三角函数的周期性与函数图像的展示

常见三角函数图像总结
一、正弦函数的图像特征
正弦函数是最常见的三角函数之一，其图像特征如下：
•周期性：正弦函数的周期为$2\\pi$，即在$[0, 2\\pi]$区间上完整呈现一个周期。

•奇函数性质：正弦函数关于原点对称，即f(f)=−f(−f)。

•取值范围：正弦函数的值域在[−1,1]之间。

二、余弦函数的图像特征
余弦函数是另一种常见的三角函数，其图像特征如下：
•周期性：余弦函数的周期也为$2\\pi$，与正弦函数一样。

•偶函数性质：余弦函数关于f轴对称，即f(f)= f(−f)。

•取值范围：余弦函数的值域同样在[−1,1]之间。

三、正切函数的图像特征
正切函数是三角函数中的另一个重要函数，其图像特征包括：
•周期性：正切函数的周期为$\\pi$，在$[0, \\pi]$区间内完成一个周期。

•奇函数性质：正切函数也是一个奇函数，即f(f)=−f(−f)。

•渐进性质：正切函数在其定义域内无限多个渐近线。

四、三角函数的图像变换
除了原始的正弦、余弦和正切函数外，这些函数还可以通
过图像的平移、伸缩和反转等方式进行变换。

其中：
•平移变换：将函数图像沿f轴或f轴平移。

•伸缩变换：改变函数图像的振幅、频率或其它参数。

•反转变换：关于f轴或f轴进行反转，改变函数图像的对称性。

综上所述，三角函数的图像总结包括正弦函数、余弦函数
和正切函数的特征，以及它们的基本变换。

深入了解这些函数的图像特性对于理解三角函数在数学和物理中的应用具有重要意义。

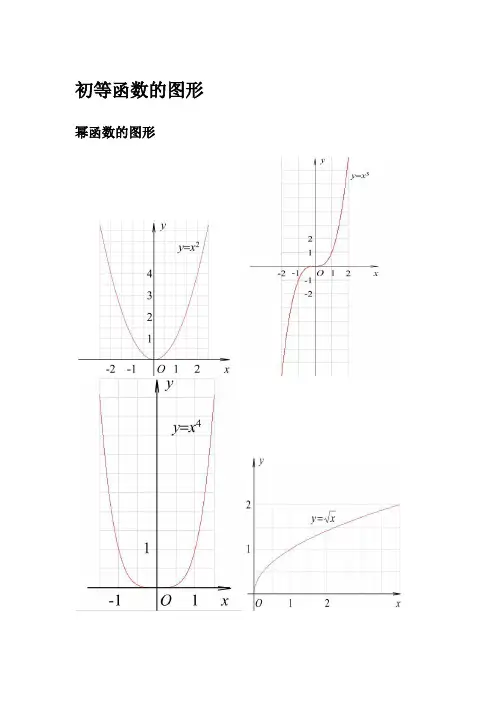
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =A tan 12tanA2-Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2aa-其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =asin 1 sec(a) =a cos 1双曲函数sinh(a)=2e -e -a a cosh(a)=2e e -a a + tg h(a)=)cosh()sinh(a a公式一设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinα cos （2kπ＋α）= cosα tan （2kπ＋α）= tanα cot （2kπ＋α）= cotα公式二设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinα cos （π＋α）= -cosα tan （π＋α）= tanα cot （π＋α）= cotα公式三任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明（全部）公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a| 一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h 正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h' 圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l 弧长公式l=a*r a是圆心角的弧度数r >0扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦：cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减，可以得到2组积化和差:相加：cosAcosB=[cos(A+B)+cos(A-B)]/2相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减，可以得到2组积化和差:相加：sinAcosB=[sin(A+B)+sin(A-B)]/2相减：sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

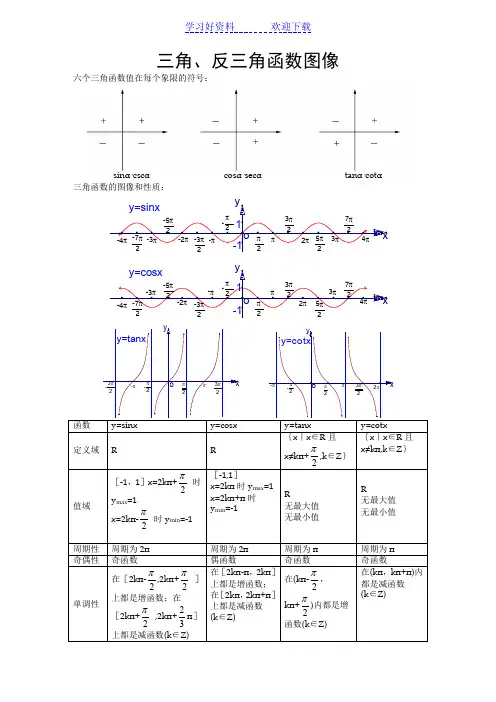
常见三角函数图像及性质三角函数在数学中具有重要的作用，主要有正弦函数、余弦函数和正切函数。

这些三角函数的图像及性质对理解三角函数在不同角度下的变化规律至关重要。

1. 正弦函数（Sine Function）正弦函数可以表示为 $y = \\sin(x)$，其中x表示自变量（角度），x表示函数值。

正弦函数的图像是一条波浪形状的曲线，在 $[-\\pi, \\pi]$ 区间内，正弦函数的图像在原点(0,0)处达到最大值1和最小值−1，且图像在x轴上对称。

正弦函数的主要性质包括：•周期性：正弦函数的周期是 $2\\pi$，即 $f(x+2\\pi) = f(x)$。

•奇函数：正弦函数是奇函数，即x(−x)=−x(x)。

•范围：正弦函数的值域为[−1,1]。

•正负性：在第一和第二象限，正弦函数为正；在第三和第四象限，正弦函数为负。

2. 余弦函数（Cosine Function）余弦函数可以表示为 $y = \\cos(x)$，余弦函数的图像是一条类似正弦函数的波浪形状曲线，不过余弦函数的图像在x轴上下移了 $\\frac{\\pi}{2}$。

余弦函数的性质包括：•周期性：余弦函数的周期也是 $2\\pi$，即$f(x+2\\pi) = f(x)$。

•偶函数：余弦函数是偶函数，即x(−x)=x(x)。

•范围：余弦函数的值域为[−1,1]。

•正负性：在第一和第四象限，余弦函数为正；在第二和第三象限，余弦函数为负。

3. 正切函数（Tangent Function）正切函数可以表示为 $y = \\tan(x)$，正切函数的图像是一条周期性的曲线，其在某些角度处会出现无穷大的值。

正切函数的图像在 $x=k\\pi + \\frac{\\pi}{2}$ 时，即 $x =\\frac{\\pi}{2}, \\frac{3\\pi}{2}, \\frac{5\\pi}{2}$ 等，会出现垂直渐近线。

正切函数的性质包括：•周期性：正切函数的周期是 $\\pi$，即 $f(x+\\pi) = f(x)$。

三角函数的周期性与解析式的变化三角函数是数学中一类重要的特殊函数，包括正弦函数、余弦函数和正切函数等。

它们在数学中具有很多重要的性质和应用。

其中，周期性与解析式的变化是三角函数的两个重要特点，下面将围绕这两个方面展开论述。

一、三角函数的周期性1. 正弦函数的周期性正弦函数是三角函数中最典型的函数之一。

它的周期性非常明显，即函数值在一定区间内以一定规律循环变化。

正弦函数的周期是2π，即在[0, 2π]区间内，函数的值会重复出现。

这个周期性的特点可以用如下的解析式来表示：y = sin(x)其中，x表示自变量，y表示函数的值。

通过这个解析式，我们可以清楚地看出正弦函数的周期性。

2. 余弦函数的周期性与正弦函数类似，余弦函数也具有明显的周期性。

余弦函数的周期也是2π，即在[0, 2π]区间内，函数的值会呈现周期性变化。

余弦函数的解析式为：y = cos(x)通过这个解析式，我们同样可以直观地感受到余弦函数的周期性。

3. 正切函数的周期性正切函数是另一个常用的三角函数，它的周期性也比较明显。

正切函数的周期是π，即在[0, π]区间内，函数的值会周期性地变化。

正切函数的解析式为：y = tan(x)通过这个解析式，我们同样可以直观地感受到正切函数的周期性。

二、解析式的变化1. 正弦函数的解析式变化正弦函数的解析式在一定条件下会发生变化。

例如，当函数中出现角度的变化时，解析式中的自变量也会随之发生相应的变化。

假设角度变量为α，那么正弦函数的解析式可以表示为：y = sin(α)通过改变α的取值，我们可以观察到函数图像的变化。

2. 余弦函数的解析式变化余弦函数与正弦函数类似，其解析式也会随着角度变化而发生变化。

余弦函数的解析式可以表示为：y = cos(α)通过改变α的取值，我们同样可以观察到函数图像的变化。

3. 正切函数的解析式变化正切函数的解析式同样会随着角度变化而发生变化。

正切函数的解析式可以表示为：y = tan(α)通过改变α的取值，我们同样可以观察到函数图像的变化。

三角函数的图像和周期三角函数是数学中非常重要的一类函数，它们的图像和周期性质对于研究函数性质和解决实际问题具有重要意义。

在本文中，我们将重点讨论正弦函数、余弦函数和正切函数的图像和周期性质。

一、正弦函数的图像和周期正弦函数是三角函数中最常见的函数之一，它的图像呈现出周期性的波动。

正弦函数的图像可以通过单位圆来表示，单位圆上一个点的纵坐标正好是该点对应的角度的正弦值。

具体来说，正弦函数的图像在坐标系中是一条连续的曲线，它的振动范围在[-1,1]之间。

当自变量（角度）增大时，函数值会逐渐增大或减小，形成连续的波动。

正弦函数的周期是2π，也就是说，当自变量增加或减少2π时，函数的值会重复。

二、余弦函数的图像和周期余弦函数也是一种常见的三角函数，它的图像和正弦函数非常相似，但相位不同。

余弦函数的图像可以通过单位圆的横坐标来表示，单位圆上一个点的横坐标正好是该点对应的角度的余弦值。

余弦函数的图像同样在坐标系中是一条连续的曲线，它的振动范围也在[-1,1]之间。

当自变量增大或减小时，函数值也会逐渐增大或减小，形成连续的波动。

余弦函数的周期也是2π，同样地，当自变量增加或减少2π时，函数的值会重复。

三、正切函数的图像和周期正切函数是三角函数中另一种重要的函数，它的图像呈现出周期性的特点。

正切函数的图像可以通过单位圆上一个点的纵坐标除以横坐标来表示，即正切值等于纵坐标除以横坐标。

正切函数的图像在坐标系中同样是一条连续的曲线，但与正弦函数和余弦函数不同的是，它在某些点上会出现无穷大或无穷小的情况。

正切函数的周期是π，也就是说，当自变量增加或减少π时，函数的值会重复。

综上所述，三角函数的图像和周期是十分重要的数学概念。

通过分析正弦函数、余弦函数和正切函数的图像和周期特性，可以帮助我们更好地理解三角函数的性质，以及在实际问题中的应用。

掌握了这些知识，我们就能更加灵活地运用三角函数解决各种数学问题。

常用三角函数图像大全三角函数是数学中常见的函数类型之一，包括正弦函数（sin）、余弦函数（cos）、正切函数（tan）等。

它们在数学和物理等领域有着广泛的应用，其图像在坐标系中展现出独特的特征。

本文将对常用三角函数的图像进行详细的介绍和展示。

正弦函数（sin）正弦函数是最基本的三角函数之一，通常用sin来表示。

它的图像是一条周期为$2\\pi$的曲线，其周期性体现在坐标系中呈现出一种波浪状的形态。

正弦函数的最大值为1，最小值为-1，且在$x=k\\pi$处达到最值，其中k为整数。

正弦函数的图像示例如下：markdown math y = \sin(x) ```余弦函数（cos）余弦函数是与正弦函数密切相关的三角函数，通常用cos 来表示。

余弦函数的图像也是一条周期为$2\\pi$的曲线，但与正弦函数的图像相比，余弦函数的波峰与波谷的位置相反。

余弦函数的最大值为1，最小值为-1，且在$x=(2k+1)\\frac{\\pi}{2}$处达到最值，其中k为整数。

余弦函数的图像示例如下：markdown math y = \cos(x) ```正切函数（tan）正切函数是另一个常用的三角函数，通常用tan来表示。

正切函数的图像在$x=k\\pi$处有无穷大的间断点，同时在$x=(k+\\frac{1}{2})\\pi$处有间断的点。

正切函数的图像是一个周期为$\\pi$的振荡函数，其变化范围为整个实数轴。

正切函数的图像示例如下：markdown math y = \tan(x) ```总结通过以上介绍，我们对常用的三角函数的图像有了更清晰的认识。

正弦函数、余弦函数和正切函数在数学中的重要性不言而喻，它们的图像特征和性质对于理解和解决各种数学问题至关重要。

希望本文对读者有所启发，更深入地了解和应用三角函数相关知识。

常见三角函数图像表正弦函数正弦函数是一个周期性的波动函数，其图像呈现出类似波浪的形状。

正弦函数的定义域是整个实数集，值域在[-1,1]之间。

在图像上，正弦函数在每个周期内经过最高点（峰值）和最低点（谷底），且在零点处过原点。

余弦函数余弦函数也是一个周期性的波动函数，其图像是正弦函数的平移。

余弦函数的定义域也是整个实数集，值域同样在[-1,1]之间。

和正弦函数不同，余弦函数在每个周期内经过最高点和最低点的中点，且在初始点处为最高点。

正切函数正切函数是一个奇函数，其图像在每π的间距处有一个无穷值点。

正切函数的周期是π，定义域为全体实数，值域为实数。

在图像上，正切函数呈现出不断递增或递减的特点，交替穿过零点。

余切函数余切函数是正切函数的倒数，也具有奇函数的特点。

它的周期同样是π，定义域为全体实数，值域是实数。

余切函数的图像呈现出在正切函数无穷值点处的连续性，交替穿过零点。

正割函数正割函数是余弦函数的倒数。

它的周期和余弦函数一样为2π，定义域为{x | x ≠ (2n + 1)π / 2, n ∈ Z}，值域为实数。

在图像上，正割函数在余弦函数的无穷点处有一个不连续点。

余割函数余割函数是正弦函数的倒数，图像为正弦函数图像的镜像。

它的周期也是2π，定义域为{x | x ≠ nπ, n ∈ Z}，值域同样为实数。

在图像上，余割函数呈现出和正弦函数相反方向的波浪形状。

通过以上对常见三角函数图像的描述，我们可以更直观地理解不同三角函数之间的关系和特点，为数学学习提供更多可能性。

三角函数的周期性与函数像的变换三角函数是数学中重要的函数之一，包括正弦函数、余弦函数和正切函数等。

这些函数具有明显的周期性特点，周期性与函数像的变换之间存在着密切的关系，下面将详细探讨这一问题。

一、三角函数的周期性1. 正弦函数的周期性正弦函数的周期为2π，即sin(x + 2π) = sin(x)，其中x为任意实数。

图像上来看，正弦函数在区间[0, 2π]上完成了一个周期的变化，之后会继续重复。

2. 余弦函数的周期性余弦函数的周期也是2π，即cos(x + 2π) = cos(x)，其中x为任意实数。

与正弦函数不同的是，余弦函数的图像是在y轴的正半轴上完成一个周期的变化。

3. 正切函数的周期性正切函数的周期为π，即tan(x + π) = tan(x)，其中x为任意实数。

正切函数的图像在每个π的间隔上变化一个周期。

二、函数像的变换1. 函数的平移变换平移变换是指将函数的图像整体向左或向右平移一定的距离。

对于三角函数而言，平移变换可以表示为f(x) = sin(x ± a)，其中a表示平移的距离。

2. 函数的垂直伸缩垂直伸缩是指改变函数图像在y轴方向的大小。

对于三角函数而言，垂直伸缩可以表示为f(x) = a*sin(x)或f(x) = a*cos(x)，其中a表示伸缩的倍数。

3. 函数的水平伸缩水平伸缩是指改变函数图像在x轴方向的大小。

对于三角函数而言，水平伸缩可以表示为f(x) = sin(ax)或f(x) = cos(ax)，其中a表示伸缩的倍数。

4. 函数的翻折变换翻折变换是指将函数的图像关于y轴或者x轴进行翻折。

对于三角函数而言，翻折变换可以表示为f(x) = sin(-x)或f(x) = cos(-x)，其中负号表示翻折。

综上所述，三角函数具有明显的周期性特点，周期为2π或π，并且可以通过平移、伸缩和翻折等变换来改变函数的图像。

这些变换是通过在函数的自变量上进行操作实现的。

三角函数图像介绍三角函数是数学中一类重要的函数，它包括正弦函数、余弦函数和正切函数等。

这些函数在数学、物理、工程等领域中都有广泛的应用。

本文将介绍三角函数的图像及其特点。

正弦函数正弦函数是最基本的三角函数之一，它的图像描述了一个周期性的波动曲线。

正弦函数的数学定义如下：y = A * sin(Bx + C) + D其中A、B、C和D都是常数参数，它们分别控制正弦函数的振幅、周期、相移和垂直偏移。

正弦函数的图像有以下几个特点：1.周期性：正弦函数的图像呈现出周期性变化，周期为2π或360度。

2.振幅：振幅控制了正弦函数图像的上下波动范围，振幅越大，波动范围越广。

3.相移：相移参数C控制了正弦函数的左右移动，当C为正数时，图像向左移动；当C为负数时，图像向右移动。

4.垂直偏移：垂直偏移参数D控制了正弦函数图像的上下平移，当D为正数时，图像向上平移；当D为负数时，图像向下平移。

下图展示了不同参数取值下的正弦函数图像：正弦函数图像正弦函数图像余弦函数余弦函数是与正弦函数密切相关的三角函数，它的图像也描述了一个周期性的波动曲线。

余弦函数的数学定义如下：y = A * cos(Bx + C) + D与正弦函数类似，余弦函数的图像也具有周期性、振幅、相移和垂直偏移等特点。

不同的是，余弦函数的波形比正弦函数向右移动了90度。

下图展示了不同参数取值下的余弦函数图像：余弦函数图像余弦函数图像正切函数正切函数是三角函数中另一种常见的函数，它的图像描述了一个周期性的振荡曲线。

正切函数的数学定义如下：y = A * tan(Bx + C) + D正切函数的图像具有以下几个特点：1.周期性：正切函数的图像以π或180度为间隔进行周期性变化。

2.垂直渐近线：正切函数的图像有两条垂直渐近线，即斜率为正无穷的直线和斜率为负无穷的直线。

3.可能存在间断点：正切函数图像中可能存在不连续的点，被称为正切函数的奇点。

下图展示了不同参数取值下的正切函数图像：正切函数图像正切函数图像总结三角函数是数学中一类重要的函数，它们的图像展示了周期性的波动曲线。