一元二次不等式解法

一元二次不等式公式解法一元二次不等式是指类似于ax+bx+c>0的不等式，其中a、b、c 为实数且a≠0。

解一元二次不等式的方法可以分为以下两种公式解法：1.配方法当a>0时，我们可以通过配方法将一元二次不等式转化为(x+m)+n>0的形式。

具体步骤如下：①将一元二次不等式转化为ax+bx+c≥0的形式。

②将a提出来，得到a(x+bx/a+c/a)≥0。

③将b/a的一半平方再减去c/a，得到(b/2a)-c/a=m，其中m为实数。

④将式子转化为a[(x+b/2a)-(b/2a)+c/a]≥0。

⑤将式子化简，得到(x+b/2a)+(4ac-b)/4a>0。

⑥将4ac-b表示为n，得到(x+b/2a)+n/4a>0。

⑦由于a>0，所以n>0，而完全平方数加上正数大于0，所以(x+b/2a)+n/4a>0，即(x+m)+n>0。

2.因式分解法当a<0时，我们可以通过因式分解法将一元二次不等式转化为(ax+b)(x+c)<0或(ax+b)(x+c)>0的形式。

具体步骤如下：①将一元二次不等式转化为ax+bx+c≤0或ax+bx+c≥0的形式。

②将a提出来，得到a(x+bx/a+c/a)≤0或a(x+bx/a+c/a)≥0。

③将x+bx/a+c/a表示为(x+d)(x+e)的形式，其中d、e为实数。

④当a<0时，(x+d)(x+e)>0；当a>0时，(x+d)(x+e)<0。

⑤当a<0时，解(x+d)(x+e)>0的方法为：找出实数d、e的大小关系，将实数轴分为三段，判断每一段上的符号，最后得到不等式的解集；当a>0时，解(x+d)(x+e)<0的方法为：找出实数d、e的大小关系，将实数轴分为三段，判断每一段上的符号，最后得到不等式的解集。

以上就是一元二次不等式的两种公式解法。

需要注意的是，在解一元二次不等式时，我们需要根据a的正负性和不等式的形式来选择不同的解法。

一元二次不等式的解法在数学中，一元二次不等式是指形如ax^2+bx+c>0或ax^2+bx+c<0的二次不等式。

解一元二次不等式的方法可以通过图像法、代入法和判别法来实现。

本文将介绍这三种解法，并通过实例来说明其具体步骤。

图像法图像法是解一元二次不等式最直观的方法之一，它通过绘制一元二次函数的图像来找到不等式的解集。

下面以一元二次不等式x^2-4x+3>0为例来说明图像法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以通过求解x的一元二次方程来得到根，即使用求根公式x = (-b±√(b^2-4ac))/(2a)。

将方程x^2-4x+3=0代入求根公式中，得到x=1和x=3。

其次，在数轴上绘制一元二次函数y=x^2-4x+3的图像。

根据函数的开口方向和图像的凹凸性，我们可以确定函数在x<1和x>3的区间上为正值，即图像在该区间上位于x轴之上。

最后，根据不等式的正号，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

代入法代入法是通过代入特定的数值来判断一元二次不等式的真假。

下面以一元二次不等式x^2-4x+3>0为例来说明代入法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以使用同样的方法得到x=1和x=3。

其次，选择一些特定的数值，代入一元二次不等式中，判断不等式的真假。

例如，选择x=0、x=2和x=4来代入不等式。

计算得到代入x=0时，不等式为3>0，代入x=2时，不等式为-1>0，代入x=4时，不等式为3>0。

根据计算结果，我们可以确定不等式在x<1和x>3的区间上为真。

最后，根据不等式的真假，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

判别法判别法是解一元二次不等式的一种常用方法，它利用一元二次不等式的判别式来确定不等式的解集。

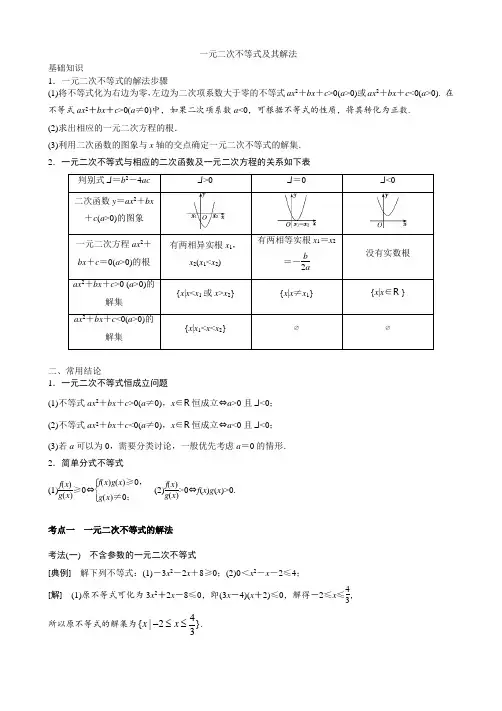
一元二次不等式及其解法基础知识1．一元二次不等式的解法步骤 (1)将不等式化为右边为零，左边为二次项系数大于零的不等式ax 2＋bx ＋c >0(a >0)或ax 2＋bx ＋c <0(a >0). 在不等式ax 2＋bx ＋c >0(a ≠0)中，如果二次项系数a <0，可根据不等式的性质，将其转化为正数. (2)求出相应的一元二次方程的根．(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的解集． 2．一元二次不等式与相应的二次函数及一元二次方程的关系如下表二、常用结论1．一元二次不等式恒成立问题(1)不等式ax 2＋bx ＋c >0(a ≠0)，x ∈R 恒成立⇔a >0且Δ<0； (2)不等式ax 2＋bx ＋c <0(a ≠0)，x ∈R 恒成立⇔a <0且Δ<0； (3)若a 可以为0，需要分类讨论，一般优先考虑a ＝0的情形． 2．简单分式不等式(1)f (x )g (x )≥0⇔⎩⎪⎨⎪⎧f (x )g (x )≥0，g (x )≠0；(2)f (x )g (x )>0⇔f (x )g (x )>0. 考点一 一元二次不等式的解法 考法(一) 不含参数的一元二次不等式[典例] 解下列不等式：(1)－3x 2－2x ＋8≥0；(2)0＜x 2－x －2≤4；[解] (1)原不等式可化为3x 2＋2x －8≤0，即(3x －4)(x ＋2)≤0，解得－2≤x ≤43，所以原不等式的解集为}342|{≤≤-x x .(2)原不等式等价于⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －2≤4⇔⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －6≤0⇔⎩⎪⎨⎪⎧ (x －2)(x ＋1)＞0，(x －3)(x ＋2)≤0⇔⎩⎪⎨⎪⎧x ＞2或x ＜－1，－2≤x ≤3. 借助于数轴，如图所示，原不等式的解集为{}x |－2≤x ＜－1或2＜x ≤3. 考法(二) 含参数的一元二次不等式[典例] 解不等式ax 2－(a ＋1)x ＋1＜0(a ＞0)． [解] 原不等式变为(ax －1)(x －1)＜0， 因为a ＞0，所以a )1(ax -(x －1)＜0. 所以当a ＞1，即1a <1时，解为1a ＜x ＜1；当a ＝1时，解集为∅；当0＜a ＜1，即1a >1时，解为1＜x ＜1a.综上，当0＜a ＜1时，不等式的解集为}11|{ax x <<； 当a ＝1时，不等式的解集为∅； 当a ＞1时，不等式的解集为}11|{<<x ax . [题组训练]1．不等式(x ＋5)(3－2x )≥6的解集是( )A.}291|{≥-≤x x x 或 B.}291|{≤≤-x x C.}129|{≥-≤x x x 或D.}129|{≤≤-x x 解析：选D 不等式(x ＋5)(3－2x )≥6可化为2x 2＋7x －9≤0，所以(2x ＋9)(x －1)≤0，解得－92≤x ≤1.所以不等式(x ＋5)(3－2x )≥6的解集是}129|{≤≤-x x .故选D. 2．已知不等式ax 2－bx －1≥0的解集是]31,21[--，则不等式x 2－bx －a ＜0的解集是( )A ．(2,3)B ．(－∞，2)∪(3，＋∞) C.)21,31( D.)31,(-∞∪),21(+∞ 解析：选A 由题意知－12，－13是方程ax 2－bx －1＝0的两根，所以由根与系数的关系得⎩⎨⎧－12＋⎝⎛⎭⎫－13＝b a，－12×⎝⎛⎭⎫－13＝－1a .解得⎩⎪⎨⎪⎧a ＝－6，b ＝5，不等式x 2－bx －a ＜0即为x 2－5x ＋6＜0，解集为(2,3)．3．求不等式12x 2－ax >a 2(a ∈R )的解集．解：原不等式可化为12x 2－ax －a 2>0，即(4x ＋a )(3x －a )>0， 令(4x ＋a )(3x －a )＝0，解得x 1＝－a 4，x 2＝a3.当a >0时，不等式的解集为)4,(a--∞∪),3(+∞a ； 当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞)； 当a <0时，不等式的解集为)3,(a --∞∪),4(+∞-a. 考点二 一元二次不等式恒成立问题 考法(一) 在R 上的恒成立问题[典例] 若不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立，则实数a 的取值范围是( )A ．(－∞，2]B ．[)2,2(-C ．(－2,2]D ．(－∞，－2) [解析] 当a －2＝0，即a ＝2时，不等式为－4<0，对一切x ∈R 恒成立．当a ≠2时，则⎩⎪⎨⎪⎧ a －2<0，Δ＝4(a －2)2＋16(a －2)<0，即⎩⎪⎨⎪⎧a －2<0，a 2<4，解得－2<a <2. ∴实数a 的取值范围是(－2,2]． [答案] C解题技法] 一元二次不等式恒成立的条件(1)ax 2＋bx ＋c >0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a >0，b 2－4ac <0.(2)ax 2＋bx ＋c <0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a <0，b 2－4ac <0.考法(二) 在给定区间上的恒成立问题[典例] 若对任意的x ∈[)2,1(-，都有x 2－2x ＋a ≤0(a 为常数)，则a 的取值范围是( ) A ．(－∞，－3] B ．(－∞，0] C ．),1[+∞[ D DD D ．]1,(-∞(解析] 法一：令f (x )＝x 2－2x ＋a ，则由题意，得⎩⎪⎨⎪⎧f (－1)＝(－1)2－2×(－1)＋a ≤0，f (2)＝22－2×2＋a ≤0，解得a ≤－3，故选A.法二：当x ∈[)2,1(-]时，不等式x 2－2x ＋a ≤0恒成立等价于a ≤－x 2＋2x 恒成立，则由题意，得a ≤(－x 2＋2x )min (x ∈[)2,1(-])．而－x 2＋2x ＝－(x －1)2＋1，则当x ＝－1时，(－x 2＋2x )min ＝－3，所以a ≤－3，故选A. 答案] A [解题技法]一元二次不等式在给定区间上的恒成立问题的求解方法(1)若f (x )>0在集合A 中恒成立，即集合A 是不等式f (x )>0的解集的子集，可以先求解集，再由子集的含义求解参数的值(或范围)． (2)转化为函数值域问题，即已知函数f (x )的值域为[m ，n ]，则f (x )≥a 恒成立⇒f (x )min ≥a ，即m ≥a ；f (x )≤a 恒成立⇒f (x )max ≤a ，即n ≤a . 考法(三) 给定参数范围求x 范围的恒成立问题[典例] 求使不等式x 2＋(a －6)x ＋9－3a >0(|a |≤1)恒成立的x 的取值范围． 解] 将原不等式整理为形式上是关于a 的不等式(x －3)a ＋x 2－6x ＋9>0. 令f (a )＝(x －3)a ＋x 2－6x ＋9，因为f (a )>0在|a |≤1时恒成立，所以 (1)若x ＝3，则f (a )＝0，不符合题意，舍去．(2)若x ≠3，则由一次函数的单调性，可得⎩⎪⎨⎪⎧ f (－1)>0，f (1)>0，即⎩⎪⎨⎪⎧x 2－7x ＋12>0，x 2－5x ＋6>0，解得x <2或x >4，综上可知，使原不等式恒成立的x 的取值范围是(－∞，2)∪(4，＋∞)． [解题技法]给定参数范围求x 范围的恒成立问题的解法解决恒成立问题一定要清楚选谁为主元，谁是参数．一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解． [题组训练]1．(2018·忻州第一中学模拟)已知关于x 的不等式x 2－4x ≥m 对任意x ∈(0,1]恒成立，则实数m 的取值范围为( )A ．(－∞，－3]B ．[－3，＋∞)C ．[－3,0)D ．[－4，＋∞)解析：选A x 2－4x ≥m 对任意x ∈(0,1]恒成立，令f (x )＝x 2－4x ，∵f (x )图象的对称轴为直线x ＝2，∴f (x )在(0,1]上单调递减，∴当x ＝1时，f (x )取到最小值，为－3，∴实数m 的取值范围是(－∞，－3]，故选A. 2．若不等式x 2＋mx －1<0对于任意x ∈[m ，m ＋1]都成立，则实数m 的取值范围是________．解析：由题意，得函数f (x )＝x 2＋mx －1在[m ，m ＋1]上的最大值小于0，又抛物线f (x )＝x 2＋mx －1开口向上，所以只需⎩⎪⎨⎪⎧ f (m )＝m 2＋m 2－1<0，f (m ＋1)＝(m ＋1)2＋m (m ＋1)－1<0，即⎩⎪⎨⎪⎧2m 2－1<0，2m 2＋3m <0，解得－22<m <0. 答案：)0,22(-3．不等式(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立，则x 的取值范围是________．解析：由题意知(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立等价于(x 2－4x )a －3x 2＋2x ＜0对a ∈(0,1)恒成立．令g (a )＝(x 2－4x )a －3x 2＋2x ，当x ＝0时，g (a )＝0，不满足题意．当x ≠0时，则⎩⎪⎨⎪⎧g (0)＝－3x 2＋2x ≤0，g (1)＝(x 2－4x )－3x 2＋2x ≤0，得x ≤－1或x ≥23.答案：(－∞，－1]∪),32[+∞ [课时跟踪检测]1．(2019·石家庄模拟)若集合A ＝{x |x 2－2x <0}，B ＝{x ||x |≤1}，则A ∩B ＝( )A ．[－1,0)B ．[－1,2)C ．(0,1]D ．[1,2)解析：选C 由x 2－2x <0得0<x <2，所以A ＝{x |0<x <2}，由|x |≤1得－1≤x ≤1，所以集合B ＝{x |－1≤x ≤1}，所以A ∩B ＝{x |0<x ≤1}，故选C. 2．不等式3x －1x －2≤0的解集为( )A.}231|{≤≤x x B.}312|{≤>x x x 或 C.}231|{<≤x x D ．{x |x <2} 解析：选C 不等式3x －1x －2≤0等价于(3x －1)(x －2)≤0，且x －2≠0，解得13≤x <2.故选C.3．不等式－3<4x －4x 2≤0的解集是( ) A.}231021|{<≤≤<-x x x 或 B ．{x |x ≤0或x ≥1} C.}2321|{<<-x x D.}2321|{≥-≤x x x 或 解析：选A 不等式可化为⎩⎪⎨⎪⎧4x (x －1)≥0，4x 2－4x －3<0，解得⎩⎪⎨⎪⎧x ≤0或x ≥1，－12<x <32，所以－12<x ≤0或1≤x <32.4．(2019·广州模拟)已知不等式ax 2－5x ＋b >0的解集为{x |－3<x <－2}，则不等式bx 2－5x ＋a >0的解集为( ) A.}3121|{-<<-x x B.}2131|{-<->x x x 或 C ．{x |－3<x <2} D ．{x |x <－3或x >2} 解析：选A 由题意得⎩⎨⎧5a＝－3－2，ba ＝－3×(－2)，解得a ＝－1，b ＝－6，所以不等式bx 2－5x ＋a >0为－6x 2－5x－1>0，即(3x ＋1)(2x ＋1)<0，所以解集为}3121|{-<<-x x ，故选A. 5．若关于x 的不等式x 2－ax －a ≤－3的解集不是空集，则实数a 的取值范围是( )A ．[]2,(-∞)B B ． (－∞，－6]]C ． ]2,6[-D ．(－∞，－6]∪[2，＋∞)解析：选D 由关于x 的不等式x 2－ax －a ≤－3的解集不是空集，得对应方程x 2－ax －a ＋3＝0有实数根，即Δ＝a 2＋4(a －3)≥0，解得a ≥2或a ≤－6，所以a 的取值范围是 (－∞，－6]∪[2，＋∞)．故选D.6．某商场若将进货单价为8元的商品按每件10元出售，每天可销售100件，现准备采用提高售价来增加利润．已知这种商品每件销售价提高1元，销售量就要减少10件．那么要保证每天所赚的利润在320元以上，销售价每件应定为( )A ．12元B ．16元C ．12元到16元之间D ．10元到14元之间解析：选C 设销售价定为每件x 元，利润为y ，则y ＝(x －8)[100－10(x －10)]， 依题意有，(x －8)[100－10(x －10)]＞320，即x 2－28x ＋192＜0，解得12＜x ＜16， 所以每件销售价应为12元到16元之间．7．存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m 的最大值为( )A ．1 B.14 C.12D ．－1解析：选C 若对于任意x ∈[－1,1]，不等式x 2＋mx －3m <0恒成立，则由函数f (x )＝x 2＋mx －3m 的图象可知⎩⎪⎨⎪⎧f (－1)＝1－m －3m <0，f (1)＝1＋m －3m <0，解得m >12.所以若存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m ≤12，所以m的最大值为12.故选C.8．(2018·北京东城区期末)设不等式x 2－2ax ＋a ＋2≤0的解集为A ，若A ⊆]3,1[，则a 的取值范围为( )A.]511,1(- B.)511,1( C.)511,2( D ．[)3,1( 解析：选A 设f (x )＝x 2－2ax ＋a ＋2，因为不等式x 2－2ax ＋a ＋2≤0的解集为A ，且A ⊆[]3,1[]， 所以对于方程x 2－2ax ＋a ＋2＝0，若A ＝∅，则Δ＝4a 2－4(a ＋2)<0，即a 2－a －2<0，解得－1<a <2；若A ≠∅，则⎩⎪⎨⎪⎧Δ＝4a 2－4(a ＋2)≥0，f (1)≥0，f (3)≥0，1≤a ≤3，即⎩⎪⎨⎪⎧a ≥2或a ≤－1，a ≤3，a ≤115，1≤a ≤3，所以2≤a ≤115.综上，a 的取值范围为]511,1(-，故选A. 9．不等式|x (x －2)|>x (x －2)的解集是________．解析：不等式|x (x －2)|>x (x －2)的解集即x (x －2)<0的解集，解得0<x <2，故不等式的解集为{x |0<x <2}． 答案：{x |0<x <2}10．若a <0，则关于x 的不等式组⎩⎪⎨⎪⎧ax －a 2<0，x 2－ax －2a 2<0的解集为________． 解析：因为a <0，所以由ax －a 2＝a (x －a )<0，得x >a ，由x 2－ax －2a 2＝(x －2a )(x ＋a )<0，得2a <x <－a .所以原不等式组的解集为(a ，－a )． 答案：(a ，－a )11．若关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，则实数a 的取值范围是________．解析：关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，所以a >0，解不等式得x 2≤a5，所以－a5≤x ≤ a5，所以3≤ a 5<4，所以9≤a5<16，即45≤a <80， 所以实数a 的取值范围是[45,80)． 答案：[45,80)12．不等式a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，则实数λ的取值范围为________．解析：因为a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，所以a 2＋8b 2－λb (a ＋b )≥0恒成立，即a 2－λba ＋(8－λ)b 2≥0恒成立，由二次不等式的性质可得Δ＝λ2b 2＋4(λ－8)b 2＝b 2(λ2＋4λ－32)≤0，所以(λ＋8)(λ－4)≤0，解得－8≤λ≤4. 答案：[－8,4]13．已知函数f (x )＝ax 2＋2ax ＋1的定义域为R . (1)求a 的取值范围； (2)若函数f (x )的最小值为22，解关于x 的不等式x 2－x －a 2－a <0. 解：(1)因为函数f (x )＝ax 2＋2ax ＋1的定义域为R ，所以ax 2＋2ax ＋1≥0恒成立， 当a ＝0时，1≥0恒成立．当a ≠0时，则有⎩⎪⎨⎪⎧a >0，Δ＝(2a )2－4a ≤0，解得0<a ≤1，综上可知，a 的取值范围是[0,1]． (2)因为f (x )＝ax 2＋2ax ＋1＝a (x ＋1)2＋1－a ，因为a >0，所以当x ＝－1时，f (x )min ＝1－a ，由题意得，1－a ＝22，所以a ＝12， 所以不等式x 2－x －a 2－a <0可化为x 2－x －34<0.解得－12<x <32，所以不等式的解集为)23,21(-。

一元二次不等式全部解法一元二次不等式是指形如ax^2 + bx + c > 0或ax^2 + bx + c < 0的不等式，其中a、b、c是已知实数且a ≠ 0。

要求解一元二次不等式，我们需要找到其解集，即使不等式成立的x的取值范围。

下面将介绍几种解一元二次不等式的方法。

方法一：图像法通过绘制二次函数的图像，我们可以直观地观察到不等式的解集。

以ax^2 + bx + c > 0为例，我们可以绘制出函数y = ax^2 + bx + c的图像，然后观察函数图像在x轴上的位置。

如果函数图像位于x轴上方，则不等式成立的x的取值范围为图像所在的区间；如果函数图像位于x轴下方，则不等式不成立的x的取值范围为图像所在的区间。

方法二：因式分解法对于一元二次不等式ax^2 + bx + c > 0，我们可以先通过因式分解将其转化为(ax + m)(ax + n) > 0的形式，其中m、n是已知实数。

然后根据乘积大于零的性质，我们可以得到两个因子同时大于零或同时小于零时不等式成立。

因此，我们需要解以下两个不等式：ax + m > 0和ax + n > 0，得到的解集再取交集，即为原不等式的解集。

方法三：配方法对于一元二次不等式ax^2 + bx + c > 0，我们可以通过配方法将其转化为完全平方的形式。

具体步骤如下：1. 将不等式移项，得到ax^2 + bx + c = 0的形式。

2. 根据二次方程的求根公式，求得方程的两个根x1和x2。

3. 根据二次函数的性质，我们可以得到该二次函数在x1和x2之间变号。

即对于ax^2 + bx + c > 0来说，当x在x1和x2之间时，不等式成立。

方法四：求解判别式对于一元二次不等式ax^2 + bx + c > 0，我们可以先求解对应的二次方程ax^2 + bx + c = 0的判别式Δ=b^2-4ac。

根据判别式的值，我们可以得到不等式的解集：1. 当Δ>0时，二次方程有两个不相等的实根x1和x2，此时不等式成立的x的取值范围为x<x1或x>x2。

一元二次不等式方程的解法含有一个未知数且未知数的最高次数为2次的的不等式叫做一元二次不等式，它的一般形式是ax2+bx+c>0或ax2+bx+c<0(a不等于0),其中ax2+bx+c实数域上的二次三项式。

一元二次不等式的解法有哪几种?1、公式法可以解所有的一元二次方程，公式法不能解没有实数根的方程(也就是b²-4ac<0的方程)。

求根公式： x=-b±√(b2-4ac)/2a。

2、配方法比较简单：首先将方程二次项系数a化为1，然后把常数项移到等号的右边，最后后在等号两边同时加上一次项系数绝对值一半的平方。

3、数轴穿根：用穿根法解高次不等式时，就是先把不等式一端化为零，再对另一端分解因式，并求出它的零点，把这些零点标在数轴上，再用一条光滑的曲线，从x轴的右端上方起，依次穿过这些零点，大于零的不等式的解对应这曲线在x轴上方部分的实数x的值的集合，小于零的则相反。

这种方法叫做序轴穿根法，又叫“穿根法”。

口诀是“从右到左，从上到下，奇穿偶不穿。

”4、一元二次不等式也可通过一元二次函数图象进行求解。

通过看图象可知，二次函数图象与X轴的两个交点，然后根据题中所需求"<0"或">0"而推出答案。

求一元二次不等式的解集实际上是将这个一元二次不等式的所有项移到不等式一侧并进行因式分解分类讨论求出解集。

解一元二次不等式，可将一元二次方程不等式转化成二次函数的形式，求出函数与X轴的交点，将一元二次不等式，二次函数，一元二次方程联系起来，并利用图象法进行解题，使得问题简化。

等式的基本性质：1、等式两边同时加(或减)同一个数或同一个代数式，所得的结果仍是等式。

用字母表示为：若a=b，c为一个数或一个代数式。

2、等式的两边同时乘或除以同一个不为0的数,所得的结果仍是等式。

用字母表示为：若a=b，c为一个数或一个代数式(不为0)。

3、不等式的两边同时加上(或减去)同一个数(或式子)，不等号的方向不变;4、不等式的两边同时乘(或除以)同一个正数，不等号的方向不变;5、不等式的两边同时乘(或除以)同一个负数，不等号的方向变。

一元二次不等式6种解法大全一元二次不等式是指形如ax²+bx+c>0或ax²+bx+c≥0的二次不等式，其中a、b、c为实数，a≠0。

这种不等式的解法有很多种，下面我将介绍其中的六种解法。

解法一：使用因式分解法。

对于形如(ax+b)(cx+d)>0或(ax+b)(cx+d)≥0的一元二次不等式，可以尝试将其因式分解为两个一次因式相乘的形式，然后根据不等式的性质讨论各个因式的取值范围，从而求得不等式的解。

解法二：使用它的图像解法。

将一元二次不等式对应的二次函数的图像画出来，然后根据图像的特点来确定使得函数大于0（或大于等于0）的x的取值范围，即为不等式的解。

解法三：使用开平方法。

对于形如x²+a≥0或x²+a>0的一元二次不等式，可以通过开平方的方法来求解。

首先将不等式移到一边，得到一个完全平方的形式，然后对不等式两边同时开平方，得到关于x的两个二次方程，根据二次方程的性质来求解。

解法四：使用代数求解法。

对于一元二次不等式ax²+bx+c>0或ax²+bx+c≥0，可以将其转化为一个关于x的二次方程ax²+bx+c=0的解的范围问题。

求得这个二次方程的解，然后根据这些解的范围来确定不等式的解。

解法五：使用数轴法。

将一元二次不等式对应的二次函数的图像画在数轴上，然后根据函数的凸性来确定函数取正值的x的取值范围，即为不等式的解。

解法六：使用区间法。

将一元二次不等式移项，化成形如ax²+bx+c<0或ax²+bx+c≤0的不等式，然后求出二次函数的零点，并根据二次函数的凸性来确定函数小于0（或小于等于0）的x的取值范围，即为不等式的解。

以上是关于一元二次不等式的六种解法，每种解法都有其独特的思路和方法。

在实际的解题过程中，可以根据具体的题目情况选择合适的解法来求解，以提高解题效率和准确性。

一元二次不等式的解法一元二次不等式是由一个二次方程构成的数学不等式，其形式通常为 ax^2 + bx + c > 0 或 ax^2 + bx + c < 0。

解一元二次不等式需要运用一些特定的方法和原理，下面将介绍一些常用的解法。

1. 图像法图像法是一种直观的解一元二次不等式的方法。

首先，我们可以将不等式的左边化简成一个二次函数的形式，例如将 ax^2 + bx + c > 0 转化为 y = ax^2 + bx + c 的图像。

然后，通过观察图像的形状和位置，确定不等式的解集。

对于一元二次不等式 ax^2 + bx + c > 0，可以按照以下步骤使用图像法解答：a) 计算二次函数的顶点坐标 (-b/(2a), f(-b/(2a)))，其中 f(x) = ax^2 + bx + c。

b) 如果 a > 0，表示二次函数开口向上，则解集为顶点坐标的右侧部分。

如果 a < 0，表示二次函数开口向下，则解集为顶点坐标的左侧部分。

c) 如果二次函数与 x 轴有交点，则解集还包括这些交点。

举例说明：假设要解一元二次不等式 x^2 + 4x + 3 > 0。

a) 通过计算，可得到顶点坐标为 (-2, -1)。

b) 由于 a > 0，解集为顶点坐标的右侧部分。

c) 二次函数与 x 轴的交点为 (-3, 0) 和 (-1, 0)。

因此，解集为 (-∞, -3) ∪ (-1, +∞)。

2. 因式分解法对于一元二次不等式，我们可以先将其因式分解为二次方程的形式，然后再解这个二次方程。

具体步骤如下：a) 将不等式左边移项，将其写成一个完全平方的形式，例如 a(x -r)(x - s) > 0 或 a(x - r)(x - s) < 0，其中 r 和 s 是待定系数。

b) 将方程 a(x - r)(x - s) = 0 求解，得到方程的根（解），记作 x = r和 x = s。

一元二次不等式6种解法大全
一元二次不等式有多种解法，以下是一些常见的解法：
1. 图像法：将一元二次不等式转化为图像，通过观察图像的变化来确定解的范围。

首先，将不等式转化为等式，再画出对应的抛物线图像，然后根据不等式的符号确定解的范围。

2. 因式分解法：将一元二次不等式进行因式分解，得到一个或多个一次因子和一个二次因子。

然后，根据这些因子的正负确定不等式的解。

3. 求导法：对一元二次不等式两边同时求导数，得到一个一次方程。

然后，通过解这个一次方程得到不等式的解。

4. 完全平方式：将一元二次不等式进行变形，使其成为完全平方式。

然后，通过对方程两边取平方根，得到不等式的解。

5. 化简法：将一元二次不等式进行化简，整理为一个或多个一次项和一个常数项的形式。

然后，根据这些项的符号确定不等式的解。

6. 区间法：将一元二次不等式转化为一个或多个区间，并确定每个区间内的解的情况。

然后，将这些区间的解合并，得到不等式的解集。

以上是一些常见的一元二次不等式的解法，具体使用哪种解法取决于不等式的形式和题目要求。

在解题过程中，可以根据需要选择适合的方法进行求解。