一元二次不等式及其解法(实根分布)

一元二次方程、解不等式、根的分布例1：解下列方程： （1）26540x x --= （2）22460x x +-=（3）22(1)(2)0x k x k k -+++=（4）2(2)20ax a x -++=（注意：对参数a 要分类讨论） 例2：解不等式： （1）23140x x --> （2）(2)(23)3x x -+≤ （3）22|1|50x x ---≥ （4）2(1)0x x a a --->解：原不等式可以化为：0))(1(>--+a x a x若)1(-->a a 即21>a 则a x >或a x -<1 若)1(--=a a 即21=a 则0)21(2>-x R x x ∈≠,21若)1(--<a a 即21<a 则a x <或a x ->1例3：关于x 的不等式02<++c bx ax 的解集为}212|{->-<x x x 或求关于x 的不等式02>+-c bx ax 的解集． 解：由题设0<a 且25-=-a b ， 1=ac从而 02>+-c bx ax 可以变形为02<+-acx a b x 即：01252<+-x x ∴221<<x 例4：关于x 的不等式01)1(2<-+-+a x a ax 对于R x ∈恒成立，求a 的取值范围。

解：当a >0时不合； 当a =0也不合∴必有：⎩⎨⎧>--<⇒⎩⎨⎧<---=∆<012300)1(4)1(022a a a a a a a 310)1)(13(0-<⇒⎩⎨⎧>-+<⇒a a a a例5：若函数)8(6)(2++-=k kx kx x f 的定义域为R ，求实数k 的取值范围。

解：显然k =0时满足 而k <0时不满足201364(8)0k k k k k >⎧⇒<≤⎨∆=-+≤⎩ ∴k 的取值范围是[0,1]例6：设函数f (x )=⎪⎪⎩⎪⎪⎨⎧≥-<<-+-≤+)1(11)11(22)1()1(2x xx x x x ，已知f (a )＞1，则a 的取值范围是( )A.(－∞，－2)∪(－21，+∞) B.(－21，21) C.(－∞，－2)∪(－21，1)D.(－2，－21)∪(1，+∞)例7：设不等式x 2－2ax +a +2≤0的解集为M ，如果M ⊆［1，4］，求实数a 的取值范围。

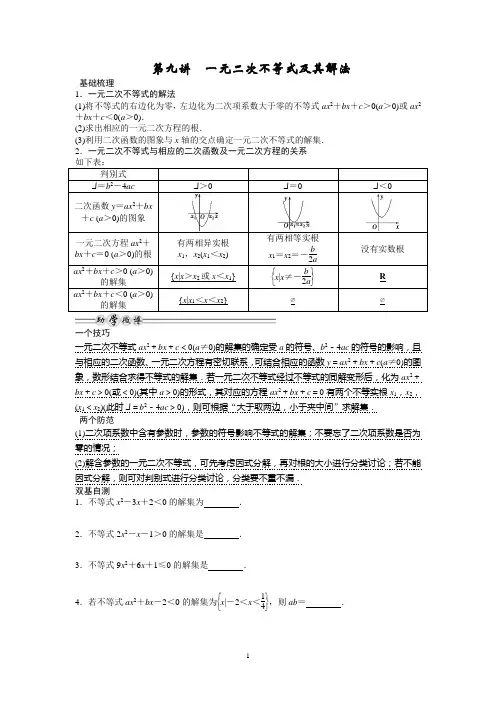
第九讲 一元二次不等式及其解法基础梳理1．一元二次不等式的解法 (1)将不等式的右边化为零，左边化为二次项系数大于零的不等式ax 2＋bx ＋c ＞0(a ＞0)或ax 2＋bx ＋c ＜0(a ＞0)．(2)求出相应的一元二次方程的根．(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的解集． 2．一元二次不等式与相应的二次函数及一元二次方程的关系 判别式 Δ＝b 2－4ac Δ＞0 Δ＝0 Δ＜0 二次函数y ＝ax 2＋bx ＋c (a ＞0)的图象一元二次方程ax 2＋bx ＋c ＝0 (a ＞0)的根 有两相异实根 x 1，x 2(x 1＜x 2) 有两相等实根x 1＝x 2＝－b2a没有实数根ax 2＋bx ＋c ＞0 (a ＞0)的解集{x |x ＞x 2或x ＜x 1} ⎩⎨⎧⎭⎬⎫x |x ≠－b 2aR ax 2＋bx ＋c ＜0 (a ＞0)的解集 {x |x 1＜x ＜x 2}∅∅一个技巧一元二次不等式ax 2＋bx ＋c ＜0(a ≠0)的解集的确定受a 的符号、b 2－4ac 的符号的影响，且与相应的二次函数、一元二次方程有密切联系，可结合相应的函数y ＝ax 2＋bx ＋c (a ≠0)的图象，数形结合求得不等式的解集．若一元二次不等式经过不等式的同解变形后，化为ax 2＋bx ＋c ＞0(或＜0)(其中a ＞0)的形式，其对应的方程ax 2＋bx ＋c ＝0有两个不等实根x 1，x 2，(x 1＜x 2)(此时Δ＝b 2－4ac ＞0)，则可根据“大于取两边，小于夹中间”求解集．两个防范(1)二次项系数中含有参数时，参数的符号影响不等式的解集；不要忘了二次项系数是否为零的情况；(2)解含参数的一元二次不等式，可先考虑因式分解，再对根的大小进行分类讨论；若不能因式分解，则可对判别式进行分类讨论，分类要不重不漏． 双基自测1．不等式x 2－3x ＋2＜0的解集为 ．2．不等式2x 2－x －1＞0的解集是 ．3．不等式9x 2＋6x ＋1≤0的解集是 ．4．若不等式ax 2＋bx －2＜0的解集为⎩⎨⎧⎭⎬⎫x |－2＜x ＜14，则ab ＝ ．5．不等式ax 2＋2ax ＋1≥0对一切x ∈R 恒成立，则实数a 的取值范围为________．考向一 一元二次不等式的解法【例1】►已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ，x ≥0，－x 2＋2x ，x ＜0，解不等式f (x )＞3.解一元二次不等式的一般步骤是：(1)化为标准形式；(2)确定判别式Δ的符号；(3)若Δ≥0，则求出该不等式对应的二次方程的根，若Δ＜0，则对应的二次方程无根；(4)结合二次函数的图象得出不等式的解集．特别地，若一元二次不等式的左边的二次三项式能分解因式，则可立即写出不等式的解集．【训练1】 函数f (x )＝2x 2＋x －3＋log 3(3＋2x －x 2)的定义域为________．考向二 含参数的一元二次不等式的解法【例2】►求不等式12x 2－ax ＞a 2(a ∈R )的解集．解含参数的一元二次不等式的一般步骤：(1)二次项若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为二次项系数为正的形式．(2)判断方程的根的个数，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．【训练2】 解关于x 的不等式(1－ax )2＜1.考向三 不等式恒成立问题【例3】►已知不等式ax 2＋4x ＋a ＞1－2x 2对一切实数x 恒成立，求实数a 的取值范围．不等式ax 2＋bx ＋c ＞0的解是全体实数(或恒成立)的条件是当a ＝0时，b ＝0，c＞0；当a ≠0时，⎩⎪⎨⎪⎧a ＞0，Δ＜0；不等式ax 2＋bx ＋c ＜0的解是全体实数(或恒成立)的条件是当a＝0时，b ＝0，c ＜0；当a ≠0时，⎩⎪⎨⎪⎧a ＜0，Δ＜0.【训练3】 已知f (x )＝x 2－2ax ＋2(a ∈R )，当x ∈[－1，＋∞)时，f (x )≥a 恒成立，求a 的取值范围．考向四 求解含参数不等式的恒成立问题 【例4】►设函数f (x )＝(x －a )2ln x ，a ∈R . (1)若x ＝e 为y ＝f (x )的极值点，求实数a ；(2)求实数a 的取值范围，使得对任意的x ∈(0,3e]，恒有f (x )≤4e 2成立． 注：e 为自然对数的底数．本题考查函数极值的概念，导数的运算法则，导数的应用，不等式的基础知识，考查学生推理论证能力．分析问题，解决问题的能力．难度较大，做好此类题目，一要有信心，二要结合题意进行恰当地转化，化难为易，化陌生为熟悉．【试一试】 设函数f (x )＝ax 3－3x ＋1，若对于任意x ∈[－1,1]，都有f (x )≥0成立，求实数a 的值．基础检测1．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，1， x ＜0，则满足不等式f (1－x 2)＞f (2x )的x 的取值范围是________．2．若存在实数x ，使得x 2－4bx ＋3b ＜0成立，则b 的取值范围是________．3．若关于x 的不等式(2ax －1)·ln x ≥0 对任意x ∈(0，＋∞)恒成立，则实数a 的值为________．4．不等式|x (x －2)|>x (x －2)的解集是________．5．若关于x 的不等式4x －2x ＋1－a ≥0在[1,2]上恒成立，则实数a 的取值范围为________．6．设函数f (x )＝mx 2－mx －1.(1)若对于一切实数x ，f (x )<0恒成立，求m 的取值范围； (2)若对于x ∈[1,3]，f (x )<－m ＋5恒成立，求m 的取值范围．第2讲一元二次不等式及其解法【2013年高考会这样考】1．会从实际情景中抽象出一元二次不等式模型．2．考查一元二次不等式的解法及其“三个二次”间的关系问题．3．以函数、导数为载体，考查不等式的参数范围问题．【复习指导】1．结合“三个二次”之间的联系，掌握一元二次不等式的解法．2．熟练掌握分式不等式、无理不等式、含绝对值不等式、高次不等式、指数不等式和对数不等式的解法．基础梳理1．一元二次不等式的解法(1)将不等式的右边化为零，左边化为二次项系数大于零的不等式ax2＋bx＋c＞0(a＞0)或ax2＋bx＋c＜0(a＞0)．(2)求出相应的一元二次方程的根．(3)利用二次函数的图象与x轴的交点确定一元二次不等式的解集．2．一元二次不等式与相应的二次函数及一元二次方程的关系判别式Δ＝b2－4ac Δ＞0Δ＝0Δ＜0二次函数y＝ax2＋bx＋c (a＞0)的图象一元二次方程ax2＋bx＋c＝0 (a＞0)的根有两相异实根x1，x2(x1＜x2)有两相等实根x1＝x2＝－b2a没有实数根ax2＋bx＋c＞0 (a＞0)的解集{x|x＞x2或x＜x1}⎩⎨⎧⎭⎬⎫x|x≠－b2aRax2＋bx＋c＜0 (a＞0)的解集{x|x1＜x＜x2}∅∅一个技巧一元二次不等式ax2＋bx＋c＜0(a≠0)的解集的确定受a的符号、b2－4ac的符号的影响，且与相应的二次函数、一元二次方程有密切联系，可结合相应的函数y＝ax2＋bx＋c(a≠0)的图象，数形结合求得不等式的解集．若一元二次不等式经过不等式的同解变形后，化为ax2＋bx＋c＞0(或＜0)(其中a＞0)的形式，其对应的方程ax2＋bx＋c＝0有两个不等实根x1，x2，(x1＜x2)(此时Δ＝b2－4ac＞0)，则可根据“大于取两边，小于夹中间”求解集．两个防范(1)二次项系数中含有参数时，参数的符号影响不等式的解集；不要忘了二次项系数是否为零的情况；(2)解含参数的一元二次不等式，可先考虑因式分解，再对根的大小进行分类讨论；若不能因式分解，则可对判别式进行分类讨论，分类要不重不漏．双基自测1．(人教A版教材习题改编)不等式x2－3x＋2＜0的解集为()．解析∵(x－1)(x－2)＜0，∴1＜x＜2.故原不等式的解集为(1,2)．2．(2011·广东)不等式2x 2－x －1＞0的解集是( )． 解析 ∵2x 2－x －1＝(x －1)(2x ＋1)＞0，∴x ＞1或x ＜－12.故原不等式的解集为⎝⎛⎭⎫－∞，－12∪(1，＋∞)． 3．不等式9x 2＋6x ＋1≤0的解集是( )． 解析 ∵9x 2＋6x ＋1＝(3x ＋1)2≥0，∴9x 2＋6x ＋1≤0的解集为⎩⎨⎧⎭⎬⎫x |x ＝－13.4．(2012·许昌模拟)若不等式ax 2＋bx －2＜0的解集为⎩⎨⎧⎭⎬⎫x |－2＜x ＜14，则ab ＝( )．解析 ∵x ＝－2，14是方程ax 2＋bx －2＝0的两根，∴⎩⎪⎨⎪⎧－2a ＝(－2)×14＝－12，－b a ＝－74，∴a ＝4，b ＝7.∴ab ＝28.5．不等式ax 2＋2ax ＋1≥0对一切x ∈R 恒成立，则实数a 的取值范围为________． 解析 当a ＝0时，不等式为1≥0恒成立；当a ≠0时，须⎩⎪⎨⎪⎧ a ＞0，Δ≤0，即⎩⎪⎨⎪⎧a ＞0，4a 2－4a ≤0.∴0＜a ≤1，综上0≤a ≤1.考向一 一元二次不等式的解法 【例1】►已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ，x ≥0，－x 2＋2x ，x ＜0，解不等式f (x )＞3.[审题视点] 对x 分x ≥0、x ＜0进行讨论从而把f (x )＞3变成两个不等式组．解 由题意知⎩⎪⎨⎪⎧ x ≥0，x 2＋2x ＞3或⎩⎪⎨⎪⎧x ＜0，－x 2＋2x ＞3，解得：x ＞1.故原不等式的解集为{x |x ＞1}．解一元二次不等式的一般步骤是：(1)化为标准形式；(2)确定判别式Δ的符号；(3)若Δ≥0，则求出该不等式对应的二次方程的根，若Δ＜0，则对应的二次方程无根；(4)结合二次函数的图象得出不等式的解集．特别地，若一元二次不等式的左边的二次三项式能分解因式，则可立即写出不等式的解集．【训练1】 函数f (x )＝2x 2＋x －3＋log 3(3＋2x －x 2)的定义域为________．解析 依题意知⎩⎪⎨⎪⎧2x 2＋x －3≥0，3＋2x －x 2＞0，解得⎩⎪⎨⎪⎧x ≤－32或x ≥1，－1＜x ＜3.∴1≤x ＜3.故函数f (x )的定义域为[1,3)．答案 [1,3)考向二 含参数的一元二次不等式的解法【例2】►求不等式12x 2－ax ＞a 2(a ∈R )的解集．[审题视点] 先求方程12x 2－ax ＝a 2的根，讨论根的大小，确定不等式的解集． 解 ∵12x 2－ax ＞a 2，∴12x 2－ax －a 2＞0， 即(4x ＋a )(3x －a )＞0，令(4x ＋a )(3x －a )＝0，得：x 1＝－a 4，x 2＝a3.①a ＞0时，－a 4＜a 3，解集为⎩⎨⎧⎭⎬⎫x |x ＜－a 4或x ＞a 3；②a ＝0时，x 2＞0，解集为{x |x ∈R 且x ≠0}；③a ＜0时，－a 4＞a 3，解集为⎩⎨⎧⎭⎬⎫x |x ＜a 3或x ＞－a 4.综上所述：当a ＞0时，不等式的解集为⎩⎨⎧⎭⎬⎫x |x ＜－a 4或x ＞a 3；当a ＝0时，不等式的解集为{x |x ∈R 且x ≠0}；当a ＜0时，不等式的解集为⎩⎨⎧⎭⎬⎫x |x ＜a 3或x ＞－a 4.解含参数的一元二次不等式的一般步骤：(1)二次项若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为二次项系数为正的形式．(2)判断方程的根的个数，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．【训练2】 解关于x 的不等式(1－ax )2＜1.解 由(1－ax )2＜1，得a 2x 2－2ax ＜0，即ax (ax －2)＜0， 当a ＝0时，x ∈∅.当a ＞0时，由ax (ax －2)＜0，得a 2x ⎝⎛⎭⎫x －2a ＜0， 即0＜x ＜2a .当a ＜0时，2a＜x ＜0.综上所述：当a ＝0时，不等式解集为空集；当a ＞0时，不等式解集为⎩⎨⎧⎭⎬⎫x ⎪⎪0＜x ＜2a ；当a ＜0时，不等式解集为⎩⎨⎧⎭⎬⎫x ⎪⎪2a＜x ＜0. 考向三 不等式恒成立问题【例3】►已知不等式ax 2＋4x ＋a ＞1－2x 2对一切实数x 恒成立，求实数a 的取值范围． [审题视点] 化为标准形式ax 2＋bx ＋c ＞0后分a ＝0与a ≠0讨论．当a ≠0时，有⎩⎪⎨⎪⎧a ＞0，Δ＝b 2－4ac ＜0.解 原不等式等价于(a ＋2)x 2＋4x ＋a －1＞0对一切实数恒成立，显然a ＝－2时，解集不是R ，因此a ≠－2，从而有⎩⎪⎨⎪⎧ a ＋2＞0，Δ＝42－4(a ＋2)(a －1)＜0，整理，得⎩⎪⎨⎪⎧ a ＞－2，(a －2)(a ＋3)＞0，所以⎩⎪⎨⎪⎧a ＞－2，a ＜－3或a ＞2， 所以a ＞2.故a 的取值范围是(2，＋∞)．不等式ax 2＋bx ＋c ＞0的解是全体实数(或恒成立)的条件是当a ＝0时，b ＝0，c＞0；当a ≠0时，⎩⎪⎨⎪⎧a ＞0，Δ＜0；不等式ax 2＋bx ＋c ＜0的解是全体实数(或恒成立)的条件是当a＝0时，b ＝0，c ＜0；当a ≠0时，⎩⎪⎨⎪⎧a ＜0，Δ＜0.【训练3】 已知f (x )＝x 2－2ax ＋2(a ∈R )，当x ∈[－1，＋∞)时，f (x )≥a 恒成立，求a 的取值范围．解 法一 f (x )＝(x －a )2＋2－a 2，此二次函数图象的对称轴为x ＝a . ①当a ∈(－∞，－1)时，f (x )在[－1，＋∞)上单调递增， f (x )min ＝f (－1)＝2a ＋3.要使f (x )≥a 恒成立， 只需f (x )min ≥a ，即2a ＋3≥a ，解得－3≤a ＜－1；②当a ∈[－1，＋∞)时，f (x )min ＝f (a )＝2－a 2， 由2－a 2≥a ，解得－1≤a ≤1.综上所述，所求a 的取值范围为[－3,1]．法二 令g (x )＝x 2－2ax ＋2－a ，由已知，得x 2－2ax ＋2－a ≥0在[－1，＋∞)上恒成立， 即Δ＝4a 2－4(2－a )≤0或⎩⎪⎨⎪⎧Δ＞0，a ＜－1，g (－1)≥0.解得－3≤a ≤1.所求a 的取值范围是[－3,1]．规范解答12——怎样求解含参数不等式的恒成立问题【问题研究】 含参数的不等式恒成立问题越来越受高考命题者的青睐，且由于新课标对导数应用的加强，这些不等式恒成立问题往往与导数问题交织在一起，在近年的高考试题中不难看出这个基本的命题趋势.对含有参数的不等式恒成立问题，破解的方法主要有：分离参数法和函数性质法.【解决方案】 解决这类问题的关键是将恒成立问题进行等价转化，使之转化为函数的最值问题.【示例】►(本题满分14分)(2011·浙江)设函数f (x )＝(x －a )2ln x ，a ∈R . (1)若x ＝e 为y ＝f (x )的极值点，求实数a ；(2)求实数a 的取值范围，使得对任意的x ∈(0,3e]，恒有f (x )≤4e 2成立． 注：e 为自然对数的底数．本题对于(1)问的解答要注意对于结果的检验，因为f ′(x 0)＝0，x 0不一定是极值点；对于(2)问的解答可以采用分离参数求最值的方法进行突破，这样问题就转化为单边求最值，相对分类讨论求解要简单的多．[解答示范] (1)求导得f ′(x )＝2(x －a )ln x ＋(x －a )2x ＝(x －a )(2ln x ＋1－ax)．(2分)因为x ＝e 是f (x )的极值点，所以f ′(e)＝(e －a )⎝⎛⎭⎫3－ae ＝0，解得a ＝e 或a ＝3e.经检验，符合题意，所以a ＝e 或a ＝3e.(4分)(2)①当0＜x ≤1时，对于任意的实数a ，恒有f (x )≤0＜4e 2成立．(5分)②当1＜x ≤3e 时，由题意，首先有f (3e)＝(3e －a )2ln(3e)≤4e 2，解得3e －2e ln (3e )≤a ≤3e ＋2eln (3e )(6分)由(1)知f ′(x )＝x －a ⎝⎛⎭⎫2ln x ＋1－ax .(8分) 令h (x )＝2ln x ＋1－ax，则h (1)＝1－a ＜0，h (a )＝2ln a ＞0，且h (3e)＝2ln(3e)＋1－a3e ≥2 ln(3e)＋1－3e ＋2eln (3e )3e ＝2⎝⎛⎭⎫ln 3e －13ln 3e ＞0.(9分)又h (x )在(0，＋∞)内单调递增，所以函数h (x )在(0，＋∞)内有唯一零点，记此零点为x 0，则1＜x 0＜3e,1＜x 0＜a .从而，当x ∈(0，x 0)时，f ′(x )＞0；当x ∈(x 0，a )时，f ′(x )＜0；当x ∈(a ，＋∞)时，f ′(x )＞0.即f (x )在(0，x 0)内单调递增，在(x 0，a )内单调递减，在(a ，＋∞)内单调递增． 所以要使f (x )≤4e 2对x ∈(1,3e]恒成立，只要 ⎩⎪⎨⎪⎧f (x 0)＝(x 0－a )2ln x 0≤4e 2，(1)f (3e )＝(3e －a )2ln (3e )≤4e 2，(2)成立．(11分) 由h (x 0)＝2ln x 0＋1－ax 0＝0，知a ＝2x 0ln x 0＋x 0.(3)将(3)代入(1)得4x 20ln 3x 0≤4e 2.又x 0＞1，注意到函数x 2ln 3x 在(1，＋∞)内单调递增，故1＜x 0≤e. 再由(3)以及函数2x ln x ＋x 在(1，＋∞)内单调递增，可得1＜a ≤3e.由(2)解得，3e －2e ln (3e )≤a ≤3e ＋2eln (3e ).所以3e －2eln (3e )≤a ≤3e.(13分)综上，a 的取值范围为3e －2eln (3e )≤a ≤3e.(14分)．本题考查函数极值的概念，导数的运算法则，导数的应用，不等式的基础知识，考查学生推理论证能力．分析问题，解决问题的能力．难度较大，做好此类题目，一要有信心，二要结合题意进行恰当地转化，化难为易，化陌生为熟悉．【试一试】 设函数f (x )＝ax 3－3x ＋1，若对于任意x ∈[－1,1]，都有f (x )≥0成立，求实数a 的值．[尝试解答] (1)若x ＝0，则不论a 取何值，f (x )＝1＞0恒成立．(2)若x ＞0，即x ∈(0,1]时，f (x )＝ax 3－3x ＋1≥0可化为a ≥3x 2－1x 3.设g (x )＝3x 2－1x3，则g ′(x )＝3(1－2x )x 4，∴g (x )在区间⎝⎛⎦⎤0，12上单调递增，在区间⎣⎡⎦⎤12，1上单调递减．∴g (x )max ＝g ⎝⎛⎭⎫12＝4，从而a ≥4. (3)若x ＜0，即x ∈[－1,0)时，f (x )＝ax 3－3x ＋1≥0可化为a ≤3x 2－1x3.设h (x )＝3x 2－1x 3，则h ′(x )＝3(1－2x )x 4，∴h (x )在[－1,0)上单调递增． ∴h (x )min ＝h (－1)＝4，从而a ≤4. 综上所述，实数a 的值为4.基础检测1．(2014·苏州模拟)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，1， x ＜0，则满足不等式f (1－x 2)＞f (2x )的x 的取值范围是________．解析：由条件得⎩⎪⎨⎪⎧1－x 2＞2x ，1－x 2＞0，解得－1＜x ＜－1＋ 2.答案：()－1，－1＋22．(2014·南通期末)若存在实数x ，使得x 2－4bx ＋3b ＜0成立，则b 的取值范围是________．解析：本题是存在性命题，只要满足Δ＝16b 2－12b ＞0即可，解得b ＜0或b ＞34.3．(2013·南京、淮安二模)若关于x 的不等式(2ax －1)·ln x ≥0 对任意x ∈(0，＋∞)恒成立，则实数a 的值为________．解析：若x ＝1，则原不等式恒成立，此时a ∈R ；若x ＞1，则ln x ＞0，于是2ax －1≥0，即a ≥⎝⎛⎭⎫12x max ，所以a ≥12；若0＜x ＜1，则ln x ＜0，于是2ax －1≤0，即a ≤⎝⎛⎭⎫12x min ，所以a ≤12.综上所述，a ＝12.4．不等式|x (x －2)|>x (x －2)的解集是________．解析：不等式|x (x －2)|>x (x －2)的解集即x (x －2)<0的解集，解得0<x <2.5．若关于x 的不等式4x －2x ＋1－a ≥0在[1,2]上恒成立，则实数a 的取值范围为________． ．解析：∵不等式4x －2x ＋1－a ≥0在[1,2]上恒成立， ∴4x －2x ＋1≥a 在[1,2]上恒成立．令y ＝4x －2x ＋1＝(2x )2－2×2x ＋1－1＝(2x －1)2－1. ∵1≤x ≤2，∴2≤2x ≤4.由二次函数的性质可知：当2x ＝2， 即x ＝1时，y 取得最小值0，∴实数a 的取值范围为(－∞，0]． 6．设函数f (x )＝mx 2－mx －1.(1)若对于一切实数x ，f (x )<0恒成立，求m 的取值范围； (2)若对于x ∈[1,3]，f (x )<－m ＋5恒成立，求m 的取值范围． 解：(1)要使mx 2－mx －1<0恒成立，若m ＝0，显然－1<0；若m ≠0，则⎩⎪⎨⎪⎧m <0，Δ＝m 2＋4m <0⇒－4<m <0.所以－4<m ≤0.(2)要使f (x )<－m ＋5在[1,3]上恒成立，即m ⎝⎛⎭⎫x －122＋34m －6<0在x ∈[1,3]上恒成立． 有以下两种方法：法一：令g (x )＝m ⎝⎛⎭⎫x －122＋34m －6， x ∈[1,3]．当m >0时，g (x )在[1,3]上是增函数，所以g (x )max ＝g (3)⇒7m －6<0，所以m <67，则0<m <67； 当m ＝0时，－6<0恒成立；当m <0时，g (x )在[1,3]上是减函数，所以g (x )max ＝g (1)⇒m －6<0，所以m <6，所以m <0.综上所述：m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67. 法二：因为x 2－x ＋1＝⎝⎛⎭⎫x －122＋34>0， 又因为m (x 2－x ＋1)－6<0，所以m <6x 2－x ＋1. 因为函数y ＝6x 2－x ＋1＝6⎝⎛⎭⎫x －122＋34在[1,3]上的最小值为67， 所以只需m <67即可． 所以，m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67. 第Ⅱ组：重点选做题1．(2014·连云港模拟)已知关于x 的不等式x 2－ax ＋2a ＜0的解集为A ，若集合A 中恰有两个整数，则实数a 的取值范围是________．4．(2014·泰州质检)设实数a ≥1，使得不等式x |x －a |＋32≥a 对任意的实数x ∈[1,2]恒成立，则满足条件的实数a 的取值范围是________．1．解析：由题意可得：Δ＝a 2－8a >0， 得a <0或a >8.当a <0时，对称轴x 0＝a 2<0，且f (0)＝2a <0. 故A 中两个整数只能为－1,0.故f (－1)＝1＋3a <0，f (－2)＝4＋4a ≥0，得－1≤a <－13. 当a >8时，x 0＝a 2>4，设A ＝(m ，n )．由于集合A 中恰有两个整数n －m ≤3.即a 2－8a ≤3，即a 2－8a ≤9.得8<a ≤9故对称轴4<a 2<5， 又f (2)＝4>0，f (3)＝9－a ≥0故A 中的两个整数为4和5.故f (4)<0，f (5)<0，f (6)≥0.即⎩⎪⎨⎪⎧ 25－3a <016－2a <036－4a ≥0，解得253<a ≤9. 综上a 的取值范围为⎣⎡⎭⎫－1，－13∪⎝⎛⎦⎤253，9. 答案：⎣⎡⎭⎫－1，－13∪⎝⎛⎦⎤253，9 4．解析：(1)当1≤a ≤32时，显然符合题意． (2)当a ≥2时，原不等式可化为x (a －x )≥a －32. 取x ＝1，成立．当x ∈(1,2]时，a ≥x 2－32x －1＝x ＋1－12(x －1). 而函数f (x )＝x ＋1－12(x －1)在(1,2]上单调递增，故a ≥f (2)＝52. (3)当32＜a ＜2时，原不等式可化为 ①⎩⎪⎨⎪⎧ 1≤x ≤a ，x (a －x )≥a －32或 ②⎩⎪⎨⎪⎧ a ≤x ≤2，x (x －a )≥a －32.参照(2)的过程解不等式组①得a ≥a ＋1－12(a －1)， 解得1＜a ≤32，矛盾，舍去； 由不等式组②得a ≤x 2＋32x ＋1＝x －1＋52(x ＋1). 同上可得－1≤a ≤32，矛盾，舍去． 综上所述，1≤a ≤32或a ≥52. 答案：⎣⎡⎦⎤1，32∪⎣⎡⎭⎫52，＋∞。

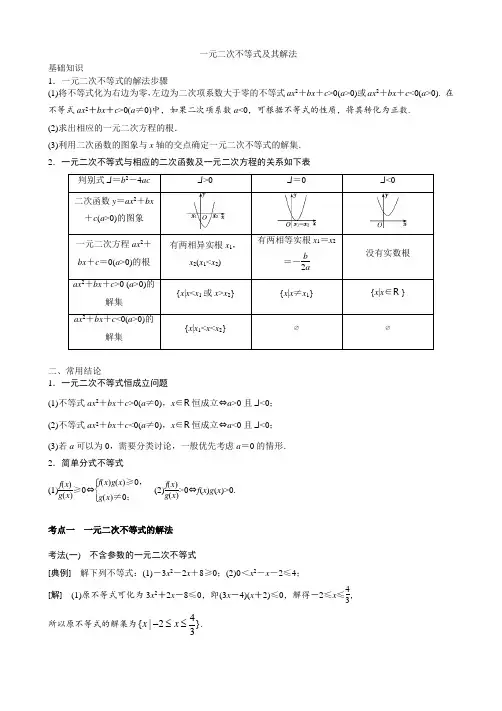
一元二次不等式及其解法基础知识1．一元二次不等式的解法步骤 (1)将不等式化为右边为零，左边为二次项系数大于零的不等式ax 2＋bx ＋c >0(a >0)或ax 2＋bx ＋c <0(a >0). 在不等式ax 2＋bx ＋c >0(a ≠0)中，如果二次项系数a <0，可根据不等式的性质，将其转化为正数. (2)求出相应的一元二次方程的根．(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的解集． 2．一元二次不等式与相应的二次函数及一元二次方程的关系如下表二、常用结论1．一元二次不等式恒成立问题(1)不等式ax 2＋bx ＋c >0(a ≠0)，x ∈R 恒成立⇔a >0且Δ<0； (2)不等式ax 2＋bx ＋c <0(a ≠0)，x ∈R 恒成立⇔a <0且Δ<0； (3)若a 可以为0，需要分类讨论，一般优先考虑a ＝0的情形． 2．简单分式不等式(1)f (x )g (x )≥0⇔⎩⎪⎨⎪⎧f (x )g (x )≥0，g (x )≠0；(2)f (x )g (x )>0⇔f (x )g (x )>0. 考点一 一元二次不等式的解法 考法(一) 不含参数的一元二次不等式[典例] 解下列不等式：(1)－3x 2－2x ＋8≥0；(2)0＜x 2－x －2≤4；[解] (1)原不等式可化为3x 2＋2x －8≤0，即(3x －4)(x ＋2)≤0，解得－2≤x ≤43，所以原不等式的解集为}342|{≤≤-x x .(2)原不等式等价于⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －2≤4⇔⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －6≤0⇔⎩⎪⎨⎪⎧ (x －2)(x ＋1)＞0，(x －3)(x ＋2)≤0⇔⎩⎪⎨⎪⎧x ＞2或x ＜－1，－2≤x ≤3. 借助于数轴，如图所示，原不等式的解集为{}x |－2≤x ＜－1或2＜x ≤3. 考法(二) 含参数的一元二次不等式[典例] 解不等式ax 2－(a ＋1)x ＋1＜0(a ＞0)． [解] 原不等式变为(ax －1)(x －1)＜0， 因为a ＞0，所以a )1(ax -(x －1)＜0. 所以当a ＞1，即1a <1时，解为1a ＜x ＜1；当a ＝1时，解集为∅；当0＜a ＜1，即1a >1时，解为1＜x ＜1a.综上，当0＜a ＜1时，不等式的解集为}11|{ax x <<； 当a ＝1时，不等式的解集为∅； 当a ＞1时，不等式的解集为}11|{<<x ax . [题组训练]1．不等式(x ＋5)(3－2x )≥6的解集是( )A.}291|{≥-≤x x x 或 B.}291|{≤≤-x x C.}129|{≥-≤x x x 或D.}129|{≤≤-x x 解析：选D 不等式(x ＋5)(3－2x )≥6可化为2x 2＋7x －9≤0，所以(2x ＋9)(x －1)≤0，解得－92≤x ≤1.所以不等式(x ＋5)(3－2x )≥6的解集是}129|{≤≤-x x .故选D. 2．已知不等式ax 2－bx －1≥0的解集是]31,21[--，则不等式x 2－bx －a ＜0的解集是( )A ．(2,3)B ．(－∞，2)∪(3，＋∞) C.)21,31( D.)31,(-∞∪),21(+∞ 解析：选A 由题意知－12，－13是方程ax 2－bx －1＝0的两根，所以由根与系数的关系得⎩⎨⎧－12＋⎝⎛⎭⎫－13＝b a，－12×⎝⎛⎭⎫－13＝－1a .解得⎩⎪⎨⎪⎧a ＝－6，b ＝5，不等式x 2－bx －a ＜0即为x 2－5x ＋6＜0，解集为(2,3)．3．求不等式12x 2－ax >a 2(a ∈R )的解集．解：原不等式可化为12x 2－ax －a 2>0，即(4x ＋a )(3x －a )>0， 令(4x ＋a )(3x －a )＝0，解得x 1＝－a 4，x 2＝a3.当a >0时，不等式的解集为)4,(a--∞∪),3(+∞a ； 当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞)； 当a <0时，不等式的解集为)3,(a --∞∪),4(+∞-a. 考点二 一元二次不等式恒成立问题 考法(一) 在R 上的恒成立问题[典例] 若不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立，则实数a 的取值范围是( )A ．(－∞，2]B ．[)2,2(-C ．(－2,2]D ．(－∞，－2) [解析] 当a －2＝0，即a ＝2时，不等式为－4<0，对一切x ∈R 恒成立．当a ≠2时，则⎩⎪⎨⎪⎧ a －2<0，Δ＝4(a －2)2＋16(a －2)<0，即⎩⎪⎨⎪⎧a －2<0，a 2<4，解得－2<a <2. ∴实数a 的取值范围是(－2,2]． [答案] C解题技法] 一元二次不等式恒成立的条件(1)ax 2＋bx ＋c >0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a >0，b 2－4ac <0.(2)ax 2＋bx ＋c <0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a <0，b 2－4ac <0.考法(二) 在给定区间上的恒成立问题[典例] 若对任意的x ∈[)2,1(-，都有x 2－2x ＋a ≤0(a 为常数)，则a 的取值范围是( ) A ．(－∞，－3] B ．(－∞，0] C ．),1[+∞[ D DD D ．]1,(-∞(解析] 法一：令f (x )＝x 2－2x ＋a ，则由题意，得⎩⎪⎨⎪⎧f (－1)＝(－1)2－2×(－1)＋a ≤0，f (2)＝22－2×2＋a ≤0，解得a ≤－3，故选A.法二：当x ∈[)2,1(-]时，不等式x 2－2x ＋a ≤0恒成立等价于a ≤－x 2＋2x 恒成立，则由题意，得a ≤(－x 2＋2x )min (x ∈[)2,1(-])．而－x 2＋2x ＝－(x －1)2＋1，则当x ＝－1时，(－x 2＋2x )min ＝－3，所以a ≤－3，故选A. 答案] A [解题技法]一元二次不等式在给定区间上的恒成立问题的求解方法(1)若f (x )>0在集合A 中恒成立，即集合A 是不等式f (x )>0的解集的子集，可以先求解集，再由子集的含义求解参数的值(或范围)． (2)转化为函数值域问题，即已知函数f (x )的值域为[m ，n ]，则f (x )≥a 恒成立⇒f (x )min ≥a ，即m ≥a ；f (x )≤a 恒成立⇒f (x )max ≤a ，即n ≤a . 考法(三) 给定参数范围求x 范围的恒成立问题[典例] 求使不等式x 2＋(a －6)x ＋9－3a >0(|a |≤1)恒成立的x 的取值范围． 解] 将原不等式整理为形式上是关于a 的不等式(x －3)a ＋x 2－6x ＋9>0. 令f (a )＝(x －3)a ＋x 2－6x ＋9，因为f (a )>0在|a |≤1时恒成立，所以 (1)若x ＝3，则f (a )＝0，不符合题意，舍去．(2)若x ≠3，则由一次函数的单调性，可得⎩⎪⎨⎪⎧ f (－1)>0，f (1)>0，即⎩⎪⎨⎪⎧x 2－7x ＋12>0，x 2－5x ＋6>0，解得x <2或x >4，综上可知，使原不等式恒成立的x 的取值范围是(－∞，2)∪(4，＋∞)． [解题技法]给定参数范围求x 范围的恒成立问题的解法解决恒成立问题一定要清楚选谁为主元，谁是参数．一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解． [题组训练]1．(2018·忻州第一中学模拟)已知关于x 的不等式x 2－4x ≥m 对任意x ∈(0,1]恒成立，则实数m 的取值范围为( )A ．(－∞，－3]B ．[－3，＋∞)C ．[－3,0)D ．[－4，＋∞)解析：选A x 2－4x ≥m 对任意x ∈(0,1]恒成立，令f (x )＝x 2－4x ，∵f (x )图象的对称轴为直线x ＝2，∴f (x )在(0,1]上单调递减，∴当x ＝1时，f (x )取到最小值，为－3，∴实数m 的取值范围是(－∞，－3]，故选A. 2．若不等式x 2＋mx －1<0对于任意x ∈[m ，m ＋1]都成立，则实数m 的取值范围是________．解析：由题意，得函数f (x )＝x 2＋mx －1在[m ，m ＋1]上的最大值小于0，又抛物线f (x )＝x 2＋mx －1开口向上，所以只需⎩⎪⎨⎪⎧ f (m )＝m 2＋m 2－1<0，f (m ＋1)＝(m ＋1)2＋m (m ＋1)－1<0，即⎩⎪⎨⎪⎧2m 2－1<0，2m 2＋3m <0，解得－22<m <0. 答案：)0,22(-3．不等式(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立，则x 的取值范围是________．解析：由题意知(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立等价于(x 2－4x )a －3x 2＋2x ＜0对a ∈(0,1)恒成立．令g (a )＝(x 2－4x )a －3x 2＋2x ，当x ＝0时，g (a )＝0，不满足题意．当x ≠0时，则⎩⎪⎨⎪⎧g (0)＝－3x 2＋2x ≤0，g (1)＝(x 2－4x )－3x 2＋2x ≤0，得x ≤－1或x ≥23.答案：(－∞，－1]∪),32[+∞ [课时跟踪检测]1．(2019·石家庄模拟)若集合A ＝{x |x 2－2x <0}，B ＝{x ||x |≤1}，则A ∩B ＝( )A ．[－1,0)B ．[－1,2)C ．(0,1]D ．[1,2)解析：选C 由x 2－2x <0得0<x <2，所以A ＝{x |0<x <2}，由|x |≤1得－1≤x ≤1，所以集合B ＝{x |－1≤x ≤1}，所以A ∩B ＝{x |0<x ≤1}，故选C. 2．不等式3x －1x －2≤0的解集为( )A.}231|{≤≤x x B.}312|{≤>x x x 或 C.}231|{<≤x x D ．{x |x <2} 解析：选C 不等式3x －1x －2≤0等价于(3x －1)(x －2)≤0，且x －2≠0，解得13≤x <2.故选C.3．不等式－3<4x －4x 2≤0的解集是( ) A.}231021|{<≤≤<-x x x 或 B ．{x |x ≤0或x ≥1} C.}2321|{<<-x x D.}2321|{≥-≤x x x 或 解析：选A 不等式可化为⎩⎪⎨⎪⎧4x (x －1)≥0，4x 2－4x －3<0，解得⎩⎪⎨⎪⎧x ≤0或x ≥1，－12<x <32，所以－12<x ≤0或1≤x <32.4．(2019·广州模拟)已知不等式ax 2－5x ＋b >0的解集为{x |－3<x <－2}，则不等式bx 2－5x ＋a >0的解集为( ) A.}3121|{-<<-x x B.}2131|{-<->x x x 或 C ．{x |－3<x <2} D ．{x |x <－3或x >2} 解析：选A 由题意得⎩⎨⎧5a＝－3－2，ba ＝－3×(－2)，解得a ＝－1，b ＝－6，所以不等式bx 2－5x ＋a >0为－6x 2－5x－1>0，即(3x ＋1)(2x ＋1)<0，所以解集为}3121|{-<<-x x ，故选A. 5．若关于x 的不等式x 2－ax －a ≤－3的解集不是空集，则实数a 的取值范围是( )A ．[]2,(-∞)B B ． (－∞，－6]]C ． ]2,6[-D ．(－∞，－6]∪[2，＋∞)解析：选D 由关于x 的不等式x 2－ax －a ≤－3的解集不是空集，得对应方程x 2－ax －a ＋3＝0有实数根，即Δ＝a 2＋4(a －3)≥0，解得a ≥2或a ≤－6，所以a 的取值范围是 (－∞，－6]∪[2，＋∞)．故选D.6．某商场若将进货单价为8元的商品按每件10元出售，每天可销售100件，现准备采用提高售价来增加利润．已知这种商品每件销售价提高1元，销售量就要减少10件．那么要保证每天所赚的利润在320元以上，销售价每件应定为( )A ．12元B ．16元C ．12元到16元之间D ．10元到14元之间解析：选C 设销售价定为每件x 元，利润为y ，则y ＝(x －8)[100－10(x －10)]， 依题意有，(x －8)[100－10(x －10)]＞320，即x 2－28x ＋192＜0，解得12＜x ＜16， 所以每件销售价应为12元到16元之间．7．存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m 的最大值为( )A ．1 B.14 C.12D ．－1解析：选C 若对于任意x ∈[－1,1]，不等式x 2＋mx －3m <0恒成立，则由函数f (x )＝x 2＋mx －3m 的图象可知⎩⎪⎨⎪⎧f (－1)＝1－m －3m <0，f (1)＝1＋m －3m <0，解得m >12.所以若存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m ≤12，所以m的最大值为12.故选C.8．(2018·北京东城区期末)设不等式x 2－2ax ＋a ＋2≤0的解集为A ，若A ⊆]3,1[，则a 的取值范围为( )A.]511,1(- B.)511,1( C.)511,2( D ．[)3,1( 解析：选A 设f (x )＝x 2－2ax ＋a ＋2，因为不等式x 2－2ax ＋a ＋2≤0的解集为A ，且A ⊆[]3,1[]， 所以对于方程x 2－2ax ＋a ＋2＝0，若A ＝∅，则Δ＝4a 2－4(a ＋2)<0，即a 2－a －2<0，解得－1<a <2；若A ≠∅，则⎩⎪⎨⎪⎧Δ＝4a 2－4(a ＋2)≥0，f (1)≥0，f (3)≥0，1≤a ≤3，即⎩⎪⎨⎪⎧a ≥2或a ≤－1，a ≤3，a ≤115，1≤a ≤3，所以2≤a ≤115.综上，a 的取值范围为]511,1(-，故选A. 9．不等式|x (x －2)|>x (x －2)的解集是________．解析：不等式|x (x －2)|>x (x －2)的解集即x (x －2)<0的解集，解得0<x <2，故不等式的解集为{x |0<x <2}． 答案：{x |0<x <2}10．若a <0，则关于x 的不等式组⎩⎪⎨⎪⎧ax －a 2<0，x 2－ax －2a 2<0的解集为________． 解析：因为a <0，所以由ax －a 2＝a (x －a )<0，得x >a ，由x 2－ax －2a 2＝(x －2a )(x ＋a )<0，得2a <x <－a .所以原不等式组的解集为(a ，－a )． 答案：(a ，－a )11．若关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，则实数a 的取值范围是________．解析：关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，所以a >0，解不等式得x 2≤a5，所以－a5≤x ≤ a5，所以3≤ a 5<4，所以9≤a5<16，即45≤a <80， 所以实数a 的取值范围是[45,80)． 答案：[45,80)12．不等式a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，则实数λ的取值范围为________．解析：因为a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，所以a 2＋8b 2－λb (a ＋b )≥0恒成立，即a 2－λba ＋(8－λ)b 2≥0恒成立，由二次不等式的性质可得Δ＝λ2b 2＋4(λ－8)b 2＝b 2(λ2＋4λ－32)≤0，所以(λ＋8)(λ－4)≤0，解得－8≤λ≤4. 答案：[－8,4]13．已知函数f (x )＝ax 2＋2ax ＋1的定义域为R . (1)求a 的取值范围； (2)若函数f (x )的最小值为22，解关于x 的不等式x 2－x －a 2－a <0. 解：(1)因为函数f (x )＝ax 2＋2ax ＋1的定义域为R ，所以ax 2＋2ax ＋1≥0恒成立， 当a ＝0时，1≥0恒成立．当a ≠0时，则有⎩⎪⎨⎪⎧a >0，Δ＝(2a )2－4a ≤0，解得0<a ≤1，综上可知，a 的取值范围是[0,1]． (2)因为f (x )＝ax 2＋2ax ＋1＝a (x ＋1)2＋1－a ，因为a >0，所以当x ＝－1时，f (x )min ＝1－a ，由题意得，1－a ＝22，所以a ＝12， 所以不等式x 2－x －a 2－a <0可化为x 2－x －34<0.解得－12<x <32，所以不等式的解集为)23,21(-。

第一课时：一元二次方程实数根的分布教学目标：使学生掌握一元二次方程实根分布问题的处理，加强求解一元二次不等式及不等式组，初步训练学生的数形结合能力。

教学重点：利用二次函数的图象，把一元二次方程根的分布−−→−转化图形问题−−→−转化代数表达式（不等式组）−−→−计算参数取值范围。

教学难点：图形问题转化成代数表达式(不等式组)并求解。

一、问题的提出若方程0)5()2(2=++++m x m x 的两根均为正数，求实数m 的取值范围.变式1：两根一正一负时情况怎样？变式2：两实根均大于5时情况又怎样？变式3：一根大于2，另一根小于-1时情况又怎样？问题：能否从二次函数图形角度去观察理解？若能试比较两种方法的优劣.方程)0(02≠=++a c bx ax 的实根，如若从二次函数图形角度去观察理解，其实质就是对应的二次函数2()0(0)f x ax bx c a =++=≠ 的抛物线与x 轴交点的横坐标.一元二次方程实根分布，实质上就是方程的根与某些确定的常数大小关系比较.二、一元二次方程实根分布仿上完成下表一元二次方程)0(02≠=++a c bx ax 实根分布图解三、练习1.m 为何实数时，方程02)1(2=+++m x m x 的两根都在-1与1之间.2、若方程0)3()1(2=-++-a x a x 的两根中，一根小于0，另一根大于2，求a 的取值范围.四、小结基本类型与相应方法：设 )0()(2≠++=a c bx ax x f ，则方程0)(=x f 的实根分布的基本类型及相应方法如下表：五作业：1．关于x 的一元二次方程222320ax x a ---=的一根大于1，另一根小于1.则a 的值是 （ ）（A ）0a >或4a <- （B ）4a <- （C ）0a > （D ）40a -<<2．方程227(13)20(x k x k k k -++--=为常数）有两实根,αβ，且01α<<，12β<<，那么k 的取值范围是 （ ）（A ）34k << （B ）21k -<<- （C ）21a -<<-或34k << （D ）无解3．设m 是整数，且方程2320x mx +-=的两根都大于95-而小于37，则m = .4.若关于x 的方程22(1)210m x mx -+-=的所有根都是比1小的正实数，则实数m 的取值范围是m ＝5. 方程2(21)(6)0x m x m +-+-=的一根不大于－1，另一根不小于1.试求：（1）参数m 的取值范围；（2）方程两根的平方和的最大值和最小值. 第二课时 一元二次方程实数根分布的应用一复习二、例子例1 已知实数a 、b 、c 满足22211a b c a b c a b c ⎧>>⎪++=⎨⎪++=⎩，求a b +的取值范围.解 由已知得1a b c +=-且222222()()(1)(1)22a b a b c c ab c c +-+---===-.所以,a b 是一元二次方程22(1)()0x c x c c --+-=的两根. 由a b c>>问题可转化为方程22(1)()0x c x c c --+-=的二根都大于c .令()f x =22(1)()x c x c c --+-，有2212()0(1)4()0c cf c c c c -⎧>⎪⎪>⎨⎪∆=--->⎪⎩ 即22123203210c c c c c c ->⎧⎪->⎨⎪--<⎩， 求得103c -<<，因此4(1,)3a b +∈.例2已知点(0,4)A 、(4,0)B .若抛物线21y x mx m =-++与线段AB (不包括端点A 及B )有两个不同的交点，则m 的取值范围是 . (1997年上海市高中数学竞赛)解： 显然直线AB 的方程为1(04)44x y x +=<<即4y x =-，代入抛物线方程并整理得2(1)(3)0x m x m +-+-=.设2()(1)(3)f x x m x m =+-+-，问题转化函数()y f x =的图象和x 轴在0到4之间有两个不同的交点，即方程2(1)(3)0x m x m +-+-=在(0,4)上有两个不相等的实根. 所以2(1)4(3)0(0)30(4)164(1)30104.2m m f m f m m m ⎧∆=--->⎪=->⎪⎪⎨=--+->⎪-⎪<<⎪⎩ 解得m 的取值范围是1733m <<. 例3关于x 的实系数二次方程20x ax b ++=的两个实数根为,αβ，证明：①如果||2,||2αβ<<，那么2||4a b <+且||4b <；②如果 2||4a b <+且||4b <，那么||2,||2αβ<<.(1993年全国高考题)证明 ①设2()f x x ax b =++，由已知，函数()y f x =的图象与x 轴在2-到2之间有两个不同的交点. 所以240,(1)22,(2)2(2)420,(3)(2)420.(4)a b a f a b f a b ⎧∆=->⎪⎪-<-<⎪⎨⎪-=-+>⎪=++>⎪⎩由(3)、(4)得(4)24b a b -+<<+，所以2||4a b <+.由(2)，得||4a <，结合(1)得2416b a <<，所以4b <. 将(3)+(4)得4b >-，因此44b -<<，即||4b <.②由于2||4a b <+且||4b <，可得4,2||448b a <<+=，所以||4a <，222a -<-<. 即函数()f x 的图象的对称轴2a x =-位于两条直线2x =-，2x =之间.因为(2)(2)(42)(42)2(4)0f f a b a b b -+=+++-+=+>，22(2)(2)(42)(42)(4)40f f a b a b b a -⋅=++-+=+-> .所以(2)0,(2)0f f ->>. 因此函数()f x 的图象与x 轴的交点位于-2和2之间，即||2,||2αβ<<.作业1．已知抛物线2(4)2(6),y x m x m m =++-+为实数.m 为何值时，抛物线与x 轴的两个交点都位于点(1,0)的右侧？2．已知,,a b c 都是正整数，且抛物线2()f x ax bx c =++与x 轴有两个不同的交点A 、B. 若A 、B 到原点的距离都小于1，求a b c ++的最小值.第三课时 应用提高例1若方程k x x =-232在[]1,1-上有实根，求实数k 的取值范围. 解法一：方程k x x =-232在[]1,1-上有实根，即方程0232=--k x x 在[]1,1-上有实根，设k x x x f --=23)(2，则根据函数)(x f y =的图象与x 轴的交点的横坐标等价于方程0)(=x f 的根. （1）两个实根都在[]1,1-上，如图：可得⎪⎪⎩⎪⎪⎨⎧≤-≤-≥≥-≥∆1210)1(0)1(0a b f f ，解得2169-≤≤-k ； （2）只有一个实根在[]1,1-上，如图：可得0)1()1(≤⋅-f f ，解得 2521≤≤-k ，综合（1）与（2）可得 实数k 的取值范围为⎥⎦⎤⎢⎣⎡-25,169 解法二：方程k x x =-232在[]1,1-上有实根，即存在[]1,1-∈x ，使得等式x x k 232-=成立，要求k 的取值范围，也即要求函数[]1,1,232-∈-=x x x k 的值域. 设[]1,1,1694323)(22-∈-⎪⎭⎫ ⎝⎛-=-==x x x x x f k 又因，则)1(169-≤≤-f k ， 可得25169≤≤-k . 解法三：令,232x x y -=则k y =，则方程k x x =-232在[]1,1-上有实根，等价于方程组⎪⎩⎪⎨⎧=-=k y x x y 232在[]1,1-上有实数解，也即等价于抛物线,232x x y -=与直线k y =在[]1,1-上有公共点，如图所示直观可得：25169≤≤-k .解法四：根据解法三的转化思想，也可将原方 程k x x =-232化成k x x +=232，然后令 k x y x y +==23,2，从而将原问题等价转化为 抛物线2x y =与直线k x y +=23在[]1,1-点时，“数形结合法”下去求参数k 的取值范围.根据图形直观可得：当直线k x y +=23过点)1,1(-， 截距k 最大；当直线k x y +=23与抛物线k x y +=23相切时，截距k 最小. 且169,25-==最小最大k k .故参数的取值范围为25169≤≤-k . 2已知实数a 、b 、c 满足021a b c m m m++=++，其中m 为正数.对于2()f x ax bx c =++. (1)若0a ≠，求证：()01m af m <+； (2) 若0a ≠，证明方程()0f x =在(0,1)内有实根.证明 (1)由021a b c m m m ++=++，求得()21am bm c m m =-+++，所以 222222211()[()()][()][]11112(1)2m m m m m af a a b c a a m m m m m m m m m=++=-=-+++++++ 又由22(1)20m m m +>+>，因此22110(1)2m m m -<++，故()01m af m <+. (2)要证明方程()0f x =在(0,1)内有实根，只须证明(0)(1)0f f ⋅< 或 (0)0,(1)0,0,0 1.2af af b a >⎧⎪>⎪⎪∆≥⎨⎪⎪<-<⎪⎩但两者都不易证明. 由01(0)1m m m <<>+，结合第(1)题()01m af m <+，对a 进行讨论： 当0a >时，有()01m f m <+. 只要证明(0)f c =和(1)f a b c =++中有一个大于零即可. 若0c >，则(0)0f >成立，问题得证；若0c ≤，由021a b c m m m ++=++求得(1)(1)2a m c m b m m++=--+，所以 (1)(1)(1)22a m c m a c f a b c a c m m m m ++=++=--+=-++. 由0,0,0a m c >>≤，知(1)0f >，命题得证. 故当0a >时，方程()0f x =在(0,1)内有实根. 同理可证，当0a <时，方程()0f x =在(0,1)内也有根.。