第2章立体上点的投影
- 格式:pps
- 大小:2.40 MB
- 文档页数:18




第二篇投影制图第二章投影的基本知识【学习目的】掌握正投影的基本原理,掌握三视图的形成及其投影规律,掌握点、线、面的投影特性。
【学习要点】投影的基本特性;物体的三视图的绘制;点、线、面的投影特性。
第一节投影方法一、投影的概念(一)投影法的概念在日常生活中,我们看到在太阳光或灯光照射物体时,在地面或墙壁上出现物体的影子,这就是一种投影现象。
投影法与自然投影现象类似,就是投影线通过物体向选定的投影面投射,并在该面上得到图形的方法,用投影法得到的图形称作投影图或投影,如图2-1所示。
图2-1 投影的产生产生投影时必须具备的三个基本条件是投影线、被投影的物体和投影面。
需要注意的是,生活中的影子和工程制图中的投影是有区别的,投影必须将物体的各个组成部分的轮廓全部表示出来,而影子只能表达物体的整体轮廓,并且内部为一个整体如图2-2所示。
(a)影子 (b)投影图2-2 投影与影子的区别二、 投影法分类根据投影线与投影面的相对位置的不同,投影法分为两种。
(一) 中心投影法投影线从一点出发,经过空间物体,在投影面上得到投影的方法(投影中心位于有限远处),如图2-3所示。
图2-3 中心投影法缺点:中心投影不能真实地反映物体的大小和形状,不适合用于绘制水利工程图样。
优点:中心投影法绘制的直观图立体感较强,适用于绘制水利工程建筑物的透视图。
(二) 平行投影法投影线相互平行经过空间物体,在投影面上得到投影的方法(投影中心位于无限远处),称为平行投影法。
平行投影法根据投影线与投影面的角度不同,又分为正投影法和斜投影法,如图2-4所示。
(a )为斜投影法,(b )为正投影法。
(b)(a)图2-4 平行投影法优点:正投影法能够表达物体的真实形状和大小,作图方法也较简单,所以广泛用于绘制工程图样。
正投影法斜投影法在以后的章节中,我们所讲述的投影都是指的正投影。
三、投影的特性(一)真实性平行于投影面的直线段或平面图形,在该投影面上的投影反映了该直线段或者平面图形的实长或实形,这种投影特性称为真实性,如图2-5所示。





第2章投影的基本知识2.1 投影法各种建筑物和机械都是根据工程图样施工、制造的。
工程图样必须准确地表达它们的形状、大小、材料和技术要求2.1.1 投影概念光线(阳光活灯光)照射物体,在墙面或地面上就会产生影子,影子只能反映物体的外形轮廓,而能表达出物体的形状和内部结构,这就是日常生活中经常看到的影子现象。
人们对这种自然现象进行科学地抽象总结,逐步形成了用投影来表示物体形状和大小地方法,即投影法。
投影法就是投射线通过物体,向选定的平面投影,并在该平面上得到图形的方法。
如图2-1所示。
图中光源S称为投影中心,从光源发出的光线称为投射线,落影的平面H称为投影面,平面H上产生的图形称为投影。
投影线、被投射物体和投影面是形成投影的三个必要条件,缺一不可,称为投影三要素。
制图标准规定空间几何元素用大写字母表示,其投影用相应的小写字母表示。
投影和影子是有区别的,影子是漆黑一团的,只能反映物体的外形轮廓,而投影可以将组成物体的各个表面和各棱线进行完整清晰的表达。
如图2-2所示:2.1.2 投影法的分类根据投射线之间的相互位置关系不同,投影法可分为中心投影法和平行投影法两大类。
1.中心投影法所有的投射线均汇交于一点的投影法称为中心投影法。
如图2-1所示。
中心投影法主要用来画透视图。
如图2.4(a)所示。
2.平行投影法如果将投影中心移到无穷远处,从投影中心发射出的投影线可看作是相互平行的,投射线相互平行的投影法称为平行投影法。
如图2-3所示。
平行投影法主要用来画轴测图。
如图2-4(b)所示。
在平行投影法中,根据投影射线与投影面的相对位置不同,又分为正投影法和斜投影法两种。
(1)正投影法:相互平行的投射线与投影面垂直的投影法称为正投影法。
根据正投影法所画出的图形称为正投影图,简称正投影。
如图2-3(a)所示。
(2)斜投影法:相互平行的投影线与投影面倾斜的投影法称为斜投影法。
根据投影法所画出的图形称为斜投影图,简称斜投影。




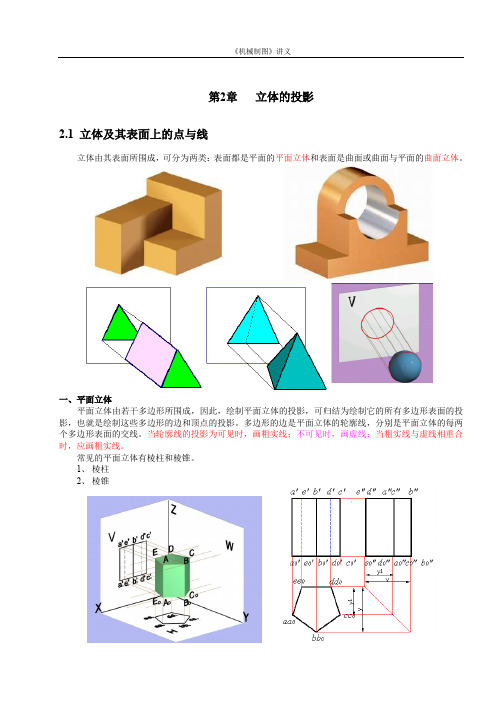
第2章立体的投影2.1 立体及其表面上的点与线立体由其表面所围成,可分为两类:表面都是平面的平面立体和表面是曲面或曲面与平面的曲面立体。
一、平面立体平面立体由若干多边形所围成,因此,绘制平面立体的投影,可归结为绘制它的所有多边形表面的投影,也就是绘制这些多边形的边和顶点的投影。
多边形的边是平面立体的轮廓线,分别是平面立体的每两个多边形表面的交线。
当轮廓线的投影为可见时,画粗实线;不可见时,画虚线;当粗实线与虚线相重合时,应画粗实线。
常见的平面立体有棱柱和棱锥。
1、棱柱2、棱锥平面立体的投影的外围轮廓总是可见的,应画粗实线;而在投影的外围轮廓内部的图线,则应根据线、面的投影分析,按前遮后、上遮下、左遮右直接判断投影的可见性,决定画粗实线或虚线,必要时还可利用交叉两直线的重影点的可见性进行判断。
二、曲面立体曲面立体由曲面或曲面与平面所围成。
有的曲面立体有轮廓线,即表面之间的交线,如圆柱;有的曲面立体有尖点,如圆锥;有的曲面立体全部由光滑的曲面所围成,如圆球。
在画曲面立体的投影时,除了画出轮廓线和尖点外,还要画出曲面投影的转向轮廓线。
曲面立体的转向轮廓线是切于曲面的诸投射线与投影面的交点的集合,也就是这些投射线所组成的平面或柱面与曲面的切线的投影,常常是曲面的可见投影和不可见投影的分界线。
曲面立体的投影就是它的所有曲面表面或曲面表面与平面表面的投影,也就是曲面立体的轮廓线、尖点的投影和曲面投影的转向轮廓线。
常见的曲面立体有圆柱、圆锥、圆球,圆环。
1、圆柱圆柱由圆柱面、顶面和底面所围成。
圆柱面由直线绕与它平行的轴线旋转而成。
因此,画圆柱的投影就是画顶面和底面及轮廓线、圆柱面投影的转向轮廓线、轴线。
当圆柱的轴线与投影面垂直时,圆柱面在轴线垂直的投影面上的投影具有积聚性。
因此,作圆柱表面2、 圆锥圆锥由圆锥面和底面所围成。
圆锥面由直线绕与它相交的轴线旋转而成。
因此,画圆锥的投影就是画尖点(即锥顶)、底面及轮廓线、圆锥面投影的转向轮廓线、轴线。



一、投影的基本知识(了解)二、工程上常用的图示法(了解)三、平行投影法的基本性质(熟悉)四、三视图的形成及其投影规律(掌握)2-1 投影的基本知识投影:用光线(灯光或阳光)照射物体时,在地面上或墙面上便产生了影子,这种现象就称为投影。
象,即把光线抽象为投射线,把物体抽象为几何形体,把地面抽象为投影面,逐步形成了投影方法。
右图中,S为投影中心,A为空间点,平面P为投影面,S与A点的连线为投射线,SA的延长线与平面P的交点a,称为A点在平面P 上的投影。
这种产生图像的方法就叫做投影法。
由空间的三维形体转变为平面二维图形就是通过投影法来实现的。
因此,投影法是整个工程图学的基础。
S 投影中心a 投影A 空间点投影面P投射线投影法投影法投影法的分类中心投影法平行投影法正投影法斜投影法画透视图画斜轴测图画工程图样及正轴测图在有限距离内,由投射中心S 发射出投射线,在投影面P 上得到物体形状的投影方法称为中心投影法。
光源SCB bcP投影特性:具有较强的直观性、较好的立体感。
中心投影法投射线aA中心投影法无法反映物体表面的真实形状和大小,投射中心、物体、投影面三者之间的相对距离对投影的大小有影响。
度量性较差。
光源SA CBabc光源S A C Ba bc P物体位置改变,投影大小也改变P当投影中心S移至无限远处时,投影线都相互平行,用这种投影法得到的图形称为平行投影法。
根据投射线于投影面所成角度的不同,平行投影法又分为正投影法和斜投影法。
正投影法斜投影法正投影法:投射线与投射面垂直,故又成为直角投影法。
斜投影法:投射线与投射面倾斜。
ABC ABC abcabcPP投射线投射线投影特性正投影法:得到的投影能够完整、真实地表达物体的形状和大小,度量方便,作图简便。
因此,在工程中得到广泛应用。
斜投影法:物体与投影面距离的远近不会影响其投影的大小,但当投影线与投影面夹角变化时,其投影大小也将发生变化。
2-2 工程上常用的图示法为满足工程设计对图样的各种不同要求,需要采用不同的图示法。

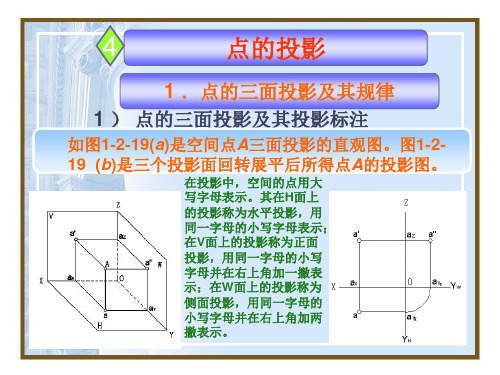
Projection of a point点的投影Relative position of two points on a solid立体上二点的相对位置Identification and labeling of coincident point重影点的判别与标注Exercises 练习题Projection of Points on a Solid立体上点的投影请点击相应标题显示其内容2WYVHxZOA Projection of a point 点的投影1. Projection of the point A 空间点A的投影请点击鼠标左键显示后面内容a —— The horizontal projection of the point A点A 在水平面 H 上的投影;a ' —— The frontal projection of the point A点A 在正平面 V 上的投影;a "—— The profile projection of the point A点A 在侧平面 W 上的投影。
a 'a " a3Z = a 'a x = a"a Yw → The distance of A to H . (A 点到水平面H 的距离)a'a"⊥OZ The height alignment , Z equal.即高平齐, Z 相等 HX O Y wY HZV WXYY Z 2. The principle of points 点的投影规律3. Relation of points projection & coordinate 点的坐标与投影的关系请点击鼠标左键显示后面内容Projection of a point 点的投影 aa' ⊥ OX The length alignment , X equal.即长对正, X 相等 aa"⊥OY The width equality , Y equal. 即宽相等, Y 相等X = a 'a z = a a Y H→ The distance of A to W . (A 点到侧平面W 的距离) Y = a a x= a"a z → The distance of A to V . (A 点到正平面V 的距离) a'aa"a x a Za Y Ha YW415105a'aa"45xzY HY wOSteps 作图步骤:(1)Drawing coordinate origin and axis. 画出坐标原点及各轴; (2)According to coordinate of point A , construct projection a',a ; 根据点A 的坐标求其V 、H 面的投影 a',a ;(3)According to rules projections of point, draw projection a". 根据点的投影规律求出第三投影 a"。
Example1. The point A (5, 10, 15) . construct three projections of A . 已知点A 的坐标为(5,10,15),求点A 的三面投影。
A请 点 击 鼠 标 左 键 显 示 后 面 内 容由于投影面的大小与视图 无关。
因此,在画三视图时, 不必画出投影面的边框。
5YZW V HVH∆Z∆Z∆Y∆Y ∆X∆XRelative position of two points 二点的相对位置Relative positions of point A & B ( A 与B 两点的相对位置)请点击鼠标左键显示后面内容Up and down → ∆Z上、下 在V 、W 面上看坐标差 ∆ZFront and back → ∆Y前、后 在H 、W 面上看坐标差 ∆YLeft and right → ∆X左、右 在V 、H 面上看坐标差 ∆Xba ' a "aBb "b 'AX6x 0 Y WY Hza'a"a下10左10后5bSteps 作图步骤:(2)Construct projection b ". 根据点的投影规律求b "。
Example2. Point B below A 10, after A 5,left A 10mm.construct projections of B . 已知B 点在A 点下面10、后面5、左面10mm 处,求B 点的三投影。
请点击鼠标左键显示后面内容AB(1)Construct projection b ',b .根据B 点的相对位置求投影b ',b 。
b'b"7Identification判别When projected to the H -Plane, up covering down.投影在H 面上重合时,上遮下(Z 坐标大的可见)。
Identification and labeling of coincident point 重影点的判别与标注请点击鼠标左键显示后面内容Labeling标注Defining 定义When two points on the solid are on the same vertical line of a projection plane, the two projectedpoints will be the same point and the two points arecalled the coincident point of the projection.当两点在某一投影面上的投影重合时称为该面的重影点。
When projected to the V -Plane, front covering back. 投影在V面上重合时,前遮后(Y 坐标大的可见)。
When projected to the W -Plane, left covering right.投影在W面上重合时,左遮右(X 坐标大的可见)。
All invisible projections of points are written in brackets. 将点在某投影面上的不可见投影加括号标注以示区别。
8b'AB 5101015 105dSteps 作图步骤:2. Construct projections D, d , d ',d "; 求D 点的三面投影d 、d '、d " 。
1. Construct projections C , c , c',c"; 求C 点的三面投影 c 、c ' 、c "。
请点击鼠标左键显示后面内容CD(c )Example3. Point C from W 5mm, from V 10mm, from H 10mm. point D from W 15mm, from V 10mm, from H 5mm.construct three projections of point C.D and distinguish its visibility. 已知C 点距W 面5mm 、距V 面10mm 、距H 面10mm, D 点距W 面15mm 、距V 面10mm 、距H 面5mm ,求C 、D 二点的三面投影,并判别其可见性。
a'a"x 0 YwY Hzb" a bc'c"d"( )d'91.Draw the third-view from its two other views shown .已知各点的两个投影,求其第三投影。
请点击题目显示其内容Exercises 练习题2. Construct the three projections of points A, B, C, D . from its coordinate and distance.根据所给定点的坐标或点到投影面的距离,画出点A 、B 、 C 、D的三面投影。
3.The point A (30,15,0). according to request draw the three projections of points A, B, C .已知A 点的坐标为(30、15、0),按要求画出点 A 、B 、C的三面投影。
4. Draw three projections of points A, B, C, D , from its coordinate.已知各点的坐标,画出点A 、B 、C 、D的三面投影。
本小节结束谢谢您的认真学习!退出前一页11b "(c ")a"a b ca" b "c "a'b 'c '1. Draw the third view from its two other views shown. 已知各点的两个投影,求其第三投影。
(1)(2)b ac a'b 'c '( )ZXY WY HZXY WY H2. Construct the three projections of points A,B,C,D. from its coordinate and distance.根据所给定的点的坐标或点到投影面的距离,画出点A、B、C、D的三面投影。
Point 点distance H距H面distance V距V面distance W距W面X Y ZA 15 10 20B 10 0 10C 15 15 0D 0 20 203. The point A (30,15,0). according to request draw the three projections of points A,B,C .已知A点的坐标为(30,15,0),按下述要求画出点A、B、C 的三面投影。
(1) B点在A点之右20mm,之前15mm,之上20mm。
C点在A点之左5mm,之后10mm,之上25mm。
(2) B点在A点之左5mm,之后5mm,之上15mm。
C点在A点之右15mm,之前10mm,之上30mm。
4.Draw three projections of points A,B,C,D from its coordinate.已知各点的坐标,求点A、B、C、D 的三面投影。