第二章立体表面交线投影2-3

(4)
a’’(b”)
AB是 侧垂 线
2-3 求作基本体表面上的点或线的其余两个投影
(1)
b’ c’
b”
a”
a c
2-3 求作基本体表面上的点或线的其余两个投影
(2)
e”
a”
d”
c” b”
e
c a
b
d
2-3 求作基本体表面上的点或线的其余两个投影
a”
(3)
f”
e”
d”
c”
b”
d f a
(b) e
内孔轮廓线应到顶。
3-14b 选择正确的第三视图（6）
（注意分析形体被切后和形体组合后的交线的投影）
3-14b 选择正确的第三视图（7）
（注意分析形体被切后和形体组合后的交线的投影）
应为相贯线
应为两内孔相贯且凸向大圆
等径时才为直线
3-14b 选择正确的第三视图（8）
（注意分析形体被切后和形体组合后的交线的投影）
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-6 补全圆锥穿孔后的水平投影和侧面投影 实线
3-6 补全圆锥穿孔后的水平投影和侧面投影
3-7 求作俯视图
3-7 求作俯视图
3-8 求作左视图
3-9 画出下列各相贯线的投影 (1)
3-9 画出下列各相贯线的投影 (2)
等径圆柱的相贯 线在V面上的投 影为两条相交的 直线
3-9 画出下列各相贯线的投影_(3)
3-9 画出下列各相贯线的投影_(4)
等径圆孔的相贯 线在侧面上的投 影为两条相交的 直线

保持物体间的相对位置关系
正投影法能够保持物体间的相对位置关系，不会改变物体的相对位 置。
易于理解和绘制
正投影法的投影面相对简单，易于理解和绘制。
立体投影图绘制方法
确定投影面和投影方向
首先确定要绘制的立体和投影面，以及投影 方向。
填充阴影
根据立体表面的光影效果，填充阴影，以增 强立体感。
绘制轮廓线
根据立体在投影面上的轮廓，绘制出轮廓线 。
虚拟现实技术在立体投影中的应用
虚拟现实技术是一种模拟真实环境的计算机技术，通过头戴式显示器等设备，使 用户沉浸在虚拟世界中。
在立体投影领域，虚拟现实技术可以用于创建逼真的立体投影效果，使用户能够 更加深入地了解和体验三维空间。
THANKS
感谢您的观看
绘制曲面立体投影图
总结词
掌握曲面立体投影图的绘制方法，包括 圆柱、圆锥和球等基本曲面的绘制技巧 。
VS
详细描述
曲面立体投影图是工程制图中另一种常见 的表达方式，主要用于表达曲面体的形态 和结构。在绘制曲面立体投影图时，需要 掌握圆柱、圆锥和球等基本曲面的绘制技 巧，以及如何将这些曲面进行组合和切割 。同时，需要注意曲面的连续性和光顺性 ，以确保投影的准确性和美观度。
绘制组合体三视图
要点一
总结词
掌握组合体三视图的绘制方法，包括组合体的构成、表达 方法和绘图步骤。
要点二
详细描述
组合体三视图是工程制图中最为复杂的一种表达方式，主 要用于表达由多个基本立体组成的复杂物体的形态和结构 。在绘制组合体三视图时，需要先对组合体的构成进行仔 细分析，选择合适的表达方法，并按照正确的绘图步骤进 行绘制。同时，需要注意各视图之间的投影关系和对应关 系，以确保三视图的一致性和完整性。

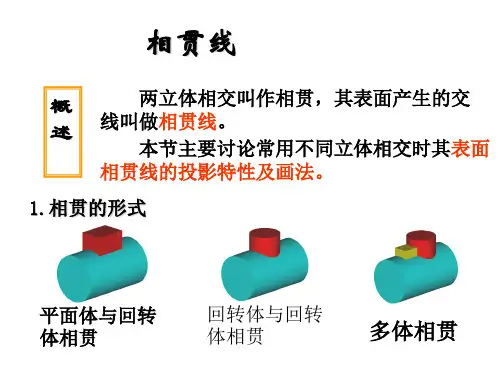
相贯线平面体与回转体相贯回转体与回转体相贯多体相贯 1.相贯的形式两立体相交叫作相贯，其表面产生的交线叫做相贯线。

本节主要讨论常用不同立体相交时其表面相贯线的投影特性及画法。

概述立体表面相交有三种形式,一种是立体的外表面相交;一种是外表面与内表面相交;一种是内表面与内表面相交.相贯线实实相贯实虚相贯虚虚相贯2.相贯线的主要性质★表面性相贯线位于两立体的表面上。

★封闭性相贯线一般是封闭的空间折线（通常由直线和曲线组成）或空间曲线。

★共有性相贯线是两立体表面的共有线。

其作图实质是找出相贯的两立体表面的若干共有点的投影。

二、平面体与回转体相贯1.相贯线的性质相贯线是由若干段平面曲线(或直线)所组成的空间折线，每一段是平面体的棱面与回转体表面的交线。

2.作图方法求交线的实质是求各棱面与回转面的截交线。

•分析各棱面与回转体表面的相对位置，从而确定交线的形状。

•求出各棱面与回转体表面的截交线。

•连接各段交线，并判断可见性。

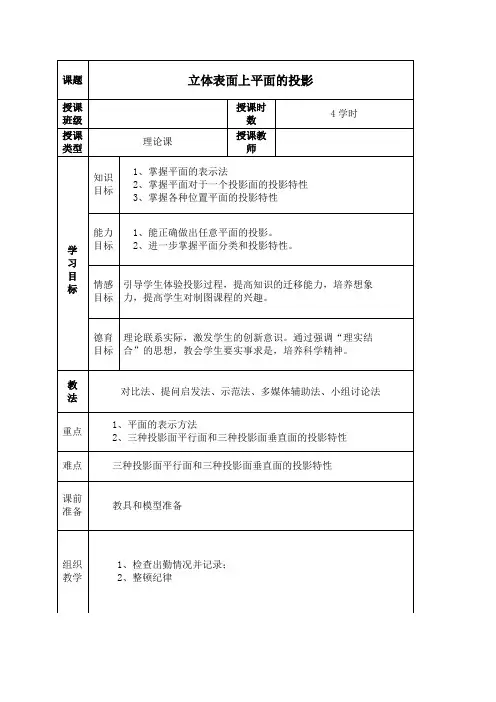
例1：补全主视图空间分析：四棱柱的四个棱面分别与圆柱面相交，前后两棱面与圆柱轴线平行，截交线为两段直线；左右两棱面与圆柱轴线垂直，截交线为两段圆弧。

投影分析：由于相贯线是两立体表面的共有线，所以相贯线的侧面投影积聚在一段圆弧上，水平投影积聚在矩形上。

例2：求作主视图三、回转体与回转体相贯1. 相贯线的性质相贯线一般为光滑封闭的空间曲线，它是两回转体表面的共有线。

2.作图方法•表面取点法利用投影的积聚性直接找点。

•辅助平面法一般是根据立体或给出的投影，分析两回转面的形状、大小及其轴线的相对位置，判断相贯线的形状特点和各投影的特点，从而选择适当的方法作图。

•先找特殊点。

⒊作图过程•补充中间点。

确定交线的弯曲趋势确定交线的范围如果两回转体相交，其中有一个是轴线垂直于投影面的圆柱，则相贯线在该投影面上的投影积聚在圆柱面上。

利用回转体表面取点的方法可以作出相贯线的其余投影。

按已知曲面立体表面上点的投影求其它投影的方法，称为表面取点法。

真实性
积聚性：当一线段与投影面垂直时，其正投影积聚为一
点；当一平面图形与投影面垂直时，其正投影积聚为 一直线。
积聚性
类似性：当一线段与投影面倾斜时，其正投影为缩短
的线段； 当一平面图形与投影面倾斜时，其正投影 为缩小的类似图形。
类似性
§2-2 三视图的形成及其对应关系
根据国标规定，用正投影法绘制出物体的图形称为视图。 下图表示的是三个不同形体，在一个投影面上的视图却是完 全相同的。
1、主视图—从前向后投射，在V 面上所得的视图。
2、俯视图—从上向下投射，在H 面上所得的视图。
3、左视图—从左向右投射，在W 面上所得的视图。
三视图的形成
三投影面的展开
V面保持不动，H面绕OX轴向下旋转90°，W面绕 OZ轴向右旋转90°，这样V、H和W三个投影面就摊 平在了同一平面上。
水 平 投 影 面 和侧立投影 面旋转后，OY轴被分成两 条，分别用OYh和OYw 表 示 。
注意：
要细心，不要把点对错了。
§2-4 直线的投影
二、各种位置直线的投影
根据直线在三投影面体系中对投影面的相对位置不同，将
直线分为：
投影面平行线 投影面垂直线
特殊位置直线
投影面倾斜线
一般位置直线
1、一般位置直线 定义：与三个投影面均成倾斜的直线
直线与 H、V、W 投影面的倾角分别用 α、β、γ表示，见图 中的标注。
即 ac:cb=a'c':c'b'=a''c'':c''b''=k
例: 判断图中点是否在直线上。
作图分析： ⑴由于AB直线为一般位置。而给出 的C点的两投影分别在AB线的同面投 影上，故可认定C点从属于AB直线。

a
定比作图方法
c
b
§2－2 直线的投影
例2 已知点C在线段AB上，求点C的正面投影。
b Z
b
V
b
c a C B
X
A
O
a
X
a
a
O
a
c YW
a
c Hb
c b
YH
§2－2 直线的投影
例3. 在直线AB上取一点C, 使AC = L，求点C的两投影。
b c
a
L
b c
a
a
X
a
b
L
c
ZAB
O
b
c
ZAB
b0
L
c0
平面对 投影面的倾 角、、
二、各种位置平面的投影特性
§2－3 平面的投影
投影面垂直面： 垂直于一个、倾斜 于另两个投影面的 平面
V面—正垂面 H面—铅垂面 W面—侧垂面
特殊位 置平面
投影面平行面： 平行于一个、同时 垂直于另两个投影 面的平面
V面—正平面 H面—水平面 W面—侧平面
投影面倾斜面： 对三个投影面都倾 斜的平面
c b
X
b O c
YW
当两直线均为
b
一般位置直线时， c
若有两个同面投影 满足上述条件，则 空间两直线相交。
d
a
YH
§2－2 直线的投影
3. 交叉两直线
既不平行又不相交的两直线
b
1(2 )
d
c
a
Ⅱ
2 Ⅰd
c
b
a1
b d
1(2 )
c
X a
O
d
c
a

的美感和特色。
立体雕塑造型
在立体雕塑造型中，交线用于表 现雕塑的轮廓和形态，强调雕塑
的立体感和空间感。
室内装饰设计
在室内装饰设计中，交线可以用 于表现墙面的纹理、图案和装饰 线条，提升室内设计的艺术感和
质感。
机械零件的加工和制造中的交线处理
1 2 3
零件加工指导
在机械零件的加工过程中，交线可以用于指导工 人进行切割、磨削、钻孔等操作，确保零件的精 确度和质量。
在工程设计和制造中，交线是 确定物体表面形状和尺寸的关 键参数，对于产品性能和制造 精度具有重要影响。
02 平面与立体表面的交线
平面与平面立体的交线
当平面与平面立体相交时，其交 线是平面与平面的交线，即一条
或多条直线。
交线的位置和数量取决于平面的 位置和方向，以及平面立体的形
状。
例如，一个长方体和一个正方形 的平面相交，其交线是四条相等
的直线段。
平面与曲面立体的交线
当平面与曲面立体相交时，其交线是 平面与曲面的交线，即一条或多条曲 线。
Hale Waihona Puke 例如，一个球体和一个圆形的平面相 交，其交线是一个圆弧。
交线的形状取决于平面的位置和方向， 以及曲面立体的形状。
特殊情况：平面与平面重合或平行
01
当平面与平面重合时，它们的交 线是一条无穷长的直线。
特殊情况：曲面与曲面重合或平行
当两个曲面完全重合或平行时，它们之间没有交线。
在这种情况下，两个曲面共享相同的几何特性，如形状、大小和方向等。
重合或平行的曲面在几何学中通常被视为同一个曲面，因此它们的交线 不存在。
04 立体表面交线的应用
工程制图中的交线绘制
确定立体形状

由于棱
锥体的棱面 无积聚性， 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影，并作出表面上各点的三面投影。
（1
）
a'
a"
b'
(b")
(b) a
回转体表面取点， 根据已知点的可见性 判断点所处的位置， 按投影关系，找出各 点的投影。
（2 ）
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性，利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性，表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
（3 ）
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性，表 面上取点利用辅助
纬圆法。
（4 ）

一、 棱柱
直棱柱---顶面和底面是两个全等且相互平行的多边形 （特征面），各侧面为矩形。 正棱柱----顶面和底面为正多边形的直棱柱。
1. 棱柱的投影
1. 棱柱的投影
分析:正六棱柱由顶面、底面和六个侧棱面组成。正六棱
柱的顶面、底面为水平面，在俯视图中反映实形。 作图:
(a) 直观图 图2-2 正六棱柱的投影
s'
m
Z
作图方法2
注意： 分清直线所在表面， 求出与所有棱线的交点。
s' c' S s"
m m
s"
m
a'
b'
M
A X B a
m
C O
a" (c")
a'
a
m
b'
c'
c
a" (c")
b"
b"
s
s b
c
b
(b) 投影图
(a) 直观图
3. 棱锥台
棱锥台---由平行于棱底的平面截去锥顶一部分形成 的立体,顶面与底面是相互平行的相似多边形,各侧面 为等腰梯形。 正棱锥台----由正棱锥截得的棱台。 四棱锥台的投影图
回 目 录
概述:
立体包含基本立体和组合体。柱、锥、球、圆环等 几何体是组成机件的基本体，基本体的组合称组合体，本 章着重研究基本体、切割体和相贯体的形体特征，立体的 投影与作图方法，在立体表面上作点、作线的方法与三视 图的画法。
§2-3
平面立体
§2-3 切割体的投影 §2-5 回转体 §2-5 相贯体的投影
截平面
截断面
截交线

X
后 前
a (a1)
c (c1 )
b (b1)
左
右
YH
1、度量关系：长对正、高平齐、宽相等。 2、位置关系：如图。
六棱 柱
空间分析
V YW
W
作图时，先画反映特征的水平投影，再 按投影规律完成其它两个投影。
a’’
六棱柱表面求点？
( b’ ) a’
b’’
b’’
b
作图分析:
b
a
(1) 由于前棱面的水平投影和侧面投影均具有积聚性,故可直接 求出a和a``。 (2) 由于左前棱面只有水平投影有积聚性,故只能利用积聚性 求出b,再根据YH=YW,由b和b`求出b``。
一、利用积聚性求相贯线
柱柱相贯 两圆柱的轴线分别垂直于不同的投影面时，相交的两圆 柱的表面相对于投影面有积聚性。
我们只讨论: 两轴线垂直相交的两圆柱的相贯线.
例24. 试求两轴线垂直相交圆柱相贯线的投影。
分析：两个圆柱体的圆柱面 分别在俯视图和左视图上具 有积聚性，因此，它们的相 贯线投影也分别处于这两个 积聚圆上，找出这两个投影， 其主视图投影就很容易求出 了。
第三章
基本立体及其表面交线的投影
§3.1 平面立体的投影 §3.2 曲面立体的投影
§3.3 平面立体的截交线
§3.4 回转体的截交线
§3.5 回转体的相贯线
常 见 的 基 本 立 体
平 面 平面+平面 立 体
棱柱
棱锥
圆柱 曲 面 立 体
曲面+平面
圆锥
曲面+曲面
圆球
圆环
画立体的投影图时，规定： 可见的轮廓线画粗实线, 不可见的轮廓线画细虚线。

第三节
基本体的视图与尺寸标注
图 房屋形体的分析
水塔形体分析
棱柱
棱锥 圆柱 圆锥 球
基本体的三视图
常见的基本几何体 平面 基本体
基本体是由各种面围成的。
曲面 基本体
平面立体的投影实质是关于其表面上点、线、面
投影的集合，且以棱边的投影为主要特征，对于可
见的轮廓线，其投影以粗实线表示，不可见的轮廓 线，则以虚线表示。在投影图中，当多种图线发生
重叠时，应以粗实线、虚线、点画线等顺序优先绘
制。
长
高
Z
宽 高
X
O 宽
YW 长
三视图对应关系为： 主、俯视图长相等（简称长对正）
YH
主、左视图高相等（简称高平齐）
俯、左视图宽相等且前后对应(宽相等）
棱柱
1、 棱柱的组成
由两个底面和几个侧棱面 组成。侧棱面与侧棱面的交线 叫侧棱线，侧棱线相互平行。 如图,为一正六棱柱，其顶 面、底面均为水平面，它们的 水平投影反映实形，正面及侧 面投影积聚为一直线。
1
a’ a
b’ b
a”(b”)
求出Ⅰ点的水平投 c” 影1。
msBiblioteka 过1作1m ∥ac，再 根据点在直线上的几 何条件，求出m 。
再根据知二求三的 方法，求出m”。（具 体步骤略)
c
正三棱锥的三面投影图
三棱锥表面上取点N
n n N
n
三棱锥表面上取点K
（k）
k
K
k
曲面立体
1、圆柱的投影
如图所示，圆柱的 轴线垂直于H面，其上 下底圆为水平面，水 平投影反映实形，其 正面和侧面投影重影 为一直线。
截交线的三视图（平行底面）

）两个投影均为类似形；任务分析平面投影的实质，就是平面形各顶点的同面投影依次连线。

各种位置平面的投影，讲解重点放在投影特性和有无实形的判断上；对于每一种位置平面形的投影，重点讲解其中的一种类型。

学习内容学生活动 教师活动考评 任务实施（一）平面对于一个投影面的投影特性空间平面相对于一个投影面的位置有平行、垂直、倾斜三种，三种位置有不同的投影特性。

1、真实性 当平面与投影面平行时，则平面的投影为实形。

2、积聚性 当平面与投影面垂直时，则平面的投影积聚成一条直线。

3、类似性 当直线或平面与投影面倾斜时，则平面的投影是小于平面实形的类似形，如图所示。

（二）各种位置平面的投影特性根据平面在三投影面体系中的位置可分为投影面倾斜面、投影面平行面、投影面垂直面三类。

前一类平面称为一般位置平面，后两类平面称为特殊位置平面。

1、投影面垂直面垂直于一个投影面且同时倾斜于另外两个投影面的平面称为投影面垂直面。

垂直于V 面的称为正垂面；垂直于H 面的称为铅垂面；垂直于W 面的称为侧垂面。

平面与投影面所夹的角度称为平面对投影面的倾角。

α、β、γ分别表示平面对H 面、V 面、W 面的倾角。

举例说明：铅垂面的投影特性1、认真听讲、理解任务的内容，对不清楚地方提出疑问。

1、老师讲课，提出问题，引导学生自主观察、认识。

1、以提问的方式观察学生的认识情况并打分。

任务实施强调：（1）两个投影均为类似形；（2）一个投影积聚为直线，并反映β、γ角。

总结投影面平行线的投影特性：两面一线。

要求学生必须掌握表2－3中的图例。

对于投影面垂直面的辨认：如果空间平面在某一投影面上的投影积聚为一条与投影轴倾斜的直线，则此平面垂直于该投影面。

讲解例题（例2－9） 如图2－39（a ）所示，四边形ABCD 垂直于V 面，已知H 面的投影abcd 及B 点的V 面投影b ′，且于H 面的倾角α= 45°，求作该平面的V 面和W 面投影。

（a ）题目 （b ）解答图2－40 求作四边形平面ABCD 的投影2、投影面平行面平行于一个投影面且同时垂直于另外两个投影面的平面称为投影面平行面。

三、正投影的基本性质
A BC
E
当空间直线或平面平行于投影面时， D 其投影反映直线的实长或平面的实形，
1.实形性
这种投影性质称为实形性。
a
b
e c d
H
目录
常德职业技术学院机械制图课程组
机械制图—第二章投影法的基本知识及三视图
三、正投影的基本性质
A C
E

2.积聚性
当直线或平面垂直于投影面时， B D 其投影积聚为一点或一条直线，这 种投影性质称为积聚性。
目录
常德职业技术学院机械制图课程组
机械制图—第二章投影法的基本知识及三视图
§2-1 投影法的基本知识
教学目标 1.了解投影法的基本概念和分类, 2.掌握正投影的基本性质。
常德职业技术学院机械制图课程组
机械制图—第二章投影法的基本知识及三视图
§2-1 投影法的基本知识
一、投影法的概念 日常生活中，当光线照射物体就会在地面上产生影子，这 就是投影现象。 实现投影的三个要素： 1.光线 —— 制图上称为投射线 2.承影面 —— 制图上称为投影面 3.物体 投影法：投射线经过物体向投影 面投射，在该面上得到图形的方 法。
宽
机械制图—第二章投影法的基本知识及三视图
1.三视图的度量对应关系
高
高
宽
长
宽
长
宽
总体三等
宽
局部三等 三等关系

V面、H面（主、俯视图）——长对正。 V面、W面（主、左视图）——高平齐。
H面、W面（俯、左视图）——宽相等。
常德职业技术学院机械制图课程组
机械制图—第二章投影法的基本知识及三视图
机械制图—第二章投影法的基本知识及三视图

一、投影的基本知识（了解）二、工程上常用的图示法（了解）三、平行投影法的基本性质（熟悉）四、三视图的形成及其投影规律（掌握）2-1 投影的基本知识投影：用光线（灯光或阳光）照射物体时，在地面上或墙面上便产生了影子，这种现象就称为投影。

象，即把光线抽象为投射线，把物体抽象为几何形体，把地面抽象为投影面，逐步形成了投影方法。

右图中，S为投影中心，A为空间点，平面P为投影面，S与A点的连线为投射线，SA的延长线与平面P的交点a，称为A点在平面P 上的投影。

这种产生图像的方法就叫做投影法。

由空间的三维形体转变为平面二维图形就是通过投影法来实现的。

因此，投影法是整个工程图学的基础。

S 投影中心a 投影A 空间点投影面P投射线投影法投影法投影法的分类中心投影法平行投影法正投影法斜投影法画透视图画斜轴测图画工程图样及正轴测图在有限距离内，由投射中心S 发射出投射线，在投影面P 上得到物体形状的投影方法称为中心投影法。

光源SCB bcP投影特性：具有较强的直观性、较好的立体感。

中心投影法投射线aA中心投影法无法反映物体表面的真实形状和大小，投射中心、物体、投影面三者之间的相对距离对投影的大小有影响。

度量性较差。

光源SA CBabc光源S A C Ba bc P物体位置改变，投影大小也改变P当投影中心S移至无限远处时，投影线都相互平行，用这种投影法得到的图形称为平行投影法。

根据投射线于投影面所成角度的不同，平行投影法又分为正投影法和斜投影法。

正投影法斜投影法正投影法：投射线与投射面垂直，故又成为直角投影法。

斜投影法：投射线与投射面倾斜。

ABC ABC abcabcPP投射线投射线投影特性正投影法：得到的投影能够完整、真实地表达物体的形状和大小，度量方便，作图简便。

因此，在工程中得到广泛应用。

斜投影法：物体与投影面距离的远近不会影响其投影的大小，但当投影线与投影面夹角变化时，其投影大小也将发生变化。

2-2 工程上常用的图示法为满足工程设计对图样的各种不同要求，需要采用不同的图示法。

直线平行于投影面 投影反映线段实长
直线倾斜于投影面 投影比空间线段短 投影不反映线段实长
ab=AB
ab=AB*cos
⒉ 直线在三个投影面中的投影特性
其投影特性取决于直线与三个投 影面间的相对位置。
正平线（平行于Ｖ面） 平行于某一投影面而 侧平线（平行于Ｗ面） 与其余两投影面倾斜 投影面平行线 水平线（平行于Ｈ面) 统称特殊位置直线 垂直于某一投影面 正垂线（垂直于Ｖ面） 投影面垂直线 侧垂线（垂直于Ｗ面） 铅垂线（垂直于Ｈ面）
a
X Z
a b
YW
b a(b)
●
YH
投影特性:
AB⊥ H
1. 在其垂直的H投影面 上， 投影有积聚性。 2. 另外两个投影，反映线 段实长，且垂直 于相应 的投影轴。
——正垂线
a(c)
●
Z
c
a
YW
X
O
c a
YH
投影特性:
AB⊥V
1. 在其垂直的V投影面 上， 投影有积聚性。 2. 另外两个投影，反映线 段实长，且垂直 于相应 的投影轴。
(1)
a
X
b
Z
d a O c
b d
YW
c c b a d
X
a
AB与CD平行。 对于一般位置直 线，只要有两组同面 投影互相平行，空间 两直线就平行。
(2) c
d Z YH c a
O
AB与CD不平行。
YW
b b
b
d
c d a
对于特殊位置直 线，只有两组同面投 影互相平行，空间直 线不一定平行。
d' d
o b
41
(1)
a' b'