2017届四川省高三“联测促改”活动理科数学试题及答案

四川省2017年高考理科数学试题及答案（考试时间:120分钟 试卷满分：150分）一、选择题：本大题共12小题,每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

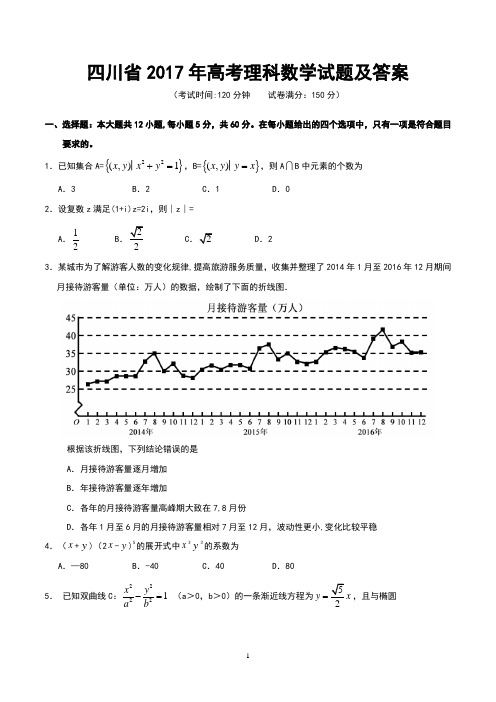
1．已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A B 中元素的个数为A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z=2i ，则∣z ∣= A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律,提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小,变化比较平稳 4．（x +y )（2x -y )5的展开式中x 3y 3的系数为A ．—80B ．-40C ．40D ．805． 已知双曲线C ：22221x y a b-= （a ＞0，b ＞0）的一条渐近线方程为5y x =，且与椭圆221123x y += 有公共焦点，则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f(x ）=cos （x+3π），则下列结论错误的是 A ．f （x)的一个周期为−2πB ．y=f （x ）的图像关于直线x=83π对称 C ．f （x+π)的一个零点为x=6πD ．f （x ）在(2π，π)单调递减 7．执行下面的程序框图,为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为 A ．—24B ．-3C ．3D ．810．已知椭圆C:22221x y a b+=，（a 〉b 〉0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A ．63B ．33C ．23D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a=A ．12-B ．13C ．12D ．112．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λ AB +μAD ，则λ+μ的最大值为A．3 B．CD．2二、填空题:本题共4小题，每小题5分,共20分。

南充市高2017届第三次高考适应性考试数学试题（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合(){}01,2121≤-=⎭⎬⎫⎩⎨⎧<><-=x x x N x x M ,则N M 等于（ ） A ．⎪⎭⎫⎢⎣⎡21,0 B ．⎥⎦⎤ ⎝⎛-1,21 C ．⎪⎭⎫⎢⎣⎡-21,1 D ．⎥⎦⎤⎝⎛-0,21 2.若iz 215+=,则z 的共轭复数为（ ） A ．i 21- B ．i 21+ C ．i 21-- D ．i 21+- 3.若角α的终边经过点()4,30--P ,则=αtan （ ）A ．34 B ．43 C ．54- D ．53- 4. 若某程序框图如图所示，则输出的p 值是（ ）A ．49B ．36 C.25 D ．165.下表提供了某厂节能降耗技术改造后再生产A 产品过程中记录的产量x （吨）与相应的生产能耗y （吨）的几组对应数据根据上表提供的数据，求出y 关于x 的线性回归方程为ˆ0.70.35yx =+那么表中t 的值为（ ） A ．3 B ．15.3 C. 5.3 D ．5.46.已知()()(]()3,,1,,1,x a x x f x a x ⎧-∈-∞⎪=⎨∈+∞⎪⎩是()+∞∞-,上的增函数，那么a 的取值范围是（ ）A ．()3,0B ．()3,1 C. ()+∞,1 D ．⎪⎭⎫⎢⎣⎡3,237.《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等，问各得几何？”其意思为：“已知甲，乙，丙，丁，戊五人分五钱，甲，乙两人所得与丙，丁，戊三人所得相同，且甲，乙，丙，丁，戊所得依次成等差数列，问五人各得多少钱？”（“钱”是古代的一种重量单位），这个问题中，甲所得为（ ） A ．45钱 B ．35钱 C.23钱 D ．34钱 8.已知向量()(),1,2,a x z b y z =-=+，且a b ⊥，若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥≤-+≥-0070x y x x y ，则z 的最大值为（ ） A ．221B ． 7 C. 14 D ．21 9. 如图，正方形ABCD 的边长为O ,2为AD 的中点，射线OP 从OA 出发，绕着点O 顺时针方向旋转至OD ,在旋转的过程中，记AOP ∠为[]()OP x x ,,0π∈所经过的在正方形ABCD 内的区域（阴影部分）的面积()x f S =，那么对于函数()x f 有以下三个结论，其中不正确的是（ ）①;233=⎪⎭⎫⎝⎛πf ②函数()x f 在⎪⎭⎫ ⎝⎛ππ,2上为减函数；③任意⎥⎦⎤⎢⎣⎡∈2,0πx 都有()()4=-+x f x f πA ．①B ．③ C.② D ．①②③10.某几何体的三视图如图所示，若该几何体的顶点都在球O 的表面上，则球O 的体积是A ．π661 B ．π2461 C. π26161⋅ D ．π66161 11. 如图，过抛物线()022>=p py x 的焦点F 的直线l 交抛物线于B A ,两点，交其准线于点C ,若BF BC 2=,且224+=AF ,则p 等于（）A ． 1B ．2 C.25D ．3 12.设函数()x f y =在R 上有定义，对于任一给定的正数t ，定义函数()()t f x f x t⎧⎪=⎨⎪⎩ ()()f x tf x t ≤> ，则称函数()t f x 为()f x 的“t 界函数”，若给定函数()221,2f x x x t =--=，则下列结论不正确的是（ ）A ．()()00t t f f f f =⎡⎤⎡⎤⎣⎦⎣⎦B ．()()22t t f f f f =⎡⎤⎡⎤⎣⎦⎣⎦ C.()()11t t f f f f =⎡⎤⎡⎤⎣⎦⎣⎦ D ．()()33t t f f f f =⎡⎤⎡⎤⎣⎦⎣⎦第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若nx x ⎪⎭⎫ ⎝⎛-1的二项展开式中各项的二项式系数的和是64,则=n ．14.已知圆的方程是122=+y x ，则经过圆上一点⎪⎪⎭⎫⎝⎛22,22M 的切线方程是 ． 15.已知数列{}n a 满足132n n a a +=+，若首项12a =，则数列{}n a 的前n 项和=n S ． 16.设()x f 是定义在R 上的偶函数，对任意的R x ∈,都有()()22+=-x f x f ,且当[]0,2-∈x 时()121-⎪⎭⎫⎝⎛=xx f ,若关于x 的方程()()()102log >=+-a x x f a 在区间[]6,2-内恰有三个不同的实根，则实数a 的取值范围是 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知在ABC ∆中，角C B A ,,所对的边分别为,,,c b a 已知.cos cos 2C A c c α=- （Ⅰ）求cb的值 （Ⅱ）若3,12=+=+αc b ,求ABC ∆的面积.S18.某市举行“中学生诗词大赛”海选，规定：成绩大于或等于90分的具有参赛资格，某校有800名学生参加了海选，所有学生的成绩均在区间[]150,30内，其频率分布直方图如图：（Ⅰ）求获得参赛资格的人数；（Ⅱ）若大赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者即答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为91，求甲在初赛中答题个数X 的分布列及数学期望().X E 19.如图，已知PD 垂直于以AB 为直径的圆O 所在平面，点D 在线段AB 上，点C 为圆O 上一点，且.22,3====AD AC PD BD(Ⅰ) 求证：;CD PA ⊥ (Ⅱ) 求二面角A PBC --余弦值.20. 已知椭圆1C 的中心为原点O ，离心率22=e ,其中一个焦点的坐标为().0,2- （Ⅰ）求椭圆1C 的标准方程；（Ⅱ）当点(),Q u v 在椭圆1C 上运动时，设动点(2,)P v u u v -+的运动轨迹为2C 若点T 满足:,2++=其中N M ,是2C 上的点.直线ON OM ,的斜率之积为21-,试说明:是否存在两个定点21,F F ,使得21TF TF +为定值?若存在,求21,F F 的坐标；若不存在，说明理由.21.已知函数()()()e x f x f e x f x-'+-=0212(e 是自然对数的底数,()0f '是函数()x f 在0=x 的导数).(Ⅰ)求函数()x f 在()()1,1f 处的切线方程； （Ⅱ）若()1232+-=x x x g ，解关于x 的不等式()()x g e x f ≥+ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系,已知直线l 与椭圆C 的极坐标方程分别为.sin 4cos 4,023sin 2cos 222θθρθρθρ+==++(Ⅰ)求直线l 与椭圆C 的直角坐标方程；（Ⅱ）若P 是直线l 上的动点，Q 是椭圆C 上的动点，求PQ 的最小值. 23.选修4-5：不等式选讲已知函数()().4,3m x x g x x f ++-=-=(Ⅰ)已知常数2,a <解关于x 的不等式()20f x a +->；（Ⅱ）若函数()x f 的图象恒在函数()x g 图象的上方，求实数m 的取值范围.试卷答案一、选择题1-5:BBACA 6-10:DDACD 11、12：BC二、填空题13.6 14. 02=-+y x 15.n S n n --=+2331 16.()2,43三、解答题17.解：（Ⅰ）因为,cos cos 2C A c c α=-所以.cos cos 2C A c c α+= 所以()C A C A A C C +=+=sin cos sin cos sin sin 2 又B C A -=+π 故B C sin sin 2= 故2sin sin =C B ,由正弦定理可得2=cb(Ⅱ)由（Ⅰ）可得c b 2=，联立⎪⎩⎪⎨⎧=+=+cb c b 212解得1,2==c b由222312a c b ==+=+，得ABC ∆为直角三角形 所以22122121=⨯⨯==bc S 18.解：（Ⅰ）由题意知[)110,90之间的频率为(),3.00125.020075.0005.00025.0201=+⨯++⨯- ()65.0200050.00125.03.0=⨯++ 故获得参赛资格的人数为52065.0800=⨯ （Ⅱ）设甲答对每一个问题的概率为P ,则()9112=-p 解得32=P 甲在初赛中答题个数X 的所有值为.5,4,3(),313132333=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==X P();27103132313231324223223=⨯⨯⎪⎭⎫ ⎝⎛+⨯⨯⎪⎭⎫ ⎝⎛==C C X P().278313252224=⎪⎭⎫⎝⎛⨯⎪⎭⎫ ⎝⎛==C X P故X 的分布列为数学期望().27107278527104313=⨯+⨯+⨯=X E 19.解：（Ⅰ）证明：由,1,3==AD BD 知,2,4==AO AB 点D 为AO 的中点， 连接OC ,因为,2===OC AC AO 所以AOC ∆为等边三角形又点D 为AO 的中点，所以,AO CD ⊥ 因为⊥PD 平面⊂CD ABC ,平面,ABC 所以,CD PD ⊥又⊂=PD D AO PD , 平面⊂AO PAB ,平面,PAB 所以⊥CD 平面PAB ,又⊂PA 平面PAB , 所以.CD PA ⊥（Ⅱ）由（Ⅰ）可知，DP DB DC ,,三线两两垂直，以D 为原点，以DP DB DC ,,所在的直线分别为x 轴，y 轴,z 轴建立空间直角坐标系，则()()(),0,3,0,0,0,3,3,3,0B C P所以()()3,3,0,0,3,3-=-=设平面PBA 与平面CPB 的法向量分别为12,,n n 显然平面PBA 的一个法向量为()11,0,0.n = 设()2,,n x y z =,由0,022=⋅=⋅n n 得⎩⎨⎧=-=-033033z y y x 解得⎩⎨⎧==zy y x 3令1=y则()23,1,1n =所以1212123cos ,15n n nn n n⋅<>===⨯所以，二面角APB C --.20.解: (Ⅰ)由题意知,c e c a === 所以 2.a =所以2222222,b a c =-=-=故椭圆1C 的方程为.12422=+y x (Ⅱ)设()()()()n m T y x P y x N y x M ,,,,,,,2211则()()12,231,3u y x x u y u x y ννν⎧=-⎪=-⎧⎪⇒⎨⎨=+⎩⎪=+⎪⎩因为点(),Q u ν在椭圆1C 上运动，所以()()2222221112242124233u y x x y x y ν⎡⎤⎡⎤+=⇒-++=⇒+=⎢⎥⎢⎥⎣⎦⎣⎦故动点P 的轨迹2C 的方程为12222=+y x由++=2得()()()()(),2,2,,2,,212122111212y y x x y x y x y y x x n m ++=++--=21212,2y y n x x m +=+=设ON OM k k ,分别为直线ON OM ,的斜率，由已知条件知212121-==⋅x x y y k k ON OM 所以022121=+y y x x 因为点N M ,在椭圆2C 上， 所以,122,12222222121=+=+y x y x故()()21222121222122442442y y y y x x x x n m +++++=+()()()6024242212122222121=+++++=y y x x y x y x从而知T 点是椭圆1306022=+y x 上的点， 所以，存在两个定点,,21F F 且为椭圆1306022=+y x 的两个焦点，使得21TF TF +为定值.其坐标分别为()()0,30,0,30-21.解：（Ⅰ）由()()()e x f x f e x f x -'+-=0212得 ()()()0212f x f e x f x '+-=' 所以()()0210f f '+='得()10-='f()(),212e x x f e x f x ---=又()()e f e f ---=211得(),11-=f所以(),12121e e f =⨯-⨯+='所以函数()x f 在()()1,1f 处的切线方程为()11-=+x e y 即01=---e y ex（Ⅱ）由（Ⅰ）知(),22e x x e x f x --+=所以()()x g e x f ≥+等价于,01212≥---x x e x 令(),1212---=x x e x h x 则().1--='x e x h x 令()()x h x '=ϕ则()1x x e ϕ'=- 当0>x 时，()()x x ϕϕ,0>'单调递增当0<x 时，()()x x ϕϕ,0<'单调递减，所以()()00x φφ≥=，即()0≥'x h 恒成立. 所以()1212---=x x e x h x 在定义域内单调递增. 又()00=h当0≥x 时，()01212≥---=x x e x h x ，当0<x 时，().01212<---=x x e x h x 所以()01212≥---=x x e x h x 的解集为[)+∞,0 22.解：（Ⅰ）,0232023sin 2cos =++⇒=++y x θρθρ及直线l 的直角坐标方程为0232=++y x,444sin 4cos sin 4cos 4222222222=+⇒=+⇒+=y x θρθρθθρ 即椭圆的直角坐标方程为1422=+y x （Ⅱ）因为椭圆14:22=+y x C 的参数方程为⎩⎨⎧==ααsin cos 2y x （α为参数） 所以可设().sin ,cos 2ααQ 因此点到直线的距离5234sin 222123sin 2cos 222+⎪⎭⎫ ⎝⎛+=+++=παααd 所以当z k k ∈+=,452ππα时，d 取最小值510， 所以PQ 的最小值为51023.解：（Ⅰ）由()20f x a +->得()32,2x a a ->-<所以32x a ->-或3 2.x a -<-所以5x a >-或1x a <+故不等式解集为()(),15,.a a -∞+-+∞（Ⅱ）因为函数()x f 的图像恒在函数()x g 图像的上方，所以()()x g x f >恒成立， 则43++-<x x m 恒成立， 因为()()74343=+--≥++-x x x x所以m 的取值范围是()7,∞-。

成都市9校2017届高三第四次联合模拟理科数学试卷 考试时间共120分钟，满分150分试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题） 注意事项：1.答题前，考生务必在答题卡上将自己的姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚，考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。

2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上，如需改动，用橡皮擦擦干净后再填涂其它答案；非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答，超出答题区域答题的答案无效；在草稿纸上、试卷上答题无效。

3.考试结束后由监考老师将答题卡收回。

第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设集合{}2230A x x x =--<,{}ln(2)B x y x ==-,则A B =A ．{}13x x -<< B ．{}12x x -<<C ．{}32x x -<<D ．{}12x x << 2．已知212zi i =++，则复数5z +的实部与虚部的和为A ．10B ．10-C ．0D ．5-3．右侧程序框图所示的算法来自于《九章算术》.若输入a 的值 为16，b 的值为24，则执行该程序框图输出的结果为 A ．6B ．7C ．8D ．94．广告投入对商品的销售额有较大影响．某电商对连续5个年度的广告费和销售额进行统计，得到统计数据如下表（单位：万元）由上表可得回归方程为10.2y x a =+，据此模型，预测广告费为10万元时的销售额约为A ．101.2B ．108.8C ．118.2D ．111.25．设0.32a =，20.3b =，()2log 0.3(1)x c x x =+>，则,,a b c 的大小关系是A ．a b c <<B ．b a c <<C ．c b a <<D ．b c a <<（第3题图）6．某公司有五个不同部门，现有4名在校大学生来该公司实习，要求安排到该公司的两个部门，且每部门安排两名，则不同的安排方案种数为 A ．60 B ．40 C ．120 D ．2407．如图为某几何体的三视图，则该几何体的外接球的表面积为A ．π227B ．π327C ．π27D ．π23278．设等差数列{}n a 满足15853a a =，且01>a ，n S 为其前n 项和，则数列{}n S 的最大项为 A ．23S B ．25S C ．24SD ．26S9．已知变量,x y 满足约束条件6,32,1,x y x y x +≤⎧⎪-≤-⎨⎪≥⎩若目标函数(0,0)z ax by a b =+>>的最小值为2，则13a b +的最小值为 A．B ．C． D．10．已知1()sin(2)2f x A x ϕ=+-（0A >，02πϕ<<）的图象在y 轴上的截距为，且()()6f x f x π=-+，若对于任意的0,2x π⎡⎤∈⎢⎥⎣⎦，都有23()m m f x -≤，则实数m 的取值范围为A ．31,2⎡⎤⎢⎥⎣⎦B ．[]1,2C ．3,22⎡⎤⎢⎥⎣⎦ D． 11．如图所示点F 是抛物线28y x =的焦点，点A B 、分别在抛物线28y x =及圆224120x y x +--=的实线部分上运动，且AB 总是平行于x 轴，则FAB ∆的周长的取值范围是A ．(6,10)B ．(8,12)C ．[6,8]D ．[8,12]（第7题图）12．若关于x 的方程2(2)22x x x e ae a x --+=-（e 为自然对数的底数）有且仅有6个不等的实数解，则实数a 的取值范围是A ．2(,)21e e +∞-B ．(,)e +∞C ．(1,)eD ．2(1,)21e e -第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题 ，每小题5分，共20分.把答案填在题中的横线上.13. 已知20(21)n x dx =+⎰，则n-的展开式中2x 的系数为 ．14. 设直线过双曲线C 的一个焦点，且与C 的一条对称轴垂直，与C 交于A 、B 两点，AB为C 的实轴长的2倍，则C 的离心率为 ．在直角三角形ABC 中，2π=C ,,3=AC 对平面内的任一点M ，平面内有一点D ,使得MA MB MD 23+=，则=∙CA CD ． 设n S 为数列{}n a 的前n 项和, 已知12a =,对任意*,p q N ∈,都有p q p q a a a +=+，则()601n S f n n +=+)(*N n ∈的最小值为 .三、解答题：本大题共6小题，前5题每题12分，选考题10分，共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17．（本小题满分12分）如图, 在△ABC 中, 点P 在BC 边上,60,2,4PAC PC AP AC ︒∠==+=. （Ⅰ）求ACP ∠；（Ⅱ）若△APB求sin ∠BAP .18．（本小题满分12分） 学校为了了解高三学生每天自主学习中国古典文学的时间，随机抽取了高三男生和女生各50名进行问卷调查，其中每天自主学习中国古典文学的时间超过3小时的学生称为“古（第11题图）P CBA（Ⅰ）根据表中数据能否判断有60%的把握认为“古文迷”与性别有关？（Ⅱ）现从调查的女生中按分层抽样的方法抽出5人进行调查，求所抽取的5人中“古文迷”和“非古文迷”的人数； （Ⅲ）现从（Ⅱ）中所抽取的5人中再随机抽取3人进行调查，记这3人中“古文迷”的人数为ξ，求随机变量ξ的分布列与数学期望．参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．19．（本小题满分12分）如图1，在直角梯形ABCD 中，AD //BC ，AB ⊥BC ，BD ⊥DC , 点E 是BC 边的中点, 将△ABD 沿BD 折起，使平面ABD ⊥平面BCD ，连接AE ,AC ,DE , 得到如图2所示的几何体.（Ⅰ）求证：AB ⊥平面ADC ； （Ⅱ）若1AD =，AB =，求二面角B AD E --的大小.E DCB AEDCB A图1 图220．（本小题满分12分）在平面直角坐标系中，0y m -+=不过原点，且与椭圆22142y x +=有两个不同的公共点,A B .（Ⅰ）求实数m 取值所组成的集合M ；（Ⅱ）是否存在定点P 使得对任意的m M ∈，都有直线,PA PB 的倾斜角互补.若存在，求出所有定点P 的坐标；若不存在，请说明理由.21．（本小题满分12分）已知函数()()ln 0af x x a x =+>.（Ⅰ）若函数()f x 有零点, 求实数a 的取值范围；（Ⅱ）证明:当2a e ≥，1>b 时, ()1ln >f b b .请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分，解答时请写清题号。

2017年四川省高考数学试卷（理科）（全国新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

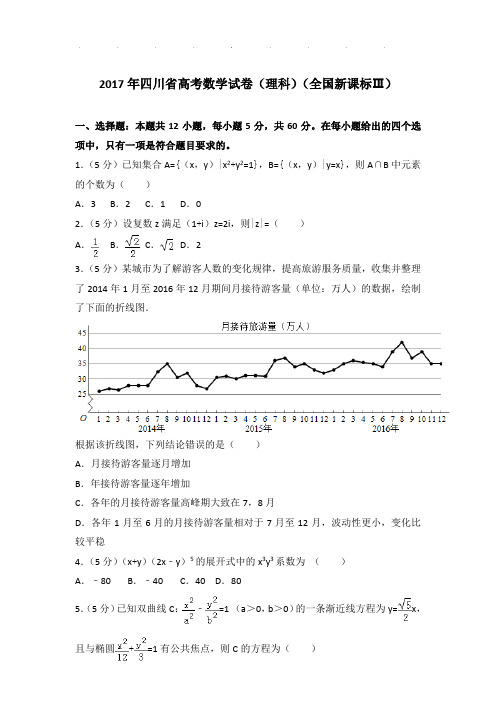
1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣ B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C．D．2二、填空题:本题共4小题，每小题5分，共20分。

成都2017届第三次高考模拟理科数学第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在一次抛硬币实验中，甲、乙两人各抛一次硬币一次，设命题p 是“甲抛的硬币正面向上”，q 是“乙抛的硬币正面向上”，则命题“至少有一人抛的硬币是正面向下”可表示为（ ）A ．()()p q ⌝∨⌝B ．()p q ∨⌝C ．()()p q ⌝∧⌝D ．()p q ⌝∨2.已知集合{}{}2|11,|10A x x B x x =-<=-<，则A B = （ ）A ． ()1,1-B ．()1,2-C ．()1,2D ．()0,1 3.若1122aii i+=++，则a =（ ） A ．5i -- B ．5i -+ C ．5i - D ． 5i +4.设()f x 是定义在R 上周期为2的奇函数，当01x ≤≤时，()2f x x x =-，则52f ⎛⎫-= ⎪⎝⎭（ ） A ．14-B ． 12- C. 14 D ．125.某几何体的三视图如图所示，则该几何体的表面积为（ ）A ．3612π+B ．3616π+ C. 4012π+ D ．4016π+ 6.设D 为ABC ∆中BC 边上的中点，且O 为AD 边上靠近点A 的三等分点，则（ ）A ．5166BO AB AC =-+B ． 1162BO AB AC =-C. 5166BO AB AC =- D ．1162BO AB AC =-+7.执行如图的程序框图，则输出x 的值是（ ）A ． 2016B ．1024 C.12D ．-1 8. 已知()00,P x y 是椭圆22:14x C y +=上的一点，12,F F 是C 的两个焦点，若120PF PF <，则0x 的取值范围是（ ）A ．⎛ ⎝⎭ B ．⎛ ⎝⎭ C. ⎛ ⎝⎭D ．⎛ ⎝⎭9. 等差数列{}n a 中的24032a a 、是函数()3214613f x x x x =-+-的两个极值点，则()2220174032log a a a = （ ）A ．624log +B ．4 C. 323log + D ．324log + 10. 函数()()2sin 4cos 1f x x x =- 的最小正周期是（ ）A ．3π B ． 23π C. π D ．2π11.某医务人员说：“包括我在内，我们社区诊所医生和护士共有17名。

四川省2017年高考理科数学试题及答案（Word 版）（考试时间：120分钟 试卷满分：150分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

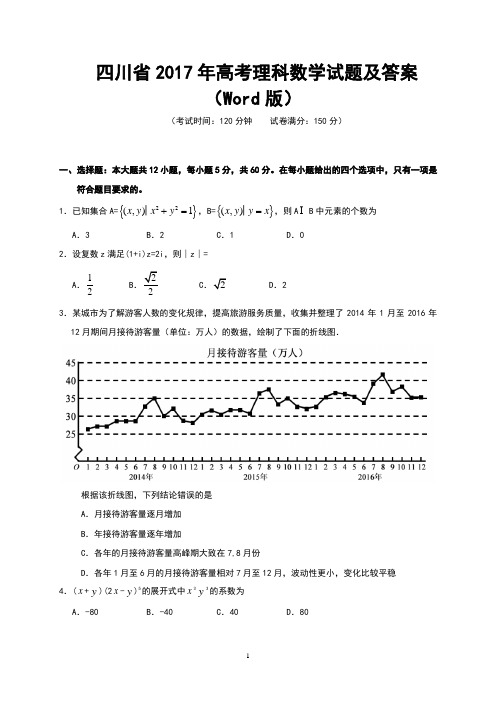
1．已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A B 中元素的个数为 A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z=2i ，则∣z ∣= A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．(x +y )(2x -y )5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．805． 已知双曲线C ：22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为52y x =,且与椭圆221123x y += 有公共焦点，则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f(x)=cos(x+3π)，则下列结论错误的是 A ．f(x)的一个周期为−2πB ．y=f(x)的图像关于直线x=83π对称 C ．f(x+π)的一个零点为x=6πD ．f(x)在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为 A ．-24B ．-3C ．3D ．810．已知椭圆C ：22221x y a b+=，（a>b>0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．63B ．33C ．23D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a=A ．12-B ．13C ．12D ．112．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λ AB +μAD，则λ+μ的最大值为 A ．3B ．22C ．5D ．2二、填空题：本题共4小题，每小题5分，共20分。

2017届高三数学理第三次调查考试题（乐山市带答案）四川省乐山市高2017届第三次调查研究考试数学（理工类）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设集合，集合，则（） A. B. C. D. 2.已知复数，则的共轭复数为（） A. B. C. D. 3.在一次跳伞训练中，甲、乙两位学员各跳一次，设命题是“甲降落在指定范围”，是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围内”可表示为（） A.B. C. D. 4.已知三个正态分布密度函数（ , ）的图象如图所示，则（） A. B. C. D. 5.如图，已知是圆的直径，点是半圆弧的两个三等分点，，，则（） A. B. C. D. 6.经统计用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系，对某小组学生每周用于数学的学习时间与数学成绩进行数据收集如表：（） x 15 16 18 19 22 y 102 98 115 115 120 由表中样本数据求得回归方程为，则点与直线的位置关系是（） A. B. C. D. 与的大小无法确定 7.如图是秦九韶算法是一个程序框图，则输出的的值为（） A. 的值 B. 的值 C. 的值 D. 的值 8.已知数列的前项和，则确定的最大正整数的值为（） A. B. C. D. 9.在平面直角坐标系中，抛物线：的焦点为，是抛物线上的一点，若的外接圆与抛物线的准线相切，且该圆的面积为，则（） A. B. C.D. 10.多面体的底面为矩形，其中（主）视图和侧（左）视图如图所示，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则该多面体的体积为（） A. B. C. D. 11.函数的部分图像如图所示，则等于（） A. B. C. D. 12.已知曲线存在两条斜率为的切线，则实数的取值范围是（） A. B. C. D. 第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13.已知等差数列的前项和为，若，则 ______. 14.若直线与垂直，则二项式展开式中的系数为________. 15.定义在上的函数满足则的值为______. 16.若函数在实数集上的图象是连续不断的，且对任意实数存在常数使得恒成立，则称是一个“关于函数”.现有下列“关于函数”的结论：①常数函数是“关于函数”；②正比例函数必是一个“关于函数”；③“关于函数”至少有一个零点；④ 是一个“关于函数”. 其中正确结论的序号是_______. 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.如图，在直角坐标系中，点是单位圆上的一个动点，过点作轴的垂线与射线交于点，与轴交于点，记，且 . （1）若，求的值；（2）求面积的最大值. 18.某商场举行购物抽奖活动，抽奖箱中放有除编号不同外，其余都相同的个小球，这个小球编号的茎叶图如图所示. 活动规则如下：从抽奖箱中随机抽取一球，若抽取的小球编号是十位数字的奇数，则为一等奖，奖金为元；若抽取的小球编号是十位数字为的奇数，则为二等奖，奖金元；若抽取的小球编号是其余号码则不中奖.现某顾客有放回的抽奖两次，两次抽奖相互独立.（1）求该顾客在两次抽奖中恰有一次中奖的概率；（2）记该顾客两次抽奖后的奖金之和为随机变量，求的数学期望.19. 如图，在三棱锥中，分别是、、的中点，平面，，二面角为 . （1）证明：；（2）求二面角的余弦值. 20.已知椭圆的左右焦点分别为，上顶点为，过点与垂直的直线交轴负半轴于点，且 + ，过、、三点的圆的半径为，过定点的直线与椭圆交于、两点（在之间）. （1）求椭圆的标准方程；（2）设直线的斜率为，在轴上是否存在点，使得以、为邻边的平行四边形为菱形？如果存在，求出的取值范围；如果不存在，请说明理由.21.已知函数 . （1）求函数的单调区间；（2）已知点和函数图像上动点 ,对任意，直线倾斜角都是钝角，求的取值范围. 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程已知曲线的参数方程是（为参数），以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程是 . （1）求曲线和的交点坐标；（2）、两点分别在曲线与上，当最大时，求的面积（是坐标原点）. 23.选修4-5：不等式选讲已知函数 . （1）求不等式的解集；（2）若关于的不等式在上无解，求实数的取值范围.乐山市高中2017届第三次调查研究考试理科数学参考答案一、选择题 1-5:CDADD 6-10:BACBC 11、12：AB 提示： 1. ，则，故选C. 2.由题知，则的共轭复数为，故选D. 3.依题意得：“甲没有降落在指定范围”，：“乙没有降落在指定范围”，因此“至少有一位学员没有降落在指定范围”可表示为，故选A. 4.正态曲线曲线关于对称，且在处取得峰值，由图得，，故，故选D. 5.连接，由点是半圆弧的三等分点，且和均为边长等于圆的半径的等边三角形，所以四边形为菱形，所以，故选D . 6. ，所以样本数据的中心点为，所以，即点满足，故选B. 7.第一次循环， ;第二次循环，；第三次循环，，此时，不成立，结束循环，输出为的值，故选A. 8. ，当时，，两式相减得整理得，是公比为的等比数列，又，解得，故，则由，即，满足要求的，所以最大正整数的值为，故选C. 9.依题意得，的外接圆半径为，的外接圆圆心应位于线段的垂直平分线上，圆心到准线的距离等于，即有，由此解得 ,故选B. 10.用割补法可把几何体分割成三个部分，可得，故选C. 11.记，则由函数图象可知， , ，则 , ,当时，，又，解得，于是，则，故选A. 12.由题得，则方程有两个解，令，且，则由图象可知，有且，即且，解得，故选B. 二、填空题13. 14. 15. 16.①④ 提示： 13.由得，则 . 14.由题，得，，展开式通项为，时，的系数为 . 15.当时，，则，得，易得的周期为，则. 16.①对任一常数函数，存在，有，，所以有，所以常数函数是“关于函数”；②令正比例函数解析式为，设存在实数，使得为一个“ 函数”，则，则，即 = ，要对任意的满足，则且，不可能，故正比例函数不可能是一个“一个关于的函数”；③“关于函数”为，当函数不恒为时，有，则与同号，又因为函数在实数集上的图象是连续不断的，的图象与轴无交点，即无零点；④对于，设存在使得，即存在使得，也就是存在使得，也就是存在使得，此方程有解，所以④正确，故正确的序号为①④. 三、解答题 17.解：（1）依题意得，所以 , 因为，且，所以 , 所以 . （2）由三角函数定义，得，从而 . , . 因为，所以当时，“=”成立，所以面积的最大值为 . 18.解：（1）设一次抽奖抽中等奖的概率为，没有中奖的概率为，则， , 则中奖的概率为 . 所以该顾客两次抽奖中，恰有一次中奖的概率为 . （2）的可能取值为 .则，， , ， . 则的分布列为 0 50 100 150 200 的数学期望为（元）. 19.（1）证明：如图，设的中点为，连接、，为的中点， . 平面，平面，又平面， , , 为的中点， . （2）解：平面，为二面角的平面角，即，以为原点，在平面内过点垂直于的直线为轴，所在直线为轴，所在的直线为轴，建立如图所示的直角坐标系.则 . 则，显然平面的一个法向量 , 设平面的法向量，则 ,即，得 . 又，又二面角的平面角为锐角，二面角的余弦值为 . 20.解：（1） , 是的中点， . . 过三点的圆的圆心为，半径为 , ，椭圆的标准方程为 . （2）直线的方程为 .设则，联立，消去整理得，，由，解得，且…7分又 . 由菱形的对角线垂直，得， . 解得，即 . ，当且仅当时等号成立，故存在满足题意的点，故的取值范围是 . 21.解：（1）函数的定义域为，，当时，，故在上单调递减；当时，，故在上单调递减；当时，，解得故在上单调递减，在上单调递增. （2）因为对任意的，直线倾斜角都是钝角，即对任意的，，即，即 . 因为，令，（i）当时，由（1）知，在上单调递减，则由，故 ,此时满足. （ii）当时，令，得，当时，即 ,函数在上单调递增，故的最大值为，解得与矛盾. 当时，即，函数在上单调递减，故的最大值为，得 ,此时 . 当时，即，函数在上单调递减，在上单调递增，故在的最大值为或，所以，即，故，综上，的取值范围为 . 22.解：（1）由，得，曲线的方程为 . 又由得，得曲线的方程为 . 联立，解得或，所以交点的坐标为 . （2）如图，可知，当共线时，最大，此时，原点到的距离为 . 则 . 23.解：（1）由题意得 . 则原不等式转化为或或 . 原不等式的解集为 . （2）由题得，由（1）知，在上的最大值为，即，解得或，即的取值范围为 .。

四川省2017届高三“联测促改”活动理综试题理科综合·生物理科综合考试时间共150分钟，满分300分。

其中物理110分，化学100分，生物90分。

生物试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），第Ⅰ卷10至11页，第Ⅱ卷12至14页，共5页。

考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效。

考试结束后，将本试题卷和答题卡一并交回。

第Ⅰ卷（选择题共42分）注意事项：必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。

第Ⅰ卷共7小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.人体肝细胞合成的糖原储存在细胞内，合成的脂肪是以VLDL（脂肪与蛋白质复合物）形式分泌出细胞外。

下列相关叙述，正确的是A.糖原和VLDL都含有C、H、O、N元素B.VLDL是以自由扩散方式分泌到细胞外的C.VLDL的合成过程必须要有内质网的参与D.糖原和脂肪是细胞生活的主要能源物质2.，美国和德国的三位科学家因揭示了囊泡运输的调控机制而获得诺贝尔生理学和医学奖。

下列有关叙述，不正确的是A.高尔基体在囊泡运输过程中起着交通枢纽作用B.细胞的囊泡运输过程依赖于生物膜的功能特性C.通过囊泡能实现内质网膜的成分向细胞膜转移D.囊泡运输障碍，可能导致神经及免疫调节紊乱3.早春开花植物雪滴兰，雪落花开，开花时花序细胞的耗氧速率远高于其他细胞，但ATP的生成量却远低于其他细胞。

据此推知，雪滴兰的花序细胞A.依靠无氧呼吸为生命活动供能B.比其他细胞中的自由水含量低C.比其他细胞的光合作用强度低D.呼吸释放的热能比其他细胞多4.下列关于生物学实验中常用技术、方法等的相关描述，正确的是A.观察植物细胞质壁分离与复原时，可用洋葱根尖分生区细胞作实验材料B.噬菌体DNA被35S标记后，用于侵染大肠杆菌能证明DNA是遗传物质C.在“探究酵母菌细胞呼吸的方式”实验中，可用重铬酸钾溶液检测CO2D.建构数学模型的方法，可以用于研究种群数量变化和酶活性变化的规律5.下列关于植物激素及类似物的叙述，正确的是A.用一定浓度赤霉素溶液处理小麦幼苗，能使植株增高B.在植物组织培养中，生长素能减弱细胞分裂素的作用C.西瓜开会后，喷施一定浓度的脱落酸可促使果实膨大D.乙烯存在于多种植物组织，主要作用是促进果实发育6.某同学选取甲、乙两个相同的透明玻璃缸，同时都加入等量的池塘水、小球藻、水草及小鱼等，随即均被密封，实验在温度适宜的暗室中进行。

2017年四川高考数学(理科数学)试题Word版真题试卷含答案2017年普通高等学校招生全国统一考试（新课标Ⅲ）四川理科数学注意事项：1.考生答卷前必须在答题卡上填写姓名和准考证号。

2.回答选择题时，在答题卡上涂黑对应题目的答案标号。

如需更改，用橡皮擦干净后再涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在试卷上无效。

3.考试结束后，将试卷和答题卡一并交回。

一、选择题（共12小题，每小题5分，共60分）1.已知集合 $A=\{(x,y)|x+y=1\}$，$B=\{(x,y)|y=x\}$，则$A\cap B$ 中元素的个数为A。

3B。

2C。

1D。

02.设复数 $z$ 满足 $(1+i)z=2i$，则 $|z|$ 等于A。

$\frac{1}{2}$B。

$\frac{\sqrt{2}}{2}$___D。

$2\sqrt{2}$3.某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图。

根据该折线图，下列结论错误的是A。

月接待游客量逐月增加B。

年接待游客量逐年增加C。

各年的月接待游客量高峰期大致在7、8月份D。

各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳4.$(x+y)(2x-y)5$ 的展开式中 $x^3y^3$ 的系数为A。

$-80$B。

$-40$___D。

$80$5.已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ 的一条渐近线方程为 $y=x$，且与椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 有公共焦点，则$C$ 的方程为A。

$\frac{x^2}{12}-\frac{y^2}{10}=1$B。

$\frac{x^2}{5}-\frac{y^2}{4}=1$C。

$\frac{x^2}{4}-\frac{y^2}{5}=1$D。