平行线的特征 ppt课件1
- 格式:ppt
- 大小:447.00 KB
- 文档页数:9

平行线的特征在几何学中,平行线是指在同一个平面上不相交且永不相交的两条直线。
平行线的研究对于很多几何问题的解决至关重要。
本文将介绍平行线的特征以及相关的概念和定理。
1. 平行线的定义平行线的定义是在欧几里得几何中最基本的概念之一。
两条线段如果在同一平面内,且它们不相交,称为平行线。
平行线可以用符号“||”表示。
例如,线段AB || 线段CD表示线段AB与线段CD平行。
2. 平行线的特征平行线具有以下特征:- 任意两条平行线的倾斜角度相等。
平行线的斜率相等或者其中一个不存在斜率。
- 平行线之间的距离是恒定的。
即使平行线在平面上不断延伸,它们之间的距离始终保持相等。
- 平行线在任何一个平面上都不会相交。
如果平行线与其他线段相交,那么它们一定不在同一个平面上。
3. 平行线的判定方法在几何学中,有几种方法可以判定两条线是否平行,包括:- 平行线的定义法:根据平行线的定义,如果两条线段不相交,即可判断它们平行。
- 夹角判定法:如果两条直线之间的夹角为180°,即为一对平行线。
- 平行线判定定理:通过已知条件,如线段的斜率或者两条线段上一点的坐标,可以应用平行线判定定理来判断线段是否平行。
4. 平行线的性质和定理在几何学中,有一些与平行线相关的重要性质和定理,包括:- 平行线的转置定理:如果一条直线与另外两条平行线相交,那么这两条平行线也互相相交。
- 平行线的逆定理:如果一条直线与一组平行线相交,并且这组平行线中的一条与该直线垂直,则该直线与该组平行线的其他线段也垂直。
- 平行线截切定理:如果一条直线截取两组平行线的一段,则这两个截断段的比例相等。
总结:平行线是几何学中的基本概念之一,具有其独特的特征和性质。
准确理解并应用平行线的特征和判定方法,对于解决各种几何问题具有重要意义。
通过研究平行线的性质和定理,我们可以推导出其他有关直线和角度的重要结论,进一步拓展和应用几何学知识。
以上就是关于平行线的特征的相关内容。

平行线的特征平行线在几何学中具有重要的作用,它们是指在同一个平面上,永远不会相交的直线。
本文将探讨平行线的特征,以及与平行线相关的性质和定理。
一、平行线的定义平行线的定义是两条直线在同一个平面上,并且永远不会相交。
这意味着两条平行线之间的距离始终相等。
二、平行线的特征1. 方向相同:平行线在平面上具有相同的方向,它们始终在相同的方向上延伸。
2. 永不相交:平行线永远不会相交。
无论延长多远,它们仍然保持平行的形状。
3. 距离相等:平行线之间的任意两点到两条平行线的距离始终相等。
这是平行线的一个重要性质。
4. 平行四边形的对边平行性:在平行四边形中,对边是平行的。
这是平行线特征的一个重要应用。
三、平行线的判定1. 同位角判定:如果两条直线被一条截线所切,并且同位角相等,那么这两条直线平行。
2. 转换判定:如果一条线与两条平行线分别相交,形成相等的内错角或外错角,那么这条线与这两条平行线平行。
3. 斜率判定:如果两条直线的斜率相等,那么这两条直线平行。
斜率是直线在坐标系中的倾斜度量。
四、平行线的应用1. 平行线与横向交错线条:在道路规划和交通设计中,平行线经常用于构建车道和交通流线的布局。
2. 平行线与角度构造:在建筑设计中,平行线被广泛应用于角度构造。
通过平行线的布局,可以创建出各种角度和形状。
3. 平行线与等距关系:平行线之间的距离相等,这一性质在几何学和测量中具有重要的应用。
五、平行线的定理1. 交替内角定理:如果两条平行线被一条截线所切,那么两条平行线上的交替内角是相等的。
2. 内错角定理:如果两条平行线被一条截线所切,那么两条平行线上的内错角是补角。
3. 锐角和钝角定理:如果两条平行线被一条截线所切,那么两条平行线上的锐角和钝角的和是180度。
六、平行线的重要性平行线的研究对几何学和应用数学具有重要意义。
它们为解决实际问题提供了基础,而且在建筑、工程、地图制作等领域也有广泛的应用。
综上所述,平行线作为几何学中的一个重要概念,具有方向相同、永不相交和距离相等等特征。

平行线的特征平行线是几何学中重要的概念之一。
在二维欧几里得空间中,如果两条直线永远不相交,那么它们被称为平行线。
本文将介绍平行线的特征及相关的性质。
1. 平行线的定义给定二维欧几里得空间中的两条直线L1和L2,如果它们满足以下条件,则称L1和L2为平行线:•L1和L2不相交。
•L1和L2存在公共的平面。
2. 平行线的性质2.1 平行线的判定已知两条直线L1和L2,判断它们是否平行的方法有多种,这里介绍两种常见的判定方法:方法一:使用线性方程判断如果直线L1的斜率等于直线L2的斜率,那么L1和L2是平行线。
方法二:使用向量判断设直线L1上一点为点A,直线L2上一点为点B。
如果向量AB与L1的方向向量平行,则L1和L2是平行线。
2.2 平行线与夹角平行线之间不存在交点,因此它们之间的夹角为0度。
即使将两条平行线延长,无论延长多远,它们之间的夹角始终保持不变。
2.3 平行线与平行四边形平行线之间的性质与平行四边形的性质密切相关。
平行四边形是有四条边都平行的四边形。
性质一:对边平行平行四边形的对边是平行的。
即如果ABCD是一个平行四边形,那么线段AB和线段CD是平行线,线段AC和线段BD是平行线。
性质二:邻边互补平行四边形的邻边是互补的。
即如果ABCD是一个平行四边形,那么角A和角C是互补角,角B和角D是互补角。
性质三:对角线等长平行四边形的对角线等长。
即如果ABCD是一个平行四边形,那么线段AC和线段BD的长度相等。
2.4 平行线与转角当两条直线相交时,会形成四个角。
其中,相邻的两个角称为相邻角,非相邻的两个角称为转角。
如果两条直线分别与一条横穿它们的其他线相交,并且转角为等量,则这两条直线是平行线。
3. 平行线的应用平行线在几何学中有广泛的应用,下面简要介绍其中的几个应用领域。
3.1 地理学在地理学中,平行线常用于地图投影中的经纬度线。
地球上的纬线是平行于赤道的圆环状线,而经线是与纬线相交在地球上的两极的直线。
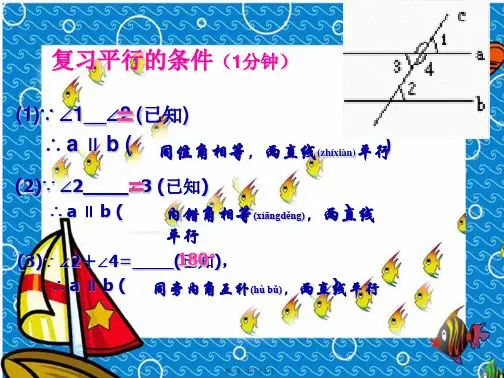



23平行线的特征平行线是在同一个平面内没有相交的直线。
下面我们来详细讨论一下平行线的特征。
1.定义:平行线是在同一个平面内没有相交的直线。
这意味着平行线永远保持相同的距离,并且永远不会相交。
2.符号表示:两条平行线通常用双竖杠,表示。
3.概念:当两条平行线被一条横线切割时,对应的对角线是平行并且长度相等的。
4.角度关系:平行线所形成的角度具有以下特征:(1)对顶角:平行线所形成的对顶角是相等的。
(2)同位角:同位角是指两条平行线被一条横线相交所形成的角,它们的度数相等。
(3)内错角:内错角是指两条平行线被一条横线相交所形成的角,它们的度数之和为180度。
(4)外错角:外错角是指两条平行线被一条横线相交所形成的角,它们的度数相等。
5.互补角和补角:对于两条平行线,如果其中一条线与另一个线的交线形成一个直角,则这两条线之间的角称为互补角。
如果两条平行线之间的角为90度,则这两条角称为补角。
6.平行线的判定定理:以下是判定两条线是否平行的几个定理:(1)同一直线上的两个点与直线上的任意一点连线,如果这两条连线所形成的角是180度,则该直线与该点连线所构成的线与原直线平行。
(2)如果两条直线与第三条直线各交于内错角,则这两条直线平行。
(3)如果两条直线与第三条直线各交于对顶角,则这两条直线平行。
(4)如果两条直线与第三条直线各交于同位角,则这两条直线平行。
7.平行线的性质:平行线具有以下性质:(1)平行线与平面上的其他线交点的距离相等。
(2)平行线上两条线段的比值等于它们所对应两个相似三角形的边长比值。
(3)平行线切割平面所形成的平行四边形相等。
(4)平行线切割平面所形成的轴对称图形相等。
(5)平行线与直线之间的角度关系可以用相应角、内错角、对顶角等概念进行描述。
总结起来,平行线的特征主要包括定义、符号表示、角度关系、互补角和补角、判定定理和性质。
通过研究平行线的特征,我们可以更好地理解和应用到几何学的各个领域,如平面几何、立体几何以及几何证明等。




平行线和垂直线的特征平行线和垂直线是几何学中常见的线段关系,它们具有不同的特征和性质。
在本文中,我们将探讨平行线和垂直线的特征及其在几何学中的应用。
一、平行线的特征平行线是指位于同一个平面上且永不相交的两条直线。
它们具有以下特征:1. 同方向性:两条平行线在无穷远处延伸时,方向总是保持一致。
无论你在平行线上移动多远,它们将始终保持相同的方向。
2. 等间距性:平行线之间的任意两条线段之间的距离是相等的。
即使这些线段在不同位置,它们之间的距离仍然保持不变。
3. 不相交性:平行线永远不会相交,无论它们延伸多远。
如果两条线段在某一点相交,那么它们不是平行线。
平行线在几何学中的应用广泛,例如在建筑设计中,我们常常使用平行线来确保建筑物的结构稳定。
此外,在平面几何中,平行线也是证明定理和解决问题的重要工具。
二、垂直线的特征垂直线是指与另一条线段相交成直角的线段。
它们具有以下特征:1. 相交成直角:垂直线与另一线段相交时,它们之间的角度为90度,即相邻角为直角。
2. 方向互为相反:两条垂直线的方向互为相反。
例如,一条向上的垂直线与一条向下的垂直线相交。
3. 无交点:垂直线没有交点,它们只是在某一点相交,并共享该点作为共同的垂足。
垂直线在几何学中也有广泛的应用。
比如,建筑设计中常常需要利用垂直线来确保结构的稳定性和垂直度。
在平面几何中,垂直线可用于构建垂直角并解决各种问题。
总结:平行线和垂直线是几何学中常见的线段关系。
它们具有一些不同的特征和性质。
平行线是永不相交且具有同一方向的两条直线,而垂直线是与另一线段相交成直角的线段。
这些特点使得平行线和垂直线在几何学的各个领域中发挥重要作用,如建筑设计和平面几何中的证明和问题解决。
对于理解几何学和应用几何学,了解平行线和垂直线的特征至关重要。