棱柱

《棱柱》说课稿尊敬的各位评委老师：大家好！今天我说课的内容是《棱柱》。

下面我将从教材分析、学情分析、教学目标、教学重难点、教法与学法、教学过程、板书设计这几个方面来展开我的说课。

一、教材分析本节课是高中数学必修二空间几何体这一章节中的重要内容。

棱柱作为一种常见的几何体，在生活中有着广泛的应用，同时也是后续学习其他几何体的基础。

通过对棱柱的学习，学生能够进一步认识空间几何体的结构特征，培养空间想象能力和逻辑思维能力，为学习立体几何的相关知识奠定坚实的基础。

教材在编排上，先通过实例引入棱柱的概念，然后详细阐述了棱柱的结构特征、分类以及表面积和体积的计算方法，内容由浅入深，符合学生的认知规律。

二、学情分析学生在初中阶段已经对一些简单的几何体有了初步的认识，但对于棱柱的结构特征和相关性质的理解还不够深入。

此时的学生已经具备了一定的观察能力和抽象概括能力，但空间想象能力还有待进一步提高。

在教学过程中，要充分利用学生已有的知识经验，通过观察、分析、归纳等活动，引导学生自主探究棱柱的相关知识，激发学生的学习兴趣和积极性。

三、教学目标1、知识与技能目标（1）理解棱柱的概念，掌握棱柱的结构特征。

（2）能够根据棱柱的结构特征判断一个几何体是否为棱柱。

（3）掌握棱柱的分类方法，了解直棱柱、正棱柱的特点。

（4）会计算棱柱的表面积和体积。

2、过程与方法目标（1）通过观察实物和模型，培养学生的观察能力和空间想象能力。

（2）通过对棱柱结构特征的分析和归纳，培养学生的抽象概括能力和逻辑思维能力。

（3）通过探究棱柱的表面积和体积的计算方法，培养学生的数学应用意识和解决问题的能力。

3、情感态度与价值观目标（1）让学生感受数学与生活的密切联系，激发学生学习数学的兴趣。

（2）通过合作学习，培养学生的团队合作精神和创新意识。

四、教学重难点1、教学重点（1）棱柱的概念和结构特征。

（2）棱柱的分类。

（3）棱柱的表面积和体积的计算。

2、教学难点（1）棱柱的结构特征的理解和应用。

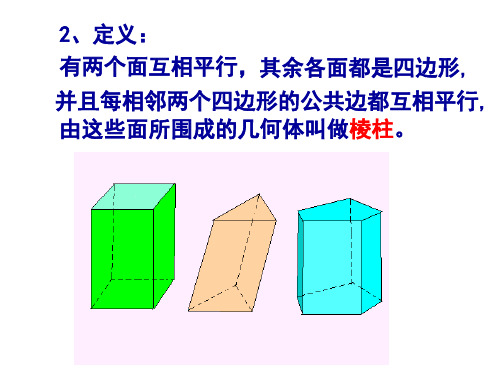
七年级数学知识点棱柱棱柱是一种三维图形，它的侧面是由若干个矩形拼接而成的，也就是说，它的侧棱都是矩形。

除此之外，棱柱还有顶面和底面，底面是一个多边形，顶面也是一个同样的多边形，两者互相平行。

在七年级的数学课程中，学生需要了解棱柱的各个特征以及计算棱柱的表面积、体积等相关知识点。

下面就对七年级数学知识点棱柱进行详细的讲解。

1、棱柱的种类棱柱的种类可以根据棱柱底面的不同多边形来分类。

如果底面是一个三角形，那么这个棱柱就被称为三棱柱；如果底面是一个正方形，那么这个棱柱就被称为正方柱；如果底面是一个六边形，那么这个棱柱就被称为六棱柱。

其他不同形状的棱柱也可以按照底面的多边形进行分类。

2、棱柱的特征除了底面、侧面和顶面之外，棱柱还有以下几个特征：(1) 棱柱的棱长棱柱的棱长指的是棱柱的侧棱的长度。

由于棱柱的侧面都是矩形，所以相邻两个侧棱的长度是相等的。

棱柱的棱长需要根据实际情况去计算。

(2) 棱柱的高棱柱的高指的是从棱柱底面到顶面的距离，也就是垂直于底面的距离。

棱柱的高的长度需要根据实际情况去计算。

(3) 棱柱的母线棱柱的母线指的是连接底面相邻顶点的线段。

对于三棱柱和四棱柱来说，它们的母线长度就是棱长；对于五棱柱及以上的棱柱来说，其母线长度需要根据实际情况去计算。

3、棱柱的表面积和体积计算棱柱的表面积和体积是数学课程中重要的知识点之一。

下面就分别对棱柱的表面积和体积进行详细的讲解。

(1) 棱柱的表面积棱柱的表面积由底面积、侧面积和顶面积三部分组成。

对于三棱柱、四棱柱和五棱柱等常用棱柱，其表面积计算公式如下：三棱柱的表面积 S = 2lh + 3B四棱柱的表面积 S = 2lh + 2B五棱柱的表面积 S = 2lh + 5B其中，l为侧棱长度，h为棱柱的高，B为底面积。

(2) 棱柱的体积棱柱的体积是指棱柱所占的空间大小，计算棱柱的体积需要先计算底面积，再乘以棱柱的高。

对于三棱柱、四棱柱和五棱柱等常用棱柱，其体积计算公式如下：三棱柱的体积 V = 1/3Bh四棱柱的体积 V = Bh五棱柱的体积 V = 5/12Bh其中，B为底面积，h为棱柱的高。

七年级上册棱柱知识点
棱柱，是由若干个侧棱为等边多边形、底面为相似同形的多边形组成的立体图形。

在七年级数学中，学生需要掌握棱柱的基本定义、特征以及面积、体积的计算方法。

一、基本定义
棱柱是一种有面积、体积的三维图形，由若干个棱、侧面为等边多边形、底面为相似同形多边形组成的，其中底面上的点到棱所在面的距离为高。

二、特征
1. 棱柱的底面和顶面平行，并且相等。

2. 侧面为等边多边形，若底面为正方形，则为正棱柱；若底面为长方形，则为长方体。

3. 棱柱的所有侧边（棱）相等。

三、表面积的计算公式
表面积指棱柱的所有表面积之和。

对于正棱柱，它的表面积等于底面周长与高的乘积再乘以2；对于长方体，它的表面积等于所有侧面积之和再加上两底面积。

例如，对于边长为2，高为3的正方形棱柱，其表面积为
2×2×2+2×2×3+2×3×3=28。

四、体积的计算公式
体积指棱柱所占空间的大小。

对于正棱柱，它的体积等于底面积与高的乘积；对于长方体，它的体积等于底面积与高的乘积。

例如，对于边长为2，高为3的正方形棱柱，其体积为
2×2×3=12。

五、应用
棱柱是日常生活中常见的立体图形之一，无论是建筑中的柱子、水杯、抽象的数学概念，都与棱柱有着紧密的联系。

在实际应用中，对棱柱的面积、体积等计算，也是十分重要的基本技能。

总之，掌握棱柱的基本定义及特征，了解表面积与体积的计算
公式，同时灵活运用，可以为数学学习和实际生活带来很多的便利。

棱柱的知识点总结棱柱的性质：1. 顶点和边的关系：棱柱有两个底面和若干个侧面，每个顶点都与若干个侧面的交点，并且与两个底面的交点。

顶点的个数等于棱柱的顶面个数和底面个数之和。

2. 棱柱的表面积和体积：棱柱的表面积等于底面积加上所有侧面积的总和，棱柱的体积等于底面积乘以高。

3. 棱柱的对称性：直棱柱在面对对角线对称和旋转180度对称的情况下，依然可以保持不变。

斜棱柱和正棱柱也有类似的对称性。

4. 棱柱的平行四边形关系：侧面都是平行四边形意味着棱柱的对边相等，且相对的对边平行。

在学习棱柱的过程中，我们还要掌握以下几个重要的知识点：1. 垂直棱柱、斜棱柱和正棱柱的特点和区别。

2. 棱柱的体积计算公式和表面积计算公式。

3. 棱柱的侧面展开图的绘制。

4. 棱柱的空间图形。

5. 棱柱的空间视图和投影。

垂直棱柱、斜棱柱和正棱柱的特点和区别：垂直棱柱：底面和顶面是平行的，并且相互垂直，侧面是平行四边形，也可以是矩形或者正方形。

垂直棱柱有很多例子，比如正方体、长方体等。

斜棱柱：底面和顶面不是平行的，侧面是平行四边形或者矩形。

斜棱柱的侧面和底面可以有不同的倾斜角度，所以斜棱柱有很多种不同的情况。

正棱柱：底面和顶面是平行的，侧面是等腰梯形。

正棱柱是一种特殊的棱柱，它具有独特的性质和特点。

对于垂直棱柱、斜棱柱和正棱柱，我们要掌握它们的特点和区别，以便能够正确识别和分类各种类型的棱柱。

棱柱的体积计算公式和表面积计算公式：棱柱的体积计算公式：V = 底面积 × 高棱柱的表面积计算公式：S = 2×底面积 + 侧面积在计算棱柱的体积和表面积时，我们要根据公式给出的参数，先计算出底面积和侧面积，然后代入公式求得棱柱的体积和表面积。

棱柱的侧面展开图的绘制：侧面展开图是指将棱柱的侧面展开平铺在平面上的图形，一般用来计算棱柱的表面积。

在绘制侧面展开图时，我们要根据棱柱的侧面形状和大小，将侧面展开成一个平面图形，然后根据展开图计算侧面积。

职高棱柱的教学教案教案标题：职高棱柱的教学教案教学目标：1. 理解棱柱的定义和特征；2. 能够识别和命名不同种类的棱柱；3. 掌握计算棱柱的表面积和体积的方法；4. 能够应用棱柱的概念解决实际问题。

教学重点：1. 棱柱的定义和特征；2. 棱柱的种类和命名；3. 棱柱的表面积和体积的计算方法；4. 棱柱在实际问题中的应用。

教学准备：1. 教师准备：教学课件、棱柱模型、计算表面积和体积的公式；2. 学生准备：教材、作业本、计算器。

教学过程：一、导入（5分钟）1. 利用教学课件展示一些与棱柱相关的图片，引发学生对棱柱的兴趣和好奇。

2. 引导学生讨论棱柱的特点和定义。

二、概念讲解（15分钟）1. 通过教学课件，详细介绍棱柱的定义和特征，包括底面、侧面、顶面、高度、棱、面等概念。

2. 根据不同的底面形状，介绍不同种类的棱柱，如正方形棱柱、长方形棱柱等，并展示相应的示意图。

三、表面积计算（20分钟）1. 解释棱柱表面积的概念，并给出计算公式。

2. 通过具体的例子，引导学生计算不同种类棱柱的表面积，包括底面积、侧面积和顶面积的计算方法。

3. 给学生布置练习题，巩固表面积计算的方法。

四、体积计算（20分钟）1. 解释棱柱体积的概念，并给出计算公式。

2. 通过具体的例子，引导学生计算不同种类棱柱的体积，包括底面积和高度的计算方法。

3. 给学生布置练习题，巩固体积计算的方法。

五、应用实例（15分钟）1. 引导学生思考棱柱在实际生活中的应用场景，如建筑、容器等。

2. 给学生提供一些实际问题，要求他们运用所学的棱柱概念和计算方法解决问题。

3. 鼓励学生展示解题过程和结果，并进行讨论和分享。

六、小结与作业布置（5分钟）1. 对本节课的重点内容进行小结，并强调棱柱的定义、特征、表面积和体积的计算方法。

2. 布置相关作业，巩固学生对棱柱的理解和计算能力。

教学反思：本节课通过导入、概念讲解、计算方法示范、实例应用等多种教学手段，旨在帮助学生全面理解和掌握棱柱的概念、特征、表面积和体积的计算方法。

棱柱的特征与计算公式棱柱是一种具有特定几何形状的立体图形。

它由多个相等的侧面组成，这些侧面都是平行四边形。

在本文中，我将详细介绍棱柱的特征以及计算它的体积和表面积的公式。

一、棱柱的特征棱柱是一个立体图形，具有以下几个特征：1. 底面和顶面：棱柱的底部和顶部是相等且平行的多边形，通常是正多边形，如正方形、正六边形等。

2. 侧面：棱柱的侧面是连接底面和顶面的矩形或平行四边形，侧面的数量与底面的边数相等。

3. 棱：棱是连接底面和顶面的边界线段，棱的数量与底面的边数相等，并且所有的棱都是相等长度的。

4. 高度：棱柱的高度是连接底面和顶面的垂直距离，也是棱柱的唯一可变参数。

二、棱柱的体积计算公式棱柱的体积是指棱柱所占据的三维空间的大小。

计算棱柱体积的公式如下：V = 底面积 ×高度其中，V表示棱柱的体积，底面积指的是底面的面积，高度指的是棱柱的高度。

例如，如果我们有一个正方形底面边长为2 cm，高度为5 cm的棱柱，我们可以使用上述公式计算其体积：V = 2 cm × 2 cm × 5 cm = 20 cm³因此，该正方形底面边长为2 cm，高度为5 cm的棱柱的体积为20 cm³。

三、棱柱的表面积计算公式棱柱的表面积是指棱柱所有面的总面积。

计算棱柱表面积的公式如下：A = 2 ×底面积 + 侧面积其中，A表示棱柱的表面积，底面积指的是底面的面积，侧面积指的是所有侧面的总面积。

底面积的计算方法取决于底面的形状，例如，如果底面是一个正方形，则底面积为边长的平方。

侧面积的计算方法取决于底面的形状和棱柱的高度，例如，如果底面是一个正方形，且高度为h，则每个侧面的面积为边长乘以高度。

综上所述，我们可以根据具体的底面形状和高度，使用上述公式计算棱柱的表面积。

结论在本文中，我们详细介绍了棱柱的特征，包括底面和顶面、侧面、棱以及高度。

同时，我们提供了计算棱柱体积和表面积的公式。

棱柱分类的三种方法
棱柱分类是指对棱柱进行分组或归类的过程。

在几何学中，常用的棱柱分类方法主要有三种：按底面形状分类、按棱数分类和按边长分类。

下面将详细介绍这三种分类方法。

一、按底面形状分类：
按底面形状分类是指根据棱柱的底面形状进行分类。

在这种分类方法下，可以分为以下几类：
1.正棱柱：底面是一个正多边形的棱柱，如正三棱柱、正四棱柱等。

2.等腰棱柱：底面是一个等腰三角形的棱柱，如等腰三棱柱。

3.矩形棱柱：底面是一个矩形的棱柱。

4.直角棱柱：底面是一个直角三角形的棱柱，如直角三棱柱。

5.不规则棱柱：底面是一个不规则多边形的棱柱。

二、按棱数分类：
按棱数分类是指根据棱柱的棱数进行分类。

在这种分类方法下，可以分为以下几类：
1.三棱柱：底面是一个三角形，棱柱有三条侧棱。

2.四棱柱：底面是一个四边形，棱柱有四条侧棱。

3.五棱柱：底面是一个五边形，棱柱有五条侧棱。

4.六棱柱：底面是一个六边形，棱柱有六条侧棱。

5.多棱柱：底面是一个正多边形，棱柱有多条侧棱。

三、按边长分类：
按边长分类是指根据棱柱底面边长的关系进行分类。

在这种分类方法下，可以分为以下几类：
1.同底棱柱：底面边长相等的棱柱。

2.等截面棱柱：除了底面外，其他横截面的边长相等的棱柱。

3.等侧棱柱：所有棱柱侧面的边长都相等的棱柱。

综上所述，棱柱分类的三种方法分别是按底面形状分类、按棱数分类和按边长分类。

这些分类方法可以帮助我们更好地了解和研究棱柱的特征和性质，对于几何学的学习和应用都有重要意义。