高二数学同步辅导教材(第2讲)

高二数学双曲线人教版【同步教育信息】一. 本周教学内容： 双曲线二. 重点、难点：1. 定义：c a PF PF 22||||21<=-到两点)0,(),0,(21c F c F -距离之差为定值2a 的点的轨迹。

2. 标准方程：12222=-b y a x 或12222=-b x a y （0,0>>b a ）3. 性质：12222=-by a x（1）X 围：),[],(∞+--∞∈a a x ，R y ∈（2）对称：x 、y 轴为对称轴，原点为对称中心 （3）顶点：)0,(a ± （4）渐近线：x ab y ±= （5）离心率：),1(∞+∈=ace 4. 第二定义：到)0,(c F 的距离与到直线l ：c a x 2=的距离之比为定值e ac=的点的轨迹为双曲线，12222=-by a x （0,0>>b a ，222c b a =+）。

【典型例题】[例1] 求满足条件的双曲线的标准方程。

（1）一条渐近线是：023=+y x ，且过点)36,8(A 的双曲线方程。

解：x y 23-= 双曲线λ=-9422y x ⎩⎨⎧<>轴轴y x 0λλ代入A 4=λ其渐近线双曲线系1361622=-y x （2）求与双曲线14522=-y x 有共同渐近线且焦距为12的双曲线。

解：λ=-4522y x 36|4||5|=+λλ4±=λ 两解 1162022±=-y x [例2] P 为平面上一点，过P 作双曲线只有一个交点的直线可作n 条。

解：∴αcos 12||||221-=⋅b PF PF21PF F S ∆2cot sin 21221ααb PF PF =⋅=[例4] 双曲线12222=-by a x 的右顶点为A ，P 为双曲线上一点（异于顶点）过A 作渐近线的平行线交OP 于E 、F 。

（1）证||||||2OF OE OP ⋅=（2）双曲线上是否存在一点P ，使4abS AEF =∆ 解：),(),0,(00y x P a AOP l ：x x y y ⋅=00AE l ：)(a x a by -= AF l ：)(a x a by --=),(000000ay bx aby ay bx abx F --),(000000ay bx aby ay bx abx E ++220220220220222||)1(||)1(||||OP x k y a x b x b a k OF OE =+=-⋅+=⋅ by x y x x k EF F E 22002||2||1||+⋅=-+=2020020200||||221y x ay b y x y S +⋅+⋅⋅=∆420ab b ay == 四点)2,25(ba ±± [例5] 双曲线C ：1322=-y x ，A （3，2），B （2，0），P 为双曲线上一点，求||21||PB PA +的最小值。

直线和圆的方程章末检测卷（二）说明：1．本试题共4页，满分150分，考试时间120分钟。

2．答题前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、试室号、座位号填写在答题卷上。

3. 答题必须使用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷上各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卷整洁，考试结束后，将答题卷交回，试卷自己保存。

第I 卷(选择题 共60分)一、单项选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求.）1．设a 为实数，若直线20x ay a ++=与直线10ax y a +++=平行，则a 值为（ ） A ．1-B ．1C ．±1D ．2【解析】由题意210a -=，1a =±，1a =时，212a a =+=，两直线重合，舍去，1a =-时，22a =-，10a +=，满足两直线平行．所以1a =-．故选：A ．2．已知过点()2,2P 的直线与圆()2215x y -+=相切，且与直线10ax y -+=垂直，则=a （ ）A ．12-B ．12C ．2-D ．2【解析】设过点(2,2)P 的直线的斜率为k ，则直线方程(22)y k x -=-，即220kx y k -+-=，=12k =-，由于直线220kx y k -+-=与直线10ax y -+=，因此112a -⨯=-，解得2a =，故选：D.3．若圆221:4C x y +=与圆222:680C x y x y m +--+=外切，则实数m 的值是（ ） A ．24-B ．16-C ．24D ．16【解析】圆221:4C x y +=的圆心为()0,0，半径为2；圆222:680C x y x y m +--+=的圆心为()3,4，半径为5=.由于两个圆外切，所以25=，解得16m =. 故选：D4．已知梯形ABCD 中，AB ∥CD ，并且点A （4，0），点B （6，6），点C （0，2），则此梯形的高为（ ） ABCD【解析】根据题意，点A （4，0），点B （6，6）， 则直线AB 的斜率k 6064-==-3，则直线AB 的方程为y ﹣0＝3（x ﹣4），即3x ﹣y ﹣12＝0； 点C 到直线AB 的距离d =梯形ABCD 中，AB ∥CD ，则此梯形的高就是点C 到直线AB； 故选：C.5．唐代诗人李颀的诗《古从军行》开头两句为“白日登山望烽火，黄昏饮马傍交河”，其中隐含了一个有趣的数学问题——“将军饮马”，即将军在白天观望烽火台之后黄昏时从山脚下某处出发，先到河边饮马再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，已知军营所在的位置为()2,0B -，若将军从山脚下的点1,03A ⎛⎫⎪⎝⎭处出发，河岸线所在直线方程为23x y +=，则“将军饮马”的最短总路程为（ ）AB ．5 CD ．163【解析】如图所示，设点()2,0B -关于直线23x y +=的对称点为()11,C x y ，在直线23x y +=上取点P ，连接PC ，则PB PC =．由题意可得1111112222322y x x y ⎧⎛⎫⋅-=- ⎪⎪+⎪⎝⎭⎨-⎪+⨯=⎪⎩，解得1104x y =⎧⎨=⎩，即点()0,4C ，所以PA PB PA PC AC +=+≥==A ，P ，C 三点共线时等号成立，所以“将军饮马” 故选：A ．6．已知直线:10l x my m -+-=，则下叙述正确的是（ ） A ．直线l 的斜率可以等于0B ．原点到直线l 的距离的最大值为32C ．直线l 可以表示过点(1,1)的所有直线D ．若直线l 的横纵截距相等，则1m =±【解析】:10l x my m -+-=，当0m =时，:10l x -=是垂直于x 轴的直线，斜率不存在；当0m ≠时，变为点斜式： ()111y x m -=-，恒过定点A ()1,1，由于10m≠，所以直线l 的斜率不会等于0，故A 错误；且:10l x my m -+-=不能表示过点(1,1)的所有直线，C 错误；设原点为O ，因为直线恒过点A ，所以当直线:10l x my m -+-=与线段OA 垂直时，原点到直线l 的距离最大，此时的最大距离就是线段OA 的长，OA B 错误；直线化为截距式：当1m =时，:l y x =，此时横纵截距为0，横纵截距相等；当1m ≠时，:111x my l m m +=--，令11m m m--=，解得：1m =-，综上：若直线l 的横纵截距相等，则1m =±，D 正确. 故选：D7．已知点()()0,2,1,1A B ，且点P 在圆22:(2)4C x y -+=上，C 为圆心，则下列说法错误的是（ ）A ．PA PB + B ．当PAB ∠最大时，APB △的面积为2C ．PA PC -的最大值为D ．PA PB -【解析】如图，当P 为线段AB 与圆C 的交点时，即PA PB AB +==此时PA PB +A 正确；由题可知点B 在圆C 内，当AP 与圆C 相切时，PAB ∠最大，此时P 与O 重合，此时12112APB S =⨯⨯=△，故B 错误；因为点P 在圆22:(2)4C x y -+=上，C 为圆心，则2PC r ==，所以当PA 最大时，PA PC -也最大，当A ，C ，P 三点共线，且C 在A ，P 之间时，其最大值为||AC =C 正确；当P 为射线BC 与圆C 的交点时，PA PB -取得最大值||AB =D 正确． 故选：B.8．在平面直角坐标系xOy 中，已知圆22221,1(9)O x y C x y ++=+=：：，直线l 与圆O 相切，与圆C 相交于,A B 两点，分别以点,A B 为切点作圆C 的切线12l l ，．设直线12l l ，的交点为P ，则OP 的最小值为（ ）A ．9B ．7C ．D ．72【解析】设点(),P m n ，()11,A x y ，()22,B x y ，()1,0C -，因为分别以点,A B 为切点作圆C 的切线12l l ，．设直线12l l ，的交点为P ， 所以CA AP ⊥，则0CA AP ⋅=，即1111(1)()()0x m x y n y +-+-=，所以22111110x x mx m y y n +--+-=，因为2211(1)9x y ++=，所以11(1)80m x ny m +++-=，即()11,x y 是方程(1)80m x ny m +++-=的解， 所以点()11,A x y 在直线(1)80m x ny m +++-=上， 同理可得()22,B x y 在直线(1)80m x ny m +++-=上， 所以切点弦AB 的方程为(1)80m x ny m +++-=， 因为直线AB 与圆O 相切，1=，解得263180n m =-≥，即72m ≤所以||OP所以当72m =时，直线AB 方程为1x =，此时min 7||2OP = 所以OP 的最小值为72.故选：D二、多项选择题（本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求。

专题二 空间向量基本定理一 知识结构图二.学法指导1．基底判断的基本思路及方法(1)基本思路：判断三个空间向量是否共面，若共面，则不能构成基底；若不共面，则能构成基底．(2)方法：①如果向量中存在零向量，则不能作为基底；如果存在一个向量可以用另外的向量线性表示，则不能构成基底．②假设a ＝λb ＋μ c ，运用空间向量基本定理，建立λ，μ的方程组，若有解，则共面，不能作为基底；若无解，则不共面，能作为基底．2．基向量的选择和使用方法(1)尽可能选择具有垂直关系的，从同一起点出发的三个向量作为基底．(2)用基向量表示一个向量时，如果此向量的起点是从基底的公共点出发的，一般考虑加法，否则考虑减法；如果此向量与一个易求的向量共线，可用数乘．3．用基底表示空间向量，一般要用向量的加法、减法、数乘的运算法则，及加法的平行四边形法则，加法、减法的三角形法则．逐步向基向量过渡，直到全部用基向量表示．三.知识点贯通知识点1 基底的判断{a ，b ，c }叫做空间的一个基底，a ，b ，c 都叫做基向量．空间任意三个不共面的向量都可以构成空间的一个基底．例题1.设x ＝a ＋b ，y ＝b ＋c ，z ＝c ＋a ，且{a ，b ，c }是空间的一个基底，给出下列向量组：①{a ，b ，x }，②{x ，y ，z }，③{b ，c ，z }，④{x ，y ，a ＋b ＋c }．其中可以作为空间一个基底的向量组有( )A ．1个B ．2个C ．3个D ．4个【答案】C【解析】如图所示，令a ＝AB →，b ＝AA 1→，c ＝AD →，则x ＝AB 1→，y ＝AD 1→，z ＝AC →，a ＋b ＋c ＝AC 1→.由于A ，B 1，C ，D 1四点不共面，可知向量x ，y ，z 也不共面，同理b ，c ，z 和x ，y ，a ＋b ＋c 也不共面，故选C 。

知识点二 用基底表示向量空间向量基本定理如果三个向量a ，b ，c 不共面，那么对任意一个空间向量p ，存在唯一的有序实数组(x ，y ，z )，使得p ＝x a ＋y b ＋z c .其中{a ，b ，c }叫做空间的一个基底，a ，b ，c 都叫做基向量．空间任意三个不共面的向量都可以构成空间的一个基底．例题2：如图，四棱锥P ­OABC 的底面为一矩形，PO ⊥平面OABC ，设OA →＝a ，OC →＝b ，OP →＝c ，E ，F 分别是PC ，PB 的中点，试用a ，b ，c 表示：BF →，BE →，AE →，EF →.【解析】 连接BO (图略)，则BF →＝12BP →＝12(BO →＋OP →)＝12(c －b －a )＝－12a －12b ＋12c . BE →＝BC →＋CE →＝BC →＋12CP →＝BC →＋12(CO →＋OP →)＝－a －12b ＋12c . AE →＝AP →＋PE →＝AO →＋OP →＋12(PO →＋OC →)＝－a ＋c ＋12(－c ＋b )＝－a ＋12b ＋12c .EF →＝12CB →＝12OA →＝12a . 知识点三 正交分解在立体几何中的应用(1)单位正交基底 如果空间的一个基底中的三个基向量两两垂直，且长度都是1，那么这个基底叫做单位正交基底．常用{i ，j ，k }表示．(2)正交分解把一个空间向量分解为三个两两垂直的向量，叫做把空间向量进行正交分解．例题3 .如图，已知平行六面体ABCD ­A 1B 1C 1D 1中，底面ABCD 是边长为a 的正方形，侧棱AA 1长为b ，且∠A 1AB ＝∠A 1AD ＝120°，求异面直线BD 1和AC 所成角的余弦值．【解析】 {AB →，AD →，AA 1→}可以作为空间的一个基底，且|AB →|＝a ，|AD →|＝a ，|AA 1→|＝b ，〈AB →，AD →〉＝90°，〈AA 1→，AB →〉＝120°，〈AA 1→，AD →〉＝120°.又BD 1→＝AD →＋AA 1→－AB →，AC →＝AB →＋AD →，∴|BD 1→|2＝|AD →|2＋|AA 1→|2＋|AB →|2＋2AD →·AA 1→－2AD →·AB →－2AA 1→·AB →＝a 2＋b 2＋a 2＋2ab cos 120°－0－2ab cos 120°＝2a 2＋b 2，|AC →|2＝|AB →|2＋2AB →·AD →＋|AD →|2＝2a 2，∴|BD 1→|＝2a 2＋b 2，|AC →|＝2a .∴BD 1→·AC →＝(AD →＋AA 1→－AB →)·(AB →＋AD →)＝AD →·AB →＋|AD →|2＋AA 1→·AB →＋AA 1→·AD →－|AB →|2－AB →·AD →＝0＋a 2＋ab cos 120°＋ab cos 120°－a 2－0＝－ab .∴|cos 〈BD 1→，AC →〉|＝|BD 1→·AC →||BD 1→||AC →|＝|－ab |2a 2＋b 2·2a ＝b 4a 2＋2b 2. ∴异面直线BD 1和AC 所成角的余弦值为b 4a 2＋2b 2. 五 易错点分析易错一 空间向量的基底例题4.设向量{a ，b ，c }是空间一个基底，则一定可以与向量p ＝a ＋b ，q ＝a －b ，构成空间的另一个基底的向量是( )A ．aB ．bC ．cD ．a 或b 【答案】C【解析】由题意和空间向量的共面定理，结合p ＋q ＝(a ＋b )＋(a －b )＝2a ，得a 与p ，q 是共面向量，同理b 与p ，q 是共面向量，所以a 与b 不能与p ，q 构成空间的一个基底；又c 与a 和b 不共面，所以c 与p ，q 构成空间的一个基底．误区警示能否作为空间向量的基底，应判断向量是否共面。

庖丁巧解牛知识·巧学一、弦切角1.定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角.2.弦切角的特点：(1)顶点在圆周上；(2)一边与圆相交；(3)一边与圆相切.误区警示弦切角定义中的三个条件缺一不可.图2-4-2各图中的角都不是弦切角.图(1)中，缺少“顶点在圆上”的条件；图(2)中，缺少“一边和圆相交”的条件；图(3)中，缺少“一边和圆相切”的条件；图(4)中，缺少“顶点在圆上”和“一边和圆相切”两个条件.图2-4-23.如图2-4-3所示，弦切角可分为三类：(1)圆心在角的外部；(2)圆心在角的一边上；(3)圆心在角的内部.图2-4-3二、弦切角定理1.弦切角定理：弦切角等于它所夹的弧所对的圆周角.2.定理的证明：由于弦切角可分为三类，即图2-4-3所示的情况，所以在证明定理时分三种情况加以讨论：当弦切角一边通过圆心时〔图2-4-4（1）〕，显然弦切角与其所夹弧所对的圆周角都是直角；当圆心O在∠CAB外时〔图2-4-4（2）〕，作⊙O的直径AQ，连结PQ，则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC；当圆心O在∠CAB内时〔图2-4-4（3）〕，作⊙O的直径AQ，连结PQ，则∠BAC=∠QAB+∠1=∠QPA+∠2=∠APC.图2-4-43.在证明弦切角定理的过程中，我们从特殊情况入手，通过猜想、分析、证明和归纳，从而证明了弦切角定理.通过弦切角定理的证明过程，要学会用运动变化的观点观察问题，进而理解从一般到特殊，从特殊到一般的认识规律.知识拓展由弦切角定理，可以直接得出一个结论：若两弦切角所夹的弧相等，则这两个弦切角也相等，我们把这一结论称为弦切角定理的推论，它也是角的变换的依据.弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半.这就建立了弦切角与弧的数量之间的关系，它为直接依据弧进行角的转换确立了基础.问题·探究问题到目前为止，对于圆中有关的角我们已学过圆心角、圆周角、弦切角，它们各自有定义、定理及和它所对的弧的度数关系，这三种角在证明题和计算题中经常用到，它们是几何综合题中不可缺少的知识点.它们相互之间有哪些联系和区别？如何把握这些联系和区别？思路:从理解圆心角、圆周角、弦切角的定义、定理及与所对、所夹的弧的关系入手思考.探究:圆心角、圆周角、弦切角是圆中三类重要的角，准确理解它们的定义、定理及与所对、所夹的弧的关系，对于我们在圆中的计算、证明，起着举足轻重的作用，将这些知识总结对比列表如下，你可以在比较中把握其异同点，从而快速、准确地应用于解决问题.名称圆心角圆周角弦切角定义顶点在圆心的角顶点在圆上；两边和圆相交顶点在圆上；一边和圆相交；另一边和圆相切图形有关定理①圆心角的度数等于它所对的弧的度数②在同圆或等圆中相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距相等同弧所对的圆周角等于它所对的圆心角的一半弦切角等于它所夹弧所对的圆周角有关推论四者关系定理的推论圆周角定理推论①、②、③弦切角定理的推论角与弧的关系∠AOB的度数=的度数∠ACB的度数=21的度∠ACB的度数=21的度典题·热题例1如图2-4-5，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB 与⊙O相交于点E，AE平分∠CAB，且AE=2，求△ABC各边的长.J图2-4-5思路分析：∠BAE为弦切角，于是∠BAE=∠C，再由AE平分∠CAB和△ABC是直角三角形可得∠C的度数，进而解直角三角形即可.解：∵AD为⊙O的切线，∴∠BAE=∠C.∵AE平分∠CAB，∴∠BAC=2∠BAE.又∵∠C+∠BAC=90°，∴∠BAE=∠C=30°.2.则有BE=1，AB=3，BC=3，AC=3深化升华本题应用弦切角、解直角三角形的知识,为基础题型，求解此类题时，要注意弦切角在角的转换中的作用，本题正是由于这一条件，沟通了角之间的数量关系.例2如图2-4-6，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F.求证：EF∥BC.图2-4-6思路分析：连结DF，构造弦切角，于是∠FDC=∠DAC，根据AD是△ABC中∠BAC的平分线,得∠BAD=∠DAC，而∠BAD与∠EFD对着同一段弧，所以相等，由此建立∠EFD与∠FDC的相等关系，根据内错角相等，可以断定两直线平行.证明：连结DF.∵AD是∠BAC的平分线，∴∠BAD=∠DAC.∵∠EFD=∠BAD，∴∠EFD=∠DAC.∵⊙O切BC于D，∴∠FDC=∠DAC.∴∠EFD=∠FDC.∴EF∥BC.方法归纳证明两条直线平行的方法有：（1）内错角相等，两直线平行；（2）同位角相等，两直线平行；（3）同旁内角互补，两直线平行等.证题时可以根据图形与已知合理选择.本题由于有切线，所以考虑弦切角和它所对的圆周角.例3如图2-4-7，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，弦BD∥XY，AC、BD相交于点E.图2-4-7（1）求证：△ABE≌△ACD；（2）若AB=6 cm，BC=4 cm，求AE的长.思路分析：第（1）问中的全等已经具备了AB=AC，再利用弦切角定理与圆周角定理可以得角的相等关系；对于（2），则利用△BCE∽△ACB建立比例式，解方程获得AE的长.（1）证明：∵XY 是⊙O 的切线，∴∠1=∠2. ∵BD ∥XY ，∴∠1=∠3.∴∠2=∠3. ∵∠3=∠4，∴∠2=∠4.∵∠ABD=∠ACD ，又∵AB=AC ，∴△ABE ≌△ACD.（2）解：∵∠3=∠2，∠BCE=∠ACB ，∴△BCE ∽△ACB. ∴CBCEAC BC. ∴AC·CE=BC 2，即AC·(AC-AE)=BC 2. ∵AB=AC=6，BC=4，∴6(6-AE)=16. ∴AE=310（cm ）. 深化升华 本题利用平行线、弦切角、圆周角等进行了角的转换，利用相似建立方程求线段的长度，综合应用时，必须非常熟悉图形中的各个量，盯准要求的数值，向图形和已知索取条件.。

2021版高中数学必修二同步学习讲义(打包39份) 人教课标版2(新教2021版高中数学必修二同步学习讲义(打包39份)人教课标版2(新教中心投影与平行投影空间几何体的三视图自学目标.介绍中心投影和平行投影.能画出来直观空间图形的三视图.能够辨识三视图所则表示的立体模型．知识点一投影的概念思索由右图你能够讲出影子就是怎样获得的吗？答案光照射到不透明物体(比如手)上，在后面的屏幕上留下影子．剖析()定义：由于光的反射，在不能透明化物体后面的屏幕上可以遗留下这个物体的影子，这种现象叫作投影．()投影线：光线．()投影面：留下物体影子的屏幕．知识点二投影的分类投影中心投影平行投影知识点三三视图思考如梦似幻！――这是无数来自全世界的游客对国家游泳中心“水立方”的第一印象．假如你站在水立方入口处的正前方或在“水立方”的左侧看水立方，你看到的是什么？若你在“水立方”的正上方观察水立方看到什么？定义光由一点向外反射构成的投影在一束平行光线反射下构成的投影特征投影线处设一点投影线平行分类正投影和斜投影根据上述三个方向观测至的平面，若想图画出来“水立方”的形状？答案“水立方”的一个侧面．“水立方”的一个表面．可以．梳理三视图的概念()定义()三视图的画法规则①正、俯视图都反映物体的长度――“长对正”；②正、侧视图都反映物体的高度――“高平齐”；③俯、侧视图都反映物体的宽度――“宽相等”．()三视图的排序顺序：先画正视图，侧视图在正视图的右边，俯视图在正视图的下边．类型一中心投影与平行投影基准()①平行投影的投影线互相平行，中心投影的投影线平行于一点；②空间图形经过中心投影后，直线变为直线，但平行线可能将变为了平行的直线；③几何体在平行投影与中心投影下存有相同的表现形式．其中恰当观点的个数为()．．．．答案解析由平行投影和中心投影的定义知，平行投影的投影线互相平行，中心投影的投影线相交于一点，故①正确；空间图形经过中心投影后，直线变成直线，但平行线有可能变成相交线，如照片中由近到远物体之间的距离越来越近，最后相交于一点，故②正确；几何体在平行投影与中心投影下有不同的表现形式，故③正确．故选.()如图所示，在正方体－′′′′中，，分别就是′，′的中点，则以下推论恰当的就是．(只填上序号)①四边形′在底面内的投影是正方形；②四边形′在面′′内的投影是菱形；③四边形′在面′′内的投影与在面′′内的投影就是全等的平行四边形．答案①③解析①四边形′的四个顶点在底面内的投影分别是，，，，所以投影是正方形，即①正确；②设正方体的棱长为，则＝，取′的中点，连接，则四边形′在面′′内的投影是四边形′，由∥′，且＝′，知四边形′是平行四边形，但＝，′＝，所以四边形′不是菱形，即②不正确；对于③，由②可知两个投影四边形是对边分别相等的平行四边形，从而③正确．思考与体悟()推论一个几何体的投影就是什么图形，先分确切就是平行投影还是中心投影，投影面的边线如何，再根据平行投影或中心投影的性质去推论．()画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得出此图形在该平面上的投影．跟踪训练()已知△，选定的投影面与△所在平面平行，则经过中心投影后所得的△′′′与△的关系是()．全等．相似．不相似．以上都不对答案解析根据题意图画出来图形例如图．由图易得＝＝＝＝，则△∽△′′′.()例如图，，分别就是正方体的面、面的中心，则四边形在该正方体的面上的正投影可能将就是图中的．(建议把所有可能将的序号都填上上)答案②③解析其中②可以就是四边形在正方体的面或面上的正投影．③可以就是四边形在正方体的面上的正投影．四边形在正方体任何一个面上的正投影都不是①④.类型二三视图的画法与辨识例一个长方体截去两个三棱锥，得到的几何体如图所示，则该几何体的三视图为()答案解析从该几何体可以看出，正视图是一个矩形内有一斜向上的对角线；俯视图是一个矩形内有一斜向下的对角线，没有斜向上的对角线，故排除、项；侧视图是一个矩形内有一斜向下的对角线，且都是实线，因为没有看不到的轮廓线，所以排除项．追踪训练将一个长方体沿相连三个面的对角线切掉一个棱锥，获得的几何体的正视图与俯视图如图所示，则该几何体的侧视图为()答案解析由几何体的正视图和俯视图所述该几何体如图所示，故其侧视图为中的图象．例画出如图所示的几何体的三视图．求解如图所示．()()。

人教A版选修2-1高二数学第2章 2.2椭圆教材同步培优、能力提升讲义及练习一、旧知回顾1.椭圆的定义：第一定义：平面内到两个定点F1、F2的距离之和等于定值2a(2a>|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.第二定义: 平面内到定点F与到定直线l的距离之比是常数e(0<e<1)的点的轨迹是椭圆,定点叫做椭圆的焦点,定直线l叫做椭圆的准线,常数e叫做椭圆的离心率.2.椭圆的标准方程及其几何性质(如下表所示)标准方程22221(0)x ya ba b+=>>22221(0)x ya bb a+=>>图形顶点(,0)a±,(0,)b±(0,)a±,(,0)b±对称轴x轴，y轴，长轴长为2a，短轴长为2b焦点1(,0)F c-、2(,0)F c1(0,)F c-、2(0,)F c焦距焦距为122(0),F F c c=>222c a b=-二、典型例题1．已知椭圆以两条坐标轴为对称轴，一个顶点是(0，13)，另一个顶点是(－10，0)，则焦点坐标为( )．A．(±13，0) B．(0，±10) C．(0，±13) D．(0，±69) 2．椭圆x2＋4y2＝1的离心率为( )．A.32B.34C.22D.233．已知椭圆C的左、右焦点坐标分别是(－2，0)，(2，0)，离心率是63，则椭圆C的方程为( )．A.x23＋y2＝1 B．x2＋y23＝1 C.x23＋y22＝1 D.x22＋y23＝14．已知椭圆的短轴长等于2，长轴端点与短轴端点间的距离等于5，则此椭圆的标准方程是________．5．已知椭圆x2k＋8＋y29＝1的离心率为12，则k的值为________．6．求椭圆x24＋y2＝1的长轴和短轴的长、离心率、焦点和顶点的坐标．7. 若F (c ，0)是椭圆22221x y a b+=的右焦点，F 与椭圆上点的距离的最大值为M ，最小值为m ，则椭圆上与F 点的距离等于2M m+的点的坐标是( ) (A)(c ，2b a±) 2()(,)b B c a -± (C)(0，±b ) (D)不存在8. 设F 1(-c ，0)、F 2(c ，0)是椭圆22x a+22y b =1(a >b >0)的两个焦点，P 是以F 1F 2为直径的圆与椭圆的一个交点,若∠PF 1F 2=5∠PF 2F 1,则椭圆的离心率为( )(A)3 (B)6 (C)22 (D)239. P 点在椭圆1204522=+y x 上，F 1、F 2是两个焦点，若21PF PF ⊥，则P 点的坐标是10. 12F F 、是椭圆2214x y +=的左、右焦点，点P 在椭圆上运动，则12||||PF PF ⋅的最大值是 ．11.设是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，P 为直线上一点，12PF F ∆是底角为的等腰三角形，则E 的离心率为（ ） ()A 12 ()B 23 ()C 34()D 4512F F 32a x =30o12.等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线x y 162=的准线交于,A B 两点，AB =则C 的实轴长为（ ）()A ()B ()C 4 ()D 813.已知1F 、2F 为双曲线22:2C x y -=的左、右焦点，点P 在C 上，12||2||PF PF =，则12cos F PF ∠= （A ）14 （B ）35 （C ）34 （D ）4514.已知抛物线关于x 轴对称，它的顶点在坐标原点O ，并且经过点0(2,)M y 。

1.2 直线的方程【知识点梳理】知识点一：直线的点斜式方程方程00()-=-y y k x x 由直线上一定点及其斜率决定，我们把00()-=-y y k x x 叫做直线的点斜式方程，简称点斜式．知识点诠释：1．点斜式方程是由直线上一点和斜率确定的，点斜式的前提是直线的斜率存在．点斜式不能表示平行于y 轴的直线，即斜率不存在的直线；2．当直线的倾斜角为0°时，直线方程为1=y y ；3．当直线倾斜角为90°时，直线没有斜率，它的方程不能用点斜式表示．这时直线方程为：1=x x ． 4．0-=-y y k x x 表示直线去掉一个点000(,)P x y ；00()-=-y y k x x 表示一条直线． 知识点二：直线的斜截式方程如果直线l 的斜率为k ，且与y 轴的交点为(0,)b ，根据直线的点斜式方程可得(0)-=-y b k x ，即=+y kx b ．我们把直线l 与y 轴的交点(0,)b 的纵坐标b 叫做直线l 在y 轴上的截距，方程=+y kx b 由直线的斜率k 与它在y 轴上的截距b 确定，所以方程=+y kx b 叫做直线的斜截式方程，简称斜截式．知识点诠释：1．b 为直线l 在y 轴上截距，截距可以取一切实数，即可以为正数、零、负数；距离必须大于或等于零； 2．斜截式方程可由过点(0,)b 的点斜式方程得到； 3．当0≠k 时，斜截式方程就是一次函数的表示形式．4．斜截式的前提是直线的斜率存在．斜截式不能表示平行于y 轴的直线，即斜率不存在的直线． 5．斜截式是点斜式的特殊情况，在方程=+y kx b 中，k 是直线的斜率，b 是直线在y 轴上的截距． 知识点三：直线的两点式方程经过两点111222(,),(,)P x y P x y （其中1212,≠≠x x y y ）的直线方程为1112122121(,)--=≠≠--y y x x x x y y y y x x ，称这个方程为直线的两点式方程，简称两点式．知识点诠释：1．这个方程由直线上两点确定；2．当直线没有斜率（21x x =）或斜率为120()=y y 时，不能用两点式求出它的方程．3．直线方程的表示与111222(,),(,)P x y P x y 选择的顺序无关．4．在应用两点式求直线方程时，往往把分式形式1112122121(,)--=≠≠--y y x x x x y y y y x x 通过交叉相乘转化为整式形式121211()()()()--=--y y x x y y x x ，从而得到的方程中，包含了x 1=x 2或y 1=y 2的情况，但此转化过程不是一个等价的转化过程，不能因此忽略由x 1、x 2和y 1、y 2是否相等引起的讨论．要避免讨论，可直接假设两点式的整式形式．知识点四：直线的截距式方程若直线l 与x 轴的交点为0(),A a ，与y 轴的交点为()0,B b ，其中0,0≠≠a b ，则过AB 两点的直线方程为1+=x ya b，这个方程称为直线的截距式方程．a 叫做直线在x 轴上的截距，b 叫做直线在y 轴上的截距．知识点诠释：1．截距式的条件是0,0≠≠a b ，即截距式方程不能表示过原点的直线以及不能表示与坐标轴平行的直线．2．求直线在坐标轴上的截距的方法：令0=x 得直线在y 轴上的截距；令 0=y 得直线在x 轴上的截距． 知识点一：直线方程的一般式关于x 和y 的一次方程都表示一条直线．我们把方程写为0++=Ax By C ，这个方程（其中A 、B 不全为零）叫做直线方程的一般式．知识点诠释：1．A 、B 不全为零才能表示一条直线，若A 、B 全为零则不能表示一条直线． 当0≠B 时，方程可变形为=--A C y x B B ，它表示过点0,⎛⎫- ⎪⎝⎭C B ，斜率为-A B 的直线．当0=B ，0≠A 时，方程可变形为0+=Ax C ，即=-Cx A，它表示一条与x 轴垂直的直线． 由上可知，关于x 、y 的二元一次方程，它都表示一条直线．2．在平面直角坐标系中，一个关于x 、y 的二元一次方程对应着唯一的一条直线，反过来，一条直线可以对应着无数个关于x 、y 的一次方程．【题型归纳目录】题型一：求直线的点斜式方程题型二：求直线的斜截式方程题型三：用两点式求直线的方程 题型四：用截距式求直线的方程 题型五：直线的一般式方程题型六：判断动直线所过定点 题型七：直线与坐标轴形成三角形问题 题型八：直线方程的综合问题 【典型例题】题型一：求直线的点斜式方程例1．（2022·江苏·高二）已知直线l 过()2,1A -，并与两坐标轴截得等腰三角形，那么直线l 的方程是（ ）． A ．10x y --=或30x y +-= B ．10x y --=或30x y -+= C ．10x y ++=或30x y -+=D ．10x y ++=或30x y +-=例2．（2022·全国·高二课时练习）经过点(3,2)-，倾斜角为60°的直线的点斜式方程是______． 例3．（2022·全国·高二课时练习）若直线l 经过点()2,3P -，斜率为2-，则直线l 的点斜式方程为______．【技巧总结】（1）利用点斜式求直线方程的步骤是：①判断斜率k 是否存在，并求出存在时的斜率；②在直线上找一点，并求出其坐标．（2）要注意点斜式直线方程的逆向运用，即由方程00()-=-y y k x x 可知该直线过定点00(),P x y 且斜率为k ．题型二：求直线的斜截式方程例4．（2022·全国·高二课时练习）直线60x +=倾斜角大小为（ ） A ．30°B ．60°C ．120°D ．150°例5．（2022·全国·高二课时练习）将直线2)y x -绕点(2,0)按逆时针方向旋转60°后所得直线方程的斜截式是______．例6．（2022·全国·高二课时练习）求与两坐标轴围成的三角形的面积是12，且斜率为32-的直线的斜截式方程．【技巧总结】（1）选用斜截式表示直线方程的依据是知道（或可以求出）直线的斜率k 和直线在y 轴上的截距b ． （2）直线的斜截式方程的好处在于它比点斜式方程少一个参数，即斜截式方程只要两个参数k 、b 即可确定直线的方程，而点斜式方程则需要三个参数k 、0x 、0y 才能确定，而且它的形式简洁明了，这样当我们仅知道直线满足一个条件时，由参数选用斜截式方程具有化繁为简的作用．（3）若直线过某一点，则这一点坐标一定满足直线方程，这一隐含条件应充分利用． 题型三：用两点式求直线的方程例7．（2022·全国·高二课时练习）已知点(1,2)A 、(1,2)B --，则直线AB 的两点式方程是______． 例8．（2022·陕西汉中·高一期中）已知直线l 过点()1,3G -，()2,1H -，则直线l 的方程为__________． 例9．（2022·全国·高二课时练习）经过点(1,2)M -､(2,3)N 的直线l 的两点式方程为___________．【技巧总结】当已知两点坐标，求过这两点的直线方程时，首先要判断是否满足两点式方程的适用条件，若满足即可考虑用两点式求方程．在斜率存在的情况下，也可以先应用斜率公式求出斜率，再用点斜式写出方程．题型四：用截距式求直线的方程例10．（2022·江苏·高二）已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数=a （ ） A ．1B ．1-C ．2-或1D ．2或1例11．（2022·全国·高二课时练习）根据下列条件，求直线的方程：（1）过点(3,2)A -，且截距是2-； （2）过点(3,0)A ，且在两坐标轴上的截距和为5．例12．（2022·江苏·高二课时练习）求过点P （2，－3），且横、纵截距互为相反数的直线方程． 例13．（2022·辽宁沈阳·高二期中）在三角形ABC 中，已知点A （4，0），B （－3，4），C （1，2）． （1）求BC 边上中线的方程；（2）若某一直线过B 点，且x 轴上截距是y 轴上截距的2倍，求该直线的一般式方程．例14．（2022·全国·高二课时练习）已知直线l 过点()1,4，且在x 轴、y 轴上的截距依次为a 和b ． （1）若a 与b 互为相反数，求直线的l 方程；（2）若0a >，0b >，当a b +取得最小值时，求直线l 的方程．【技巧总结】应用截距式求直线方程时，一定要注意讨论截距是否为零． 题型五：直线的一般式方程例15．（2022·江苏·高二）直线l 过点()1,2-，且在两坐标轴上截距相等，则直线l 的一般式方程为___________． 例16．（2022·重庆市两江中学校高二阶段练习）已知三角形的三个顶点(2,1),(3,3),(0,4)A B C --．（1）求BC 边所在直线的方程；（2）求BC 边上的高所在直线方程； （3）求BC 边的中垂线所在直线方程．例17．（2022·全国·高三专题练习）已知直线l ：120(R)kx y k k -++=∈，直线l 与两坐标轴围成一个等腰直角三角形，求此时直线l 的方程．例18．（2022·全国·高二课时练习）根据下列条件，写出直线方程的一般式：（1）经过点（0，2），且倾斜角为3π； （2）经过点（－2，3）和点（－1，0）；（3）经过点（2，1），在x ，y 轴上有不为0且相等的截距．【技巧总结】对于直线方程的一般式，一般作如下约定：x 的系数为正，x ，y 的系数及常数项一般不出现分数，一般按含x 项、y 项、常数项顺序排列．求直线方程的题目，无特别要求时，结果写成直线方程的一般式．题型六：判断动直线所过定点例19．（2022·四川达州·高一期末（文））直线()()1120a x a y --++=恒过定点（ ） A ．()1,1B ．()1,1-C ．()1,1-D ．()1,1--例20．（2022·河南·扶沟县第二高中高一阶段练习）不论k 为何实数，直线()()()213110k x k y k --+--=恒通过一个定点，这个定点的坐标是（ ） A ．()5,2 B ．()2,3 C ．()5,9D ．1,32⎛⎫- ⎪⎝⎭例21．（2022·北京市十一学校高一阶段练习）不论m 为何实数，直线2130x my m --+=恒过一个定点，则这个定点的坐标为（ ） A ．()1,0B ．()2,3C ．()3,2D ．31,2⎛⎫ ⎪⎝⎭例22．（2022·江苏·高二）对任意实数a ，直线y =ax -3a +2所经过的定点是（ ） A ．()2,3B ．()3,2C ．()2,3-D ．()3,2-【技巧总结】 合并参数题型七：直线与坐标轴形成三角形问题例23．（2022·云南省楚雄天人中学高二阶段练习）已知一条动直线()()311620m x m y m ++---=， （1）求证：直线恒过定点，并求出定点P 的坐标； （2）若直线不经过第二象限，求m 的取值范围；（3）若直线与x ､y 轴的正半轴分别交于A ，B 两点，O 为坐标原点，AOB 的面积为6，求直线的方程． 例24．（2022·全国·高二课时练习）过点()1,2P 作直线l 分别与x ，y 轴正半轴交于点A ，B ．（1）若AOB 是等腰直角三角形，求直线l 的方程；（2）对于①OA OB +最小，①AOB 面积最小，若选择___________作为条件，求直线l 的方程． 例25．（2022·全国·高三专题练习）已知直线:120()l kx y k k R -++=∈．若直线l 交x 轴负半轴于A ，交y 轴正半轴于B ，AOB 的面积为(S O 为坐标原点），求S 的最小值并求此时直线l 的方程． 例26．（2022·吉林·长春外国语学校高二开学考试）已知直线():210R l kx y k k -++=∈． （1）若直线l 不能过第三象限，求k 的取值范围；（2）若直线l 交x 轴负半轴于点A ，交y 轴正半轴于点B ，O 为坐标原点，设AOB 的面积为S ，求S 的最小值及此时直线l 的方程．例27．（2022·江苏·高二课时练习）已知直线l 经过点P （4， 1），且与两坐标轴在第一象限围成的三角形的面积为8，求直线l 的点斜式方程．例28．（2022·内蒙古·呼和浩特市教育教学研究中心高一期末）已知一条动直线()31640m x my m ++--=， （1）求证：直线恒过定点，并求出定点P 的坐标；（2）若直线与x 、y 轴的正半轴分别交于A 、B 两点，O 为坐标原点，是否存在直线同时满足下列条件：①AOB 的周长为12；①AOP 的面积为4．若存在，求出方程；若不存在，请说明理由．例29．（2022·全国·高二课前预习）已知直线l 过点(2,1)P ，且与x 轴、y 轴的正半轴分别为交于A 、B 两点，O 为坐标原点，则OAB 面积的最小值为__________，此时的直线方程为__________．例30．（2022·江苏·高二）过点(1,1)P 作直线l ，与两坐标轴相交所得三角形面积为4，则直线l 有（ ） A ．1条B ．2条C ．3条D ．4条【技巧总结】（1）由于已知直线的倾斜角（与斜率有关）及直线与坐标轴围成的三角形的面积（与截距有关），因而可选择斜截式直线方程，也可选用截距式直线方程，故有“题目决定解法”之说．（2）在求直线方程时，要恰当地选择方程的形式，每种形式都具有特定的结论，所以根据已知条件恰当地选择方程的类型往往有助于问题的解决．例如：已知一点的坐标，求过这点的直线方程，通常选用点斜式，再由其他条件确定该直线在y 轴上的截距；已知截距或两点，选择截距式或两点式．在求直线方程的过程中，确定的类型后，一般采用待定系数法求解，但要注意对特殊情况的讨论，以免遗漏．题型八：直线方程的综合问题例31．（2022·全国·高二课时练习）已知直线l 过点(2,3)P -，且与x 轴、y 轴分别交于A 、B 两点．若点P 恰为AB 的中点，求直线l 的方程．例32．（2022·全国·高二课时练习）已知三角形的三个顶点的坐标分别是()3,8A ､()3,2B -､()3,0C -． （1）求BC 边所在直线的方程；（2）求BC 边上的中线所在直线的方程．例33．（2022·全国·高二课时练习）已知ABC 的顶点()1,3A ，AB 边上的中线所在的直线方程为10y -=，AC 边上的高所在直线的方程为210x y -+=．分别求AC ，AB 边所在直线的方程．例34．（2022·江苏·高二课时练习）已知点()000,P x y 不在直线1:2340l x y ++=上，直线2l 过点()000,P x y ，且它的斜率与直线1l 的斜率相等，证明：直线2l 的方程可以写成()()00230x x y y -+-=．例35．（2022·山东威海·高二期中）已知,(0,0),3ABC A B ABC π∠=，y 轴为BC 边中线（1）求AC 边所在直线方程； （2）求CAB ∠角平分线所在直线方程．【技巧总结】在一般情况下，使用斜截式比较方便，这是因为斜截式只需要两个独立变数，而点斜式需要三个独立变数．在求直线方程时，要根据给出的条件采用适当的形式．一般地，已知一点的坐标，求过这点的直线，通常采用点斜式，再由其他条件确定斜率；已知直线的斜率，常用斜截式，再由其他条件确定在y 轴上的截距；已知截距或两点选择截距式或两点式．从结论上看，若求直线与坐标轴所围成的三角形的面积或周长，则选择截距式求解较方便，但不论选用哪一种形式，都要注意各自的限制条件，以免遗漏．【同步练习】一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（2022·广西·高二学业考试）已知直线l 的倾斜角为60，且经过点()0,1，则直线l 的方程为（ ）A ．y =B ．2y =-C ．1y =+D ．3y =+2．（2022·广西·高二学业考试）已知直线:20l x y c ++=经过点(1,1)，则c 的值为（ ）A ．-3B ．-5C ．-7D ．-93．（2022·江苏·高二）已知k ∈R ，223b k k =-+，则下列直线的方程不可能是y kx b =+的是（ ）A ．B ．C ．D ．4．（2022·江苏·高二）如果AB >0且BC <0，那么直线Ax ＋By ＋C ＝0不经过第（ ）象限 A ．一B ．二C ．三D ．四5．（2022·全国·高二课时练习）1:1l x =与直线sin cos 1042x y ππααα⎛⎫+-=<< ⎪⎝⎭的夹角是（ ）A ．αB ．2πα-C ．2πα-D ．πα-6．（2022·上海市复兴高级中学高二期末）已知直线l 过点()3,4P ，且与坐标轴分别相交于点A ､B ，若OAB 的面积为24，其中O 为坐标原点，则这样的直线有（ ） A ．1条B ．2条C ．3条D ．4条7．（2022·全国·高二专题练习）直线1l ：310x y -+=，直线2l 过点()1,0，且它的倾斜角是1l 的倾斜角的2倍，则直线2l 的方程为（ ） A ．61y x =+B ．()61y x =-C ．()314y x =- D ．()314y x =-- 8．（2022·全国·高二课时练习）若直线()0,0ax by ab a b +=>>过点()1,1，则该直线在x 轴与y 轴上的截距之和的最小值为（ ）． A ．1B ．2C ．3D ．4二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．（2022·江苏·高二）下列说法正确的是（ ） A ．直线()32y ax a a R =-+∈必过定点()3,2 B ．直线32y x =-在y 轴上的截距为2C10y -+=的倾斜角为60°D ．过点()1,2-且平行于直线230x y -+=的直线方程为20x y += 10．（2022·江苏·高二）已知直线l 的方程是0Ax By C ++=，则下列说法中正确的是（ ） A ．若0A B C ⋅⋅≠，则直线l 不过原点 B ．若0A B ⋅>，则直线l 必过第四象限 C ．若直线l 不过第四象限，则一定有0A B ⋅< D ．若0A B ⋅<且0A C ⋅>，则直线l 不过第四象限 11．（2022·江苏·高二）下列说法正确的是（ ） A ．11y y x x --＝k 不能表示过点M （x 1，y 1）且斜率为k 的直线方程 B ．在x 轴，y 轴上的截距分别为a ，b 的直线方程为1x ya b+=C ．直线y ＝kx +b 与y 轴的交点到原点的距离为bD ．过两点A （x 1，y 1）B （x 2，y 2）的直线方程为212212()()()()0x x y y y y x x -----=12．（2022·江苏·高二）直线12,l l 的方程分别为1:0l x ay b ++=，2:0l x cy d ++=，它们在坐标系中的位置如图所示，则下列结论中正确的是（ ）A ．0,0b d ><B ．0,0b d <>C ．a c >D ．a c <三、填空题：本题共4小题，每小题5分，共20分．13．（2022·四川达州·高一期末（文））直线y x b =+的倾斜角为______．14．（2022·江苏·高二）经过直线()()1232a x a y -++=的定点，且斜率为2-的直线方程为__________． 15．（2022·江苏·高二）直线:(12)(1)130l m x m y m +-+--=分别交x 轴､y 轴的正半轴于A ､B 两点，当AOB 面积最小时，直线l 的方程为___________．16．（2022·甘肃·高台县第一中学模拟预测（理））已知直线()()()11230k x k y k R ++--=∈恒过定点A ，点A 在直线()10,0x ym n m n+=>>上，则2m n +的最小值为___________．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步棸． 17．（10分）（2022·重庆·万州纯阳中学校高二阶段练习）已知三角形ABC 的顶点坐标为A （-1，5）、B （-2，-1）、C （4，3），（1）求AB 边所在的直线方程； （2）求AB 边的高所在直线方程． 18．（12分）（2022·全国·高二课时练习）已知直线2(2)68a y x a a -=+-+不经过第二象限，求实数a 的取值范围． 19．（12分）（2022·全国·高二课时练习）已知直线l 经过点(5,2)A -，且在两坐标轴上的截距相等，求直线l 的方程． 20．（12分）（2022·天津市红桥区教师发展中心高二期中（文））完成下面问题：（1）求直线25200x y +-=分别在x 轴，y 轴上的截距；（2）求平行于直线20x y -+=，的直线的方程；（3）已知两点(7,1)M -，(5,4)N -，求线段MN 的垂直平分线的方程． 21．（12分）（2022·全国·高二课前预习）已知直线l 的倾斜角的正弦值为35，且它与坐标轴围成的三角形的面积为6，求直线l 的方程． 22．（12分）（2022·全国·高二）（1）已知直线1y =-的倾斜角为α，另一直线l 的倾斜角2βα=，且过点()2,1M -，求l 的方程．（2）已知直线l 过点()2,3P -，且与两坐标轴围成的三角形面积为4，求直线l 的方程．。

和角公式【重难点命题方向】公式的应用重要公式1．cos(α－β)＝cos αcos β＋sin αsin β(Cα－β) cos(α＋β)＝____________________________ (Cα＋β)sin(α－β)＝____________________________ (Sα－β)sin(α＋β)＝______________________________ (Sα＋β)tan(α－β)＝tan α－tan β1＋tan αtan β(Tα－β)tan(α＋β)＝tan α＋tan β1－tan αtan β(Tα＋β) 题型一求值例1已知33cos,,2,52πααπ⎛⎫=∈ ⎪⎝⎭求cos3πα⎛⎫-⎪⎝⎭．例2已知23sin,cos,34αβ==-且α、β都是第二象限角，求cos()αβ+和sin()αβ-的值．例3已知12cos,sin,2923βααβ⎛⎫⎛⎫-=--=⎪ ⎪⎝⎭⎝⎭且,022ππαπβ<<<<，求cos.2αβ+例4 求下列各式的值．(1)105tan ； (2)75tan 175tan 1-+．例5 已知,5)tan(,3)tan(=-=+βαβα求βα2tan ,2tan ．题型二 化简 例6 化简(1));45sin()30cos()45cos()30sin(x x x x --+-+(2).65sin 35cos 25sin 55cos-(3)cos(20)cos(25)cos(70)sin(155)x x x x ︒+︒--︒-︒+．例7 化简下列各式：(1)sin x x ； cos )x x -.4cos 464sin 42)3(⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ππ例8 化简（1） 28tan 17tan 28tan 17tan ⋅++;（2）60tan 40tan 20tan 200tan 31200tan 310tan 310tan 31++-++-倍角公式【重难点命题方向】 公式的应用重要公式 二倍角公式sin 2α＝__________________；cos 2α＝________________＝__________＝__________； tan 2α＝______________.概念深化二倍角余弦公式的逆用22cos 1sin ,22cos 1cos 22ααα-=+=，这两个公式通常又称为降幂扩角公式，它们在三角函数的求值、化简单具有广泛的应用．题型一 求值 例1 （1）求125cos12cosππ的值；（2）已知),,2(,135sin ππαα∈=求α2sin 、α2cos 、α2tan 的值；（3）求10cos 310sin 1-的值．题型二 求角的集合例2 函数]2,0[,2sin sin 2)(2π∈+=x x x x f 求使)(x f 为正值的x 的集合．题型三 公式的应用 例3．已知函数f (x )＝⎝⎛⎭⎪⎫1＋1tan x sin 2x ＋m sin ⎝ ⎛⎭⎪⎫x ＋π4sin ⎝⎛⎭⎪⎫x －π4. (1)当m ＝0时，求f (x )在区间⎣⎢⎡⎦⎥⎤π8，3π4上的取值范围；(2)当tan α＝2时，f (α)＝35，求m 的值．三角函数的图像与性质【重难点命题方向】2.函数sin()(0,0)y A x b A ωϕω=++≠>的最小正周期T = ．函数sin()(0,0)y A x A ωϕω=+≠>的最小正周期 ，值域 ．把函数sin y x =的图象上所有点（当0ϕ>时）向左或（当0ϕ<时）向右平行移动ϕ个单位长度，就得到函数 的图象．函数sin y x =的图象上所有点的横坐标不动，把纵坐标（当0A >时）乘上A ，就得到函数 的图象．函数sin y x =的图象上所有点的纵坐标不动，把横坐标乘上 ，就得到函数sin (0)y x ωω=>的图象．把函数sin (0)y x ωω=>的图象上所有点（当0ϕ>时）向左或（当0ϕ<时）向右平行移动 个单位长度，就得到函数sin()y x ωϕ=+的图象．概念深化五点作图法画出sin()(0,0)y A x b A ωϕω=++≠≠在一个周期内图象的步骤： ①列表②描点；③用平滑曲线连接五点．典例精析类型一 定义域、值域例1 求下列函数的定义域：（1）y =（2）tan(2)3y x π=-．类型二 函数的奇偶性例2 判断下列函数的奇偶性：（1）()cos f x x x =；（2）()sin()2f x x π=+（3）()tan()6f x x π=-．类型三 作图例3 用五点作图法作出函数2sin()3y x π=+在一个周期内的图象．例4 作出函数y =类型四 单调性及应用 例5 求函数2sin(2)4y x π=-的单调区间．例6 求下列函数的最值及取得最值时x 的值：（1）2cos sin ([,])43y x x x ππ=+∈-；（2）2sin()([0,])3y x x ππ=--∈．类型五 周期、对称问题例7 已知函数sin()(0,)2y x πωϕωϕ=+><的最小正周期为1，且关于直线13x =对称，求函数的解析式．类型六 图象变换例8用五点法在同一平面直角坐标系中画出函数sin y x =、2sin y x =、2sin()3y x π=-、2sin(2)3y x π=-在一个周期内的图象，并根据所画图象说明2sin(2)3y x π=-的图象可由sin y x =的图象经过怎样的变换而得到．例9 把函数()y f x =图象上的每一个点向左平移3π个单位长度，再把横坐标缩小到原来的12倍（纵坐标不变），得到函数2sin()3y x π=+的图象．（1）求()y f x =的解析式；（2）求()y f x =的周期和单调增区间．类型七 函数图象的应用例10 已知函数sin()(0,0,)y A x A ωϕωϕπ=+>>< 的图象如图所示，求它的解析式．例11 若方程2sin(2)6x a π-=在区间[0,]2π内有两个根，则实数a 的取值范围是 ．一题一练：方程sin lg x x =实根的个数为A ．2个B ．3个C ．4个D ．无数个 【基础限时训练】一、选择题1、下列函数最小正周期为4π的是（ ）A ．sin 4y x =B ．sin 2y x =C ．1sin 2y x =D ．1sin 4y x = 2、函数sin(2)3y x π=-的一条对称轴方程是（ ）A ．2x π=B ．6x π=C ．12x π=-D ．4x π=3、函数sin(2)6y x π=-+的增区间是（ ）A ．2[,]()63k k k Z ππππ++∈ B ．[,]()36k k k Z ππππ-+∈C ．[,]()63k k k Z ππππ-+∈ D ．5[,]()36k k k Z ππππ++∈ 4、函数3cos tan (0,)22y x x x x ππ=≤<≠的图象是（ ）A ．BC ．D ．二、填空题 5、已知()sin3xf x π=，则(1)(2)(3)(2007)f f f f ++++= ．6、函数y =的定义域为 ．7、已知函数()2sin()3f x x π=-，有下列命题： ①()y f x =的图象关于点(,0)6π-对称；②()y f x =的图象关于直线6x π=-对称；③若12()()0f x f x ==，则12()x x k k Z π-=∈； ④()y f x =的图象与2cos()3y x π=-的图象重合． 其中正确命题的序号是 ． 【拔高限时训练】 一、选择题1、把函数2sin()3y x π=-图象上每一个点的横坐标扩大到原来的2倍（纵坐标不变），则所得函数图象的解析式为（ ） A ．sin()3y x π=-B ．2sin(2)3y x π=-C ．12sin()26y x π=-D ．12sin()23y x π=-2、函数sin sin y x x =+的值域为（ ）A ．[2,2]-B ．[2,0]-C ．[0,2]D ．[1,2]- 3、函数)24sin(x -π的单调增区间为（ ） A ．3[,]()88k k k Z ππππ-+∈B ．5[,]()88k k k Z ππππ++∈C ．3[,]()88k k k Z ππππ-+∈D ．37[,]()88k k k Z ππππ++∈4、已知函数2sin()(0)103kx y k π=+≠，若函数在任意一个长度为2的区间上的函数值至少包含一个最大值和一个最小值，则最小的正整数k 为（ ）A ．63B ．62C ．16D ．31 二、填空题5、已知函数sin()(0,0,)2y A x A πωϕωϕ=+>><图象上相邻的两个最值点的坐标分别为(,2)12π、7(,2)12π-，则其解析式为 ． 三、解答题6、已知函数sin()(0,0,)2y A x b A πωϕωϕ=++>><的图象如图所示，求它的解析式．7、求下列函数的值域：（1）12sin 2sin x y x-=+；（2）2sin(2)1([0,])62y x x ππ=-+∈．。

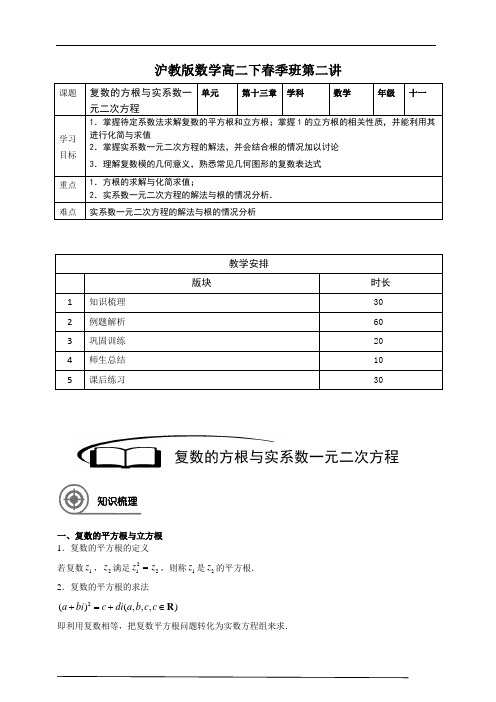
沪教版数学高二下春季班第二讲课题 复数的方根与实系数一元二次方程单元第十三章 学科数学年级十一学习 目标1．掌握待定系数法求解复数的平方根和立方根；掌握1的立方根的相关性质，并能利用其进行化简与求值2．掌握实系数一元二次方程的解法，并会结合根的情况加以讨论3．理解复数模的几何意义，熟悉常见几何图形的复数表达式 重点 1．方根的求解与化简求值；2．实系数一元二次方程的解法与根的情况分析． 难点 实系数一元二次方程的解法与根的情况分析一、复数的平方根与立方根 1．复数的平方根的定义若复数1z ，2z 满足212z z =，则称1z 是2z 的平方根．2．复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等，把复数平方根问题转化为实数方程组来求． 教学安排版块 时长1 知识梳理 302 例题解析 603 巩固训练 204 师生总结 10 5课后练习30复数的方根与实系数一元二次方程知识梳理3．复数的平方根的性质复数(0)z z ≠总有两个平方根1z ，2z ，且120z z +=（见图1）． 4．复数的立方根的定义类似的，若复数1z ，2z 满足312z z =，则称1z 是2z 的立方根．5．1的立方根 设复数1322i ω=-+，则21,,ωω都是1的立方根． 6．ω的性质 ①210ωω++=， ②31ω=， ③21322i ωω==--． 可运用这些性质化简相关问题（见图2）． 7．其他有用结论2(1)2i i -=-，2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式，那么（1）0∆>⇔方程有两个不相等的实根242b b aca-±-；（2）0∆=⇔方程有两个相等的实根2b a-； （3）0∆<⇔方程有两个共轭虚根242b ac b ia-±-，在（3）的情况下，方程的根与系数关系（韦达定理）仍然成立． 求解复数集上的方程的方法：（1）设(,)z x yi x y =+∈R 化归为实数方程来解决（化归思想）．（2）把z 看成一个未知数（而不是实部和虚部两个未知数），用复数的性质来变形（整体思想）． （3）对二次方程，直接用一元二次方程的求根公式（公式法）． 图1图2三、常见几何图形的复数表达式 复数1z ，2z 为定值，且12z z ≠．（1）线段12Z Z 的中垂线方程：12||||z z z z -=-； （2）以1Z 为圆心，半径为r 的圆方程：1||z z r -=； （3）以1Z 、2Z 为焦点，长轴长为2(0)a a >的椭圆方程：12||||2z z z z a -+-=（其中12||2z z a -<）； （4）以1Z 、2Z 为焦点，实轴长为2(0)a a >的双曲线方程：12||||||2z z z z a ---=（其中12||2z z a ->）．1、复数的平方根与立方根 【例1】求4-及86i -的平方根．【难度】★【答案】4-的平方根为2i 或2i -；86i -的平方根为3i -或3i -+ 【例2】计算：（1）615212(13)(13)112(1)22i i i i i ---⎛⎫-+ ⎪⎝⎭；（2）50820028223(22)112313i i i i i i ⎛⎫-+++-++ ⎪ ⎪ ⎪-+-⎝⎭⎝⎭． 例题解析【注意】 （1）在复数集C 中的一元二次方程的求根公式和韦达定理仍适用，但根的判别式仅 在实数集上有效； （2）实系数一元二次方程在复数集中一定有根，若是虚根则一定成对出现； （3）齐二次实系数二次方程2211220(,,)az bz z cz a b c R ++=∈，将等式两端除以2z 后，将得到一个关于12zz 得实系数一元二次方程；（不作要求） （4）虚系数一元二次方程20(0ax bx c a a b c ++=≠，，，至少有一个为虚数）①判别式判断实根情况失效； ②虚根成对出现的性质失效； 如220x ix --=，虽然70∆=>，但该方程并无实根，不过韦达定理仍适用.【难度】★★【答案】（1）513；（2）247+【例3】记122ω=-+，求1ωω+，221ωω+． 【难度】★★ 【答案】11ωω+=-，2211ωω+=-【例4】已知等比数列123,,,,n z z z z L ，其中11z =，2z x yi =+，3z y xi =+（,,0x y x ∈>R ）． （1）求,x y 的值；（2）试求使1230n z z z z ++++=L 的最小正整数n ；（3）对（2）中的正整数n ，求123n z z z z g g gL g 的值． 【难度】★★【答案】（1）12x y ⎧=⎪⎪⎨⎪=⎪⎩；（2）12n =；（3）1-．【巩固训练】1．复数34i +的平方根是 ．【难度】★ 【答案】(2)i ±+2．计算：（11996= ． （2）151512(1)(1)(1)i -=-+ ． 【难度】★ 【答案】（1）122-；（2）03．已知ω满足等式210ωω++=．（1）计算4(1)ωω++；304050ωωω++；224(1)(1)ωωωω-+-+；（2）求证：对任意复数u ，有恒等式33233(1)()()3(1)u u u u ωω+++++=+； （3）计算：21n n ωω++，*n ∈N ． 【难度】★★【答案】（1）1-；0；4；（2）略；（3）*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式：2223x x ++ 【难度】★【答案】222223244x x x x ⎛⎫⎛⎫-+-++=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭2x x ⎛=+- ⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=，求()41z z ++的值 【难度】★★【答案】由210z z ++=得，211022z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1．若虚数z 满足327z =，则32315z z z +++的值为 ． 【难度】★★ 【答案】332．1≠ω，13=ω，求32302ωωω+++Λ的值.【难度】★★【答案】122i ω=-+时，原式=15-；122ω=--时，原式；3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ，求方程的解．【难度】★【答案】920m ∆=-当0∆>时，即920m <时，32x ±=；当0∆=时，即920m =时，32x =；当0∆<时，即920m >时，32i x ±=．【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根，且2αβ∈R ，求βα的值．【难度】★★【答案】∵2αβ∈R ，∴2222ααβαββαβ=⇒=，即330αβ-=∴12αβ=-± 【例9】已知12,x x 是实系数方程20x x p ++=的两个根，且满足12||3x x -=，求实数p 的值． 【难度】★★ 【答案】14p ∆=-，（1）当0∆≥时，即14p ≤时，12,x x 是实根，∴12||3x x -==，即32p =⇒=-；（2）当0∆<时，即14p >时，12,x x 是共轭虚根，设1(,)x a bi a b =+∈R ，则2x a bi =-， ∴123|||2|2||32x x bi b b -===⇒=±，由1221x x a +==-，得12a =-．从而21215||2p x x x ===．综上，2p =-或52．【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根，求||||αβ+的值．【难度】★★【答案】212m ∆=-，（1）当0∆≥时，即m ≥m ≤-30αβ=>，∴||||||||m αβαβ+=+=；（2）当0∆<时，即m -<<||||2||αβα+===【例11】已知复数12,z z 满足1||2z =，2||1z =，12||2z z -=，求12z z ． 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=， ∴12121z z z z ⋅+⋅=， ∴122211211z zz z z z z z ⋅⋅+⋅⋅=， ∴122141z zz z +=． 令12z t z =，则141t t+=， ∴240t t -+=，∴122t i =±，即1212z z =．【例12】（1）方程20()x px k p -+=∈R 有一个根为12i +，求实数k 的值； （2）方程240x x k -+=有一个根为12i +，求k 的值． 【难度】★【答案】（1）由题意：另一个根为12i -，∴(12)(12)5k i i =+-=； （2）由题意2(12)4(12)074i i k k i +-++=⇒=+．【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根，且一个根的模是2，求实数a 、b 的值． 【难度】★★【答案】设()t t ∈R 是方程的一实根，则2(2)()i 0t at a bt b -++-=．则220,0t at a bt b ⎧-+=⎨-=⎩．（1）当0b =时，此方程为220x ax a -+=．①有实根，0∆≥即1a ≥或0a ≤． 当根为2时，440a a -+=．得43a =．当根为2-时，440a a ++=．得45a =-． ②有一对共轭虚根即01a <<．模为2，即有4a =（舍）．（2）当0b ≠时，则1t =，此时1a =．又因为模为2，所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1．下列命题在复数集中是否正确？为什么？（1）若,,a b c ∈R ，0a ≠，且240b ac -≥，则方程20ax bx c ++=有两个实数根； （2）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则12b x x a +=-，12c x x a=； （3）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则221212||()x x x x -=-；（4）若,,a b c ∈R ，0a ≠，且α是方程20ax bx c ++=的根，则α也是方程的根． 【难度】★★【答案】（1）、（2）、（4）正确，（3）不正确2．若12,x x 为方程270x x -+=的两个根，则212||x x -= ．【难度】★★ 【答案】273．已知,0x y ≠且022=++y xy x ，求20092009()()x y x y x y+++的值. 【难度】★★【答案】14．关于x 的方程222(31)10x m x m --++=的两根为αβ、，且||||3αβ+=，求实数m 的值． 【难度】★★【答案】53m =-或m =5．设αβ、为方程220x x t ++=，（t ∈R ）的两个根，()||||f t αβ=+，（1）求()f t 的解析式；（2）证明关于t 的方程()f t m =，当2m >时恰有两个不等的根，且两根之和为定值． 【难度】★★【答案】（1）0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩．．．（2）证明：函数()y f t =的图像关于直线12t =对称（证略） 当(1,)t ∈+∞时，()f t 为增函数，且()(2,)f t ∈+∞； 当(,0)t ∈-∞时，()f t 为减函数，且()(2,)f t ∈+∞．所以当2m >，方程()f t m =在区间(1,)+∞上有唯一解1t ，在区间(,0)-∞上也有唯一解2t ， 则121212t t +=⨯=．4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中，1z ，2z ，m 都是复数，且21241620z z i -=+，设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值． 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=．∴2121|(4)|74m z z --=，即|(45)|7m i -+=， 这表明复数m 在以(4,5)C 为圆心，7为半径的圆周上，∴max ||7m =，min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<．【例14】已知22016220160122016(1)x x a a x a x a x ++=++++g g g ，试求0362016a a a a ++++g g g 的值。

第2讲椭圆（一）热点透析考察目标 1.考查椭圆的定义及应用；2.考查椭圆的方程、几何性质；3.考查直线与椭圆的位置关系．达成目标 1.熟练掌握椭圆的定义、几何性质；2.会利用定义法、待定系数法求椭圆方程；3.重视数学思想方法的应用，体会解析几何的本质——用代数方法求解几何问题．知识回顾1.椭圆的概念在平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a>0，c>0，且a，c为常数：(1)若a>c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a<c，则集合P为空集.2.椭圆的标准方程和几何性质附件：当堂过手训练（快练五分钟，稳准建奇功！）1.判断下面结论是否正确(请在括号中打“√”或“×”)(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆. (×)(2)椭圆上一点P与两焦点F1，F2构成△PF1F2的周长为2a＋2c(其中a为椭圆的长半轴长，c为椭圆的半焦距).( √ ) (3)椭圆的离心率e 越大，椭圆就越圆.( × ) (4)方程mx 2＋ny 2＝1(m >0，n >0，m ≠n )表示的曲线是椭圆.( √ ) 2.已知椭圆的焦点在y 轴上，若椭圆x 22＋y 2m ＝1的离心率为12，则m 的值是( )A.23B.43C.53D.83答案 D解析 由题意知a 2＝m ，b 2＝2，∴c 2＝m －2. ∵e ＝12，∴c 2a 2＝14，∴m －2m ＝14，∴m ＝83.3.(2013·广东)已知中心在原点的椭圆C 的右焦点为F (1,0)，离心率等于12，则C 的方程是( )A.x 23＋y 24＝1 B.x 24＋y 23＝1 C.x 24＋y 22＝1D.x 24＋y 23＝1 答案 D解析 由题意知c ＝1，e ＝c a ＝12，所以a ＝2，b 2＝a 2－c 2＝3.故所求椭圆方程为x 24＋y 23＝1.4.如果方程x 2＋ky 2＝2表示焦点在y 轴上的椭圆，那么实数k 的取值范围是__________. 答案 (0,1)解析 将椭圆方程化为x 22＋y 22k＝1，∵焦点在y 轴上，∴2k>2，即k <1，又k >0，∴0<k <1.5.已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的两焦点为F 1、F 2，以F 1F 2为边作正三角形，若椭圆恰好平分正三角形的另两条边，则椭圆的离心率为________. 答案3－1解析 设过左焦点F 1的正三角形的边交椭圆于A ，则|AF 1|＝c ，|AF 2|＝3c ，有2a ＝(1＋3)c ， ∴e ＝c a ＝21＋3＝3－1.二、高频考点专题链接题型一 椭圆的定义及标准方程例1 (1)已知圆(x ＋2)2＋y 2＝36的圆心为M ，设A 为圆上任一点，且点N (2,0)，线段AN 的垂直平分线交MA 于点P ，则动点P 的轨迹是( )A.圆B.椭圆C.双曲线D.抛物线(2)已知椭圆以坐标轴为对称轴，且长轴是短轴的3倍，并且过点P (3,0)，则椭圆的方程为________.(3)已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P 1(6，1)、P 2(－3，－2)，则椭圆的方程为________.提示 (1)题主要考虑椭圆的定义； (2)题要分焦点在x 轴和y 轴上两种情况； (3)可以用待定系数法求解.答案 (1)B (2)x 29＋y 2＝1或y 281＋x 29＝1(3)x 29＋y 23＝1 解析 (1)点P 在线段AN 的垂直平分线上， 故|P A |＝|PN |， 又AM 是圆的半径，∴|PM |＋|PN |＝|PM |＋|P A |＝|AM |＝6>|MN |， 由椭圆定义知，P 的轨迹是椭圆.(2)若焦点在x 轴上，设方程为x 2a 2＋y 2b 2＝1(a >b >0)，∵椭圆过P (3,0)，∴32a 2＋02b 2＝1，即a ＝3，又2a ＝3×2b ，∴b ＝1，方程为x 29＋y 2＝1.若焦点在y 轴上，设方程为y 2a 2＋x 2b 2＝1(a >b >0).∵椭圆过点P (3,0).∴02a 2＋32b 2＝1，即b ＝3.又2a ＝3×2b ，∴a ＝9，∴方程为y 281＋x 29＝1.∴所求椭圆的方程为x 29＋y 2＝1或y 281＋x 29＝1.(3)设椭圆方程为mx 2＋ny 2＝1(m >0，n >0且m ≠n ). ∵椭圆经过P 1、P 2点，∴P 1、P 2点坐标适合椭圆方程.则⎩⎪⎨⎪⎧6m ＋n ＝1， ①3m ＋2n ＝1， ②①、②两式联立，解得⎩⎨⎧m ＝19，n ＝13.∴所求椭圆方程为x 29＋y 23＝1.注意 (1)求椭圆的方程多采用定义法和待定系数法，利用椭圆的定义定形状时，一定要注意常数2a >|F 1F 2|这一条件.(2)求椭圆标准方程的基本方法是待定系数法，具体过程是先定形，再定量，即首先确定焦点所在位置，然后再根据条件建立关于a ，b 的方程组.如果焦点位置不确定，要考虑是否有两解，有时为了解题方便，也可把椭圆方程设为mx 2＋ny 2＝1 (m >0，n >0，m ≠n )的形式.(1)过点(3，－5)，且与椭圆y 225＋x 29＝1有相同焦点的椭圆的标准方程为________.(2)已知P 是椭圆x 2100＋y 236＝1上一点，F 1、F 2分别是椭圆的左、右焦点，若∠F 1PF 2＝60°，则△PF 1F 2的面积为________.答案 (1)y 220＋x 24＝1 (2)12 3解析 (1)方法一 椭圆y 225＋x 29＝1的焦点为(0，－4)，(0,4)，即c ＝4.由椭圆的定义知，2a ＝(3－0)2＋(－5＋4)2＋(3－0)2＋(－5－4)2，解得a ＝2 5.由c 2＝a 2－b 2可得b 2＝4.所以所求椭圆的标准方程为y 220＋x 24＝1.方法二 因为所求椭圆与椭圆y 225＋x 29＝1的焦点相同，所以其焦点在y 轴上，且c 2＝25－9＝16.设它的标准方程为y 2a 2＋x 2b 2＝1(a >b >0).因为c 2＝16，且c 2＝a 2－b 2，故a 2－b 2＝16.①又点(3，－5)在所求椭圆上，所以(－5)2a 2＋(3)2b 2＝1，即5a 2＋3b2＝1.②由①②得b 2＝4，a 2＝20，所以所求椭圆的标准方程为y 220＋x 24＝1.(2)根据椭圆的定义，得|PF 1|＋|PF 2|＝20，①在△PF 1F 2中，由余弦定理，得|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|cos 60°＝256.②①2－②得|PF 1|·|PF 2|＝48.∴S △PF 1F 2＝12|PF 1|·|PF 2|sin 60°＝12 3.题型二 椭圆的几何性质例2 (1)在Rt △ABC 中，AB ＝AC ＝1，如果一个椭圆通过A ，B两点，它的一个焦点为点C ，另一个焦点在AB 上，求这个椭圆的离心率. (2)如图，焦点在x 轴上的椭圆x 24＋y 2b 2＝1的离心率e ＝12，F ，A 分别是椭圆的一个焦点和顶点，P 是椭圆上任意一点，求PF →·P A →的最大值和 最小值.提示 本题主要考查椭圆的几何性质及其应用，解题(1)的关键是根据题意求出a ，c 的值；解题(2)的关键是表示出PF →·P A →，根据椭圆的性质确定变量的取值范围.解 (1)设椭圆的焦半径为c ，设另一个焦点为F ，如图所示， ∵AB ＝AC ＝1，△ABC 为直角三角形， ∴1＋1＋2＝4a ，则a ＝2＋24.设F A ＝x ，∴⎩⎪⎨⎪⎧x ＋1＝2a ，1－x ＋2＝2a ，∴x ＝22，∴1＋(22)2＝4c 2，∴c ＝64，e ＝ca＝6－ 3. (2)设P 点坐标为(x 0，y 0).由题意知a ＝2， ∵e ＝c a ＝12，∴c ＝1，∴b 2＝a 2－c 2＝3.所求椭圆方程为x 24＋y 23＝1.∴－2≤x 0≤2，－3≤y 0≤ 3.又F (－1,0)，A (2,0)，PF →＝(－1－x 0，－y 0)， P A →＝(2－x 0，－y 0)，∴PF →·P A →＝x 20－x 0－2＋y 20＝14x 20－x 0＋1＝14(x 0－2)2. 当x 0＝2时，PF →·P A →取得最小值0， 当x 0＝－2时，PF →·P A →取得最大值4. 注意 (1)求椭圆的离心率的方法①直接求出a ，c 来求解e .通过已知条件列方程组，解出a ，c 的值.②构造a ，c 的齐次式，解出e .由已知条件得出关于a ，c 的二元齐次方程，然后转化为关于离心率e 的一元二次方程求解.③通过取特殊值或特殊位置，求出离心率.(2)椭圆的范围或最值问题常常涉及一些不等式.例如，－a ≤x ≤a ，－b ≤y ≤b,0<e <1等，在求椭圆相关量的范围时，要注意应用这些不等关系.(1)已知点F 1，F 2是椭圆x 2＋2y 2＝2的两个焦点，点P 是该椭圆上的一个动点，那么|PF 1→＋PF 2→|的最小值是( )A.0B.1C.2D.2 2(2)(2013·辽宁)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F ，椭圆C 与过原点的直线相交于A ，B 两点，连接AF ，BF .若|AB |＝10，|AF |＝6，cos ∠ABF ＝45，则C 的离心率e ＝________.答案 (1)C (2)57解析 (1)设P (x 0，y 0)，则PF 1→＝(－1－x 0，－y 0)， PF 2→＝(1－x 0，－y 0)，∴PF 1→＋PF 2→＝(－2x 0，－2y 0)， ∴|PF 1→＋PF 2→|＝4x 20＋4y 20＝22－2y 20＋y 20＝2－y 20＋2.∵点P 在椭圆上，∴0≤y 20≤1，∴当y 20＝1时，|PF 1→＋PF 2→|取最小值2.故选C.(2)如图，在△ABF 中，|AB |＝10，|AF |＝6，且cos ∠ABF ＝45，设|BF |＝m ， 由余弦定理，得 62＝102＋m 2－20m ·45，∴m 2－16m ＋64＝0，∴m ＝8.因此|BF |＝8，AF ⊥BF ，c ＝|OF |＝12|AB |＝5.设椭圆右焦点为F ′，连接BF ′，AF ′，由对称性，|BF′|＝|AF|＝6，∴2a＝|BF|＋|BF′|＝14.∴a＝7，因此离心率e＝ca ＝5 7.题型三直线与椭圆的位置关系例3已知椭圆x2 a2＋y2b2＝1(a>b>0)的一个顶点为B(0,4)，离心率e＝55，直线l交椭圆于M，N两点.(1)若直线l的方程为y＝x－4，求弦MN的长.(2)如果△BMN的重心恰好为椭圆的右焦点F，求直线l方程的一般式.提示直线与圆锥曲线的关系问题，一般可以直接联立方程，“设而不求”，把方程组转化成关于x或y的一元二次方程，利用根与系数的关系及弦长公式求解.解(1)由已知得b＝4，且ca ＝55，即c2a2＝15，∴a2－b2a2＝15，解得a2＝20，∴椭圆方程为x220＋y216＝1.则4x2＋5y2＝80与y＝x－4联立，消去y得9x2－40x＝0，∴x1＝0，x2＝409，∴所求弦长|MN|＝1＋12|x2－x1|＝402 9.(2)椭圆右焦点F的坐标为(2,0)，设线段MN的中点为Q(x0，y0)，由三角形重心的性质知BF →＝2FQ →，又B (0,4)，∴(2，－4)＝2(x 0－2，y 0)，故得x 0＝3，y 0＝－2，即得Q 的坐标为(3，－2).设M (x 1，y 1)，N (x 2，y 2)，则x 1＋x 2＝6，y 1＋y 2＝－4，且x 2120＋y 2116＝1，x 2220＋y 2216＝1， 以上两式相减得(x 1＋x 2)(x 1－x 2)20＋(y 1＋y 2)(y 1－y 2)16＝0， ∴k MN ＝y 1－y 2x 1－x 2＝－45·x 1＋x 2y 1＋y 2 ＝－45×6－4＝65， 故直线MN 的方程为y ＋2＝65(x －3)， 即6x －5y －28＝0.注意 (1)解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题.涉及弦中点的问题常常用“点差法”解决，往往会更简单.(2)设直线与椭圆的交点坐标为A (x 1，y 1)，B (x 2，y 2)，则|AB |＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2] ＝ (1＋1k2)[(y 1＋y 2)2－4y 1y 2](k 为直线斜率). 提醒：利用公式计算直线被椭圆截得的弦长是在方程有解的情况下进行的，不要忽略判别式.已知椭圆G ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为63，右焦点为(22，0).斜率为1的直线l 与椭圆G 交于A ，B 两点，以AB 为底边作等腰三角形，顶点为P (－3,2).(1)求椭圆G 的方程；(2)求△P AB 的面积.解 (1)由已知得c ＝22，c a ＝63，解得a ＝2 3. 又b 2＝a 2－c 2＝4，所以椭圆G 的方程为x 212＋y 24＝1. (2)设直线l 的方程为y ＝x ＋m ，由⎩⎪⎨⎪⎧y ＝x ＋m ，x 212＋y 24＝1.消去y 得4x 2＋6mx ＋3m 2－12＝0.①设A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)(x 1<x 2)，AB 中点为E (x 0，y 0)，则x 0＝x 1＋x 22＝－3m 4，y 0＝x 0＋m ＝m 4. 因为AB 是等腰△P AB 的底边，所以PE ⊥AB ，所以PE 的斜率k ＝2－m 4－3＋3m 4＝－1，解得m ＝2. 此时方程①为4x 2＋12x ＝0，解得x 1＝－3，x 2＝0，所以y 1＝－1，y 2＝2.所以|AB |＝32，又点P (－3,2)到直线AB ：x －y ＋2＝0的距离d ＝|－3－2＋2|2＝322. 所以△P AB 的面积S ＝12|AB |·d ＝92.反思总结：高考中圆锥曲线的离心率问题典例：(10分)(1) 如图，椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左焦点为F 1， 上顶点为B 2，右顶点为A 2，过点A 2作x 轴的垂线交直线F 1B 2于点P ，若|P A 2|＝3b ，则椭圆C 的离心率为________.(2)已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1(－c,0)、 F 2(c,0)，若椭圆上存在点P 使a sin ∠PF 1F 2＝c sin ∠PF 2F 1，则该椭圆的离心率的取值范围为 ________.提示 椭圆的离心率利用方程思想，只需利用题目条件得到a ，b ，c 的一个关系式即可.若得到的关系式含b ，可利用a 2＝b 2＋c 2转化为只含a ，c 的关系式.解析 (1)由题设知|B 2O ||P A 2|＝|F 1O ||F 1A 2|⇒b 3b＝c a ＋c ＝13，e ＝12. (2)依题意及正弦定理，得|PF 2||PF 1|＝a c (注意到P 不与F 1F 2共线)， 即|PF 2|2a －|PF 2|＝a c， ∴2a |PF 2|－1＝c a ，∴2a |PF 2|＝c a ＋1>2a a ＋c， 即e ＋1>21＋e，∴(e ＋1)2>2. 又0<e <1，因此2－1<e <1.答案 (1)12(2)(2－1,1) 注意 离心率是椭圆的重要几何性质，是高考重点考查的一个知识点.这类问题一般有两类：一类是根据一定的条件求椭圆的离心率；另一类是根据一定的条件求离心率的取值范围.无论是哪类问题，其难点都是建立关于a ，b ，c 的关系式(等式或不等式)，并且最后要把其中的b 用a ，c 表达，转化为关于离心率e 的关系式，这是化解有关椭圆的离心率问题难点的根本方法.方法技巧1.求椭圆的标准方程时，应从“定形”“定式”“定量”三个方面去思考.“定形”就是指椭圆的对称中心在原点，以坐标轴为对称轴的情况下，能否确定椭圆的焦点在哪个坐标轴上.“定式”就是根据“形”设出椭圆方程的具体形式，“定量”就是指利用定义和已知条件确定方程中的系数a ，b 或m ，n .2.讨论椭圆的几何性质时，离心率问题是重点，求离心率的常用方法有以下两种：(1)求得a ，c 的值，直接代入公式e ＝c a求得； (2)列出关于a ，b ，c 的齐次方程(或不等式)，然后根据b 2＝a 2－c 2，消去b ，转化成关于e 的方程(或不等式)求解.总结1.判断两种标准方程的方法为比较标准形式中x 2与y 2的分母大小.2.注意椭圆的范围，在设椭圆x 2a 2＋y 2b 2＝1 (a >b >0)上点的坐标为P (x ，y )时，则|x |≤a ，这往往在求与点P 有关的最值问题中特别有用，也是容易被忽略而导致求最值错误的原因.巩固练习(时间：40分钟)一、选择题1.已知椭圆C 的短轴长为6，离心率为45，则椭圆C 的焦点F 到长轴的一个端点的距离为( ) A.9B.1C.1或9D.以上都不对 答案 C解析 ⎩⎪⎨⎪⎧ b ＝3c a ＝45a 2＝b 2＋c 2，解得a ＝5，b ＝3，c ＝4.∴椭圆C 的焦点F 到长轴的一个端点的距离为a ＋c ＝9或a －c ＝1.2.设F 1、F 2分别是椭圆x 225＋y 216＝1的左、右焦点，P 为椭圆上一点，M 是F 1P 的中点，|OM |＝3，则P 点到椭圆左焦点的距离为( ) A.4 B.3 C.2D.5 答案 A解析 由题意知|OM |＝12|PF 2|＝3， ∴|PF 2|＝6，∴|PF 1|＝2×5－6＝4.3.已知椭圆x 210－m ＋y 2m －2＝1的焦距为4，则m 等于 ( )A.4B.8C.4或8D.以上均不对 答案 C解析 由⎩⎪⎨⎪⎧ 10－m >0m －2>0，得2<m <10， 由题意知(10－m )－(m －2)＝4或(m －2)－(10－m )＝4，解得m ＝4或m ＝8.4.(2012·江西)椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别是A 、B ，左、右焦点分别是F 1、F 2，若|AF 1|，|F 1F 2|，|F 1B |成等比数列，则此椭圆的离心率为( ) A.14 B.55 C.12 D.5－2答案 B解析 由题意知|AF 1|＝a －c ，|F 1F 2|＝2c ，|F 1B |＝a ＋c ，且三者成等比数列，则|F 1F 2|2＝|AF 1|·|F 1B |，即4c 2＝a 2－c 2，a 2＝5c 2，所以e 2＝15，所以e ＝55. 5.已知圆M ：x 2＋y 2＋2mx －3＝0(m <0)的半径为2，椭圆C ：x 2a 2＋y 23＝1的左焦点为F (－c,0)，若垂直于x 轴且经过F 点的直线l 与圆M 相切，则a 的值为( ) A.34 B.1 C.2 D.4答案 C解析 圆M 的方程可化为(x ＋m )2＋y 2＝3＋m 2，则由题意得m 2＋3＝4，即m 2＝1(m <0)，∴m ＝－1，则圆心M 的坐标为(1,0).由题意知直线l 的方程为x ＝－c ，又∵直线l 与圆M 相切，∴c ＝1，∴a 2－3＝1，∴a ＝2.二、填空题6.(2013·福建)椭圆Г：x 2a 2＋y 2b2＝1(a >b >0)的左，右焦点分别为F 1，F 2，焦距为2c .若直线y ＝3(x ＋c )与椭圆Г的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于________.答案 3－1解析 由直线方程为y ＝3(x ＋c )，知∠MF 1F 2＝60°，又∠MF 1F 2＝2∠MF 2F 1，所以∠MF 2F 1＝30°，MF 1⊥MF 2，所以|MF 1|＝c ，|MF 2|＝3c所以|MF 1|＋|MF 2|＝c ＋3c ＝2a .即e ＝c a ＝3－1. 7.已知椭圆x 2a 2＋y 2b 2＝1 (a >b >0)的离心率等于13，其焦点分别为A 、B ，C 为椭圆上异于长轴端点的任意一点，则在△ABC 中，sin A ＋sin B sin C的值等于________. 答案 3解析 在△ABC 中，由正弦定理得sin A ＋sin B sin C ＝|CB |＋|CA ||AB |，因为点C 在椭圆上，所以由椭圆定义知|CA |＋|CB |＝2a ，而|AB |＝2c ，所以sin A ＋sin B sin C ＝2a 2c ＝1e＝3. 8.椭圆x 24＋y 2＝1的左，右焦点分别为F 1，F 2，点P 为椭圆上一动点，若∠F 1PF 2为钝角，则点P 的横坐标的取值范围是________.答案 (－263，263) 解析 设椭圆上一点P 的坐标为(x ，y )，则F 1P →＝(x ＋3，y )，F 2P →＝(x －3，y ).∵∠F 1PF 2为钝角，∴F 1P →·F 2P →<0，即x 2－3＋y 2<0，① ∵y 2＝1－x 24，代入①得x 2－3＋1－x 24<0， 34x 2<2，∴x 2<83. 解得－263<x <263，∴x ∈(－263，263). 三、解答题9.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，其中左焦点F (－2,0). (1)求椭圆C 的方程；(2)若直线y ＝x ＋m 与椭圆C 交于不同的两点A ，B ，且线段AB 的中点M 在圆x 2＋y 2＝1上，求m 的值.解 (1)由题意，得⎩⎪⎨⎪⎧ c a ＝22，c ＝2，a 2＝b 2＋c 2.解得⎩⎪⎨⎪⎧a ＝22，b ＝2. ∴椭圆C 的方程为x 28＋y 24＝1. (2)设点A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)，线段AB 的中点为M (x 0，y 0)，由⎩⎪⎨⎪⎧x 28＋y 24＝1，y ＝x ＋m .消去y 得，3x 2＋4mx ＋2m 2－8＝0， Δ＝96－8m 2>0，∴－23<m <23，∵x 0＝x 1＋x 22＝－2m 3，∴y 0＝x 0＋m ＝m 3， ∵点M (x 0，y 0)在圆x 2＋y 2＝1上， ∴(－2m 3)2＋(m 3)2＝1，∴m ＝±355. 10.设椭圆x 2a 2＋y 2b2＝1(a >b >0)的左，右焦点分别为F 1，F 2.点P (a ，b )满足|PF 2|＝|F 1F 2|. (1)求椭圆的离心率e .(2)设直线PF 2与椭圆相交于A ，B 两点.若直线PF 2与圆(x ＋1)2＋(y －3)2＝16相交于M ，N 两点，且|MN |＝58|AB |，求椭圆的方程.解 (1)设F 1(－c,0)，F 2(c,0)(c >0)，整理得2(c a )2＋c a －1＝0，解得c a ＝－1(舍)，或c a ＝12. 所以e ＝12. (2)由(1)知a ＝2c ，b ＝3c ，可得椭圆方程为3x 2＋4y 2＝12c 2，直线PF 2的方程为y ＝3(x －c ).A ，B 两点的坐标满足方程组⎩⎪⎨⎪⎧3x 2＋4y 2＝12c 2，y ＝3(x －c ). 消去y 并整理，得5x 2－8cx ＝0.解得x 1＝0，x 2＝85c . 得方程组的解⎩⎪⎨⎪⎧ x 1＝0，y 1＝－3c ，⎩⎨⎧ x 2＝85c ，y 2＝335c .不妨设A (85c ，335c )，B (0，－3c )， 所以|AB |＝ (85c )2＋(335c ＋3c )2＝165c . 于是|MN |＝58|AB |＝2c . 圆心(－1，3)到直线PF 2的距离 d ＝|－3－3－3c |2＝3|2＋c |2. 因为d 2＋(|MN |2)2＝42， 所以34(2＋c )2＋c 2＝16. 整理得7c 2＋12c －52＝0，得c ＝－267(舍)，或c ＝2. 所以椭圆方程为x 216＋y 212＝1. 拓展训练(时间：30分钟)1.(2013·四川)从椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点P 向x 轴作垂线，垂足恰为左焦点F 1，A 是椭圆与x 轴正半轴的交点，B 是椭圆与y 轴正半轴的交点，且AB ∥OP (O 是坐标原点)，则该椭圆的离心率是( ) A.24 B.12C.22D.32 答案 C解析 由题意可设P (－c ，y 0)(c 为半焦距)，k OP ＝－y 0c ，k AB ＝－b a，由于OP ∥AB ， ∴－y 0c ＝－b a ，y 0＝bc a， 把P ⎝⎛⎭⎫－c ，bc a 代入椭圆方程得(－c )2a 2＋⎝⎛⎭⎫bc a 2b 2＝1， 而⎝⎛⎭⎫c a 2＝12，∴e ＝c a ＝22.选C. 2.已知F 1、F 2是椭圆的两个焦点，满足MF 1→·MF 2→＝0的点M 总在椭圆内部，则椭圆离心率的取值范围是( ) A.(0,1)B.(0，12]C.(0，22) D.[22，1) 答案 C解析 ∵满足MF 1→·MF 2→＝0的点M 在圆x 2＋y 2＝c 2上，∴圆x 2＋y 2＝c 2在椭圆内部，即c <b ，∴c 2<b 2＝a 2－c 2,2c 2<a 2，∴e 2<12，即e ∈(0，22). 3.在椭圆x 216＋y 24＝1内，通过点M (1,1)，且被这点平分的弦所在的直线方程为( ) A.x ＋4y －5＝0B.x －4y －5＝0C.4x ＋y －5＝0D.4x －y －5＝0答案 A解析 设直线与椭圆交点为A (x 1，y 1)，B (x 2，y 2)，则⎩⎨⎧ x 2116＋y 214＝1， ①x 2216＋y 224＝1， ②由①－②，得(x 1＋x 2)(x 1－x 2)16＋(y 1＋y 2)(y 1－y 2)4＝0， 因⎩⎪⎨⎪⎧x 1＋x 2＝2，y 1＋y 2＝2，所以y 1－y 2x 1－x 2＝－4(x 1＋x 2)16(y 1＋y 2)＝－14， 所以所求直线方程为y －1＝－14(x －1)， 即x ＋4y －5＝0.4.点P 是椭圆x 225＋y 216＝1上一点，F 1，F 2是椭圆的两个焦点，且△PF 1F 2的内切圆半径为1，当P 在第一象限时，P 点的纵坐标为________.答案 83解析 |PF 1|＋|PF 2|＝10，|F 1F 2|＝6， 21F PF S ∆＝12(|PF 1|＋|PF 2|＋|F 1F 2|)·1＝8＝12|F 1F 2|·y P ＝3y P .所以y P ＝83. 5.设F 1、F 2分别是椭圆x 225＋y 216＝1的左、右焦点，P 为椭圆上任一点，点M 的坐标为(6,4)，则|PM |＋|PF 1|的最大值为________.答案 15解析 |PF 1|＋|PF 2|＝10，|PF 1|＝10－|PF 2|，|PM |＋|PF 1|＝10＋|PM |－|PF 2|，易知M 点在椭圆外，连接MF 2并延长交椭圆于P 点，此时|PM |－|PF 2|取最大值|MF 2|，故|PM |＋|PF 1|的最大值为10＋|MF 2|＝10＋(6－3)2＋42＝15. 6.已知中心在原点，焦点在x 轴上的椭圆C 的离心率为12，且经过点M (1，32). (1)求椭圆C 的方程；(2)是否存在过点P (2,1)的直线l 1与椭圆C 相交于不同的两点A ，B ，满足P A →·PB →＝PM →2？若存在，求出直线l 1的方程；若不存在，请说明理由.解 (1)设椭圆C 的方程为x 2a 2＋y 2b 2＝1(a >b >0)， 由题意得⎩⎨⎧1a 2＋94b 2＝1，c a ＝12，a 2＝b 2＋c 2，解得a 2＝4，b 2＝3.故椭圆C 的方程为x 24＋y 23＝1. (2)假设存在直线l 1且由题意得斜率存在，设满足条件的方程为y ＝k 1(x －2)＋1，代入椭圆C 的方程得，(3＋4k 21)x 2－8k 1(2k 1－1)x ＋16k 21－16k 1－8＝0. 因为直线l 1与椭圆C 相交于不同的两点A ，B ，设A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，所以Δ＝[－8k 1(2k 1－1)]2－4(3＋4k 21)·(16k 21－16k 1－8)＝32(6k 1＋3)>0， 所以k 1>－12. 又x 1＋x 2＝8k 1(2k 1－1)3＋4k 21，x 1x 2＝16k 21－16k 1－83＋4k 21， 因为P A →·PB →＝PM →2，即(x 1－2)(x 2－2)＋(y 1－1)(y 2－1)＝54， 所以(x 1－2)(x 2－2)(1＋k 21)＝PM →2＝54. 即[x 1x 2－2(x 1＋x 2)＋4](1＋k 21)＝54. 所以[16k 21－16k 1－83＋4k 21－2·8k 1(2k 1－1)3＋4k 21＋4]·(1＋k 21)＝4＋4k 213＋4k 21＝54，解得k 1＝±12. 因为k 1>－12，所以k 1＝12. 于是存在直线l 1满足条件，其方程为y ＝12x .。

1 第2讲 圆锥曲线【考纲要求】圆锥曲线：1、圆锥曲线方程的求解2、直线与圆锥曲线综合性问题 3、圆锥曲线的离心率问题 【教学重难点】重点：直线与圆锥曲线综合性问题 难点：直线与圆锥曲线综合性问题 【重难点命题方向】椭 圆1．椭圆的概念在平面内与两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．集合P ＝{M ||MF 1|＋|MF 2|＝2a }，|F 1F 2|＝2c ，其中a ＞0，c ＞0，且a ，c 为常数： (1)若a ＞c ，则集合P 为椭圆； (2)若a ＝c ，则集合P 为线段； (3)若a ＜c ，则集合P 为空集． 2．椭圆的标准方程和几何性质标准方程 x 2a 2＋y 2b2＝1(a ＞b ＞0) y 2a 2＋x 2b 2＝1(a ＞b ＞0)图形性质范围 －a ≤x ≤a －b ≤y ≤b －b ≤x ≤b －a ≤y ≤a 对称性 对称轴：x 轴、y 轴对称中心：(0，0)顶点A 1(－a ，0)，A 2(a ，0)B 1(0，－b )，B 2(0，b ) A 1(0，－a )，A 2(0，a ) B 1(－b ，0)，B 2(b ，0)轴 长轴A 1A 2的长为2a 短轴B 1B 2的长为2b焦距 |F 1F 2|＝2c 离心率 e ＝ca，e ∈(0，1) a ，b ，c 的关系c 2＝a 2－b 2[做一做]1．已知中心在原点的椭圆C 的右焦点为F (1，0)，离心率等于12，则C 的方程是( )2 A.x 23＋y 24＝1 B.x 24＋y 23＝1 C.x 24＋y 22＝1 D.x 24＋y 23＝1 2．(2015·浙江省名校联考)已知F 1，F 2是椭圆x 24＋y23＝1的两个焦点，过点F 2作x 轴的垂线交椭圆于A ，B 两点，则△F 1AB 的周长为________．3．若直线x －2y ＋2＝0经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为( ) A.x 25＋y 2＝1 B.x 24＋y 25＝1 C.x 25＋y 2＝1或x 24＋y 25＝1 D ．以上答案都不对 4．(2015·江苏常州调研)若方程x 25－k ＋y2k －3＝1表示椭圆，则k 的取值范围是________．考点一__椭圆的定义及标准方程________________(1)(2015·洛阳市高三年级统考)已知中心在原点的椭圆C 的右焦点为F (15，0)，直线y＝x 与椭圆的一个交点的横坐标为2，则椭圆方程为( )A.x 216＋y 2＝1 B ．x 2＋y 216＝1 C.x 220＋y 25＝1 D.x 25＋y 220＝1 (2)(2014·高考大纲全国卷)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点为F 1、F 2，离心率为33，过F 2的直线l 交C 于A 、B 两点．若△AF 1B 的周长为43，则C 的方程为( )A.x 23＋y 22＝1B.x 23＋y 2＝1C.x 212＋y 28＝1D.x 212＋y 24＝1 (3)已知F 1，F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点，P 为椭圆C 上的一点，且PF 1→⊥PF 2→.若△PF 1F 2的面积为9，则b ＝________．考点二__椭圆的几何性质(高频考点)____________(1)已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的一个焦点是圆x 2＋y 2－6x ＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为( )A ．(－3，0)B ．(－4，0)C ．(－10，0)D ．(－5，0)(2)椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为( )A ．－21B ．21C ．－1925或21 D.1925或21(3)(2014·高考江西卷)设椭圆C ：x 2a 2＋y2b2＝1(a ＞b ＞0)的左，右焦点为F 1，F 2，过F 2作x 轴的垂线与C 相交于A ，B 两点，F 1B 与y 轴相交于点D ，若AD ⊥F 1B ，则椭圆C的离心率等于________.若本例(3)条件变为“过F 1，F 2的两条互相垂直的直线l1，l 2的交点在椭圆的内部”，求离心率的取值范围．2.(1)已知椭圆的长轴长是8，离心率是34，则此椭圆的标准方程是( )A.x 216＋y 27＝1B.x 216＋y 27＝1或x 27＋y 216＝1C.x 216＋y 225＝1D.x 216＋y 225＝1或x 225＋y 216＝1 (2)设e 是椭圆x 24＋y 2k ＝1的离心率，且e ∈(12，1)，则实数k 的取值范围是( )3 A ．(0，3) B ．(3，163) C ．(0，3)∪(163，＋∞) D ．(0，2)(3)已知椭圆短轴上的两个顶点分别为B 1，B 2，焦点为F 1，F 2，若四边形B 1F 1B 2F 2是正方形，则这个椭圆的离心率e 等于( )A.22B.12C.32D.33(4) (2015·安徽合肥质检)如图，焦点在x 轴上的椭圆x 24＋y 2b 2＝1的离心率e ＝12，F ，A 分别是椭圆的一个焦点和顶点，P 是椭圆上任意一点，则PF →·P A →的最大值为________．考点三__直线与椭圆的位置关系________________(2014·高考陕西卷) 已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点(0，3)，离心率为12，左，右焦点分别为F 1(－c ，0)，F 2(c ，0)．(1)求椭圆的方程；(2)若直线l ：y ＝－12x ＋m 与椭圆交于A ，B 两点，与以F 1F 2为直径的圆交于C ，D 两点，且满足|AB ||CD |＝534，求直线l 的方程．双曲线1．双曲线的概念平面内动点P 与两个定点F 1、F 2(|F 1F 2|＝2c ＞0)的距离之差的绝对值为常数2a (0＜2a ＜2c )，则点P 的轨迹叫双曲线．这两个定点叫双曲线的焦点，两焦点间的距离叫焦距．集合P ＝{M |||MF 1|－|MF 2||＝2a }，|F 1F 2|＝2c ，其中a 、c 为常数且a ＞0，c ＞0： (1)当a ＜c 时，P 点的轨迹是双曲线； (2)当a ＝c 时，P 点的轨迹是两条射线； (3)当a ＞c 时，P 点不存在．2．双曲线的标准方程和几何性质标准方程x2a2－y2b2＝1(a＞0，b＞0)y2a2－x2b2＝1(a＞0，b＞0)图形性质范围x≥a或x≤－a，y∈R x∈R，y≤－a或y≥a 对称性对称轴：坐标轴，对称中心：原点顶点A1(－a，0)，A2(a，0)A1(0，－a)，A2(0，a)渐近线y＝±ba x y＝±ab x离心率e＝ca，e∈(1，＋∞)实虚轴线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a；线段B1B2叫做双曲线的虚轴，它的长|B1B2|＝2b；a叫做双曲线的半实轴长，b叫做双曲线的半虚轴长a、b、c的关系c2＝a2＋b2(c＞a＞0，c＞b＞0)[做一做]1．(2014·高考课标全国卷Ⅰ)已知双曲线x2a2－y23＝1(a>0)的离心率为2，则a＝() A．2 B.62 C.52 D．12．已知中心在原点的双曲线C的右焦点为F(3，0)，离心率等于32，则C的方程是() A.x24－y25＝1 B.x24－y25＝1C.x22－y25＝1 D.x22－y25＝13．(2014·高考北京卷)设双曲线C经过点(2，2)，且与y24－x2＝1具有相同渐近线，则C的方程为________；渐近线方程为________．考点一__双曲线的定义________________________(1)(2014·高考大纲全国卷)已知双曲线C的离心率为2，焦点为F1、F2，点A在C上．若|F1A|＝2|F2A|，则cos∠AF2F1＝()A.14 B.13 C.24 D.23(2)P是双曲线x2a2－y2b2＝1(a＞0，b＞0)右支上一点，F1，F2分别为左、右焦点，且焦距为2c，则△PF1F245 的内切圆圆心M 的横坐标是( )A ．aB ．BC ．cD ．a ＋b －c 考点二__求双曲线的标准方程__________________(1)(2015·东北三校联合模拟)与椭圆C ：y 216＋x 212＝1共焦点且过点(1，3)的双曲线的标准方程为( )A ．x 2－y 23＝1B ．y 2－x 212＝1 C.y 22－x 22＝1 D.y 23－x 2＝1(2)(2014·高考江西卷)过双曲线C ：x 2a 2－y 2b2＝1的右顶点作x 轴的垂线，与C 的一条渐近线相交于点A .若以C 的右焦点为圆心、半径为4的圆经过A ，O 两点(O 为坐标原点)，则双曲线C 的方程为( )A.x 24－y 212＝1B.x 27－y 29＝1C.x 28－y 28＝1D.x 212－y 24＝1 考点三__双曲线的几何性质(高频考点)__________(1)(2014·高考广东卷)若实数k 满足0<k <5，则曲线x 216－y 25－k ＝1与曲线x 216－k －y 25＝1的( )A ．实半轴长相等B ．虚半轴长相等C ．离心率相等D ．焦距相等(2)(2014·高考重庆卷)设F 1、F 2分别为双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，双曲线上存在一点P 使得(|PF 1|－|PF 2|)2＝b 2－3ab ，则该双曲线的离心率为( )A. 2B.15 C ．4 D.17(3)(2014·高考山东卷)已知a >b >0，椭圆C 1的方程为x 2a 2＋y 2b 2＝1，双曲线C 2的方程为x 2a 2－y 2b2＝1，C 1与C 2的离心率之积为32，则C 2的渐近线方程为( )A ．x ±2y ＝0 B.2x ±y ＝0 C ．x ±2y ＝0 D．2x ±y ＝03.(1)(2015·忻州市高三联考)已知双曲线C ：x 2n －y 24－n＝1的离心率为3，则C 的渐近线方程为( )A ．y ＝±2xB ．y ＝±2xC ．y ＝±22xD ．y ＝±32x(2)(2015·唐山模拟)已知双曲线x 2－y 2＝4左支上一点P (a ，b )到直线y ＝x 的距离为2，则a ＋b ＝( )A ．2B ．－2C ．4D ．－46 (3)(2015·湖北宜昌调研)已知F 1，F 2是双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点，过F 1且垂直于x 轴的直线与双曲线的左支交于A 、B 两点，若△ABF 2是正三角形，那么双曲线的离心率为( )A. 2B. 3 C ．2 D ．3考点四__与双曲线有关的综合问题______________(2015·湖南宁远一中测试)已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的离心率为2，焦点到渐近线的距离等于3，过右焦点F 2的直线l 交双曲线于A 、B 两点，F 1为左焦点．(1)求双曲线的方程；(2)若△F 1AB 的面积等于62，求直线l 的方程．4.(2015·铜陵模拟)若双曲线E ：x 2a2－y 2＝1(a ＞0)的离心率等于2，直线y ＝kx －1与双曲线E 的右支交于A ，B 两点．(1)求k 的取值范围；(2)若|AB |＝63，求k 的值．【基础限时训练】1．已知0＜θ＜π4，则双曲线C 1：x 2sin 2θ－y 2cos 2θ＝1与C 2：y 2cos 2θ－x 2sin 2θ＝1的( )A ．实轴长相等B ．虚轴长相等C ．离心率相等D ．焦距相等2．(2015·福建宁德模拟)已知椭圆x 2a 2＋y 29＝1(a >0)与双曲线x 24－y 23＝1有相同的焦点，则a 的值为( )A. 2B.10 C ．4 D.34 3．(2014·高考课标全国卷Ⅰ)已知F 为双曲线C ：x 2－my 2＝3m (m >0)的一个焦点，则点F 到C 的一条渐近线的距离为( )A. 3 B ．3 C.3m D ．3m4．(2015·河南开封模拟)设F 1，F 2分别为双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左，右焦点．若在双曲线右支上存在点P ，满足|PF 2|＝|F 1F 2|，且F 2到直线PF 1的距离等于双曲线的实轴长，则该双曲线的离心率为( )A.43B.537 C.54D.4145．(2015·兰州市、张掖市高三联考)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点分别为F 1、F 2，以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3，4)，则此双曲线的方程为( )A.x 216－y 29＝1B.x 23－y 24＝1C.x 29－y 216＝1D.x 24－y 23＝1 6．已知双曲线x 29－y2a＝1的右焦点的坐标为(13，0)，则该双曲线的渐近线方程为________．7．(2015·浙江六市六校联盟模拟)如图所示，已知双曲线以长方形ABCD 的顶点A ，B 为左、右焦点，且双曲线过C ，D 两顶点．若AB ＝4，BC ＝3，则此双曲线的标准方程为________．8．(2015·武汉模拟)已知F 1，F 2分别是双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点，P 为双曲线右支上的任意一点．若|PF 1|2|PF 2|＝8a ，则双曲线的离心率e 的取值范围是________．9．已知双曲线关于两坐标轴对称，且与圆x 2＋y 2＝10相交于点P (3，－1)，若此圆过点P 的切线与双曲线的一条渐近线平行，求此双曲线的方程．10．已知离心率为45的椭圆的中心在原点，焦点在x 轴上，双曲线以椭圆的长轴为实轴，短轴为虚轴，且焦距为234.(1)求椭圆及双曲线的方程；(2)设椭圆的左、右顶点分别为A 、B ，在第二象限内取双曲线上一点P ，连结BP 交椭圆于点M ，连结P A 并延长交椭圆于点N ，若BM →＝MP →，求四边形ANBM 的面积．【老师5分钟答疑】。

进入虚拟课堂高三数学同步辅导教材（第2讲）一、本讲进度导数、多项式函数的导数2.1导数的背景 2.2导数的概念 2.3多项式函数的导数，课本P30～39二、学习指导本讲通过运动物体在某一时刻的瞬时速度（0lim →∆t t s ∆∆）、曲线在某一点处的切线的斜率（0lim →∆x xy ∆∆）、生产的边际成本（0lim→∆q qc∆∆）三个实例（ 也导数的三个重要应用，特别地，曲线在某一点处切线的斜率即是导数的几何意义）.抽象出它们共同的、实质性的东西：函数的变化量△y 与自变量的变化△x 的比值当△x →0时的极限，并定义为函数f (x)在这一点处的导数.（课本P33页）并进而定义了导函数（简称导数）（课本P34页）.导数应用很广泛，经常需要求导，如果都用定义求一遍，不胜其烦，人们就用定义推导出一些常见函数的导函数，并作为公式加以应用.课本内只介绍了两个求导公式：C /=0，及/)(n x =1-n nx（n 为正整数）课P36已予推导；两个法则：[f (x )±g (x ) ]/=/f (x )±g /(x ). [Cf （x ）]/=C /f (x) .请同学们根据定义自行证明一下上述两个法则后再往下看：[f (x )±g (x ) ]/= 0lim>∆x xx g x f x x g x x f ∆±-∆+±∆+)]()([)]()([= 0lim >∆x xx g x x g x f x x f ∆-∆+±-∆+)]()([)]()([=0lim >∆x x x f x x f ∆-∆+)()(±0lim >∆x xx g x x g ∆-∆+)()(=)(/x f ±)(/x g/)]([x Cf =0lim >∆x x x Cf x x Cf ∆-∆+)()(=0lim >∆x （C ·x x f x x f ∆-∆+)()(）=C 0lim >∆x xx f x x f ∆-∆+)()(=)(/x Cf .有了这些工具，我们就能求出一切多项式函数的导数了. 另外，∵x y ∆∆=xx f x x f ∆-∆+)()(00≈)(0/x f ， ∴△y ≈)(0/x f ·△x . 当△x 很小时，可把它作为一个简单易记的近似计算公式。