2014 第25届希望杯高一级全国获奖名单

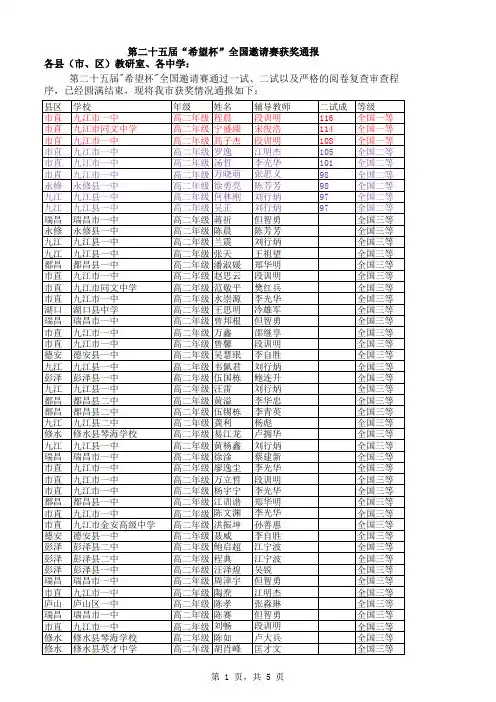
邓效天四广济中心小学镇海 1.412E+11鲍晨（1）广济中心小学四年级王天澍四余姚市崇文书院培训学校 1.412E+11蔡南鹏（3）江北实验小学四年级鲍晨四广济中心小学 1.412E+11陈飞扬（2）宁波江北实验小学四年级何语晨四惠贞书院 1.412E+11陈俊炜南苑小学四年级潘薇羽四江东实验小学 1.412E+11陈可心宁波市海曙中心小学四年级徐睿四宁波市曙光小学 1.412E+11陈志源（2）象山新港小学四年级张鑫亮四镇明中心 1.412E+11储浩展宁波海曙中心小学四年级1.412E+11崔月镇明中心小学四年级冯薏诺四慈溪慈吉小学 1.412E+11代豫宁（3）宁波镇明中心小学四年级顾国琛四宁波高新区实验小学 1.412E+11戴煊朗宁波爱菊艺术学校四年级郭昊东四广济中心小学 1.412E+11邓效天广济中心小学四年级韩越四广济中心 1.412E+11董家烨宁波江东外国语实验小学四年级卢昕冉四象山新港小学 1.412E+11董思涵宁波市实验小学四年级王贝宁四江东实验小学 1.412E+11董玉灵广济中心小学四年级王任聪四宁波宋诏桥小学 1.412E+11董誉江东第二实验小学四年级1王圣宇四东湖小学 1.412E+11费天睿孙文英小学四年级谢天琦四江东中心华光校区 1.412E+11冯奕程广济中心小学四年级许劭洋四江东实验 1.412E+11冯致远宁波广济中心小学四年级叶斯语四广济中心小学 1.412E+11高若晗（3）江东第二实验小学四年级马子媛四江东中心 1.412E+11龚亦婷（3）镇海中心小学四年级谷硕四宁波江北广厦小学 1.412E+11谷硕（2）宁波江北广厦小学四年级王欣楠四镇明中心 1.412E+11顾国琛（3）宁波高新区实验小学四年级杨涵宇四宋诏桥小学 1.412E+11顾家铭宁波市江北中心小学四年级刘京四宁波市东钱湖中心小学 1.412E+11顾晓宁（3）东钱湖中心小学四年级陈飞扬四宁波江北实验小学 1.412E+11郭昊东广济中心小学四年级陈志源四象山新港小学 1.412E+11郭一佑广济中心小学实验校区四年级卢薪宇四宁波市实验小学 1.412E+11郭知承宁波江花小学四年级缪无四镇明中心 1.412E+11何语晨（1）惠贞书院四年级裘天琦四宁波江北实验小学 1.412E+11贺奕飞（3）广济中心小学四年级虞璟轩四江东中心小学 1.412E+11洪思涵宁波市镇海骆驼中心小学四年级章之恒四宁波市镇海骆驼中心小学 1.412E+11洪思妍（3）宁波市曙光小学四年级胡 航四余姚市崇文书院培训学校 1.412E+11胡崇迪象山第三小学四年级卢宇宸四宁波江东幸福苑小学 1.412E+11胡予扬宁波北仑长江小学四年级杨启凡四宁波海曙中心小学 1.412E+11华嘉煜（3）快乐小家四年级葛春晓四宁波炼化小学 1.412E+11华俊伊广济中心小学四年级牛宇天四宁波广济中心小学 1.412E+11黄贰城中小学四年级陶科铭四镇明小学实验校区1.412E+11黄祺恺华高艺校四年级1.412E+11李函益东海实验学校四年级姓名年级学校1.412E+11李扬磊广济中学四年级陈秋宇四宁波炼化小学 1.412E+11李昱喆宁波贝阳奥数学习中心四年级庞祎祺四江东二小学西 1.412E+11林嘉豪象山新港小学四年级蔡南鹏四江北实验小学 1.412E+11林乐成象山石浦小学四年级代豫宁四宁波镇明中心小学 1.412E+11林李科轶象山新港小学四年级丁瑜璐四镇海中心学校 1.412E+11林宇翔（3）江东第二实验小学四年级卢凌越四岷山小学1.412E+11林钰博象山新港小学四年级潘健辉四1.412E+11刘京（2）宁波市东钱湖中心小学四年级王鸿宇四宁波市镇海区中心学校 1.412E+11楼天驰（3）奉化锦屏小学四年级王嵘杰四宁波市实验小学1.412E+11卢凌越岷山小学四年级薛彦辰四市实验 1.412E+11卢昕冉小学四年级陈赉四慈溪慈吉小学 1.412E+11卢薪宇宁波市实验小学四年级张 金四慈溪慈吉小学 1.412E+11卢宇宸（2）宁波江东幸福苑小学四年级谢勤淼四余姚市崇文书院培训学校 1.412E+11马海钟鄞州区东湖小学四年级潘益霄四朝晖实验小学 1.412E+11牟一帆广济中心小学四年级朱立涛四洪塘小学 1.412E+11倪宇澄宁波市镇明中心小学四年级潘炬辉四慈溪慈吉小学 1.412E+11牛宇天（2）宁波广济中心小学四年级高若晗四江东第二实验小学 1.412E+11潘健辉（3）四年级洪思妍四宁波市曙光小学 1.412E+11潘薇羽江东实验小学四年级周楚焜四镇明中心 1.412E+11裘天琦（2）宁波江北实验小学四年级董航四广济中心实验校区 1.412E+11邵晓阳宁波市实验小学四年级徐碧妍四宁波炼化小学 1.412E+11沈霖孙文英小学四年级何佳莹四高塘小学 1.412E+11舒淇（3）宁波高塘小学四年级华嘉煜四快乐小家 1.412E+11宋玄烨奉化锦屏小学四年级黄贰四城中小学 1.412E+11陶融江东第二实验小学四年级林宇翔四江东第二实验小学 1.412E+11王贝宁（2）江东实验小学四年级楼天驰四奉化锦屏小学 1.412E+11王鸿宇宁波市镇海区中心学校四年级卢泓谕四广济中心 1.412E+11王嘉瑶镇明中心小学四年级戚思源四江东二小 1.412E+11王铃菱学四年级王天宜四高塘小学 1.412E+11王旻迟（3）江东第二实验小学四年级应钧衡四宁波海曙中心小学 1.412E+11王任聪（2）宁波宋诏桥小学四年级张熙妍四江东实验小学 1.412E+11王嵘杰（3）宁波市实验小学四年级谢传朋四高桥镇望春小学 1.412E+11王圣宇东湖小学四年级邹敏四镇安小学 1.412E+11王粟潘天寿四年级四年级方凯乐四镇明中心 1.412E+11王昕怡宁波市镇海区应行久外语实验小学四年级舒淇四宁波高塘小学 1.412E+11王孜涵快乐小家四年级顾家铭四宁波市江北中心小学 1.412E+11王子辰（3）北仑区长江小学四年级贺奕飞四广济中心小学 1.412E+11王梓涵宁波市幸福苑实验小学四年级胡贤哲四宁波炼化小学 1.412E+11魏欣晨观海卫镇中心小学四年级江来四宁波炼化小学 1.412E+11文天勤江北中心小学四年级董家烨四宁波江东外国语实验小学 1.412E+11翁翔（3）宁波市镇海骆驼中心小学四年级董思涵四宁波市实验小学 1.412E+11邢倍宁宁波贝阳奥数学习中心四年级龚亦婷四镇海中心小学 1.412E+11徐睿（1）宁波市曙光小学四年级顾晓宁四东钱湖中心小学 1.412E+11徐臻诚宁波江东中心小学中山校区四年级邵晓阳四宁波市实验小学 1.412E+11徐子航宁波江东中心小学华光分校四年级王旻迟四江东第二实验小学 1.412E+11杨晨镇海骆驼中心学校四年级翁翔四宁波市镇海骆驼中心小学 1.412E+11杨涵宇宋诏桥小学四年级袁钧四宁波高塘小学 1.412E+11杨启凡（2）宁波海曙中心小学四年级赵伊晗四象山新港小学 1.412E+11杨雁南王笙舲小学四年级周子皓四江东实验小学 1.412E+11叶斯语广济中心小学四年级范子怡四宁波炼化小学 1.412E+11叶曜嘉海曙中心小学四年级王子辰四北仑区长江小学 1.412E+11尹松屹宁波钟公庙中心小学四年级赵子易四海曙中心 1.412E+11应钧衡宁波海曙中心小学四年级1.412E+11余亦璠宁波镇海中心学校四年级1.412E+11虞璟轩（2）江东中心小学四年级1.412E+11郁凯文宁波宋诏桥小学四年级1.412E+11袁钧宁波高塘小学四年级1.412E+11袁欣怡宁波市孙文英小学四年级1.412E+11曾旭东曙光小学四年级1.412E+11张润恒宁波镇明中心小学四年级1.412E+11张熙妍江东实验小学四年级1.412E+11张欣瑜海曙中心小学四年级1.412E+11张一韵李惠利小学四年级1.412E+11张愉笛宁波广济中心小学分校四年级1.412E+11张哲奔象山新港小学四年级1.412E+11章之恒宁波市镇海骆驼中心小学四年级1.412E+11赵伊晗象山新港小学四年级1.412E+11郑钰霖宁波江东外国语实验小学四年级1.412E+11周佳何宁波广济中心小学四年级1.412E+11周轩宁波贝阳奥数学习中心四年级61.412E+11周雨奇宁波江东中心小学华光校区四年级1.412E+11周子皓江东实验小学四年级1.412E+11朱子腾潘天寿四7四年级1.412E+11卓元圆江北中心小学四年级1.412E+11邹敏镇安小学四年级陈凌宇四年级江东二小西陈露敏四年级江花小学陈吾玚四年级市实验丁瑜璐（3）四年级镇海中心学校董航（3）四年级广济中心实验校区董懿璇四年级江东二小方凯乐（3）四年级镇明中心龚云琦四年级江北实验郭若铭四年级华泰小学韩越（2）四年级广济中心何佳莹（3）四年级高塘小学胡璟玙四年级镇海中心学校卢泓谕（3）四年级广济中心陆行四年级海小陆一昕四年级市实验1马子媛（2）四年级江东中心缪无（2）四年级镇明中心庞皓中四年级广济中心庞祎祺（3）四年级江东二小学西戚思源（3）四年级江东二小史佳仪四年级市实验孙焕四年级镇明中心陶科铭（2）四年级镇明小学实验校区王瀚搏四年级江东中心王天宜（3）四年级高塘小学王添锦四年级江北中心王欣楠（2）四年级镇明中心王一涵四年级镇明中心谢天琦（2）四年级江东中心华光校区徐可迪四年级江东二小徐亦宽四年级镇海中心许劭洋（2）四年级江东实验薛彦辰（3）四年级市实验阎兴宇四年级镇海中心小学杨明宇四年级镇明中心杨宇琪四年级镇明中心於子轩四年级海曙中心张榜四年级江东中心华光校区张赫四年级江东二小西张鑫亮（1）四年级镇明中心赵子易（3）四年级海曙中心周楚焜（3）四年级镇明中心周一巍四年级广济实验祝铭浩四年级江东二小。

希望杯
希望杯，一直受到原国家教委的肯定，并被列入原国家教委批准的全国性竞赛活动的名单中，同时愈来愈多的数学家、数学教育家对邀请赛给予热情的关心和支持。

到第十届为止，参赛城市已超过500个，参赛学生累计598万余人。

“希望杯”全国数学邀请赛已经成为中学生中规模最大、影响最广的学科课外活动之一。

“希望杯”邀请赛自1990年以来，已经连续举行了二十五届。

25年来，主办单位始终坚持比赛面向多数学校、多数学生，从命题、评奖到组织工作的每个环节，都围绕着一个宗旨：激发广大中学生学习的兴趣，培养他们的自信，不断提高他们的能力和素质。

“希望杯”全国数学邀请赛在济南举行
佚名
【期刊名称】《中国校外教育：上旬》
【年(卷),期】2016(000)004
【摘要】4月10日，第十四届小学”希望杯”全国数学邀请赛、第二十七届中学”希望杯“全国数学邀请赛山东赛区决赛在济南举行。

近400名考生参加了此次大赛。

山东省青少年活动中心作为大赛山东组委会负责此次山东赛区的筹备组织工作。

【总页数】1页(P169-169)
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.“希望杯”全国数学邀请赛在济南举行 [J], ;
2.建模思想在小学数学教学中的渗透——一个“希望杯”全国数学邀请赛试题的启示 [J], 曹军;蔡炯辉;鲁慧媛
3.《第十四届“希望杯”全国数学邀请赛》（初一第1试）答案／9月份《数学
竞赛训练题》参考答案 [J], 煜明
4.立足基本思路,引领思路突破*——一道"希望杯"全国数学邀请赛试题的解法及变式探究 [J],
5.立足基本思路,引领思路突破—一道“希望杯”全国数学邀请赛试题的解法及变
式探究 [J], 张宁
因版权原因，仅展示原文概要，查看原文内容请购买。

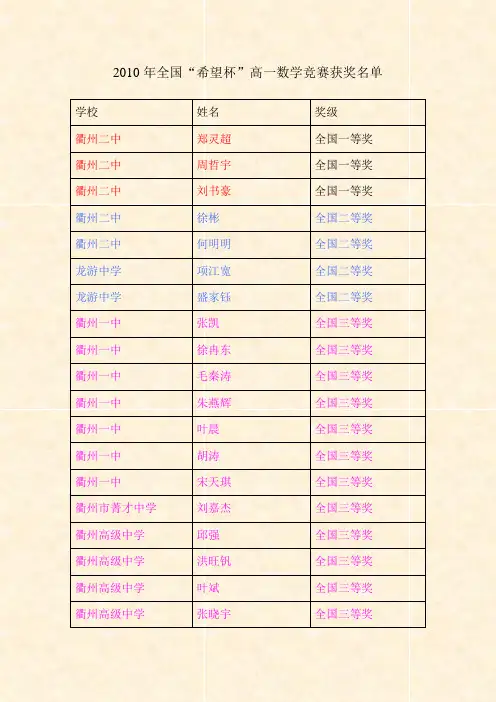
2010年全国“希望杯”高一数学竞赛获奖名单学校姓名奖级衢州二中郑灵超全国一等奖衢州二中周哲宇全国一等奖衢州二中刘书豪全国一等奖衢州二中徐彬全国二等奖衢州二中何明明全国二等奖龙游中学项江宽全国二等奖龙游中学盛家钰全国二等奖衢州一中张凯全国三等奖衢州一中徐冉东全国三等奖衢州一中毛秦涛全国三等奖衢州一中朱燕辉全国三等奖衢州一中叶晨全国三等奖衢州一中胡涛全国三等奖衢州一中宋天琪全国三等奖衢州市菁才中学刘嘉杰全国三等奖衢州高级中学邱强全国三等奖衢州高级中学洪旺钒全国三等奖衢州高级中学叶斌全国三等奖衢州高级中学张晓宇全国三等奖衢州高级中学李豪全国三等奖衢州二中刘伟荣全国三等奖衢州二中姜航全国三等奖衢州二中毛佳文全国三等奖衢州二中吴世豪全国三等奖衢州二中郑美林全国三等奖衢州二中江心怡全国三等奖衢江区衢州三中汪家南全国三等奖衢江区衢州三中李佳晖全国三等奖衢江区衢州三中林双龙全国三等奖衢江区杜泽中学林建梅全国三等奖衢江区杜泽中学刘佳明全国三等奖衢江区杜泽中学徐哲坤全国三等奖衢江区大洲中学曾鑫全国三等奖龙游中学张涛全国三等奖龙游中学朱焕东全国三等奖龙游中学余嘉伟全国三等奖龙游中学吴浩全国三等奖龙游横山中学徐文华全国三等奖龙游二高童广军全国三等奖龙游二高何俊全国三等奖龙游二高毛志成全国三等奖龙游二高陆敏全国三等奖龙游二高宁益航全国三等奖龙游二高徐鹏翔全国三等奖龙游二高夏丽全国三等奖开化中学胡昌辉全国三等奖开化中学汪起涛全国三等奖开化华埠中学陈艳梅全国三等奖江山中学胡华杰全国三等奖江山中学周小明全国三等奖江山中学刘浩全国三等奖江山中学段怡全国三等奖江山五中叶斌全国三等奖江山五中刘璜全国三等奖江山实验中学杨敢全国三等奖江山实验中学周域霖全国三等奖江山实验中学汪舳珂全国三等奖江山实验中学王美丽全国三等奖江山实验中学邱鹏飞全国三等奖江山实验中学刘起全国三等奖江山滨江高中严伟全国三等奖江山滨江高中陈张衢妹全国三等奖江山滨江高中王康全国三等奖江山滨江高中邵博政全国三等奖常山紫港中学张志龙全国三等奖常山紫港中学江婷婷全国三等奖常山一中王志成全国三等奖常山一中曾丹园全国三等奖常山一中汪路庭全国三等奖常山一中吴诗敏全国三等奖常山一中王艳静全国三等奖常山一中洪俊全国三等奖。

2014 第25届全国希望杯高一年级第二试 含详细答案2012年4月8日 上午9：00至11：00校名________________ 班_________ 姓名__________ 辅导老师_________ 成绩_____一、选择题（每题4分，40分）1．加果一个几何体的主视图和左视图均为矩形，而俯视图为一个圆．则这个几何体是（ ）（A ）棱锥． (B) 直棱柱． (C)圆锥． ( D)圆柱．2．已知43232()41027,()256f x x x x g x x x x =-+-=--+，{|()0}A x f x =>， {|()0,}B x g x x A ==∈且，则B 中元素的个数是（ ）（A ）1． (B) 2． (C)3． ( D)无穷多．3．关于x 的方程121ln x a =-有正根，则实数a 的取值范围是（ ） （A ）（0，1）． (B) (1,)e ． (C) (1,)+∞． ( D) (,)e +∞．4．If 22y x = where x and y are real numbers ，then the minimum vale of 224z y x =++ is( )（A ）3． (B) 4． (C) 5． ( D) 6．5．设()f x 是R 上的偶函数，并且(6)()(3)f x f x f +=+，若(2)2014f =，则(2014)f 等于（ ）（A ）2012． (B) 2013． (C)2014． ( D) 2015．6．苦关于x 的方程|23|0xk --=有两个不怕年的实数恨，则k 的取值范围是（ ）（A ）[0,3)． (B) (0,3)． (C) (0,)+∞． ( D) (,3)-∞．7．已知x ，y 是实数，且28y x x =+-，则y 的最大值是（ ） （A ）6． (B)254． (C) 978． ( D) 1298． 8．若对于任意的实数x ，不等式|1|||10x x a ---≤恒成立，则a 的取值范围是（ ）（A ）[3,4]-． (B) [4,3]-． (C) [9,11]-． (D) [11,9]-． 9．已知,,,a b m n R ∈，且222222m n a m b n >+．令22,M m n n a b =+=+．则M 与N 的大小关系是（ ）( A ) M > N . ( B ) M ≥N . ( C ）M ＜N ． (D) M ≤N ．.10．若函数2()2||21f x x a x a ax =---+有且只有3个零点，则实数a 的值是（ ）（A ）-1． (B) 6． (C) 1． ( D) 2．二、填空题（每小题4分，共40分）11．函数169log ()()2x x f x +=的定义域是 ．12．如图1．三棱锥A-BCD 的顶点B, C ，D 在平面α内，CA=AB=BC=CD=DB=2,AD=6．若将该三棱锥以BC 为轴转动，到点A 落在平面α内为止．则A 、D 两点所经过的路程之和是 ．13．己知函数21122()()k k f x x k Z -++=∈是奇函数，且在(0,)+∞上是增函数，则k 的值是 ．14．若函数1,0,()1,0,x x f x x x -+<⎧=⎨->⎩ 则不等式(1)(1)3x x f x +++≤的解集是 ． 15．如图2所示，已知AB 切⊙O 于点A,B,直线AC 交⊙O 于点C,和D,若AD=DC,BC=2,则BD= ．16．设()f x 是R 上的减函数，且(0)3,(3)1f f ==-，已知{||()1|2P x f x t =+-<，{|()1}Q x f x =<-．若P 是Q 的真子集，则实数t 的取值范围是 ．17．若函数2()(2)(21)f x a x ax a =+-+-的两个零点分别在区间（-2，-1）和区间（0，1）内，则a 的取值范围是 ．18．关于x 的不等式222(2)kx x >-恰有4个整数解，则实数k 的取值范围是 ．19．设1m >，若,x y 满足,,1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩时，函数z x my =+的最大值是4，则m 的值是 ．20．As shown in Fig.3,AB=6,BC=8,CA=10．Point P is inside of the triangleABC.DE,FG ,and IH all pass point P and are parallel to AB,BC, andCA,respectively ．The lengths of DE,FG and IH are all equal to d,and d= ．(英汉小词典，parallel 平行）下三、解答题每题都要写出推算过程．21．（本题满分10分）记 ()lg(3|3|)f x x =--的定义域为A,集合2{|(1)0}B x x a x a =-++<．若A B B =．求实数a 的取值范围．22．（本题满分15分）在△ABC 中，,,a b c 分别是角 A 、B 、C 的对边． 已知228(sin sin )()sin A C a b B -=-，且△ABC 的外接圆半径是4．（1）求角C;（2）求△ABC 的面积的最大值．23．（本题满分15分）已知函数2()(0,)a f x x x a R x=+≠∈． （1）判断函数()f x 的奇偶性；（2）当[2,)x ∈+∞时，若()f x 是增函数，求实数a 的取值范围．参考答案1-5. DBBBC, 6-10. BDCAC.11. (0,)+∞. 12.3π. 13. 1或2. 14. (,1]-∞ 15.1. 16. (,3]-∞-. 17.11(,)24--. 18. 92(,]509. 19. 27+. 20. 21047. 21．[-2，4]．22．（1）3C π=；（2）123．23．（1）当0a =时，2()f x x =是偶函数；当0a ≠时，()f x 是非奇非偶函数；（2）(,16]-∞． 2 分）2 1.由3|3|0x -->，得(2,4)A =-，（2分）由己知，得{|(1)()0}B x x x a =--<.若B =∅，则1a =.若B ≠∅．则(,1)B a =．(1)当1a >时，(1,)B a =，由AB B =，得(1,)(2,4)a -，推得14a <≤．(2)当1a <时，(,1)B a =.由类似推理．21a -≤<．所以实数a 的取值范围是(2,4]-．（10分） 22. (l) 已知条件及正弦定理，2228()42a c b a c R R-⋅=-⋅． 又4R =，所以222a c ab b -=-，即222c a b ab =+-． 再与余弦定理对比可得1cos 2C =． 因为C 是△ABC 的内角, 所以3C π=．(7分)(2) 因为4R =．于是由正弦定理，得2sin c R C ==．又222482c a b ab ab ab ab ==+-≥-=，即048ab <≤，所以1sin 24S ab C ==≤ 所以当且仅当a b =，即△ABC为等边三角形时，其面积取得最大值 ( 13分)23．(l)当0a =时，2()f x x =为偶函数．（3分）当0a ≠时，()f x 既不是奇函数也不是偶函数；（6分）(2)设122x x >≥，易知22121212()()()a a f x f x x x x x -=+-+22121211()x x a x x =-+- 12121212[()]x x x x x x a x x -=+-． 由122x x >≥，得1212()16x x x x +>，12120,0x x x x ->>，所以要使()f x 在区间[2,)+∞是增函数只需12()()0f x f x ->，即1212()0x x x x a +->恒成立．则16a ≤. 即实数a 的取值范围是(,16]-∞．（15分）。

希望杯第一届（1990年）初中一年级第一试试题................................................ 003-005 希望杯第一届（1990年）初中一年级第二试试题................................................ 010-012 希望杯第二届（1991年）初中一年级第一试试题................................................ 017-020 希望杯第二届（1991年）初中一年级第二试试题................................................ 023-026 希望杯第三届（1992年）初中一年级第一试试题................................................ 031-032 希望杯第三届（1992年）初中一年级第二试试题................................................ 037-040 希望杯第四届（1993年）初中一年级第一试试题................................................ 047-050 希望杯第四届（1993年）初中一年级第二试试题................................................ 055-058 希望杯第五届（1994年）初中一年级第一试试题................................................ 063-066 希望杯第五届（1994年）初中一年级第二试试题 ............................................... 070-073 希望杯第六届（1995年）初中一年级第一试试题................................................ 077-080 希望杯第六届（1995年）初中一年级第二试试题................................................ 084-087 希望杯第七届（1996年）初中一年级第一试试题................................................ 095-098 希望杯第七届（1996年）初中一年级第二试试题................................................ 102-105 希望杯第八届（1997年）初中一年级第一试试题................................................ 110-113 希望杯第八届（1997年）初中一年级第二试试题................................................ 117-120 希望杯第九届（1998年）初中一年级第一试试题................................................ 126-129 希望杯第九届（1998年）初中一年级第二试试题................................................ 135-138 希望杯第十届（1999年）初中一年级第二试试题................................................ 144-147 希望杯第十届（1999年）初中一年级第一试试题................................................ 148-151 希望杯第十一届（2000年）初中一年级第一试试题............................................ 158-161 希望杯第十一届（2000年）初中一年级第二试试题............................................ 166-169 希望杯第十二届（2001年）初中一年级第一试试题............................................ 170-174 希望杯第十二届（2001年）初中一年级第二试试题............................................ 175-178 希望杯第十三届（2002年）初中一年级第一试试题............................................ 181-184 希望杯第十三届（2001年）初中一年级第二试试题............................................ 185-189 希望杯第十四届（2003年）初中一年级第一试试题............................................ 192-196 希望杯第十四届（2003年）初中一年级第二试试题............................................ 197-200希望杯第十五届（2004年）初中一年级第一试试题 (202)希望杯第十五届（2004年）初中一年级第二试试题 (203)希望杯第十六届（2005年）初中一年级第一试试题............................................ 213-218 希望杯第十六届（2005年）初中一年级第二试试题 (203)希望杯第十七届（2006年）初中一年级第一试试题............................................ 228-233 希望杯第十七届（2006年）初中一年级第二试试题............................................ 234-238 希望杯第十八届（2007年）初中一年级第一试试题............................................ 242-246 希望杯第十八届（2007年）初中一年级第二试试题............................................ 248-251 希望杯第十九届（2008年）初中一年级第一试试题............................................ 252-256 希望杯第十九届（2008年）初中一年级第二试试题............................................ 257-262 希望杯第二十届（2009年）初中一年级第一试试题............................................ 263-266 希望杯第二十届（2009年）初中一年级第二试试题............................................ 267-271 希望杯第二十一届（2010年）初中一年级第一试试题........................................ 274-276 希望杯第二十一届（2010年）初中一年级第二试试题........................................ 277-283 希望杯第二十二届（2011年）初中一年级第一试试题........................................ 284-286希望杯第一届（1990年）初中一年级第1试试题一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么( )A．a，b都是0．B．a，b之一是0．C．a，b互为相反数．D．a，b互为倒数．2．下面的说法中正确的是( )A．单项式与单项式的和是单项式．B．单项式与单项式的和是多项式．C．多项式与多项式的和是多项式．D．整式与整式的和是整式．3．下面说法中不正确的是( )A. 有最小的自然数．B．没有最小的正有理数．C．没有最大的负整数．D．没有最大的非负数．4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么( )A．a，b同号．B．a，b异号．C．a＞0．D．b＞0．5．大于－π并且不是自然数的整数有( )A．2个．B．3个．C．4个．D．无数个．6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身．这四种说法中，不正确的说法的个数是( )A．0个．B．1个．C．2个．D．3个．7．a代表有理数，那么，a和－a的大小关系是( )A．a大于－a．B．a小于－a．C．a大于－a或a小于－a．D．a不一定大于－a．8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( ) A．乘以同一个数．B．乘以同一个整式．C．加上同一个代数式．D．都加上1．9．杯子中有大半杯水，第二天较第一天减少了10%，第三天又较第二天增加了10%，那么，第三天杯中的水量与第一天杯中的水量相比的结果是( )A．一样多．B．多了．C．少了．D．多少都可能．10．轮船往返于一条河的两码头之间，如果船本身在静水中的速度是固定的，那么，当这条河的水流速度增大时，船往返一次所用的时间将( )A．增多．B．减少．C．不变．D．增多、减少都有可能．二、填空题（每题1分，共10分）1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______． 2．198919902－198919892=______． 3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5．1－2＋3－4+5－6+7－8+…+4999－5000=______．6.当x=-24125时,代数式(3x 3－5x 2+6x －1)－(x 3－2x 2+x －2)+(－2x 3+3x 2+1)的值是____． 7．当a=－0.2，b=0.04时，代数式272711()(0.16)()73724a b b a a b --++-+的值是______.8．含盐30%的盐水有60千克，放在秤上蒸发，当盐水变为含盐40%时，秤得盐水的重是______克．9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半，一共需要______天．10．现在4点5分，再过______分钟，分针和时针第一次重合．答案与提示一、选择题1．C 2．D 3．C 4．D 5．C 6．B 7．D 8．D 9．C 10．A提示：1．令a=2，b=－2，满足2+(－2)=0，由此2．x2，2x2，x3都是单项式．两个单项式x3，x2之和为x3+x2是多项式，排除A．两个单项式x2，2x2之和为3x2是单项式，排除B．两个多项式x3+x2与x3－x2之和为2x3是个单项式，排除C，因此选D．3．1是最小的自然数，A正确．可以找到正所以C“没有最大的负整数”的说法不正确．写出扩大自然数列，0，1，2，3，…，n，…，易知无最大非负数，D正确．所以不正确的说法应选C．5．在数轴上容易看出：在－π右边0的左边（包括0在内）的整数只有－3，－2，－1，0共4个．选C．6．由12=1，13=1可知甲、乙两种说法是正确的．由(－1)3=－1，可知丁也是正确的说法．而负数的平方均为正数，即负数的平方一定大于它本身，所以“负数平方不一定大于它本身”的说法不正确．即丙不正确．在甲、乙、丙、丁四个说法中，只有丙1个说法不正确．所以选B．7．令a=0，马上可以排除A、B、C，应选D．8．对方程同解变形，要求方程两边同乘不等于0的数．所以排除A．我们考察方程x－2=0，易知其根为x=2．若该方程两边同乘以一个整式x－1，得(x－1)(x－2)=0，其根为x=1及x=2，不与原方程同解，排除B．若在方程x－2=0两边加上同一个代数式去了原方程x=2的根．所以应排除C．事实上方程两边同时加上一个常数，新方程与原方程同解，对D，这里所加常数为1，因此选D．9．设杯中原有水量为a，依题意可得，第二天杯中水量为a×(1－10%)=0.9a；第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a；第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了，选C．10．设两码头之间距离为s，船在静水中速度为a，水速为v0，则往返一次所用时间为设河水速度增大后为v，(v＞v0)则往返一次所用时间为由于v－v0＞0，a+v0＞a－v0，a+v＞a－v所以(a+v0)(a+v)＞(a－v0)(a－v)∴t0－t＜0，即t0＜t．因此河水速增大所用时间将增多，选A．二、填空题提示：2．198919902－198919892=(19891990+19891989)×(19891990－19891989) =(19891990+19891989)×1=39783979．3．由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2－1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22－1)(22+1)(24+1)(28+1)(216+1)=(24－1)(24+1)(28+1)(216+1)=(28－1)(28+1)(216+1)=(216－1)(216+1)=232－1．2(1+x)－(x－2)=8,2+2x－x+2=8解得；x=45．1－2+3－4+5－6+7－8+…+4999－5000=(1－2)+(3－4)+(5－6)+(7－8)+…+(4999－5000)=－2500．6．(3x3－5x2+6x－1)－(x3－2x2+x－2)+(－2x3+3x2+1)=5x+27．注意到：当a=－0.2，b=0.04时，a2－b=(－0.2)2－0.04=0，b+a+0.16=0.04－0.2+0.16=0．8．食盐30%的盐水60千克中含盐60×30%（千克）设蒸发变成含盐为40%的水重x克，即0.001x千克，此时，60×30%=(0.001x)×40%解得：x=45000（克）．10．在4时整，时针与分针针夹角为120°即希望杯第一届（1990年）初中一年级第2试试题一、选择题（每题1分，共5分）以下每个题目里给出的A，B，C，D四个结论中有且仅有一个是正确的．请你在括号填上你认为是正确的那个结论的英文字母代号．1．某工厂去年的生产总值比前年增长a%，则前年比去年少的百分数是( )A．a%．B．(1+a)%． C.1100aa+D.100aa+2．甲杯中盛有2m毫升红墨水，乙杯中盛有m毫升蓝墨水，从甲杯倒出a毫升到乙杯里, 0＜a＜m，搅匀后，又从乙杯倒出a毫升到甲杯里，则这时( )A．甲杯中混入的蓝墨水比乙杯中混入的红墨水少．B．甲杯中混入的蓝墨水比乙杯中混入的红墨水多．C．甲杯中混入的蓝墨水和乙杯中混入的红墨水相同．D．甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定．3.已知数x=100,则( )A．x是完全平方数．B．(x－50)是完全平方数．C．(x－25)是完全平方数．D．(x+50)是完全平方数．4．观察图1中的数轴：用字母a，b，c依次表示点A，B，C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5．x=9，y=－4是二元二次方程2x2+5xy+3y2=30的一组整数解，这个方程的不同的整数解共有( )A．2组．B．6组．C．12组．D．16组．二、填空题（每题1分，共5分）1．方程|1990x－1990|=1990的根是______．2．对于任意有理数x，y，定义一种运算*，规定x*y=ax+by－cxy，其中的a，b，c表示已知数，等式右边是通常的加、减、乘运算．又知道1*2=3，2*3=4，x*m=x（m≠0），则m的数值是______．3．新上任的宿舍管理员拿到20把钥匙去开20个房间的门，他知道每把钥匙只能开其中的一个门，但不知道每把钥匙是开哪一个门的钥匙，现在要打开所有关闭着的20个房间，他最多要试开______次．4．当m=______时，二元二次六项式6x2+mxy－4y2－x+17y－15可以分解为两个关于x，y的二元一次三项式的乘积．5．三个连续自然数的平方和（填“是”或“不是”或“可能是”）______某个自然数的平方．三、解答题（写出推理、运算的过程及最后结果．每题5分，共15分）1．两辆汽车从同一地点同时出发，沿同一方向同速直线行驶，每车最多只能带24桶汽油，途中不能用别的油，每桶油可使一辆车前进60公里，两车都必须返回出发地点，但是可以不同时返回，两车相互可借用对方的油．为了使其中一辆车尽可能地远离出发地点，另一辆车应当在离出发地点多少公里的地方返回？离出发地点最远的那辆车一共行驶了多少公里？2．如图2，纸上画了四个大小一样的圆，圆心分别是A，B，C，D，直线m通过A，B，直线n通过C，D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5(S－1)，直线m，n之间被圆盖住的面积是8，阴影部分的面积S1，S2，S3满足关系式S3=13S1=13S2,求S．3.求方程11156x y z++=的正整数解.答案与提示一、选择题1．D 2．C 3．C 4．C 5．D提示：1．设前年的生产总值是m，则去年的生产总值是前年比去年少这个产值差占去年的应选D．2．从甲杯倒出a毫升红墨水到乙杯中以后：再从乙杯倒出a毫升混合墨水到甲杯中以后：乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C．∴x－25=(10n+2+5)2可知应当选C．4．由所给出的数轴表示（如图3）：可以看出∴①＜②＜③，∴选C．5．方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x，y是整数，∴2x+3y，x+y也是整数．由下面的表可以知道共有16个二元一次方程组，每组的解都是整数，所以有16组整数组，应选D．二、填空题提示：1．原方程可以变形为|x－1|=1，即x-1=1或-1，∴x=2或0．2．由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0，∴bm=0．∵m≠0，∴b=0．∴等式改为x*y=ax-cxy．∵1*2=3，2*3=4，解得a=5，c=1．∴题设的等式即x*y=5x-xy．在这个等式中，令x=1，y=m，得5-m=1，∴m=4．3．∵打开所有关闭着的20个房间，∴最多要试开4．利用“十字相乘法”分解二次三项式的知识，可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解：3x -52x +3现在要考虑y，只须先改写作然后根据-4y2，17y这两项式，即可断定是：由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式，所以m=5．5．设三个连续自然数是a-1，a，a+1，则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2，显然，这个和被3除时必得余数2．另一方面，自然数被3除时，余数只能是0或1或2，于是它们可以表示成3b，3b+1，3b+2（b是自然数）中的一个，但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1，(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时，余数要么是0，要么是1，不能是2，所以三个连续自然数平方和不是某个自然数的平方．三、解答题1．设两辆汽车一为甲一为乙，并且甲用了x升汽油时即回返，留下返程需的x桶汽油，将多余的(24-2x)桶汽油给乙．让乙继续前行，这时，乙有(24-2x)+(24-x)=48-3x桶汽油，依题意，应当有48-3x≤24，∴x≥8．甲、乙分手后，乙继续前行的路程是这个结果中的代数式30(48-4x)表明，当x的值愈小时，代数式的值愈大，因为x≥8，所以当x=8时，得最大值30(48-4·8)=480（公里），因此，乙车行驶的路程一共是2(60·8+480)=1920（公里）．2．由题设可得即2S-5S3=8……②∴x，y，z都＞1，因此，当1＜x≤y≤z时，解(x，y，z)共(2，4，12)，(2，6，6)，(3，3，6)，(3，4，4)四组．由于x，y，z在方程中地位平等．所以可得如下表所列的15组解．希望杯第二届（1991年）初中一年级第1试试题一、选择题（每题1分，共15分）以下每个题目的A，B，C，D四个结论中，仅有一个是正确的，请在括号内填上正确的那个结论的英文字母代号．1．数1是( )A．最小整数．B．最小正数．C．最小自然数．D．最小有理数．2．若a＞b，则( )A.11a b; B．-a＜-b．C．|a|＞|b|．D．a2＞b2．3．a为有理数，则一定成立的关系式是( )A．7a＞a．B．7+a＞a．C．7+a＞7．D．|a|≥7．4．图中表示阴影部分面积的代数式是( )A．ad+bc．B．c(b-d)+d(a-c)．C．ad+c(b-d)．D．ab-cd．5．以下的运算的结果中，最大的一个数是( )A．(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686．3.1416×7.5944+3.1416×(-5.5944)的值是( ) A．6.1632． B．6.2832．C．6.5132．D．5.3692．7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A．16． B．15． C．14． D．13．8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x ．B.甲方程的两边都乘以43x; C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34. 10．如图: ，数轴上标出了有理数a ，b ，c 的位置,其中O 是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A ．27． B ．28． C ．29． D ．30．12.当x=12,y=-2时,代数式42x y xy -的值是( )A ．-6．B ．-2．C ．2．D ．6．13．在-4，-1，-2.5，-0.01与-15这五个数中，最大的数与绝对值最大的那个数的乘积是( )A ．225．B ．0.15．C ．0.0001．D ．1．14.不等式124816x x x xx ++++>的解集是( ) A ．x ＜16． B ．x ＞16．C ．x ＜1． D.x>-116. 15．浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题（每题1分，共15分）1． 计算：(-1)+(-1)-(-1)×(-1)÷(-1)=______． 2． 计算：-32÷6×16=_______.3．计算：(63)36162-⨯=__________.4．求值：(-1991)-|3-|-31||=______．5．计算:111111 2612203042-----=_________.6．n为正整数，1990n-1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009．则n的最小值等于______．7. 计算：19191919199191919191⎛⎫⎛⎫---⎪ ⎪⎝⎭⎝⎭=_______.8. 计算：15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10．不超过(-1.7)2的最大整数是______．11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13．一个质数是两位数，它的个位数字与十位数字的差是7，则这个质数是______．14.一个数的相反数的负倒数是119,则这个数是_______.15．如图11，a，b，c，d，e，f均为有理数．图中各行，各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1．C 2．B 3．B 4．C 5．C 6．B 7．B 8．B 9．C 10．B 11．D 12．A 13．B 1 4．A 15．D提示：1．整数无最小数，排除A；正数无最小数，排除B；有理数无最小数，排除D．1是最小自然数．选C．有|2|＜|-3|，排除C；若2＞-3有22＜(-3)2，排除D；事实上，a＞b必有-a＜-b．选B．3．若a=0，7×0=0排除A；7+0=7排除C|0|＜7排除D，事实上因为7＞0，必有7+a＞0+a=a．选B．4．把图形补成一个大矩形，则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d)．选C．5．运算结果对负数来说绝对值越小其值越大。

“希望杯”全国数学邀请赛简介 这⼀邀请赛⾃1990年以来，已经连续举⾏了⼆⼗⼆届。

22年来，主办单位始终坚持⽐赛⾯向多数学校、多数学⽣，从命题、评奖到组织⼯作的每个环节，都围绕着⼀个宗旨：激发⼴⼤中学⽣学习的兴趣，培养他们的⾃信，不断提⾼他们的能⼒和素质。

这⼀活动只涉及初⼀、初⼆、⾼⼀、⾼⼆四个年级，不涉及初三、⾼三，不与奥赛重复，不与中考、⾼考挂钩，不增加师⽣负担，因此受到⼴⼤师⽣的欢迎。

该竞赛⼀直受到原国家教委的肯定，并被列⼊原国家教委批准的全国性竞赛活动的名单中，同时愈来愈多的数学家、数学教育家对邀请赛给予热情的关⼼和⽀持。

到第⼗届为⽌，参赛城市已超过500个，参赛学⽣累计598万。

“希望杯”全国数学邀请赛已经成为中学⽣中规模、影响最⼴的学科课外活动之⼀。

据介绍，该竞赛活动分两试进⾏。

第⼀试（每年三⽉进⾏）以各地（省、市、县、〔区〕、学校）为单位组织参赛学⽣，在全国各参赛学校同时进⾏，各测试点按命题委员会下发的评分标准进⾏阅卷、评分，从中按七分之⼀的⽐例按成绩择优选拔参加第⼆试的选⼿。

第⼆试（每年四⽉进⾏）由当地《数理天地》编委分会或地、市级教研室或教育学院、教科所、教师进修学校统⼀组织，测试结束后，各测试点将试卷密封，向组委会挂号寄出，由命题委员会阅卷，从中按⼋分之⼀的⽐例按成绩评定⼀、⼆、三等奖，分别授予⾦、银、铜奖牌及获奖证书。

对组织⼯作做得出⾊的地区或学校，组委会颁发“希望杯”数学邀请赛组织奖。

⽇本国算数奥林匹克委员会对此项赛事⾮常关注，该委员会事务局局长若杉荣⼆先⽣专程来华同邀请赛组委会洽谈参赛事宜，并从1996年开始，已连续三年组织⽇本部分中学⽣参加了竞赛活动，由此开创了我国社会团体举办同类竞赛⾛出国门的先例。

近年来，美国、德国的有关组织也与组委会联系合作事宜。

希望杯杯徽 ★圆形，表⽰⼴阔的天空。

★英⽂hope（希望）形如⼀只展翅飞翔的鸟。

喻义：“希望杯”全国数学邀请赛为⼴⼤的青少年在科学思维能⼒上的健康发展开辟了⼀个⼴阔的空间，任他们⾃由翱翔。

直线平分固定的三角形面积的类型云南省玉溪第一中学㊀㊀６５３１００㊀㊀武增明㊀㊀直线平分固定的三角形的面积归纳起来主要有两种类型：（１）动直线平分固定的三角形的面积；（２）定直线平分固定的三角形的面积．下面通过实例谈一谈这两种类型的具体情况．１㊀动直线平分固定的三角形的面积１．１㊀动直线平分固定的三角形的面积，求动直线在ｙ轴上的截距的取值范围例１㊀（２０１３年高考全国新课标卷Ⅱ㊃理１２）已知点Ａ（－１，０），Ｂ（１，０），Ｃ（０，１），直线ｙ＝ａｘ＋ｂ（ａ＞０）将әＡＢＣ分割为面积相等的两部分，则ｂ的取值范围是（㊀㊀）．Ａ．（０，１）㊀㊀㊀㊀㊀㊀Ｂ．（１－２２，１２）Ｃ．（１－２２，１３］㊀㊀㊀Ｄ．［１３，１２）解㊀如图１所示，点Ｆ（－ｂａ，０）在线段ＡＢ上时，可求得Ｅ（１－ｂａ＋１，ａ＋ｂａ＋１），则ＳәＥＦＢ＝１２（１＋ｂａ）㊃ａ＋ｂａ＋１＝１２ＳәＡＢＣ＝１２，整理可得ａ＝ｂ２１－２ｂ，由－１＜－ｂａ＜０，ａ＝ｂ２１－２ｂ＞０ìîíïïïï可解得１３ɤｂ＜１２；图１㊀㊀㊀㊀㊀㊀㊀㊀㊀图２如图２所示，当点Ｆ（－ｂａ，０）在点Ａ左侧时，可求得Ｅ（１－ｂａ＋１，ａ＋ｂａ＋１），Ｇ（１－ｂａ－１，ａ－ｂａ－１），则Ｓ四边形ＡＢＥＧ＝ＳәＢＥＦ－ＳәＡＦＧ＝１２（１＋ｂａ）㊃ａ＋ｂａ＋１－１２（－１＋ｂａ）㊃ａ－ｂａ－１＝１２ＳәＡＢＣ＝１２，整理可得ａ２＝－２ｂ２＋４ｂ－１，由－ｂａ＜－１，ａ２＝－２ｂ２＋４ｂ－１＞０ìîíïïï可解得１－２２＜ｂ＜１３或１＜ｂ＜１＋２２（舍去），综上可得ｂ的取值范围为（１－２２，１２），故应选Ｂ．评注㊀（１）当年高考，此题难住了不少考生，现在回过头看看，确实较难．图３（２）此题虽然有较简单的解法，但是许多考生不易想到．在此不妨给出较简单的解法：可以利用极限位置和特值法．由于ａ＞０，可以先考虑极端情况：ａ＝０，此时直线ｙ＝ｂ与边ＡＢ平行，易得ｂ＝１－２２；再考虑另一种极限位置即斜率不存在，如图３，将ＣＯ顺时针旋转，与ｙ轴交于点Ｐ，与ＢＣ，ＡＢ分别交于点Ｅ，Ｆ，若ＥＦ平分әＡＢＣ，则әＣＥＰ的面积必须等于әＯＦＰ的面积．由１２ＰＥ㊃ＰＣ㊃ｓｉｎøＣＰＥ＝１２ＰＦ㊃ＰＯ㊃ｓｉｎøＯＰＦ，即ＰＥ㊃ＰＣ＝ＰＦ㊃ＰＯ可知，点Ｐ的纵坐标必须小于１２，因此答案为Ｂ．例２㊀设ａ为任意正实数，әＡＢＣ的三个顶点为Ａ（０，０），Ｂ（１，０），Ｃ（０，１）．如果直线ｙ＝ａｘ＋ｂ将三角形分成面积相等的两部分，试问ａ，ｂ之间有何关系？（用ａ表示ｂ）．当ａȡ１时，ｂ＝ａ（ａ＋１）２－ａ；当０＜ａ＜１时，ｂ＝１－ａ＋１２（过程略）．读者不妨自己试一试．此题出自‘数学通讯“丛书编审组编，１９９３年５月第１版，华中师范大学出版社出版的‘高中数学辅教导学 从基础到能力“丛书之五，综合训练（１），第２５７页习题１１ ２第三题中的第３题．此题可以说是上述例１的题源，即由此题稍作改编而得，其解答思路和方法完全相同．１４中学数学杂志㊀２０１５年第５期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ＺＨＯＮＧＸＵＥＳＨＵＸＵＥＺＡＺＨＩ㊀１．２㊀动直线平分固定的三角形的面积，求动直线在三角形内的线段的长度的最值（取值范围）例３㊀（２０１４年第２５届 希望杯 全国数学邀请赛高二第２试第１７题）已知ＲｔәＡＢＣ中，øＡ＝３０ʎ，ＳәＡＢＣ＝１．用与øＡ两边都相交的直线ｍ将әＡＢＣ的面积二等分，则直线ｍ在әＡＢＣ内的线段的长度的最小值是㊀㊀㊀㊀．图４解㊀如图４，设ｍ交ＡＣ于点Ｄ，交ＡＢ于点Ｅ，ＡＤ＝ｘ，ＡＥ＝ｙ，则ＤＥ２＝ＡＤ２＋ＡＥ２－２ＡＥ㊃ＡＤ㊃ｃｏｓＡ＝ｘ２＋ｙ２－２ｘｙ㊃３２＝ｘ２＋ｙ２－３ｘｙȡ２ｘｙ－３ｘｙ＝（２－３）ｘｙ．㊀㊀㊀㊀㊀①依题意，有ＳәＡＤＥ＝１２ＳәＡＢＣ＝１２，即１２ｘｙｓｉｎ３０ʎ＝１２，解得ｘｙ＝２．㊀㊀㊀㊀㊀②将②代入①，得ＤＥ２ȡ４－２３＝（３－１）２．得ＤＥȡ３－１（当且仅当ｘ＝ｙ＝２时等号成立）．所以ＤＥ的最小值是３－１．评注㊀此题题设中 әＡＢＣ是直角三角形 这个条件是多余的．２㊀定直线平分固定的三角形的面积２．１㊀定直线平分固定的三角形的面积且经过三角形的一个顶点，求此直线的方程例４㊀已知әＡＢＣ顶点分别为Ａ（２，８），Ｂ（－４，０），Ｃ（６，０），求过点Ｂ且将әＡＢＣ面积平分的直线的方程．解㊀取ＡＣ中点Ｄ，则Ｄ（４，４），因为ＳәＡＢＤ＝ＳәＣＢＤ，所以所求直线方程为ｙ－４＝４－０４－（－４）（ｘ－４），即ｘ－２ｙ＋４＝０．２．２㊀定直线平分固定的三角形的面积且不经过三角形的顶点也不与三角形的边平行，求此直线的方程例５㊀已知әＡＢＣ的三个顶点Ａ（４，１），Ｂ（２，－１），Ｃ（０，５），点Ｄ在边ＡＢ上，且ＡＤ＝２ＤＢ，点Ｅ在边ＡＣ上．若ＤＥ平分әＡＢＣ的面积，求直线ＤＥ的方程．解㊀由әＡＤＥ的面积是әＡＢＣ面积的一半可得１２ＡＤ㊃ＡＥ㊃ｓｉｎＡ１２ＡＢ㊃ＡＣ㊃ｓｉｎＡ＝１２．由ＡＤ＝２ＤＢ，得ＡＤＡＢ＝２３，于是ＡＥＡＣ＝３４，即ＡＥ＝３４ＡＣ，所以ＡＥң＝３４ＡＣң，从而（ｘＥ－４，ｙＥ－１）＝３４（－４，４），由此得ｘＥ＝１，ｙＥ＝４，即Ｅ（１，４）．由ＡＤ＝２ＤＢ，得ＡＤң＝２ＤＢң，从而（ｘＤ－４，ｙＤ－１）＝２（２－ｘＤ，－１－ｙＤ），由此得ｘＤ＝４３，ｙＤ＝－１３，即Ｄ（４３，－１３）．故直线ＤＥ的方程为１３ｘ＋ｙ－１７＝０．２．３㊀定直线平分固定的三角形的面积且平行于三角形的一边，求此直线的方程例６㊀已知Ａ（１，１），Ｂ（５，３），Ｃ（４，５），直线ｌ平分әＡＢＣ的面积且ｌʊＡＢ，求点Ｃ到ｌ的距离和ｌ的方程．图５解㊀如图５，ＳәＣＤＥＳәＣＡＢ＝１２⇔１２ＣＤ㊃ＣＥ㊃ｓｉｎＣ１２ＣＡ㊃ＣＢ㊃ｓｉｎＣ＝１２⇔ＣＤ㊃ＣＥＣＡ㊃ＣＢ＝１２．әＣＤＥʐәＣＡＢ⇒ＣＤＣＡ＝ＣＥＣＢ．所以ＣＥ２ＣＢ２＝１２⇔ＣＥ＝２２ＣＢ⇔ＣＥң＝２２ＣＢң⇒（ｘＥ－４，ｙＥ－５）＝２２（１，－２）⇒ｘＥ＝４＋２２，ｙＥ＝５－２⇒Ｅ（４＋２２，５－２）．因为ｌʊＡＢ，所以ｋｌ＝ｋＡＢ，又ｋＡＢ＝１２，于是ｋｌ＝１２．故直线ｌ的方程为ｙ－５＋２＝１２（ｘ－４－２２），即２ｘ－４ｙ＋１２－５２＝０．点Ｃ到ｌ的距离ｄ＝８－２０＋１２－５２４＋１６＝１０２．综上，点Ｃ到ｌ的距离为１０２，ｌ的方程为２ｘ－４ｙ＋１２－５２＝０．作者简介㊀武增明，男，１９６５年５月生，云南省玉溪市易门县人，中学高级教师，玉溪市数学学科带头人，玉溪市劳模．在省级及其以上数学专业刊物上发表教育教学论文１４０余篇．主要从事高中数学教学及其研究．２４㊀ＺＨＯＮＧＸＵＥＳＨＵＸＵＥＺＡＺＨＩ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀中学数学杂志㊀２０１５年第５期。

教育精品资料目录1.第一届小学“希望杯”全国数学邀请赛（第1试） (2)2. 第一届小学“希望杯”全国数学邀请赛（第2试） (5)3. 第二届小学“希望杯”全国数学邀请赛（第1试） (7)4. 第二届小学“希望杯”全国数学邀请赛（第2试） (10)5. 第三届小学“希望杯”全国数学邀请赛（第1试） (12)6. 第三届小学“希望杯”全国数学邀请赛（第2试） (15)7. 第四届小学“希望杯”全国数学邀请赛（第1试） (17)8. 第四届小学“希望杯”全国数学邀请赛（第2试） (20)9. 第五届小学“希望杯”全国数学邀请赛（第1试） (22)10. 第五届小学“希望杯”全国数学邀请赛（第2试） (24)11. 第六届小学“希望杯”全国数学邀请赛（第1试） (26)12. 第六届小学“希望杯”全国数学邀请赛（第2试） (28)13. 第七届小学“希望杯”全国数学邀请赛（第1试） (30)14. 第七届小学“希望杯”全国数学邀请赛（第2试） (34)15. 第八届小学“希望杯”全国数学邀请赛（第1试） (37)16. 第八届小学“希望杯”全国数学邀请赛（第2试） (39)17. 第九届小学“希望杯”全国数学邀请赛（第1试） (41)18. 第九届小学“希望杯”全国数学邀请赛（第2试） (43)19. 第十届小学“希望杯”全国数学邀请赛（第1试） (45)20. 第十届小学“希望杯”全国数学邀请赛（第2试） (47)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C 中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。