2015年浙江省希望杯四年级决赛获奖名单

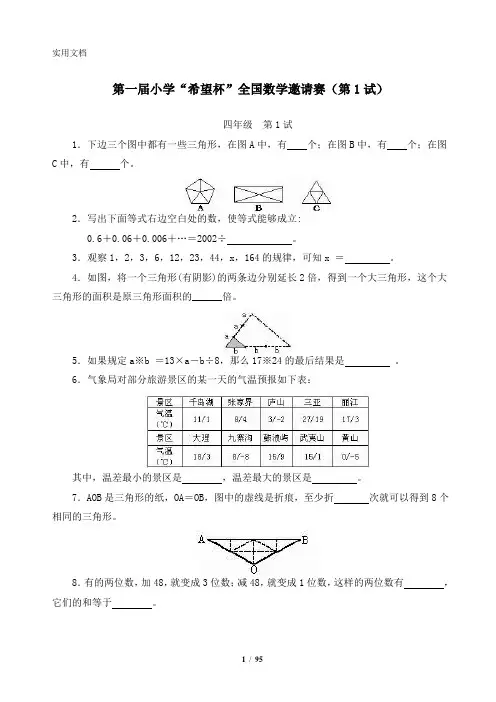
第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

教育精品资料目录1.第一届小学“希望杯”全国数学邀请赛〔第1试〕 (2)2. 第一届小学“希望杯”全国数学邀请赛〔第2试〕 (5)3. 第二届小学“希望杯”全国数学邀请赛〔第1试〕 (7)4. 第二届小学“希望杯”全国数学邀请赛〔第2试〕 (10)5. 第三届小学“希望杯”全国数学邀请赛〔第1试〕 (12)6. 第三届小学“希望杯”全国数学邀请赛〔第2试〕 (15)7. 第四届小学“希望杯”全国数学邀请赛〔第1试〕 (17)8. 第四届小学“希望杯”全国数学邀请赛〔第2试〕 (20)9. 第五届小学“希望杯”全国数学邀请赛〔第1试〕 (22)10. 第五届小学“希望杯”全国数学邀请赛〔第2试〕 (24)11. 第六届小学“希望杯”全国数学邀请赛〔第1试〕 (26)12. 第六届小学“希望杯”全国数学邀请赛〔第2试〕 (28)13. 第七届小学“希望杯”全国数学邀请赛〔第1试〕 (30)14. 第七届小学“希望杯”全国数学邀请赛〔第2试〕 (34)15. 第八届小学“希望杯”全国数学邀请赛〔第1试〕 (37)16. 第八届小学“希望杯”全国数学邀请赛〔第2试〕 (39)17. 第九届小学“希望杯”全国数学邀请赛〔第1试〕 (41)18. 第九届小学“希望杯”全国数学邀请赛〔第2试〕 (43)19. 第十届小学“希望杯”全国数学邀请赛〔第1试〕 (45)20. 第十届小学“希望杯”全国数学邀请赛〔第2试〕 (47)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛〔第1试〕四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C 中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

浙江希望杯引言：浙江希望杯作为长期以来在浙江省内举办的一项盛大活动，旨在推动学生综合素质的提升，为广大学子提供一个展现才华的舞台。

自活动举办以来，已经有无数优秀的参赛选手通过浙江希望杯展现了自己的才华，成为了各行业的佼佼者。

本文将介绍浙江希望杯的举办背景、组织架构、活动内容以及对参赛选手的意义。

一、背景浙江希望杯起源于对专业技能竞赛缺乏的认识，为了促进综合素质教育的发展，浙江省教育部门开始策划组织一项大规模的学生综合素质竞赛。

经过广泛调研和多次研讨，浙江希望杯于XX年首次举办，至今已经连续举办了十年。

二、组织架构浙江希望杯的组织架构包括主办单位和协办单位。

主办单位通常由浙江省教育厅和浙江省学生文化艺术中心共同担任。

协办单位则是各级教育机构、学校和社会团体。

这些单位共同负责活动的策划、组织和赛事的落地实施。

三、活动内容浙江希望杯的活动内容涵盖了多个方面的竞赛项目。

其中，最重要的是学科竞赛，包括数学、语文、英语等学科的知识竞赛。

此外还有艺术类比赛，如音乐、舞蹈、书法等，以及体育类比赛，如足球、篮球、田径等。

这些竞赛项目的设置旨在全面考察学生的综合素养和才艺，并为广大学子提供一个展示自我、分享经验的机会。

四、对参赛选手的意义参加浙江希望杯对于学生来说有着重要的意义。

首先，参赛选手通过准备和参赛的过程，可以提高自己的学科知识水平和技能技巧。

其次，比赛过程中的交流和互动，能够让学生从其他参赛选手身上汲取经验和启示，提高自身的竞争力。

此外，获得浙江希望杯的奖项将成为学生个人履历的重要标志，为他们未来的发展提供更多机会和选择。

结语：浙江希望杯的举办为广大学生提供了一个展现才华和挑战自我的平台。

通过参与各类竞赛项目，学生可以全面发展自己的综合素质，提高学科水平和技能技巧。

同时，浙江希望杯也鼓励学生之间的交流与互动，激发他们的学习热情和创新意识。

相信在浙江希望杯的影响下，更多优秀的学生将走上成才之路，为社会的发展做出贡献。

第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

第十二届小学“希望杯”全国数学邀请赛四年级第Ⅰ试试题2014年3月16日上午8:30至10:00以下每题6分，共120分1、过元旦时，班委会用730元为全班同学每人买了一份价值17元的纪念品，剩余16元，那么，这个班共有学生（）名。

2、买5斤黄瓜用了11元8角，比买4斤西红柿少用1元4角，那么，每斤西红柿的价格是（）元（）角。

3、图1是4×4的方格图，有3个小正方形有阴影，若再将一个小正方形涂阴影，使方格图成为轴对称图形，则不同的涂法有（）种。

4、小东和小荣同时从甲地出发到乙地，小东每分钟行50米，小荣每分钟行60米，小荣到达乙地后立即返回，若两人从出发到相遇用了10分钟，则甲、乙两地相距（）米。

5、如图2，从一张长50厘米、宽20厘米的长方形纸片上剪去边长分别是12厘米和4厘米的两个正方形，则剩余部分图形的周长是（）厘米。

6、图3是长方形，将它分成7部分，至少要画（）条直线。

7、甲、乙两个油桶中共有100千克油，将乙桶中的15千克油注入甲桶，此时甲桶中的油是乙桶中的油的4倍。

那么，原来甲桶中油比乙桶中的油多（）千克。

8、甲、乙、丙三校合办画展，参展的画中，有41幅不是甲校的，有38幅不是乙校的，甲、乙两校参展的画共43幅，那么，丙校参展的画有（）幅。

9、一个正方形的面积与一个长方形的面积相等，若长方形的长是1024，宽是1，则正方形的周长是（）。

10、如图4，每个小正方形的边长都是1，那么。

图中面积为2的阴影长方形共有（）个。

11、如图5，将一张圆形纸片对折，再对折，又对折，……，到第六次对折后，得到的扇形的面积是5，那么，圆形纸片的面积是（）。

12、自然数a 是3的倍数，a -1是4的倍数，a -2是5的倍数，则a 最小是（）。

13、四年级的两个班共有学生72人，其中有女生35人，四（1）班有学生36人，四（2）班有男生19人，则四（1）班有女生（）人。

14、如图6，阴影小正方形的边长是2，最外边的大正方形的边长是6，则正方形 ABCD 的面积是（）。

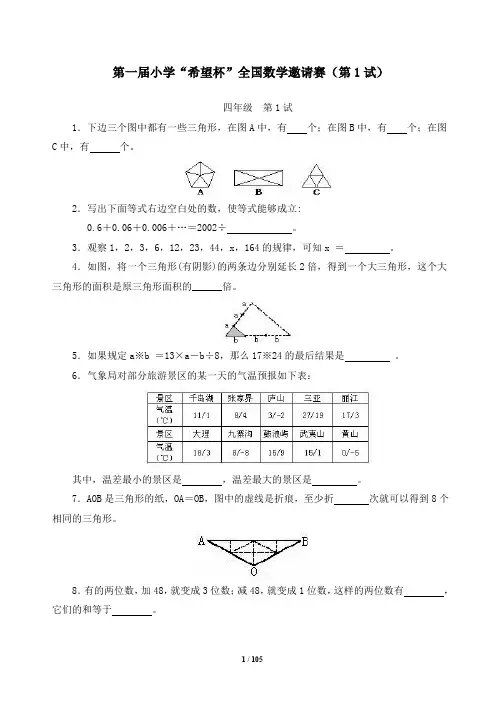
第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

金牌初一合肥市新航培训中心高英明安徽金牌初一濠江中學容逸朗澳门金牌初一培正中學古宏澳门金牌初一新巨人培训学校尹伊北京金牌初一福州励志中学林毅福建金牌初一福州华伦中学陈誉杰福建金牌初一福州第十九中卢祺福建金牌初一厦门一中程思浩福建金牌初一晋江市季延初级中学施泽楷福建金牌初一石狮中英文实验学校柯法至福建金牌初一开平市金山中学胡文正广东金牌初一开平市金山中学邝鑫康广东金牌初一深圳市华瑞教育黄禹欢广东金牌初一深圳市华瑞教育魏千皓广东金牌初一深华教育陈毅骏广东金牌初一深圳博尔思教育陈嘉广东金牌初一深圳市高级中学初中部陈蔓佳广东金牌初一广州学而思杨诗田广东金牌初一海珠区六中珠江中学徐栎广东金牌初一华南师大附中廖星玥广东金牌初一广州大学附属中学利茵广东金牌初一纪中三鑫双语学校范钶广东金牌初一纪中三鑫双语学校古云天广东金牌初一中山纪念中学黄乐明广东金牌初一广西师范大学附属外国语学校董芳圻广西金牌初一贵阳十九中罗全宇贵州金牌初一海口新卓力文化培训中心陈麟发海南金牌初一邢台市天元培训学校熊丘桓河北金牌初一石家庄外国语学校刘宇扬河北金牌初一石家庄外国语学校严梓昊河北金牌初一石家庄润智学校俞骁阳河北金牌初一邢台市天元培训学校熊丘桓河北金牌初一郑州市枫杨外国语学校崔世博河南金牌初一郑州市枫杨外国语学校杨偲宽河南金牌初一郑州市枫杨外国语学校袁竞择河南金牌初一哈工大附中刘枭男黑龙江金牌初一哈工大附中谷肇兴黑龙江金牌初一湖北华一寄宿学校贾逸珂湖北金牌初一湖北华一寄宿学校胡靖佳湖北金牌初一雅礼实验吴佳英湖南金牌初一冷水江市第七中学陈俊贤湖南金牌初一冷水江市第七中学吴成智湖南金牌初一酿溪中学邹冬骏湖南金牌初一长沙市南雅中学吴乙弘湖南金牌初一长沙市南雅中学陈子云湖南金牌初一辽源市实验中学郑皓天吉林金牌初一吉林师范大学附属中学李京瀚吉林金牌初一江苏书人教育范泽玥江苏金牌初一江苏书人教育薛东昀江苏金牌初一江苏书人教育张海平江苏金牌初一江苏书人教育邹嘉骐江苏金牌初一徐州书人教育卢辰博江苏金牌初一扬州书人教育袁天瑞江苏金牌初一苏州市新东方学校谢林锋江苏金牌初一常州外国语学校王想江苏金牌初一苏州学而思文化培训中心姚骧江苏金牌初一南昌市百德学校余不悔江西金牌初一南昌新东方学校董一航江西金牌初一浮梁县一中王诗哲江西金牌初一抚顺市第五十中学李瑞辽宁金牌初一呼伦贝尔市海拉尔五中浩树奇内蒙古金牌初一呼伦贝尔市甘河韩卓内蒙古金牌初一呼和浩特市实验中学刘栩屾内蒙古金牌初一呼和浩特市启秀中学兰震内蒙古金牌初一包头市北重一中贾浩宇内蒙古金牌初一包头市北重二中李驰内蒙古金牌初一济南历城二中张钊山东金牌初一西安铁一中谢卓言陕西金牌初一西北工业大学附中胥皓然陕西金牌初一西北工业大学附中曹倍源陕西金牌初一西安高新一中初中校区刘雨萱陕西金牌初一上海进华中学卢珽宇上海金牌初一新华初级中学沈株涵上海金牌初一上宝中学冯钰玮上海金牌初一上外附中罗曼娜上海金牌初一兰生复旦中学瞿天雍上海金牌初一上海中学东校吴骐锋上海金牌初一宜宾黄冈实验学校薛飞杨四川金牌初一成都市三原外国语学校周书锴四川金牌初一射洪中学外语实验学校蔡忠良四川金牌初一丹秋名师堂学校王钺洛四川金牌初一宁波镇海蛟川书院陈与时浙江金牌初一宁波镇海蛟川书院孙翌凯浙江金牌初一宁波镇海蛟川书院徐婷蕾浙江金牌初一宁波镇海蛟川书院孙言笑浙江金牌初一宁波镇海蛟川书院周栩屹浙江金牌初一宁波镇海蛟川书院张文望浙江金牌初一宁波镇海蛟川书院宋雨婷浙江金牌初一宁波镇海蛟川书院邹慕尧浙江金牌初一宁波镇海蛟川书院段儒剑浙江金牌初一宁波镇海蛟川书院张开颜浙江金牌初一宁波镇海蛟川书院尹清扬浙江金牌初一宁波镇海蛟川书院李晗芃浙江金牌初一宁波镇海蛟川书院林逸舟浙江金牌初一宁波镇海蛟川书院崔博宇浙江金牌初一富阳永兴中学马圣博浙江金牌初一桐庐县叶浅予中学应舒畅浙江金牌初一桐庐县叶浅予中学张诗远浙江金牌初一温州新星学校陈启轩浙江金牌初一温州新星学校黄钱生浙江金牌初一温州新星学校金政浙江金牌初一温州新星学校项铭铭浙江金牌初一温州新星学校章圣楠浙江金牌初一苍南潜龙学校颜明浙江金牌初一泰顺育才学校翁乐其浙江金牌初一上外附属浙江宏达学校陈奕希浙江金牌初一上外附属浙江宏达学校陈加诺浙江金牌初一现代实验学校吴迪浙江金牌初一现代实验学校蒋哲宇浙江金牌初一现代实验学校肖彤浙江金牌初一求是实验中学徐嘉辉浙江金牌初一求是实验中学朱晗捷浙江金牌初一求是实验中学赵诗瑶浙江金牌初一求是实验中学朱卓锋浙江金牌初一二十一世纪外国语学校刘伯仁浙江金牌初一桐乡六中姚问浙江金牌初一桐乡六中施潇艺浙江金牌初一嘉兴市实验初级中学万致远浙江金牌初一嘉兴市实验初级中学曹宇航浙江金牌初一嘉善县泗洲中学李少群浙江金牌初一嘉善县泗洲中学方涵浙江金牌初一博才实验学校敬睿悦浙江金牌初一博才实验学校汤天怡浙江金牌初一博才实验学校李舒怡浙江金牌初一嘉兴一中实验学校王睿祺浙江金牌初一嘉兴一中实验学校倪宇冰浙江金牌初一平湖市东湖中学胡宇恒浙江金牌初一重庆市大帝学校覃沛阳重庆金牌初一重庆市九龙坡区教育培训学校王淋枫重庆银牌初一安徽省合肥市育苗培训学校姜凡希安徽银牌初一合肥市新航培训中心饶兴豪安徽银牌初一培正中學唐健維澳门银牌初一鏡平學校許楚堅澳门银牌初一学而思培训学校陈锐恒北京银牌初一厦门大学附属实验中学黄哲涛福建银牌初一福清西山学校刘丝曼福建银牌初一福州华伦中学罗成杰福建银牌初一福州华伦中学何家骏福建银牌初一福州十八中陈震宇福建银牌初一福州时代中学楼成福建银牌初一福州长乐侨中陈子涵福建银牌初一泉州七中金山校区陈伟镔福建银牌初一泉州市培元中学刘嘉森福建银牌初一安溪县凤城中学郭文楷福建银牌初一安溪县凤城中学许坤钊福建银牌初一泉州市外国语中学郑雯文福建银牌初一泉州市外国语中学林灿坤福建银牌初一安溪县东溪中学陈应炀福建银牌初一泉州市现代中学林雅菲福建银牌初一安溪县第八中学张岚杨福建银牌初一泉州市第六中学郑艺辉福建银牌初一泉州市第三中学吴钧霆福建银牌初一泉州市第十五中学张立豪福建银牌初一五缘实验学校谢林珊福建银牌初一莲花中学周轩霆福建银牌初一泉州实验中学丁正午福建银牌初一晋江市季延初级中学王欣荣福建银牌初一石狮市瀚博文化培训学校王思增福建银牌初一树人学校房奕嘉甘肃银牌初一清远市博爱学校温北晨广东银牌初一开平市金山中学邝润发广东银牌初一开平市金山中学司徒佑权广东银牌初一开平市金山中学杨宇骊广东银牌初一开平市金山中学黄嘉辉广东银牌初一开平市金山中学温育民广东银牌初一开平市金山中学袁卓荣广东银牌初一开平市金山中学关均淋广东银牌初一开平市金山中学刘思一广东银牌初一开平市金山中学周润杨广东银牌初一开平市金山中学张景斌广东银牌初一开平市金山中学劳树森广东银牌初一深圳市高级中学初中部徐子川广东银牌初一深圳学而思毛瀚燚广东银牌初一深圳学而思林胤广东银牌初一深圳学而思徐钰翔广东银牌初一深圳学而思雷岳龙广东银牌初一海珠区六中珠江中学唐语阳广东银牌初一华南师大附中冯宣瑞广东银牌初一广州市第七中学徐有成广东银牌初一广州市执信中学陈百铭广东银牌初一惠阳高级中学许哲涛广东银牌初一福泉奥林匹克学校陈睿广东银牌初一纪中三鑫双语学校潘毓哲广东银牌初一纪中三鑫双语学校彭睿广东银牌初一纪中三鑫双语学校盛宁广东银牌初一纪中三鑫双语学校林欣洋广东银牌初一纪中三鑫双语学校吴政达广东银牌初一中山纪念中学陈若霖广东银牌初一惠州市第一中学黄俊铭广东银牌初一顺德德胜学校吴基洋广东银牌初一顺德德胜学校陈思佳广东银牌初一桂林市奎光学校李南佳广西银牌初一广西师范大学附属外国语学校赵锦曦广西银牌初一广西师范大学附属外国语学校李琳广西银牌初一柳州市博学教育陈文川广西银牌初一柳州市博学教育李卢楷广西银牌初一南宁市二十六中聂一宁广西银牌初一南宁市西大附中赖玉轩广西银牌初一南宁市十一中韦正豪广西银牌初一普安县地瓜镇地瓜中学朱宸瑶贵州银牌初一三都水族自治县鹏城中学潘洪创贵州银牌初一贵阳市春雷思维培训学校唐仙镒贵州银牌初一贵阳市春雷思维培训学校纵雨芯贵州银牌初一贵阳市春雷思维培训学校何俊豪贵州银牌初一北师大附中文国睿贵州银牌初一贵阳十九中冯文镜贵州银牌初一乐湾国际学校喻星匀贵州银牌初一开智培训学校姚云天贵州银牌初一开智培训学校姚骏奕贵州银牌初一六枝特区三中王家瑞贵州银牌初一六枝特区第二中学赛尧贵州银牌初一六枝特区第二中学王学瑾贵州银牌初一贵阳一中新世界国际学校韦宇宁贵州银牌初一贵定县第二中学庭开旭贵州银牌初一贵阳市十七中学盛易天贵州银牌初一贵阳市七中刘海鹏贵州银牌初一海口新思维文化艺术培训中心李芯童海南银牌初一海口市育龙青少年活动中心黄旭东海南银牌初一海口市育龙青少年活动中心李卓阳海南银牌初一海口市育龙青少年活动中心王瀚海南银牌初一海南省青少年俱乐部素质教育活动中心韩钰海南银牌初一海南省青少年俱乐部素质教育活动中心蔡文凯海南银牌初一海口新卓力文化培训中心吴鼎海南银牌初一海口新卓力文化培训中心朱素瑶海南银牌初一海口景山学校王浩成海南银牌初一海口实验中学梁言海南银牌初一海南师范附中钱世豪海南银牌初一邢台市小天才培训学校石家豪河北银牌初一邢台市小天才培训学校董思远河北银牌初一邢台市第十九中学王子川河北银牌初一邢台市天元培训学校时代校区王辰轩河北银牌初一石家庄润智学校杨菁露河北银牌初一石家庄润智学校吴重佑河北银牌初一石家庄鑫鹏学校赵翊帆河北银牌初一石家庄外国语学校屈佳璇河北银牌初一石家庄新星第28中学刘博河北银牌初一邯郸市第一中学王研哲河北银牌初一郑州市枫杨外国语学校贾明易河南银牌初一郑州市枫杨外国语学校蒋博文河南银牌初一郑州市枫杨外国语学校吴浩泽河南银牌初一郑州市枫杨外国语学校张芮扬河南银牌初一郑州市枫杨外国语学校马铭遥河南银牌初一洛阳市彩虹学校兰浩轩河南银牌初一大庆外国语学校蒋柏瑞黑龙江银牌初一大庆博奥学校张旭鹏黑龙江银牌初一哈工大附中林宇航黑龙江银牌初一松雷中学杨英奇黑龙江银牌初一湖北华一寄宿学校徐天骁湖北银牌初一十堰市东风分局第七中学张晓越湖北银牌初一十堰市实验中学林志豪湖北银牌初一常德市长麓（茂林）培训学校邓浩湖南银牌初一常德市长麓（茂林）培训学校张茂轩湖南银牌初一凤凰县华鑫实验学校龙诗睿湖南银牌初一雅礼实验刘景赫湖南银牌初一雅礼实验蔡心怡湖南银牌初一冷水江市第二中学张慧湖南银牌初一冷水江市第二中学陈慧颖湖南银牌初一冷水江市明礼实验中学段嘉骏湖南银牌初一酿溪中学李共幸湖南银牌初一酿溪中学李振湖南银牌初一酿溪中学唐龙湖南银牌初一酿溪中学谢玉婷湖南银牌初一坪上镇中学肖孚璐湖南银牌初一湖南省新化县第十五中学伍昭阳湖南银牌初一长沙市南雅中学陈思文湖南银牌初一长沙市南雅中学伍骏程湖南银牌初一长沙市南雅中学方千里湖南银牌初一长沙市南雅中学邹瑞航湖南银牌初一长沙市南雅中学王林亿湖南银牌初一吉林市二十九中苏园茗吉林银牌初一吉林师范大学附属中学侯琳琳吉林银牌初一四平市第十七中学刘家维吉林银牌初一四平市第十七中学隋建新吉林银牌初一长春市解放大路学校鲍志灏吉林银牌初一长春鸿宇晁祎吉林银牌初一长春市师大（贯通）玄朕吉林银牌初一盐城市盐阜中学江可欣江苏银牌初一盐城市文峰中学滕昊江苏银牌初一江苏书人教育陈庭宇江苏银牌初一江苏书人教育胡程悦江苏银牌初一江苏书人教育殷天成江苏银牌初一江苏书人教育张嘉彬江苏银牌初一江苏书人教育林宇轩江苏银牌初一江苏书人教育金正秋江苏银牌初一江苏书人教育李睿博江苏银牌初一江苏书人教育肖潇江苏银牌初一江苏书人教育周子骏江苏银牌初一江苏书人教育庄永强江苏银牌初一金升外国语实验学校成蕊江苏银牌初一海安神墨教育培训中心杨悠优江苏银牌初一吴江市青云实验中学王振宇江苏银牌初一吴江市青云实验中学秦永平江苏银牌初一常州外国语学校王星越江苏银牌初一苏州学而思文化培训中心吴宇深江苏银牌初一南昌市百德学校陈政博江西银牌初一南昌新东方学校甘睿骜江西银牌初一乐平市第二中学徐宇航江西银牌初一乐平市第二中学袁尹杰江西银牌初一浮梁县一中李彤江西银牌初一浮梁县新平中学计炜轩江西银牌初一赣州市第一中学朱卓远江西银牌初一赣州市第一中学周可心江西银牌初一赣州市第一中学殷文骅江西银牌初一抚顺市第五十中学洪图辽宁银牌初一东北育才外国语学校鲍姝含辽宁银牌初一呼伦贝尔市海拉尔五中李松林内蒙古银牌初一呼伦贝尔市海拉尔五中夏越千内蒙古银牌初一呼伦贝尔市满洲里十中王敬泽内蒙古银牌初一鄂尔多斯市东胜区正东中学张俊扬内蒙古银牌初一呼和浩特市实验中学张浦内蒙古银牌初一呼和浩特市实验中学段禹琪内蒙古银牌初一呼和浩特市实验中学蒙杰内蒙古银牌初一呼和浩特市实验中学王泽宇内蒙古银牌初一包头市包钢三中魏颢晨内蒙古银牌初一包头市包钢三中王敬一内蒙古银牌初一包头市包钢三中祁芃内蒙古银牌初一包头市35中孙浩森内蒙古银牌初一包头市29中李泽显内蒙古银牌初一包头市北重四中刘洋内蒙古银牌初一利津县第一实验学校庄瑞毅山东银牌初一青岛超银中学鞍山路校区迟凯文山东银牌初一青岛超银中学广饶路校区于奕童山东银牌初一运城东康中学苏家祺山西银牌初一运城东康中学闫子航山西银牌初一杨凌高新中学甘凤轩陕西银牌初一西安高新一中初中校区杨启志陕西银牌初一西安高新一中初中校区李沅芷陕西银牌初一西安高新一中初中校区苏子珺陕西银牌初一西安高新一中初中校区冯成洁陕西银牌初一西安高新一中初中校区邓思行陕西银牌初一西北工业大学附中董凡可陕西银牌初一西北工业大学附中张一驰陕西银牌初一西安铁一中张佳伟陕西银牌初一上海中学东校马宇飞上海银牌初一上海进华中学季灏上海银牌初一上宝中学王宸上海银牌初一上宝中学马易成上海银牌初一兰生复旦中学孟嘉音上海银牌初一兰生复旦中学王亦悦上海银牌初一宜宾黄冈实验学校罗祥富四川银牌初一宜宾翠屏棠湖外语学校张钰睿四川银牌初一成都市三原外国语学校刘迦一四川银牌初一成都市嘉祥外国语学校郫县分校王云萱四川银牌初一射洪中学外语实验学校高邓泽君四川银牌初一丹秋名师堂学校陈竞文四川银牌初一天津市二十五中学孙绍聪天津银牌初一乌鲁木齐市兵团一中张艺锐新疆银牌初一喀什地区第二中学陈李杰新疆银牌初一喀什地区第二中学王蒙新疆银牌初一华兵实验中学王湘天穆新疆银牌初一克拉玛依市南湖中学肖涵睿新疆银牌初一水富县云天化中学施吉胤云南银牌初一宁波镇海蛟川书院周骏东浙江银牌初一宁波镇海蛟川书院汤奕骁浙江银牌初一宁波镇海蛟川书院方嘉文浙江银牌初一宁波镇海蛟川书院陈奎谕浙江银牌初一宁波镇海蛟川书院褚天乐浙江银牌初一宁波镇海蛟川书院林听浙江银牌初一宁波镇海蛟川书院郭浚哲浙江银牌初一宁波镇海蛟川书院吴思妍浙江银牌初一宁波镇海蛟川书院徐艺珊浙江银牌初一宁波镇海蛟川书院黄钟宏浙江银牌初一宁波镇海蛟川书院叶梦倩浙江银牌初一平阳新纪元学校陈智钻浙江银牌初一平阳昆阳镇第二中学繆心安浙江银牌初一温州新星学校苏畅浙江银牌初一温州新星学校陈奕浙江银牌初一温州新星学校董卓伦浙江银牌初一温州新星学校方舟浙江银牌初一温州新星学校姜增铤浙江银牌初一温州新星学校李潇浙江银牌初一温州新星学校林佳栩浙江银牌初一温州新星学校林柯浙江银牌初一温州新星学校刘畅浙江银牌初一温州新星学校吴荻浙江银牌初一宁海镇明中心梅文九浙江银牌初一杭州锦绣中学邱瑞晨浙江银牌初一杭州绿城育华学校郑楚泓浙江银牌初一桐乡六中张雨杨浙江银牌初一桐乡六中崔雨桐浙江银牌初一博才实验学校朱奕诚浙江银牌初一博才实验学校范亦心浙江银牌初一博才实验学校由思琪浙江银牌初一博才实验学校顾恬文浙江银牌初一博才实验学校徐立傲浙江银牌初一嘉兴一中实验学校章钰清浙江银牌初一嘉兴一中实验学校沈子皓浙江银牌初一嘉兴一中实验学校马涵语浙江银牌初一嘉兴一中实验学校吴文骏浙江银牌初一嘉兴一中实验学校汪旻宇浙江银牌初一嘉兴一中实验学校戴子涵浙江银牌初一嘉兴一中实验学校朱嘉策浙江银牌初一嘉兴一中实验学校陈祎祺浙江银牌初一北师大南湖附属学校杨光浙江银牌初一求是实验中学徐梦琪浙江银牌初一求是实验中学祝镪浙江银牌初一求是实验中学张泽濠浙江银牌初一求是实验中学孙佶恺浙江银牌初一上外秀洲外国语学校俞书璇浙江银牌初一武原中学赵言彬浙江银牌初一现代实验学校吴乾城浙江银牌初一现代实验学校陈斌浙江银牌初一嘉善县第四中学徐江昊浙江银牌初一海宁市紫微初中周亿涵浙江银牌初一海宁市南苑中学朱弈弛浙江银牌初一上外附属浙江宏达学校娄陈博文浙江银牌初一上外附属浙江宏达学校董烨浙江银牌初一重庆市九龙坡区教育培训学校白涵之重庆。

第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

2015年第十三届小学“希望杯”全国数学邀请赛试卷（四年级第1试）一、填空题：1．（3分）计算：2468×629÷（1234×37）=．2．（3分）有一个除法算式，被除数和除数的和是136，商是7，则除数是．3．（3分）定义：a⊕b=a+b+ab，则（2⊕3）⊕4的值为．4．（3分）买一支水彩笔需要1元7角，用15元钱最多可以买这样的水彩笔支．5．（3分）王雷是国庆节那天出生的，若他年龄的3倍减去8刚好是他出生那月的总天数，则王雷今年岁．6．（3分）数一数，图中共有个三角形．7．（3分）某班30人参加跳绳比赛，开始时有4人迟到没有参加比赛，这时平均成绩为20个，后来这4位同学赶到了比赛场地，分别跳了26，27，28，29个．这时全班同学的平均成绩是个．8．（3分）明明临摹一本字帖练习毛笔字，临摹第一遍时，他每天写25个字，临摹第二遍时，他每天多写3个字，结果刚好比第一遍少用了3天，则这本字帖共有字．9．（3分）如图有16个1×1的小正方形组成，图中△ABC的面积是．10．（3分）乌龟和兔子在全长为1000米的赛道上比赛，兔子的速度是乌龟速度的15倍．但兔子在比赛的过程中休息了一会儿，醒来时发现乌龟刚好到达终点，而此时兔子还差100米才到终点．则兔子休息期间乌龟爬行了米．11．（3分）任意一个一位奇数与任意一个一位偶数相乘，不同的乘积有个．12．（3分）一个长方形的相框长为40厘米，宽为32厘米，放入一张长为32厘米宽为28厘米的相片，则相框中没有被照片覆盖的部分的面积是平方厘米．13．（3分）爷爷，爸爸，小明的年龄分别是60岁，35岁，11岁，则再过年爷爷的年龄等于小明和爸爸年龄的和．14．（3分）一个长方形的长和宽都增加3厘米后，面积增加了90平方厘米，则原长方形的周长是厘米．15．（3分）甲筐和乙筐内原来分别放有54个和63个鸡蛋，若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍，那么应从乙筐内取出个鸡蛋放入甲筐．16．（3分）王蕾和姐姐从家步行去体育馆打羽毛球，已知姐姐每分钟比王蕾多走20米，25分钟后姐姐到体育馆，这时姐姐发现没有带球拍，于是立即按原路返回取球拍，在离体育馆300米的地方遇到了王蕾，则王蕾家到体育馆的路程是米．17．（3分）如图，用小正方形摆成下列图形，按摆放规律，第25个图形需要小正方形个．18．（3分）若abc+cba=1069，则这样的abc有个．19．（3分）某地希望杯组委会给参加希望杯考试的考生安排考场，若每个考场安排30名考生，则会有一个考场有26名考生；若每个考场安排26个考生，则会有一个考场有20名考生，并且要比前一种方案多用9个考场，则该地区参加考试的考生有个．20．（3分）如图有3个边长是6的正方形组成，则图中阴影部分的面积是．2015年第十三届小学“希望杯”全国数学邀请赛试卷（四年级第1试）参考答案与试题解析一、填空题：1．（3分）计算：2468×629÷（1234×37）=34．【分析】根据除法的性质进行简便计算．【解答】解：2468×629÷（1234×37）=2468×629÷1234÷37=2468÷1234×（629÷37）=2×17=34故答案为：34．【点评】完成本题要注意分析式中数据，运用合适的简便方法计算．2．（3分）有一个除法算式，被除数和除数的和是136，商是7，则除数是17．【分析】方法一：被除数和除数的和是136，商是7，说明被除数是除数的7倍，被除数与除数的和就是除数的（7+1）倍，用136除以（7+1）即可求出除数，由此求解；方法二：根据被除数=商×除数，设除数是x，则被除数就是7x，再根据“被除数与除数的和是136”，列出方程并解方程即可．【解答】解：方法一：136÷（7+1）=136÷8=17答：除数是17．方法二：设除数是x，被除数是7x，由题意得：7x+x=1368x=136x=17答：除数是17．故答案为：17．【点评】解决本题可以看成和倍问题进行求解：两数和÷倍数和=1倍的数；也可以设出未知数，根据被除数、除数和商三者之间的关系找出等量关系列出方程求解．3．（3分）定义：a⊕b=a+b+ab，则（2⊕3）⊕4的值为59．【分析】根据题意得出a⊕b等于a加上b再加上a与b的积，由此利用此方法计算（2⊕3）⊕4的值，据此解答．【解答】解：（2⊕3）⊕4=（2+3+2×3）⊕4=11⊕4=11+4+11×4=59故答案为：59．【点评】先理解新运算的计算方法，然后按照先算小括号再算括号外的顺序带入数据计算即可．4．（3分）买一支水彩笔需要1元7角，用15元钱最多可以买这样的水彩笔8支．【分析】1元7角=1.7角，求用15元钱最多可以买这样的水彩笔多少支，就是求15里面有几个1.7，用除法解答即可．【解答】解：1元7角=1.7角15÷1.7≈8（支）答：用15元钱最多可以买这样的水彩笔8支．故答案为：8．【点评】本题考查了有余数除法应用题，要注意得数用“去尾法”求值．5．（3分）王雷是国庆节那天出生的，若他年龄的3倍减去8刚好是他出生那月的总天数，则王雷今年13岁．【分析】因为国庆节在10月，10月有31天，所以根据“他年龄的3倍减去8刚好是他出生那月的总天数，”知道王雷的年龄的3倍再减去8等于31，由此先求出王雷年龄的3倍，再求出王雷的年龄．【解答】解：（31+8）÷3=39÷3=13（岁）；答：王雷今年13岁．故答案为：13．【点评】解答此题的关键是知道10月有31天，再根据“王雷的年龄的3倍再减去8等于31”这个数量关系解决问题．6．（3分）数一数，图中共有24个三角形．【分析】不在同一直线上三点可以确定一个三角形，据此即可求解．【解答】解：（5+1+1+1+1）+（4+2+2+1）+3+2+1=9+9+3+2+1=24（个）答：图中共有24个三角形．故答案为：24．【点评】本题主要考查了三角形的认识，按正确的顺序计算三角形的个数是解决本题的关键．7．（3分）某班30人参加跳绳比赛，开始时有4人迟到没有参加比赛，这时平均成绩为20个，后来这4位同学赶到了比赛场地，分别跳了26，27，28，29个．这时全班同学的平均成绩是21个．【分析】根据30人参加跳绳比赛，开始时有4人迟到没有参加比赛，这时平均成绩为20个，先算出30﹣4=26人的成绩，（30﹣4）×20=520，然后再加上26、27、28、29，再除以30即可解答．【解答】解：（30﹣4）×20=520（个）520+26+27+28+29=630（个）630÷30=21（个）答：这时全班同学的平均成绩是21个．故答案为：21．【点评】本题考查了平均数的含义以及应用．8．（3分）明明临摹一本字帖练习毛笔字，临摹第一遍时，他每天写25个字，临摹第二遍时，他每天多写3个字，结果刚好比第一遍少用了3天，则这本字帖共有700字．【分析】设临摹第一遍时，用了x天，则临摹第二遍时用了x﹣3天，根据等量关系：临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字，列方程解答即可得临摹第一遍时天数，再求这本字帖共有多少页即可．【解答】解：设临摹第一遍时，用了x天，25x=（25+3）×（x﹣3）25x=28x﹣843x=84x=28，28×25=700（字）答：这本字帖共有700字．故答案为：700．【点评】本题考查了列方程解应用题，关键是根据等量关系：临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字，列方程．9．（3分）如图有16个1×1的小正方形组成，图中△ABC的面积是7．【分析】正方形减去边上三个直角三角形的面积即可求解；正方形的边长4，左上角三角形的底是4，高是2；右下角三角形的底是1，高是4；左下角三角形的底是3，高是2，把这些数据代入正方形和三角形的面积公式求解即可．【解答】解：4×4﹣4×2÷2﹣4×1÷2﹣3×2÷2=16﹣4﹣2﹣3=7答：图中△ABC的面积是7．故答案为：7．【点评】此题解答的关键在于把要求三角形的面积转化成正方形的面积与另外三个三角形的面积差，再分别根据它们的面积公式求解．10．（3分）乌龟和兔子在全长为1000米的赛道上比赛，兔子的速度是乌龟速度的15倍．但兔子在比赛的过程中休息了一会儿，醒来时发现乌龟刚好到达终点，而此时兔子还差100米才到终点．则兔子休息期间乌龟爬行了940米．【分析】根据题意，兔子一共跑了1000﹣100=900（米），因为兔子的速度是乌龟的15倍，所以在兔子跑的同时乌龟跑了900÷15=60（米），而实际乌龟跑了1000米，所以它在兔子睡着的时候乌龟跑了1000﹣60=940（米），解决问题．【解答】解：1000﹣（1000﹣100）÷15=1000﹣900÷15=1000﹣60=940（米）；答：兔子休息期间乌龟爬行了940米．故答案为：940．【点评】此题的解答思路：先求出兔子一共跑的路程，再根据兔子速度是乌龟的5倍，求出在兔子跑的同时乌龟跑的路程，进而解决问题．11．（3分）任意一个一位奇数与任意一个一位偶数相乘，不同的乘积有19个．【分析】因为0是最小的偶数，5个奇数（1，3，5，7，9）乘4个偶数（2、4、6、8）一共是4×5=20个数，去掉得数是18和得数是6的两个相同的，还有18个，再加上0，就是19个，据此解答．【解答】解：5个奇数（1，3，5，7，9）乘偶数（2、4、6、8）一共是5×4=20个得数，去掉3×6=2×9，2×3=1×6两个相同的，还有18个，再加上0，就是19个；答：不同的乘积有19个；故答案为：19．【点评】关键是别忘记把相同的乘积给减去，注意0是偶数．12．（3分）一个长方形的相框长为40厘米，宽为32厘米，放入一张长为32厘米宽为28厘米的相片，则相框中没有被照片覆盖的部分的面积是384平方厘米．【分析】放入一张长为32厘米宽为28厘米的相片，则被照片覆盖的部分的面积是这张相片的面积，分别求出相框和相片的面积，然后用相框的面积减去相片的面积即可．【解答】解：40×32﹣32×28=32×（40﹣28）=32×12=384（平方厘米）答：相框中没有被照片覆盖的部分的面积是384平方厘米．故答案为：384．【点评】此题考查了长方形面积公式的灵活运用．13．（3分）爷爷，爸爸，小明的年龄分别是60岁，35岁，11岁，则再过14年爷爷的年龄等于小明和爸爸年龄的和．【分析】设经过x年后爷爷的年龄等于小明和爸爸年龄的和，那么经过x年后，爷爷，爸爸，小明的年龄分别是：60+x，35+x，11+x，根据“爷爷的年龄等于小明和爸爸年龄的和”列出方程解答即可【解答】解：设经过x年后爷爷的年龄等于小明和爸爸年龄的和，由题意得：35+x+11+x=60+x2x+46=60+xx=14，答：经过14年后爷爷的年龄等于小明和爸爸年龄的和．故答案为：14．【点评】本题等量关系明显，用方程较易解决．14．（3分）一个长方形的长和宽都增加3厘米后，面积增加了90平方厘米，则原长方形的周长是54厘米．【分析】根据题意，长和宽分别增加了3厘米，这个长方形的面积就增加了90平方米（如下图）：增加的面积包括2部分，下面的长方形，面积是3（3+a），右上角的小长方形，面积是3b，它们的和是3（3+a）+3b等于90，求出a+b的和，再用（a+b）×2计算即可．【解答】解：设长方形原来的长是a厘米，宽是b厘米，现在的长是a+3厘米，宽是b+3厘米，图下图：3（3+a）+3b=909+3a+3b=90a+b=2727×2=54（平方厘米）答：原长方形的周长是54厘米．【点评】此题主要考查长方形周长的计算，关键是求出原来长方形的长与宽的和，再根据长方形的公式解答．15．（3分）甲筐和乙筐内原来分别放有54个和63个鸡蛋，若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍，那么应从乙筐内取出24个鸡蛋放入甲筐．【分析】甲筐和乙筐内原来分别放有54个和63个鸡蛋，总共有54+63=117个鸡蛋；若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍，这两筐的鸡蛋总数不变，还是117个，根据和倍公式求出这时乙筐的鸡蛋个数，即117÷（2+1）=39个，那么乙筐比原来少的就是放入甲筐的个数，即63﹣39=24个．【解答】解：54+63=117（个）117÷（2+1）=117÷3=39（个）；63﹣39=24（个）．答：应从乙筐内取出24个鸡蛋放入甲筐．故答案为：24．【点评】本题关键是两筐鸡蛋总个数不变，根据倍数关系，由和倍公式求出后来乙筐鸡蛋的个数，然后再进一步解答．16．（3分）王蕾和姐姐从家步行去体育馆打羽毛球，已知姐姐每分钟比王蕾多走20米，25分钟后姐姐到体育馆，这时姐姐发现没有带球拍，于是立即按原路返回取球拍，在离体育馆300米的地方遇到了王蕾，则王蕾家到体育馆的路程是1500米．【分析】在离图书馆300米处相遇时，王蕾和姐姐的路程差为300×2=600米，由于姐姐每分钟比王蕾多走20米，因此两人相遇时经历的时间是=30分钟，然后可得姐姐走300米的时间，进而可得姐姐的速度，从而可求得王蕾家到图书馆的路程．【解答】解：在离图书馆300米处相遇时，王蕾和姐姐的路程差为300×2=600（米），两人相遇时经历的时间==30（分钟），姐姐返回走的300米花费的时间=30﹣25=5（分钟），姐姐的速度==60（米/分钟），王雷家到图书馆的路程=60×25=1500（米）答：王蕾家到体育馆的路程是1500米．故答案为：1500．【点评】本题考查了相遇问题，关键在于能根据相遇时两人的路程差求出相遇时经历的时间．17．（3分）如图，用小正方形摆成下列图形，按摆放规律，第25个图形需要小正方形625个．【分析】观察得知：第一个图有1个正方形形组成，即12个；第二个图有1+3=4个正方形形组成，即22个；第三个图有1+3+5=9个正方形形组成，即32个；第四个图有1+3+5+7=16个正方形形组成，即42个；…以此类推：第n个图有1+3+5+7+…+.2n﹣1=n2个正方形形组成．据此解答即可．【解答】解：由分析可得：第25个图形需要小正方形：1+3+5+7+…+49=252=625（个）答：第25个图形需要小正方形625个．故答案为：625．【点评】解答本题的关键是：正确找出第几个图与所含正方形形个数的关系，进而得出它们之间的关系．18．（3分）若abc+cba=1069，则这样的abc有8个．【分析】解：（1）abc+cba=100a+10b+c+100c+10b+a=101a+101c+20b=101×（a+c）+20b=1069；（2）根据101×（a+c）+20b=1069的个位数字9可知：a+c 的个位一定是9；又因为a、c最大值均不超过9，因此a+c=9，可得b一定是8；（3）分析a+c=9有多少种情况：因为a、c 都出现在第一位上，因此均不可能为0．然后推出当a=1、2、3、4、5、6、7、8 时c的值，解决问题．【解答】解：（1）由abc+cba=1069，可得abc+cba=100a+10b+c+100c+10b+a=101a+101c+20b=101×（a+c）+20b=1069；（2）因为101×（a+c）+20b=1069的个位数字9，a+c 的个位一定是9；又因为a、c最大值均不超过9，因此a+c=9，可得b一定是8；（3）因为a+c=9，因为a、c 都出现在第一位上，因此均不可能为0．当a=1 时，c=8；当a=2 时，c=7；当a=3时，c=6；当a=4时，c=5；当a=5时，c=4；当a=6时，c=3；当a=7时，c=2；当a=8时，c=9；因此每种组合对应着一种情况，故abc存在8个不同的数．综上，这样的abc有8个．故答案为：8．【点评】此题由关系式入手，101×（a+c）+20b=1069的个位数字9，从而得出a+c 的个位一定是9，这是解题的关键．19．（3分）某地希望杯组委会给参加希望杯考试的考生安排考场，若每个考场安排30名考生，则会有一个考场有26名考生；若每个考场安排26个考生，则会有一个考场有20名考生，并且要比前一种方案多用9个考场，则该地区参加考试的考生有1736个．【分析】首先分析把题意转换为标准的盈亏问题，转换为30人的考场则少4人，26人的考场则多26×8+20=228人即可求解．【解答】解：依题意可知：题意转换为30人的考场则少4人，26人的考场则多26×8+20=228人．考场个数为（228+4）÷（30﹣26）=58（场）．学生共58×30﹣4=1736（人）故答案为：1736【点评】本题考查对盈亏问题的理解和运用，关键问题是分析出两次的盈亏数字，问题解决．20．（3分）如图有3个边长是6的正方形组成，则图中阴影部分的面积是36．【分析】如图，灰色小长方形加上灰色直角三角形加上阴影部分正好是一个梯形．梯形的上底等于小正方形边长的，下底和高都等于正方形边长的2倍，由此可求出梯形的面积；灰色长方形的长等于小正方形的边长，宽等于长的一半，由此可求出小长方形的面积；灰色直角三角形的面积两直角边分别是小正方形边长的2倍、小正方形边长，由此可求出这个直角三角形的面积；梯形面积﹣灰色长方形面积﹣灰色三角形面积=阴影部分面积．【解答】解：如图，（6×+6×2）×（6×2）÷2﹣6××6﹣6×2×6÷2=（3+12）×12÷2﹣6××6﹣6×2×6÷2=15×12÷2﹣6××6﹣6×2×6÷2=90﹣18﹣36=36，故答案为：36．【点评】此题是考查组成图形的面积，通过辅助部分组成一直角梯形，面积可求，两辅助部分面积也可求，梯形面积减去两辅助部分面积就是阴影部分面积．。

2014—2015年度奥数全国总决赛浙江选手披“金”戴“银”2015年2月9日—13日，2014-2015年度世界少年奥林匹克数学竞赛全国总决赛在北京、长沙、广州、哈尔滨四地同步举行并举行了隆重的颁奖典礼。

据悉本次全国总决赛有来自全国各赛区5000多名选手参加，浙江赛区共计344名选手参加了小学三年级至初中三年级七个年级段的比赛。

经过两轮比赛的激烈角逐，浙江选手共获得242枚奖牌，其中金奖37枚、银奖75枚、铜奖130枚。

来自乐清北白象第一小学三年级选手林兆赫、宁波市实验小学四年级选手傅立凯、温州市上陡门小学五年级选手王铭炜、富阳市永兴小学六年级选手姚彬、湖州市德清县华盛达外国语学校七年级选手孙宇凡等37位选手分别获得了金奖。

选手们通过本次比赛不仅收获了荣誉、开阔了眼界，还增强了他们的自信心和不断挑战新高的勇气与决心。

与此同时所有获奖选手还有机会参加下一阶段更高级别的比赛，如世界少年奥林匹克数学竞赛全球总决赛（特别金奖、金奖选手参加，全球总决赛将于2015年8月中旬在斯里兰卡举行）、世界少年奥林匹克数学竞赛亚洲精英赛（银奖、铜奖选手参加，亚洲精英赛将于2015年8上旬在香港和韩国举行）。

2014—2015世界少年奥林匹克数学竞赛全国总决赛获奖名单姓名性别年级学校奖项林兆赫男三年级乐清北白象第一小学金奖全葛睿睿女三年级宁波市广济中心小学实验校区金奖施衍羽男四年级乐清育英学校小学分校金奖傅立凯男四年级宁波市实验学校金奖黄际豪男四年级宁波市海曙中心小学金奖史宇颉男四年级宁波市海曙中心小学金奖乐卓彦男四年级宁波市海曙中心小学金奖王铭炜男五年级温州市上陡门小学金奖陈磊男五年级宁波市高塘小学金奖黄贰男五年级宁海县城中小学金奖余昊哲男五年级岱山实验小学金奖张佳艺男五年级宁波市江东实验小学金奖侯淳皓男五年级宁波市海曙中心小学金奖金森达男五年级瓯海娄桥一小金奖张义彬男五年级丽水囿山小学金奖章子奕男五年级丽水莲都小学金奖吕浩华男五年级丽水囿山小学金奖丛中笑男五年级杭州长江实验小学金奖姚彬男六年级富阳市永兴小学金奖俞皓曦男六年级宁波市江东实验小学金奖张宇粟男六年级宁波市海曙中心小学金奖俞欣怡女六年级宁波市海曙中心小学金奖陈科睿男六年级宁波市广济中心小学分校金奖胡家齐男六年级宁波市实验小学金奖许天翔男六年级宁波市幸福苑学校金奖陈骏扬男六年级宁波市镇明中心小学金奖鲍宇星男六年级宁波市鄞州区东湖小学金奖周羽荃女六年级宁波市镇明中心小学金奖沈奕彬男六年级宁波市江东实验小学金奖应韪朱倩女六年级宁波市鄞州区东湖小学金奖贺于桐女六年级宁波市江东二小金奖林雨蓝女六年级宁波市江北实验小学金奖戴锦阳男六年级乐清白象九小金奖孙宇凡男七年级德清县华盛达外语学校金奖周逸凡男七年级宁波东海实验学校金奖胡帅男七年级宁波市外国语学校金奖朱世豪男七年级瑞安新纪元学校金奖徐睿男三年级温州平阳昆阳镇第一小学银奖周裕凯男三年级瑞安实验小学银奖应文韬男三年级宁波市镇明中心小学银奖陈睿泽男三年级柳市三小银奖蒋月雅女三年级乐清外国语学校银奖陈星赫男四年级瑞安新纪元实验学校银奖蔡丰泽男四年级瑞安新纪元实验学校银奖周傲启男四年级宁波市广济中心小学银奖林予涵男四年级宁波市北仑区长江小学银奖赵柳舟男四年级云和实验学校银奖林睿焓男四年级云和实验学校银奖陈杭楠男四年级丽水囿山小学银奖方潇男四年级乐清育英学校银奖詹尔力男四年级乐清外国语学校银奖林与萧男四年级丽水遂昌育才小学银奖叶一鸣男四年级泰顺育才小学银奖鲍晨男五年级宁波光济中心小学银奖王一凡男五年级丽水缙云紫薇小学银奖朱徐洋男五年级德清县实验中学银奖王泽宁女五年级宁波市江东中心小学银奖魏弘阳男五年级宁波市江东实验小学银奖沈博闻男五年级宁波市华泰小学银奖王炫哲男五年级宁波市江东中心小学银奖孟诗语女五年级宁波市邱隘实验小学银奖周致宇男五年级温州市建设小学银奖林俊宇男五年级瓯北第二小学银奖陈麒旭男五年级温州市南浦小学银奖张羽就女五年级丽水大洋路小学银奖吴彦含男五年级丽水大洋路小学银奖陈可倪女五年级柳市三小银奖陈梦茜女五年级乐清外国语学校银奖李鹏程男五年级乐清外国语学校银奖石子涵男五年级乐清外国语学校银奖林易成男五年级丽水遂昌育才小学银奖杨霖锐男五年级青田县塔山实验小学银奖楼尚尚男五年级丽水莲都区中山小学银奖蔡易展男六年级丽水缙云实验小学银奖江府衡男六年级丽水缙云县实验小学银奖徐诗韵女六年级德清县实验学校银奖章轶杰男六年级宁波市镇明中心小学银奖杨骐开男六年级宁波市海曙中心小学银奖张鹤蓝男六年级宁波市国家高新区实验学校银奖郑天铭男六年级宁波市海曙中心小学银奖李雨航男六年级宁波市实验小学银奖周嘉树男六年级宁波市实验小学银奖张宇翔男六年级宁波市广济中心小学实验校区银奖赵正浩男六年级宁波市实验小学银奖周鹏男六年级宁波市新城实验小学银奖江翌琳女六年级宁波市华天小学银奖胡日臻男六年级宁波市江北中心小学银奖赵艺然男六年级宁波市江北中心小学银奖张欣瑜女六年级宁波市镇海区骆驼中心学校银奖金培捷男六年级宁波市孙文英小学银奖曹天鑫男六年级宁波市实验小学银奖吴湛男六年级象山县实验小学银奖吴蕾蕾女六年级象山实验小学银奖张添任男六年级宁波市江北中心小学银奖马铮浩男六年级宁波市江北实验小学银奖施昱女六年级宁波市海曙中心小学银奖吴峥男六年级宁波市镇海区应行久外语实验学校银奖朱波男六年级宁波市国家高新区实验学校银奖潘宁静女六年级宁波市镇明中心小学银奖郑全超男六年级宁波市实验小学银奖张旦阳男六年级宁波市镇明中心小学银奖谢仲霖男六年级宁波市镇明中心小学银奖张煜安女六年级宁波市海曙中心小学银奖林生阳男六年级宁波市江北实验小学银奖葛董琳女六年级宁波市海曙中心小学银奖王可唯男六年级宁波市镇明中心小学银奖陈彦熙男六年级宁波市江北中心小学银奖何奕霏女六年级丽水实验学校银奖陈贞男七年级衢州华茂外国语学校银奖叶昊宇男八年级瑞安市集云实验学校银奖王晟男八年级浙江德清县武康中学银奖潘文斌男九年级宁波市江北实验中学银奖陈强男三年级瑞安塘下实验小学铜奖缪泽浩男三年级瑞安莘滕实验小学铜奖翁嘉盛男三年级瑞安新纪元实验学校铜奖缪恩南男三年级瑞安市安阳实验小学铜奖陈泽宇男三年级丽水青田实验小学铜奖缪德湖男三年级苍南龙港海城小学铜奖伍耀文男三年级瑞安新纪元实验学校铜奖吴锦睿男三年级瑞安新纪元实验学校铜奖赵一强男三年级瑞安实验小学铜奖谢昊远男三年级瑞安新纪元实验学校铜奖黄照宇男三年级瑞安安阳实验小学铜奖林之正男三年级瓯海景山小学铜奖蔡尚蓁男三年级乐清育英学校小学铜奖章嘉冀男三年级德清县武康实验小学铜奖邵元明男三年级德清县实验学校铜奖李志儒男三年级德清县实验小学铜奖胡曦文女三年级乐清白象六小铜奖刘怡辉男四年级温州育英学校铜奖刘洋溢男四年级瑞安新纪元实验学校铜奖留煊昊男四年级丽水青田实验小学铜奖李嘉豪男四年级浙江衢州市新星学校铜奖钱炯成男四年级龙湾海城一小铜奖郑燮男四年级乐清城南二小铜奖陈谷瑜男四年级瑞安实验二小铜奖尤哲凯男四年级瑞安汀田实验小学铜奖申屠子暄女四年级杭州市桐庐县春江小学铜奖徐意博男四年级乐清育英学校小学分校铜奖徐乐航男四年级乐清育英学校小学分校铜奖董适男四年级泰顺县实验二小铜奖江皓楠男四年级宁波市广济中心小学铜奖陈延炫男四年级丽水实验小学铜奖林纪彤女四年级云和实验学校铜奖张淳男四年级乐清外国语学校铜奖叶城肇男四年级乐清外国语学校铜奖黄智博男四年级乐清外国语学校铜奖陶湘园女四年级泰顺育才外国语学校铜奖林子桥男四年级乐清旭阳寄宿学校铜奖傅炳坤男四年级乐清白象九小铜奖陈锦浩男四年级乐清白象一小铜奖汤雨欣女四年级乐清白象九小铜奖潘樾男五年级平阳昆阳镇第一小学铜奖沈文豪男五年级温州市沙城镇沙城二小铜奖吴韶韵女五年级泰顺育才小学铜奖陈豪男五年级温州市私立第一实验铜奖陆清洲男五年级绍兴市上虞滨江小学铜奖项天歌男五年级瑞安市实验小学铜奖戴雨航男五年级瑞安市仙降镇中心小学铜奖孔维程男五年级温州瑞安万桥天成小学铜奖陈以勒男五年级温州市南浦小学铜奖张焕然男五年级温州市南浦小学铜奖陈致乔男五年级乐清建设路小学铜奖林炜盛男五年级瑞安马鞍山实验小学铜奖郭展睿男五年级丽水遂昌育才小学铜奖王之韩男五年级平阳鳌江小学铜奖陈昱行男五年级瑞安马鞍山实验小学铜奖王楚淏男五年级温州市上陡门小学铜奖周于越男五年级杭州市桐庐县春江小学铜奖钱奕宁男五年级德清县新市完全小学铜奖张润恒男五年级宁波市镇明中心小学铜奖徐臻诚男五年级宁波市江东中心小学铜奖金文韬男五年级温州市少年艺术学校铜奖傅梓萌男五年级丽水人民路小学铜奖程熙冉男五年级乐清外国语学校铜奖王力男五年级乐清外国语学校铜奖朱锦琛男五年级乐清外国语学校铜奖黄子欣女五年级瑞安马鞍山实验小学铜奖吴涵男五年级瑞安集云实验小学铜奖杨浩泽男五年级乐清白象一小铜奖王浩然男六年级瑞安安阳实验小学铜奖虞普开男六年级丽水缙云县实验小学铜奖余樵男六年级温州市广场路小学铜奖林子睿男六年级丽水云和江滨实验铜奖肖兢克男六年级瑞安莘滕实验小学铜奖赵鹏腾男六年级乐清北白象第一小学铜奖杨颂恩男六年级温州平阳鳌江七小铜奖薛雨馨女六年级苍南龙港湖前小学铜奖夏歆婷女六年级瑞安新纪元实验学校铜奖丁正枫男六年级丽水缙云县实验小学铜奖申屠宇豪男六年级杭州市桐庐县春江小学铜奖孙相杰男六年级杭州市桐庐县窄溪小学铜奖朱名扬男六年级杭州市桐庐县圆通小学铜奖申屠枭邦男六年级杭州市桐庐县圆通小学铜奖沈佳骏男六年级德清县实验学校铜奖胡中正男六年级平阳龙港湖前小学铜奖叶颖颖女六年级德清县实验学校铜奖冯洯女六年级宁波市江东中心小学铜奖陶钧辉男六年级宁波市范桂馥小学铜奖林亮男六年级宁波市镇明中心小学实验校区铜奖许恒远男六年级宁波市镇明中心小学铜奖杜煜泽男六年级宁波市江东第二实验小学铜奖俞嘉民男六年级丹城二小铜奖钱可涵女六年级宁波市镇明中心小学铜奖易小凡男六年级宁波市实验小学铜奖汪赛芸女六年级宁波市国家高新区实验学校铜奖李锦楠男六年级宁波市华泰小学铜奖李家杰男六年级宁波市海曙中心小学铜奖吕瑱琪女六年级宁波孙文英小学铜奖陈明昊男六年级瑞安新纪元实验学校铜奖陈谙羽女六年级温州籀园小学铜奖杨心苹女六年级丽水实验学校铜奖倪瑜阳男六年级乐清虹桥一小铜奖郑尔佳女六年级乐清外国语学校铜奖尹晗女六年级杭州文一街小学铜奖欧洋洲男六年级瑞安蓝翔教育学校铜奖杨子董男六年级旭阳寄宿学校铜奖陈景致男六年级龙湾实验小学铜奖徐子涵男七年级瑞安安阳实验中学铜奖陈柏翔男七年级温州瑞安安阳中学铜奖周凯悦男七年级瑞安鲍田中学铜奖周煜博男七年级永嘉县瓯北第五中学铜奖彭晨旭男七年级瑞安湖岭鹿木中心学校铜奖杨浩然男七年级浙江德清县武康中学铜奖钟耀东男七年级兴宁中学铜奖黄喆男七年级衢州华茂外国语学校铜奖朱紫婷女八年级台州外国语学校铜奖张浩宇男八年级瑞安市安阳实验中学铜奖上官昊男八年级瑞安市安阳实验中学铜奖白搏凯男八年级瑞安市玉海实验中学铜奖郑瑾女八年级瑞安市安阳实验中学铜奖郑舒琪女八年级瑞安市滨江中学铜奖邱崇晟男八年级瑞安市安阳实验中学铜奖蔡雨哲女八年级瑞安市安阳实验中学铜奖周吴杰男八年级浙江德清县武康中学铜奖张思雯女八年级浙江德清县武康中学铜奖韩孟霖男八年级绍兴市第一初级中学铜奖王梓汲男九年级台州外国语学校铜奖蒋俊豪男九年级台州外国语学校铜奖孙嘉颖女九年级浙江德清县武康中学铜奖朱政毅女九年级浙江德清县武康中学铜奖严杰男九年级德清县华盛达外语学校铜奖。

第十五届小学希望杯全国数学邀请赛四年级第2试真题1. 计算：1100÷25×4÷11=_________2. 有15个数,它们的平均数是17,加入1个数后,平均数变成20,则加入的数是_________3. 若abc和def是两个三位数,且a=b+1, b=c+2, abc×3+4=def=,则def=4. 已知a+b=100,若a除以3,余数是2,b除以7,余数是5,则a×b的值最大是_________5. 如图所示,两个完全相同的等腰三角形中各有一个正方形,图乙中的正方形面积为36平方厘米,则图甲中的正方形面积为_________平方厘米6. 边长为20的正方形的面积恰好等于边长为a和边长为b的两个正方形的面积的和,若a和b都是自然数,则a+b=_________7. 今年是2017年,年份的数字和是10,则本世纪内,数字和是10的所有年份的和是_________8. 在纸上画2个圆,最多可以得到2个交点,画3个圆,最多可得到6个交点.那么,如果在纸上画10个圆,最多可得到________个交点9. 小红带了面额50元,20元,10元的人民币各5X,6X,7X,她买了230元的商品,那么有________种付款方式.10. 甲、乙、丙的三个数的和是2017,甲比乙的2倍少3,乙比丙的3倍多20,则甲是________11. 篮球比赛中,三分线外投中1球得3分,三分线内投中1球得2分,罚篮投中1球得1分,某球队在一次比赛中共投进32球,得65分,已知2分球的个数比三分球的个数的4倍多3个,则这个球队在比赛中罚篮共投中________球12. 篮球比赛中,三分线外投中1球得3分,三分线内投中1球得2分,罚篮投中1球得1分,某球队在一次比赛中共投进32球,得65分,已知2分球的个数比三分球的个数的4倍多3个,则这个球队在比赛中罚篮共投中________球二、解答题〔每小题15分,共60分.〕每题都要写出推算过程.1313.甲、乙两人同时从A、B两地出发,相向而行,甲每分钟走70米,乙每分钟走60米,两人在距离中点80米的地方相遇,求A,B两地之间的距离14.老师给学生分水果,准备了两种水果,其中橘子的个数比苹果的个数的3倍多3个,每人分2个苹果,则余下6个苹果,每人分7个橘子,最后一人只能分得1个橘子,求学生的人数15. 两个相同的正方形重合在一起,将上层的正方形向右移动3厘米,再向下移动5厘米,得到图中的图形,已知阴影部分的面积是57平方厘米,求正方形的边长.16.商店推出某款新手机的分期付款活动,有两种方案供选择：方案一：第一个月付款800元,以后每月付款200元方案二：前一半时间每月付款350元,后一半时间每月付款150元两种方案付款总额和时间都相同,求这款手机的价格.第十五届小学希望杯全国数学邀请赛四年级第2试真题答案01.计算：1100÷25×4÷11=_________[答案]16[学习时间点]启智数学B体系三年级秋季第1讲[考点]乘除法凑整[解析]1100÷25×4÷11=1100÷11÷25×4=100÷25×4=1602.有15个数,它们的平均数是17,加入1个数后,平均数变成20,则加入的数是_________[答案]65[学习时间点]启智数学B体系四年级秋季第3讲[考点]平均数,两组平均数间的关系[解析]第一组数的总和是15×17=255,加入一个数之后,第二组数总共有15+1=16个数,其平均数是20,那么第二组数的总和是16×20=320.加入的数是320-255=65.03[答案]964[学习时间点]启智数学B体系三年级暑假第5讲[考点]枚举法[解析]由题目可知,a=b+1=c+2+1=c+3,所以a=c+3,b=c+2,现在从小到大进行枚举：当c=0时,b=2,a=3,第一个三位数是320,所以答案是320×3+4=964,符合题意.当c=1时,b=3,a=4,第二个三位数是431,此时431×3+4=1297,不是三位数,不符合题意,并且之后的答案都不会是三位数.所以答案是964.04已知a+b=100,若a除以3,余数是2,b除以7,余数是5,则a×b的值最大是_________[答案]2491[学习时间点]启智数学B体系四年级春季第4讲[考点]整除,余数,和定积大[解析]a可以表示成3x+2的形式,b可以表示成7y+5的形式,代入a+b=100中去,得到3x+7y=93,因为3x和93都可以被3整除,根据整除的可减性,可知7y也可以被3整除,又因为7不能被3整除,所以得知y可以被3整除,所以b进一步可以表示成21z+5的形式,因为b<100,所以b只可能是5、26、47、68、89这5个数,而此时a分别对应是95、74、53、32、11这5个数.两个数的和确定的时候,这两个数的差越小,积越大,所以a×b的值最大是53×47=2491.05如图所示,两个完全相同的等腰三角形中各有一个正方形,图乙中的正方形面积为36平方厘米,则图甲中的正方形面积为_________平方厘米[答案]32[学习时间点]启智数学B体系四年级暑假第7讲[考点]割补法[解析]根据图形补的方法,可以将图乙补成所示图形,可以发现所补图形〔即大正方形〕面积的正好是图乙面积的2倍,又是图乙中的小正方形面积的4倍,所以图乙、图甲的面积是36×2=72平方厘米.根据图形割的方法,可以将图甲割成所示图形,可以发现图甲被分割成9个小的,面积相等的等腰三角形,所以1个小的等腰三角形面积是72÷9=8平方厘米,图甲的正方形面积则是8×4=32平方厘米.06边长为20的正方形的面积恰好等于边长为a和边长为b的两个正方形的面积的和,若a和b都是自然数,则a+b=_________[答案]28[学习时间点]启智数学B体系四年级秋季第13讲[考点]勾股定理,整除[解析]在勾股定理中学到过最基本的一个算式是,而题目中的算式是,又知道5可以被20整除,20÷5=4,所以,再根据得知：a÷4=3以与b÷4=4；或者是a÷4=4以与b÷4=3.所以a、b的值分别是12、16或者是16、12,而a+b则一定是12+16=28.07今年是2017年,年份的数字和是10,则本世纪内,数字和是10的所有年份的和是_________[答案]18396[学习时间点]启智数学B体系三年级秋季第9讲[考点]等差数列,加减法巧算[解析]本世纪的年份是从20##-2099年,即20ab年,因为年份的数字和是10,所以2+0+a+b=10,得a+b=8,年份最小的是20##,最大的是2080年.且年份从小到大每变化一次,十位加1同时个位减1,所以其年份是一组以9为公差,首项为2008,末项为2080的9项等差数列,其和=2008+2017+……+2072+2080=〔2000+8〕+〔2000+17〕+……+〔2000+72〕+〔2000+80〕=2000×9+〔8+17+……+72+80〕=18000+〔8+80〕×9÷2=18396.08在纸上画2个圆,最多可以得到2个交点,画3个圆,最多可得到6个交点.那么,如果在纸上画10个圆,最多可得到________个交点[答案]90[考点]图形找规律[解析]在稿纸上尝试画4个圆时,发现：最多可得到12个交点.现在开始找规律：,2个圆对应2个交点,3个圆对应6个交点,4个圆对应12个交点.可发现2=1×2；6=2×3；12=3×4,找到规律后应用于题目中去：画10个圆时,最多可以得到〔10-1〕×10=90个交点.09小红带了面额50元,20元,10元的人民币各5X,6X,7X,她买了230元的商品,那么有________种付款方式. [答案]11[学习时间点]启智数学B体系三年级寒假第1讲[考点]分类枚举[解析]1、用了0X50元的情况时：小红最多用了20×6+10×7=190元,不符合题意；2、用了1X50元的情况时,小红需要用20元和10元的人民币买230-50=180元,只有：20×6+10×6=180这1种情况；3、用了2X50元的情况时,小红需要用20元和10元的人民币买230-50×2=130元,有20×6+10×1；20×5+10×3；20×4+10×5；20×3+10×7这4种情况；4、用了3X50元的情况时,小红需要用20元和10元的人民币买230-50×3=80元,有20×4+10×0；20×3+10×2；20×2+10×4；20×1+10×6这4种情况；5、用了4X50元的情况时,小红要需要用20元和10元的人民币买230-50×4=30元,有20×1+10×1；20×0+10×3这2情况；5、用了5X50元的情况时：因为50×5=250>230,不符合题意综合以上情况,总共有1+4+4+2=11种付款方式.10甲、乙、丙的三个数的和是2017,甲比乙的2倍少3,乙比丙的3倍多20,则甲是________[答案]1213[考点]和差倍线段图,设份数[解析]由线段图可知,令丙为1份,乙是3份多20,甲线段到红色端点处,有3份+20+3份+20,总共是6份多40,可实际上甲线段只到右边的黑色端点处,未到红色顶端处,所以甲线段实际长度为6份多37.那现在丙是1份,乙是3份多20,甲是6份多37,三者的和是2017,可知道1+3+6=10份是对应2017-37-20=1960的,所以1份是1960÷10=196,则甲是196×6+37=1213.11篮球比赛中,三分线外投中1球得3分,三分线内投中1球得2分,罚篮投中1球得1分,某球队在一次比赛中共投进32球,得65分,已知2分球的个数比三分球的个数的4倍多3个,则这个球队在比赛中罚篮共投中________球[答案]4[学习时间点]启智数学B体系三年级秋季第11讲[考点]鸡兔同笼,寻找问题中的"头〞和"腿〞[解析]可以让题目中的2分球与三分球之间成整倍关系,即65-2×3=59分,32-3=29球.那题目可转化成：共进29球,得59分,且此时已知2分球的个数是三分球个数的4倍,那根据多元素鸡兔同笼的做法,可将2分球与三分球合体为一个物体,即〔2×4+3×1〕÷〔1+4〕=2.2,即将2分球与三分球合体为"2.2分球〞,那题目可转化为：罚球有1个头,1条腿.5个"2.2分球〞有11条腿.总共有29个头,59条腿.那进一步扩倍,将所有腿分成5条小腿,即题目转变成：罚球有1个头,5条小腿,1个"2.2分球〞有1个头,11条小腿.总共有29个头,59×5=295条小腿.每个"2.2分球〞比罚球多11-5=6条小腿.假设所有的29个头都是"2.2分球〞,那么应该会有29×11=319条小腿,可实际上只有295条小腿,多出了319-295=24条小腿,那罚球的数量应为24÷6=4个,即这个球队在比赛中罚篮共投中4球.12篮球比赛中,三分线外投中1球得3分,三分线内投中1球得2分,罚篮投中1球得1分,某球队在一次比赛中共投进32球,得65分,已知2分球的个数比三分球的个数的4倍多3个,则这个球队在比赛中罚篮共投中________球[答案]4[学习时间点]启智数学B体系三年级秋季第11讲[考点]鸡兔同笼,寻找问题中的"头〞和"腿〞[解析]可以让题目中的2分球与三分球之间成整倍关系,即65-2×3=59分,32-3=29球.那题目可转化成：共进29球,得59分,且此时已知2分球的个数是三分球个数的4倍,那根据多元素二、解答题〔每小题15分,共60分.〕每题都要写出推算过程.13甲、乙两人同时从A、B两地出发,相向而行,甲每分钟走70米,乙每分钟走60米,两人在距离中点80米的地方相遇,求A,B两地之间的距离[答案]2080米[学习时间点]启智数学B体系三年级春季第13讲[考点]行程问题线段图；速度差和路程差的分析；速度和与路程和的分析[解析]由路线图可知,甲走了一半路程多80米,乙走了一半路程少80米,甲乙的路程差为80+80=160米,因为速度差×时间=路程差,速度差为80-70=10米/分,所以时间为160÷10=16分钟,相遇问题中,根据相遇问题的公式：速度和×时间=总路程,得：A、B两地距离为〔70+60〕×16=2080米.14老师给学生分水果,准备了两种水果,其中橘子的个数比苹果的个数的3倍多3个,每人分2个苹果,则余下6个苹果,每人分7个橘子,最后一人只能分得1个橘子,求学生的人数[学习时间点]启智数学B体系四年级暑假第3讲[考点]和差倍综合应用题,画线段图,份数扩倍,盈亏问题思想[解析]题目中出现和差倍关系,那先假设苹果为1份,可是因为每人分2个苹果,所以需要扩倍份数.由线段图可知：苹果有2份,橘子有6份多3个,每个学生分7个橘子,最后一人只有1个,可以假设橘子多出6个〔红色线段部分〕,则橘子给每个学生分7个,正好可以分完.同理,可以让苹果总数少6个,正好每个学生分2个.从线段图可得知：2份学生=2份水果-6个〔苹果与学生的线段图〕→1份学生=1份水果-3个→7份学生=7份水果-21个且7分学生=6份水果+9个〔橘子与学生的线段图〕,所以：7份水果-21个=6份水果+9个.得到1份水果是30个,所以学生是有30-3=27人.15两个相同的正方形重合在一起,将上层的正方形向右移动3厘米,再向下移动5厘米,得到图中的图形,已知阴影部分的面积是57平方厘米,求正方形的边长.[答案]9厘米[学习时间点]启智数学B体系四年级暑假第6讲、第7讲[考点]巧算面积,图形拼接,寻找份数[解析]将原正方形分成4块,先看第①、第④块的面积和与第③、第④块的面积和,因为正方形四条边长相等,其关系只与5厘米、3厘米的两条边长相关.所以设第①、第④块的面积和是5份,则第③、第④块的面积和则是3份,且得知〔①+④〕+〔③+④〕=阴影部分面积+④=57+3×5=72平方厘米,总共是有5+3=8份占72平方厘米,所以一份是72÷8=9平方厘米,①+④=5×9=45平方厘米,所以正方形边长是45÷5=9厘米.16商店推出某款新手机的分期付款活动,有两种方案供选择：方案一：第一个月付款800元,以后每月付款200元方案二：前一半时间每月付款350元,后一半时间每月付款150元两种方案付款总额和时间都相同,求这款手机的价格.[答案]3000元[学习时间点]启智数学B体系三年级暑假第3讲[考点]基本应用题,寻找题目数量关系,寻找题目条件变化下的不变量.[解析]题目中有部分条件发生变化,但是不变化的有两个量：付款总额、时间,根据题目数量关系：平均月付款额=付款总额÷时间,得知两个方案的平均月付款额是相同的.那方案二中,因为前一半每月付款350元,后一半时间每月付款150元,所以方案二的平均月付款额是〔350+150〕÷2=250元,所以第一个方案的平均月付款额也是250元,那方案一中,第一个月超出了平均月付款额800-250=550元,而后的每个月都得多分配250-200=50元,则需要550÷50=11个月来分配这多出来的550元,所以第一个方案用了11+1=12个月,根据方案一算得：这款手机的价格是800+200×11=3000元.。

教育精品资料目录1.第一届小学“希望杯”全国数学邀请赛（第1试） (2)2. 第一届小学“希望杯”全国数学邀请赛（第2试） (5)3. 第二届小学“希望杯”全国数学邀请赛（第1试） (7)4. 第二届小学“希望杯”全国数学邀请赛（第2试） (10)5. 第三届小学“希望杯”全国数学邀请赛（第1试） (13)6. 第三届小学“希望杯”全国数学邀请赛（第2试） (16)7. 第四届小学“希望杯”全国数学邀请赛（第1试） (18)8. 第四届小学“希望杯”全国数学邀请赛（第2试） (21)9. 第五届小学“希望杯”全国数学邀请赛（第1试） (23)10. 第五届小学“希望杯”全国数学邀请赛（第2试） (26)11. 第六届小学“希望杯”全国数学邀请赛（第1试） (28)12. 第六届小学“希望杯”全国数学邀请赛（第2试） (30)13. 第七届小学“希望杯”全国数学邀请赛（第1试） (32)14. 第七届小学“希望杯”全国数学邀请赛（第2试） (36)15. 第八届小学“希望杯”全国数学邀请赛（第1试） (39)16. 第八届小学“希望杯”全国数学邀请赛（第2试） (41)17.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。