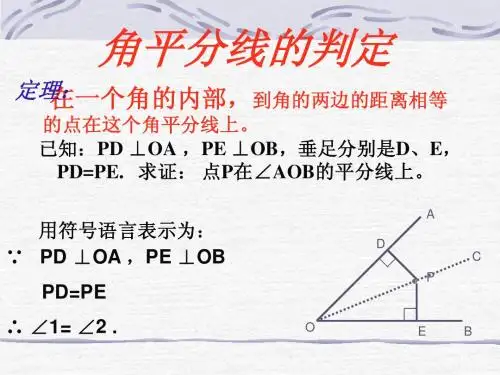
角平分线的判定定理

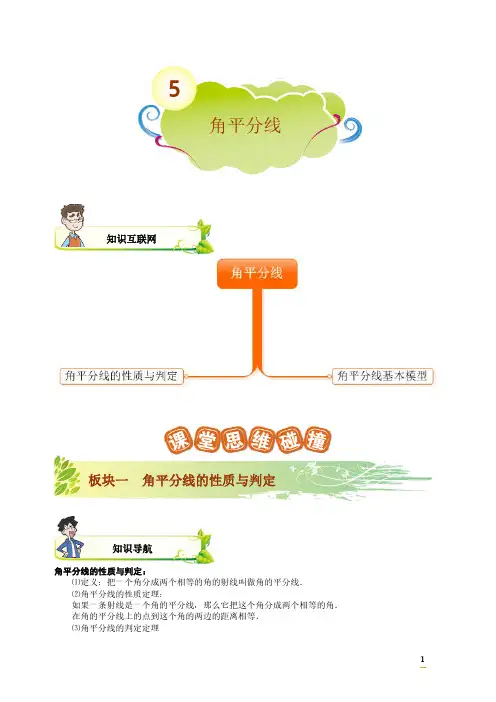
5角平分线知识互联网板块一角平分线的性质与判定知识导航角平分线的性质与判定：⑴定义：把一个角分成两个相等的角的射线叫做角的平分线．⑵角平分线的性质定理：如果一条射线是一个角的平分线，那么它把这个角分成两个相等的角．在角的平分线上的点到这个角的两边的距离相等．⑶角平分线的判定定理12如果一条射线的端点与角的顶点重合，且把一个角分成两个等角，那么这条射线是这个角的平分线；在角的内部，到角两边距离相等的点在这个角的平分线上．夯实基础【例1】⑴证明：三角形三个角的角平分线交于一点．⑵已知：如图，ABC △的两条外角平分线交于点P ．求证：PB 平分ABC ∠．BAP【解析】⑴如图，在ABC △中，设BAC ABC ∠∠、的平分线的交点为I ，过I 点作ID AB ⊥于D ，IE AC ⊥于E ，IF BC ⊥于F ，连接IC ．∵AI BI 、都是角平分线，∴ID IE =，ID IF =，∴IE IF =，∴IC 是ACB ∠的平分线，∴三角形三个角的平分线交于一点．这一点称之为三角形的内心，常用大写字母I 来表示，三角形的内心到三角形三条边的距离相等，它是三角形内切圆的圆心．⑵如图，过P 作PM BA ⊥于M ，PN AC ⊥于N ，PQ BC⊥于Q ．由角平分线的性质定理，易证PM PN =，PN PQ =，故PM PQ =，因此根据角平分线的判定定理，PB 平分ABC ∠，得证．这一点称之为三角形的旁心，三角形的旁心到三角形三条边的距离相等，它是三角形旁切圆的圆心．旁心有3个．【例2】如图，点C 为线段AB 上一点，ACM △、CBN △是等边三角形．请你证明：CF 平分AFB ∠．M D NEC BFAGM H D NEC BF AI FE DCB ANMC B AQ P3【解析】过点C 作CG AN ⊥于G ，CH BM ⊥于H ，由ACN MCB △≌△，利用AAS 进而再证BCH NCG △≌△，可得AFC BFC ∠=∠，故CF 平分AFB ∠．【点评】此图在前面的学习中做过介绍，老师可以先带着学生简单复习一下相关结论。

角平分线的性质定理及其逆定理定理一、角平分线的性质定理及其逆定理1.角平分线的性质定理：角平分线上的点到这个角的两边的距离相等。

2.角平分线的逆定理：在角的内部，且到角的两边距离相等的点，在这个角的平分线上。

不难发现，定理1的条件是定理2的结论，同时它的结论又是定理2的条件，它们互为逆定理。

定理1说明了角平分线上点的纯粹性，即：只要是角平分线上的点，它到此角两边一定等距离，而无一例外；定理2反映了角平分线的完备性，即只要是到角两边距离相等的点，都一定在角平分线上，而绝不会漏掉一个。

在实际应用中，前者用来证明线段相等，后者用来证明角相等或证明点在一个角的平分线上。

用数学语言可表示如下：例题一：（1）∵OC平分∠AOB，点P在射线OC上，PD⊥OA于D，PE⊥OB于E∴PD=PE（定理1）（2）∵PD⊥OA，PE⊥OB，PD=PE∴OC平分∠AOB（定理2）例题二：如图，△ABC的ㄥB平分线BD与ㄥC的外角的平分线CE相较于点P。

求证：点P到三边AB、BC、CA所在直线的距离相等。

从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等这题对吗？。

三角形角平分线定理三角形角平分线定理是指：三角形内一条角的角平分线把这条角分成两个相等角，并且这条角平分线所在的边与三角形外一边的两个对边的比等于被分角的两边的比。

三角形角平分线定理是一个重要且有用的几何定理，它可以帮助我们推导解决许多与三角形相关的问题。

本文将详细介绍三角形角平分线定理以及其应用。

一、三角形角平分线定理的定义与性质三角形角平分线定理可以描述为：设三角形ABC中，AD是角BAC的角平分线，则有以下两个性质成立：1. 角BAD与角DAC的度数相等，即∠BAD = ∠DAC。

2. AB/BC = BD/DC。

角平分线的定义是指一条线段或射线从一个角的顶点出发，将该角分成两个相等的角。

根据角平分线的定义，我们可以得出性质1。

性质2则是说明了角平分线所在边与三角形外一边的两个对边的比例关系。

这个比例关系在解决一些三角形相关问题时非常有用，比如计算未知边长或角度大小等。

二、三角形角平分线定理的证明现在我们来证明三角形角平分线定理中的性质2。

首先，我们假设角BAD = α，角CAD = β，角DAC = α，角BDA = β。

根据正弦定理，我们可以得到以下两个等式：sinα/BD = sinβ/AB (1)sinα/DC = sinβ/AC (2)将(1)除以(2)，可以得到：(AB/BD)/(AC/DC) = sinα/sinα = 1由于左边等式的分数形式是BD/DC的比，因此我们可以得出：AB/BC = BD/DC这就证明了三角形角平分线定理中的性质2。

三、三角形角平分线定理的应用三角形角平分线定理有着广泛的应用，特别是在解决与三角形相关的题目时，可以通过应用该定理得到简洁而准确的答案。

以下是三个典型的应用案例：1. 求角平分线所分角的大小已知三角形ABC中，BD为角BAC的角平分线，要求角BAD的大小。

根据三角形角平分线定理的性质1，我们知道角BAD与角DAC的大小相等，即∠BAD = ∠DAC。

八年级角平分线知识点总结角平分线是几何知识中的一个重要概念，也是初中数学中常见的考点之一。

在八年级中学习了角平分线的相关知识后，许多同学还存在一定的困惑。

因此，本文将对八年级角平分线的知识点做一个总结，以帮助大家更好地掌握该知识。

一、角平分线的定义和性质1. 定义所谓“角平分线”，是指将一个角平分为两个角的线段。

在角上下方形成两个新的角，它们的大小相等。

2. 性质(1) 角平分线把原来的角分成两个大小相等的角。

(2) 角平分线的两侧所对的两个角相等。

(3) 在三角形中，若一条线段是一个角的平分线，则它所在的线段所对的两侧角的大小之比等于它所在的线段所对的两侧边的长度之比。

二、与角平分线有关的定理1. 外角定理所谓“外角”，是指一个三角形的一个内角所对的另一个角。

外角定理是指一个三角形的一个外角等于它的不相邻两个内角之和。

2. 内角定理一个多边形的内角和等于这个多边形的狄利克雷函数乘以180°。

三、角平分线的应用了解了角平分线的定义和性质以及与角平分线有关的定理，我们就可以在解题过程中灵活应用，其中最常见的就是角平分线定理的应用。

在三角形中，若已知一条角平分线及其所分割的两边长度，则可以利用角平分线定理求解三角形中其它角的大小。

例如，已知在三角形ABC中，角BAD的平分线交BC边于点E，且BE=7，EC=5，则可以利用角平分线定理求解角DAB和角DAC的大小。

根据角平分线定理，有：$\dfrac{BD}{DC}=\dfrac{AB}{AC}$因此，$\dfrac{BD}{DC}=\dfrac{BE}{EC}=\dfrac{7}{5}$又有：$\dfrac{BD}{DC}=\dfrac{\sin \angle BAD}{\sin \angle DAC}$因此，$\dfrac{\sin \angle DAB}{\sin \angle DAC}=\dfrac{7}{5}$由于$\angle DAB+\angle DAC=180^\circ$，因此可以列出以下方程组：$\begin{cases} \dfrac{\sin \angle DAB}{\sin \angleDAC}=\dfrac{7}{5} \\ \sin \angle DAB+\sin \angle DAC=1\end{cases}$解得$\sin \angle DAB=\dfrac{7}{12}$，$\sin \angleDAC=\dfrac{5}{12}$，$\angle DAB=\sin^{-1} \dfrac{7}{12}$，$\angle DAC=\sin^{-1} \dfrac{5}{12}$，即$\angle DAB \approx 36.87^\circ$，$\angle DAC \approx 26.57^\circ$。

高中数学角平分线定理角平分线定理是高中数学中一个重要的几何定理，它是在三角形中研究角平分线性质时的一个基本定理。

角平分线定理是指：若一条线段从一个角的顶点出发，平分这个角，并且与这个角的两边相交于两点，那么这条线段就称为这个角的角平分线，并且它将这个角分成两个相等的部分。

角平分线定理在解决三角形问题时具有重要的作用。

我们可以通过角平分线定理来证明一些性质或者解决一些问题。

下面我们将介绍角平分线定理的一些应用。

角平分线定理可以帮助我们证明两条角平分线互相垂直的性质。

假设在三角形ABC中，角BAD和角CAD的角平分线相交于点D，我们想要证明BD和CD相互垂直。

根据角平分线定理，我们知道角BAD和角CAD被角平分线BD所平分，所以角BAD和角CAD 的度数相等。

同样地，角BAD和角CAD被角平分线CD所平分，所以角BAD和角CAD的度数也相等。

因此，角BAD和角CAD的度数相等，从而BD和CD相互垂直。

角平分线定理还可以帮助我们解决一些关于角度比例的问题。

假设在三角形ABC中，角BAD和角CAD的角平分线相交于点D，我们想要求证BD和CD的长度比。

根据角平分线定理，我们知道角BAD和角CAD被角平分线BD所平分，所以角BAD和角CAD的度数相等。

根据三角形内角和定理，我们知道角BAD和角CAD的度数之和等于180度。

因此，角BAD和角CAD的度数都是90度。

根据三角形中角的度数之和等于180度，我们可以得知角ABC的度数为180度- 90度- 90度= 0度。

这意味着角ABC是一个平角，也就是说，角ABC是一条直线。

根据三角形内角和定理，我们知道角BAD和角CAD的度数之和等于180度，所以它们的度数都是90度。

因此，根据角平分线定理，BD和CD的长度比为1:1。

除了上述应用，角平分线定理还可以帮助我们证明一些关于相似三角形的性质。

假设在三角形ABC和三角形DEF中，角BAD和角CAD的角平分线分别与角EDF和角FDF的角平分线相交于点D和点E，我们想要证明三角形ABC和三角形DEF相似。

角平分线定理角平分线定理是高中数学中的重要定理之一。

它描述了角平分线与三角形内部的关系。

在本文中，我们将简要介绍角平分线定理的定义、证明和应用。

角平分线定理是指：在一个三角形中，如果一条线段从一个顶点出发，将对角线平分成两条相等的线段，那么这条线段就是该角的平分线。

证明角平分线定理的一个常用方法是通过角的对等性。

我们可以假设在三角形ABC中，角BAD的平分线CE将角BAD平分成两个相等的角，即∠CAE≅∠EAD。

我们需要证明线段CE平分了角BAC。

首先，我们延长线段CE，使其与边BC相交于点F。

根据三角形内角和定理，可知∠CAF+∠BAC+∠BFA=180°。

由于∠CAE≅∠EAD，所以∠CAF≅∠EAF。

将这个结论代入上述等式中得到∠CAF+∠BAC+∠BFA=180°变为∠EAF+∠BAC+∠BFA=180°。

通过对等性，我们还可以得出∠EAD≅∠EAF。

将这一事实代入上述等式得到∠EAD+∠BAC+∠BFA=180°变为∠EAD+∠BAC+∠BAD=180°。

由于∠BAC+∠BAD=180°（三角形内角和定理），可得∠EAD+∠BAD=∠EAD+∠BAC+∠BAD。

根据等式两边的角相等性，我们可以得出∠EAD=∠EAD+∠BAC，进一步得出∠BAC=0°。

这说明线段CE平分了角BAC，从而证明了角平分线定理。

角平分线定理的应用非常广泛。

在几何证明中，我们常常可以利用角平分线定理来证明一些关于三角形的性质。

例如，利用角平分线定理可以证明等腰三角形的底角相等，证明三角形内角平分线交于一点等。

此外，在解题中角平分线定理也经常被使用。

根据角平分线定理，我们可以推导出一些重要的性质，如外接角平分线定理和内接角平分线定理。

这些性质可以帮助我们解决各种与角平分线有关的问题，例如求证两条角平分线垂直相交、求证两条角平分线平行等。

总结一下，角平分线定理是一条非常重要的几何定理，它描述了角平分线与三角形内部的关系。

直角三角形角平分线定理
直角三角形的角平分线定理是指：在一个直角三角形中，如果从直角顶点引一条线段，将对角线分成两段，那么这条线段所在的直线就是这个直角顶点的两个相邻角的平分线。

具体来说，设一个直角三角形ABC，其中∠C=90度，AD为BC的中线，DE是AC的垂线，则AD是∠A和∠B的平分线，即∠CAD=∠BAD=∠A/2，∠CBD=∠ABD=∠B/2。

这个定理的证明可以利用几何知识进行证明，例如相似三角形、角度和定理等。

但简单来说，我们可以利用三角函数的定义，根据正弦、余弦、正切等函数来计算证明。

总之，直角三角形的角平分线定理在几何学中有着重要的应用价值，可以帮助我们更好地理解和应用三角形的相关知识。

三角形角平分线的定理三角形角平分线的定理是初中数学中的一个重要定理，它是指在一个三角形中，如果一条直线从一个角平分另一个角，那么这条直线所在的线段将把对边分成两个相等的线段。

这个定理的主要内容包括以下几个方面：一、定理的表述三角形角平分线的定理可以用以下的方式表述：在三角形ABC中，如果BD是角B的平分线，那么AB/AC=BD/CD。

其中，AB、AC、BD、CD分别表示三角形ABC中的边和角平分线。

二、定理的证明三角形角平分线的定理的证明可以通过以下的方式进行：1. 假设BD是角B的平分线，那么∠ABD=∠CBD。

2. 由于∠ABD=∠CBD，所以三角形ABD与三角形CBD是全等的。

3. 因此，AB/BD=CB/BD，即AB/CB=BD/CD。

4. 所以，AB/AC=AB/(AB+CB)=BD/(BD+CD)=BD/CD。

5. 因此，BD是角B的平分线，那么AB/AC=BD/CD。

三、定理的应用三角形角平分线的定理在初中数学中有很多应用，其中最常见的应用包括以下几个方面：1. 求角平分线所在的线段长度如果已知一个三角形中的两个边和一个角的大小，可以通过三角函数求出第三条边的长度，然后再利用角平分线的定理求出角平分线所在的线段长度。

2. 求角平分线所在的点的坐标如果已知一个三角形中的三个顶点的坐标，可以通过向量的方法求出角平分线所在的点的坐标。

3. 判断角平分线是否在三角形内部如果一个三角形中的一个角的平分线不在三角形内部，那么这个三角形就不是一个普通的三角形，而是一个退化的三角形。

四、总结三角形角平分线的定理是初中数学中的一个重要定理，它可以帮助我们求解三角形中的各种问题。

在学习这个定理的过程中，我们需要掌握定理的表述、证明和应用，以便在实际问题中灵活运用。

等边三角形角平分线定理定理：等边三角形中, 三条角平分线交于一个点，并且这个点是重心、垂心、外心、内心的交点。

证明：1. 假设三角形ABC是一个等边三角形，三个角的测量都是60度。

2. 连接三角形的顶点A与底边BC的中点D，同时也连接角A的平分线AE。

同样，连接B与平分线CF, C与平分线BG.3. 由于等边三角形中，三个角的测量都是60度，所以可以得到角DAB=30度，角FAE=30度，角GBC=30度。

4. 同样由于等边三角形中，AB=BC=AC，可以得到三角形ABD与三角形ACD 是相等的，即AB=AC，角DAB=角DAC=30度。

5. 这意味着线段AD是三角形ABC的一个角平分线。

同样由于线段BE和CF 也分别是角B和角C的平分线，我们可以得到三角形ABC中的三条角平分线。

6. 接下来，我们要证明这三条角平分线会交于同一个点。

假设它们交于点O。

7. 由于角DAB=30度，角FAE=30度，角GBC=30度，所以可以得到角BOC=120度。

8. 同时，由于线段AD是角A的平分线，所以可以得到角BAD=angleCAD=30度。

9. 又因为AB=AC，所以可以得到三角形ABO与三角形ACO是相等的，即AB=AC, AO=AO, 和角BAO=角CAO=30度。

10. 因此，三角形ABO与ACO是相等且全等的，从而可以得到BO=CO，即点O位于线段BC的中垂线上。

11. 可以类似地证明点O也位于线段AB和线段AC的中垂线上，所以它是三角形ABC的重心。

12. 另一方面，由于三角形ABC是等边三角形，所以利用此前已经证明过的结论，点O也是三角形ABC的垂心、外心和内心的交点。

综上所述，等边三角形中，三条角平分线交于一个点，并且这个点是重心、垂心、外心、内心的交点。

三角形中的角平分线定理三角形中的角平分线定理是基本的几何定理之一，它给出了关于三角形内部角平分线的性质和特点。

在本文中，我们将深入探讨角平分线定理的定义、证明以及相关应用。

定义：在一个三角形中，如果一条线段从一个角的顶点出发，且将该角划分为两个相等的角，那么这条线段就是该角的角平分线。

证明：为了证明角平分线定理，我们假设在三角形ABC中，角A的角平分线AD将角A划分为两个相等的角。

我们需要证明AD是BC边上角BAC的角平分线。

首先，由三角形内角和定理可知，角A + 角B + 角C = 180°。

因为AD是角A的角平分线，所以角BAD和角DAC相等，即角BAD = 角DAC。

根据三角形内角和定理，角BAD + 角DAC + 角B = 180°。

由于角BAD = 角DAC，我们可以将该等式改写为2 ×角BAD + 角B = 180°。

进一步整理可得2 ×角BAD = 180° - 角B，即角BAD = (180° - 角B)/2。

又因为角A + 角BAD = (180° - 角B)/2 + 角B = 180°/2 = 90°，可以得出角BAD = 90° - 角B/2。

同样地，我们可以利用类似的步骤证明角CAD = 90° - 角C/2。

由于角BAD = 90° - 角B/2，角CAD = 90° - 角C/2，我们可以得出结论：角BAC的角平分线AD将角BAC划分成两个相等的角BAD和角CAD。

应用：三角形中的角平分线定理不仅仅局限于理论证明，它在解决实际问题时也有着广泛的应用。

首先，角平分线定理可以用于求解三角形内部角的大小。

当我们知道了角平分线的长度和其他两个角的大小时，可以通过角平分线定理计算出未知角的大小。

其次，角平分线定理还可以用于证明两条线段相互平分对方所在的角。

角平分线定理角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。

■ 三角形的角平分线定义：三角形顶点到其内角的角平分线交对边的点连的一条线段，叫三角形的角平分线。

【注】三角形的角平分线不是角的平分线，是线段。

角的平分线是射线。

■拓展：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。

■定理1：在角平分线上的任意一点到这个角的两边距离相等。

■逆定理：在一个角的内部（包括顶点），且到这个角的两边距离相等的点在这个角的角平分线上。

■定理2：三角形一个角的平分线分对边所成的两条线段和这个角的两邻边对应成比例，如：在△ABC中，BD平分∠ABC，则AD：DC=AB：BC提供四种证明方法：已知，如图，AM为△ABC的角平分线，求证AB／AC=MB／MC已知和证明1图证明：方法1：（面积法）S△ABM=(1/2)·AB·AM·sin∠BAM,S△ACM=(1/2)·AC·AM·sin∠CAM,∴S△ABM：S△ACM=AB:AC又△ABM和△ACM是等高三角形，面积的比等于底的比，证明2图即三角形ABM面积S：三角形ACM面积S=BM:CM ∴AB／AC=MB／MC方法2（相似形）过C作CN‖AB交AM的延长线于N则△ABM∽△NCM∴AB/NC=BM/CM又可证明∠CAN=∠ANC∴AC=CN∴AB／AC=MB／MC证明3图方法3（相似形）过M作MN‖AB交AC于N则△ABC∽△NMC,∴AB/AC=MN/NC,AN/NC=BM/MC又可证明∠CAM=∠AMN∴AN=MN∴AB/AC=AN/NC∴AB／AC=MB／MC方法4（正弦定理）作三角形的外接圆，AM交圆于D，由正弦定理，得，证明4图AB/sin∠BMA=BM/sin∠BAM,∴AC/sin∠CMA=CM/sin∠CAM又∠BAM=∠CAM，∠BMA+∠AMC=180°sin∠BAM=sin∠CAM,sin∠BMA=sin∠AMC, ∴AB／AC=MB／MC。

角平分线的三个定理公式证明说到角平分线的定理，真是让人有点头疼的一个话题，不过别担心，我们慢慢聊，一起来把这个“难题”变得简单有趣。

先来个热身，想象一下，一个三角形就像一块美味的蛋糕，三个角就像三种不同的口味，而角平分线就是把这个蛋糕切得又好看又好吃的神奇刀具。

你看，一条线从角的顶点伸出，把这个角一分为二，就像把巧克力口味和香草口味分得清清楚楚，太棒了吧？咱们得说说第一个定理。

它告诉我们，如果你有一个三角形，角平分线所对的边上，两个小线段的比例正好和相邻两边的比例一样。

听起来有点复杂，其实就像是在说，如果你把这个三角形的某个角切开了，那么对面的那条边就像是个神奇的秤，称出了两边的比例。

想象一下你和朋友一起去买饮料，你买了可乐，他买了果汁，你们两个的饮料总量和价格都得成正比，不然怎么公平呢？这个定理就像在给你们打下了一个公平的基础，让你们都能喝到满意的饮料。

接着再说说第二个定理。

这一条有点意思，简单来说，就是如果你知道了三角形的两边和夹角，你就能利用角平分线来找到一个点，让这个点和三角形的两个顶点连成的线段和角平分线相等。

就像你在公园里散步，突然发现有一条小路把你和朋友们的聚集地分开，你想到了用一条线把它切成两个相等的区域。

这个时候，角平分线就是你的好帮手，它能让你不费吹灰之力找到完美的聚会地点。

再说到第三个定理，这个可真是个宝藏定理！它告诉我们，如果一个角平分线和三角形的另一条边相交，那交点到这条边的距离和两个角的比值也有关系。

简单地说，就是你在一场比赛中，不同的队伍在场上的表现得到了平衡。

如果有一方表现特别优秀，角平分线就像个公正的裁判，确保比赛不会太失衡。

想象一下，如果没有这个裁判，比赛一定会变成一场混乱的“打斗”，没有人知道胜负了，真是让人心烦。

说了这么多，其实这三个定理都有个共同点，就是它们都在强调一个“公正”二字。

就像生活中，我们每个人都希望能得到公平的对待，不管是在工作、学习还是在朋友间的交往。

角平分线定理
角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.
三角形的角平分线定义：三角形顶点到其内角的角平分线交对边的点连的一条线段，叫三角形的角平分线.
注：三角形的角平分线不是角的平分线，是线段.角的平分线是射线.
拓展：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心).
定理1：角平分线上的任意一点到这个角的两边距离相等.
逆定理：在一个角的内部（包括顶角），且到这个角的两边距离相等的点在这个角的角平分线上.
定理2：三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例，。