线段的垂直平分线的性质和判定定理

线段的垂直平分线知识要点分析1. 线段垂直平分线性质定理及判定定理线段垂直平分线上的点到这条线段两个端点的距离相等。

(这个结论是经常用来证明两条线段相等的根据之一.)到一条线段两个端点距离相等的点在这条线段的垂直平分线上。

2. 三角形三条边的垂直平分线定理三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

(这是一个证明三条直线交于一点的证明根据.)3. 尺规作图尺规作图的概念：只用没有刻度的直尺和圆规进行作图，称尺规作图。

能写出尺规作图的步骤作已知线段的垂直平分线已知底边及底边上的高，求作一个等腰三角形。

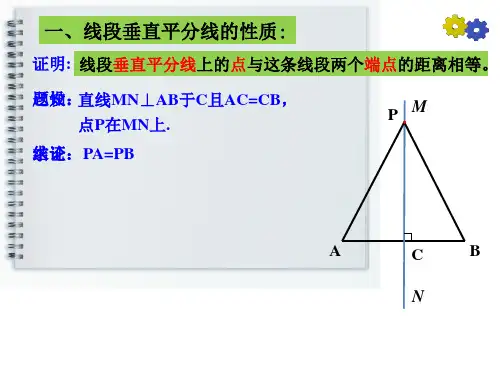
【典型例题】考点一：线段垂直平分线性质定理和判定定理例1. 如图，A、B表示两个仓库，要在A、B一侧的河岸边建造一个码头，使它到两个仓库的距离相等，码头应建在什么位置？例2、已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的点. 求证：PA=PB.想一想：你能写出这个定理的逆命题吗？它是真命题吗？如果是，请你证明它。

这个定理的逆命题：到一条线段两个端点距离相等的点在这条线段的垂直平分线上证明：取AB的中点C，过PC作直线.APBC21这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.考点二：尺规作图例3、用尺规作线段的垂直平分线已知：线段AB（如图）. A B求作：线段AB的垂直平分线.现在同学们会作一条已知线段的垂直平分线了，那么你能作出一个三角形的三边的垂直平分线吗？如果能，请试一试观察一下三角形三条边的垂直平分线交于一点吗？如果交于一点，你能证明出来吗？例4、已知：在△ABC中，设AB、BC的垂直平分线交于点P，连接AP，BP，CP.求证：P点在AC的垂直平分线上.这就是我们今天学习的又一个定理三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

例5、边及底边上的高，求作等腰三角形.已知：线段a、h求作：△ABC，使AB=AC，BC=a，高AD=h(先分析,作出示意图形,再按要求去作图.)考点三：三角形三条边的垂直平分线的性质例6. 已知：△ABC中，AB=AC，AD是BC边上的一条中线，AB的垂直平分线交AD于O求证：OA=OB=OC.严格性之于数学家,犹如道德之于人.证明的规范性在于：条理清晰，因果相应,言必有据.这是证明者谨记和遵循的原则 一、选择题1、如果一个三角形两边的垂直平分线的交点在第三边上，那么这个三角形是（ ）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不能确定*2、已知，如图，在△ABC 中，OB 和OC 分别平分∠ABC 和∠ACB ，过O 作DE ∥BC ，分别交AB 、AC于点D 、E ，若BD+CE ＝5，则线段DE 的长为 （ ）A. 5 B. 6 C. 7D. 82题图 3题图3、如图所示，有A 、B 、C 三个居民小区的位置成三角形，现决定在三个小区之间建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）A 、AB 、BC 两边高线的交点处B 、AC 、BC 两边中线的交点处C 、AC 、BC 两边垂直平分线的交点处D 、∠A 、∠B 的平分线交点处 二、填空题4、如图所示，△ABC 中，∠C=90°，DE 是AB的中垂线，AB=2AC ，BC=18cm ，则BE 的长度为4题图 7题图*5、锐角△ABC 中，∠A=60°，AB ，AC 两边的垂直平分线交于点O ，则∠BOC 的度数是 __________。

线段的垂直平分线的性质
性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的
距离相等；三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点
的距离相等等。

1、垂直平分线垂直且平分其所在线段。

2、垂直平分线上任意一点，到线段两端点的距离相等。

3、三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的
距离相等。

4、垂直平分线的判定：必须同时满足（1）直线过线段中点；（2）直线⊥线段。

若图形（这个图形可以是直线的、折线的、曲线的）关于某条直线对称，这条轴就称
为对称轴。

以五角星为例，它有五条对称轴。

垂直平分线是存在某条线段时才会有这个概念。

它的定义是经过某一条线段的中点，
并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）。

它有一定的局限性。

轴对称图形的对称轴是对称图形中任意两个对应点连线段的垂直平分线。

感谢您的阅读，祝您生活愉快。

线段垂直平分线定理知识总结一、线段垂直平分线的性质定理说明：1、这里的距离指的是点与点之间的距离，也就是两点之间线段的长度。

2、在使用该定理时必须保证两个前提条件：一是垂直于线段，二是平分这条线段。

例题、如图所示，在△ABC 中，已知AC=27，AB 的垂直平分线交AB 于点D ，交AC 于点E ，△BCE 的周长等于50，求BC 的长。

分析：题中给出了线段垂直平分线这个条件，所以可以考虑运用其性质定理，从而得出AE=BE ，把BE 与AE 进行等量代换，再根据△BCE 的周长及AC 的长，可求出BC 的长。

解：因为ED 是线段AB 的垂直平分线， 所以BE=AE 。

因为△BCE 的周长等于50， 即BE ＋EC ＋BC=50， 所以AE ＋EC ＋BC=50。

又因为AE ＋EC=AC=27， 所以BC=50－27=23。

二、线段垂直平分线定理的逆定理证明某一条直线是另一条线段的垂直平分线有两种方法：第一种：根据线段垂直平分线的定义，也就是经过线段的中点，并且垂直于这条EDCBA线段的直线，叫做这条线段的垂直平分线。

使用这种方法必须满足两个条件：一是垂直二是平分；第二种：可以证明有两个点都在线段的垂直平分线上，根据两点确定一条直线，就可以判断这两点所在的直线就是这条线段的垂直平分线。

例题1、如图所示，P 为线段AB 外的一点，并且PA=PB 。

求证：点P 在线段AB 的垂直平分线上。

分析：要想说明某一点在线段的垂直平分线上，可以根据线段的垂直平分线的定义来进行判断。

证明：过点P 作PC ⊥AB ，垂足为点C 。

因为PA=PB ， 所以∠A=∠B 。

又因为PC ⊥AB ， 所以∠PAB=∠PBA=90°. 在△PAC 和△PBC 中A B PAC PBC PC PC ∠=∠⎧⎪∠=∠⎨⎪=⎩所以△PAC ≌△PBC ， 所以AC=BC 。

又因为PC ⊥AB ，所以PC 垂直平分线段AB ，所以点P 在线段AB 的垂直平分线上。

垂直平分线知识点
垂直平分线是经过某一条线段的中点，并且垂直于这条线段的直线。

以下是垂直平分线的一些知识点：
1.性质：垂直平分线上的任意一点到这条线段两个端点的距离相等，即线段垂直平分线上的点到线段两个端点的距离相等。

2.判定：如果直线过线段中点，并且垂直于这条线段，那么这条直线就是这条线段的垂直平分线。

3.三角形中的垂直平分线：三角形三条边的垂直平分线相交于一点，这一点叫做三角形的外心，并且这一点到三角形三个顶点的距离相等。

4.与对称轴的关系：如果一个图形关于某一直线对称，那么这个直线就是对应点连线的垂直平分线。

总之，垂直平分线是数学中的一个重要概念，它具有一些独特的性质和判定方法，并且在三角形等图形问题中有着广泛的应用。

线段的垂直平分线知识总结一、线段垂直平分线的性质定理说明：1、这里的距离指的是点与点之间的距离，也就是两点之间线段的长度。

2、在使用该定理时必须保证两个前提条件：一是垂直于线段，二是平分这条线段。

例题、如图所示，在△ABC 中，已知AC=27，AB 的垂直平分线交AB 于点D ，交AC 于点E ，△BCE 的周长等于50，求BC 的长。

分析：题中给出了线段垂直平分线这个条件，所以可以考虑运用其性质定理，从而得出AE=BE ，把BE 与AE 进行等量代换，再根据△BCE 的周长及AC 的长，可求出BC 的长。

解：因为ED 是线段AB 的垂直平分线， 所以BE=AE 。

因为△BCE 的周长等于50， 即BE ＋EC ＋BC=50， 所以AE ＋EC ＋BC=50。

又因为AE ＋EC=AC=27， 所以BC=50－27=23。

二、线段垂直平分线定理的逆定理EDCBA证明某一条直线是另一条线段的垂直平分线有两种方法：第一种：根据线段垂直平分线的定义，也就是经过线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

使用这种方法必须满足两个条件：一是垂直二是平分；第二种：可以证明有两个点都在线段的垂直平分线上，根据两点确定一条直线，就可以判断这两点所在的直线就是这条线段的垂直平分线。

例题1、如图所示，P 为线段AB 外的一点，并且PA=PB 。

求证：点P 在线段AB 的垂直平分线上。

分析：要想说明某一点在线段的垂直平分线上，可以根据线段的垂直平分线的定义来进行判断。

证明：过点P 作PC ⊥AB ，垂足为点C 。

因为PA=PB ， 所以∠A=∠B 。

又因为PC ⊥AB ， 所以∠PAB=∠PBA=90°. 在△PAC 和△PBC 中A BPAC PBC PC PC ∠=∠⎧⎪∠=∠⎨⎪=⎩所以△PAC ≌△PBC ， 所以AC=BC 。

又因为PC ⊥AB ，所以PC 垂直平分线段AB ，所以点P 在线段AB 的垂直平分线上。

线段垂直平分线和角平分线的性质
和判定
线段垂直平分线：
它是在一条线段上的两个端点之间画出的一条垂直于该线段的线段，其中两段等长。

性质：
1.线段垂直平分线是一条垂直于给定线段的线段；
2.它将给定线段分成两段等长的线段；
3.它的端点位于给定线段的端点。

判定：
可以使用叉乘或者勾股定理来判断线段垂直平分线，如果a×b=0，则a线段垂直于b线段；如果|a–
b|=|a+b|，则a线段和b线段等长；如果a和b都满足上述条件，则a线段就是给定线段的垂直平分线。

角平分线：
它是在一个角的两边画出的一条线段，其中两段之间的夹角是该角的一半。

性质：
1.角平分线是一条穿过角的线段；
2.它将角分割成两个等分的角；
3.它的端点位于角的两条边上。

判定：
可以使用叉乘法判断角平分线，如果a×b=0，则a线段和b线段垂直；如果|a+b|= 2*|a|，则a和b之间的夹角是180°的一半；如果a和b都满足上述条件，则a线段就是角的平分线。

《线段的垂直平分线》观评课记录
课题：线段的垂直平分线
一、自评
本节课，我通过生活中的实例引入，激发学生的好奇心和求知欲，然后利用动手操作引出线段的垂直平分线的定义，为他们独立思考、相互交流和亲自发现提供了广阔的空间。

但整节课互动环节还是不够，在以后的教学设计中会注意这一点。

总之，对课堂的设计，我始终在努力贯彻以教师为主导，以学生为主体，以问题为基础，以能力、方法为主线，有计划培养学生的自学能力、观察和实践能力、思维能力、应用知识解决问题的能力和创造能力为指导思想。

并且能从各种实际出发，充分利用各种教学手段来激发学生的学习兴趣，培养学生的创新意识。

二、评课
观察总结：
1、首先利用情景引入，比较贴近学生实际生活，让学生明白数学是与生活相关的，引起学生的学习兴趣。

2、在学生证明线段垂直平分线的性质时，注意辅助线的做法一定要强调好，而且注意这里用多种方法证明（全等、三线合一），而且用“三线合一”来证明此性质是最简单、明了的。

3、教态自然，语言流畅，师生配合默契，课堂气氛融洽。

线段的垂直平分线与角平分线【知识框架】1、线段垂直平分线的性质（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示：如图1.∵ CD ⊥AB.且AD ＝BD∴ AC ＝BC.定理的作用：证明两条线段相等 （2）线段关于它的垂直平分线对称. 2、线段垂直平分线的判定定理：到一条线段两个端点距离相等的点在这条线段的垂直平分线上. 定理的数学表示：如图2.∵ AC ＝BC∴ 点C 在线段AB 的垂直平分线m 上.定理的作用：证明一个点在某线段的垂直平分线上. 3、关于线段垂直平分线性质定理的推论（1）关于三角形三边垂直平分线的性质：三角形三边的垂直平分线相交于一点.并且这一点到三个顶点．．．．．的距离相等.性质的作用：证明三角形内的线段相等.（2）三角形三边垂直平分线的交点位置与三角形形状的关系：若三角形是锐角三角形.则它三边垂直平分线的交点在三角形内部； 若三角形是直角三角形.则它三边垂直平分线的交点是其斜边的中点；若三角形是钝角三角形.则它三边垂直平分线的交点在三角形外部. 反之.也成立。

4、角平分线的性质定理：角平分线的性质定理：角平分线上的点到这个角的两边的距离相等.定理的数学表示：如图4.∵ OE 是∠AOB 的平分线.F 是OE 上一点.且CF ⊥OA 于点C.DF ⊥OB 于点D. ∴ CF ＝DF.定理的作用：①证明两条线段相等；②用于几何作图问题； 角是一个轴对称图形.它的对称轴是角平分线所在的直线. 5、角平分线性质定理的逆定理：角平分线的判定定理：在角的内部到角的两边距离相等的点在这个角的角平分线上. 定理的数学表示：如图5.∵点P 在∠AOB 的内部.且PC ⊥OA 于C.PD ⊥OB 于D.且PC ＝PD.图1图2图4∴点P在∠AOB的平分线上.定理的作用：用于证明两个角相等或证明一条射线是一个角的角平分线注意角平分线的性质定理与判定定理的区别和联系.（1）关于三角形三条角平分线交点的定理：三角形三条角平分线相交于一点.并且这一点到三边的距离相等.定理的数学表示：如图6.如果AP、BQ、CR分别是△ABC的内角∠BAC、∠ABC、∠ACB的平分线.那么：① AP、BQ、CR相交于一点I；②若ID、IE、IF分别垂直于BC、CA、AB于点D、E、F.则DI＝EI＝FI.定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题.（2）三角形三条角平分线的交点位置与三角形形状的关系：三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.7、关于线段的垂直平分线和角平分线的作图：（1）会作已知线段的垂直平分线；（2）会作已知角的角平分线；（3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.【典型例题】例1、如图1.在△ABC 中.BC ＝8cm.AB 的垂直平分线交AB 于点D.交边AC 于点E.△BCE 的周长等于18cm.则AC 的长等于（ ） A ．6cm B ．8cm C ．10cm D ．12cm【跟踪练习】（1）如图.AB=AC=14cm,AB 的垂直平分线交AB 于点D.交AC 于点E. 如果△EBC 的周长是24cm.那么BC=_________;（2）如图.AB=AC=14cm,AB 的垂直平分线交AB 于点D.交AC 于点E. 如果BC=8cm.那么△EBC 的周长是______;（3）如图.AB=AC,AB 的垂直平分线交AB 于点D.交AC 于点E. 如果∠A=28度.那么∠EBC=___.例2、已知： AB=AC.DB=DC.E 是AD 上一点.求证：BE=CE.【跟踪练习】已知：在△ABC 中.ON 是AB 的垂直平分线,OA=OC.求证：点O 在BC 的垂直平分线.例3、在△ABC 中.AB=AC.AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°.△ABC 的底角∠B的大小为_______________。