6、已知圆的周长求直径或半径

圆的周长计算公式例题
例题1：求圆的周长，已知半径是5cm。

解：根据公式2πr，将半径r替换成5cm，得到周长
=2π×5cm≈31.42cm。

所以圆的周长是31.42cm。

例题2：已知圆的周长是18cm，求圆的半径。

例题3：求圆的周长，已知直径是10m。

解：由于直径是半径的两倍，所以半径r=10m/2=5m。

根据公式2πr，将半径r替换成5m，得到周长=2π×5m≈31.42m。

所以圆的周长是
31.42m。

例题4：已知圆的周长是36π cm，求圆的直径。

例题5：已知圆的周长是100周长单位，求圆的半径。

通过以上例题的解答，我们可以发现圆的周长计算公式2πr可以很
方便地帮助我们求解圆的周长、半径和直径。

在实际生活和工作中，我们
经常会遇到需要计算圆的周长的问题，比如建筑设计、数学几何等领域。

掌握圆的周长计算公式将对我们的工作和学习有很大的帮助。

六年级数学上册圆形知识点六年级数学上册圆形知识点一、认识圆形1、圆的定义：圆是由曲线围成的一种平面图形。

2、圆心：将一张圆形纸片对折两次，折痕相交于圆中心的一点，这一点叫做圆心。

一般用字母O表示。

它到圆上任意一点的距离都相等.3、半径：连接圆心到圆上任意一点的线段叫做半径。

一般用字母r表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

4、直径：通过圆心并且两端都在圆上的线段叫做直径。

一般用字母d表示。

直径是一个圆内最长的线段。

5、圆心确定圆的位置，半径确定圆的大小。

6、在同一个圆内或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的直径都相等。

7.在同圆或等圆内，直径的长度是半径的2倍，半径的长度是直径的1/2。

用字母表示为：d=2r或r=d/28、轴对称图形：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。

折痕所在的这条直线叫做对称轴。

9、长方形、正方形和圆都是对称图形，都有对称轴。

这些图形都是轴对称图形。

10、只有1条对称轴的图形有：角、等腰三角形、等腰梯形、扇形、半圆。

只有2条对称轴的图形是：长方形;只有3条对称轴的图形是：等边三角形;只有4条对称轴的图形是：正方形;有无数条对称轴的图形是：圆、圆环。

11、画对称轴要用铅笔画，同时要用尺子(三角板)画出虚线，这条虚线两端要超出图形一点。

二、圆的周长1、圆的周长：围成圆的曲线的长度叫做圆的周长。

用字母C表示。

2、圆周率实验：(滚动法)在圆形纸片上做个记号，与直尺0刻度对齐，在直尺上滚动一周，得到圆的周长。

或者用线围绕圆形纸片一周量出线的长度就是圆的周长(测绳法)。

发现，圆周长与它直径的比值(圆周长除以直径)是一个固定数即3倍多一点，我们把它叫做圆周率用字母π表示。

3、圆周率：任意一个圆的周长与它的直径的比值是一个固定的数，我们把它叫做圆周率。

用字母π(pai) 表示。

世界上第一个把圆周率算出来的人是我国的数学家祖冲之。

西师大版六年级数学上册第二单元教案圆的周长第1课时教学内容教科书第23页例1、例2，课堂活动第1、2题，练习五第1~5题。

教学目标1.使学生掌握圆周率的近似值，理解和掌握圆周长公式，并能正确计算圆的周长和解答简单的实际问题。

2.让学生在知识的主动建构过程中掌握一些数学的思想方法，发挥学生学习的主动性、独立性、合作性，对学生进行辨证唯物主义教育和爱国主义教育。

教学重、难点掌握并理解圆的周长计算公式及其推导过程。

教具、学具准备圆规、直尺、课件、圆纸片、线。

教学过程一、导入新课出示情境图：谁的铁环滚一圈的距离长一些？为什么？教师：铁环滚动一周的距离我们就叫做铁环的周长。

教师：围成圆的曲线的长叫做圆的周长。

今天我们就一起来研究圆的周长。

板书课题：圆的周长。

二、感知圆的周长与直径的关系1.老师出示一个圆(实物)。

谁来指一指这个圆的周长？课件出示一个圆。

谁来指一指这个圆的周长？学生指出并回答。

(略)2.观察。

课件演示右图：问题：这两个圆周长有什么关系？你是怎么知道的？小结：直径相等，圆的周长就相等。

3.课件演示右图：问题：这两个圆的周长哪一个长一些？为什么？学生回答后，课件演示由曲变直，对学生的推断进行检验。

4.小结。

问题：通过刚才的观察，你有什么发现？学生：圆的周长和直径有关系。

三、探究圆的周长与直径的倍数关系圆的周长和直径有怎样的关系呢？我们一起来作一个实验，测量学具中圆形的周长和直径，然后再用周长除以直径得出它们的商。

1.小组讨论，制定探究步骤。

出示探究建议：(1)测量圆的周长和直径；(2)记录数据；(3)进行计算；(4)得出结论。

2.说明活动要求。

每个组的同学先测量出学具中圆形的周长和直径，然后再用周长除以直径，并把这些数据和计算的结果填在表里。

圆的直径圆的周长周长除以直径的商(保留两位小数)3.小组合作，进行探究。

4.汇报交流。

(1)交流测量的方法。

提问：谁来介绍一下，你们组是怎样测量圆的周长的？学生汇报测量的方法。

六年级数学圆的认识知识点六年级数学圆的认识知识点在我们的学习时代，很多人都经常追着老师们要知识点吧，知识点也可以通俗的理解为重要的内容。

你知道哪些知识点是真正对我们有帮助的吗？下面是店铺为大家整理的六年级数学圆的认识知识点，欢迎阅读，希望大家能够喜欢。

六年级数学圆的认识知识点一、认识圆形1、圆的定义：圆是由曲线围成的一种平面图形。

2、圆心：将一张圆形纸片对折两次，折痕相交于圆中心的一点，这一点叫做圆心。

一般用字母O表示。

它到圆上任意一点的距离都相等.3、半径：连接圆心到圆上任意一点的线段叫做半径。

一般用字母r表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

4、直径：通过圆心并且两端都在圆上的线段叫做直径。

一般用字母d表示。

直径是一个圆内最长的线段。

5、圆心确定圆的位置，半径确定圆的大小。

6、在同一个圆内或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的直径都相等。

7.在同圆或等圆内，直径的长度是半径的2倍，半径的长度是直径的1/2。

用字母表示为：d=2r或r=d/28、轴对称图形：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。

折痕所在的这条直线叫做对称轴。

9、长方形、正方形和圆都是对称图形，都有对称轴。

这些图形都是轴对称图形。

10、只有1条对称轴的图形有：角、等腰三角形、等腰梯形、扇形、半圆。

只有2条对称轴的图形是：长方形;只有3条对称轴的图形是：等边三角形;只有4条对称轴的图形是：正方形;有无数条对称轴的图形是：圆、圆环。

11、画对称轴要用铅笔画，同时要用尺子(三角板)画出虚线，这条虚线两端要超出图形一点。

二、圆的周长1、圆的周长：围成圆的曲线的长度叫做圆的周长。

用字母C表示。

2、圆周率实验：(滚动法)在圆形纸片上做个记号，与直尺0刻度对齐，在直尺上滚动一周，得到圆的周长。

或者用线围绕圆形纸片一周量出线的长度就是圆的周长(测绳法)。

发现，圆周长与它直径的比值(圆周长除以直径)是一个固定数即3倍多一点，我们把它叫做圆周率用字母π表示。

求圆的周长习题及答案求圆的周长习题及答案圆是几何学中的一种基本图形，它具有许多独特的性质和特点。

其中一个重要的性质就是它的周长。

在本文中，我们将探讨一些关于求圆周长的习题，并提供相应的答案。

习题一：已知圆的半径为5cm，求其周长是多少？解答：圆的周长可以通过公式C = 2πr来计算，其中C表示周长，π是一个常数，约等于3.14，r表示半径。

根据已知条件，将半径r代入公式中，即可得到周长C = 2 × 3.14 × 5 = 31.4cm。

习题二：已知圆的直径为8cm，求其周长是多少？解答：圆的直径是连接圆上两个点的线段，它的长度等于半径的两倍。

因此，我们可以通过直径求得半径，然后再利用公式C = 2πr计算周长。

根据已知条件，直径d = 8cm，半径r = d/2 = 8/2 = 4cm。

将半径r代入公式中，即可得到周长C = 2 × 3.14 × 4 = 25.12cm。

习题三：已知圆的周长为18.84cm，求其半径是多少？解答：根据已知条件，我们可以利用公式C = 2πr来计算半径。

将已知的周长C = 18.84cm代入公式中，得到18.84 = 2 × 3.14 × r。

解方程可得r = 18.84 / (2 × 3.14) ≈ 3cm。

习题四：已知圆的周长为36cm，求其直径是多少？解答：根据已知条件，我们可以利用公式C = 2πr来计算直径。

将已知的周长C = 36cm代入公式中，得到36 = 2 × 3.14 × r。

解方程可得r = 36 / (2 × 3.14) ≈ 5.73cm。

由于直径等于半径的两倍，所以直径d ≈ 5.73 × 2 ≈ 11.46cm。

习题五：已知圆的周长为50cm，求其面积是多少？解答：圆的面积可以通过公式A = πr²来计算，其中A表示面积，π是一个常数，约等于3.14，r表示半径。

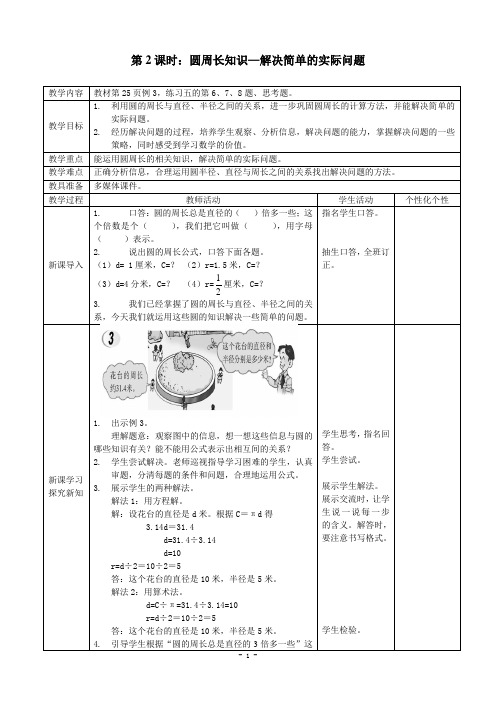
第2课时：圆周长知识—解决简单的实际问题教学内容教材第25页例3，练习五的第6、7、8题、思考题。

教学目标1.利用圆的周长与直径、半径之间的关系，进一步巩固圆周长的计算方法，并能解决简单的实际问题。

2.经历解决问题的过程，培养学生观察、分析信息，解决问题的能力，掌握解决问题的一些策略，同时感受到学习数学的价值。

教学重点能运用圆周长的相关知识，解决简单的实际问题。

教学难点正确分析信息，合理运用圆半径、直径与周长之间的关系找出解决问题的方法。

教具准备多媒体课件。

教学过程教师活动学生活动个性化个性新课导入1.口答：圆的周长总是直径的（）倍多一些；这个倍数是个（），我们把它叫做（），用字母（）表示。

2.说出圆的周长公式，口答下面各题。

（1）d= 1厘米，C=？（2）r=1.5米，C=？（3）d=4分米，C=？（4）r=21厘米，C=？3.我们已经掌握了圆的周长与直径、半径之间的关系，今天我们就运用这些圆的知识解决一些简单的问题。

指名学生口答。

抽生口答，全班订正。

新课学习探究新知1.出示例3。

理解题意：观察图中的信息，想一想这些信息与圆的哪些知识有关？能不能用公式表示出相互间的关系？2.学生尝试解决。

老师巡视指导学习困难的学生，认真审题，分清每题的条件和问题，合理地运用公式。

3.展示学生的两种解法。

解法1：用方程解。

解：设花台的直径是d米。

根据C＝πd得3.14d＝31.4d=31.4÷3.14d=10r=d÷2＝10÷2＝5答：这个花台的直径是10米，半径是5米。

解法2：用算术法。

d=C÷π=31.4÷3.14=10r=d÷2＝10÷2＝5答：这个花台的直径是10米，半径是5米。

4.引导学生根据“圆的周长总是直径的3倍多一些”这学生思考，指名回答。

学生尝试。

展示学生解法。

展示交流时，让学生说一说每一步的含义。

解答时，要注意书写格式。

学生检验。

圆的周长和面积的练习题圆是数学中一个重要的几何形状，它具有许多独特的特点和性质。

本文将提供一系列关于圆的周长和面积的练习题，帮助读者加深对圆形的认识并提升解题能力。

通过探索这些练习题，读者将能够熟练计算圆的周长和面积，并在日常生活中灵活运用相关知识。

练习题一：计算圆的周长题目：一个圆的半径为8厘米，计算其周长。

解析：圆的周长可以通过公式C = 2πr来计算，其中C代表周长，π代表圆周率（取近似值3.14），r为半径。

根据题目，半径r为8厘米，代入公式可得：C = 2 × 3.14 × 8 = 50.24厘米因此，该圆的周长为50.24厘米。

练习题二：计算圆的面积题目：一个圆的半径为12米，计算其面积。

解析：圆的面积可以通过公式A = πr²来计算，其中A代表面积，π代表圆周率，r为半径。

根据题目，半径r为12米，代入公式可得：A = 3.14 × 12² = 452.16平方米因此，该圆的面积为452.16平方米。

练习题三：已知圆的周长，求半径题目：一个圆的周长为18.84厘米，求其半径。

解析：已知圆的周长C和半径r的关系为C = 2πr。

将已知条件代入该公式，可以得到：18.84 = 2 × 3.14 × r解方程，求出r的值：r = 18.84 ÷ (2 × 3.14) ≈ 3厘米因此，该圆的半径约为3厘米。

练习题四：已知圆的面积，求直径题目：一个圆的面积为706.5平方米，求其直径。

解析：已知圆的面积A和直径d的关系为A = π × (d/2)²。

将已知条件代入该公式，可以得到：706.5 = 3.14 × (d/2)²解方程，求出d的值：(d/2)² = 706.5 ÷ 3.14d/2 ≈ √(706.5 ÷ 3.14)d ≈ 2 × √(706.5 ÷ 3.14) ≈ 37.7因此，该圆的直径约为37.7米。

第5讲 圆一、认识圆形1. 圆的定义，圆是由曲线围成的一种平面图形。

2. 圆心:将一张圆形纸片对折两次，折痕相交于圆中心的一点，这一点叫做圆心。

一般用字母O 表示它到圆上任意一点的距离都相等。

3. 半径:连接圆心到圆上任意一点的线段叫做半径。

一般用字母r 表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

4. 直径:通过圆心并且两端都在圆上的线段叫做直径。

一般用字母 d 表示。

直径是一个圆内最长的线段。

5. 圆心确定圆的位置，半径确定圆的大小。

6. 在同一个圆内或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的直径都相等。

7. 在同圆或等圆内，直径的长度是半径的2倍，半径的长度是直径的21。

用字母表示为:d=2r 或r=2d 。

8. 轴对称图形:如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形折痕所在的这条直线叫做对称轴。

9、长方形、正方形和圆都是对称图形，都有对称轴。

这些图形都是轴对称图形。

10. 只有1条对称轴的图形有: 角、等腰三角形、等腰梯形、扇形、半圆。

只有2条对称轴的图形是长方形;只有3条对称轴的图形是:等边三角形;只有4条对称轴的图形是:正方形有无数条对称轴的图形是: 圆、圆环。

11. 画对称轴要用铅笔画，同时要用尺子(三角板)画出虚线，这条虚线两端要超出图形一点。

【例1】（2020秋•兴县期中）用圆规画圆，圆规两脚间的距离是圆的 ． 决定圆的大小， 确定圆的位置．【分析】圆规在画圆时，有针的一脚不动，即圆心，有笔头的一脚旋转一周，得到圆，两脚之间的距离就是圆的半径，所以圆心决定圆的位置，半径决定圆的大小． 【解答】解：由分析可知：用圆规画圆，圆规两脚间的距离是圆的半径．半径决定圆的大小，圆心确定圆的位置．故答案为：半径，半径，圆心．【点评】此题主要考查了圆的画法和各部分作用．【例2】（2021秋•峄城区期末）在每个图形下面填写上图中的数学信息。