流体力学习题解答
- 格式:doc
- 大小:150.50 KB
- 文档页数:6
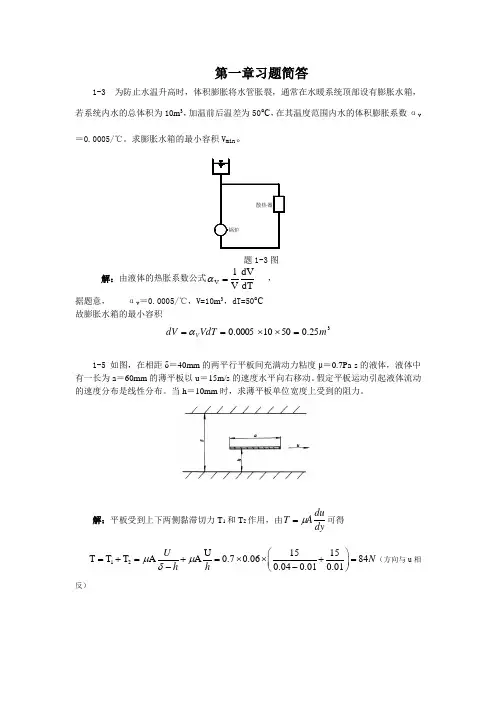
第一章习题简答1-3 为防止水温升高时,体积膨胀将水管胀裂,通常在水暖系统顶部设有膨胀水箱,若系统内水的总体积为10m 3,加温前后温差为50°С,在其温度范围内水的体积膨胀系数αv=0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解:由液体的热胀系数公式dTdVV 1V =α , 据题意, αv =0.0005/℃,V=10m 3,dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-7 温度为20°С的空气,在直径为2.5cm 的管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少?解:温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系,且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250,c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ (与课本后的答案不一样。

第一章 绪论1-1 连续介质假设的条件是什么?答:所研究问题中物体的特征尺度L ,远远大于流体分子的平均自由行程l ,即l/L<<1。
1-2 设稀薄气体的分子自由行程是几米的数量级,问下列二种情况连续介质假设是否成立? (1)人造卫星在飞离大气层进入稀薄气体层时; (2)假象地球在这样的稀薄气体中运动时。
答:(1)不成立。
(2)成立。
1-3 粘性流体在静止时有没有切应力?理想流体在运动时有没有切应力?静止流体没有粘性吗? 答:(1)由于0=dy dv ,因此0==dydvμτ,没有剪切应力。
(2)对于理想流体,由于粘性系数0=μ,因此0==dydvμτ,没有剪切应力。
(3)粘性是流体的根本属性。
只是在静止流体中,由于流场的速度为0,流体的粘性没有表现出来。
1-4 在水池和风洞中进行船模试验时,需要测定由下式定义的无因次数(雷诺数)νUL=Re ,其中U 为试验速度,L 为船模长度,ν为流体的运动粘性系数。
如果s m U /20=,m L 4=,温度由C ︒10增到C ︒40时,分别计算在水池和风洞中试验时的Re 数。
(C ︒10时水和空气的运动粘性系数为410013.0-⨯和410014.0-⨯,C ︒40时水和空气的运动粘性系数为4100075.0-⨯和410179.0-⨯)。
答:C ︒10时水的Re 为:()()72410154.6/10013.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒10时空气的Re 为:()()72410714.5/10014.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时水的Re 为:()()82410067.1/100075.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时空气的Re 为:()()62410469.4/10179.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。

1、流体与固体的最大区别是流体______。
(第01章流体力学:1) A.易流动B.可压缩C.A和 BD.不可压缩流体与固体的根本区别在于流动性。
正是由于流体具有流动性,所以流体没有固定的形状。
3、下列是______流体的物理性质。
(191079:第01章流体力学:3) A.粘度,流动速度,流体质量B.密度,压缩性,表面张力C.流体速度,流体重量,密度D.粘度,流体重量,表面张力流体主要的力学性质有:重度、密度、压缩性、膨胀性、粘滞性、表面张力、含气量及空气分离压等。
6、如图 (191082:第01章流体力学:6)ABCD16、同种流体的密度随_____的变化而变化。
(191092:第01章流体力学:16)A.温度B.压力C.温度和压力D.A、B、C都不对这是由流体膨胀性和压缩性所决定的。
17、如图 (191093:第01章流体力学:17)ABCD22、若200cm3待测液从恩氏粘度计流出的时间为102s,则恩氏粘度为_____. (191098:第01章流体力学:22)A.102B.200C.2D.l26、流体的运动一停止,流体_____。
(191102:第01章流体力学:26) A.就具有可压缩性B.就不呈现粘滞性C.粘度就随温度升高而降低D.内压力就消失31、牛顿内摩擦定律适用于_____。
(191107:第01章流体力学:31) A.层流流动B.紊流流动C.A和BD.任意流动牛顿内摩擦定律仅仅适用于层流流动。
36、当其他条件不变,流体的温度升高时,其动力粘度_____。
A.增大B.减小C.不变D.不一定液体和气体的粘度随温度的变化规律不同。
液体的粘度随温度的升高而减小,而气体的粘度随温度的升高而增大。
这是因为液体分子间距小,不规则运动弱,因此内摩擦力主要取决于分子间的内聚力。
温度升高时,分子间距增大,内聚力相应减小,因而粘度就要减小。
对于气体内摩擦力主要取决于分子间不规则运动的动量交换。

2.在现实生活中可视为牛顿流体的有水 和空气 等。
3.流体静压力和流体静压强都是压力的一种量度。
它们的区别在于:前者是作用在某一面积上的总压力;而后者是作用在某一面积上的平均压强或某一点的压强。
4.均匀流过流断面上压强分布服从于水静力学规律。
5.和液体相比,固体存在着抗拉、抗压和抗切三方面的能力。
7.流体受压,体积缩小,密度增大 的性质,称为流体的压缩性 ;流体受热,体积膨胀,密度减少 的性质,称为流体的热胀性 。
8.压缩系数β的倒数称为流体的弹性模量 ,以E 来表示 12.液体静压强分布规律只适用于静止、同种、连续液体。
13.静止非均质流体的水平面是等压面,等密面和等温面。
14.测压管是一根玻璃直管或U 形管,一端连接在需要测定的容器孔口上,另一端开口,直接和大气相通。
16.作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。
17.通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18. 流线不能相交(驻点处除外),也不能是折线,因为流场内任一固定点在同一瞬间只能有一个速度向量,流线只能是一条光滑的曲线或直线。
20.液体质点的运动是极不规则的,各部分流体相互剧烈掺混,这种流动状态称为紊流。
21.由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速k v ',其中kv '称为上临界速度,k v 称为下临界速度。
23.圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。
25.紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。
26.速度的大小、方向或分布发生变化而引起的能量损失,称为局部损失。
29.湿周是指过流断面上流体和固体壁面接触的周界。
31.串联管路总的综合阻力系数S 等于各管段的阻抗叠加。
32.并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s++=。
管嘴与孔口比较,如果水头H 和直径d 相同,其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。

(完整版)工程流体力学习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d )【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp=ρ。
解:不考虑黏性的流体称为理想流体。
(c )【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。

第二章2-2解:由P gh ρ=得h 水 =Pg ρ水=3350101109.8⨯⨯⨯=5.1m 335010=3.21.6109.8Ph m gρ⨯==⨯⨯四氯化碳四氯化碳 335010=0.37513.6109.8Ph m g ρ⨯==⨯⨯水银水银2-3 解:(1)体积弹性模量 /dpEv d ρρ=+在重力场中流体的压强形式为:dpg dzρ=- d dp gdz Evρρρ∴=-=两边积分,带入边界条件:00,0,z p ρρ===0lnEvp Ev Ev ghρ∴=- 11222212.5*160N F *40000NF L L s F s ==⎛⎫=== ⎪⎝⎭题解:有杠杆原理知:F 所以: 6、如题2-6图所示,封闭容器中盛有ρ=800kg/3m的油,1300h mm =,油下面为水,2500h mm =,测压管中水银液位读数400hmm =,求封闭容器中油面上的压强p 的大小。
解:12g 0p h gh gh ρρρ++-=油水水银12g p gh h gh ρρρ=--水银油水333313.6109.840010109.8500100.8--=⨯⨯⨯⨯-⨯⨯⨯-⨯=44.6110pa ⨯2-7:解:(1)、2224F gh s 10009.81001010101098Nρ--==⨯⨯⨯⨯⨯=2)m 121216G [s h h s h ]1000199109.81.95g Nρ-=⨯⨯=⨯⨯⨯=(-)+02h(3)因为在21h h -处谁对容器有向上的压力2-8,解:由同一液面压强相等可列:(0)()gh sin /6p(0)1239.21/^3p p h l kn m θθπ===∴=液2-9 解:设A 点距左U 形管测压计水银页面高度为H 则B 点距右U 型管测压计水银高度为H+hB A B h gh g H h gh gh gh m ag ρρρρρρA P -P -+P P -P =-=-⨯⨯P 水水水水则(+)=则()=(13600-1000)9.80.3=370442.10,解:选取右侧U 形管汞柱高作为等压面,有:1132()m B P g h h gh gh gh p ρρρρ++-+=+酒汞汞水B p 42.7410pa =-⨯2-11解:左边液面压强与右边液面压强相等知,.66g .66.89g .82g .8211g ⨯+-⨯=⨯+-⨯未知水未知水)()(ρρρρ解得333102.31m kg 103.85⨯=⋅⨯=-未知ρ3m kg -⋅2-12 解:设左支管液面到另一液体分界面的距离为1h ,右支管为2h ,则有:1112222P gh P gh gh ρρρ+=++或121122121221()()P P g h h ghP P gh gh ghρρρρρρ-=--+-=-+=-得 1221()P P h gρρ-=-2-13解:gh P gh ρρ+=水水银P=gh gh ρρ∴-水银水127400.07891.8F PS N∴==⨯=2-14解:以闸门与液面交点为O 点,沿闸门向下方向建立坐标S ,取微元ds ,在面积bds 内,液体压力对链轴取矩()()0.2sin600.2dM ghbds s g s sdsρρ=-+=-+ 所以)0sin 600.2Mgb s sds ρ=-+Q对链轴取矩)cos600.2Q M Q =由力矩平衡得 0Q M M +=化简)1.*1.9320.302Q -=得 26778Q N=()()D 33352.151y y *1132***2*4121232,8832**10*10*12*89.6*10xcC c xc cD c I y sI b a y s d y F g h s ρ=+==========题解:依题意知又即:*16、一个很长的铅垂壁面吧海水和淡水隔开,海水深7m ;试确定淡水多深时壁面所受液体作用力合力为零。

流体⼒学习题解答第⼀章习题答案选择题(单选题)1.1 按连续介质的概念,流体质点是指:(d )(a )流体的分⼦;(b )流体内的固体颗粒;(c )⼏何的点;(d )⼏何尺⼨同流动空间相⽐是极⼩量,⼜含有⼤量分⼦的微元体。
1.2 作⽤于流体的质量⼒包括:(c )(a )压⼒;(b )摩擦阻⼒;(c )重⼒;(d )表⾯张⼒。
1.3 单位质量⼒的国际单位是:(d )(a )N ;(b )Pa ;(c )kg N /;(d )2/s m 。
1.4 与⽜顿内摩擦定律直接有关的因素是:(b )(a )剪应⼒和压强;(b )剪应⼒和剪应变率;(c )剪应⼒和剪应变;(d )剪应⼒和流速。
1.5 ⽔的动⼒黏度µ随温度的升⾼:(b )(a )增⼤;(b )减⼩;(c )不变;(d )不定。
1.6 流体运动黏度ν的国际单位是:(a )(a )2/s m ;(b )2/m N ;(c )m kg /;(d )2/m s N ?。
1.7 ⽆黏性流体的特征是:(c )(a )黏度是常数;(b )不可压缩;(c )⽆黏性;(d )符合RT p=ρ。
1.8 当⽔的压强增加1个⼤⽓压时,⽔的密度增⼤约为:(a )(a )1/20000;(b )1/10000;(c )1/4000;(d)1/2000。
1.9 ⽔的密度为10003kg/m ,2L ⽔的质量和重量是多少?解:10000.0022m V ρ==?=(kg )29.80719.614G mg ==?=(N )答:2L ⽔的质量是2kg ,重量是。
体积为3m 的油料,重量为4410N ,试求该油料的密度是多少?解:44109.807899.3580.5m G g V V ρ====(kg/m 3)答:该油料的密度是m 3。
1.11 某液体的动⼒黏度为Pa s ?,其密度为8503/kg m ,试求其运动黏度。
解:60.005 5.88210850µνρ-===?(m 2/s )答:其运动黏度为65.88210-?m 2/s 。

流体力学习题库(含答案)一、单选题(共70题,每题1分,共70分)1、低温泵的气相平衡线的作用是防止泵的( )。
A、憋压B、超温C、汽蚀D、汽缚正确答案:D2、若被输送液体的黏度增大时,离心泵的效率( )。
A、减小B、增大C、不变D、不定正确答案:A3、当地大气压为745mmHg测得一容器内的绝对压强为350mmHg,则真空度为( )A、395mmHgB、350mmHgC、410mmHg正确答案:A4、单位质量的流体所具有的( )称为流体的比容。
A、位能B、动能C、体积D、黏度正确答案:C5、喷射泵是利用流体流动时的( )的原理来工作的。
A、动能转化为静压能B、热能转化为静压能C、静压能转化为动能正确答案:C6、机械密封与填料密封相比( )的功率消耗较大。
A、填料密封B、机械密封C、差不多正确答案:A7、下列不属于离心泵的主要构件是 ( )A、泵轴B、泵壳C、叶轮D、轴封装置正确答案:A8、一台离心泵开动不久,泵入口处的真空度正常,泵出口处的压力表也逐渐降低为零,此时离心泵完全打不出水。
发生故障的原因是( )A、吸入管路堵塞B、忘了灌水C、吸入管路漏气D、压出管路堵塞正确答案:A9、某液体在内径为D0的水平管路中稳定流动,其平均流速为u0,当它以相同的体积流量通过等长的内径为D2(D2=D0/2)的管子时,若流体为层流,则压降ΔP为原来的( )倍。
A、32B、8C、4D、16正确答案:A10、造成离心泵气缚原因是( )A、泵不能抽水B、安装高度太高C、入口管路阻力太大D、泵内流体平均密度太小正确答案:D11、离心泵的轴功率N和流量Q的关系为( )A、Q增大,N增大B、Q增大,N先增大后减小C、Q增大,N减小D、Q增大,N先减小后增大正确答案:A12、在静止的连通的同一种连续流体内,任意一点的压强增大时,其他各点的压强则( )A、减小B、不变C、相应增大D、不一定正确答案:C13、往复泵的流量调节采用( )A、出口支路B、出口阀开度C、入口阀开度D、入口支路正确答案:A14、为了防止( )现象发生,启动离心泵时必须先关闭泵的出口阀A、汽蚀B、电机烧坏C、气缚D、叶轮受损正确答案:B15、某泵在运行的时候发现有汽蚀现象应( )A、停泵向泵内灌液B、降低泵的安装高度C、检查进口管路是否漏液D、检查出口管阻力是否过大正确答案:C16、选离心泵是根据泵的( )A、扬程和轴功率选择B、转速和轴功率选择C、轴功率和流量选择D、扬程和流量选择正确答案:D17、流体运动时,能量损失的根本原因是由于流体存在着 ( )。

第1章 绪论【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d ) 【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】 流体运动黏度υ的国际单位是:(a )m2/s ;(b )N/m2;(c )kg/m ;(d )N 〃s/m2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】 理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp =ρ。
解:不考虑黏性的流体称为理想流体。
(c ) 【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
(c ) 【1.7】下列流体哪个属牛顿流体:(a )汽油;(b )纸浆;(c )血液;(d )沥青。
解:满足牛顿内摩擦定律的流体称为牛顿流体。

【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯相对密度 330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P p dV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆t p V V ?,相比之下可以忽略由压力变化引起的体积改变,则 由 200L β+=t V V dT 得 1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。

流体力学习题和解答1. 15℃的空气在直径200mm 的圆管中流动,假定距管壁1mm 处的速度为0.3m/s,试求每米管长上的摩擦阻力。
2. 如图所示,已知动力润滑轴承内轴的直径D=0.2m,轴承宽度b=0.3m,间隙δ=0.8mm,间隙内润滑油的动力粘度s Pa 245.0⋅=μ,消耗的功率P=50.7W,试求轴的转速n 为多少? [2830 rpm]题2图 题5图3. 直径为0.46m 的水平圆盘,在较大的平板上绕其中心以90rpm 的转速旋转。
已知两壁面间的间隙为0.23mm,间隙内油的动力粘度为0.4Pa·s,如果忽略油的离心惯性的影响,试求转动圆盘所需的力矩?4. 两平行平板之间的间隙为2mm,间隙内充满密度为885kg/m 3、运动粘度为0.00159 m 2/s的油,试求当两板相对速度为4m/s 时作用在平板上的摩擦应为多少?5. 如图所示,活塞直径d=152.4mm,缸径D=152.6mm,活塞长L=30.48cm,润滑油的运动粘度41091440-⨯ν.=m 2/s,密度ρ=920kg/m3。
试求活塞以v=6m/s 的速度运动时,克服摩擦阻力所消耗的功率。
6. 重500N 的飞轮的回转半径为30cm,转速为600rpm,由于轴承中润滑油的粘性阻滞,飞轮以0.02rad/s2的角减速度放慢,已知轴的直径为2cm,轴套的长度为5cm,它们之间的间隙为0.05mm,求润滑油的动力粘度。
7. 内径8mm 的开口玻璃管,插入20℃的水中,已知水与玻璃的接触角θ=10o,试求水在玻璃管中上升的高度。
8. 内径8mm 的开口玻璃管,插入20℃的水银中,已知水银与玻璃的接触角约为1400,试求水银液面在管中下降的高度。
[1.36mm]1. 如图所示,用U 形管测压计测量管道A 、B 中的压强差,若A 管中的压强为510744.2⨯Pa ,B 管中的压强为510372.1⨯ Pa ,试确定U 形管中两液面的高度差h 为多少。
一、填 空 题2.在现实生活中可视为牛顿流体的有水 和空气 等。
3.流体静压力和流体静压强都是压力的一种量度。
它们的区别在于:前者是作用在某一面积上的总压力;而后者是作用在某一面积上的平均压强或某一点的压强。
5.和液体相比,固体存在着抗拉、抗压和抗切三方面的能力。
7.流体受压,体积缩小,密度增大 的性质,称为流体的压缩性 ;流体受热,体积膨胀,密度减少 的性质,称为流体的热胀性 。
9.1工程大气压等于98.07千帕,等于10m 水柱高,等于735.6毫米汞柱高。
11.流体静压强的方向必然是沿着作用面的内法线方向。
17.通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18. 流线不能相交(驻点处除外),也不能是折线,因为流场内任一固定点在同一瞬间只能有一个速度向量,流线只能是一条光滑的曲线或直线。
20.液体质点的运动是极不规则的,各部分流体相互剧烈掺混,这种流动状态称为紊流。
21.由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv ',其中k v '称为上临界速度,k v 称为下临界速度。
23.圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。
24.根据λ繁荣变化特征,尼古拉兹实验曲线可分为五个阻力区,分别是层流区;临界区;紊流光滑区;紊流过渡区和紊流粗糙区。
26.速度的大小、方向或分布发生变化而引起的能量损失,称为局部损失。
27.正方形形断面管道(边长为a),其水力半径R 等于4a R =,当量直径de 等于a d e =。
30.层流运动时,沿程阻力系数λ与(Re)f 有关,紊流运动沿程阻力系数λ在光滑管区与(Re)f 有关,在过渡区与)(Re,d K f 有关,在粗糙区与)(dK f 有关。
38.几何相似是指流动空间几何相似。
即形成此空间任意相应两线段夹角相同,任意相应线段长度保持一定的比例 。
二、判 断 题1.当平面水平放置时,压力中心与平面形心重合。
流体力学练习题及答案一、单项选择题1、下列各力中,不属于表面力的是( )。
A .惯性力B .粘滞力C .压力D .表面张力2、下列关于流体粘性的说法中,不准确的说法是( )。
A .粘性是实际流体的物性之一B .构成流体粘性的因素是流体分子间的吸引力C .流体粘性具有阻碍流体流动的能力D .流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中,流体质点的加速度包括当地加速度和迁移加速度,迁移加速度反映( )。
A .由于流体质点运动改变了空间位置而引起的速度变化率B .流体速度场的不稳定性C .流体质点在流场某一固定空间位置上的速度变化率D .流体的膨胀性4、重力场中平衡流体的势函数为( )。
A .gz -=πB .gz =πC .z ρπ-=D .z ρπ=5、无旋流动是指( )流动。
A .平行B .不可压缩流体平面C .旋涡强度为零的D .流线是直线的6、流体内摩擦力的量纲[]F 是( )。
A . []1-MLt B . []21--t ML C . []11--t MLD . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ,则流动属于( )。
A .三向稳定流动B .二维非稳定流动C .三维稳定流动D .二维稳定流动8、动量方程 的不适用于( ) 的流场。
A .理想流体作定常流动in out QV QV F )()(ρρ∑-∑=∑B.粘性流体作定常流动C.不可压缩流体作定常流动D.流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时,以下陈述错误的是:沿流动方向( ) 。
A.流量逐渐减少B.阻力损失量与流经的长度成正比C.压强逐渐下降D.雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失()。
A.一定不相等B.之和为单位质量流体的总能量损失C.一定相等D.相等与否取决于支管长度是否相等11、边界层的基本特征之一是()。
习 题 六1. 已知不可压缩平面流动的速度分布u=x 2+2x-4y ,v=-2xy-2y 。
确定流动:(1)是否满足连续性条件;(2)是否有旋;(3)驻点位置;(4)如存在速度势函数和流函数,求出它们。
4题2. 已知不可压缩平面流动的速度势为:(1)ϕ=r Q ln 2π;(2)ϕ=xyarctan 2πΓ。
求:(1)速度分布;(2)流函数和流动图案。
5题图3. 求以下平面流动的涡量场,并判断由给定涡量场能否唯一地确定相应的速度场。
(1) u=-y ,v=0;(2)u=-(x+y ),v=y ;(3)u=-y ,v=x ;4. 已知平面流场的速度分布量为:r>a ,u=222y x y a +-ω,v=222yx x a +ω;r ≤a ,u=-y ω,v=x ω。
ω为常数,a 为半径,求图中三条封闭曲线C 1,C 2,C 3的环量1Γ,2Γ,3Γ。
5. 证明以下分别用速度势和流函数表示的两个流场实际实际上是同一流场:22y x x -+=ϕ和y xy +=2ψ6. 不压缩流体平面流动的速度势为x y x +-=22ϕ,求其相应的流函数。
7. 在(1,0)和(-1,0)两点各有强度为4π的点源,试求在(0,0),(0,1),(0,-1),(1,1)的速度。
8. 两个速度环量相等且为s m /102=Γ的旋涡,分别位于y=3±处。
求(1)原点处的分速度u ,v ;(2)A (4,0)点处的u ,v ;(3)B (6,5)点处的u ,v ;(4)流线方程。
15题图9. 已知不可压缩流体平面流动的速度势为22y x -=ϕ,求在点(2,1.5)处的压强。
设驻点的压强为101kN/m 2,流体的密度为3/19.1m kg =ρ。
10. 根据固定壁面可以和流线等价交换的原则,决定如下平面流动的速度势和沿壁面的速度分布。
(1) 一强度为Q 的点源位于(a ,0)处,y 轴为固定壁面。
(2) 一强度为Q 的点汇位于(0,a )处,x 轴为固定壁面。
11. x 轴上的两点(a ,0),(-a ,0)处分别放置强度为Q 的一个点源和一个点汇。
证明叠加后组合流动的流函数为: 2222arctan 2a y x ay Q -+=πψ 12.速度为V ∞的平行流和强度为Q 的点源叠加,形成绕半无穷体的流动。
求其流函数和速度势,并证明柱形体的外形方程为r=Q (θπθπsin 2/)∞-V ,它的宽度为Q/ V ∞。
13.在平面xoy 上的点(a ,0),(-a ,0)处各放置一个强度为Q 的点源,在点(0,a ),(0,-a )处各放置一个强度为Q 的点汇。
求组合流动流函数,并证明通过这四点的圆周就是这组合流动的一条流线。
14. 已知复势函数W=(a+ib )lnz+z ,其中a ,b 是常数,求流体运动的流线。
15. 已知复势函数W=1/z ,求流体运动的流线和等势线。
16.已知复势函数为(1)W=1+iz ;(2)W=(1+i )ln44-+z z ;(3)W=6iz+i24/z ;问:(1)流动由哪几种基本流动组成,它们的坐标位置?绘出流动图形;(2)计算经过封闭曲线x 922=+y 的流量,及沿此曲线的速度环量。
17.圆柱体长l=5m ,直径D=1m ,垂直立于平板车上。
平板车以V 1=20m/s 的速度匀速前进。
若此圆柱体以每秒5转绕垂直轴顺时针旋转,并受到垂直于平板行驶方向的侧风作用,风速V 2=15m/s 。
求圆柱体所受流体作用力的大小和方向(空气密度为1.2kg/m 3,忽略圆柱体两端三维效应)。
32题图啊 18. 设有半径为a ,强度为Γ的圆周形涡丝,求经过圆心的对称轴z 上的任一点M 的诱导速度。
33题图 19. 设有一条强度为Γ的X 形涡丝,其两端伸向无穷远,求图示的点M 处的诱导速度。
34图参考答案: 4.,02222=--+=∂∂+∂∂x x y v x u 不可压缩,ψ存在;)42(21)(21+-=∂∂-∂∂=y y u x v y ω, 有旋,φ不存在驻点:x 2+2x-4y=0且2xy+2y=0得(-1,-41),(0,0),(-2,0)==∂∂u yψx 2+2x-4y ,得)(2222x f y xy y x +-+=ψ,v x-=∂∂ψ,所以2xy+2y+f`(x)=2xy+2yf`(x)=0,f(x)=0, 2222y xy y x -+=ψ5.(1)ϕ=r Q ln 2π,v r Q r r πϕ2=∂∂= ,v 0=∂∂=θϕθr ,r Q v r r πθψ2==∂∂ ,θψv r -=∂∂=0 ,所以θπψ2Q = (2)ϕ=x y arctan 2πΓ=θπ2Γ ,tg x y =θ ,v r r v r r πθϕϕθ2,0Γ=∂∂==∂∂= r v r v r r πψθψθ2,0Γ-=-=∂∂==∂∂,所以r ln 2πψΓ-=8.yu x v z ∂∂-∂∂=Ω 。
(1)u=-y,v=0,1=Ωz ;(2)u=-(x+y),v=y,1=Ωz ; (3)u=-y,v=x, 2=Ωz 9.r>a ,u=222y x y a +-ω,v=222yx xa +ω;r ≤a ,u=-y ω,v=x ω。
r a ≤时,ω2=Ωz ;r>a 时,0=Ωz对曲线C1⎰=Ω=ΓAn adA 22ωπ;对曲线C2:0=Γ;对曲线C3:2221412a a a ωππ==Γ10.22y x x -+=ϕ,. u=,12+=∂∂x xϕv=y y 2-=∂∂ϕ y xy +=2ψ ,u=12+=∂∂x y ψ,v=-y x2-=∂∂ψ12.x y x +-=22ϕ 。
12+=∂∂==∂∂x xu y ϕψ ,)(2x f y xy ++=ψ, 因为-y yv x 2-=∂∂==∂∂ϕψ 所以 -(2y+f`(x))=-2y, f(x)=C=0 , y xy +=2ψ 13.W)]1ln()1[ln(2)]1ln()1[ln(2++-=++-=z z z z Qz π,)1111(2)1111(2iyx iy x z z iv u dz dW ++++-=++-=-= 在点(0,0):u-iv=0,u=0,v=0 ;点(0,1):u-iv=-2i,u=0,v=2.点(0,-1):u-iv=2i,u=0,v=-2; 点(-1,-1):u-iv=-i 51254+,u=-54,v=-51215. W 10)],3ln()3[ln(2=Γ-++Γ=z z i z π. ]3131[5-++=-=z z i iv u dz dW π 点(0,0)处:u-iv=0,u==,v=0; 点A(4,0)处:u-iv=-i π740,u=0,v=π740点B(6,5)处:u-iv=]343510695[5i i --+--π, u=-3431069(5),3411061(25+=+ππv )i y x In Inri iInr i W 22(5222)(2+-Γ=Γ-Γ=-Γ=+=πθππθπθπφϕ 所以22(5y x In +=πφ18. 22y x -=ϕ, u=x x2=∂∂ϕ, v=y y 2-=∂∂ϕ, V )(422222y x v u +=+= , 点(2,1.5)处,V 252= p+022p V =ρ,p=p Pa Pa 100985875.140=-20. (1) W=)]ln()[ln(2a z a z Q++-π,y 轴上u=0,v=22y a y Q +π (2)W=)]ln()[ln(2ai z ai z Q ++-π, u-iv=]11[2ai z ai z Q dz dW ++-=π ,x 轴上z=x u-iv=2222]11[2ax x Q ai x ai x Q +=++-ππ 21. W=)]ln()[ln(2a z a z Q +--π 令z-a=r 11θi e,z+a=r 22θi e .W=]ln [ln 22121θθπ-+-r r Q ,)(221θθπψ-=Q而tg(222222212121211)ay x ay a x y a x ya x y tg tg tg tg -+=-++--=+-=-θθθθθθ , 222212a y x ay arctg-+=-θθ, 22222ay x ayarctg Q -+=πψ 23. W=V z Q z ln 2π+∞ ,θπψ2Q y V +=∞,求驻点u-iv=V zQ 12π+∞, 令u=v=0,则z=-∞V Q π2 ,即x 0=-∞V Qπ2,y 00= 驻点:πθ=,所以过驻点的流线为: θπ2Q y V +∞=ππ2Q y=)(2θππ-∞V Q ,或r=)(sin 2θπθπ-∞V Q ,当时0→θ,y=∞V Q2 24.W)]ln()ln()ln()[ln(2ai z ai z a z a z QZ +---++-=π,u-iv=]1111[2iaz ia z a z a z Q dz dW +---++-=π=442222242]22[2a z z a Q a z z a z z Q -=+--ππ 。
圆周上z=ae θi ,u-iv=θθθθθππ224422)1(42i i i i i ee e a Q e a ae a Q ---=- =θθθπθθθπ2sin cos sin 2sin 2sin cos 2i a Q i i a Q --=- 所以u=-θπcos 12a Q , v=θπsin 12a Q ,v 022sin cos =+-=+=aQa Q v u r ππθθv ][222cos sin θθπθπθπθθθctg tg aQctg a Q tg a Q v u +=+=+-=,在次圆周上只有切向速度,而法向速度v r =0,可见圆周是流线。
27. W=(a+ib)(lnr+i θ)+x+iy ,const y r b a =++=ln θψ 28. W=1/z=22y x iyx +- ,12221C const y x x ==+=ϕ ,(x21212)C y C =+- ,22221C yx y =+-=ψ, x 22222)(C C y =++ 30. (1) W=1+iz,均匀流,V i =∞ (2)W=(1+i )ln44-+z z ,在圆周x 2223=+y 上,流量,速度环量为零 (3)W=6iz+i24/z=6i(z+4/z)32. V 252221=+V V ,F l V L Γ=ρ, R R Rv ωππθ22==Γ,所以F l R V L ωπρ22=因为V=25m/s , R=0.5m ,s rad /10πω=,l=5m,所以F N L 7402=33.⎰⨯Γ=L rrdl V 24π投影到z 轴上 V=a r aa r ad r sin 24sin 42203ππθππΓ=⋅Γ⎰,因为sina=a/r ,r 222z a +=V=2/3222][2z a a +Γ34.tga=al ,V=aa l a l a a a a l πππππππππ2)cos 1(2]cos [cos 4)]2cos()2[cos(4)]cos(0[cos 4Γ++Γ=-Γ++--Γ+--Γsina。