流体力学例题

pai 定理 工程流体力学例题例 1 开口容器内盛有液体，容器下部壁面有孔通大气。

显然在孔的不同高度上流出的速度也不同。

试计算通过此孔的流量Q 。

设自由面高度不变，不计摩擦，几何尺寸如图（4.13）所示。

解 出口面上的任一微面 dh b ⨯上的速度可以利用连续方程及动量方程求得gh 2e=V式中h 为此微元面距自由面的高度。

出口体积流量为})()2{(2322b 2/32/32/2/2/12/2/d H dH g b dh h g b Vdh Q d H d H d H d H --+===⎰⎰+-+-2a e g p p H ρ+= 例2大容器有背压的小孔流出。

开口容器内盛有液体，容器下部有小孔，小孔与另一盛有液体的容器通，如图（4.14）所示。

两容器中自由液面高度分别为1H ,2H ,压力位a p ，设不计摩擦,1H ,2H 为常数，试求小孔流出速度。

解 小孔出口压力（a ）在S A 面与e A 面之间应用伯努利方程（b ）利用（a ）、（b ），并注意到eV V S <<，可得到出口速度公式)g 221e H H V -=（例3 文丘里管流量计为了测量管道中的流量，可以将收缩—扩张管接到管道中去。

如图（4.15）所示。

通过测量颈部及来流段的压力差以确定流体的平均速度。

为了测量这个压力差，可以利用U 型管测压器。

试建立颈部g2g p 0g 2g p 2ee 2a 1VV H S ++=+=ρρ)1)(()()g-g1212121122z p z p ρρρρρρ，，（）（--=---=++l l l l l l 2/1,12212222)]1)(()/-1g2[(ρρ---==l l A A A V A Q 2/1,122122)]1)(()/(-1g 2[A ρρ---=l l A V 流速与U 型管中液面高度差的关系。

解 对1—1，2—2截面利用连续方程与伯努利方程1221A A V V = (a)z pV z p V ggg g 2222112122++=++ρρ(b)由此两式可得 )()(2)/(1221121222z p z p A A V gg g +-+=-ρρ（c ） 由此可见，只要能测出p p 12-就可完全确定V2。

《例题力学》典型例题例题1：如图所示，质量为m ＝5 kg 、底面积为S ＝40 cm ×60 cm 的矩形平板，以U ＝1 m/s 的速度沿着与水平面成倾角θ＝30的斜面作等速下滑运动。

已知平板与斜面之间的油层厚度δ＝1 mm ，假设由平板所带动的油层的运动速度呈线性分布。

求油的动力粘性系数。

解：由牛顿内摩擦定律，平板所受的剪切应力du Udy τμμδ=＝ 又因等速运动，惯性力为零。

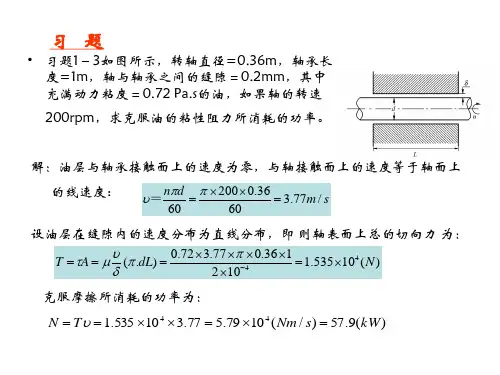
根据牛顿第二定律：0m ==∑F a ，即：gsin 0m S θτ-⋅=()324gsin 59.8sin 301100.1021N s m 1406010m U S θδμ--⋅⨯⨯⨯⨯==≈⋅⋅⨯⨯⨯ 例题2：如图所示，转轴的直径d ＝0.36 m 、轴承的长度l ＝1 m ，轴与轴承的缝隙宽度δ＝0.23 mm ，缝隙中充满动力粘性系数0.73Pa s μ=⋅的油，若轴的转速200rpm n =。

求克服油的粘性阻力所消耗的功率。

解：由牛顿内摩擦定律，轴与轴承之间的剪切应力()60d d n d uy πτμμδ=＝粘性阻力（摩擦力）：F S dl ττπ=⋅= 克服油的粘性阻力所消耗的功率：()()3223223230230603.140.360.732001600.231050938.83(W)d d n d n n lP M F dl πππμωτπδ-==⋅⋅=⨯⨯=⨯⨯⨯=⨯⨯=例题3：如图所示，直径为d 的两个圆盘相互平行，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以恒定角速度ω旋转，此时所需力矩为T ，求间隙厚度δ的表达式。

解：根据牛顿黏性定律 d d 2d r r F A r r ωωμμπδδ== 2d d 2d r T F r r r ωμπδ=⋅=42420d d 232dd d T T r r πμωπμωδδ===⎰432d Tπμωδ=例题4：如图所示的双U 型管，用来测定比水小的液体的密度，试用液柱高差来确定未知液体的密度ρ（取管中水的密度ρ水＝1000 kg/m 3）。

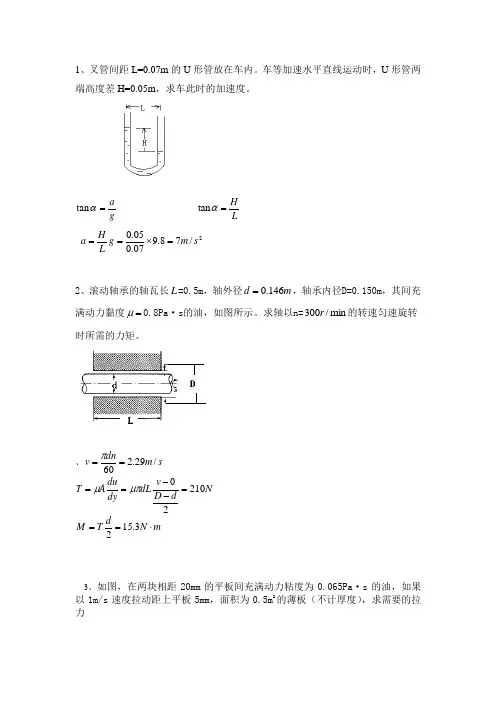
1、叉管间距L=0.07m 的U 形管放在车内。

车等加速水平直线运动时，U 形管两端高度差H=0.05m ，求车此时的加速度。

g a =αtan LH =αtan 2/78.907.005.0s m g L H a =⨯==2、滚动轴承的轴瓦长L =0.5m ，轴外径m d 146.0=，轴承内径D=0.150m ，其间充满动力黏度=μ0.8Pa ·s 的油，如图所示。

求轴以n=min /300r 的转速匀速旋转时所需的力矩。

、s m dnv /29.260==πN d D v dL dydu A T 2102=--==μπμm N dT M ⋅==3.1523、如图，在两块相距20mm 的平板间充满动力粘度为0.065Pa ·s 的油，如果以1m/s 速度拉动距上平板5mm ，面积为0.5m 2的薄板（不计厚度），求需要的拉力dy du AT μ= N huA dy du AT 5.61===μμ N hH u A dy du AT 17.22=-==μμ N T T T 67.821=+=4、用复式U 形管差压计测量A 、B 两点的压力差。

已知：mm h 3001=，mm h 5002=。

水31000m kg =ρ，水银内313600m kg m =ρ，3800m kg ='ρ。

求B A p p -。

A B p h h h g gh h h p =+∆++'-∆-)(211ρρρPa p p B A 32144-=-5、有一敞口容器，长=L 2米，高=H 1.5米，等加速水平直线运动，求当水深h 分别为1.3米和0.5米时，使容器中的液体开始溢出的最大加速度。

g a =αtan L h H )(2tan -=α 2/96.1)(2s m g Lh H a =-= xH hL 21=34=x x H g a ==αtan s m g a /11892==6、有一敞口容器，长2米，高1.3 米，宽B=1m ，等加速水平直线运动，水深0.5米。

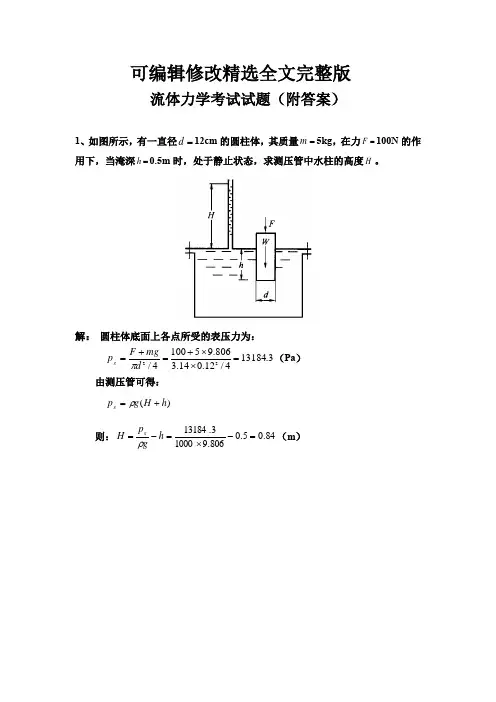
可编辑修改精选全文完整版流体力学考试试题（附答案）1、如图所示，有一直径=d 12cm 的圆柱体，其质量=m 5kg ，在力=F 100N 的作用下，当淹深=h 0.5m 时，处于静止状态，求测压管中水柱的高度H 。

解： 圆柱体底面上各点所受的表压力为：3.131844/12.014.3806.951004/22=⨯⨯+=+=d mg F p g π（Pa ）由测压管可得：)(h H g p g +=ρ则：84.05.0806.910003.13184=-⨯=-=h gp H gρ（m ）2、为测定90º弯头的局部阻力系数，在A 、B 两断面接测压管，流体由A 流至B 。

已知管径d =50 mm ，AB 段长度L AB = 0.8 m ，流量q = 15 m 3/h ，沿程阻力系数λ=0.0285，两测压管中的水柱高度差Δh = 20 mm ，已知水银的密度为13600kg/m 3，求弯头的局部阻力系数ξ。

解：)/(12.2405.0360015422s m d q v v v v B A =⨯⨯====ππ 对A 、B 列伯努利方程：f BB B A A A h gv z g P g v z g P +++=++2222水水ρρ 2211z gPz g P z g Pz g P B B A A +=++=+水水水水ρρρρf BA h gv z g P g v z g P +++=++∴22222211水水ρρ vv v B A == 又64.005.08.00285.0)1100013600(12.202.08.92)(2)2(222)(22222221212211=--⨯⨯⨯=-∆-∆=-=∴+=+=∆-∆=-+-=+-+=∴d l h h v g g v d l h v g gv g v d l h h h h gh g z z g P P z gP z gP h f f f λρρλξξλρρρρρξλ水汞水汞水水水又3、一变直径管段AB ，内径d A =0.2m ，d B =0.4m ，高度差Δh =1m ，压强表指示p A =40kPa ，p B =70kPa ，已知管中通过的流量q v =0.2m 3/s ，水的密度ρ=1000kg/m 3，试判断管中水流的方向。

课堂例题第一章例1 使水的体积减小0.1%及1%时，应增大压强各为多少？（K =2000MPa ）解： d V /V =-0.1%∆p =-2000×106×（-0.1%）=2×106Pa=2.0Mpad V /V = -1%∆p = -2000×106×（-1%）=20 Mpa例2 一平板距离另一固定平板0.5mm ，两板间充满液体，上板在每平方米上有2N 的力作用下以0.25m/s 的速度移动，求该流体的粘度？解： 第二章例1:测压装置。

A 中p e =2.45×104Pa, h=500mm,h 1=200mm, h 2=100mm, h 3=300mm, ρ2=800kg/m3,求B 中气体表压。

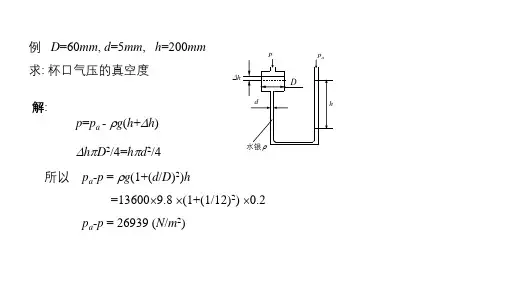
解：1、2、3、4四个等压面，1点忽略气体密度，得例2 求斜壁圆形闸门的总压力,已知d=0.5m,a=1m,α=60°解：由式 得总压力V dV dp K -=V dV K dp -=∴h U A F μ=0005.025.02μ=)(004.0s Pa ⋅=μ)(111h h g p p e e ++=ρ13111312)(gh h h g p gh p p e e e ρρρ-++=-=2213112223)(gh gh h h g p gh p p e e e ρρρρ+-++=+=332213113334)(gh gh gh h h g p gh p p e e e ρρρρρ-+-++=-=Pap p e Be 345384-==Ap A gh F ce c p ==ρ)(20834sin )2(2N d d a g F p =+=παρ例3：圆柱扇形闸门,已知H=5m,闸门宽B=10m,α=60°。

求曲面ab 上总压力解： 总压力大小和方向为第三章例1离心水泵吸水装置，d=200mm,q V =170m 3/h,泵入口前真空为330mmHg,如不计能量损失，求水泵的吸水高度。

水水银题1图1、如图所示，用多管水银测压计测水箱表面的压强。

图中高程的单位为m 。

试求水箱表面的相对压强。

（ 水银的密度3/13600m kg =ρ）2、如图所示，密度3920/kg m ρ=的油在管中流动。

用水银压差计测量长度3l m =的管流的压差，其读数为90h mm ∆=。

已知管径25dmm =，测得的油的流量434.510/Q m s -=⨯，试求油的运动粘性系数。

3、图示一密闭容器，上层为空气，中层为ρ=800kg/m 3的石油，下层为ρ=1200kg/m 3的甘油。

试求：当测压管中甘油表面高程为9.14m 时压力表G 的读数。

题型一：曲面上静水总压力的计算问题（注：千万注意方向，绘出压力体）1、AB 曲面为一圆柱形的四分之一，半径R=0.2m ，宽度（垂直纸面）B=0.8m ，水深H=1.2m ，液体密度3/850m kg =ρ，AB 曲面左侧受到液体压力。

求作用在AB 曲面上的水平分力和铅直分力。

（10分） 解：（1）水平分力：RB RH g A h P z c x ⋅-==)2(ργ…….(3分) N 1.14668.02.0)22.02.1(8.9850=⨯⨯-⨯⨯=，方向向右（2分）。

（2）铅直分力：绘如图所示的压力体，则B R R R H g V P z ⎥⎥⎦⎤⎢⎢⎣⎡+-==4)(2πργ……….（3分）1.15428.042.014.32.0)2.02.1(8.98502=⨯⎥⎥⎦⎤⎢⎢⎣⎡⨯+⨯-⨯⨯=，方向向下（2分）。

2．有一圆滚门，长度l=10m ，直径D=4.2m ，上游水深H1=4.2m ，下游水深H2=2.1m ，求作用于圆滚门上的水平和铅直分压力。

ldQhG BA空 气 石 油甘 油7.623.661.529.14m11解题思路：（1）水平分力：l H H p p p x )(21222121-=-=γ 方向水平向右。

（2）作压力体，如图，则l D Al V p z 4432πγγγ⨯=== 方向垂直向上。

第一章：绪论例1-1 200 ºC体积为的2.5m3水，当温度升至800ºC时，其体积增加多少？解： 200 ºC时：ρ1=998.23kg/m3 800CºC时：ρ2=971.83kg/m3即：则：例1-2使水的体积减小0.1%及1%时，应增大压强各为多少？（K=2000MPa）d V/V =-0.1%=-2000×106×（-0.1%）=2×106Pa=2.0MPad V /V = -1%= -2000×106×（-1%）=20 MPa例1-3输水管l=200m，直径d=400mm，作水压试验。

使管中压强达到55at后停止加压，经历1小时，管中压强降到50at。

如不计管道变形，问在上述情况下，经管道漏缝流出的水量平均每秒是多少？水的体积压缩率κ =4.83×10-10m2 /N 。

解水经管道漏缝泄出后，管中压强下降，于是水体膨胀，其膨胀的水体积水体膨胀量5.95 l 即为经管道漏缝流出的水量，这是在1小时内流出的。

设经管道漏缝平均每秒流出的水体积以Q 表示，则例1-4：试绘制平板间液体的流速分布图与切应力分布图。

设平板间的液体流动为层流，且流速按直线分布，如图1-3所示。

解：设液层分界面上的流速为u,则：切应力分布：图1-3上层下层：在液层分界面上：--流速分布：上层：下层：例1-5：一底面积为40 ×45cm2，高为1cm的木块，质量为5kg，沿着涂有润滑油的斜面向下作等速运动，如图1-4所示，已知木块运动速度u =1m/s，油层厚度d =1mm，由木块所带动的油层的运动速度呈直线分布，求油的粘度。

解：∵等速∴αs =0由牛顿定律：∑F s=mαs=0m gsinθ－τ·A=0（呈直线分布）图1-4∵ θ=tan-1(5/12)=22.62°例1-6: 直径10cm的圆盘，由轴带动在一平台上旋转，圆盘与平台间充有厚度δ=1.5mm的油膜相隔，当圆盘以n =50r/min旋转时，测得扭矩M =2.94×10-4 N·m。

典 型 例 题 1 基本概念及方程【1－1】底面积A ＝0.2m ×0.2m 的水容器，水面上有一块无重密封盖板，板上面放置一个重量为G 1＝3000N 的铁块，测得水深h ＝0.5m ，如图所示。

如果将铁块加重为G 2＝8000N ，试求盖板下降的高度Δh 。

【解】:利用体积弹性系数计算体积压缩率：E p v v //∆=∆ )/(00B p p np E +=p 为绝对压强。

当地大气压未知，用标准大气压Pa p 501001325.1⨯=代替。

Pa A G p p 51011076325.1/⨯=+=Pa A G p p 52021001325.3/⨯=+=因 01/p p 和 02/p p 不是很大，可选用其中任何一个，例如，选用02/p p 来计算体积弹性系数：Pa B p p np E 9020101299.2)/(⨯=+=在工程实际中，当压强不太高时，可取 Pa E 9101.2⨯=512104827.6/)(///-⨯=-=∆=∆=∆E p p E p v v h hm h h 55102413.310604827--⨯=⨯=∆【2－2】用如图所示的气压式液面计测量封闭油箱中液面高程h 。

打开阀门1，调整压缩空气的压强，使气泡开始在油箱中逸出，记下U 形水银压差计的读数Δh 1＝150mm ，然后关闭阀门1，打开阀门2，同样操作，测得Δh 2＝210mm 。

已知a ＝1m ，求深度h 及油的密度ρ。

【解】水银密度记为ρ1。

打开阀门1时，设压缩空气压强为p 1，考虑水银压差计两边液面的压差，以及油箱液面和排气口的压差，有同样，打开阀门2时，两式相减并化简得代入已知数据，得所以有2 基本概念及参数【1－3】测压管用玻璃管制成。

水的表面张力系数σ＝0.0728N/m ，接触角θ＝8º，如果要求毛细水柱高度不超过5mm ，玻璃管的内径应为多少？ 【解】由于因此【1－4】高速水流的压强很低，水容易汽化成气泡，对水工建筑物产生气蚀。

流体力学计算题及答案第二章例1：用复式水银压差计测量密封容器内水面的相对压强，如图所示。

已知：水面高程z 0=3m,压差计各水银面的高程分别为z 1=0.03m , z 2=0.18m , z 3=0.04m, z 4=0.20m, 水银密度3/13600m kg ρ='，水的密度3/1000m kg ρ= 。

试求水面的相对压强p 0。

解：ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2：用如图所示的倾斜微压计测量两条同高程水管的压差。

该微压计是一个水平倾角为θ的在xoz 坐标系中，自由表面1的方程：gr z 2220ω=对于容器边缘上的点，有：m L z m d r 4.015.02==== )/(67.1815.04.08.922220s rad r gz =⨯⨯==∴ω∵ωπ=260n /∴==⨯=n r 160260186721783ωππ..(/min)(2)当抛物面顶端碰到容器底部时，这时原容器中的水将被甩出一部分，液面为图中2所指。

在'''x o z 坐标系中：自由表面2的方程： gr z 2220ω'='当m H z m dr 5.0,15.02=='==时)/(87.2015.05.08.92222s rad r z g =⨯⨯='='ωmin)/(3.199287.20602602r ππωn =⨯='=∴这时，有：14214222ππd H d H h ⋅=-()mm Hh Hh H 2502222==∴=-∴例6：已知：一块平板宽为 B ，长为L,倾角θ，顶端与水面平齐。

求：总压力及作用点。

解：总压力：LB θL γA h γF c 2sin ⋅==压力中心D ：方法一：dA θy γy ydF dM sin ==3sin sin sin 322L BθγBdy y θγdA y θγM L A===⎰⎰DFy M = L F M yD32/==∴方法二：62212123LL BL L BL L A y J y y c cx c D +=+=+=例7：如图，已知一平板，长L,宽B,安装于斜壁面上，可绕A 转动。