理论力学第四章讲义
- 格式:pps
- 大小:596.50 KB
- 文档页数:24









CATALOG OF CHAPTER 4§4.1 SPACIAL ROTATIONAL FRAME OF REFERENCE§4.2 THE EFFECTS INDUCED BY THE EARTH’S ROTATIONCH4 ROTATIONAL FRAME OF REFERENCE §4.1 Spacial Rotational Frame ofReference(一)Kinematicsthe stationary frame of reference S:Setting up a stationary coordinate system o-ξηζ;the spacial rotational frame of reference S':Setting up a moving coordinate system o-xyz;⇳The origin is coincident with that of the stationarycoordinate system ,∴r r '= ozηξζxy P⇳The angular velocity is always through the originpoint O ;ωIn the stationary frame , the time derivative of anyphysical quantity isGG k dtdG j dt dG i dt dG z y x ⨯+++=ωˆˆˆ)ˆˆˆ(k G j G i G dtd dt G d z y x ++= the component expressionfor the vector Gthe moving framein the ozηξζxy PωG dtG d dt G d⨯+=ω*The first term :“the relative rate of change ”, which represents the variation with time relative to frame S ’;The second term :“the convected rate of change ”, which represents the variation with time due to the motion of the frame S 'itself.The expression can be written asozηξζxy PωThe velocity of any point P in space relative to thestationary framedt r d v =rdtr d ⨯+=ω*rv ⨯+'=ωThe acceleration of any point P in space relative to the stationary framedt v d a =vdtv d ⨯+=ω*Substituting the formula of velocity into it:)()(***r dtr d r dt r d dt d a ⨯+⨯+⨯+=ωωω)(***2*2r dtr d dt r d r dt d dt r d ⨯⨯+⨯+⨯+⨯+=ωωωωωcombinationdtr d r r dt d dt r d a**2*22)(⨯+⨯⨯+⨯+=⇒ωωωωωωωω⨯+=dt d dt d *dtd ω*=v r r a a '⨯+⨯⨯+⨯+'=⇒ ωωωω2)(relative accelerationconvected accelerationCoriolis’ acceleration)1.4.4(rotating with constant angular velocityv r r a a '⨯+⨯⨯+⨯+'= ωωωω2)(v R a a '⨯+-'=∴ ωω22orωR//R )()]([//2//R R R R +-+⋅=ωωω()RR R 2//2//ωωωω--=R R R 2//2//2ωωω--=R 2ω-=r r r2)()(ωωωωω-⋅=⨯⨯)2.4.4(the planar rotational frame of reference S '(such as a flat )ozηζxyS ' The origin is coincident with that of the stationary coordi-nate system:RotatING around the axis perpendicular to itself.A particle is moving on the flat:jy i x r ˆˆ+= r r '= kz ˆωω=P(二)Dynamics 1. Dynamical Equations()v m r m r m F a m '⨯-⨯⨯-⨯-='⇒ ωωωω2主①②③Multiplying the formula (4.4.1) by m :()v m r m r m a m a m '⨯+⨯⨯+⨯+'=⇒ ωωωω2v r r a a '⨯+⨯⨯+⨯+'= ωωωω2)(There are three kinds of inertial forces induced by therotation of the frame S ’.()v m r m r m r m F a m '⨯-+⋅-⨯-='⇒ ωωωωω22主①②③rm 2ω+:centrifugal inertia force:Coriolis forcev m '⨯-ω2v m R m F a m '⨯-+='⇒ ωω22主constant angular velocity v m R m a m a m '⨯+-'=⇒ ωω22v R a a '⨯+-'= ωω22over2. Relative Equilibrium()v m r m r m F a m '⨯-⨯⨯-⨯-=' ωωωω2主v m R m F a m '⨯-+=' ωω22主constant angular velocityA particle is in the state of equilibrium relative to thenon-inertial frame, then:0,0='='a v()0=⨯⨯-⨯-r m r m Fωωω主02=+R m Fω主⎩⎨⎧⇒constant angular velocity§4.2 THE EFFECTS INDUCED BY THE ERATH’S ROTATION (一)Centrifugal Inertia Force ωNSoTRm 2ω引F gm Assuming thata.The angular velocity is constant vector along the earth’s axis;b.A particle is at rest relative to the earth.2=+R m F ω主02=++⇒R m T F ω引Rm F g m 2ω+=⇒引Then :Due to the effect of the centrifugal inertia force. the gravity is the resultant force of the gravitational force and the centrifugal force.The latitude is higher, the gravity is bigger; at the poles the gravity is equal to the gravitational force.ωNSoTRm 2ω引F gm(二)Coriolis ForceAssuming thata.The angular velocity is a constant vector along the earth’s axis;the unit vectors kj i ˆ,ˆ,ˆ* Adhere to the earth’s surface* Point to south horizontally, east horizontally, and upwards vertically respectively ωNSi ˆjˆkˆW Eλki z x ˆˆωωω+=k i ˆsin ˆcos λωλω+-=kˆi ˆωλλωNSi ˆjˆkˆWEλ引主F F =k mg ˆ-=gm =Substituting them into the dynamical equations :b.The effects of the centrifugal inertia force is neglected :2≈R m ωc.Only the gravitational force amongthe initiative forces is considered;)ˆˆˆ()ˆsin ˆcos (2ˆk zj y i x k i m k mg ++⨯+---=λωλωv m R m F a m '⨯-+=' ωω22主Coriolis forceωNSi ˆjˆkˆWEλ⎪⎭⎪⎬⎫+-=+-==λωλλωλωcos 2)cos sin (2sin 2y m mg z m z x m y m y m x m Working out the formula above, it givesthe Northern Hemisphere :0sin ,0cos >>λλ0sin ,0cos <>λλthe Southern Hemisphere :)1.2.4(赤道附近空气因热上升,在高空向两极推进;两极地带空气因冷下降,在地面附近向赤道推进;→形成对流,称“贸易风”受科氏力的影响,原本南北向的气流向东西向偏转。
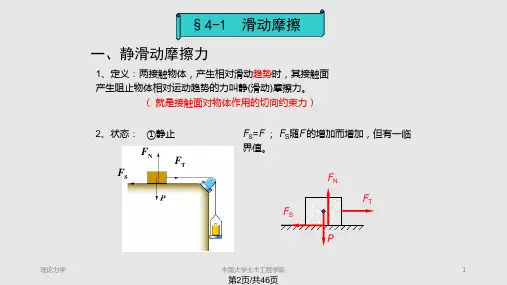
由动力学方程(4.2.1)用以上动力学方程解释科氏力的影响I. Trade Wind 贸易风南北向(x 轴)速度产生东西向(y 轴)的科氏力;ωNSW E热热冷冷由(4.2.1) 式,科氏力指向西方;河流:ωNSWEv '科F自北向南运动:0,0==>z y x 故:右岸的冲刷甚于左岸,比较陡峭。