理论力学第四章
- 格式:pptx
- 大小:1.81 MB
- 文档页数:45

理论力学第四章习题答案理论力学第四章习题答案在理论力学的学习过程中,习题是非常重要的一部分。
通过解答习题,我们可以巩固理论知识,加深对概念和原理的理解,并培养解决实际问题的能力。
本文将为大家提供理论力学第四章习题的详细答案,希望能够对大家的学习有所帮助。
1. 一个质点在力F作用下做直线运动,已知力的大小与时间的关系为F = kt,其中k为常数。
求质点的速度与时间的关系。
解答:根据牛顿第二定律F = ma,将力的大小与时间的关系代入,得到ma = kt。
由于质点做直线运动,所以速度的变化率等于加速度,即v = ∫a dt。
将上式代入,得到v = ∫(kt/m) dt = (k/m)∫t dt = (k/m)(t^2/2) + C。
其中C为积分常数。
因此,质点的速度与时间的关系为v = (k/m)(t^2/2) + C。
2. 一个质点在力F作用下做直线运动,已知力的大小与位置的关系为F = -kx,其中k为常数。
求质点的加速度与位置的关系。
解答:根据牛顿第二定律F = ma,将力的大小与位置的关系代入,得到ma = -kx。
由于质点做直线运动,所以加速度的变化率等于速度的变化率,即a =dv/dt。
将上式代入,得到dv/dt = -kx/m。
将变量分离,得到dv = (-kx/m) dt。
对两边同时积分,得到∫dv = ∫(-kx/m) dt。
积分后得到v = (-kx^2/2m) + C1,其中C1为积分常数。
再次对上式积分,得到∫v dx = ∫((-kx^2/2m) + C1) dx。
积分后得到x = (-kx^3/6m) + C1x + C2,其中C2为积分常数。
因此,质点的加速度与位置的关系为a = (-kx/m)。
3. 一个质点在势能函数U(x) = kx^2/2下做直线运动,已知质点的质量为m。
求质点的速度与位置的关系。
解答:根据势能函数U(x) = kx^2/2,可以求得力的大小与位置的关系为F = -dU(x)/dx = -kx。








第四章空间力系本章将研究空间力系的简化和平衡条件。
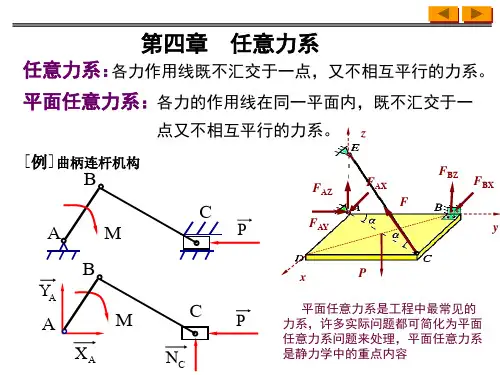
工程中常见物体所受各力的作用线并不都在同一平面内,而是空司分布的,例如车床主轴、起重设备、高压输电线塔和飞机的起落架等结构。
设计这些结构时,需用空间力系的平衡条件进行计算。
与平面力系一样,空间力系可以分为空间汇交力系、空司力偶系和空间任意力系来研究。
§4-1 空间汇交力系1.力在直角坐标轴上的投影和力沿直角坐标轴的分解若已知力F与正交坐标系Oxyz三轴间的夹角分别为α、β、γ,如图4-1所示,则力在三个轴上的投影等于力F的大小乘以与各轴夹角的余弦,即X=cosαY=cosβ (4-1)Z=cosγ当力与坐标轴Ox、Oy间的夹角不易确定时,可把力先投影到坐标平面Oxy上,得到力,然后再把这个力投影到x、y轴上。
在图4-2中,已知角γ和,则力在三个坐标轴上的投影分别为X=sinγcosY=sinγsin (4-2)Z=cosγ若以、、表示力F沿直角坐标轴x、y、z的正交分量,以i、j、k分别表示沿x、y、z坐标轴方向的单位矢量,如图4-3所示,则图4-2=++=X i+Y j+Z k (4-3)由此,力在坐标轴上的投影和力沿坐标轴的正交分矢量间的关系可表示为:=X i,=Y j,=Z k (4-4)如果己知力F在正交轴系Oxyz的三个投影,则力F的大小和方向余弦为=cos(,i)=cos(,j)= (4-5)cos(,k)=例4-1图4-4所示的圆柱斜齿轮,其上受啮合力的作用。
已知斜齿轮的齿倾角(螺旋角) β和压力角α,试求力沿x、y和z轴的分力。
解:先将力向z轴和Oxy平面投影,得Z=-sinα=cosα再将力向x、y轴投影,得X=-sinβ=-cosαsinβY=-cosβ=-cosαcosβ则沿各轴的分力为=-cosαsinβi,=-cosαcosβj,=-sinαk式中i、j、k为沿x、y、z轴的单位矢量,负号表明各分力与轴的正向相反。