第2课时 与坡度、方位角有关的应用问题
- 格式:ppt
- 大小:1.23 MB
- 文档页数:8


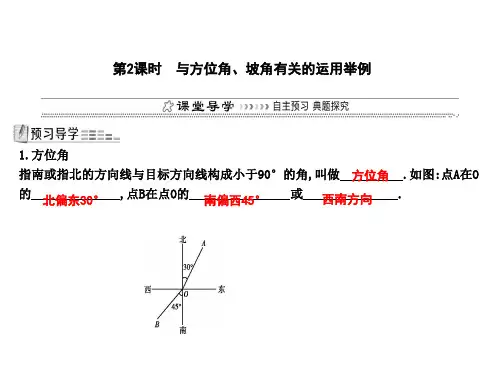

第2课时 与方位角、坡角有关的运用举例 1.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,如图,从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么B处船与小岛M的距离为( B )
(A)20海里 (B)20海里 (C)15海里 (D)20海里 2.说出下列各角的方位. $
∠NOA是 北偏东55° ,? ∠BOS是 南偏东30° ,? ∠COS是 南偏西35° ,? ∠NOD是 西北方向 .? 3.某人沿着坡度为1∶的山坡向上走50 m,这时他离水平地面 25 m.? 4.在倾斜角为30°的斜坡上植树,若要求两棵树的水平距离为6 m,则斜坡上相邻两树的坡面距离为 4 m.? ! 5.一船上午9点位于灯塔A的东北方向,在与灯塔A相距64海里的B
港出发,向正西航行,到10时30分时恰好在灯塔的正北的C处,则此船
的速度为 海里/时.? 6.如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tan α的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O,B,C,A,P在同一平面内,求山坡的坡度.(参考数据 sin °≈,tan °≈,sin 37°≈,tan 37° ≈
解:如图,过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形. 在Rt△PBD中,∵∠BDP=90°,∠BPD=°, ∴BD=PD·tan∠BPD=PD·tan °; ~ 在Rt△CPD中,∵∠CDP=90°,∠CPD=37°,
∴CD=PD·tan∠CPD=PD·tan 37°; ∵CD-BD=BC,
∴PD·tan 37°-PD·tan °=80, ∴解得PD=320, ∴BD=PD·tan °≈320×=160, ∵OB=220, @ ∴PE=OD=OB-BD=60,

第2课时与方向角、坡角有关的解直角三角形应用题1.能运用解直角三角形解决航行问题.2.能运用解直角三角形解决斜坡问题.3.理解坡度i=坡面的铅直高度坡面的水平宽度=tan坡角.阅读教材P76,自学“例5”和“归纳”,掌握利用解直角三角形的知识解决方位角的实际问题.自学反馈独立完成后小组内交流①利用解直角三角形的知识解决实际问题的一般过程是:a.将实际问题抽象为数学问题,画出图形,转化为解的问题;b.根据条件的特点,适当地选用去解直角三角形;c.得到数学问题的答案;d.最后得到问题的答案.②已知外婆家在小明家的正东方,学校在外婆家的北偏西40°,外婆家到学校与小明家到学校的距离相等,则学校在小明家的方向.活动1 小组讨论例1如图,海中一小岛A,该岛四周10海里内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处,之后,货轮继续向东航行,你认为货轮向东航行的途中会有触礁的危险吗?解:如图,过点A作AD⊥BC交BC的延长线于点D.在Rt△ABD中,∵tan∠BAD=BD AD,∴BD=AD·tan55°.在Rt△ACD中,∵tan∠CAD=CD AD,∴CD=AD·tan25°.∵BD=BC+CD,∴AD·tan55°=20+AD·tan25°.∴AD=205525tan tan︒-︒≈20.79>10.∴轮船继续向东行驶,不会遇到触礁危险.应先求出点A距BC的最近距离,若大于10则无危险,若小于或等于10则有危险. 活动2 跟踪训练(独立完成后展示学习成果)如图所示,A、B两城市相距100 km.现计划在这两座城市间修筑一条高速公路(即线段AB).经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50 km为半径的圆形区域内,请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:3≈1.732,2≈1.414)解这类题目时,首先弄清楚方位角的含义;其次是通过作垂线构造直角三角形,将问题转化为解直角三角形.阅读教材P77练习2,自学关于坡度的问题,弄懂坡度与坡角的实际意义,理解铅垂高度与水平宽度的实际意义.自学反馈独立完成后小组内交流①拦水大坝的横断面为梯形,其中坡度i是指与的比,这个值与坡角的值相等.②坡度i一般写成1∶m的形式,坡度i的值越大,表明坡角越,即坡越陡.③已知一大坝的坡角为45°,则它的坡度i的值等于.通过书上的例题掌握“化整为零,积零为整”“化曲为直,以直代曲”的方法来解决一些实际和数学问题.活动1 小组讨论例2 如图,水库大坝的横断面是梯形,坝顶宽6 m,坝高23 m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i′=1∶2.5,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长.(精确到0.1 m)解:如图,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,在Rt△ABE和Rt△CDF中,BEAE=13,CFFD=12.5,∴AE=3BE=3×23=69(m),FD=2.5CF=2.5×23=57.5(m). ∴AD=AE+EF+FD=69+6+57.5=132.5(m).∵斜坡的坡度i=13≈0.333 3,∴BEAE=0.333 3,即tanα=0.333 3.∴α≈18°26′.∵BEAB=sinα,∴AB=BEsin≈230.3162≈72.7(m).答:斜坡AB的坡角α约为18°26′,坝底宽AD为132.5 m,斜坡AB的长约为72.7 m.这类问题,首先要弄清楚坡度、坡角等名词的含义;其次,要将梯形予以分割,分割成特殊的四边形和直角三角形.活动2 跟踪训练如图,已知在山脚的C处测得山顶A的仰角为45°,沿着坡角为30°的斜坡前进400 m到点D 处,测得点A的仰角为60°,求出AB的高度.第2小题,要过点D作AB和BC的垂线,构造两个直角三角形和一个矩形,将AB 分成两段来求.活动3 课堂小结1.本节学习的数学知识:利用解直角三角形的知识解决实际问题.2.本节学习的数学方法:数形结合的思想和数学建模的思想.教学至此,敬请使用学案当堂训练部分.【预习导学1】自学反馈①直角三角形锐角三角函数等实际②北偏东40°【合作探究1】活动2 跟踪训练过点P作PD垂直AB于点D,可求得PD≈63.4 m>50 m,所以计划修筑的这条高速公路不会穿越保护区.【预习导学2】自学反馈①坡面的铅垂高度它的水平宽度正切②大③1【合作探究2】活动2 跟踪训练AB=(2003+200)m。