用脉冲响应求传递函数

脉冲响应与传递函数的关系脉冲响应和传递函数是信号处理领域中两个重要的概念。

它们之间存在着密切的关系，相互之间可以进行转换和推导。

本文将介绍脉冲响应和传递函数的基本概念，并探讨它们之间的关系。

我们来了解一下脉冲响应的概念。

脉冲响应是指系统对单位脉冲信号的响应。

单位脉冲信号是一个持续时间很短的信号，幅度为1，其它时间段内幅度为0。

当单位脉冲信号经过系统时，系统会产生一个响应信号，这个响应信号就是系统的脉冲响应。

脉冲响应可以描述系统对任意输入信号的响应情况。

脉冲响应通常用h(t)表示，其中t表示时间。

传递函数是描述系统输入输出关系的函数。

它是输入信号的拉普拉斯变换和输出信号的拉普拉斯变换之比。

传递函数通常用H(s)表示，其中s是复变量。

传递函数可以反映系统对不同频率信号的响应特性。

通过传递函数，我们可以了解系统的频率响应、相位响应等信息。

脉冲响应和传递函数之间的关系可以通过拉普拉斯变换来推导。

假设系统的传递函数为H(s)，脉冲响应为h(t)，那么它们之间的关系可以表示为：H(s) = L{h(t)}其中L表示拉普拉斯变换。

这个公式表明传递函数是脉冲响应的拉普拉斯变换。

通过传递函数，我们可以得到系统的脉冲响应，从而了解系统对不同输入信号的响应情况。

反过来，如果已知系统的传递函数H(s)，我们可以通过拉普拉斯反变换来求得系统的脉冲响应h(t)。

这样，我们就可以通过传递函数来确定系统的脉冲响应。

脉冲响应和传递函数在信号处理中具有广泛的应用。

在滤波器设计中，我们可以通过传递函数来设计滤波器的频率响应，从而实现对输入信号的滤波。

在系统建模和控制系统设计中，我们可以通过传递函数来分析和设计系统的稳定性和性能。

总结起来，脉冲响应和传递函数是信号处理领域中重要的概念。

它们之间存在着密切的关系，相互之间可以进行转换和推导。

通过传递函数，我们可以了解系统对不同频率信号的响应特性；通过脉冲响应，我们可以了解系统对任意输入信号的响应情况。

3-2 脉冲响应函数对于线性定常系统，其传递函数)(s Φ为)()()(s R s C s =Φ式中)(s R 是输入量的拉氏变换式，)(s C 是输出量的拉氏变换式。

系统输出可以写成)(s Φ与)(s R 的乘积，即)()()(s R s s C Φ= （3-1） 下面讨论，当初始条件等于零时，系统对单位脉冲输入量的响应。

因为单位脉冲函数的拉氏变换等于1，所以系统输出量的拉氏变换恰恰是它的传递函数，即)()(s s C Φ= （3-2） 由方程(3-2)可见，输出量的拉氏反变换就是系统的脉冲响应函数，用)(t k 表示，即1()[()]k t s -=Φ脉冲响应函数)(t k ，是在初始条件等于零的情况下，线性系统对单位脉冲输入信号的响应。

可见，线性定常系统的传递函数与脉冲响应函数，就系统动态特性来说，二者所包含的信息是相同的。

所以，如果以脉冲函数作为系统的输入量，并测出系统的响应，就可以获得有关系统动态特性的全部信息。

在具体实践中，与系统的时间常数相比，持续时间短得很多的脉动输入信号就可以看成是脉冲信号。

设脉冲输入信号的幅度为11t ，宽度为1t ，现研究一阶系统对这种脉动信号的响应。

如果输入脉动信号的持续时间t )0(1t t <<，与系统的时间常数T 相比足够小，那么系统的响应将近似于单位脉冲响应。

为了确定1t 是否足够小，可以用幅度为12t ，持续时间(宽度)为21t 的脉动输入信号来进行试验。

如果系统对幅度为11t ，宽度为1t 的脉动输入信号的响应，与系统对幅度为12t ，宽度为21t 的脉动输入信号的响应相比，两者基本上相同，那么1t 就可以认为是足够小了。

图3-3(a)表示一阶系统脉动输入信号的响应曲线；图3-3(c)表示一阶系统对脉冲输入信号的响应曲线。

应当指出，如果脉动输入信号T t 1.01<(图3-3(b)所示)，则系统的响应将非常接近于系统对单位脉冲信号的响应。

传递函数辨识(2)：脉冲响应两点法和三点法丁锋;徐玲;刘喜梅【摘要】本工作利用系统的脉冲响应观测数据,提出了辨识一阶系统、二阶系统传递函数参数的两点法、三点法等,以及确定传递函数参数的差分方程法和面积法.所提出的方法能够避免直接求解超越方程,且原理简单,实现方便.%By means of the system impulse response data,this paper presents two-point methods and three-point methods for identifying the parameters of first-order systems and second-order systems,which are described by transfer functions,and presents the difference equation method and the area method for identifying transfer functions.The proposed algebraic methods of determining the parameters of the transfer functions have simple mechanism and ease to understand,and avoid solving some transcendental equations.【期刊名称】《青岛科技大学学报（自然科学版）》【年(卷),期】2018(039)002【总页数】15页(P1-15)【关键词】传递函数;参数估计;系统辨识;阶跃响应;脉冲响应【作者】丁锋;徐玲;刘喜梅【作者单位】青岛科技大学自动化与电子工程学院,山东青岛266042;江南大学物联网工程学院,江苏无锡214122;江南大学物联网工程学院,江苏无锡214122;青岛科技大学自动化与电子工程学院,山东青岛266042【正文语种】中文【中图分类】TP273传递函数是一种参数模型。

简述脉冲响应函数和传递函数的关系
脉冲响应函数和传递函数是控制系统中两个重要的概念。

它们之间有着密切的关系，本文将从两者的定义、性质和联系三个方面进行阐述。

脉冲响应函数是指系统对单位脉冲信号的响应函数，通常用h(t)表示。

传递函数是指系统的输入输出关系，通常用H(s)表示。

在时域中，脉冲响应函数和传递函数之间的关系可以用卷积定理表示为： h(t) = L^{-1}[H(s)]
其中，L^{-1}表示拉普拉斯反变换。

这个公式表明，脉冲响应函数是传递函数的拉普拉斯反变换，而传递函数是脉冲响应函数的拉普拉斯变换。

因此，脉冲响应函数和传递函数是密切相关的。

脉冲响应函数和传递函数都具有一些重要的性质。

脉冲响应函数具有线性性、时不变性和因果性等特点。

传递函数具有线性性、时不变性、稳定性和因果性等特点。

这些性质保证了系统的可靠性和稳定性。

脉冲响应函数和传递函数之间的联系可以用于系统的分析和设计。

通过求解传递函数，可以得到系统的频率响应和稳定性等信息。

而通过求解脉冲响应函数，可以得到系统的时域响应和阶跃响应等信息。

这些信息对于系统的控制和优化具有重要的意义。

脉冲响应函数和传递函数是控制系统中两个重要的概念，它们之间有着密切的关系。

脉冲响应函数是传递函数的拉普拉斯反变换，而传递函数是脉冲响应函数的拉普拉斯变换。

通过求解脉冲响应函数和传递函数，可以得到系统的时域响应和频域响应等信息，这对于系统的分析和设计具有重要的意义。

传递函数单位脉冲响应单位脉冲响应是指系统对于单位脉冲信号的响应情况。

在信号处理和系统控制中，单位脉冲响应是一种重要的概念，它能够描述系统对于输入信号的反应情况，对于系统的特性分析和设计具有重要的意义。

在信号处理和系统控制领域中，我们经常遇到各种各样的信号，如正弦信号、方波信号、脉冲信号等。

这些信号在系统中传递时，会受到系统自身的特性影响，从而产生不同的响应。

单位脉冲响应就是一种用来描述系统对于单位脉冲信号的响应情况的方法。

单位脉冲信号是一种理想化的信号，其幅度为1，宽度为0，持续时间为无穷小。

在数学上，单位脉冲信号可以用冲激函数来表示，通常用δ(t)表示。

单位脉冲信号在时间域上的图像是一个脉冲，幅度为1，宽度为无穷小。

在系统分析和设计中，我们常常需要知道系统对于单位脉冲信号的响应情况。

这是因为单位脉冲信号具有特殊的性质，它包含了所有频率的正弦信号的线性组合。

通过对系统的单位脉冲响应进行分析，我们可以了解系统在不同频率下的响应情况，从而判断系统的稳定性和性能。

单位脉冲响应可以通过系统的冲激响应函数来表示，通常用h(t)表示。

冲激响应函数描述了系统对于单位脉冲信号的响应情况。

对于线性时不变系统，单位脉冲响应和冲激响应函数是等价的。

单位脉冲响应可以通过实验或数学计算来获取。

在实验中，我们可以输入单位脉冲信号到系统中，然后测量系统的输出信号，通过对输入输出信号进行比较，可以得到系统的单位脉冲响应。

在数学计算中，我们可以通过系统的微分方程或差分方程来求解单位脉冲响应。

单位脉冲响应具有一些重要的性质。

首先，单位脉冲响应是系统的固有属性，不依赖于输入信号。

这意味着，只要系统的结构不变，单位脉冲响应就不会改变。

其次，单位脉冲响应可以用来描述系统的时域特性和频域特性。

通过对单位脉冲响应进行傅里叶变换，可以得到系统的频率响应函数，从而了解系统在不同频率下的响应情况。

单位脉冲响应在信号处理和系统控制中具有广泛的应用。

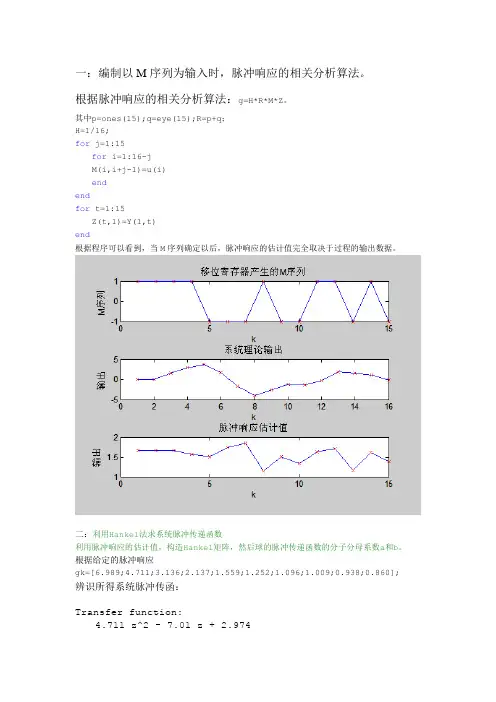
一：编制以M序列为输入时，脉冲响应的相关分析算法。

根据脉冲响应的相关分析算法：g=H*R*M*Z。

其中p=ones(15);q=eye(15);R=p+q；H=1/16;for j=1:15for i=1:16-jM(i,i+j-1)=u(i)endendfor t=1:15Z(t,1)=Y(1,t)end根据程序可以看到，当M序列确定以后，脉冲响应的估计值完全取决于过程的输出数据。

二：利用Hankel法求系统脉冲传递函数利用脉冲响应的估计值，构造Hankel矩阵，然后球的脉冲传递函数的分子分母系数a和b。

根据给定的脉冲响应gk=[6.989;4.711;3.136;2.137;1.559;1.252;1.096;1.009;0.938;0.860]; 辨识所得系统脉冲传函：Transfer function:4.711 z^2 - 7.01 z + 2.974----------------------------------z^3 - 2.154 z^2 + 1.611 z - 0.4266Sampling time: 0.1三：差分方程法求系统的传递函数由脉冲响应构建线性方程组矩阵，由Aa=B，确定待定系数a，随后生成关于X的特征多项式，求出x的n个解，得到传递函数的极点s，构造c的系数矩阵，求出c.便可确定系统传递函数。

根据所给脉冲响应：gk=[0;0.196;0.443;0.624;0.748;0.831];辨识所得系统传函：Transfer function:8.327e-017 s^2 - 0.01701 s + 0.8613------------------------------------s^3 + 2.607 s^2 + 0.8313 s + 0.01011四：加权最小二乘算法系统的输入信号为一个周期的M序列，z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)用理想的输出值作为观测值，给样本矩阵HL和ZL赋值，加权矩阵取单位阵I，则c=c2*c3，其中c1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c简称最小二乘估计值。

如何求传递函数传递函数是系统理论中非常重要的概念，它描述了信号在线性时不变系统中的传递过程。

在控制系统、信号处理等领域中，传递函数作为系统的数学模型，被广泛应用于系统分析与设计中。

那么，如何求传递函数呢？我们需要了解传递函数的定义。

传递函数是输入信号与输出信号的关系函数，通常用H(s)表示，其中s是复变量。

传递函数描述了系统对输入信号的响应过程，可以通过对系统的输入输出进行分析求得。

下面我们将介绍两种常见的求传递函数的方法。

一、脉冲响应法脉冲响应法是一种常用的求传递函数的方法。

它的基本思想是通过对系统输入一个单位脉冲信号，然后观察系统的输出响应，从而得到传递函数。

具体步骤如下：1. 将系统的输入信号设置为单位脉冲信号δ(t)，其中δ(t)表示单位冲激函数。

2. 记录系统的输出响应h(t)，即系统对单位脉冲信号的响应。

3. 对记录的输出响应进行傅里叶变换，得到系统的频率响应H(jω)，其中ω是频率变量。

4. 将频率响应H(jω)除以单位脉冲信号的傅里叶变换F(jω)=1，即可得到传递函数H(jω)。

通过脉冲响应法求得的传递函数是系统的拉普拉斯变换形式，可以直接用于系统分析与设计。

二、频率响应法频率响应法是另一种常用的求传递函数的方法。

它的基本思想是通过对系统输入一个正弦信号，然后观察系统的输出响应，从而得到传递函数。

具体步骤如下：1. 将系统的输入信号设置为正弦信号x(t)=Acos(ωt)，其中A是振幅，ω是角频率。

2. 记录系统的输出响应y(t)，即系统对正弦信号的响应。

3. 对记录的输入信号和输出响应进行傅里叶变换，得到输入信号的频率谱X(jω)和输出响应的频率谱Y(jω)。

4. 将输出响应的频率谱Y(jω)除以输入信号的频率谱X(jω)，即可得到传递函数H(jω)=Y(jω)/X(jω)。

通过频率响应法求得的传递函数是系统的频域形式，可以用于频率特性分析和滤波器设计等应用。

需要注意的是，在实际应用中，由于系统的输入和输出通常是连续信号，所以需要进行傅里叶变换将其转换为频域信号。

第三章3－3 已知各系统的脉冲响应，试求系统的闭环传递函数()s Φ：()()1.25(1)()0.0125;(2)()510sin 445;(3)()0.11t t k t e k t t t k t e --==++=-解答： （1） []0.0125()() 1.25s L k t s Φ==+（2）[])222223222()()5sin 4cos 425452442142511616116s L k t L t t t s s s s s s s s ⎡⎤Φ==++⎢⎥⎣⎦⎫=++⎪++⎭⎛⎫+++ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭（3）[]()111()()0.1110313s L k t s s s s ⎡⎤⎢⎥Φ==-=⎢⎥+⎢⎥+⎣⎦ 3-4 已知二阶系统的单位阶跃响应为)6.1sin(5.1210)(1.532.1︒-+-=t t h et试求系统的超调量σ%，峰值时间tp和调节时间ts.解答：因为0<ξ<1，所以系统是欠阻尼状态。

阻尼比ξ=cos(1.53︒)=，自然频率26.0/2.1==w n，阻尼振荡频率wd=6.16.01212=-⨯=-=ξw w n d 1． 峰值时间tp的计算96.16.1===ππwt dp2． 调节时间ts的计算9.226.05.35.3=⨯==w t ns ξ3． 超调量σ%的计算%48.9%1006.0%100%221/6.01/=⨯=⨯=-⨯---eeππξξσ3-5设单位反馈系统的开环传递函数为)6.0(14.0)(++=s s s s G ，试求系统在单位阶跃输入下的动态性能。

解答：方法一：根据比例-微分一节推导出的公式)135(6.014.0)12/()1()(+⨯⨯+=++=s s s s s s K s G w T n d ξ1)5.2(4.0114.0)6.0(14.01)6.0(14.0)2()(1)()(22222+++=+++=+++++=+++=+=s s s s s s s s s s s zs z S G s G s s s w w s w nn dn ξφ)1()](1[12)1sin(1)(222222ξξξξξξξπψξddnddndnn ddn tarctg z arctg z r t w r t h www w zw e n d -+--+-=-+-=ψ+-+=-把z=1/Td=,1=wn,5.0=ξd代入可得)3.8323sin(5.005.11)7.9623sin(5.005.11)( ---=--+=t e t t e t t h峰值时间的计算0472.1)1(2=-=ξξβdddarctg ，-1.6877=ψ158.312=--=ξβψdndpwt超调量得计算%65.21%10011%22=⨯--=-ξξξσddetrpd调节时间得计算29.6)ln(21ln )2ln(2131222=--+-+=-ww w z t ndn n d sd z ξξξ方法二：根据基本定义来求解闭环传递函数为114.0)6.0(14.01)6.0(14.0)(1)()(2+++=+++++=+=s s s s s s s s S G s G s s φ当输入为单位阶跃函数时 )232()21(21.0)232()21(2)21(116.01)1(14.0)(22++-++++-+=++--+=+++=s s s s s s s s s s s C s s 得单位阶跃响应)23sin(1.0)23cos(1)(2121t t t h e et --⨯--=)3.8423sin(121 +-=-t et )0(≥t 1． 峰值时间tp的计算 对h(t)求导并令其等于零得023)23cos()23sin(3.843.842121=⨯+-+︒-︒-t e t epp t t p p 3)23tan(3.84=+︒t p t p = 2. 超调量σ%的计算 %100)()()(%⨯∞∞-=h h h t p σ=%3. 调节时间ts得计算05.0)84.523sin(21≤-⨯-t est s5.33=t s3-6.已知控制系统的单位阶跃响应为6010()10.2 1.2t t h t e e --=+- ，试确定系统的阻尼比ζ和自然频率n ω。

简述脉冲响应函数和传递函数的关系
脉冲响应函数和传递函数在信号系统中经常用到。

当需要分析和设计系统的时候，我们需要了解这两个函数的关系，以便更好地控制和优化系统的性能。

脉冲响应函数是指系统在输入一个单位脉冲时，响应的输出信号。

它是描述系统特性的一种函数，可以反映系统对瞬态输入信号的响应。

在时间域中，脉冲响应函数是系统零状态响应的拉普拉斯变换。

因此，如果知道了脉冲响应函数，就能够求出任意输入信号的响应。

传递函数描述了系统的输入和输出之间的关系。

它是输入和输出之间的比值或者函数表达式，通常是在复频域中表示的。

传递函数是一个重要的概念，因为它可以用来确定系统的稳态和瞬态响应。

系统的传递函数和脉冲响应函数之间存在密切的联系。

事实上，传递函数可以通过系统的脉冲响应函数求得。

具体地说，需要进行拉普拉斯变换，将脉冲响应函数转换到复频域中，并对其进行数学操作，就可以得到系统的传递函数。

一般情况下，当系统的输入是个时间函数时，它的输出也是时间函数。

然而，当系统的传递函数是已知的时候，系统的输出信号可以直接从给定的输入信号计算出来。

这是因为给定的输入信号可以分解成一系列单位脉冲信号的加权和，而这些单位脉冲信号的响应就是脉冲响应函数。

换句话说，如果给定的输入信号为f(t)，那么输出信号y(t)就可以表示为：
y(t) = f(t) * h(t)
其中，“*”表示卷积，h(t)表示系统的脉冲响应函数。

matlab求脉冲传递函数
脉冲传递函数是描述线性时不变系统的频域特性的函数。

在MATLAB中，可以使用不同的方法来求脉冲传递函数。

以下是一种常见的方法：
首先，假设你有系统的传递函数H(s)，可以通过MATLAB的控制系统工具箱来求取脉冲传递函数。

假设传递函数为H(s)，可以使用以下命令来求取脉冲传递函数：
matlab.
impulse(H);
这将绘制系统的脉冲响应，并且可以从图形中获得脉冲传递函数的信息。

另一种方法是使用MATLAB的符号计算工具箱来求取脉冲传递函数。

首先，定义传递函数H(s)作为符号变量，然后使用laplace函数将其转换为时域表达式。

接着，使用ilaplace函数将时域表达式转换为脉冲传递函数。

下面是一个示例：
matlab.
syms s t.
H = (s+1)/(s^2+3s+2); % 举例传递函数。

h = ilaplace(H, s, t);
这将给出传递函数H(s)对应的脉冲传递函数h(t)的表达式。

除了这些方法，还有其他一些方法可以用来求取脉冲传递函数，具体取决于系统的特性和所需精度。

在实际应用中，还可以使用数
字信号处理工具箱中的函数来计算离散系统的脉冲传递函数。

总之，MATLAB提供了多种方法来求取脉冲传递函数，可以根据
具体情况选择合适的方法来进行计算。