K型相似练习题

四川省自贡市成考专升本2021-2022学年生态学基础模拟练习题三附答案学校:________ 班级:________ 姓名:________ 考号:________一、单选题(30题)1. 自然界中某个种群数量突然发生变化，必然牵动整个食物网，首先反映在( )。

A.其数量上B.食物链上C.营养级上D.消费者身上2. 下面四种生物属于K型生长的是( )。

A.苍蝇B.大象C.稗草D.盐虾3.腔肠动物附着在寄居蟹背上，当寄居蟹在海底爬行时，扩大了腔肠动物的觅食范围，同时，腔肠动物的刺细胞又对蟹起着伪装和保护作用。

寄居蟹和腔肠动物的这种关系为( )。

A.互利共生B.偏利共生C.原始协作D.负相互作用4.A.种群初始数量B.环境容量C.种群增长率D.增长时间5.种群平衡是指（）A．种群的出生率和死亡率均为零B、种群数量在较长时期内维持在几乎同一水平C、种群迁入和迁出相等D、种群的出生率和死亡率相等6.与K对策生物相比，r对策生物一般( )。

A.出生率高、寿命较短B.生率低、寿命长C.出生率低、寿命较短D.出生率高、寿命长7.下列范围不属于生物圈的是（）。

A.大气圈的上层B.全部水圈C.岩石的上层D.大气圈的下层8.景观生态学研究的对象是（）。

A.种群B.群落C.生态系统D.景观9. 只有在环境资源分布均匀、种群中个体间没有彼此吸引或排斥的情况下，种群的内分布型才会出现（）A.随机型B.均匀型C.成群型D.聚集型10. 从纯生态学角度讲，人类( )最为经济。

A.肉食B.素食C.杂食D.以上三种饮食方式差不多11.生物对高温适应的特点是( )。

A.降低细胞含水量，增加可溶性糖B.降低细胞含水量，减少可溶性糖C.增加细胞含水量，增加可溶性糖D.增加细胞含水量，减少可溶性糖12. 泛群系是( )群落分类的最大单位。

A.英美学派B.法瑞学派C.北欧学派D.苏联学派13. 种群中的某些个体身体表面的颜色可以随着环境的颜色而改变，以避免被天敌发现捕杀，又不易被猎物察觉，使之获得的食物充足，这样的个体在种群中的竞争能力强，会有更高的存活率并能繁殖更多的后代。

《图形的相似》拔高练习一、选择题（本大题共5小题，共25.0分）1．（5分）如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（）A．B．C．D．2．（5分）已知线段a＝3，b＝4，则a、b的比例中项为（）A．3.5B．12C．2D．±3．（5分）下列四条线段中，不能成比例的是（）A．a＝4，b＝8，c＝5，d＝10B．a＝2，b＝2，c＝，d＝5 C．a＝1，b＝2，c＝3，d＝4D．a＝1，b＝2，c＝2，d＝44．（5分）下列四组线段中，不成比例线段的是（）A．2cm，5cm，10cm，25cm B．4cm，7cm，4cm，7cmC．2cm，cm，cm，4cm D．cm，cm，2cm，5cm 5．（5分）下列a、b、c、d四条线段，成比例线段的是（）A．a＝12，b＝4，c＝5，d＝12B．a＝15，b＝3，c＝5，d＝1C．a＝13，b＝2，c＝8，d＝12D．a＝5，b＝0.02，c＝0.7，d＝0.3二、填空题（本大题共5小题，共25.0分）6．（5分）如图，AB∥CD∥EF，如果AC＝2，AE＝5，DF＝3.6，那么BD＝．7．（5分）已知线段a，b，c满足＝＝，且a+2b+c＝26，则a＝，b＝，c＝．8．（5分）若，则﹣的值是．9．（5分）如图，已知l1∥l2∥l3，若＝，EF＝4，则DE＝．10．（5分）如图，AE、BD交于点C，AB∥DE，若AC＝4，BC＝2，DC＝1，则EC＝．三、解答题（本大题共5小题，共50.0分）11．（10分）已知＝＝，求的值．12．（10分）如图，在平行四边形ABCD中，点E为边BC上一点，联结AE并延长交DC的延长线于点M，交BD于点G，过点G作GF∥BC交DC于点F，＝．（1）若BD＝20，求BG的长；（2）求的值．13．（10分）如图，已知点D、E分别在△ABC的边BA、CA的延长线上，且AE ＝3，AC＝6，AD＝2，AB＝4．（1）求证：DE∥BC；（2）若BC＝5，求ED的长．14．（10分）黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值．如图1，我们已经学过，点C将线段AB分成两部分，如果AC：AB＝BC：AC，那么称点C为线段AB的黄金分割点．如图2，△ABC中，AB＝AC ＝1，∠A＝36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．15．（10分）已知＝＝＝＝k，求k值．《图形的相似》拔高练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（）A．B．C．D．【分析】根据平行线分线段成比例定理进行判断即可．【解答】解：A、由AB∥CD∥EF，则，所以A选项的结论正确；B、由AB∥CD∥EF，则，所以B选项的结论正确；C、由AB∥CD∥EF，则，所以C选项的结论正确；D、由AB∥CD∥EF，则，所以D选项的结论错误；故选：D．【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．2．（5分）已知线段a＝3，b＝4，则a、b的比例中项为（）A．3.5B．12C．2D．±【分析】根据比例中项的定义列方程求解即可．【解答】解：∵设线段c为a，b的比例中项，∴c2＝ab，∵线段a＝3，b＝4，∴c2＝12，∴c＝2，c＝﹣2（舍去）．故选：C．【点评】本题考查了比例线段，熟记比例中项的定义是解题的关键，要注意线段的长度是正数．3．（5分）下列四条线段中，不能成比例的是（）A．a＝4，b＝8，c＝5，d＝10B．a＝2，b＝2，c＝，d＝5 C．a＝1，b＝2，c＝3，d＝4D．a＝1，b＝2，c＝2，d＝4【分析】根据比例线段的概念，让最小的和最大的相乘，另外两条相乘，看它们的积是否相等即可得出答案．【解答】解：A、4×10＝5×8，能成比例；B、2×5＝2×，能成比例；C、1×4≠2×3，不能成比例；D、1×4＝2×2，能成比例．故选：C．【点评】此题考查了比例线段，理解成比例线段的概念，注意在线段两两相乘的时候，要让最小的和最大的相乘，另外两条相乘，看它们的积是否相等进行判断．4．（5分）下列四组线段中，不成比例线段的是（）A．2cm，5cm，10cm，25cm B．4cm，7cm，4cm，7cmC．2cm，cm，cm，4cm D．cm，cm，2cm，5cm 【分析】根据比例线段的概念，让最小的和最大的相乘，另外两条相乘，看它们的积是否相等即可得出答案．【解答】解：A．2×25＝5×10，四组线段中能成比例，不符合题意；B．4×7＝4×7，四组线段中能成比例，不符合题意；C．×4≠×2，四组线段不能成比例，符合题意；D．×5＝×2，四组线段中能成比例，不符合题意；故选：C．【点评】此题考查了比例线段，理解成比例线段的概念，注意在线段两两相乘的时候，要让最小的和最大的相乘，另外两条相乘，看它们的积是否相等进行判断．5．（5分）下列a、b、c、d四条线段，成比例线段的是（）A．a＝12，b＝4，c＝5，d＝12B．a＝15，b＝3，c＝5，d＝1C．a＝13，b＝2，c＝8，d＝12D．a＝5，b＝0.02，c＝0.7，d＝0.3【分析】根据比例线段的概念：如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．【解答】解：A．4×12≠5×12，所以不成比例，不符合题意；B．1×15＝3×5，所以成比例，符合题意；C．2×13≠8×12，所以不成比例，不符合题意；D．0.02×5≠0.3×0.7，所以不成比例，不符合题意；故选：B．【点评】本题考查线段成比例的知识．解决本类问题只要计算最大最小数的积以及中间两个数的积，判断是否相等即可，相等即成比例，不相等不成比例．二、填空题（本大题共5小题，共25.0分）6．（5分）如图，AB∥CD∥EF，如果AC＝2，AE＝5，DF＝3.6，那么BD＝ 2.4．【分析】根据平行线分线段成比例定理即可得到结论．【解答】解：∵AC＝2，AE＝5，∴CE＝3，AB∥CD∥EF，∴，即，∴BD＝2.4，故答案为：2.4【点评】本题考查平行线分线段成比例定理，用到的知识点是平行线分线段成比例定理，关键是找准对应关系，列出比例式．7．（5分）已知线段a，b，c满足＝＝，且a+2b+c＝26，则a＝6，b＝4，c＝12．【分析】设比值为k，然后用k表示出a、b、c，再代入等式求解得到k，然后求解即可．【解答】解：设＝＝＝k，则a＝3k，b＝2k，c＝6k，∵a+2b+c＝26，∴3k+4k+6k＝26，解得：k＝2，∴a＝6，b＝4，c＝12，故答案为：6，4，12．【点评】本题考查了比例的性质，比例线段，利用“设k法”用k表示出a、b、c可以使计算更加简便．8．（5分）若，则﹣的值是﹣．【分析】将﹣变形为﹣，再代入计算即可求解．【解答】解：∵，∴＝，∴﹣＝﹣＝﹣．故答案为：﹣．【点评】本题考查了比例的性质，熟记比例的性质是解题的关键．9．（5分）如图，已知l1∥l2∥l3，若＝，EF＝4，则DE＝．【分析】根据平行线分线段成比例定理列出比例式，代入计算．【解答】解：∵l1∥l2∥l3，解得，DE＝，故答案为：．【点评】本题考查的是平行线分线段成比例定理，灵活运用定理，找准对应关系是解题的关键．10．（5分）如图，AE、BD交于点C，AB∥DE，若AC＝4，BC＝2，DC＝1，则EC＝2．【分析】由AB∥DE，即可证得△ABC∽△ECD，然后由相似三角形的对应边成比例，即可求得CE的长．【解答】解：∵AB∥DE，∴△ABC∽△ECD，∴，∵AC＝4，BC＝2，DC＝1，∴，解得：CE＝2．故答案为：2【点评】此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．三、解答题（本大题共5小题，共50.0分）11．（10分）已知＝＝，求的值．【分析】设＝＝＝k，根据比例的性质得出x＝2k，y＝3k，z＝4k，代入求出即可．【解答】解：设＝＝＝k，所以＝＝﹣1．【点评】本题考查了比例的性质，能选择适当的方法求解是解此题的关键．12．（10分）如图，在平行四边形ABCD中，点E为边BC上一点，联结AE并延长交DC的延长线于点M，交BD于点G，过点G作GF∥BC交DC于点F，＝．（1）若BD＝20，求BG的长；（2）求的值．【分析】（1））由GF∥BC推出＝即可解决问题；（2）由AB∥CD，AB＝CD，推出＝，＝，可得＝解决问题；【解答】解：（1）∵GF∥BC，∴＝，∵BD＝20，＝∴BG＝8．（2）∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴＝，∴＝，∴＝，∴＝．【点评】本题考查平行四边形的性质，平行线分线段成比例定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．13．（10分）如图，已知点D、E分别在△ABC的边BA、CA的延长线上，且AE ＝3，AC＝6，AD＝2，AB＝4．（1）求证：DE∥BC；（2）若BC＝5，求ED的长．【分析】（1）根据平行线分线段成比例证明即可；（2）根据平行线的性质和相似三角形的判定定理得出△EAD∽△CAB，根据相似三角形的性质求出即可．【解答】证明：（1）∵AE＝3，AC＝6，AD＝2，AB＝4，∴，∴，∴DE∥BC；（2）∵DE∥BC，∴△EAD∽△CAB，∴，∵BC＝5，∴，∴ED＝2.5．【点评】本题考查了平行线的性质，相似三角形的性质和判定的应用，能推出△EAD∽△CAB是解此题的关键．14．（10分）黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值．如图1，我们已经学过，点C将线段AB分成两部分，如果AC：AB＝BC：AC，那么称点C为线段AB的黄金分割点．如图2，△ABC中，AB＝AC ＝1，∠A＝36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．【分析】（1）利用等腰三角形的性质和三角形内角和定理可计算出∠ABC＝∠C ＝72°，∠ABD＝∠CBD＝36°，∠BDC＝72°，则可得到AD＝BD＝BC，然后根据相似三角形的判定方法易得△BDC∽△ABC，利用相似比得到BC2＝CD•AC，于是有AD2＝CD•AC，则可根据线段黄金分割点的定义得到结论；（2）设AD＝x，则CD＝AC﹣AD＝1﹣x，由（1）的结论得到x2＝1﹣x，然后解方程即可得到AD的长．【解答】（1）证明：∵AB＝AC＝1，∴∠ABC＝∠C＝（180°﹣∠A）＝（180°﹣36°）＝72°，∵BD平分∠ABC交AC于点D，∴∠ABD＝∠CBD＝∠ABC＝36°，∴∠BDC＝180°﹣36°﹣72°＝72°，∴DA＝DB，BD＝BC，∴AD＝BD＝BC，易得△BDC∽△ABC，∴BC：AC＝CD：BC，即BC2＝CD•AC，∴AD2＝CD•AC，∴点D是线段AC的黄金分割点；（2）解：设AD＝x，则CD＝AC﹣AD＝1﹣x，∵AD2＝CD•AC，∴x2＝1﹣x，解得x1＝，x2＝，即AD的长为．【点评】本题考查了黄金分割，相似三角形的判定和性质，解一元二次方程，熟练掌握相似三角形的判定和性质是解题的关键．15．（10分）已知＝＝＝＝k，求k值．【分析】依据等比性质可得，＝k，分两种情况讨论，即可得到k的值．【解答】解：∵＝＝＝＝k，∴由等比性质可得，＝k，当a+b+c+d≠0时，k＝＝；当a+b+c+d＝0时，b+c+d＝﹣a，∴k＝＝＝﹣2；综上所述，k的值为或﹣2．【点评】本题主要考查了比例的性质的运用，解决问题的关键是掌握比例的性质．。

咽部疾病练习题A型题1、Ok 1、关于咽的解剖以下哪种说法是错误 AA咽上起自软腭，下达第6颈椎平面，为一长约12cm的肌膜管。

B咽是呼吸和消化的共同通道。

C咽前面分别通向鼻腔、口腔和喉。

D咽两侧有颈部的大血管和神经通过。

E2、Ok 2、鼻咽癌侵犯颅内常经 DA圆孔。

B卵圆孔。

C枕骨大孔。

D破裂孔。

3、3、扁桃体的神经主要来自(B)A迷走神经。

B舌咽神经。

C舌下神经。

D外展神经。

Ok 4、扁桃体的主要生理功能为(D)A呼吸功能。

B吞咽功能。

C消化功能。

D免疫功能。

Ok 5、急性扁桃体炎常见的并发症有©A口底峰窝织炎。

B咽后脓肿。

C扁桃体周围脓肿。

D食管周围脓肿。

Ok 6、小儿扁桃体手术选用麻醉以哪种方式为好：(A)A全身麻醉插管，保持呼吸道通畅。

B1%的卡因表面麻醉。

C局部浸润麻醉。

D无麻醉。

7、咽后壁脓肿在直接喉镜下穿刺切开的体位是(C)A平卧位。

B高头位后仰。

C低头足高位。

D侧卧位。

E以上都不是。

Ok 8、以下哪种情况不适宜做扁桃体摘除术(D)A扁桃体角化症。

B扁桃体肿瘤。

C幼儿扁桃体肥大引起呼吸和吞咽困难。

D急性风湿热活动期，扁桃体作为病灶。

E慢性扁桃体炎引起邻近器官疾患，如急性鼻炎等。

9、颈侧切开术适用于 AA摘除咽侧肿块。

B摘除扁桃体。

C摘除鼻咽纤维血管瘤。

D切除鼻咽癌。

E切除舌根肿瘤。

10、正常情况下扁桃体伤口白膜形成于手术后A32小时。

B6－12小时。

C24小时以后。

D5－7天。

E以上都不是。

K型题（A ①+ ②+ ③ B ①+ ③ C ②+ ④ D ④ E ①+ ②+ ③+④）Ok 1、关于鼻咽解剖以下哪些说法是错误的？B①腺样体位于咽隐窝处。

②鼻咽侧壁有咽鼓管口、咽鼓管隆突和咽隐窝。

③鼻咽前壁为软腭。

④咽鼓管周围的淋巴组织称咽鼓管扁桃体。

Ok 2、咽淋巴内环包括 E①腺样体。

②舌扁桃体。

③咽鼓管扁桃体。

④腭扁桃体。

3、ok 3、增殖体肥大的主要症状有 E①鼻阻塞。

②张口呼吸。

第一章骨学第一章骨学1 选择题[A型题]1．桡神经沟位于A．肱骨上端B．肱骨体C．肱骨下端D．尺骨体E．桡骨体2．眶下孔位于A．颧骨B．鼻骨C．上颌骨D．下颌骨E．颞骨3．骺软骨A．位于骺的表面B．属于透明软骨C．成人的骺软骨呈线状D．属于纤维软骨E．随着年龄的增长而渐长4．属于桡骨下端的结构是A．桡神经沟B．桡切迹C．尺切迹D．尺神经沟E．桡骨头5．犁骨A．左右各一B．位于筛板紧下方C．构成骨性鼻中隔上部D．构成骨性鼻中隔下部E．属于脑颅骨6．眶上裂A．位于颅前窝B．属于筛骨上的结构C．属于额骨上的结构D．属于蝶骨上的结构E．是蝶骨和筛骨间的裂隙7．肩胛骨A．侧缘称腋缘B．侧缘称脊柱缘，外侧角上有关节盂C．肩峰末端膨大形成喙突D．前面有肩胛冈E．后面为肩脚下窝。

8．腕骨包括A．距骨B．骰骨C．楔骨D．月骨E．跖骨9．外踝位于A．胫骨下端B．胫骨上端C．腓骨上端D．腓骨下端E．股骨下端10．髋臼上有A．耳状面B．月状面C．臀面D．髌面E．以上皆非11．一般椎骨不包括A．椎体B．椎弓C．椎孔D．侧块E．棘突12．关于胸椎叙述正确的是A．关节突呈矢状位B．椎体小C．椎孔最大D．有肋凹E．棘突呈方板状13．颈椎特有的结构A．横突肋凹B．关节突C．棘突D．横突孔E．椎孔14．骶骨和髋骨均有得结构是A．粗线B．月状面C．耳状面D．弓状线E．髋臼15．不成对的面颅骨有A．鼻骨B．泪骨C．舌骨D．腭骨E．额骨16．成对的脑颅骨有A．颧骨B．犁骨C．顶骨D．蝶骨E．枕骨17．颅后窝有A．颈动脉沟B．乙状窦沟C．外耳门D．三叉神经压迹E．筛孔18．脑膜中动脉沟起自A．圆孔B．卵圆孔C．棘孔E．茎乳孔19．肱骨骨折的最易发部位是A．解剖颈B．外科颈C．肱骨干D．肱骨下端E．尺神经沟20．不属于颅中窝的结构有A．眶上裂B．眶下裂C．颈动脉沟D．视神经管E．卵圆孔21．颅底面能见到而外面看不见的结构有A．圆孔B．卵圆孔C．棘孔D．破裂孔E．颈静脉孔22．骶管麻醉的穿刺部位应正对A．骶前孔C．骶管裂孔D．骶角E．骶岬23．颅中窝有A．筛孔B．垂体窝C．颈动脉管外口D．颈静脉孔E．鸡冠24．眶与鼻腔相交通是通过A．眶下裂B．眶下管C．眶下孔D．鼻泪管E．圆孔25．构成骨性鼻中隔的是A．犁骨和腭骨B．上颌骨和犁骨C．筛骨垂直板和犁骨D．下鼻甲和犁骨E．犁骨和鼻骨26．中鼻甲属于A．上颌骨B．蝶骨C．筛骨D．上鼻甲的一部分E．鼻骨27．关于鼻旁窦正确的说法是A．都开口于上鼻道B．都开口于中鼻道C．口腔感染时易波及到鼻旁窦D．鼻腔感染时易波及到鼻旁窦E．上颌窦开口于下鼻道28．分泌物引流最不畅的鼻旁窦是A．上颌窦B．筛窦前、中群。

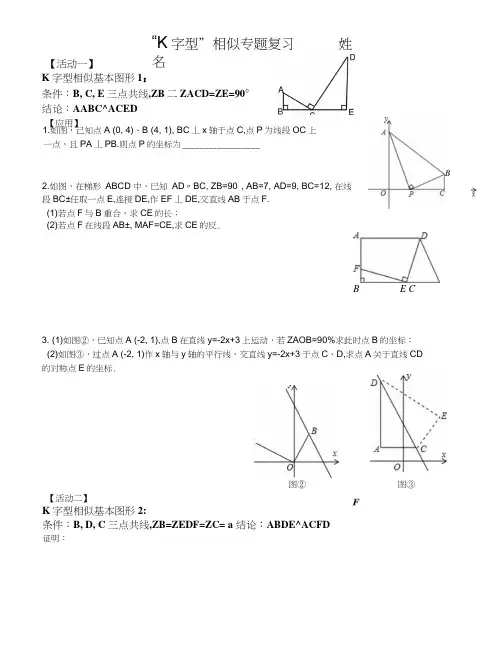
3. (1)如图②，已知点A (-2, 1),点B 在直线y=-2x+3上运动，若ZAOB=90%求此时点B 的坐标；(2)如图③，过点A (-2, 1)作x 轴与y 轴的平行线，交直线y=-2x+3于点C 、D,求点A 关于直线CD的对称点E 的坐标.图② 图③【活动二】K 字型相似基本图形2:条件：B, D, C 三点共线,ZB=ZEDF=ZC= a 结论：ABDE^ACFD证明： “K 字型”相似专题复习 姓名【活动一】 K 字型相似基本图形1：条件：B, C, E 三点共线,ZB 二ZACD=ZE=90°结论：AABC^ACED【应用】 1.如图，己知点A (0, 4)、B (4, 1), BC 丄x 轴于点C,点P 为线段OC 上一点，且PA 丄PB.则点P 的坐标为 __________________2.如图，在梯形 ABCD 中，已知 AD 〃BC, ZB=90°, AB=7, AD=9, BC=12, 在线段BC±任取一点E,连接DE,作EF 丄DE,交直线AB 于点F.(1)若点F 与B 重合，求CE 的长；B(2)若点F 在线段AB±, MAF=CE,求CE 的反.BE C【应用】1.如图，在平面直角坐标中，四边形OABC是等腰梯形，CB〃OA, 0A=7, BC=1, AB=5,点P为x轴上的一个动点，点P不与点0、点A重合.连接CP,过点P作PD交AB于点D.（1）______________________________ 直接写出点B的坐标 .（2）当点P在线段OA上运动吋，使得ZCPD=ZOAB,且BD: AD=3:2 ,求点P的坐标.4 222如图，已知直线归0（与抛物线『=——%2 +一交于点A （3, 6）.27 3（1）求直线y=kx的解析式和线段OA的氏度；（2）若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点0、A不重合），点D （m, 0）是x轴正半轴上的动点，且满足ZBAE=ZBED=ZAOD.探究：m在什么范围时，符合条件的E点的个数分别是1 个、2个？（2012-天津）已知一个矩形纸片OACE,将该纸片放置在平面直角坐标系中，点A （lb C）•点B （0, 0,点P为BC边上的动点（点P不与点B、（:重合），经过点6 P折叠该纸片，得点B'和折痕OP.设BP=t.< I〉如图①，当ZB0P-30w时，求点P的坐标；（II）如图②，经过点P再次折叠纸片，使点C落在克线PB'上，得点L 和折痕PQ,若A4n, 试用含有t的式子表示呀（HD在（H）的乗件下.当点C'恰好落在边O.A上时，求点P的坐标（直接写出结果即可）.。

图形的相似（填空题：一般）1、：的比值是（___________）；把4 : 0.8化为最简单的整数比是（___________）。

2、在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20 cm，则它的宽约为．3、如果=k（b+d+f≠0），且a+c+e=3（b+d+f），那么k=_____．4、已知线段AB的长为10厘米，点P是线段AB的黄金分割点，那么较长的线段AP的长等于_______厘米．（结果保留根号）5、已知是线段的黄金分割点，若，则_________。

6、已知，则＝________．7、已知：点P是线段MN的黄金分割点，(PM>PN),MN=4cm,则MP= .8、已知线段AB=20cm，点C是线段AB的黄金分割点，则较长线段AC的长为______cm．9、若，则的值为_________.10、已知点是线段的一个黄金分割点，且，则长为___________ .11、已知，则=________．12、如果，那么=__________．13、若，则=________________．14、配置一种盐水，盐和水的质量比是1:2，盐是盐水质量的________.15、如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米．甲身高1.8米,乙身高1.5米,则甲的影长是米．16、如图，在△ABC与△ADE中，，要使△ABC与△ADE相似，还需要添加一个条件，这个条件可以是__________．17、如图，在△ABC中，点D为AC上一点，且，过点D作DE∥BC交AB于点E，连接CE，过点D作DF∥CE交AB于点F．若AB=15，则EF=___________．18、将一个矩形沿着一条对称轴翻折，如果所得到的矩形与这个矩形相似，那么我们就将这样的矩形定义为“白银矩形”．事实上，“白银矩形”在日常生活中随处可见，如：我们常见的A4纸就是一个“白银矩形”．请根据上述信息求A4纸的较长边与较短边的比值，这个比值是________．19、如果，那么__________。

中考数学重难考点突破---“K”字型几何相似题型研究与练习相似基本图形中除了常见的“A”字型、“X”字型相似外，还有一个“K”字型相似，也常用于各种相似图形中“K”字型相似由特殊到一般，题型往往丰富多彩，也是近几年中考题中常见的一种基本图形．了解一个基本图形，有助于我们在复杂图形中渗透其中的奥秘，从而找到解决问题的突破口．类型1 “K”字型相似基本图形1图1例1 条件：如图1，B，C，E三点共线，∠B＝∠ACD＝∠E＝90°.结论：△ABC∽△CED.请证明结论正确【分析】(1)证明两个三角形相似有哪些方法？(2)除了∠B＝∠E＝∠ACD之外，图中还可以找出哪些角相等？【答案】(1)证明两个三角形相似常用的判定方法有：两角对应相等的两个三角形相似；两边对应成比例且夹角相等的两个三角形相似；三边对应成比例的两个三角形相似等．(2)根据余角的性质还可以得到∠A＝∠DCE，∠ACB＝∠D，从而可证得△ABC∽△CED.【应用】如图2，已知点A(0，4)，B(4，1)，BC⊥x轴于点C，点P为线段OC上一点，且PA⊥PB，则点P的坐标为________．图2【分层分析】(1)根据“K”字型相似，图中可以找到哪两个三角形相似？根据相似三角形又可以得到怎样的比例式？(2)设P(x，0)，则根据比例式列出方程即可求得x的值，从而得到点P的坐标．【解题方法点醒】“K”字型相似基本图形1，在于寻找三个直角相等，熟记基本图形有利于快速找到相似三角形，从而通过建立方程解决问题．【答案】【分层分析】(1)根据“K”字型相似，可得到△AOP∽△PCB，所以AOPC＝OPCB.(2)设P(x，0)，因为AO＝OC＝4，BC＝1，所以OP＝x，PC＝4－x，所以4 4－x ＝x1，解得x＝2，从而得到点P的坐标为(2，0)．[答案] (2，0) [解析] ∵PA⊥PB，∴∠APO＋∠BPC＝90°.∵AO⊥x轴，∴∠APO＋∠PAO＝90°，∴∠PAO＝∠BPC.又∵BC⊥x轴，AO⊥x轴，∴∠BCP＝∠POA＝90°，∴△BCP∽△POA，∴AOPC＝OPCB.∵点A(0，4)，B(4，1)，∴AO＝4，BC＝1，OC＝4. 设P(x，0)，则OP＝x，PC＝4－x，∴44－x＝x1，解得x＝2，∴点P的坐标为(2，0)．类型2 “K”字型相似基本图形2例2 条件：如图3，B，D，C三点共线，∠B＝∠EDF＝∠C＝∠α.图3结论：△BDE∽△CFD.请证明：结论正确【分层分析】(1)“K”字型相似基本图形2与基本图形1有何联系？(2)如何证明∠E＝∠CDF?【答案】【分层分析】(1)两个图形都有三个角相等，基本图形1是三个直角相等，而基本图形2是基本图形1的一般情况，更具普遍性，两个图形的形状均类似于字母“K”，因此称之为“K”字型相似图形．(2)∵∠B＝∠EDF＝∠C＝∠α，由外角性质可知∠EDC＝∠B＋∠E＝∠α＋∠E.又∵∠EDC＝∠EDF＋∠FDC＝∠α＋∠CDF，∴∠E＝∠CDF.证明：∵∠B＝∠EDF＝∠C＝∠α，由外角性质可知∠EDC＝∠B＋∠E＝∠α＋∠E.又∵∠EDC＝∠EDF＋∠FDC＝∠α＋∠FDC，∴∠E＝∠FDC.又∵∠B＝∠C，∴△BDE∽△CFD.【应用】1．如图4，在平面直角坐标系中，四边形OABC是梯形，CB∥OA，OC＝BA，OA＝7，BC＝1，AB＝5，点P为x轴上的一个动点，点P不与点O，A重合．连结CP，过点P作PD交AB于点D.图4(1)直接写出点B 的坐标：________；(2)当点P 在线段OA 上运动时，使得∠CPD＝∠OAB，且BD∶AD＝3∶2，求点P 的坐标． 【分层分析】(1)过点B 作BQ⊥x 轴于点Q ，依题意可得OQ ＝4，AQ ＝3，已知AB ＝5，根据勾股定理求出QB 即可解答．(2)根据“K ”字型相似，图中可以找到哪两个三角形相似？根据相似三角形又可以得到怎样的比例式？【答案】【分层分析】(1)过点B 作BQ⊥x 轴于点Q ，易求得BQ ＝4，故得到点B 的坐标为(4，4)． (2)由“K ”字型相似可得到△POC∽△DAP， 所以OC AP ＝OP AD，设OP ＝x ，OC ＝AB ＝5，AD ＝25AB ＝2，AP ＝7－x ，所以57－x ＝x 2，解得x ＝2或x ＝5，所以点P 的坐标为(2，0)或(5，0)． 解：(1)过点B 作BQ⊥x 轴于点Q. ∵AB ＝OC ，∴AQ ＝(7－1)÷2＝3， 在Rt △BQA 中，BA ＝5，由勾股定理，得BQ ＝AB 2－AQ 2＝4， ∴点B 的坐标为(4，4)． (2)∵∠CPA＝∠OCP＋∠COP， 即∠CPD＋∠DPA＝∠COP＋∠OCP， 而∠CPD＝∠OAB＝∠COP， ∴∠OCP ＝∠APD，∴△OCP∽△APD，∴OCAP＝OPAD.∵BDAD＝32，∴AD＝2.设OP＝x，OC＝AB＝5，AP＝7－x，∴57－x＝x2，解得x＝2或x＝5，∴点P的坐标为(2，0)或(5，0)．2．如图5，已知直线y＝kx与抛物线y＝－427x2＋223交于点A(3，6)．图5(1)求直线y＝kx的函数表达式和线段OA的长度．(2)若点B为抛物线上对称轴右侧的点，点E在线段OA上(与点O，A不重合)，点D(m，0)是x轴正半轴上的动点，且满足∠BAE＝∠BED＝∠AOD.探究：m在什么范围内时，符合条件的点E分别有1个、2个？【分层分析】(1)利用待定系数法求出直线y＝kx的函数表达式，根据A点坐标用勾股定理求出线段OA 的长度．(2)①延长AB交x轴于点F，由∠BAE＝∠AOD可求出点F的坐标为________，进而再求得点B的坐标为________，然后由两点间距离公式可求得线段AB的长为________；②由已知条件∠BAE＝∠BED＝∠AOD，可得到“K”字型相似的基本图形2，故可得到△________∽△________，设OE＝a，则由对应边的比例关系可以得到________．从而得到关于a 的一元二次方程为____________，然后根据根的判别式可以分别得到a的值分别为1个、2个时m的取值范围．【解题方法点醒】“K”字型相似基本图形2，根据三个角相等，联想到“K”字型基本图形1，便于快速找到相似三角形，从而利用相似的有关性质解决问题．【答案】【例题分层分析】(1)直线y＝kx的函数表达式为y＝2x，OA＝32＋62＝3 5.(2)①点F的坐标为(152，0)，点B的坐标为(6，2)，AB＝5.②根据“K”字型相似的基本图形2，可得到△ABE∽△OED，设OE＝a，则AE＝3 5－a(0＜a＜3 5)，由△ABE∽△OED得AEAB＝ODOE，∴3 5－a5＝ma，∴a2－3 5a＋5m＝0，依题意知m>0，∴当Δ＝0，即(－3 5)2－20m＝0，m＝94时，符合条件的点E有1个；当Δ＞0，即(－3 5)2－20m＞0，0＜m＜94时，符合条件的点E有2个．解：(1)把点A(3，6)的坐标代入y＝kx，得6＝3k，∴k＝2，∴y＝2x，OA＝32＋62＝3 5.(2)如图，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R.∵∠AOD＝∠BAE，∴AF＝OF，∴OC＝AC＝12OA＝325.∵∠ARO＝∠FCO＝90°，∠AOR＝∠FOC，∴△AOR∽△FOC，∴OFOC＝AOOR＝3 53＝5，∴OF＝325×5＝152，∴点F 的坐标为⎝ ⎛⎭⎪⎫152，0.设直线AF 的函数表达式为y ＝ax ＋b(a≠0)，把点A(3，6)，F ⎝ ⎛⎭⎪⎫152，0的坐标代入，解得a＝－43，b ＝10，∴y ＝－43x ＋10，由⎩⎪⎨⎪⎧y ＝－43x ＋10，y ＝－427x 2＋223，解得⎩⎨⎧x 1＝3，y 1＝6(舍去)，⎩⎨⎧x 2＝6，y 2＝2，∴B(6，2)，∴AB ＝5. ∵∠BAE ＝∠BED，∠ABE ＋∠BAE＝∠DEO＋∠BED， ∴∠ABE ＝∠DEO.∵∠BAE ＝∠EOD，∴△ABE ∽△OED. 设OE ＝a ，则AE ＝3 5－a(0＜a ＜3 5)， 由△ABE∽△OED 得AE AB ＝ODOE， 即3 5－a 5＝ma，∴a 2－3 5a ＋5m ＝0. 依题意得m>0，∴当Δ＝0，即(－3 5)2－20m ＝0，m ＝94时，符合条件的点E 有1个；当Δ＞0，即(－3 5)2－20m ＞0，0＜m ＜94时，符合条件的点E 有2个．专 题 训 练1． 如图6，已知矩形ABCD 的顶点A ，D 分别落在x 轴、y 轴上，OD ＝2OA ＝6，AD ∶AB ＝3∶1，则点C 的坐标是( )A ．(2，7)B ．(3，7)C ．(3，8)D ．(4，8)图62．如图7，在矩形ABCD中，把DA沿AF对折，使得点D与CB边上的点E重合，若AD＝10，AB＝8，则EF＝________．图73．如图8，D是等边△ABC边AB上的点，AD＝2，BD＝4.现将△ABC折叠，使得点C与点D重合，折痕为EF，且点E，F分别在边AC和BC上，则CFCE＝________．图84．如图9，在直角梯形ABCF中，CB＝14，CF＝4，AB＝6，CF∥AB，在边CB上找一点E，使以E，A，B为顶点的三角形和以E，C，F为顶点的三角形相似，则CE＝________．图95．如图10，在直角梯形ABCD中，∠A＝90°，∠B＝120°，AD＝3，AB＝6.在底边AB上取点E，在射线DC上取点F，使得∠DEF＝120°.(1)当点E是AB的中点时，线段DF的长度是________；(2)若射线EF经过点C，则AE的长是________．图106．将形状、大小完全相同的两个等腰三角形如图11所示放置，点D在AB边上，△DEF绕点D旋转，腰DF和底边DE分别交△CAB的两腰CA，CB于M，N两点．若CA＝5，AB＝6，AD∶AB＝1∶3，则MD＋12MA·DN的最小值为________．图117．如图12，在四边形ABCD中，已知AD∥BC，∠B＝90°，AB＝7，AD＝9，BC＝12，在线段BC上任取一点E，连结DE，作EF⊥DE，交直线AB于点F.(1)若点F与B重合，求CE的长；(2)若点F在线段AB上，且AF＝CE，求CE的长．图128．如图13，在△ABC中，AB＝AC，点P，D分别是BC，AC边上的点，且∠APD＝∠B.(1)求证：AC·CD＝CP·BP；(2)若AB＝10，BC＝12，当PD∥AB时，求BP的长．图139．△ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF的顶点E 与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.(1)如图14①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE.(2)如图14②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP＝2，CQ ＝9时BC的长．图1410．在△ABC中，AB＝AC，∠BAC＝120°，P为BC的中点，小明拿着含有30°角的透明直角三角板，使30°角的顶点落在点P上，三角板绕点P旋转．(1)如图15①，当三角板的一直角边和斜边分别与AB，AC交于点E，F时，连结EF，请说明△BPE∽△CFP.(2)操作：将三角板绕点P旋转到图②的情形时，三角板的两边分别交BA的延长线、边AC 于点E，F，连结EF.①探究1：△BPE与△CFP相似吗？请说明理由；②探究2：△BPE与△PFE相似吗？请说明理由．图15参考答案1.【答案】A2.【答案】53.【答案】544.【答案】2或12或285 [解析] 两个三角形相似，可能是△EFC ∽△EAB ，也可能是△EFC ∽△AEB ，所以应分两种情况讨论，进而求CE 的值即可．5.【答案】(1)6 (2)2或5[解析] (1)过点E 作EG ⊥DF ，由E 是AB 的中点，得出DG ＝3，从而得出∠DEG ＝60°，由∠DEF＝120°，得∠FEG ＝60°，由tan ∠FEG ＝FG GE，即可求出GF 的长，进而得出DF 的长． (2)过点B 作BH ⊥DC ，延长AB ，过点C 作CM ⊥AB 于点M ，则BH ＝AD ＝3，再由锐角三角函数的定义求出CH 及BC 的长，设AE ＝x ，则BE ＝6－x ，利用勾股定理用x 表示出DE 及EC 的长，再判断出△EDC ∽△BCE ，由相似三角形的对应边成比例即可得出关于x 的方程，求出x 的值即可．6.【答案】2 3[解析] 先求出AD ＝2，BD ＝4，由“K ”字型相似可得△AMD 和△BDN 相似，根据相似三角形对应边成比例可得MA BD ＝MD DN，求出MA ·DN ＝4MD ，再将所求代数式整理得出完全平方的形式，然后根据非负数的性质求出最小值即可．7.解：(1)当点F 和B 重合时，∵EF ⊥DE ，∴DE ⊥BC .∵∠B ＝90°，∴AB ⊥BC ，∴AB ∥DE .∵AD ∥BC ，∴四边形ABED 是平行四边形，∴AD ＝EF ＝9，∴CE ＝BC －EF ＝12－9＝3.(2)过点D作DM⊥BC于点M，∵∠B＝90°，∴AB⊥BC，∴DM∥AB.∵AD∥BC，∴四边形ABMD是矩形，∴AD＝BM＝9，AB＝DM＝7，CM＝12－9＝3.设AF＝CE＝a，则BF＝7－a，EM＝a－3，BE＝12－a，可证△FBE∽△EMD，∴BFEM＝BEDM，即7－aa－3＝12－a7，解得a＝5或a＝17.∵点F在线段AB上，∴AF＝CE＜AB＝7，∴CE＝5.8.解：(1)证明：∵∠APC＝∠PAB＋∠B，∠APD＝∠B，∴∠DPC＝∠PAB，又AB＝AC，∴∠ABP＝∠PCD，∴△ABP∽△PCD，∴ABCP＝BPCD，∴ACCP＝BPCD，∴AC·CD＝CP·BP.(2)∵PD∥AB，∴∠DPC＝∠B，∴∠PAB＝∠B，又∠B＝∠C，∴∠PAB＝∠C.∴△PBA ∽△ABC ，∴BP AB ＝AB BC， ∴BP ＝AB 2BC ＝10212＝253. 9.解：(1)证明：∵△ABC 是等腰直角三角形，∴∠B ＝∠C ＝45°，AB ＝AC ，∵AP ＝AQ ，∴BP ＝CQ ，∵E 是BC 的中点，∴BE ＝CE ，在△BPE 和△CQE 中，∵⎩⎨⎧BE ＝CE ，∠B ＝∠C，BP ＝CQ ，∴△BPE ≌△CQE (SAS )；(2)∵△ABC 和△DEF 是两个全等的等腰直角三角形，∴∠B ＝∠C ＝∠DEF ＝45°，∵∠BEQ ＝∠EQC ＋∠C ，即∠BEP ＋∠DEF ＝∠EQC ＋∠C ，∴∠BEP ＋45°＝∠EQC ＋45°，∴∠BEP ＝∠EQC ，∴△BPE ∽△CEQ ，∴BP CE ＝BE CQ， ∵BP ＝2，CQ ＝9，BE ＝CE ，∴BE 2＝18，∴BE ＝CE ＝3 2，∴BC ＝6 2.10.解：(1)∵在△ABC 中，∠BAC ＝120°，AB ＝AC ，∴∠B ＝∠C ＝30°.∵∠B ＋∠BPE ＋∠BEP ＝180°，∴∠BPE ＋∠BEP ＝150°.又∵∠BPE ＋∠EPF ＋∠CPF ＝180°，∠EPF ＝30°，∴∠BPE ＋∠CPF ＝150°，∴△BPE∽△CFP(两角对应相等的两个三角形相似)．(2)①△BPE∽△CFP，理由同(1)．②△BPE与△PFE相似．理由：由①△BPE∽△CFP，得CP∶BE＝PF∶PE，而CP＝BP，因此BP∶BE＝PF∶PE.又∵∠EBP＝∠EPF，∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似)．。

一、选择题1、直接染料染色时，加Na2SO4起作用。

A 促染B 缓染C 匀染2、B型活性染料固色温度为A 30℃B 60℃C 90℃3、以下关于直接染料特点说法错误的是A 色泽鲜艳，色谱齐全B 可用于棉染色C 皂洗牢度好4、以下染料不用于棉织物染色的是 C 。

A 还原染料B 活性染料C 分散染料5、活性染料染棉时，与棉纤维结合的方式是A 离子键B 共价键C 氢键6、活性染料浸染时，加入的固色剂为A 元明粉B 纯碱C 食盐D 碳酸氢钠7、K型活性染料染色与固色的温度分别为A 30℃、60℃B 60℃、90℃C 30℃、30℃8、M型活性染料染色与固色的温度分别为A 60℃、60℃B 60℃、90℃C 30℃、30℃9、以下关于活性染料特点说法错误的是A 色泽鲜艳，色谱齐全B 湿牢度高C 不易水解，利用率高10、拼色打样时，染料只数一般不超过A 1B 2C 3D 411、广泛用于染色和印花的助溶剂是（）A、纯碱B、尿素C、拉开粉12、KN型活性染料染色时应选择( )。

A、染色温度40—70℃，固色温度80—95℃。

B、染色温度40—60℃，固色温度60—70℃C、染色温度60—90℃，固色温度60—95℃13、轧染时，为防止活性染料的泳移，要在染液中加入( )。

A、尿素B、防染盐SC、海藻酸钠14、织物轧染时，应选择( )。

A、直接性大的染料B、直接性小的染料C、不用考虑直接性15、活性染料染棉时，碱过少，则得色―――――――――――――（）Ａ．浓Ｂ．淡Ｃ．牢16、称织物3g放入烧杯中，移取活性染料母液25mL，移取元明粉溶液25mL，再加水40mL，则该工艺浴比为（）Ａ．1：30 Ｂ．1：40 Ｃ．1：5017、下列染料在水中带正电荷的是（）Ａ．直接染料Ｂ．活性染料Ｃ．阳离子染料二、填空1、在印染厂中，染色时的三原色是指、、。

2、直接染料浸染时，加元明粉起作用，加平平加O起（）作用。

3、活性染料浸染时加元明粉起作用，加Na2CO3起（）作用。

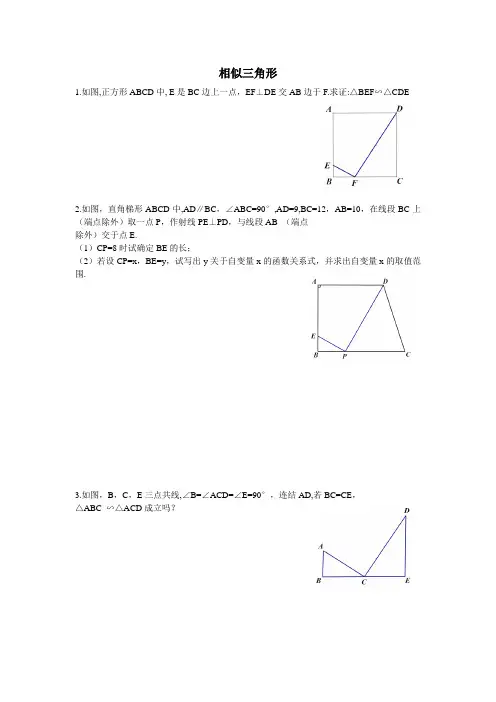
相似三角形1.如图,正方形ABCD中, E是BC边上一点，EF⊥DE交AB边于F.求证:△BEF∽△CDE2.如图，直角梯形ABCD中,AD∥BC，∠ABC=90°,AD=9,BC=12，AB=10，在线段BC上（端点除外）取一点P，作射线PE⊥PD，与线段AB （端点除外）交于点E.（1）CP=8时试确定BE的长；（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式，并求出自变量x的取值范围.3.如图，B，C，E三点共线,∠B=∠ACD=∠E=90°，连结AD,若BC=CE，△ABC ∽△ACD成立吗？4.如图: △ABC中,∠B= ∠C ，D为BC上一点，作∠EDF=∠B= ∠C= α，并且∠EDF 的一边与AB交于E点，另一边与AC（或延长线）交于F点，则△BDE∽△CFD吗？5.如图: △ABC中，∠B= ∠C ，D为BC上中点，以D为顶点作∠EDF，使∠EDF=∠B= ∠C= α，并且∠EDF的一边与AB交于E点，另一边与AC（或延长线）交于F点，则有△BDE ∽△DFE ？6.M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α，且DM交AC于F，ME交BC于G．（1）写出图中三对相似三角形4，求FG长．（2）连结FG，若α＝45°，AF＝3，AB＝27.如图平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7，AB=4，∠BAO=60°，点P为线段OA上的—个动点，点P不与点O、点A重合．连结CP，过点P作射线PD交直线AB于点D．(1)当点P运动什么位置时，使得∠CPD=60°，此时D在线段AB上，且BD:BA=5:8，求点P的坐标．(2)（2）动点P运动使得∠CPD=60°，且符合条件的点P有且只有1个，求线段AD、OP 的长；（3）同（2）条件，若符合条件的点P有且只有2个，求线段AD取值范围？8.如图1，已知直线y=kx 与抛物线y=3222742+-x 交于点A （3，6）． （1）求直线y=kx 的解析式和线段OA 的长度； （2）点P 为抛物线第一象限内的动点，过点P 作直线PM ，交x 轴于点M （点M 、O 不重合），交直线OA 于点Q ，再过点Q 作直线PM 的垂线，交y 轴于点N ．试探究：线段QM 与线段QN 的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；（3）如图2，若点B 为抛物线上对称轴右侧的点，点E 在线段OA 上（与点O 、A 不重合），点D （m ，0）是x 轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m 在什么范围时，符合条件的E 点的个数分别是1个、2个？。

秦九韶与k进制练习题一．选择题（共16小题）1．把77化成四进制数的末位数字为（）A．4 B．3 C．2 D．12．用秦九韶算法求多项式f（x）=x4+2x3+x2﹣3x﹣1，当x=2时的值，则v3=（）！A．4 B．9 C．15 D．293．把67化为二进制数为（）A．110000 B．1011110 C．1100001 D．10000114．用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=时的值时，需要做乘法和加法的次数分别是（）A．6，6 B．5，6 C．5，5 D．6，55．使用秦九韶算法计算x=2时f（x）=6x6+4x5﹣2x4+5x3﹣7x2﹣2x+5的值，所要进行的乘法和加法的次数分别为（）A．6，3 B．6，6 C．21，3 D．21，6\6．把27化为二进制数为（）A．1011（2）B．11011（2）C．10110（2）D．10111（2）7．用秦九韶算法计算多项式f（x）=5x5+4x4+3x3﹣2x2﹣x﹣1在x=﹣4时的值时，需要进行的乘法、加法的次数分别是（）A．14，5 B．5，5 C．6，5 D．7，58．二进制数（2）对应的十进制数是（）A．401 B．385 C．201 D．258《9．小明中午放学回家自己煮面条吃，有下面几道工序：①洗锅盛水2分钟；②洗菜6分钟；③准备面条及佐料2分钟；④用锅把水烧开10分钟；⑤煮面条和菜共3分钟．以上各道工序，除了④之外，一次只能进行一道工序．小明要将面条煮好，最少要用（）分钟．A．13 B．14 C．15 D．2310．用秦九韶算法在计算f（x）=2x4+3x3﹣2x2+4x﹣6时，要用到的乘法和加法的次数分别为（）A．4，3 B．6，4 C．4，4 D．3，411．用秦九韶算法求多项式f（x）=1+2x+x2﹣3x3+2x4在x=﹣1时的值，v2的结果是（）A．﹣4 B．﹣1 C．5 D．612．下列各数85（9）、210（6）、1000（4）、111111（2）中最大的数是（）A．85（9）B．210（6）C．1000（4）D．111111（2）13．十进制数89化为二进制的数为（）A．1001101（2）B．1011001（2）C．0011001（2）D．1001001（2）14．烧水泡茶需要洗刷茶具（5min）、刷水壶（2min）、烧水（8min）、泡茶（2min）等个步骤、从下列选项中选最好的一种算法（）A．第一步：洗刷茶具；第二步：刷水壶；第三步：烧水；第四步：泡茶B．第一步：刷水壶；第二步：洗刷茶具；第三步：烧水；第四步：泡茶C．第一步：烧水；第二步：刷水壶；第三步：洗刷茶具；第四步：泡茶D．第一步：烧水；第二步：烧水的同时洗刷茶具和刷水壶；第三步：泡茶15．在下列各数中，最大的数是（）A．85（9）B．210（6）C．1000（4）D．11111（2）.16．把23化成二进制数是（）A．00110 B．10111 C．10101 D．11101二．填空题（共11小题）17．用秦九韶算法求多项式f（x）=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4的值时，其中V1的值=_________．18．把5进制的数412（5）化为7进制是_________．19．用秦九韶算法计算多项式f（x）=8x4+5x3+3x2+2x+1在x=2时的值时，v2=_________．)20．用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=时的值时，至多需要做乘法和加法的次数分别是_________和_________．21．军训基地购买苹果慰问学员，已知苹果总数用八进位制表示为abc，七进位制表示为cba，那么苹果的总数用十进位制表示为_________．22．若六进制数Im05（6）（m为正整数）化为十进数为293，则m=_________．23．用秦九韶算法求多项式f（x）=5x5+2x4+﹣+﹣当x=5时的值的过程中v3=_________．24．完成下列进位制之间的转化：1234=_________（4）．/25．把十进制数51化为二进制数的结果是_________．26．进制转化：403（6）=_________（8）．27．完成右边进制的转化：1011（2）=_________（10）=_________（8）．三．解答题（共3小题）28．将多项式x3+2x2+x﹣1用秦九韶算法求值时，其表达式应写成_________．29．写出将8进制数23760转化为7进制数的过程．30．已知一个5次多项式为f（x）=4x5﹣3x3+2x2+5x+1，用秦九韶算法求这个多项式当x=2时的值．答案与评分标准一．选择题（共16小题）1．把77化成四进制数的末位数字为（）A．4 B．3 C．2 D．1考点：排序问题与算法的多样性。

巧用“K”型图作者：严伟娟来源：《新高考·升学考试》2018年第01期在数学问题的解决过程中，有意识地提炼一些典型的数学模型，可以有效地提高解题速度和准确率，“K”型图在几何图形中较为常见，本文浅谈该基本图形在解题中集中常见的应用.一、探究“K”型图的基本模型如图1①：∠C=∠D=∠1=90°时，则△APC∽△PBD；如图1②：∠C=∠D=∠1=60°时，△APC∽△PBD；如图1③：∠C=∠D=∠1=n°时，△APC∽△PBD.图1③证明如下：在△APC中，∠A+∠C+∠APC=180°，而∠BPD+∠1+∠APC=180°，且∠C=∠1，∴∠A=∠BPD，又∵∠C=∠D，∴△APC∽△PBD.图1①和图1②是图1③的特殊情况，此处就不再证明.因这三个图形形似字母K，我们把这三个图形统称为“K”型图.虽然基本K型图有3种，但究其本质，可以归纳为：满足一条直线上有3个相等的角的图就是K型图.这3个角无论是直角、锐角、钝角，结论都成立，所以也有把这个基本图形称为“一线三角”图形.二、“K”型图的基本应用1. 有直角的“K”型图例1. 如图2在矩形ABCD中，AB=10，AD=8，F是CD上一动点，沿EF折叠后，点C 恰好落在AB上G处，E在BC上，BG=6时，能求折痕EF的长吗？简析：要求EF，发现它在Rt△CEF中，可以通过勾股定理求出，但首要是先求出CE和CF，由于翻折，CE=GE，可以设CE=x，则BE=8-x，在Rt△BGE中，由勾股定理列出方程：（8-x）2+62=x2，解得：x=254；类似的考虑CF也放到直接三角形中去，自然而然地想到过点F作FM⊥AB，垂足为M，图中出现基本图形①，易证出△FMG∽△GBE，根据相似三角形的性质得到FMFG=BGGE，8FG=6254，解得FG=253，在Rt△CFE中，由勾股定理得：EF=CE2+FG2=2532+2542=12512.翻折问题较好地考查了学生的空间想象能力和动手操作的能力，直角三角形折叠问题是历年中考的一个热点问题，寻找基本图形①成为了解题的关键.变式练习：（1）如图3，在正方形ABCD中，点C的坐标为（4，3），求A、D点坐标.（2）如图4，在矩形ABCD中，点A的坐標为（-3，1），求D、C点坐标.提示：两题均是过点C作CE⊥x轴，垂足为E，过点A作AF⊥x轴，垂足为F，过点D 作DG⊥AF，垂足为G，图中出现基本图形①，再证出三角形相似，并利用相似三角形的性质即可求出.2. 没有直角的“K”型图图5例2. 如图5所示，在等边△QCD中，P为CD上一点，B为QD上一点，且∠1=60°，CP=1，BD= 23，求△QCD的边长.简析：本题由条件立刻可以知道∠1=∠C=∠D=60°，这是基本图形②的最直接应用.可以快速证明出：△QCP∽△PDB，根据相似三角形的性质得到CQCP=DPBD，CQ1=CQ-123，解得CQ=3.变式练习：在△ABC中，AB=AC，∠BAC=120°，P为BC的中点，小明拿着含有30°角的透明直角三角板，使30°角的顶点落在点P上，三角板绕点P旋转.（1）如图6，当三角板的一直角边和斜边分别与AB、BC交于点E、F时，连接EF，请说明△BPE∽△CFP；（2）操作：将三角板绕点P旋转到图7情形时，三角板的两边分别交BA的延长线、边AC于点E、F，连接EF.探究：△BPE与△CFP相似吗？请说明理由.提示：两题均是直接利用基本图形③解决问题.3. “K”型图在综合题中的运用例3.已知，如图8，点B（2，4）在抛物线y=x2上，点A（1，0），矩形ABCD有两个顶点在该抛物线上，AD=mAB，求m的值.简析：过点B和D分别作BM⊥x轴，DN⊥x轴，垂足为分别为M、N，图中出现基本图形①，证出△ADN∽△BAM，并利用相似三角形的性质列出：DNAM=ANBM=ADAB=m，DN1=AN4=m，∴DN=m，AN=4m.∴D（1-4m，m），将点D的坐标带入抛物线解析式，（1-4m）2=m，求解即可；同理，当点C（2-4m，m+4）在函数图象上时，解法亦同.变式练习：如图9，在平面直角坐标系内，反比例函数和二次函数y=k（x2+x-1）的图象交于点A （1，k）和点B（-1，-k）. 设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值.提示：本题中由题意可得：Q（-12，-54k），利用勾股定理AQ2+BQ2=AB2，或者根据OQ=OA=OB，都可以列出方程，解出k的值.但是，从几何的角度发现∠AQB=90°，而且在平面直角坐标系中，点的坐标和线段长度换算时，常常作和坐标轴垂直的线，这样，我们的“K”型图就出现了.我们可以通过Q做平行于x轴的垂线l，过点A和B再向直线l作垂线，垂直为M、N，则由“K”型相似得到，△MAQ∽△NQB，MQ、MA、NB、NQ这四条线段易用k的代数式表示，再通过它们成比例列出关于k的方程，问题就迎刃而解了.在初中数学的学习过程中，数学解题能力的提高，需要借助丰富的解题经验，这里既有思维方式上的经验，也有一些典型的知识块的积累，适当提炼一些基本图形，可以增强整体意识，快速抓住问题的本质，简化思维过程，提高解题效率.。

第一章骨学第一章骨学1 选择题[A型题]1.桡神经沟位于A.肱骨上端B.肱骨体C.肱骨下端D.尺骨体E.桡骨体2.眶下孔位于A.颧骨B.鼻骨C.上颌骨D.下颌骨E.颞骨3.骺软骨A.位于骺的表面B.属于透明软骨C.成人的骺软骨呈线状D.属于纤维软骨E.随着年龄的增长而渐长4.属于桡骨下端的结构就是A.桡神经沟B.桡切迹C.尺切迹D.尺神经沟E.桡骨头5.犁骨A.左右各一B.位于筛板紧下方C.构成骨性鼻中隔上部D.构成骨性鼻中隔下部E.属于脑颅骨A.位于颅前窝B.属于筛骨上的结构C.属于额骨上的结构D.属于蝶骨上的结构E.就是蝶骨与筛骨间的裂隙7.肩胛骨A.内侧缘称腋缘B.内侧缘称脊柱缘,外侧角上有关节盂C.肩峰末端膨大形成喙突D.前面有肩胛冈E.后面为肩脚下窝。

8.腕骨包括A.距骨B.骰骨C.楔骨D.月骨E.跖骨9.外踝位于A.胫骨下端B.胫骨上端C.腓骨上端D.腓骨下端E.股骨下端10.髋臼上有A.耳状面B.月状面C.臀面D.髌面E.以上皆非11.一般椎骨不包括A.椎体B.椎弓C.椎孔E.棘突12.关于胸椎叙述正确的就是A.关节突呈矢状位B.椎体小C.椎孔最大D.有肋凹E.棘突呈方板状13.颈椎特有的结构A.横突肋凹B.关节突C.棘突D.横突孔E.椎孔14.骶骨与髋骨均有得结构就是A.粗线B.月状面C.耳状面D.弓状线E.髋臼15.不成对的面颅骨有A.鼻骨B.泪骨C.舌骨D.腭骨E.额骨16.成对的脑颅骨有A.颧骨B.犁骨C.顶骨D.蝶骨E.枕骨17.颅后窝有A.颈动脉沟B.乙状窦沟C.外耳门D.三叉神经压迹E.筛孔18.脑膜中动脉沟起自A.圆孔B.卵圆孔C.棘孔D.破裂孔E.茎乳孔19.肱骨骨折的最易发部位就是A.解剖颈B.外科颈C.肱骨干D.肱骨下端E.尺神经沟20.不属于颅中窝的结构有A.眶上裂B.眶下裂C.颈动脉沟D.视神经管E.卵圆孔21.颅底内面能见到而外面瞧不见的结构有A.圆孔B.卵圆孔C.棘孔D.破裂孔E.颈静脉孔22.骶管麻醉的穿刺部位应正对A.骶前孔B.骶后孔C.骶管裂孔D.骶角E.骶岬23.颅中窝有A.筛孔B.垂体窝C.颈动脉管外口D.颈静脉孔E.鸡冠24.眶与鼻腔相交通就是通过A.眶下裂B.眶下管C.眶下孔D.鼻泪管E.圆孔25.构成骨性鼻中隔的就是A.犁骨与腭骨B.上颌骨与犁骨C.筛骨垂直板与犁骨D.下鼻甲与犁骨E.犁骨与鼻骨26.中鼻甲属于A.上颌骨B.蝶骨C.筛骨D.上鼻甲的一部分E.鼻骨27.关于鼻旁窦正确的说法就是A.都开口于上鼻道B.都开口于中鼻道C.口腔感染时易波及到鼻旁窦D.鼻腔感染时易波及到鼻旁窦E.上颌窦开口于下鼻道28.分泌物引流最不畅的鼻旁窦就是A.上颌窦B.筛窦前、中群。

相似三角形练习题一、选择题一、下列各组图形中不是位似图形的是（）A．B．C．D．二、若2：3=7：x，则x=（）A．2B．3C．3.5D．10.53、两个相似三角形的一组对应边别离为5cm和3cm，若是它们的面积之和为136cm2，则较大三角形的面积是（）A．36cm2B．85cm2C．96cm2D．100cm2 4、如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD，若B（1，0），则点C的坐标为（）A．（1，-2）B．（-2，1）C．（）D．（1，-1）五、如图，已知点A在反比例函数y=(x < 0)上，作Rt△ABC，点D是斜边AC的中点，连DB并延长交y轴于点E，若△BCE的面积为8，则k的值为( )A .8B .12C .16D .20六、如图，平面直角坐标系中，直线y=-x+a与x、y轴的正半轴别离交于点B和点A，与反比例函数y=-的图象交于点C，若BA：AC=2：1，则a的值为（）A．2B．-2C．3D．-37、如图，△ABC与△DEF是位似图形，位似比为2：3，已知AB=4，则DE的长等于( )A .6B .5C .9D .八、如图，已知在△ABC中，点D、E、F别离是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于( )A .5∶8B .3∶8C .3∶5D .2∶5九、如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③=；④=AD•AB．其中单独能够判定△ABC∽△ACD的个数为( )A .1B .2C .3D .410、如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，动点P从点B动身，沿着B-A-D在菱形ABCD的边上运动，运动到点D停止，点P′是点P关于BD的对称点，PP′交BD于点M，若BM=x，△OPP′的面积为y，则y与x之间的函数图象大致为（）A．B．C．D．1一、在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC 的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t（秒）．设△OMN的面积为S，则能反映S与t之间函数关系的大致图象是（）A．B．C．D．1二、如图，已知在梯形ABCD中，AD∥BC，BC=2AD，若是对角线AC与BD相交于点O，△AOB、△BOC、△COD、△DOA的面积别离记作S1、S2、S3、S4，那么下列结论中，不正确的是（）A．S1=S3B．S2=2S4C．S2=2S1D．S1•S3=S2•S4二、填空题13、如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是 __________ cm．14、如图，在△PMN中，点A、B别离在MP和NP的延长线上，==，则= __________ ．三、解答题1五、已知=,求下列算式的值．（1）;（2）1六、如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，极点E、H别离在AB、AC上，已知BC=40cm，AD=30cm．（1）求证：△AEH∽△ABC；（2）求这个正方形的边长与面积。

相似几何模型之“K”字型例题1、⑴问题：如图1,在四边形ABCD中，点P为AB上一点,ZDPC=ZA=ZB=90°，求证：AD•BC=AP•BP;(2)探究：如图2,在四边形ABCD中，点P为AB上一点，当Z DPC=Z A=Z B=0时，上述结论是否依然成立？说明理由．(3)应用：请利用(1)(2)获得的经验解决问题：如图3,在AABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度，由点A出发，沿边AB 向点B运动，且满足Z CPD=Z A,设点P的运动时间为(秒)，当DC=4BC时，求t的值．A ．1B ．2C ．3D ．4例题2、如图,在等边△ABC 中，将A ABC 沿着MN 折叠。

使点A 落在边BC 上的点D 处。

⑴若AB =4,当A BMP 为直角三角形时，求AM 的长。

(2)当BD :CD =1:3时，求AM-.AN 的值。

【巩固练习】1.如图，已知AABC 和AADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F,AB=9,BD =3,则CF 等于()2.如图坐标系中，0(0,0),A (6,6J 3),B (12,0),将AOAB 沿直线线CD 折叠，使点A 恰好落在线段OB 上的点E 处，若OE=24,则CE ：DE 的值是.5AE3•正方形ABCD边长为4,M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM丄MN.⑴设BM=x,CN=y,求y与x之间的函数关系式.(2)在点M,N运动的过程中，求CN的最小值.4.如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，AB4=16，点D与点A关于y轴对称,tan Z ACB=§,Z CDE=Z CAO，点E、F分别是线段AD、AC上的动点(点E不与点A、D重合)，且Z CEF=Z ACB.(1)求AC的长和点D的坐标；(2)证明：△AEF^^DCE;(3)当A EFC为等腰三角形时，求点E的坐标.5•如图•等腰直角三角形ABC中，Z A=90°,P为BC的中点，小明拿着含45°角的透明三角形，使45°角的顶点落在点P,且绕P旋转.(1)如图①：当三角板的两边分别AB、AC交于E、F点时，试说明△BPE S^CFP.(2)将三角板绕点P旋转到图②，三角板两边分别交BA延长线和边AC于点EF.探究1：△BPE与A CFF.还相似吗？(只需写结论)探究2：连接EF,△BPE与A EFF是否相似？请说明理由.图②图①6.【试题再现】如图1,Rt^ABC中，Z ACB=90°,AC=BC,直线I过点C,过点A、B分别作AD丄/于点D,BELl于点E,则DE=AD+BE（不用证明）.（1）【类比探究】如图2,在A ABC中，AC=BC,且Z ACB=Z ADC=Z BEC=100°,上述结论是否成立？若成立,请说明理由：若不成立,请写出一个你认为正确的结论．（2）【拓展延伸】①如图3,在A ABC中，AC=nBC,且Z ACB=Z ADC=Z BEC=100°,猜想线段DE、AD、BE之间有什么数量关系？并证明你的猜想.②若图1的Rt^ABC中,Z ACB=90°,AC=nBC,并将直线l绕点C旋转一定角度后与斜边AB相交，分别过点A、B作直线l的垂线，垂足分别为点D和点E,请在备用图上画出图形，并直接写出线段DE、AD、BE之间满足的一种数量关系（不要求写出证明过程）.-g__/—_D存备用團【例题讲解】（构造“K”字型）基本构造方法例题1.如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为(4,8),将矩形沿对角线AC翻折，B点落在D点的位置，且AD交尹轴于点那么点D 的坐标为.k例题2•如图，矩形ABCD中，AB=2AD,点A(O,1),点C、D在反比例函数y=x(k>0)的图象上，AB与x轴的正半轴相交于点E，若E为AB的中点，则k的值为.例题3、如图，直线a〃b〃c,a与b之间的距离为3,b与c之间的距离为6,a、b、c分别经过等边三角形ABC的三个顶点，则三角形的边长为.C本次课课后练习1、如图，直线\J\J\,等腰直角三角形ABC的三个顶点A，B，C分别在°l2，13上,乙ACB=90°，AC交l2于点D,已知*与12的距离为1，12与13的距离为3,则A ABC的面积为A5k2.如图，边长为4的正方形ABCD的顶点A在y轴上，顶点D在反比例函数y=-（x>0）的图象上，已知点B的坐标是］3,4）则k 的值为（）2727A.7B・C・4D・61683.如图，AB=4,射线BM和AB互相垂直，点D是AB上的一个动点，点E在射线BM上,BE=|D B，作EF丄DE并截取EF=DE，连结AF并延长交射线BM于点C.设BE=x,BC=y，则y关于x的函数解析式是（）12x A^y=~X^4 _2x一3x「8xB•尸—c.y=—戸D^y=-x^44.如图，在矩形AOBC中，点A的坐标（一2,1）,点C的纵坐标是4,则B、C两点的坐分别是（A. 〔4, 2)、)J2'4)B.〔I，3)」C. 討、〔-2'4D.[4 I)、〔一I'4)5.如图，在平面直角坐标系中，矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、mD在反比例函数y=x（m>°）的图象上，若tanZADB=2.则点D的坐标为.。

专题11 相似三角形中的“K”字型相似模型【模型展示】如图，直角三角形被斜边上的高分成的两个直角三角形与原三角形相似，即△ACD∽△ABC∽△CBD.CA222“三垂直”模型如图，∠B＝∠D＝∠ACE＝90°，则△ABC∽△CDE.“一线三等角”模型如图，∠B＝∠ACE＝∠D，则△ABC∽△CDE.特别地，连接AE，若C为BD的中点，则△ACE∽△ABC∽△CDE.【题型演练】一、单选题1．如图，矩形纸片ABCD中，AB=6，BC=8，E是边CD上一点，连接AE．折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上．若DE=4，则AF的长为（）A．163B．4C．3D．2【答案】C【分析】由矩形的性质可得AB=CD=6，AD=BC=8，∠BAD=∠D=90°，通过证明∠ABF∠∠DAE，可得AF DEAB AD=，即可求解．【详解】解：∠矩形ABCD，∠∠BAD=∠D=90°，BC=AD=8∠∠BAG+∠DAE=90°∠折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，∠BF垂直平分AG∠∠ABF+∠BAG=90°∠∠DAE=∠ABF，∠∠ABF∠∠DAE∠AF ABDE AD=即648AF=解之：AF=3．故答案为：C．【点评】本题考查了翻折变换，矩形的性质，相似三角形的判定与性质，熟练掌握翻折变换和矩形的性质，证明三角形相似是解题的关键．2．如图，边长为10的等边ABC中，点D在边AC上，且3AD=，将含30°角的直角三角板（30F∠=︒）绕直角顶点D旋转，DE、DF分别交边AB、BC于P、Q．连接PQ，当//EF PQ 时，DQ长为（）A．6B C．10D．【答案】B【分析】过点Q作QK AC⊥于K，根据等边三角形，和含30︒角的直角三角形，易证得ADP BPQ∽△△，从而求得线段BP，AP，BQ，CQ，CK，QK，DK的长度，最后在Rt DQK△中利用勾股定理可以求得DQ 的长度．【详解】解：过点Q 作QK AC ⊥于K ，在等边ABC 中，60∠=∠=∠=︒A B C ，10AB BC AC ， 在Rt EFD 中，60E ∠=︒，30F ∠=︒，∠//EF PQ ，∠60DPQ ∠=︒，30DQP ∠=︒，∠APD ADP APD QPB ∠+∠=∠+∠，∠ADP QPB ∠=∠，又∠∠A =∠B =60°，∠ADP BPQ ∽△△， ∠AD AP PD BP BQ QP==， ∠在Rt PQD △中，30DQP ∠=︒， ∠12PD QP =， 即12PD QP =， ∠12AD AP PD BP BQ QP ===， ∠3AD =， ∠312BP =， ∠6BP =，已知10AB =∠1064AP AB BP =-=-=， ∠412BQ =， ∠8BQ =，∠1082CQ BC BQ =-=-=，在Rt CQK △中，60C ∠=︒，∠30KQC ∠=︒， ∠2122CQ KC ===， ∠DK AC AD KC =--，∠10316DK =--=，而sin KQ C CQ ∠=,∠sin 602KQ ︒==∠KQ =在Rt DQK △中，DQ∠DQ =即DQ =故选：B ．【点睛】本题考查了等边三角形的性质，特殊三角函数值，一线三等角的相似模型，正确找到相似三角形是解题的关键．3．如图，在矩形ABCD 中，CD ＝4，E 是BC 的中点，连接AE ，tan∠AEB 43=，P 是AD 边上一动点，沿过点P 的直线将矩形折叠，使点D 落在AE 上的点D 处，当APD '△是直角三角形时，PD 的值为（ ）A ．23或67B ．83或247C ．83或307D ．103或187【答案】B【分析】根据矩形的性质得到AB ＝CD ，∠B ＝90°，根据勾股定理求得AE ，当∠APD '是直角三角形时，分两种情况分类计算即可；【详解】∠四边形ABCD 是矩形，∠AB ＝CD ，∠B ＝90°，∠CD ＝4，tan∠AEB 43=，∠BE ＝3，在Rt ∠ABE 中，AE 5=，∠E 是BC 的中点，∠AD ＝6，由折叠可知，PD ＝PD '，设PD ＝x ，则PD '＝x ，AP ＝6﹣x ，当∠APD '是直角三角形时，∠当∠AD 'P ＝90°时，∠∠AD 'P ＝∠B ＝90°，∠AD ∠BC ，∠∠P AD '＝∠AEB ，∠∠ABE ∠∠PD 'A ， ∠AP PD AE AB '=， ∠654x x -=， ∠x 83=， ∠PD 83=； ∠当∠APD '＝90°时，∠∠APD '＝∠B ＝90°，∠∠P AE ＝∠AEB ，∠∠APD '∠∠EBA ， ∠AP PD BE AB '=， ∠634x x -=， ∠x 247=， ∠PD 247=； 综上所述：当∠APD '是直角三角形时，PD 的值为83或247； 故选：B ．【点睛】本题主要考查了矩形的性质，勾股定理，直角三角形的性质，相似三角形的判定与性质，准确计算是解题的关键．4．如图，在矩形ABCD 中，4AB =，5AD =，E 、F 、G 、H 分别为矩形边上的点，HF 过矩形的中心O ，且HF AD =．E 为AB 的中点，G 为CD 的中点，则四边形EFGF 的周长为（ ）A ．B ．C ．D ．【答案】B【分析】连接EG ，证明四边形EHGF 是矩形，再证明AEH DHG △∽△，求得AH 与DH 的长度，由勾股定理求得EH 与HG ，再由矩形的周长公式求得结果．【详解】解：连接EG ，四边形ABCD 是矩形，AB CD ∴=，//AB CD ， E 为AB 的中点，G 为CD 的中点，AE DG ∴=，//AE DG ，∴四边形AEGD 是平行四边形，AD EG ∴=，矩形是中心对称图形，HF 过矩形的中心O ．EG ∴过点O ，且OH OF =，OE OG =，∴四边形EHGF 是平行四边形，HF AD EG ==，∴四边形EHGF 是矩形，90EHG ∴∠=︒，90A D ∠=∠=︒，90AHE AEH AHE DHG ∴∠+∠=∠+∠=︒，AEH DHG ∴∠=∠，AEH DHG ∴△∽△， ∴AH AE DG DH=，设AH x =，则5DH x =-，122AE DG AB ===， ∴225x x=-， 解得，1x =或4，1AH ∴=或4，当1AH =时，4DH =，则HE =HG∴四边形EFGH 的周长2=⨯=同理，当4AH =时，四边形EFGH 的周长2=⨯=；故选：B ．【点睛】本题主要考查了矩形的性质，相似三角形的性质与判定，勾股定理，关键在于证明四边形EHGF 是矩形．5．如图，E 、F 、G 、H 分别为矩形的边AB 、BC 、CD 、DA 的中点，连接AC 、HE 、EC 、GA 、GF ，已知AG ∠GF ，AC 则下列结论：∠∠DGA =∠CGF ；∠∠DAG ∠∠CGF ；∠AB =2；∠BE CF ．正确的个数是（ ）A ．2个B ．3个C ．4个D ．5个 【答案】B【分析】由余角的定义可推出90DGA CGF ∠+∠=︒，并不能说明DGA CGF ∠=∠，说明∠错误；再根据90DAG DGA ∠+∠=︒，可推出DAG CGF ∠=∠，进而可证明DAG CGF ，说明∠正确；连接BD ，由三角形中位线可知12GF BD =DAG CGF 可进一步推出2CF CG CG CF =，即2CF =，即BE =，说明∠正确；在Rt GCF 中，222GF CF CG =+，即可求出CG 长度，即可求出AB=2，说明∠正确．【详解】解：∠90AGF ∠=︒，∠90DGA CGF ∠+∠=︒，∠不能说明DGA CGF ∠=∠，故∠错误．∠90DAG DGA ∠+∠=︒，∠DAG CGF ∠=∠，又∠90ADG GCF ∠=∠=︒∠DAG CGF ，故∠正确．如图连接BD ，由题意可知AC BD =∠G 和F 分别为CD 和BC 的中点，∠12GF BD = ∠DAG CGF ∠AD DG GC CF =，即2CF CG CG CF=，∠CF =在Rt GCF 中，222GF CF CG =+，即222)CG =+, 解得1CG =∠22AB CG ==，故∠正确．∠BE CG =，∠CF BE ，即BE ，故∠正确． 综上正确的有∠∠∠共3个．故选B ．【点睛】本题考查矩形的性质，余角，三角形中位线，三角形相似的判定和性质以及勾股定理，综合性强．能够连接常用的辅助线和证明DAG CGF 是解答本题的关键．6．如图，在ABC 中，490,5cm,cos 5C AB B ∠=︒==．动点D 从点A 出发沿着射线AC 的方向以每秒1cm 的速度移动，动点E 从点B 出发沿着射线BA 的方向以每秒2cm 的速度移动．已知点D 和点E 同时出发，设它们运动的时间为t 秒．连接BD ．下列结论正确的有（ ）个∠4BC =；∠当AD AB =时，tan 2ABD ∠=；∠以点B 为圆心、BE 为半径画B ，当2513t =时，DE 与B 相切； ∠当CBD ADE ∠=∠时，2511t． A ．1B ．2C ．3D ．4 【答案】D【分析】利用锐角三角函数求出BC 可判断∠，利用勾股定理求AC ，BD ，AG ，再用正切锐角三角函数定义求值可判断∠，利用相似三角形判定与性质，可判断∠，利用相似三角形判定与性质建构方程，解方程求解可判断∠【详解】解：在ABC 中，490,5cm,cos 5C AB B ∠=︒==． 4cos 545BC AB B =⋅=⨯=， 故∠4BC =正确；作AG ∠BD 于G ，在Rt∠ABC 中，3AC =，∠AD =AB =5，AG ∠BD∠CD =AD -AC=5-3=2，DG =BG ，在Rt∠DCB 中，BD =∠DG =BG在Rt∠BGA 中，AG =∠tan 2AG ABD BG ∠===， 故∠当AD AB =时，tan 2ABD ∠=正确；AD =t ，BE =2t ，cos A =35AC AB =， 当2513t =时，2513AD t ==，2550221313BE t ==⨯=， ∠50155251313AE AB BE t =-=-=-=， ∠1531325513AE AD ==， ∠cos A ==AE AC AD AB，∠DAE =∠BAC ， ∠∠ADE ∠∠ABC ，∠∠AED =∠ACB =90°，∠∠DEB =90°，∠DE 与B 相切，故∠以点B 为圆心、BE 为半径画B ，当2513t =时，DE 与B 相切正确；过E 作EH ∠AC 于H ，当CBD ADE ∠=∠时，∠∠EHD =∠DCB =90°，∠∠EHD ∠∠DCB ， ∠HE DH CD CB=， ∠AE =5-2t ，∠AH =()35-25t ，EH =()45-25t ，3CD t =-，6113355HD AD AH t t t =-=-+=-， ∠()4115235534t t t --=-， 整理得211801250t t -+=，因式分解得()()112550t t --=， ∠2511t 或5t =（舍去），故∠当CBD ADE ∠=∠时，2511t正确；正确的结论有4个．故选择D ．【点睛】本题考查锐角三角函数求边长，勾股定理，相似三角形判定与性质，圆的切线判定，一元二次方程的解法，掌握锐角三角函数求边长，勾股定理，相似三角形判定与性质，圆的切线判定，一元二次方程的解法是解题关键．二、填空题7．如图，正方形ABCD 的对角线AC ，BD 相交于点O，AB =E 为OC 上一点，2OE =，连接BE ，过点A 作AF BE ⊥于点F ，与BD 交于点G ，则EF 的长是______．【分析】根据 正方形的性质求出5AO BO CO ===，证明EBO EAF ∽△△得到EF AE OE BE =，即可求出答案.【详解】解：四边形ABCD 是正方形，AB =90AOB ∠=︒∴，OA=OB=OC=OD ，∠222OA AB =,∠5AO BO CO ===，AF BE ⊥，EBO EAF ∴∠=∠，EBO EAF ∴∽△△，即EF AE OE BE= 2OE =，5OB OA ==，BE ∴=7AE =，2EF ∴=EF =. 【点睛】此题考查正方形的性质，勾股定理，相似三角形的判定及性质，解题中熟练掌握并运用各知识点是解题的关键.8．如图，在矩形ABCD 中，9AB =，12BC =，F 是边AD 上一点，连接BF ，将ABF △沿BF 折叠使点A 落在G 点，连接AG 并延长交CD 于点E ，连接GD ．若DEG △是以DG 为腰的等腰三角形，则AF 的长为________．或9 2【分析】分两种情形：如图1中，当GD=GE时，过点G作GM∠AD于M，GN∠CD于N．设AF=x，证明∠BAF∠∠ADE，推出AB AFDA DE=，可得DE=43x，再证明AM=MD=6，在Rt∠FGM中，利用勾股定理构建方程求解．如图2中，当DG=DE时，利用相似三角形的性质求解即可．【详解】解：如图1中，当GD=GE时，过点G作GM∠AD于M，GN∠CD于N．设AF=x．∠四边形ABCD是矩形，∠AD=BC=12，∠BAF=∠ADE=90°，由翻折的性质可知，AF=FG，BF∠AG，∠∠DAE+∠BAE=90°，∠ABF+∠BAE=90°，∠∠ABF=∠DAE，∠∠BAF=∠ADE=90°，∠∠BAF∠∠ADE，∠AB AF DA DE=，∠912xDE=，∠DE=43x，∠GM∠AD，GN∠CD，∠∠GMD=∠GND=∠MDN=90°，∠四边形GMDN是矩形，∠GM=DN=EN=23 x，∠GD=GE，∠∠GDE=∠GED，∠∠GDA+∠GDE=90°，∠GAD+∠GED=90°，∠∠GDA=∠GAD，∠GA =GD =GE ，∠GM ∠DE ，∠AM =MD =6，在Rt ∠FGM 中，则有()222()263x x x =-+，解得x =（舍弃），∠AF ． 如图2中，当DG =DE 时，由翻折的性质可知，BA =BG ，∠∠BAG =∠BGA ，∠DG =FE ，∠∠DGE =∠DEG ，∠AB ∠CD ，∠∠BAE =∠DEG ，∠∠AGB =∠DGE ，∠B ，G ，D 共线，∠BD 15=，BG =BA =9，∠DG =DE =6，∠∠BAF ∠∠ADE ， ∠AF AB DE AD =， ∠9612AF =， ∠AF =92，综上所述，AF 或92．【点睛】本题考查矩形的性质，翻折变换，相似三角形的判定和性质，解直角三角形等知识，解题的关键是学会利用参数构建方程解决问题，属于中考填空题中的压轴题．9．如图，ABC 为等边三角形，点D ，E 分别在边AB ，AC 上，3BD =，将ADE 沿直线DE 翻折得到FDE ，当点F 落在边BC 上，且4BF CF =时，DE AF ⋅的值为______．【分析】根据∠ABC 为等边三角形，∠ADE 与∠FDE 关于DE 成轴对称，可证∠BDF ∠∠CFE ，根据BF =4CF ，可得CF =4，根据AF 为轴对称图形对应点的连线,DE 为对称轴，可得DE ∠AF ，根据S 四边形ADFE =12DE AF ⋅=S △CEF =-S △ABC -S △CEF ，进而可求DE AF ⋅= 【详解】解：如图，作∠ABC 的高AL ，作∠BDF 的高DH ，∠∠ABC 为等边三角形，∠ADE 与∠FDE 关于DE 成轴对称，∠∠DFE =∠DAE = 60°，AD = DF ，∠∠CFE +∠FEC =∠CFE +∠DFB = 120°，∠∠DFB = ∠CEF ，又∠B =∠C = 60°，∠∠BDF ∠∠CFE ， ∠BD CF BE CE= ， 即BF CF CE BD ⋅=， 设CF = x (x > 0)，∠BF =4CF ，∠BF = 4x ，∠BD =3， ∠243x CE =， ∠45BC BF CF x x x =+=+=，∠53AD AB BD BC BD DF x =-=-==-，2453x AE EF x ==-， ∠∠BDF ∠∠CFE ， ∠DF BD EF CF=， ∠2533453x x x x -=- 解得：x =2，∠CF =4，∠BC =5x =10，∠在Rt ∠ABL 中，∠B =60°，∠AL =AB∠S △ABC=1102⨯⨯= ∠在Rt ∠BHD 中，BD =3，∠B =60°，∠DH =BDsin60°=3= ∠S △BDF=11822BF DH ⋅=⨯= ∠∠BDF ∠∠CFE ， ∠223924BDF CFE S BD S CF ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭， ∠S△BDF =∠S △CEF ， 又∠AF 为轴对称图形对应点的连线,DE 为对称轴，∠AD =DF ，∠ADF 为等腰三角形，DE ∠AF ，∠S 四边形ADFE =12DE AF ⋅=S △CEF =-S △ABC -S △CEF==，∠DE AF⋅=故答案为．【点睛】本题主要考查等边三角形的和折叠的性质，一线三等角证明k型相似，以及“垂美四边形”的性质：对角线互相垂直的四边形的面积＝对角线乘积的一半．三、解答题10．如图，在矩形ABCD中，E为AD的中点，EF∠EC交AB于F，延长FE与直线CD相交于点G，连接FC（AB＞AE）．(1)求证：∠AEF∠∠DCE；(2)∠AEF与∠ECF是否相似？若相似，证明你的结论；若不相似，请说明理由；(3)设ABkBC=，是否存在这样的k值，使得∠AEF与∠BFC相似？若存在，证明你的结论并求出k的值；若不存在，请说明理由．【答案】(1)见解析(2)相似，证明见解析(3)存在，k【分析】(1)由题意可得∠AEF＋∠DEC＝90°，又由∠AEF＋∠AFE＝90°，可得∠DEC＝∠AFE，据此证得结论；(2)根据题意可证得Rt∠AEF∠Rt∠DEG(ASA)，可得EF＝EG，∠AFE＝∠EGC，可得CE垂直平分FG，∠CGF是等腰三角形，据此即可证得∠AEF与∠ECF相似；(3)假设∠AEF与∠BFC相似，存在两种情况：∠当∠AFE＝∠BCF，可得∠EFC＝90°，根据题意可知此种情况不成立；∠当∠AFE＝∠BFC，使得∠AEF与∠BFC相似，设BC＝a，则AB＝ka，可得AF＝13ka，BF＝23ka，再由∠AEF∠∠DCE，即可求得k值．（1）证明：∠EF∠EC，∠∠FEC＝90°，∠∠AEF＋∠DEC＝90°，∠∠AEF＋∠AFE＝90°，∠∠DEC＝∠AFE，又∠∠A＝∠EDC＝90°，∠∠AEF∠∠DCE；（2）解：∠AEF∠∠ECF．理由：∠E为AD的中点，∠AE＝DE，∠∠AEF＝∠DEG，∠A＝∠EDG，∠∠AEF∠∠DEG(ASA)，∠EF＝EG，∠AFE＝∠EGC．又∠EF∠CE，∠CE垂直平分FG，∠∠CGF是等腰三角形．∠∠AFE＝∠EGC＝∠EFC．又∠∠A＝∠FEC＝90°，∠∠AEF∠∠ECF；（3）解：存在k使得∠AEF与∠BFC相似．理由：假设∠AEF与∠BFC相似，存在两种情况：∠当∠AFE＝∠BCF，则有∠AFE与∠BFC互余，于是∠EFC＝90°，因此此种情况不成立；∠当∠AFE＝∠BFC，使得∠AEF与∠BFC相似，设BC＝a，则AB＝ka，∠∠AEF∠∠BCF，∠12AFAE BF BC ， ∠AF ＝13ka ，BF ＝23ka ， ∠∠AEF ∠∠DCE ， ∠AE AF DC DE =，即113212ka a ka a =，解得，k =．∠存在k ∠AEF 与∠BFC 相似． 【点睛】本题考查了矩形的性质，相似三角形的判定及性质，全等三角形的判定与及性质，等腰三角形的判定及性质，采用分类讨论的思想是解决本题的关键．11．（1）问题如图1，在四边形ABCD 中，点P 为AB 上一点，当90DPC A B ∠=∠=∠=︒时，求证：AD BC AP BP ⋅=⋅．（2）探究若将90°角改为锐角或钝角（如图2），其他条件不变，上述结论还成立吗？说明理由．（3）应用如图3，在ABC 中，AB =45B ∠=︒，以点A 为直角顶点作等腰Rt ADE △．点D 在BC 上，点E 在AC 上，点F 在BC 上，且45EFD∠=︒，若CE CD 的长．【答案】（1）见解析；（2）成立，理由见解析；（3）5CD =【分析】（1）由∠DPC =∠A =B =90°，可得∠ADP ＝∠BPC ，即可证到∠ADP ∽∠BPC ，然后运用相似三角形的性质即可解决问题；（2）由∠DPC ＝∠A ＝∠B ＝α，可得∠ADP =∠BPC ，即可证到∠ADP ∽∠BPC ，然后运用相似三角形的性质即可解决问题；（3）先证∠ABD ∽∠DFE ，求出DF =4，再证∠EFC ∽∠DEC ，可求FC ＝1，进而解答即可．【详解】（1）证明：如题图1，∠∠DPC =∠A =∠B =90°，∠∠ADP ＋∠APD =90°，∠BPC ＋∠APD = 90°， ∠∠ADP = ∠BPC ，∠∠ADP ∽∠BPC ，AD AP BP BC∴=， ∠AD ⋅BC = AP ⋅BP ，（2）结论仍然成立，理由如下，BPD DPC BPC ∠=∠+∠，又BPD A ADP ∠=∠+∠，DPC BPC A ADP ∴∠+∠=∠+∠，DPC A ∠=∠，设DPC A α∠=∠=，BPC ADP ∴∠=∠，ADP BPC ∴∽△△，AD AP BP BC∴=， ∠AD ⋅BC = AP ⋅BP ，（3）45EFD ∠=︒，45B ADE ∴∠=∠=︒，BAD EDF ∴∠=∠，ABD DFE ∴∽，AB AD DF DE∴=， ADE 是等腰直角三角形，DE ∴=， 2AB =4DF ∴=，45,45EFD ADE ∠=︒∠=︒，135EFC DEC ∴∠=∠=︒，EFC DEC ∴∽，FC EC EC CD∴=， 5EC =4CD DF FC FC =+=+， ()245EC FC CD FC FC ∴=⋅=⋅+=， 1FC ∴=，【点睛】本题考查相似三角形的综合题，三角形的相似；能够通过构造45°角将问题转化为一线三角是解题的关键．12．【感知】如图∠，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），90A B DPC ∠=∠=∠=︒．易证DAP PBC △△∽．（不需要证明）【探究】如图∠，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），A B DPC ∠=∠=∠．若4PD =，8PC =，6BC =，求AP 的长．【拓展】如图∠，在ABC 中，8AC BC ==，12AB =，点P 在边AB 上（点P 不与点A 、B 重合），连结CP ，作CPE A ∠=∠，PE 与边BC 交于点E ，当CPE △是等腰三角形时，直接写出AP 的长．【答案】【探究】3；【拓展】4或203． 【分析】探究：根据相似三角形的性质列出比例式，计算即可；拓展：证明∠ACP ∠∠BPE ，分CP =CE 、PC =PE 、EC =EP 三种情况，根据相似三角形的性质计算即可．【详解】探究：证明：∠DPB ∠是APD △的外角，∠DPB A PDA ∠=∠+∠，即DPC CPB A PDA ∠+∠=∠+∠，∠A DPC ∠=∠，∠PDA CPB ∠=∠，又∠A B ∠=∠，∠DAP PBC △△∽， ∠PD AP PC BC=， ∠4PD =，8PC =，6BC =， ∠486AP =， 解得：3AP =；拓展：∠AC =BC ，∠∠CPB 是∠APC 的外角，∠∠CPB =∠A +∠PCA ，即∠CPE +∠EPB =∠A +∠PCA ，∠∠A =∠CPE ，∠∠ACP =∠BPE ，∠∠A =∠B ，∠∠ACP ∠∠BPE ，当CP =CE 时，∠CPE =∠CEP ，∠∠CEP ＞∠B ，∠CPE =∠A =∠B ，∠CP =CE 不成立；当PC =PE 时，∠ACP ∠∠BPE ，则PB =AC =8，∠AP =AB -PB =12-8=4；当EC =EP 时，∠CPE =∠ECP ，∠∠B =∠CPE ，∠∠ECP =∠B ，∠PC =PB ，∠∠ACP ∠∠BPE ， ∠AC AP PC BP BE EP ==， 即8128PB PB PB BE BE-==-， 解得：163PB =， ∠AP =AB -PB =16201233-=， 综上所述：∠CPE 是等腰三角形时，AP 的长为4或203． 【点睛】本题考查的是相似三角形的判定和性质、等腰三角形的性质、三角形的外角性质，灵活运用分情况讨论思想是解题的关键．13．如图，在矩形ABCD 中，E 是BC 上一点，DF AE ⊥于点F ，设()0AD AEλλ=>．（1）若1λ=，求证：CE FE =；（2）若3,4AB AD ==，且D B F 、、在同一直线上时，求λ的值．【答案】（1）证明见解析；（2）1615【分析】（1）根据矩形的性质可得，90//B AD BC AB CD AD BC ∠=︒==，，，，再根据已知条件DF AE ⊥，即可证明DFA ∠ABE △，则AF BE =，进而通过线段的和差关系求得； （2）由勾股定理求得BD 的长度，再由ABD △的面积求得AF 的长度，则可用勾股定理求得DF 的长度，则可得BF 的长度，再由DFA ∠ABE △，求得EB 的长度，在Rt ABE 中，根据勾股定理即可求得AE ，即可求得λ的值．【详解】（1）∠1λ=， ∠1AD AE=， ∠AD AE =，又∠四边形ABCD 是矩形，∠90//B AD BC AB CD AD BC ∠=︒==，，，，∠DAF AEB ∠=∠，∠DF AE ⊥，∠90DFA B ∠=∠=︒，∠在DFA 和ABE △中，DFA B DAF AEB AD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∠DFA ∠ABE △，∠AF BE =，∠=AE AD BC =，∠AE AF BC BE -=-，∠CE FE =；（2）如图，D B F 、、三点共线，∠3,4AB AD ==，∠5BD =，∠DF AE ⊥， ∠1122ABD S AB AD BD AF =⋅=⋅△， ∠341255AB AD AF BD ⋅⨯===，∠165DF ==， ∠169555BF BD DF =-=-=， ∠//AD BE ， ∠在ADF △和EBF △中，FAD FEB ADF EBF AFD EFB ∠=∠∠=∠∠=∠，，，∠ADF △∠EBF △， ∠AD DF EB BF=， 即164595EB =， ∠94EB =，∠154AE ==， ∠14161554AD AE λ===．【点睛】本题考查了矩形的性质、三角形全等的判定和性质、三角形相似的判定和性质、勾股定理、三角形面积、相似比等，解答本题的关键是熟练掌握运用以上知识点，利用勾股定理求解线段的长．14．如图，矩形ABCD 中，AB ＝1，BC ＝3，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ，点G 在线段EF 上，满足FG∠GE ＝1∠2，设BE ＝x ． （1）求证：AD DF AB BE=； （2）当点G 在∠ADF 的内部时，用x 的代数式表示∠ADG 的余切；（3）当∠FGD ＝∠AFE 时，求线段BE 的长．【答案】（1）见解析；（2）361x x --；（3． 【分析】（1）根据题意可证明∠DAF ＝∠BAE ，又由于∠ABE ＝∠ADF ＝90°，即证明∠ADF∠∠ABE ，所以AD DF AB BE=． （2）作GH∠CF 于H ，根据题意可求出DF ＝3BE ＝3x ，根据平行线分线段成比例得出13GH FH FG EC FC FE ===，即可列出关于x 的等式，从而得出GH 和FH 的长，即可求出HD 的长，cot∠ADG ＝cot∠DGH ＝GH HD，即可求出结果． （3）作EM//GD 交DC 于点M ，即可知12FD FG DM GE ==，可求出DM ，从而求出CM ，根据图形可证明∠ABE∠∠ECM ，即可得到AB EC BE CM=，即列出关于x 的方程，解出x 即可． 【详解】（1）如图，因为AF∠AE ，∠∠EAF ＝∠BAD ＝∠ADF ＝90°．∠同角的余角相等，∠∠DAF ＝∠BAE ．∠∠ABE ＝∠ADF ＝90°．∠∠ADF∠∠ABE ． ∠AD DF AB BE=．（2）由31DF AD BE AB ==，得DF ＝3BE ＝3x ． 如图，作GH∠CF 于H ，那么GH//BC//AD ． 根据题意结合平行线分线段成比例得：13GH FH FG EC FC FE ===． ∠EC BC BE =-，FC CD DF =+， ∠13313GH FH x x ==-+．即GH ＝1(3)3x -，FH ＝1(31)3x +． 在Rt∠GHD 中，HD ＝DF －FH ＝13(31)3x x -+＝123x -＝1(61)3x -， ∠∠ADG ＝∠DGH ，∠cot∠ADG ＝cot∠DGH ＝GH HD ＝1(3)31(61)3x x --=361x x --．（3）当点G 在∠ADF 内部时，很明显∠FGD 和∠AFE 不相等．所以点G 在∠ADF 外部． 如图，作EM//GD 交DC 于点M ，那么12FD FG DM GE ==． ∠DM ＝6x ，∠MC ＝1－6x ．如果∠FGD ＝∠AFE ，那么AF//GD//EM ．∠∠AEM ＋∠EAF ＝180°．∠∠AEM ＝90°．∠∠ABE∠∠ECM ． ∠AB EC BE CM =．即1316x x x-=-． 整理，得x 2－9x ＋1＝0．解得1x =23x >（不符合题意，舍去）．所以BE【点睛】本题考查三角形相似的判定与性质，矩形，余角，平行线的性质．综合性较强，作出辅助线是解答本题的关键．15．如图，已知四边形ABCD ，∠B ＝∠C ＝90°，P 是BC 边上的一点，∠APD ＝90°． （1）求证：ABP PCD △△；（2）若BC ＝10，CD ＝3，PD ＝AB 的长．【答案】（1）证明见解析；（2）8．【分析】（1）先根据直角三角形的两锐角互余、角的和差可得BAP CPD ∠=∠，再根据相似三角形的判定即可得证；（2）先利用勾股定理求出PC 的长，从而可得BP 的长，再利用相似三角形的性质即可得．【详解】（1）90,90B C APD ∠=∠=︒∠=︒，90BAP APB CPD APB ∠+∠=∠+∠=∴︒，BAP CPD ∴∠=∠，在ABP 和PCD 中，BAP CPD B C ∠=∠⎧⎨∠=∠⎩，ABP PCD ~∴；（2）在Rt PCD 中，3,CD PD ==6PC ∴，10BC =，4PB BC PC ∴=-=，由（1）已证：ABP PCD △△，AB PB PC CD ∴=，即463AB =， 解得8AB =．【点睛】本题考查了相似三角形的判定与性质、勾股定理等知识点，熟练掌握相似三角形的判定与性质是解题关键．16．如图，四边形ABCD 和四边形AEFG 都是矩形，C ，F ，G 三点在一直线上，连接AF 并延长交边CD 于点M ，若∠AFG ＝∠ACD ．（1）求证：∠∠MFC ∠∠MCA ；∠若AB ＝5，AC ＝8，求CF BE的值． （2）若DM ＝CM ＝2，AD ＝3，请直接写出EF 长．【答案】（1）∠见解析；∠FC EB ＝85；（2）EF 【分析】（1）∠根据两角对应相等两三角形相似，证明即可．∠证明∠AEF∠∠ABC ，推出AF AC ＝AE AB ，推出AF AE ＝AC AB，推出∠FAC∠∠EAB ，可得结论． （2）利用勾股定理求出AM ，AC ，由MFC∠∠MCA ，推出CM AM ＝FM CM ，求出MF ，AF ，由∠AEF∠∠ABC ，推出EF BC ＝AF AC ，可得结论． 【详解】（1）∠证明：∠∠AFG ＝∠ACD ，∠∠FCA +∠F AC ＝∠FCA +∠MCF ，∠∠F AC ＝∠MCF ，∠∠FMC ＝∠CMA ，∠∠MFC ∠∠MCA ．∠解：∠四边形AEFG ，四边形ABCD 都是矩形，∠FG ∠AE ，CD ∠AB ，∠∠AFG ＝∠F AE ，∠ACD ＝∠CAB ，∠∠AFG ＝∠ACD ，∠∠F AE ＝∠CAB ，∠∠AEF ＝∠ABC ＝90°，∠∠AEF ∠∠ABC ， ∠AF AC ＝AE AB ， ∠AF AE ＝AC AB， ∠∠F AE ＝∠CAB ，∠∠F AC ＝∠EAB ，∠∠F AC ∠∠EAB ， ∠FC EB ＝AC AB ＝85． （2）解：∠四边形ABCD 是矩形，∠∠D ＝90°，AD ＝BC ＝3，∠DM ＝MC ＝2，AD ＝3，∠CD ＝4，AM AC 5， ∠∠MFC ∠∠MCA ， ∠CM AM ＝FM CM，∠FM ＝2CM AM∠AF ＝AM ﹣FM ∠∠AEF ∠∠ABC ， ∠EF BC ＝AF AC ，∠3EF ＝135，∠EF【点睛】本题属于相似形综合题，考查了矩形的性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找相似三角形解决问题，属于中考压轴题．17．如图，在正方形ABCD 中，点E 在AD 上，EF ⊥BE 交CD 于点F ．（1）求证：ABE DEF ∆∆；（2）连结BF ，若ABEEBF ∆∆，试确定点E 的位置并说明理由． 【答案】（1）见解析；（2）点E 为AD 的中点．理由见解析【分析】（1）根据同角的余角相等证明∠ABE =∠DEF ，再由直角相等即可得出两三角形相似的条件；（2）根据相似三角形的对应边成比例，等量代换得出AB AB DE AE=，即可得出DE =AE ． 【详解】（1）证明∠四边形ABCD 是正方形，∠∠A =∠D =90°，∠∠AEB +∠ABE =90°，∠EF ∠BE ，∠∠AEB +∠DEF =90°，∠∠ABE =∠DEF ．在∠ABE 和∠DEF 中， ABE DEF A D ∠=∠⎧⎨∠=∠⎩∠∠ABE ∠∠DEF ；（2）∠∠ABE ∠∠DEF ， ∠AB BE DE EF=， ∠∠ABE ∠∠EBF ，∠AB BE AE EF=，∠AB AB DE AE=，∠DE=AE，∠点E为AD的中点．【点睛】本题主要考查了相似三角形的判定和性质，根据等角的余角相等证出两角相等是解决（1）的关键，根据相似三角形的对应边成比例等量代换是解决（2）的关键．18．如图，正方形ABCDP是BC边上的一动点，∠APB、∠APC的角平分线PE、PF分别交AB、CD于E、F两点，连接EF．（1）求证：∠BEP∠∠CPF；（2）当∠P AB＝30°时，求∠PEF的面积．【答案】（1）详见解析；（2）2-【分析】（1）由于PE平分∠APB，PF平分∠APC，所以∠EPF＝90°，然后根据相似三角形的判定即可求证∠BEP∠∠CPF；（2）由题意可知∠BPE＝30°，60°，根据含30度的直角三角形的性质即可求出答案．【详解】（1）∠PE平分∠APB，PF平分∠APC，∠∠APE＝12∠APB，∠APF＝12∠APC，∠∠APE+∠APF＝12（∠APB+∠APC）＝90°，∠∠EPF＝90°，∠∠EPB+∠BEP＝∠EPB+∠FPC＝90°，∠∠BEP＝∠FPC，∠∠B＝∠C＝90°，∠∠BEP∠∠CPF；（2）∠∠PAB＝30°，∠∠BPA＝60°，∠∠BPE＝30°，在Rt∠ABP中，∠PAB ＝30°，AB∠BP ＝1，在Rt∠BPE 中，∠BPE ＝30°，BP ＝1，∠EP ∠CP1，∠FPC ＝60°，∠PF ＝2CP ＝2，∠∠PEF 的面积为：12PE•PF ＝2 【点睛】本题考查相似三角形的综合问题，解题的关键是熟练运用相似三角形的性质与判定，含30度角的直角三角形的性质，本题属于中等题型．19．如图，四边形ABCD 是矩形，点P 是对角线AC 上一动点（不与A 、C 重合），连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，已知3AD =，5AC =．设AP 的长为x ．(1)AB =___________；当1x =时，PE =_________； (2)试探究：否是定值?若是，请求出这个值；若不是，请说明理由；(3)当PCE 是等腰三角形时，请求出x 的值．【答案】(1)4AB =,34PE PB = (2)PE PB 为定值，34PE PB = (3)75x =或4x = 【分析】（1）作PM AB ⊥于M 交CD 于N ．由BMP PNE ∆∆∽，推出PE PN PB BM =，只要求出PN 、BM 即可解决问题；（2）结论：PE PB的值为定值．证明方法类似（1）； （3）分两种情形讨论求解即可解决问题；（1）解：作PM AB ⊥于M 交CD 于N ．四边形ABCD 是矩形，3BC AD ∴==，5AC =，90ABC ∠=︒，4AB ∴=．在Rt APM △中，1PA =，35PM =，45AM =， 165BM AB AM ∴=-=， 3MN AD ==，125PN MN PM ∴=-=， 90PMB PNE BPE ∠=∠=∠=︒，90BPM EPN ∴∠+∠=︒，90EPN PEN ∠+∠=︒，BPM PEN ∴∠=∠，BMP PNE ∴△∽△， ∴12351645PE PB===， 故答案为4，34． （2） 结论：PE PB的值为定值． 理由：由PA x =，可得35PM x =．45AM x =，445BM x =-，335PN x =-， BMP PNE △∽△， ∴33354445x PE PN PB BM x -===-； （3）∠当点E 在线段CD 上时，连接BE 交AC 于F ．90PEC ∠>︒，所以只能EP EC =，EPC ECP ∴∠=∠，90BPE BCE ∠=∠=︒，BPC BCP ∴∠=∠，BP BC ∴=，BE ∴垂直平分线段PC ，在Rt BCF 中，cos CF BC BCF BC AC∠==， ∴335CF =， 95CF ∴=， 1825PC CF ∴==， 187555x PA ∴==-=． ∠当点E 在DC 的延长线上时，设BC 交PE 于G ．90PCE ∠>︒，所以只能CP CE =．CPE E ∴∠=∠，90GPB GCE ∠=∠=︒，PGB CGE ∠=∠，PBG E CPE ∴∠=∠=∠，90ABP PBC ∠+∠=︒，90APB CPE ∠+∠=︒，4AB AP ∴==，综上所述，x 的值为75或4． 【点睛】本题属于四边形综合题、考查了矩形的性质、相似三角形的判定和性质、勾股定理以及等腰三角形的构成条件等重要知识，同时还考查了分类讨论的数学思想，难度较大．20．【推理】如图1，在正方形ABCD 中，点E 是CD 上一动点，将正方形沿着BE 折叠，点C 落在点F 处，连结BE ，CF ，延长CF 交AD 于点G ．（1）求证：BCE CDG △△≌． 【运用】（2）如图2，在【推理】条件下，延长BF 交AD 于点H ．若45HD HF =，9CE =，求线段DE 的长．【拓展】（3）将正方形改成矩形，同样沿着BE 折叠，连结CF ，延长CF ，BF 交直线AD 于G ，两点，若AB k BC =，45HD HF =，求DE EC 的值（用含k 的代数式表示）．【答案】（1）见解析；（2）DE =（3【分析】（1）根据ASA 证明BCE CDG △△≌； （2）由（1）得9CE DG ==，由折叠得BCF BFC ∠=∠，进一步证明HF HG =，由勾股定理得2222HF FE DH DE +=+，代入相关数据求解即可；（3）如图，连结HE ，分点H 在D 点左边和点H 在D 点右边两种情况，利用相似三角形的判定与性质得出DE 的长，再由勾股定理得2222HF FE DH DE +=+，代入相关数据求解即可．【详解】（1）如图，BFE △由BCE 折叠得到，BE CF ∴⊥，90ECF BEC ∴∠+∠=︒． 又四边形ABCD 是正方形，90D BCE ∴∠=∠=︒，90ECF CGD ∴∠+∠=︒，BEC CGD ∴∠=∠， 又 正方形,ABCD,BC CD ∴=，()BCE CDG AAS ∴△△≌．（2）如图，连接EH ，由（1）得BCE CDG △△≌， 9CE DG ∴==，由折叠得BC BF =，9CE FE ==，BCF BFC ∴∠=∠．四边形ABCD 是正方形，//AD BC ∴，BCG HGF ∴∠=∠，又BFC HFG ∠=∠，HFG HGF ∴∠=∠，HF HG ∴=． 45HD HF =，9DG =， 4HD ∴=，5HF HG ==．90D HFE ∠=∠=︒2222HF FE DH DE ∴+=+，2222594DE ∴+=+，DE ∴=DE =-． （3）如图，连结HE ，由已知45HD HF =可设4DH m =，5HG m =，可令DE x EC=， ∠当点H 在D 点左边时，如图，同（2）可得，HF HG =，9DG m ∴=，由折叠得BE CF ⊥，90ECF BEC ∴∠+∠=︒，又90D ∠=︒，90ECF CGD ∴∠+∠=︒，BEC CGD ∴∠=∠，又90BCE D ∠=∠=︒，CDG BCE ∴△∽△，DG CD CE BC∴=， CD AB k BC BC ==， 91m k CE ∴=， 9m CE FE k∴==， 9mx DE k ∴=． 90D HFE ∠=∠=︒，2222HF FE DH DE ∴+=+，222299(5)(4)m mx m m k k ⎛⎫⎛⎫∴+=+ ⎪ ⎪⎝⎭⎝⎭，x ∴=x =舍去）．DE EC∴=∠当点H 在D 点右边时，如图，同理得HG HF =，DG m ∴=，同理可得BCE CDG △∽△， 可得m CE FE k ==，mx DE k∴=， 2222HF FE DH DE +=+，2222(5)(4)m mx m m k k ⎛⎫⎛⎫∴+=+ ⎪ ⎪⎝⎭⎝⎭，x ∴=x =．DE EC∴=【点睛】此题主要考查了正方形的性质，矩形的性质，折叠的性质，全等三角形的判定与性质，勾股定理，相似三角形的判定与性质，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．21．在矩形ABCD 中，点E 是CD 边上一点，将ADE 沿AE 折叠，使点D 恰好落在BC 边上的点F 处．（1）如图1，若3tan 4EFC ∠=，求:AB BC 的值；（2）如图2，在线段BF 上取一点G ，使AG 平分BAF ∠，延长AG ，EF 交于点H ，若FG BG CF =+，求:AB BC 的值．【答案】（1）45；（2）35． 【分析】（1）根据3tan 4EFC ∠=，可设3CE k =，则4CF k =，5DE EF k ==，再证明ABF FCE ~，由相似三角形性质即可用k 表示出BF ，从而求得比值；（2）过点G 作GM AF ⊥于点M ，由FG BG CF =+可得1122FG BC AF ==，再证MFG BFA ，从而12GM FM FG AB BF AF ===，设BG x =，由角平分线性质可得：BG MG x ==，2AB AM x ==，设FM y =，则2BF y =，由222AB BF AF +=列方程即可求出43y x =，再根据AB AB BC AF=即可求出比值． 【详解】解：（1）∠四边形ABCD 是矩形，90B C D ︒∴∠=∠=∠=，由折叠的性质得：90AFE D ︒∠=∠=，EF ED =，AF AD =，3tan 4CE EFC CF ∴∠==， 设3CE k =，则4CF k =，5DE EF k ∴==，又90AFB BAF ︒∠+∠=，90AFB EFC ∠+∠=︒，BAF EFC ∴∠=∠，∠ABF FCE ~，AB BF CF CE∴=， ∠843k BF k k=， 6BF k ∴=，∠6410BC BF CF k k k =+=+=，84105AB k BC k ∴==； （2）如解图2，过点G 作GM AF ⊥于点M ，FG BG CF =+，=FG BG CF BC ++， 1122FG AD BC ∴== AD AF =，12FG AF ∴= MFG BFA ∠=∠，90FMG FBA ︒∠=∠=， MFGBFA ∴， ∠12GM FM FG AB BF AF ===， 设BG x =， AG 平分,,BAF GB AB GM AF ∠⊥⊥， BG MG x ∴==，2AB AM x ==， 设FM y =，则2BF y =，222AB BF AF +=222(2)(2)(2)x y x y ∴+=+，解得43y x = 而=AF AM MF +，∠410233x x x +=， ∠231053AB AB x BC AF x ===． 【点睛】本题考查了四边形的综合问题，也考查了三角形相似的判定与性质、勾股定理、三角函数和角平分线的性质．解题的关键是掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．难点是构造垂直利用角平分线性质得线段相等并利用相似进行求解．22．问题提出（1）如图1，在矩形ABCD 中，4cm AB =，点E 为AB 的中点，点F 在BC 上，过点E 作//EG BC交FD 于点G ．若5cm EG =，则EFD △的面积为_________．问题探究（2）如图2，在矩形ABCD 中，6cm,9cm AB BC ==，点P 是AD 边上一动点，点Q 是CD 的中点将．ABP 沿着BP 折叠，点A 的对应点是A '，将QDP △沿着PQ 折叠，点D 的对应点是D ．请问是否存在这样的点P ，使得点P 、A '、D 在同一条直线上？若存在，求出此时AP 的长度；若不存在，请说明理由．问题解决（3）某精密仪器厂接到生产一种特殊四边形金属部件的任务，部件要求：如图3，在四边形ABCD 中，4cm BC =，点D 到BC 的距离为5cm,AD CD ⊥，且CD =．若过点D 作//BC MN ，过点A 作MN 的垂线，交MN 于点E ，交CB 的延长线于点H ，过点C 作CF MN ⊥于点F ，连接AC ．设AE 的长为(cm)x ，四边形ABCD 的面积为()2cm y ． ∠根据题意求出y 与x 之间的函数关系式；∠在满足要求和保证质量的前提下，仪器厂希望造价最低．已知这种金属材料每平方厘米造价60元，请你帮忙求出这种四边形金属部件每个的造价最低费用． 1.73)【答案】（1）210cm ；（2）存在，6cm AP =或3cm AP =；（3）∠210y x =+⎝⎭；∠963.3元．【分析】（1）先由矩形的性质得//,4AD BC CD AB ==，再由三角形面积公式求解即可； （2）由折叠的性质得：,APB A PB DPQ D PQ ∠=∠∠'=∠'，再证BAP PDQ ∽，然后根据相似三角形的性质列比例式求解；（3）∠先证得AED DFC ∽，然后根据相似三角形的性质求得DE DF ==，然后根据面积公式列式求解；∠根据二次函数性质求最值【详解】解：（1）∠四边形ABCD 是矩形，∠//,4AD BC CD AB ==．∠//EG BC ，∠////AD EG BC ．∠点E 为AB 的中点，∠EFD EGD EGF S S S =+111222EG CD =⨯⨯+12EG CD ⨯⨯ 12EG CD =⨯⨯ 1542=⨯⨯ 10=故答案为：210cm ；（2）存在，理由如下：∠四边形ABCD 是矩形，∠90,9,6cm BAD ADC BC AD AB CD ∠=∠=︒===．∠Q 是CD 的中点，∠3cm DQ =．由折叠的性质得：,APB A PB DPQ D PQ ∠=∠∠'=∠'，当点P 、A '、D 三点在同一条直线上时，180APB A PB DPQ D PQ ∠+∠+∠+=''∠︒， ∠90APB DPQ ∠+∠=︒．∠90APB ABP ∠+∠=︒，∠ABP DPQ ∠=∠．∠∠90BAP PDQ ∠=∠=︒，∠BAP PDQ ∽， ∠AB AP PD DQ =，即693AP AP =-， 解得：6cm AP =或3cm AP =；（3）∠根据题意做出辅助线，如图所示．由题意得：5CF EH ==．∠AD CD ⊥，∠90EDA CDF ∠+∠=︒．∠CF MN ⊥，∠90DCF CDF ∠+∠=︒，∠EDA DCF ∠=∠．又∠90AED DFC ∠=∠=︒，∠AED DFC ∽， ∠CF DF CD DE AE DA==． 由AE x =，则5AH x =-．∠5,CF CD ==，∠5DF DE x==∠DE DF ==， ∠EACF DEA DFC ABC y S S S S =--+四边形1111(5)542222x x ⎫=+⨯-⨯+⨯⨯⎪⎪⎝⎭(5)x -2210x x =- 210x =++⎝⎭∠由∠知，210y x =+⎝⎭，当x =时，四边形ABCD 的面积取得最小值为210cm ⎛+ ⎝⎭，∠最低造价为1060963.3⎛⨯≈ ⎝⎭（元）， ∠四边形金属部件每个的造价最低费用约为963.3元．【点睛】本题是四边形综合题目，考查了矩形的性质、相似三角形的判定与性质、翻折变换的性质、梯形面积公式、三角形面积公式以及二次函数的应用等知识；本题综合性强，熟练掌握矩形的性质和翻折变换的性质，证明三角形相似是解题的关键，属于中考常考题型．。

相似三角形一、知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。

2.平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例。

３.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.４．相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。

③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示：①全等三角形一定是相似三角形,其相似比k=1．所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△ABC∽△A′B′Ｃ′的对应边的比,即相似比为k，则△Ａ′B′Ｃ′∽△ＡBＣ的相似比，当且仅当它们全等时,才有k＝ｋ′＝1.③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出．5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交，所得的三角形与原三角形相似；②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。

温馨提示：（１)判定三角形相似的几条思路：①条件中若有平行,可采用判定定理1；②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例；③条件中若有两边对应成比例,可找夹角相等;但是，在选择利用判定定理２时，一对对应角相等必须是成比例两边的夹角对应相等.④条件中若有等腰关系，可找顶角相等或底角相等,也可找腰和底对应成比例。

（2）在综合题中,注意相似知识的灵活运用，并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。

(3）运用相似的知识解决一些实际问题，要能够在理解题意的基础上，把它转化为纯数学知识的问题，要注意培养当数学建模的思想。

三年级上册语文练习题大全三年级语文上册的练习题一、我会写，看我写的字多美。

(5分)zīshìkuānyùyuánzhùgǔlìwēixiǎn()()()()()二、我会划去带点字的错误读音。

(6分)讲述(sùshù)不假(jiājiǎ)思索给(jǐgěi)予卡(kǎqiǎ)片他俩(liǎngliǎ)系(jìxì)绳子三、这些字好相似，你能辨别吗?快试试吧!(5分)买()热()予()险()即()卖()势()矛()脸()既()四、我会照样子，把下列的词语补充完整。

(12分)1、例：圆(溜)(溜)胖()()金()()雾()()乐()()我还能写两个这样的词：2、例：(风)餐(露)宿()默不()应有()()彬彬()()()不转()恋恋()()如()()偿五、我会写出带点词的反义词。

(4分)1、这里危险，快到()的地方去。

2、井口很窄，一点也不()，往外爬的时候千万要小心。

3、虽然这个实验失败了多次，但这次终于获得了()。

4、孩子们都兴高采烈，只有金吉娅()。

六、我会填。

(8分)1、_______________，__本善。

__相远，__________________。

2、_______________，__________________。

亲师友，习礼仪。

3、玉不琢，不成器。

_________________，________________。

你积累了《三字经》里的句子有多少，请展示一下。

(写一句) _______________________________________________________第二部分阅读积累与应用(30分)(一)课内阅读(16分)就在英子刚刚站定的那一(该、刻)，教室里骤然间响起了掌声，那掌声热烈而持久。

在掌声里，我们看到，英子的泪水(流、留)了下来。

掌声渐渐平息，英子也镇定了情绪，开始讲述自己的一个故事。

第1篇欢迎来到小狗赛跑智力测试！在这个充满乐趣和挑战的测试中，你将扮演一位智慧的主人，通过解答一系列问题来帮助你训练你的小狗，使其在赛跑比赛中脱颖而出。

请准备好你的大脑，让我们一起开始这场脑力激荡的冒险吧！第一部分：基础训练1. 你的小狗喜欢在清晨还是傍晚进行训练？为什么？- A. 清晨，因为那时空气清新，小狗精力充沛。

- B. 傍晚，因为那时小狗已经休息了一整天，更容易集中注意力。

2. 以下哪种训练方法对你的小狗最为有效？- A. 通过食物奖励来激励小狗。

- B. 通过玩具和游戏来吸引小狗的注意力。

- C. 通过严厉的命令和惩罚来训练小狗。

3. 你的小狗在比赛中容易分心，以下哪种方法可以帮助它集中注意力？- A. 在比赛前给小狗戴上眼罩，减少外界干扰。

- B. 在赛道周围放置一些障碍物，让小狗学会绕过它们。

- C. 在比赛前进行一些简单的集中注意力训练。

4. 以下哪种食物最适合作为训练奖励？- A. 干燥的狗粮。

- B. 新鲜的肉类。

- C. 特制的训练饼干。

5. 你的小狗在训练中总是落后于其他小狗，以下哪种方法可以帮助它提高速度？- A. 增加训练强度，让小狗跑得更快。

- B. 逐渐缩短训练时间，让小狗保持最佳状态。

- C. 改变训练路线，让小狗适应不同的地形。

第二部分：高级策略6. 在比赛中，你的小狗总是因为转弯不灵活而落后，以下哪种方法可以帮助它改善？- A. 在训练中增加转弯练习，让小狗适应快速转弯。

- B. 在赛道上设置一些转弯标志，引导小狗正确转弯。

- C. 让小狗跟随其他小狗转弯，学习它们的技巧。

7. 你的小狗在比赛中总是容易受伤，以下哪种方法可以帮助它提高耐力和减少受伤风险？- A. 在训练中增加力量训练，提高小狗的肌肉强度。

- B. 在训练中增加耐力训练，让小狗适应长时间奔跑。

- C. 在训练前后进行适当的热身和拉伸，预防肌肉拉伤。

8. 你的小狗在比赛中总是过于兴奋，以下哪种方法可以帮助它保持冷静？- A. 在比赛前给小狗戴上口套，限制它的活动范围。