直线射线线段的基础知识

直线射线与线段的性质直线、射线和线段是几何中常见的基本概念，它们在空间中有一些独特的性质。

本文将探讨直线、射线和线段的性质，以便更好地理解它们在几何学中的应用。

一、直线的性质直线是最基本的几何图形之一，具有以下几个重要性质：1. 直线是无限延伸的。

它没有起点和终点，可以一直向两个方向无限延伸下去。

2. 直线上的任意两点可以确定一条直线。

也就是说，直线由无数个点组成，任意两点可以确定且只能确定一条直线。

3. 直线上的任意一点，都在直线上。

直线上的任意一点，都能通过直线上的其他点，经过无数个无重叠的线段相连而形成。

4. 直线上的任意两点之间的距离是无穷大。

由于直线可以无限延伸，因此直线上的任意两点之间的距离是无限远的。

5. 直线可以平分角。

如果将一条直线作为角的边，那么该直线将角平分成两个相等的角。

二、射线的性质射线是直线的一种特殊形式，具有以下几个性质：1. 射线有一个起点，但没有终点。

从起点出发，射线可以一直向一个方向无限延伸下去。

2. 射线上的任意一点，都在射线上。

射线上的任意一点，都能通过射线的起点，经过无数个无重叠的线段相连而形成。

3. 射线可以平分角。

如果将一条射线作为角的边，那么该射线将角平分成两个相等的角。

三、线段的性质线段是直线的一种有限形式，具有以下几个性质：1. 线段有一个起点和一个终点。

线段在起点和终点之间有限的长度。

2. 线段上的任意一点，都在线段上。

线段上的任意一点，都能通过线段的起点和终点，经过无数个无重叠的线段相连而形成。

3. 线段的长度是有限的。

线段长度是起点和终点之间的距离，具体数值可以通过直尺等工具进行测量。

4. 线段不能平分角。

因为线段有限，无法像直线和射线那样将角分成两个相等的角。

综上所述，直线、射线和线段具有各自独特的性质。

了解这些性质有助于我们更好地理解几何学中的相关概念和定理，为解决实际问题提供准确的数学基础。

同时，这些性质的理解还可以拓宽我们对空间图形的认知，提高几何思维能力和问题解决能力。

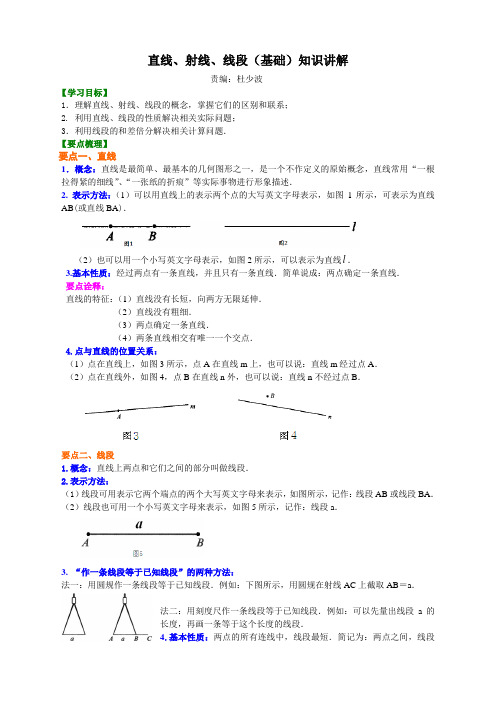
直线、射线、线段（基础）知识讲解责编：杜少波【学习目标】1．理解直线、射线、线段的概念，掌握它们的区别和联系；2. 利用直线、线段的性质解决相关实际问题；3．利用线段的和差倍分解决相关计算问题．【要点梳理】要点一、直线1．概念：直线是最简单、最基本的几何图形之一，是一个不作定义的原始概念，直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述．2. 表示方法：（1）可以用直线上的表示两个点的大写英文字母表示，如图1所示，可表示为直线AB(或直线BA)．（2）也可以用一个小写英文字母表示，如图2所示，可以表示为直线l．3.基本性质：经过两点有一条直线，并且只有一条直线．简单说成：两点确定一条直线．要点诠释：直线的特征：（1）直线没有长短，向两方无限延伸．（2）直线没有粗细．（3）两点确定一条直线．（4）两条直线相交有唯一一个交点．4.点与直线的位置关系：（1）点在直线上，如图3所示，点A在直线m上，也可以说：直线m经过点A．（2）点在直线外，如图4，点B在直线n外，也可以说：直线n不经过点B．要点二、线段1.概念：直线上两点和它们之间的部分叫做线段．2.表示方法：（1）线段可用表示它两个端点的两个大写英文字母来表示，如图所示，记作：线段AB或线段BA．（2）线段也可用一个小写英文字母来表示，如图5所示，记作：线段a．3. “作一条线段等于已知线段”的两种方法：法一：用圆规作一条线段等于已知线段．例如：下图所示，用圆规在射线AC上截取AB＝a．法二：用刻度尺作一条线段等于已知线段．例如：可以先量出线段a的长度，再画一条等于这个长度的线段．4.基本性质：两点的所有连线中，线段最短．简记为：两点之间，线段最短．如图6所示，在A ，B 两点所连的线中，线段AB 的长度是最短的．要点诠释：（1）线段是直的，它有两个端点，它的长度是有限的，可以度量，可以比较长短．（2）连接两点间的线段的长度，叫做这两点的距离． （3）线段的比较：①度量法：用刻度尺量出两条线段的长度，再比较长短．②叠合法：利用直尺和圆规把线段放在同一条直线上，使其中一个端点重合，另一个端点位于重合端点同侧，根据另一端点与重合端点的远近来比较长短．5.线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点．如图7所示，点C 是线段AB 的中点，则12AC CB AB ==，或AB ＝2AC ＝2BC ．要点诠释：若点C 是线段AB 的中点，则点C 一定在线段AB 上．要点三、射线1.概念：直线上一点和它一侧的部分叫射线，这个点叫射线的端点．如图8所示，直线l 上点O 和它一旁的部分是一条射线，点O 是端点．l2.特征：是直的，有一个端点，不可以度量，不可以比较长短，无限长．3.表示方法：（1）可以用两个大写英文字母表示，其中一个是射线的端点，另一个是射线上除端点外的任意一点，端点写在前面，如图8所示，可记为射线OA ．（2）也可以用一个小写英文字母表示，如图8所示，射线OA 可记为射线l ． 要点诠释：(1)端点相同，而延伸方向不同，表示不同的射线．如图9中射线OA ，射线OB 是不同的射线．(2)端点相同且延伸方向也相同的射线，表示同一条射线．如图10中射线OA 、射线OB 、射线OC 都表示同一条射线．要点四、直线、射线、线段的区别与联系1.直线、射线、线段之间的联系（1）射线和线段都是直线上的一部分，即整体与部分的关系．在直线上任取一点，则可将直线分成两条射线；在直线上取两点，则可将直线分为一条线段和四条射线．（2）将射线反向延伸就可得到直线；将线段一方延伸就得到射线；将线段向两方延伸就得到直线． 图6 图7图8 图9 图102．三者的区别如下表要点诠释：（1）联系与区别可表示如下：（2）在表示直线、射线与线段时，勿忘在字母的前面写上“直线”“射线”“线段”字样．【典型例题】类型一、相关概念1.下列说法中，正确的是( )A．射线OA与射线AO是同一条射线B．线段AB与线段BA是同一条线段C．过一点只能画一条直线D．三条直线两两相交，必有三个交点【答案】B【解析】射线OA的端点是O，射线AO的端点是A，所以射线OA与射线AO不是同一条射线，故A 错误；过一点能画无数条直线，所以C错误；三条直线两两相交，有三个交点或一个交点(三条直线相交于一点时)，所以D错误；线段AB与线段BA是同一条线段，所以B正确．【总结升华】直线和线段用两个大写字母表示时，与字母的前后顺序无关，但射线必须是表示端点的字母写在前面，不能互换．举一反三：【变式1】以下说法中正确的是（）A．延长线段AB到C B．延长射线ABC．直线AB的端点之一是A D．延长射线OA到C【答案】A【变式2】如图所示，请分别指出图中的线段、射线和直线的条数，并把它们分别表示出来.【答案】解：如下图所示，在直线上点A左侧和点C右侧分别任取点X和Y.图中有6条射线：射线AX、射线AY、射线BX、射线BY、射线CX、射线CY.有3条线段：线段AB(或BA)、线段BC(或CB)、线段AC(或CA)有1条直线：直线AC(或AB，BC).类型二、有关作图2．如图所示，线段a，b，且a＞b．用圆规和直尺画线段：(1)a+b；(2)a-b．【答案与解析】解：(1) 画法如图(1)，画直线AF，在直线AF上画线段AB＝a，再在AB的延长线上画线段BC＝b，线段AC就是a与b的和，记作AC＝a+b．(2) 画法如图(2)，画直线AF，在直线AF上画线段AB＝a，再在线段AB上画线段BD＝b，线段AD 就是a与b的差，记作AD＝a-b．【总结升华】在画线段时，为使结果更准确，一般用直尺画直线，用圆规量取线段的长度．举一反三：【变式1】如图，C是线段AB外一点，按要求画图：（1）画射线CB；（2）反向延长线段AB；（3）连接AC，并延长AC至点D，使CD=AC．【答案】解：【高清课堂：直线、射线、线段397363 按语句画图3（3）】【变式2】用直尺作图：P 是直线a 外一点，过点P 有一条线段b 与直线a 不相交.【答案】解：类型三、有关条数及长度的计算3.如图，A 、B 、C 、D 为平面内任意三点都不在同一条直线上的四点，那么过其中两点，可画出 条直线.【思路点拨】根据两点确定一条直线即可计算出直线的条数．【答案】6条直线【解析】由两点确定一条直线知，点A 与B,C,D 三点各确定一条直线，同理点B 与C 、D 各确定一条直线，C 与D 确定一条直线，综上：共有直线：3+2+1=6（条）.【总结升华】平面上有n 个点，其中任意三点不在一条直线上，则最多确定的直线条数为：(1)123...(1)2n n n -++++-=． 举一反三：【变式1】如图所示，已知线段AB 上有三个定点C 、D 、E ．(1)图中共有几条线段？(2)如果在线段CD 上增加一点，则增加了几条线段？你能从中发现什么规律吗？【答案】解：(1)线段的条数：4＋3＋2＋1＝10(条)；(2)如果在线段CD 上增加一点P ，则P 与其它五个点各组成一条线段，因此，增加了5条线段. （注解：若在线段AB 上增加一点，则增加2条线段，此时线段总条数为1＋2；若再增加一点，则又增加了3条线段，此时线段总条数为1＋2＋3；…；当线段AB 上增加到n 个点(即增加n －2个点)时，线段的总条数为1＋2＋……＋(n －1)＝21n(n －1) .） 【变式2】)如图直线m 上有4个点A 、B 、C 、D ，则图中共有________条射线．【答案】84.（2016春•启东市月考）已知点C 在线段AB 上，线段AC=7cm ，BC=5cm ，点M 、N 分别是AC 、BC 的中点，求MN 的长度．【思路点拨】根据M 、N 分别为AC 、BC 的中点，根据AC 、BC 的长求出MC 与CN 的长，由MC+CN 求出MN 的长即可．【答案与解析】解：∵AC=7cm ，BC=5cm ，点M 、N 分别是AC 、BC 的中点，∴MC=AC=3.5cm ，CN=BC=2.5cm ，则MN=MC+CN=3.5+2.5=6（cm ）．【总结升华】此题考查了线段的和差，熟练掌握线段中点定义是解本题的关键．【高清课堂：直线、射线、线段397363画图计算例2】举一反三：【变式】在直线l 上按指定方向依次取点A 、B 、C 、D ，且使AB ：BC ：CD=2：3：4，如图所示，若AB 的中点M 与CD 的中点N 的距离是15cm ，求AB 的长.【答案】解：依题意，设AB ＝2x cm ，那么BC ＝3x cm ，CD ＝4x cm ．则有：MN=BM+BC+CN= x+3x+2x=15 解得：52x = 所以AB=2x =5252⨯=cm. 类型四、最短问题5.（2015•新疆）如图所示，某同学的家在A 处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（ ）A ．A →C →D →B B ． A →C →F →BC ． A →C →E →F →BD ．A →C →M →B【答案】B ．【解析】根据两点之间的线段最短，可得C、B两点之间的最短距离是线段CB的长度，所以想尽快赶到书店，一条最近的路线是：A→C→F→B．【总结升华】“两点之间线段最短”在实际生活中有广泛的应用，此类问题要与线段的性质联系起来，这里线段最短是指线段的长度最短，连接两点的线段的长度叫做两点间的距离，线段是图形，线段长度是数值．举一反三：【变式】 (1)如图1所示，把原来弯曲的河道改直，A、B两地间的河道长度有什么变化?(2)如图2，公园里设计了曲折迂回的桥，这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比，这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理．【答案】解：(1)河道的长度变小了．(2)由于“两点之间，线段最短”，这样做增加了游人在桥上行走的路程，有利于游人更好地观赏湖面风光，起到“休闲”的作用．。

第四章 几何图形初步4.2 直线、射线、线段一、知识考点知识点1【直线】1、直线：把线段向两端无限延伸形成的图形叫做直线。

2、特点：是直的；无粗细之分；无端点；不可以度量；不可以比较长短，无限长。

3、基本性质：经过两点有且只有一条直线（两点确定一条直线）；4、直线有两种表示方法:（1）用直线上任意两点的大写字母,如:表示为直线AB 或直线BA 。

（2）也可以用一个小写字母表示,如:直线l5、直线和点的位置关系：（1）在直线上:点O 在直线l 上,或者说说直线l 经过点O（2）点在直线外:点P 在直线l 外,或者说说直线l 不经过点P6、交点：当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做他们的交点。

O Pl知识点2【射线】1、射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

2、特点：是直的,有一个端点,不可以度量,不可以比较长短,无限长。

3、射线有两种表示方法：（1）可以用两个大写英文字母表示，其中一个是射线的端点,另一个是射线上除端点外的任意的一点,端点写在前面。

(如图：可以记作射线OM,但不能记作射线MO) （2）可以用一个小写英文字母表示,比如:射线OM也可以记为射线l。

4、射线的画法：画射线一要画出射线端点，二要画出射线经过一点,并向一旁延伸的情况。

知识点3【线段】1、线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

2、特点：线段是直的,它有两个端点,他的长度是有限的,可以度量的,可以比较长短。

3、基本性质：(1) 线段公理：两点之间的所有连线中,线段最短（两点之间，线段最短）(2) 两点之间的距离：两点之间线段的长度，叫做这两点之间的距离。

注意：两点间的距离是指线段的长度,是一个数值,而不是指线段本身。

(3) 线段的中点到两端点的距离相等。

(4) 线段的大小关系和它们的长度的大小关系是一致的4、线段有两种表示方法：（1）可以用它的两个端点的大写英文字母来表示，如线段AB（或线段BA）（2）可以用一个小写字母来表示,如线段a5、线段的画法：用直尺和尺规作图（尺规作图）已知：线段a(如图所示),用直尺和圆规画一条线段,使它等于已知线段a第一步：任意画一条射线AC第二步：用圆规量取已知线段a的长度。

直线、射线、线段1.直线：直，向两边无限延伸，无宽窄。

2.直线的性质（公理）：经过两点能够做一条直线，且只有一条直线。

两点确定一条直线。

．．．．．．．．．3．关系【同一平面内】1）相交（垂直） 2）平行相交：如果两条直线有一个．．公共点，则两条直线相交。

平行：两条直线没有公共点。

关系【不在同一平面内】1）相交（垂直） 2）平行 3）异面直线1.射线：直线上一点和它一旁的部分。

2.射线直线关系：射线是直线的一部分。

3.规律若直线上有N个点，则有2N条射线。

射线只能．．反向延伸。

1.线段：直线上两点和它们之间的的部分。

2.线段的性质（公理）：连接两点的所有线中，线段最短。

两点之间线段最短．．．．．．．．。

3.两点间的距离叫连结两点间的线段的长度．．。

距离不是线段，线段是一个几何图形，而距离是一个数值，它反映的是线段长短。

重要规律当一条直线有N个点时射线 2N条线段 N（N-1）÷2（射线和线段都是直线上的一部分：将射线反向延伸就可得到直线；将线段一方延伸就得到射线，两方延伸就得到直线。

）线段的比较一、线段的比较大小【长度】1.度量法2.叠合法：a.两条线段一个端点重合。

b.共线c.看另一端位置二．线段和、差、倍、分倍、分1.线段的中点线段上一点把这条线段分成两条相等的线段。

若三条线段中满足两条线段之和等于第三线段，则三点共线。

角1.角的定义：（1）有公共端点的两条射线所组成的图形叫做角，这个公共端点叫做角的顶点，这两条射线叫做角的边.（2）角也可看成是由一条射线绕着它的端点旋转而成的图形.（3）角定义包含两层含义：①有公共端点；②两条射线.2. 1周角=2平角=4直角 【度、分、秒的转换计算】160160''''︒==（1）平角是指射线旋转到与起始位置成一直线时所成的角.（2）周角是指射线旋转回到起始位置所成的角.注意：平角的特点是两边成一条直线，但直线与平角的意义是不同的，不要误认为直线就是平角.同样，周角的特点是两边重合成一条射线，不要误说射线就是周角，射线和周角的意义也是不一样的.3.角的平分线一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线4.余角：如果两个角的和等于90︒（直角），就说这两个角互为余角.5.补角：如果两个角的和等于180︒（平角），就说这两个角互为补角.90,αβαβ+=︒⇔互余180,αβαβ+=︒⇔互补6.方向表示（应用题）（1）东北方向（即北偏东45︒或东偏北45︒）————射线OA（2）北偏西60︒方向（或西偏北30︒方向） ————射线OB7.时钟上的时针与分针的角度注意半点的时候时针的位置5：30时，时针与分针的夹角的度数为：8.角的个数数角的个数必须不重不漏，从一点引出n （n ≥2）条射线组成的角有n （n-1）÷2个。

七年级上学期数学知识点：直线、射线、线段鉴于数学知识点的重要性，小编为您提供了这篇七年级上学期数学知识点：直线、射线、线段，希望对同学们的数学有所帮助。

1、基本概念图形直线射线线段端点个数无一个两个表示法直线a直线AB(BA) 射线AB 线段a线段AB(BA)作法叙述作直线AB;作直线a 作射线AB 作线段a;作线段AB;连接AB延长叙述不能延长反向延长射线AB 延长线段AB;反向延长线段BA2、直线的性质经过两点有一条直线，并且只有一条直线.简单地：两点确定一条直线.3、画一条线段等于已知线段(1)度量法(2)用尺规作图法4、线段的大小比较方法(1)度量法(2)叠合法5、线段的中点(二等分点)、三等分点、四等分点等定义：把一条线段平均分成两条相等线段的点.图形：A M B符号：若点M是线段AB的中点，则AM=BM=AB，AB=2AM=2BM.6、线段的性质两点的所有连线中，线段最短.简单地：两点之间，线段最短.7、两点的距离连接两点的线段长度叫做两点的距离.宋以后，京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。

至元明清之县学一律循之不变。

明朝入选翰林院的进士之师称“教习”。

到清末，学堂兴起，各科教师仍沿用“教习”一称。

其实“教谕”在明清时还有学官一意，即主管县一级的教育生员。

而相应府和州掌管教育生员者则谓“教授”和“学正”。

“教授”“学正”和“教谕”的副手一律称“训导”。

于民间，特别是汉代以后，对于在“校”或“学”中传授经学者也称为“经师”。

在一些特定的讲学场合，比如书院、皇室，也称教师为“院长、西席、讲席”等。

8、点与直线的位置关系(1)点在直线上 (2)点在直线外.宋以后，京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。

至元明清之县学一律循之不变。

明朝入选翰林院的进士之师称“教习”。

到清末，学堂兴起，各科教师仍沿用“教习”一称。

其实“教谕”在明清时还有学官一意，即主管县一级的教育生员。

线段射线和直线课堂讲解
一、线段、射线和直线的定义：
1. 线段：有两个端点的一段直线，可以向两个方向无限延伸。

2. 射线：有一个固定端点，另一侧无限延伸。

3. 直线：没有端点，两侧都无限延伸。

二、线段、射线和直线的特性：
1. 线段：线段是两点之间所有点的集合，它有一个固定的长度。

2. 射线：射线是有一个固定端点，另一侧无限延伸的直线。

它有一个方向。

3. 直线：直线是向两个方向无限延伸的直线，没有固定的长度。

三、线段、射线和直线的表示方法：
1. 线段：用两个大写字母表示，例如线段AB。

2. 射线：用一个大写字母和一个箭头表示，例如射线AB。

3. 直线：用两个大写字母或一个小写字母表示，例如直线AB或直线l。

四、线段、射线和直线的应用：
1. 线段：在几何学中，线段是基础图形之一，可以用来研究长度、角度等几何量。

在实际生活中，线段可以用来表示道路、桥梁等物体的一部分。

2. 射线：在几何学中，射线可以用来研究角度、射影等几何量。

在实际生活中，射线可以用来表示光线、雷达等物体的发射方向。

3. 直线：在几何学中，直线是最基础的图形之一，可以用来研究平行、垂直等几何量。

在实际生活中，直线可以用来表示道路、铁路等物体的延伸方向。

“直线、射线、线段”知识要点
一、直线
1、直线是向两方无限延伸的的一条笔直的线，如代数中的数轴，就是一条直线（它只规定了原点、方向和长度单位）；
2、一个点可以用一个大写字母表示。

一条直线可以用一个小写字母表示。

如图1中的直线可以记作l ，如果A 点，B 点在直线l 上，那么直线l 也可以记作直线AB ；
3、一个点P 与一条直线l 有两种位置关系，如图2，①P 点在直线l 上，②P 点在直线l 外；
4、两条直线a 和b ，如果它们只有一个公共点O ，这两条直线的位置关系叫做相交，公共点O 叫做交点。

如图3；
5、公里：经过两点有一条直线，并且只有一条直线。

（即，过两点有且只有一条直线）；
6、经过一点有无数条直线。

如图4。

二、射线、线段
1、直线上一点和它的一旁的直线部分叫做射线，这点叫做射线的端点。

一条射线可以用表示端的字母和表示射线上两一点的字母来表示，例如，在图5中的射线，记做射线OA ，注意，表示端点的字母要写在前面，有时也可以用一个小写字母来表示，如射线OA 也可以写成射线l 。

2、直线上两点和它们之间的部分叫做线段，这两点叫做线段的端点。

以A 、B 为端点
的线段记做线段AB ，或线段BA ，也可以用一个小写字母a 来表示，如图６。

三、直线、射线和线段的区别
１、直线可向两方无限延伸，没有端点，长度无限；
２、射线可向一方无限延伸，有一个端点，长度无限；
３、线段有两个短点，有一定的长度。

A
B l 图1 l P l P 图 2 a b O 图 3 a b c d O 图 4 O A l 图 5 B A 图 6 a。

M O a线段、射线、直线【知识要点】知识点1、线段、直线、射线的概念：线段：一段拉直的棉线可近似地看作线段，线段有两个端点。

线段的画法：（1）画线段时，要画出两个端点之间的部分，不要画出向任何一方延伸的情况．（2）以后我们说“连结 ”就是指画以A 、B 为端点的线段．射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

如手电筒、探照灯射出的光线等。

射线的画法：画射线 一要画出射线端点 ；二要画出射线经过一点，并向一旁延伸的情况．直线：将线段向两个方向无限延长就形成了直线，直线没有端点。

如笔直的铁轨等。

直线的画法：用直尺画直线，但只能画出一部分，不能画端点。

知识点2、线段、直线、射线的表示方法：（1） 点的记法：用一个大写英文字母（2） 线段的记法：①用两个端点的字母来表示 ②用一个小写英文字母表示 如图：记作线段AB 或线段BA ， 记作线段a ，与字母顺序无关 此时要在图中标出此小写字母（3） 射线的记法：用端点及射线上一点来表示，注意端点的字母写在前面如图：记作射线OM,但不能记作射线MO（4） 直线的记法：①用直线上两个点来表示 ②用一个小写字母来表示如图：记作直线AB 或直线BA ， 记作直线l与字母顺序无关。

此时要在图中标出此小写字母知识点3、线段、射线、直线的区别与联系：联系：三者都是直的，线段向一个方向延长可得到射线，线段向两个方向延长可得到直线，故射线、线段都是直线的一部分，线段是射线的一部分。

区别：直线可以向两方延伸，射线可以向一方无限延伸，线段不能延伸，三者的区别见下表：BA BAlB AaMOBAkB A名称图形表示方法界限端点长度线段线段AB（或线段BA）（字母无序）线段a 两方有界两个有射线射线AB(字母有序) 一方有界，一方无限一个无直线直线AB（或直线BA）（字母无序）直线l 两方无限无无知识点4、直线的基本性质（重点）（1）经过一点可以画无数条直线（2）经过两点只可以画一条直线直线的基本性质：经过两点有且只有一条直线（也就是说：两点确定一条直线）注：“确定”体现了“有”，又体现了“只有”。

一、线段、直线和射线1.定义射线：线段的一段无限延长得到的线叫射线。

直线：线段的两段无限延伸得到的线叫直线。

2.线段、直线和射线的特点线段：两个端点、有限长、可以测量直直的线射线：一个端点、另一个端可以无限延伸、无限长、不可测量直直的线直线：两个端点、两端可以无限延伸、无限长、不可测量直直的线过一点可以画无数条射线，过一点可以画无数条直线，过两点只能画一条直线。

二、角1.由一点引出的两条射线所组成的图形叫角，用符号“”表示。

相交的点是角的顶点，两条射线是角的边。

2. 角通常用符号“”表示，上图的角可以记作：三、角的度量1.测量角的工具叫量角器。

角的计量单位是“度”，用符号“°”表示。

把半圆平分成180 等份，每一份所对的大小记作1°角的大小与角的两边画出的长短没关系。

角的大小与两边张开的大小有关。

2. 量角的步骤：（1）点与点重合，中心点和角的顶点重合；线与边重合，0°刻度线和角一条边重合。

（2）读准数，从0°刻度线重合的边看，看有0°刻度线的那一圈刻度，另一条边所对的刻度就是角的度数。

三、角的分类锐角：小于90°锐角< 90°直角：等于90°一直角= 90°钝角：大于90°且小于180°90°< 钝角< 180°平角：等于180°一平角=180°=2直角周角：等于360°一周角=360°=2平角=4直角锐角<直角<钝角<平角<周角3. 画角步骤：①画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。

②在量角器65°刻度线的地方点一个点。

③以画出的射线的端点为端点，通过刚画的点，再画一条射线。