生活中的立体图形完整版

精品"正版〞资料系列,由本公司独创 .旨在将"人教版〞、〞苏教版"、〞北师大版"、〞华师大版"等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友 .本资源创作于2021年8月,是当前最|新版本的教材资源 .包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最|正确选择 .1 生活中的立体图形第二课时【学习目标】1、知识与技能：进一步认识并描述几何体的特征.2、过程与方法：通过实例进一步认识点,线,面.感受点,线,面之间的关系.3、情感、态度和价值观：丰富学习体验,开阔思维空间,激发对空间图形的探知欲望.【学习重点】进一步认识并描述几何体的特征.【学习难点】进一步认识点,线,面.感受点,线,面之间的关系学习过程一、温故知新1.举例说明几何体按形状分哪几类?2.圆柱和圆锥的相同点是,不同点是.思考:图形是由_______、_______、________构成的,面与面相交得到____,线与线相交得到_____.二、自主学习1.看课本p52.试一试,解决以下问题①找出图1 -4中的点、线、面.②图1 -4中的哪些线是直的,哪些线是曲的?那些面是平的?哪些面是曲的?三、合作交流.讨论解决: ①p6议一议(1 )六棱柱是有几个面围成的?圆柱是有几个面围成的?他们都是平的吗?(2 )圆柱的侧面和底面相交成几条线?他们是直的还是曲的?(3 )六棱柱有几个顶点?经过每一个顶点有几条棱?看课本p6 想一想(1 )我们可以得到：点动成( ) ,线动成( ) , ( )动成体.(2 )你能举例说明这一结论吗?能力提升：我们都知道,面动成体.（1）圆柱可以看做由哪个平面图形旋转得到?球体呢?（2）课本图1 - -5中各个花瓶的外表可以看做由哪个平面图形绕虚线旋转一周而得到?用线连一连.四、归纳总结圆柱柱体棱柱分类棱锥锥体圆锥生活中的立体图形- - - - - - - - 球体体构成面面线线点五、例题解析在桌面上,棱长为a的假设干个正方体摆放成如下图的模型①模型中共有 个正方体.②对模型的所有暴露面喷漆 (不含底面 ),那么喷漆面的总面积是 . 六、课堂达标：1.下雨看起来是一根线,这说明 .电扇转起来象一个整体的圆盘, 这说明 . 2.三棱锥是由 个面围成的? 有 个顶点, 有 条棱 . 3.五棱柱、圆锥分别是由几个面围成的 ?他们是直的还是曲的 ?七、谈收获：本节课你学习了那些知识?感受了那些问题类型和解决问题的方法? 八、小试牛刀： 一、选择题1、下面的几何体是棱柱的是 ( )2、圆柱是由以下 ( )图形绕虚线旋转一周而成 .二、填空题：A B C DADBC1. 在日常生活中,我们见到类似棱柱、圆柱、圆锥、正方体、长方体以及球体的物体有哪些?请举例说出来：.2. 圆柱体有个面围成,长方体有个面成.3. 由点动成,由线动成,由动成体.4. 观察以下图,正方体有个顶点, 条棱, 个面,这些面的形状都是.5.三棱锥是由面围成的,有顶点,有棱.三、解答题：1、至|少找出以下几何体的4个共同点.八、布置作业(1 )p7 随堂练习(2 )观察身边的几何体,想象一下它们是由什么平面图形旋转而成的?以下为赠送内容别想一下造出大海,必须先由小河川开始 .成功不是只有将来才有,而是从决定做的那一刻起,持续积累而成!人假设软弱就是自己最|大的敌人,人假设勇敢就是自己最|好的朋友 .成功就是每天进步一点点!如果要挖井,就要挖到水出为止 .即使爬到最|高的山上,一次也只能脚踏实地地迈一步 .今天拼搏努力,他日谁与争锋 .在你不害怕的时候去斗牛,这不算什么；在你害怕的时候不去斗牛,这没什么了不起；只有在你害怕的时候还去斗牛才是真正的了不起 .行动不一定带来快乐,但无行动决无快乐 .只有一条路不能选择- -那就是放弃之路；只有一条路不能拒绝| - -那就是成长之路 .坚韧是成功的一大要素,只要在门上敲得够久够大声,终会把人唤醒的 .只要我努力过,尽力过,哪怕我失败了,我也能拍着胸膛说："我问心无愧 ."用今天的泪播种,收获明天的微笑 .人生重要的不是所站的位置,而是所朝的方向 .弱者只有千难万难,而勇者那么能披荆斩棘；愚者只有声声哀叹,智者却有千路万路 .坚持不懈,直到成功!最|淡的墨水也胜过最|强的记忆 .凑合凑合,自己负责 .有志者自有千计万计,无志者只感千难万难 .我中|考,我自信!我尽力我无悔!听从命运安排的是凡人；主宰自己命运的才是强者；没有主见的是盲从,三思而行的是智者 .相信自己能突破重围 .努力造就实力,态度决定高度 .把自己当傻瓜,不懂就问,你会学的更多 .人的活动如果没有理想的鼓舞,就会变得空虚而渺小 .安乐给人予舒适,却又给人予早逝；劳作给人予磨砺,却能给人予长久 .眉毛上的汗水和眉毛下的泪水,你必须选择一样!假设不给自己设限,那么人生中就没有限制你发挥的藩篱 .相信自己我能行!任何业绩的质变都来自于量变的积累 .明天的希望,让我们忘了今天的痛苦 .世|界上最|重要的事情,不在于我们身在何处,而在于我们朝着什么方向走 . 爱拼才会赢努力拼搏,青春无悔!。

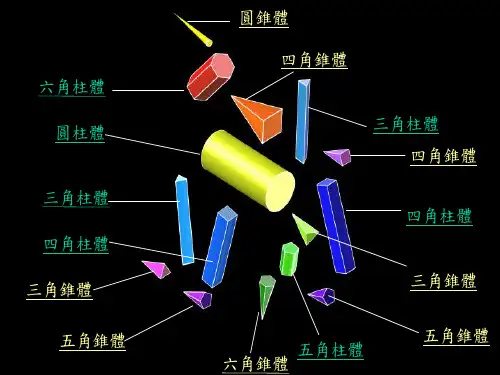
生活中的立体图形
华东师范大学出版社七年级上册
你认识它们吗？
你认识它们吗？
你认识它们吗？
你认识它们吗？
柱体
•1、圆柱：两个底面都是大小相等的圆形，侧面由曲面组成。

•2、棱柱：两个底面都是多边形，侧面都是平行四边形。

椎体
•1、圆锥：只有一个底面，且是圆形，侧面由曲面组成。

•2、棱锥：只有一个底面，且是多边形，侧面都是三角形。

球体：由一个曲面围成
由旋转得到几何体
•1、圆柱：由长方形围绕一个轴旋转得到•2、圆锥：由三角形围绕一个轴旋转得到•3、球体：由圆形围绕一个轴旋转得到
棱柱和棱锥
三棱柱三棱锥
棱柱和棱锥
四棱柱四棱锥
棱柱和棱锥
五棱柱五棱锥
棱柱和棱锥
六棱柱六棱锥
下列图形中为圆柱体的是：
难点：棱柱的顶点数、棱数、面数n棱柱顶点数棱数面数
n=3 n=4 n=5 n
695
8126
10157
2n3n n+2
结论：顶定点数+面数—棱数=2
难点：棱锥的顶点数、棱数、面数n棱锥顶点数棱数面数
n=3 n=4 n=5 n
464
585
6106
n+12n n+1
结论：顶点数+面数—棱数=2。

第01讲生活中的立体图形1.认识柱体、椎体、球体，并能够熟练的进行立体图形的分类；2.掌握柱体、椎体、球体的特征；3.掌握柱体特征及其面的个数、棱的条数、顶点个数之间的关系；4.掌握立体图形的表面积、体积公式；5.掌握棱柱的顶点数、棱数、面数的计算方法；6.掌握立体图形的表面积和体积的计算方法.知识点01 认识立体图形（1）几何图形：从实物中抽象出的各种图形叫几何图形．几何图形分为立体图形和平面图形．（2）立体图形：有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一个平面内，这就是立体图形．知识点02 立体图形的分类（1）按形状分类：球，柱体（圆柱、棱柱），椎体（圆锥、棱锥），台体（圆台、棱台）.（2）按构成分类：旋转体（由平面围成的立体图形），旋转体（绕某一轴旋转一周）.知识点03 点、线、面、体（1）体与体相交成面，面与面相交成线，线与线相交成点．（2）从运动的观点来看：点动成线，线动成面，面动成体．点、线、面、体组成几何图形，点、线、面、体的运动组成了多姿多彩的图形世界．（3）从几何的观点来看：点是组成图形的基本元素，线、面、体都是点的集合．（4）长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体，几何体简称体．（5）面有平面和曲面之分，如长方体由6个平面组成，球由一个曲面组成．知识点04 棱柱与棱锥的顶点、面、棱数（1）几何体的表面积＝侧面积+底面积（上、下底的面积和）（2）常见的几种几何体的表面积的计算公式：题型01几何体的识别【典例1】下列标注的图形与名称不相符的是（）A．圆锥B．四棱柱C．三棱锥D．圆柱【变式1】下面的立体图形按从左到右的顺序依次是（）A．长方体、圆柱、圆锥、正方体B．长方体、圆柱、球、正方体C．棱柱、棱柱、球、正方体D．长方体、棱柱、圆锥、棱柱题型02立体图形的分类【典例1】如图，下列几何体，是柱体的有______，球体的有______．（填序号）【变式1】如图所示，请将下列几何体分类．题型03几何体中点、棱、面【典例1】几何知识．（1）长方体有_____个面，_____条棱，_____个顶点．（2）圆柱体由_____个面围成，圆锥由_____个面围成，它们的底面都是_____．（3）已知三棱柱有5个面、6个顶点、9条棱，四棱柱有6个面、8个顶点、12条棱，五棱柱有7个面、10个顶点、15条棱，……，由此类推n棱柱有_____个面，_____个顶点，_____条棱．【变式1】如图所示，是我们熟悉的三棱柱、五棱柱和六棱柱．(1)填写下表：题型04点、线、面、体四者之间的关系【典例1】当你用笔在纸上写字时，你的笔尖实现了（）A．点动成线B．线动成面C．面动成体D．以上都不对【变式1】如图，直角三角形绕它的一条直角边所在的直线旋转一周，形成的几何体是__________，这其中蕴含的数学事实是__________．题型05平面图形旋转后所得的立体图形【典例1】图中的圆柱体是由下面哪个图形旋转而成的（）A．B．C．D．【变式1】下列各选项中的图形，绕虚线旋转一周，所得的几何体是圆锥的是（）A．B．C．D．一、选择题1．下列图形是平面图形的是（）A．正方体B．圆C．球D．圆锥2．下列几何体中，不属于棱柱的是（）A．B．C．D．3．中华武术是中国传统文化之一，是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念，注重内外兼修，诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等，逐步形成了独具民族风貌的武术文化体系.“枪挑一条线，棍扫一大片”，从数学的角度解释为（）A．点动成线，线动成面B．线动成面，面动成体C．点动成线，面动成体D．点动成面，面动成线4．如图，把图形绕着给定的直线旋转一周后形成的几何体是（）A．B．C．D．二、填空题5．五棱柱的面的个数为______．6．在正方体、长方体、圆柱、圆锥、球、六棱柱、六棱锥中属于柱体有___个．7．笔尖在纸上快速滑动写出了一个又一个字，这说明了_____；直角三角形绕它的直角边旋转一周，形成了一圆锥体，这说明了_____，“齐天大圣”孙悟空有一个宝贝﹣金箍棒，当他快速旋转金箍棒时，展现在我们眼前的是一个圆的形象，这说明_____．8．如图是一个底面各边都相等的六棱柱，它的底面边长为2cm，高为5cm．这个棱柱共有______条棱，______个面，侧面积是______2cm．三、解答题9．将如图几何体分类，并说明理由．10．下列是我们常见的几何体，按要求将其分类（只填写编号）．(1)如果按“柱”“锥球”来分，柱体有______，椎体有______，球有______；(2)如果按“有无曲面”来分，有曲面的有______，无曲面的有______．(1)根据要求填写表格：操作探究：。

第一节 生活中的立体图形(一)常见的几何体1、 圆柱与圆锥的相同与不同相同点: 底面都是圆面，侧面都是曲面不同点： （1）圆柱有两个大小相同的底面,而圆锥只有一个底面 （2）圆柱没有顶点, 而圆锥有一个顶点2、 棱柱与圆柱的相同与不同相同点: 都有上、下两个底面，都有侧面 不同点：（1）棱柱的底面是形状和大小完全相同的多边形,圆柱的底面是圆。

（2）棱柱的侧面是长方形，圆柱的侧面是曲面圆柱圆锥 正方体 长方体 棱柱 球棱锥（3）棱柱有顶点，圆柱没有顶点3、棱柱、棱锥的命名是按底面的边数来命名的：三棱柱四棱柱五棱柱六棱柱三棱锥四棱锥五棱锥六棱锥4、按“柱锥球”划分：(1) 柱体：棱柱圆柱 (2) 锥体：棱锥圆锥（3)球体5、棱柱有直棱柱和斜棱柱。

（本书只讨论直棱柱简称棱柱）[练习题]一、填空题1、正方体（立方体）有个面，各个面都是，个顶点，条棱，经过每个顶点有条棱，这些棱的长度都2、一个正方体的所有棱长的和为36 cm，则它的表面积是3、圆柱是由个面围成的，其中一个是面，两个是面，它的侧面和底面相交成条线，它们是（直的，曲的）。

4、圆锥体由个面围成的，底面形状是二、选择题1、一个几何体有一个顶点，一个侧面，一个底面，则这个几何体是（）A、棱柱B、棱锥C、圆锥D、圆柱2、五棱柱的棱和侧面数分别是（）A、5，5B、15，5C、10，7D、5，73、下列说法不正确的是（）A、长方体和正方体都有六个面。

B、圆锥的底面是圆面。

C、棱柱的上下底面是完全相同的图形。

D、三棱柱有三个面，三条棱。

4、下列几何体没有曲面的是（）A、球B、棱锥C、圆锥D、圆柱5、下列几何体有八个面的是（）A、六棱锥B、八棱锥C、六棱柱D、八棱柱6、七棱柱共有（）条棱。

A、7B、14C、16D、217、下列说法正确的是（）A、棱柱的侧面可以是三角形。

B、正方体和长方体都是特殊的棱柱。

C、所有几何体的侧面都能展开成平面图形。

D、棱柱的各条棱都相等。