生活中的立体图形
- 格式:ppt
- 大小:3.44 MB
- 文档页数:44
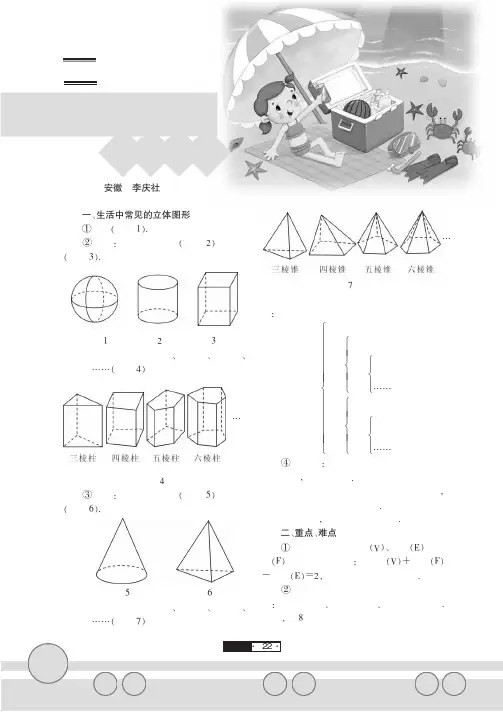
线平行一、生活中常见的立体图形①球体(如图1).②柱体:柱体分为圆柱(如图2)和棱柱(如图3).图1图2图3而棱柱又分为三棱柱、四棱柱、五棱柱、六棱柱……(如图4)图4③锥体:锥体分为圆锥(如图5)和棱锥(如图6).图5图6而棱锥又分为三棱锥、四棱锥、五棱锥、六棱锥……(如图7)图7它们之间的关系可以用下面的示意图来表示:立体图形球体柱体圆柱棱柱三棱柱四棱柱五棱柱……………………………………锥体圆锥棱锥三棱锥四棱锥五棱锥………………………………………………………………………④多面体:由若干个平面多边形所围成的几何体,叫做多面体.多面体是从另外的角度观察几何体的,它与前面的分类有重叠部分.如长方体既可以叫做四棱柱,又可以叫做六面体.二、重点、难点①凸多面体的顶点数(V )、棱数(E )和面数(F )之间满足关系式:顶点数(V )+面数(F )-棱数(E )=2,这就是著名的欧拉公式.②我们可以用运动的观点观察几何图形:点运动成线、线运动成面、面运动形成体.例如,图8中的圆锥可以看作是由直角三角数学篇生活中常见的安徽李庆社立体图形……22··数学篇线平行形绕着它的一条直角边所在的直线旋转一周得到的立体图形.图8三、典型例题分析例1写出下列立体图形的名称.图9分析:识别立体图形,关键是要搞清楚它们的特征.锥体只有一个底面,柱体有两个底面;圆柱、圆锥先找圆形底面,再由侧面确定是圆锥还是圆柱;棱锥的侧面是三角形,棱柱的侧面是长方形.解:这4个立体图形的名称依次是,三棱柱、四棱锥、圆柱、圆锥.例2下列立体图形中属于四棱柱的是().图10分析:四棱柱属于棱柱,它有两个互相平行且形状大小一样的四边形底面,有四个侧面而且都是长方形.图形A 称为圆台.图形B 是四棱锥.图形D 是四棱锥被截去一个角,它叫作六面体,也叫作棱台.解:选C.例3圆柱可以看作是由一个()经过旋转得到的.A .矩形B .直角梯形C .直角三角形D .半圆分析:用运动的观点容易得出,矩形绕它的一边所在的直线旋转一周得到圆柱体;半圆绕它的直径所在的直线旋转一周得到球体;直角三角形绕它的一条直角边所在的直线旋转一周得到圆锥;直角梯形绕着垂直于底边的腰所在的直线旋转一周得到圆台.解:选A .例4图11-1是正方体木块,把它切去一块,可得到如图11-2、11-3、11-4、11-5所示的木块.我们知道,正方体木块有8个顶点、12条棱、6个面,请你将图11-2、11-3、11-4、11-5中的木块的顶点数、棱数、面数填入下表.观察上表,请你归纳上述各种木块的顶点数、棱数、面数之间的数量关系,并表示出来.分析:首先由图形确定各自的顶点数、棱数、面数,再观察每个图形中三个数据之间的关系,然后根据数据间的关系推断出一般的规律.解:表格中应填入的四行数据分别为7,12,7;8,12,6;6,9,5;10,15,7.可得出数量关系:顶点数+面数-棱数=2.图顶点数棱数面数11-1812611-211-311-411-5图11-1图11-2图11-3图11-4图11-523··。


生活中常见的立体图形及其特征立体图形是我们日常生活中的常见事物,它们不仅令我们生活更美好,还有很多有趣的特征和用途。
本文将从常见的立体图形入手,探讨它们的特征和应用,让我们了解到立体图形的奥秘。
一、正方体正方体是一种常见的正交多面体,它有六个平面、八个顶点和12条边。
正方体是最稳定的立方体,因为它的6个面都是相等的,也就是说,正方体所承受的压力和重力是相等的。
正方体在我们的日常生活中广泛应用,例如玩具、箱子和建筑等领域。
二、圆柱体圆柱体是一种由一个圆和与其垂直的柱面组成的几何体。
它有两个平面、一个侧面、两个底面和一个轴线,圆柱体也是我们日常生活中的一种常见事物,比如可乐瓶、水管、笔筒等。
三、圆锥体圆锥体是一种由一个圆锥和一个底面组成的几何体,它有一个平面、一个侧面、一个底面和一个轴线。
圆锥体与圆柱体类似,但它的形状更加特殊,因此它有着更广泛的应用,例如圆锥机、储物柜、喇叭等。
四、棱柱棱柱是一个由两个平行的底面和由这些底面到每个底面所垂直的平面面组成的多面体。
棱柱的特征是它的“棱”,也就是说它是由多个长方形组成的,正方形是最常见的。
棱柱在我们的日常生活中也有着广泛的应用,例如铅笔盒、棉花糖、灯罩等。
五、棱锥棱锥是一个由一个多边形和所有连接多边形到一个点的线段组成的几何体。
棱锥的特征是它的“锥”,也就是说它的形状呈尖锐的角度。
棱锥也有广泛的应用,例如灯泡、安全帽等。
六、球体球体是一个由一条半径为r的球面和半径为r的半球组成的三维形体。
球体的特征是它的完美圆形,这种形状在我们的日常生活中也随处可见,例如足球、篮球、地球仪等。
七、金字塔金字塔是一个由一个多边形底面和一个顶点连接底面每个角的三角形组成的几何体。
金字塔的特征是它的形状,它的形状特殊,所以它也有很多特殊的用途,如建筑、博物馆等。
总结立体图形在我们的日常生活中随处可见,它们的特征各不相同,在不同的应用领域也有不同的用途,例如在建筑领域中,我们会用金字塔和棱锥来烘托建筑的氛围;在玩具制作领域中,我们常见到的正方体和球体;在工程制造领域中,我们可以看到的是圆柱体和圆锥体。
第01讲生活中的立体图形1.认识柱体、椎体、球体,并能够熟练的进行立体图形的分类;2.掌握柱体、椎体、球体的特征;3.掌握柱体特征及其面的个数、棱的条数、顶点个数之间的关系;4.掌握立体图形的表面积、体积公式;5.掌握棱柱的顶点数、棱数、面数的计算方法;6.掌握立体图形的表面积和体积的计算方法.知识点01 认识立体图形(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.知识点02 立体图形的分类(1)按形状分类:球,柱体(圆柱、棱柱),椎体(圆锥、棱锥),台体(圆台、棱台).(2)按构成分类:旋转体(由平面围成的立体图形),旋转体(绕某一轴旋转一周).知识点03 点、线、面、体(1)体与体相交成面,面与面相交成线,线与线相交成点.(2)从运动的观点来看:点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.(3)从几何的观点来看:点是组成图形的基本元素,线、面、体都是点的集合.(4)长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体简称体.(5)面有平面和曲面之分,如长方体由6个平面组成,球由一个曲面组成.知识点04 棱柱与棱锥的顶点、面、棱数(1)几何体的表面积=侧面积+底面积(上、下底的面积和)(2)常见的几种几何体的表面积的计算公式:题型01几何体的识别【典例1】下列标注的图形与名称不相符的是()A.圆锥B.四棱柱C.三棱锥D.圆柱【变式1】下面的立体图形按从左到右的顺序依次是()A.长方体、圆柱、圆锥、正方体B.长方体、圆柱、球、正方体C.棱柱、棱柱、球、正方体D.长方体、棱柱、圆锥、棱柱题型02立体图形的分类【典例1】如图,下列几何体,是柱体的有______,球体的有______.(填序号)【变式1】如图所示,请将下列几何体分类.题型03几何体中点、棱、面【典例1】几何知识.(1)长方体有_____个面,_____条棱,_____个顶点.(2)圆柱体由_____个面围成,圆锥由_____个面围成,它们的底面都是_____.(3)已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……,由此类推n棱柱有_____个面,_____个顶点,_____条棱.【变式1】如图所示,是我们熟悉的三棱柱、五棱柱和六棱柱.(1)填写下表:题型04点、线、面、体四者之间的关系【典例1】当你用笔在纸上写字时,你的笔尖实现了()A.点动成线B.线动成面C.面动成体D.以上都不对【变式1】如图,直角三角形绕它的一条直角边所在的直线旋转一周,形成的几何体是__________,这其中蕴含的数学事实是__________.题型05平面图形旋转后所得的立体图形【典例1】图中的圆柱体是由下面哪个图形旋转而成的()A.B.C.D.【变式1】下列各选项中的图形,绕虚线旋转一周,所得的几何体是圆锥的是()A.B.C.D.一、选择题1.下列图形是平面图形的是()A.正方体B.圆C.球D.圆锥2.下列几何体中,不属于棱柱的是()A.B.C.D.3.中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为()A.点动成线,线动成面B.线动成面,面动成体C.点动成线,面动成体D.点动成面,面动成线4.如图,把图形绕着给定的直线旋转一周后形成的几何体是()A.B.C.D.二、填空题5.五棱柱的面的个数为______.6.在正方体、长方体、圆柱、圆锥、球、六棱柱、六棱锥中属于柱体有___个.7.笔尖在纸上快速滑动写出了一个又一个字,这说明了_____;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____,“齐天大圣”孙悟空有一个宝贝﹣金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明_____.8.如图是一个底面各边都相等的六棱柱,它的底面边长为2cm,高为5cm.这个棱柱共有______条棱,______个面,侧面积是______2cm.三、解答题9.将如图几何体分类,并说明理由.10.下列是我们常见的几何体,按要求将其分类(只填写编号).(1)如果按“柱”“锥球”来分,柱体有______,椎体有______,球有______;(2)如果按“有无曲面”来分,有曲面的有______,无曲面的有______.(1)根据要求填写表格:操作探究:。







生活中的立体图形引言立体图形是指在三维空间中具有长度、宽度和高度的图形。
在我们的日常生活中,我们经常会遇到各种各样的立体图形,例如盒子、球体和圆柱体等等。
这些立体图形不仅仅是一种几何形状,它们在我们的生活中扮演着重要的角色,就像我们周围的建筑物、容器和各种物体一样。
本文将介绍生活中常见的几种立体图形以及它们的应用。
一、盒子盒子是一种常见的立体图形,它具有六个面,包括四个侧面、一个底面和一个顶面。
盒子通常用来储存物品或包装物品。
在我们的日常生活中,我们经常会使用盒子来存放食物、书籍、衣物等等。
此外,盒子还经常用于运输物品,在物流行业中扮演着重要的角色。
二、球体球体是另一个常见的立体图形,它是由一个平面围绕着一个点旋转形成的图形。
球体在体育运动、音乐乐器和家居装饰中都有重要的应用。
在体育运动中,例如足球、篮球和网球,都是使用球体形状的球进行比赛。
此外,许多乐器,如打击乐器中的铜钹和木琴,也具有球体形状。
在家居装饰中,人们经常使用球体形状的装饰物来增添居家的美感。
三、圆柱体圆柱体是一个由圆形底面和一个平行于底面的圆形顶面连接而成的立体图形。
它不仅仅在我们的日常生活中发挥着储存和运输物品的作用,还在建筑、工程和设计领域中被广泛应用。
在建筑中,圆柱体形状常用于柱子和柱头的设计,为建筑物增添了美观和稳定性。
在工程领域中,圆柱体常用于管道和容器的设计和制造。
在设计领域中,圆柱体形状的物体常用于产品设计,例如圆柱形的笔筒和香薰瓶等。
四、棱柱体棱柱体是一个由多个相等的侧面连接而成的立体图形,它有两个平行且相等的底面。
棱柱体在建筑、工程和数学等领域有广泛的应用。
在建筑中,棱柱体常用于建筑物的设计,例如建筑立面的设计。
在工程领域中,棱柱体形状的物体常用于制造容器和管道。
在数学中,棱柱体经常被用作教学工具,帮助学生理解几何概念。
结论生活中的立体图形在我们的日常生活中无处不在。
从盒子到球体,再到圆柱体和棱柱体等等,这些立体图形不仅仅是一种几何形状,它们还扮演着各种重要的角色。
生活中的立体图形
生活中,我们常常被各种各样的立体图形所包围。
从简单的立方体到复杂的多
面体,这些图形无时无刻不在提醒着我们生活的多样性和丰富性。
首先,让我们来看看立方体。
它是最简单的立体图形之一,由六个正方形组成。
在我们的日常生活中,许多物品都是立方体的形状,比如盒子、饼干罐、书架等等。
这些立方体的物品给我们带来了方便和整洁,让我们的生活更加有序。
接下来,我们再来看看圆柱体。
它是一个有两个圆形底面和一个侧面的立体图形。
在我们的生活中,圆柱体也是非常常见的,比如水杯、筒形花瓶、圆柱形蜡烛等等。
圆柱体的形状给我们的生活增添了一些美感和艺术气息,让我们的生活更加丰富多彩。
另外,我们还有许多其他的立体图形,比如球体、锥体、多面体等等。
它们都
在我们的生活中扮演着不同的角色,给我们的生活带来了不同的乐趣和便利。
总的来说,生活中的立体图形无处不在,它们丰富了我们的生活,让我们的生
活更加多姿多彩。
让我们珍惜这些立体图形,感受它们给我们带来的美好。
希望我们能够在生活中发现更多立体图形,让我们的生活更加精彩!。
的图形世界2023-11-04•引言•常见的立体图形•立体图形的性质与特点目录•立体图形在生活中的应用•立体图形的制作与设计•总结与展望01引言篮球、足球、乒乓球等。
球形物体茶杯、可乐罐、笔筒等。
圆柱形物体冰淇淋蛋卷、陀螺等。
锥形物体积木、书柜、电脑主机等。
立方体物体生活中的立体图形立体图形定义三维空间中占有空间的实体形状,立体图形是各部分不都在同一平面内的几何图形。
立体图形分类多面体、旋转体以及其他较为特殊的立体图形。
其中,多面体是由若干个平面组成的几何体,旋转体是由一个平面图形围绕某一条直线旋转一周所得到的几何体。
立体图形的定义与分类02常见的立体图形定义长方体是一种具有六个面、十二条棱、八个顶点的立体图形。
每个面都是矩形或正方形,相对的两个面互相平行且大小相等。
形状特点长方体的六个面都是矩形或正方形,十二条棱分别平行且相等。
八个顶点分别位于每个面的四个角上。
体积和面积长方体的体积可以通过其长、宽、高的乘积计算得到,即V=abc(其中a、b、c分别表示长、宽、高)。
而其表面积可以通过六个面的面积之和计算得到,即S=2(ab+bc+ac)。
定义圆柱体是一种具有一个底面、一个顶面以及一个侧面(圆筒)的立体图形。
底面和顶面互相平行且大小相等,侧面展开后为矩形。
形状特点圆柱体的底面是一个圆,直径为d,半径为r。
顶面也是一个圆,直径与底面相同。
侧面展开后为一个矩形,长为底面的周长,宽为圆柱体的高h。
体积和面积圆柱体的体积可以通过底面积乘以高得到,即V=πr²h(其中π表示圆周率,r表示底面半径,h表示高)。
而其表面积则包括底面积、顶面积和侧面积,即S=2πr²+ch(其中c表示底面周长)。
球体定义01球体是一种具有一个曲面、没有棱的立体图形。
球体的曲面叫做球面,球心与球面之间的距离叫做半径。
形状特点02球体是一个完全对称的图形,无论从哪个方向观察,它的形状都是相同的。
球体的表面积和体积都是通过半径来计算的。
《生活中的立体图形》教案设计与说明(精选11篇)《生活中的立体图形》教案设计与说明篇1一、学习目标:1、通过观看生活中的大量物体,熟悉基本的几何体。
2、经过比较不同的物体学会观看物体间的不同特征,体会几何体间的联系与区分。
3、进一步熟悉点、线、面、体,感受点、线、面、体之间的关系;4、通过观看、操作等实践活动,进一步进展同学的空间观念;学习重点:1、在详细的情境中,熟悉一些基本的几何体,并能描述这些几何体的特征。
2、熟悉点、线、面、体,感受点、线、面、体之间的关系学习难点:1、是描述几何体的特征,对几何体进行分类。
2、熟悉点、线、面、体,感受点、线、面、体之间的关系二、自学导引自学检测:1、画出在学校的时候学习的平面图形和几何图形,并将它们分类,说出分类的标准和理由。
2、在生活你还见到那些几何体?三、典例精析1、指出下列几何体的名称2、争论并填写下表:①生活常见的几何体有那些?②这些几何体有什么特征③圆柱体与圆锥体有什么的相同之处和不同之处④圆柱体与棱柱体有什么的相同之处和不同之处?⑤棱柱的分类;⑥几何体的分类(1)、几何体特征表:分类名称图形主要特征柱棱柱球球(2)、相同点与不同点:分类相同点不同点圆柱圆锥分类相同点不同点圆柱棱柱3、小组活动,争论并沟通下列问题及其解答:(对比观看,理解相关性质)(1)正方体是由_____个面围成的;圆柱是由______个面围成的;它们都是平的吗?(2)圆柱的侧面和底面相交成_____条线?它们是直的还是曲的?(3)正方体有______个顶点?经过每个顶点有______条边?(4)图形是由______ _______ _______构成的。
(5)面与面相交得到______,线与线相交得到______。
四、随堂演练:1、用笔点一点,让点动起来,然后把你得到的图形平移,观看图形。
2、想象下列平面图形绕轴旋转一周,可以得到哪些立体图形?(1)(2)(3)(4)(5) a b c d e总结:点动成,线动成,动成体。