电路原理课件-一阶电路的全响应
- 格式:ppt
- 大小:1.27 MB
- 文档页数:36
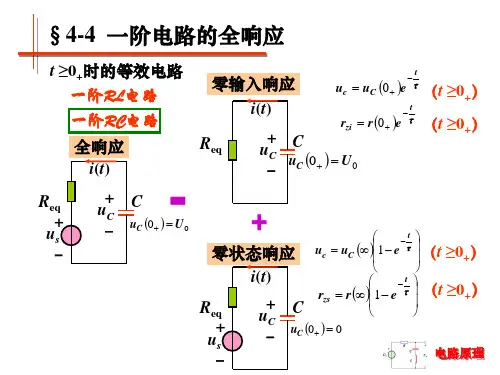


一阶电路的全响应一阶电路的全响应一、全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应,称为一阶电路的全响应(complete response)。
图5.5-1(a)所示的一阶RC电路,直流电压源Us是外加激励,时开关S处于断开状态,电容的初始电压。
时开关闭合,现讨论时电路响应的变化规律。
时,响应的初始值为时,响应的稳态值为用叠加定理计算全响应:开关闭合后,电容电压的全响应,等于初始状态U0单独作用时产生的零输入响应和电压源Us单独作用时产生的零状态响应的代数和,如图5.5-1(b)、(c)所示。
图5.5-1(b)中,零输入响应为图5.5-1(c)中,零状态响应为根据叠加定理,图5.5-1(a)电路的全响应为用表示全响应,表示响应的初始值,表示稳态值。
全响应的变化规律1、当时,即初始值大于稳态值,则全响应由初始值开始按指数规律逐渐衰减到稳态值,这是动态元件C或L对电路放电。
2、当时,即初始值小于稳态值,则全响应由初始值开始按指数规律逐渐增加到稳态值,这是电路对动态元件C或L充电。
3、当时,即初始值等于稳态值,则全响应。
电路换路后无过渡过程,直接进入稳态,动态元件C或L既不对电路放电,也不充电。
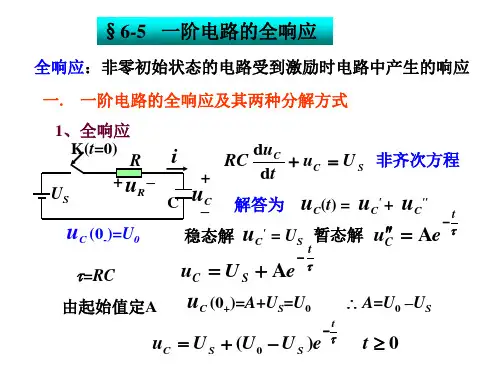
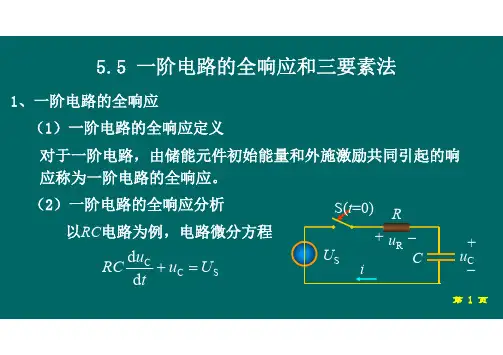
二、全响应的三要素计算方法全响应的三要素初始值稳态值时间常数例5.5-1 图5.5-2(a)所示电路,已知C=5uF,t<0时开关S处于断开状态,电路处于稳态,t=0时开关S闭合,求时的电容电流。
解:欲求电容电流,只要求出电容电压即可。
1、确定初始状态。
作时刻的电路,如图5.5-2(b)所示,这时电路已处于稳态,电容相当于开路,则。
由换路定则得初始状态2、确定电容电压的稳态值。
作t→∞时的电路,如图5.5-2(c)所示,这时电路也处于稳态,电容也相当于开路,则3KΩ电阻两端的电压则电容电压的稳态值为3、求时间常数τ。
求从电容C两端看进去的戴维南等效电阻R的电路如图5.5-2(d)所示,这时将15V和5V电压源都视为短路,等效电阻为6KΩ和3KΩ电阻的并联,即R=6K∥3K=2KΩ所以,时间常数为4、求全响应。
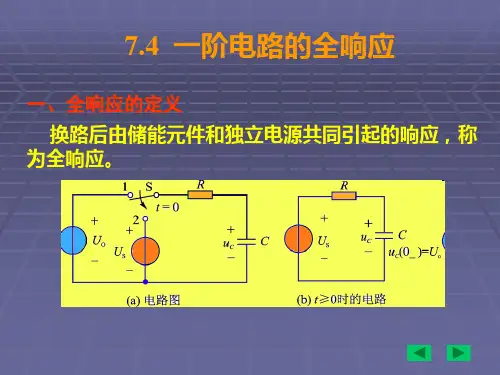


§5.4 一阶电路的全响应与三要素在上两节中分别研究了一阶电路的零输入响应和零状态响应,电路要么只有外激励源的作用,要么只存在非零的初始状态,分析过程相对简单。
本节将讨论既有非零初始状态,又有外激励源共同作用的一阶电路的响应,称为一阶电路的全响应。
5.4.1 RC 电路的全响应电路如图5-9所示,将开关S 闭合前,电容已经充电且电容电压0)0(U u c =-,在t=0时将开关S 闭合,直流电压源S U 作用于一阶RC 电路。
根据KVL ,此时电路方程可表示为:C u图 5-19 一阶RC 电路的全响应S C CU u tu RC=+d d (5-19) 根据换路原则,可知方程(5-19)的初始条件为 0)0()0(U u u C C ==-+令方程(5-9)的通解为 C CC u u u ''+'= 与一阶RC 电路的零状态响应类似,取换路后的稳定状态为方程的特解,则S CU u =' 同样令方程(5-9)对应的齐次微分方程的通解为τtCAe u -=''。
其中RC =τ为电路的时间常数,所以有τtS C AeU u -+=将初始条件与通解代入原方程,得到积分常数为 S U U A +=0所以电容电压最终可表示为τtS S c e U U U u --+=)(0 (5-20)电容充电电流为etS C R U U t u C i τ--==0d d这就是一阶RC 电路的全响应。
图5-20分别描述了s U ,0U 均大于零时,在0U U s >、0=s U 、0U U s <三种情况下c u 与i 的波形。
(a) (b)图5-20C u ,i 的波形图将式(5-20)重新调整后,得)1(0ττtS tC e U eU u ---+=从上式可以看出,右端第一项正是电路的零输入响应,第二项则是电路的零状态响应。
显然,RC 电路的全响应是零输入响应与零状态响应的叠加,即 全响应 = 零输入响应 + 零状态响应研究表明,线性电路的叠加定理不仅适用于RC 电路,在RC 电路的分析过程中同样适用,同时,对于n 阶电路也可应用叠加定理进行分析。



一阶动态电路的全响应好嘞,今天我们来聊聊一阶动态电路的全响应。
说到这,大家可能会觉得有点复杂,不过别担心,我会用轻松的方式给你讲明白的。
想象一下,你在家里喝茶,偶尔抬头看看窗外,看到那微风吹过的树叶,忽然想起了电路。
听起来是不是有点奇怪?但电路其实就像生活中的很多事情,有时候一阵风吹来,你的反应会慢半拍,这就跟一阶动态电路一样。
一阶动态电路是什么呢?简单说,就是那种反应不那么迅速的电路。
就像你在思考一件事情时,脑子里可能会卡壳。
电流流动的速度不是瞬间就能达到,而是有个逐渐适应的过程。
就像你早上醒来,不是一下子就能进入状态,得喝杯咖啡,等一等才行。
电路也是,输入信号来了,输出信号得等一等,慢慢才能反应过来。
这种反应过程就叫全响应。
我们来想象一下,一个简单的电路。
假设有个电阻和电容,电压信号突然加上去。
这时候,电容就像个小水库,水库里的水不能一下子装满,得一点点来,慢慢充水。
这个过程就是电容充电的过程,电流逐渐增大,电压也渐渐上升。
你可以把它想象成一个人慢慢适应新环境,刚到一个派对,开始有点紧张,慢慢就能放开来,跟大家聊得热火朝天。
然后啊,电路的全响应不仅仅是充电,放电也是一回事。
电容充好电了,假如这个电源突然断了,电容里的电就像气球里的空气,开始慢慢漏出去。
这时候,电压又会渐渐下降,直到完全放空。
这种变化其实在生活中也很常见,比如你跟朋友聊天,聊得正嗨,结果突然有人打断了,你可能一时没反应过来,脑子里还在回味刚才的话题。
说到这里,可能会有人问,全响应有什么用呢?嘿,这可大有用处了。
你想啊,很多电子设备都需要控制信号的变化速率。
比如说在音响里,如果信号变化太快,可能会造成声音失真,就像是你跟朋友聊天,他话说得太快,你根本跟不上。
反过来,如果反应太慢,又会造成滞后,影响使用体验。
我们再说说这个电路的时间常数。
这个时间常数就像你给电路加个标签,告诉它“嘿,反应时间差不多是多久”。
时间常数越大,反应越慢;越小,反应越快。