一阶电路的全响应

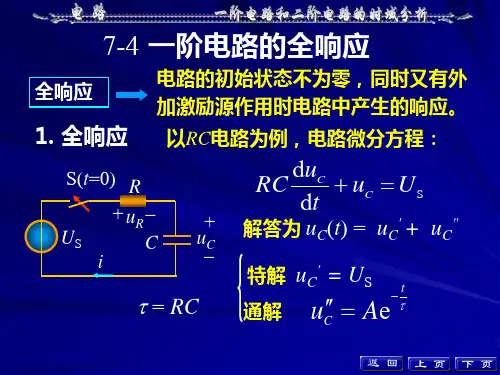
电路原理课件-一阶电路的全响应

稳态分量
t 0
t
暂态分量

i R (t ) i Rf [i R (0 ) i Rf ]e

t 0
电容中的电流响应为
U0 iC ( t ) I s i R ( t ) e R
U0 iC ( 0 ) I s R iCf 0
t RC
I se
2 10 0 V 4V 5
2. 求稳态值
uC1 f uC 2 f 0
3. 求时间常数
RC RC1 C2 25 s
4. 写出响应表达式
uC 1 (t ) 4e

t 25 V
uC1(0-)=10
uC(t)/V
t 0
4 uC2(0-)=0 0 τ 电容电压曲线
3) 求τ
Req 14 2 1 s 14 7
4) 写出i (t)
iL (t ) 4 (1 4)e
7 t
4 5e
7 t
A
t 0
例4 在图示电路中，电感电流iL(0)=0。t=0时，开关S1闭合后，经过0.1s，再闭合开关S2。试求电感电流iL(t)。解： 1、0+≤ t ≤0.1-s时
U0 Is R iC(0-)=0 0
零状态分量
i R( t ) iC (t) t
零输入分量
t
U0 - Is R
-U0/R
一阶电路对阶跃激励的全响应的一般表达式
r (t ) rf (t ) r (0 ) rf (0 ) eFra bibliotek
t

t 0
全响应的初始值、稳态解和电路的时间常数，称为一阶线性电路全响应的三要素。这种方法就叫做三要素法。

一阶电路的全响应

i(∞) 10 / 5A 2A
+ 10V
-
3
i(t) (2 2e5t ) A
S2(t=0.2s)
返回上页下页
t > 0.2s
i(0.2 ) (2 2e50.2 )A 1.26A
i(0.2 ) 1.26A
2 L / R 1/2s 0.5s
i(∞) 10/2A 5A
i(t) (5 3.74e2(t0.2) ) A
+ 10V
uC (∞) (10 1)V 11V –
+ uC
－
1A +
u
－
返回上页下页
RC (11) 1s 2s
全响应： uC (t) (11 Ae0.5t )V
1
1 1
uC (t) (11 10e0.5t )V
iC
(t
)
duC dt
5e0.5t A
+ 10V –
+ －uC
1A +
返回上页下页
或求出稳态分量全响应
代入初值有
iL (∞) 24 /12A 2A
iL (t) (2 Ae20t )A
6＝2＋A
A=4
例4-2 t=0时 ,开关S闭合，求t >0后的iC、uC及电流源两端的电压（uC(0－)=1V，C=1F）。
解这是RC电路全响
应问题，有
1
1 1
稳态分量：
iL (t) [6 (2 6)e5t ]A (6 4e5t )A t 0
i1(t) [2 (0 2)e5t ]A (2 2e5t )A
i2 (t) [4 (2 4)e5t ]A (4 2e5t )A
返回上页下页

(电路分析)一阶电路的全响应

一阶电路的全响应一阶电路的全响应一、全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应，称为一阶电路的全响应（complete response）。

图5.5-1（a）所示的一阶RC电路，直流电压源Us是外加激励，时开关S处于断开状态，电容的初始电压。

时开关闭合，现讨论时电路响应的变化规律。

时，响应的初始值为时，响应的稳态值为用叠加定理计算全响应：开关闭合后，电容电压的全响应，等于初始状态U0单独作用时产生的零输入响应和电压源Us单独作用时产生的零状态响应的代数和，如图5.5-1（b）、（c）所示。

图5.5-1（b）中，零输入响应为图5.5-1（c）中，零状态响应为根据叠加定理，图5.5-1（a）电路的全响应为用表示全响应，表示响应的初始值，表示稳态值。

全响应的变化规律1、当时，即初始值大于稳态值，则全响应由初始值开始按指数规律逐渐衰减到稳态值，这是动态元件C或L对电路放电。

2、当时，即初始值小于稳态值，则全响应由初始值开始按指数规律逐渐增加到稳态值，这是电路对动态元件C或L充电。

3、当时，即初始值等于稳态值，则全响应。

电路换路后无过渡过程，直接进入稳态，动态元件C或L既不对电路放电，也不充电。

二、全响应的三要素计算方法全响应的三要素初始值稳态值时间常数例5.5-1 图5.5-2（a）所示电路，已知C=5uF，t<0时开关S处于断开状态，电路处于稳态，t=0时开关S闭合，求时的电容电流。

解：欲求电容电流，只要求出电容电压即可。

1、确定初始状态。

作时刻的电路，如图5.5-2（b）所示，这时电路已处于稳态，电容相当于开路，则。

由换路定则得初始状态2、确定电容电压的稳态值。

作t→∞时的电路，如图5.5-2（c）所示，这时电路也处于稳态，电容也相当于开路，则3KΩ电阻两端的电压则电容电压的稳态值为3、求时间常数τ。

求从电容C两端看进去的戴维南等效电阻R的电路如图5.5-2（d）所示，这时将15V和5V电压源都视为短路，等效电阻为6KΩ和3KΩ电阻的并联，即R=6K∥3K=2KΩ所以，时间常数为4、求全响应。

一阶电路的全响应——三要素公式【PPT课件】

6A
2
Is
US 3H
(a)
u
大学电路与系统
(2)求解零状态响应iLf(t)和uf(t) 。
零状态响应是初始状态为零,仅由独立源所引起的 R2
响应;故 iLf(0+)=0,电感相当于开路。画出其0+等效 12V
电路,如图 (b)所示,所以
R3 US
iLf(0+) uf(0+) R4
RLiL
L1uS
(a)
(b)
制作
若用y(t)表示响应,用f (t)表示外加激励,上述方程统一表示为
ddy(tt)1y(t)bf(t)
τ为时常数,对RC电路, τ= RC; 对RL电路, τ= L/R。
第 5-2 页
前一页
下一页返回本章目录
y(t) = yh(t) + yp(t)
特征根 s = - 1/τ, yh(t) = Ke- t/τ ,
学电路与
1316uL(0)13863
系统
得uL(0+) = 6V, i(0+) = uL(0+) /6=1A
(a) 3Ω
i(0+) 3A
18V uL(0+)
6Ω
6A
(b) 0+图
3Ω
多媒
(3)画∞等效电路,如图(c)。
i(∞) 3A
体室
显然有 uL(∞) = 0, i(∞) = 0,
18V uL(∞) iL(∞) 6Ω
路与
iL(0+) =iL(0-)=12/(2+1)=12/3=4(A)
系统
uC (0+)= uC(0-)=1×iL(0-)=4(V)

(电路分析)一阶电路的全响应

一阶电路的全响应一阶电路的全响应一、全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应，称为一阶电路的全响应（complete response）。

图5.5-1（a）所示的一阶RC电路，直流电压源Us是外加激励，时开关S处于断开状态，电容的初始电压。

时开关闭合，现讨论时电路响应的变化规律。

时，响应的初始值为时，响应的稳态值为用叠加定理计算全响应：开关闭合后，电容电压的全响应，等于初始状态U0单独作用时产生的零输入响应和电压源Us单独作用时产生的零状态响应的代数和，如图5.5-1（b）、（c）所示。

图5.5-1（b）中，零输入响应为图5.5-1（c）中，零状态响应为根据叠加定理，图5.5-1（a）电路的全响应为用表示全响应，表示响应的初始值，表示稳态值。

全响应的变化规律1、当时，即初始值大于稳态值，则全响应由初始值开始按指数规律逐渐衰减到稳态值，这是动态元件C或L对电路放电。

2、当时，即初始值小于稳态值，则全响应由初始值开始按指数规律逐渐增加到稳态值，这是电路对动态元件C或L充电。

3、当时，即初始值等于稳态值，则全响应。

电路换路后无过渡过程，直接进入稳态，动态元件C或L既不对电路放电，也不充电。

二、全响应的三要素计算方法全响应的三要素初始值稳态值时间常数例5.5-1 图5.5-2（a）所示电路，已知C=5uF，t<0时开关S处于断开状态，电路处于稳态， t=0时开关S闭合，求时的电容电流。

解：欲求电容电流，只要求出电容电压即可。

1、确定初始状态。

作时刻的电路，如图5.5-2（b）所示，这时电路已处于稳态，电容相当于开路，则。

由换路定则得初始状态2、确定电容电压的稳态值。

作t→∞时的电路，如图5.5-2（c）所示，这时电路也处于稳态，电容也相当于开路，则3KΩ电阻两端的电压则电容电压的稳态值为3、求时间常数τ。

求从电容C两端看进去的戴维南等效电阻R的电路如图5.5-2（d）所示，这时将15V和5V电压源都视为短路，等效电阻为6KΩ和3KΩ电阻的并联，即R=6K∥3K=2KΩ所以，时间常数为4、求全响应。

一阶电路的全响应

3.所谓“陷阱”。
例如：电路原已稳定，求开关动作后的电
流i。
解： t 0 , iL (0 ) 2 A
1H 5
5 + 由换路定则：
iL
t=0 i
10V
-
t 0 , iL(0 ) 2 A
如果认为 R0 0
得 R0 0
用三要素公式，得 iL () 0
R0 t
iL (t) 2e L A
电流源的电流is。其通解为
t
r(t ) rh (t ) rp (t ) Ae rp (t )
t=0+代入，得： A r(0 ) rp (0 )
因而得到
r(t)
rp (t )
[r(0
)
rp (0
)]e
t
,
t
0
一阶电路任意激励下uC(t)和iL(t)响
应的公式
推广应用于任意激励下任一响应
开关闭合前，电路已稳定，电容相当于开路，电流源电流全部流入4电阻中，
uC (0 ) 4 2 8V
由于开关转换时，电容电流有界，电容
电压不能跃变，故
uC (0 ) uC (0 ) 8V
画0+图如右2A
4
2 i(0+)
+
+
8V 4
-
10V
-
i(0 ) 10 uC (0 ) 10 8 1A
例19 开关在a时电路已稳定。t=0倒向
b,t=R1C倒向c，求t0的iC(t)并画波形
解： t<0 时， c
R1
uC(0-)=0 。第一次换路后由换路定则得：
R2
+
Us
-
b

一阶电路的全响应

vCh
图11.24 RC串联零输入电路图图11.25 t > 0时的等效电路图图11.26 电容电压vC波形图0
t(s)
2006-1-1
！
2
1.1 全响应的解(1)
当t = 0时，开关S由1掷向2处。此时直流电压源VS2作用于电路，其等效电路如图11.25所示。根据换路定理可知：vC(0+) = vC(0−) = VS1。又根据基尔霍夫电压定律列写电压方程有vC + Ri = VS2 (t > 0)。由于电流i与电容电压 vC关联，因此存在以下关系
+ + +
RS S t = 0
+
vC − C
R1 i1 iC
i2
+
vC − C
RS
R1 i1 iC
Req
i2
VS
R2
VS
R2
VOC
−
−
−
图11.28 例11.3图图11.29 t > 0时的等效电路图11.30 化简为戴维南等效电路
+
iC vC C −
2006-1-1
！
7
1.3 三要素法
解当t < 0时，由于电路已经处于稳定状态，因此可知电容电压vC(0−) = 0。当t = 0时，开关S闭合。根据换路定理可知，vC(0+) = vC(0−) = 0。为方
当t = 0时，开关S由1掷向2处。根据换路定理可知，iL(0+) = iL(0−) = −0.5(A)。为方便，画出其等效电路图如图11.33所示。将电感以外的电路化简为戴维南等效电路，如图11.34所示，那么其开路电压VOC = −2.5(V)，等效电阻Req = 1.5(Ω)。则电感电流终了值iL(∞) = VOC/Req = −1.667(V)，时间常数

一阶电路的全响应

一阶电路的全响应一阶电路的全响应一.全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应，称为一阶电路的全响应(complete response)。

图5. 5-1 (a)所示的一阶RC电路，直流电压源Us是外加激励•时开关S处于断开状态.电容的初始电压叫2°时开关闭合.现讨论f上°时电路响应的变化规律。

2 °4时，响应的初始值为叫(―)二％时，响应的稳态值为叫(8)=°$1(8)= 0川亞丿川宦理计算全响应:开关闭合后，电容电压叫⑦的全响应•等于初始状态U0取独作用时产生的零输入响应叫购和电I W ' I'JU'r Hj时产生的零状态响应叫11⑦的代如II,如图5・5・1 (b) . (c)所示。

图5. 5-1 (b)中，零输入响应为= = (ao)图5. 5-1 (c)中.零状态响应为du''(f)dt(CO)1、、厂（°+）1（8）时川初始值大于稳态值.2、屮®J'%00）时川初始值小于稳态值. 则全响应由初始值开始按抬数规律逐渐増加到稳态值，这是电路对动8、当® Jr （8）时.电路换路后无过渡过程，直接进入稳态.动态根据叠加定理•图5. 5-1 （a）电路的全响应为◎（f） = Q（f） + 冬"（f）=弘五4■兀Q 一＜码t i=,十（九一匚）「冠=十血Oh） - （C 0皿=1/(0 +y® =-譽尸+牛二=1（8）+哄4）-「（8护用‘①表示全响应，农示响应的初始值，心校示稳态值。

—阶电路全响应非零初始状态的一阶动态电路，包括RC电路和RL电路，在外加激励的作用下，电路中任何一条支路上的全响应为啲=r(0 十)E T+ F(CD)(1 - g『)全响应的变化规律则全响应由初始值开始按抬数规律逐渐衰减到稳态值，这是动态元件C或L对电路放电。

一阶电路的全响应

t
0)
5 55
55
iL (t )=
6 5
(
6 5
6
)e
t 3
5
6 5
12
e
t 3
(
A)(
t
5
0)
【例2】如图(a)电路，uc(0-)=2V，t=0时K闭合，试用三要素法求t≧0时uc(t)及i1(t)。
K i1(t) 2
K i1(0+) 26Biblioteka -+6
-
+
+
+
Us 12V
2i1 1F +
uc(t) -
令t=0+，则：
-0
y(0+ )=Ae y() A y(0+ )-y()
故：
-t
y(t)=y() [ y(0 ) y()]e
-t
y(t)=y() [ y(0 ) y()]e
三要素：
① 初始值y(0+)
② 终值y()
③ 时间常数=RC或
L R
2、三要素法的应用
i(t) 1
1
K
iL(t)
—— 电路的时间常数。
(c) t= 等效图
1
1
（3）时间常数
L
R
（图d）
0
R0 2
5
R0 =1
(2//1)
3
等效内阻，从动态元件两端看出去
(d) 求时等效图
L = 5 3(s)
R0 5 / 3
-t
（4）由 y(t)=y() [ y(0 ) y()]e
i(t )=
9
(1
9
)e

一阶电路的全响应

一阶电路的全响应
电路是一种用来控制电流和电压的装置。

它们由电子元件如电阻、电容和电感组成，用来制造各种不同的电路。

其中，一阶电路是一种
简单的电路，它只包含一个电阻、电容或电感元件。

一阶电路的全响
应指电路在输入信号变化的过程中，电路中的电压和电流如何随着时
间变化。

在一阶电路中，电压和电流是随时间而变化的，称为变量。

在电
路稳定后，变量不再发生变化，称为恒定值。

一阶电路的全响应有三
个部分：零状态响应、强制响应和完全响应。

首先，零状态响应是指电路中元件上原有的电荷和电流在没有外
部输入信号时的响应。

在没有输入信号时，电路中的电荷和电流会随
时间变化，直到它们达到恒定值。

这个响应通常是指电路的初始状态，也称为初始响应。

其次，强制响应是指电路在输入信号发生变化时，由于外部输入
信号的作用，电路中的电荷和电流发生了变化。

这个响应是由于外部
输入信号强制电路中的元件发生变化而引起的。

最后，完全响应是指在零状态响应和强制响应的基础上，电路中
的电荷和电流发生的全部变化。

它是由零状态响应和强制响应的叠加
而得到的。

它包含了所有的电路响应，因此也被称为总响应。

一阶电路的全响应对于理解电路的行为和性能非常重要。

它可以帮助我们判断电路的稳定性和可靠性，也可以提供对电路故障的判断依据。

因此，在电路设计和维修中，深入理解一阶电路的全响应是非常有必要的。

电路原理一阶电路的全响应

20i3
1 di3(t) dt
30
0.095 0.028e35t t 0
3. 求i1(t) i1(t) i2(t) i3(t)
0.238 0.029e35t t 0
例3. 图示电路换路前已工作了很长的时间。试用三要素法求换路后u(t)、i(t)。
解：1）求 iL(0+) iL(0 ) 0.2A
4-4-1 求题4-4-1图所示电路中的电容电压uc(t)，并绘出曲线。
解：1）求uc(0+)
uc (0 ) uc (0 ) 297 3 40 200V
20 40
2）求ucf
3) 求τ
3
ucf
40 2V 20 40
20 40 4 104 s
20 40 3
4) 写出uc (t)
注意： 1、零输入响应、零状态响应是全响应的特例，都可采用三要素法进行求解；
2、以uc(t)和iL(t)为第一求解变量； 3、三要素法只能用于求解一阶电路的响应。
例2. 图示电路换路前已工作了很长的时间，求换路后各
支路的电流。
思路：先用三要素法求i3(t)
解: 1. 求i3(t) 1) 求i3(0+)
t
uC (t) (U0 RI s )e RC RI s t 0
解法二：全响应=零输入响应+零状态响应
➢由原始状态uc(0)=U0引起的零输入响应电容电压为
t
uczi (t ) U0e RC
t 0
➢电路对阶跃电流激励Is (t)的零状态响应电容电压为
uczs(t )
RIs 1
t
e RC
uc (t)
ucf
(uc (0 ) ucf

一阶电路的全响应

使用稳定的电源电压，避免电压波动对实验结果的影响。
注意安全事项
在实验过程中，要注意安全事项，如避免触电、短路等危险情况。
仿真模拟软件应用举例
Multisim软件
Multisim是一款常用的电路仿真软件，可以用于模拟一阶电路的全响应过程，通过虚拟实验来验证理论分析结果。
PSpice软件
PSpice是另一款专业的电路仿真软件，具有强大的电路分析和模拟功能，可以用于一阶电路的暂态响应和稳态响应分析。
电感L的影响
在RL电路中，电感L的大小直接影响时间常数τ。电感L越大，时间常数τ越大，电路变化越慢；反之，电感L越小，时间常数τ越小，电路变化越快。同时，电阻R的大小也会影响时间常数τ 的大小。
05 全响应过程分析与描述
零输入响应、零状态响应概念区分
零输入响应
指电路在没有外部激励的情况下，仅由初始储能（如电容电压、电感电流）引起的响应。
一阶电路简介
一阶电路定义
仅含有一个动态元件（电容或电感）的线性电路。
一阶电路特点
电路结构简单，动态过程易于分析。
常见的一阶电路
RC电路、RL电路等。
全响应概念及重要性
全响应定义
一阶电路在激励和初始状态共同作用下的响应。
全响应的组成
全响应的重要性
全响应反映了电路在实际工作条件下的动态特性，是电路分析和设计的重要依据。同时，全响应也是理解更复杂电路响应的基础。
时间常数是描述一阶电路暂态过程变化快慢的重要参数，用希腊字母τ（tau）表示。它反映了电路从一种稳定状态过渡到另一种稳定状态所需的时间。
计算公式
对于一阶RC电路，时间常数τ等于电阻R与电容C的乘积，即τ=RC；对于一阶RL电路，时间常数τ等于电感L与电阻R的比值，即τ=L/R。

一阶电路的全响应

分析（1） iL (t) (I0 IS )e L IS
全响应＝瞬态响应＋稳态响应自由分量＋强制分量以外加信号的形式
画出波形设 I0>IS
I0
iL (t)
IS
I0 -IS
0
t
Rt
iL (t) (I0 IS )e L IS
电感电流由初始值I0慢慢放电，最后稳定在IS
t
全响应是外加电源与储能元件上初始储能共同产生的电路响应。
看一个电路为例如下图
Is
t=0 iR
iL
换路前电路稳定，L 相当于短路线，在两个电
R
R
L 源的共同作用下：
+Us
iL (0 ) IS
US R
I0
iL (0 ) iL (0 ) I0
t>0+时，此时电压源已不起作用，电流源作用于电
﹌﹌﹌﹌⑴ ﹌﹌﹌﹌﹌
﹌﹌﹌﹌ ⑵﹌﹌﹌﹌﹌
Rt
uL (t) R(I0 IS )e L
t 0分析（2）Fra bibliotektRt
iL (t) I0 e L IS (1 e L )
全响应＝零输入响应＋零状态响应 (这个表达式体现叠加性)
全响应是储能元件上初始储能与外加电源共同产生的电路响应
Rt
路，电感元件的初始储能同时作用于电路。
t=∞时，电路又稳定下来，L相当于短路线，在电
流源的作用下
iL () IS
Is
t=0 iR
iL
R
R
L
+Us
列出方程:
diL dt
R L
iL
R L
I
iL (0 ) I0
解方程可得到解答，归纳为两种不同表达式，表现出不同的意义

L22-1一阶电路的全响应

例1 求换路后的uC(t)。
uC Us
U0<Us
uC 零状态响应 U0
t
t
uC (t ) U0e RC US (1 e RC )
0
全响应＝零输入响应＋零状态响应
零输入响应 t
1 S (t=0) R iC
+ US_
2 + U0_
+ uR _ C +_uc
+
+
R u_R
U0_
C u_+Ct ≤0- Nhomakorabea电路uC (0+ ) = uC (0- ) = U0
一阶电路的全响应
例1 如下图所示电路，开关在 t=0 时刻由2接至1。开关
动作前，电路已达稳态。求换路后的uC(t)。
1 S (t=0) R iC
uC
uC uh up
US
Ae
t RC
US
RC
duC dt
uC
0
t
uh Ae RC
up US
一阶电路的全响应
例1 求换路后的uC(t)。
1 S (t=0) R iC
+ US_
2 + U0_
+ uR _ C +_uc
RC
duC dt
uC
US
t
uC (t ) uh up Ae RC US
例1 求换路后的uC(t)。
uC(t) U0<Us 稳态响应
Us uC
U0
全响应＝暂态响应＋稳态响应
-t
uC (t) (U0 - US )e τ US
0 U0-Us
暂态响应 t
一阶电路的全响应

一阶电路全响应

t

(t 0)
零状态响应
零输入响应
便于叠加计算
二. 三要素法分析一阶电路
以一阶RC电路全响应说明： t
u c U s (U 0 U S ) e
稳态分量t→∞ 电容电压uc（∞）

时间常数

电容电压初值uc（0）
t /
上式可以写成： c ( t ) U c ( ) [U c (0 ) U c ( )]e U
S
(U
0
U
S
t
)e

t 0
自由分量(暂态解)
uc US U0 0 uc
全解
uC'
稳态解
uC"
t
暂态解
U0 -US
(2). 全响应= 零状态响应 + 零输入响应
uC U
零状态响应
S
(1 e

t

) U 0e

t

(t 0)
零输入响应
K(t=0) US
R
R
i
C uC = – i
K(t=0)
R
R
i
u C –C
C i U0 +
K(t=0)
+u –
+
US
+u –
R
R
i
C uC – +
+
+u –
uC (0-)=U0
+
uC (0-)=0
uc
等效
uC (0-)=U0
uc
uC (0-)=U0
C
+
-

一阶RC电路的全响应

+
u" C
uC'= US uC"=Aept
uC (0)=U0
t
uC US Ae =RC
uC (0+)=A+US=U0
t
uC U S (U0 U S )e
(t>0)
强制分量自由分量
A=U0 US
t
uC US (U0 US )e (t 0)
6.6 一阶电路的全响应
全响应：非零初始状态的电路受到激励时电路中产生的响应。
一、一阶电路的全响应及其两种分解方式 1. 全解 = 强制分量(稳态解)+自由分量(暂态解)
以RC电路为例
S(t=0) R i
RC duC dt
uC
US
非齐次方程
US
+ uR –
C
+ 解答为
uC
–
uC(t)=uC'
强制分量(稳态解)
自由分量(暂态解)
uC
US
u'u" C
U0 US
2. 全响应= 零状态响应 + 零输入响应
S(t=0) R i
S(t=0) R i1
US
= + uR– C
+ uC
–
US
+ + uR1C–
+ –uC1
uC (0)=U0
uC 1(0-)=0
t
t
uC US (1 e ) U0e
(t 0)
零状态响应
零输入响应
uC
全响应
US
S(t=0) R i2
+ uR2 – C

一阶电路的全响应

合集下载

电路原理课件-一阶电路的全响应

一阶电路的全响应

(电路分析)一阶电路的全响应

一阶电路的全响应——三要素公式【PPT课件】

(电路分析)一阶电路的全响应

一阶电路的全响应

一阶电路的全响应

一阶电路的全响应

一阶电路的全响应

一阶电路的全响应

电路原理一阶电路的全响应

一阶电路的全响应

一阶电路的全响应

L22-1一阶电路的全响应

一阶电路全响应

一阶RC电路的全响应

文档推荐

最新文档