(电路分析)一阶电路的全响应

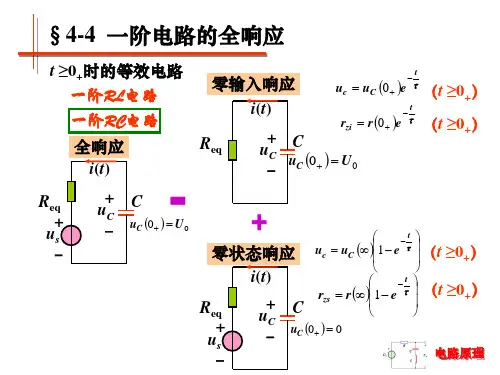
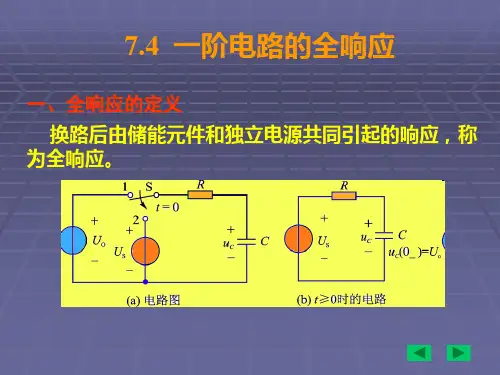
§5.4 一阶电路的全响应与三要素在上两节中分别研究了一阶电路的零输入响应和零状态响应，电路要么只有外激励源的作用，要么只存在非零的初始状态，分析过程相对简单。

本节将讨论既有非零初始状态，又有外激励源共同作用的一阶电路的响应，称为一阶电路的全响应。

5.4.1 RC 电路的全响应电路如图5-9所示，将开关S 闭合前，电容已经充电且电容电压0)0(U u c =-，在t=0时将开关S 闭合，直流电压源S U 作用于一阶RC 电路。

根据KVL ，此时电路方程可表示为：C u图 5-19 一阶RC 电路的全响应S C CU u tu RC=+d d （5-19） 根据换路原则，可知方程（5-19）的初始条件为 0)0()0(U u u C C ==-+令方程（5-9）的通解为 C CC u u u ''+'= 与一阶RC 电路的零状态响应类似，取换路后的稳定状态为方程的特解，则S CU u =' 同样令方程（5-9）对应的齐次微分方程的通解为τtCAe u -=''。

其中RC =τ为电路的时间常数，所以有τtS C AeU u -+=将初始条件与通解代入原方程，得到积分常数为 S U U A +=0所以电容电压最终可表示为τtS S c e U U U u --+=)(0 （5-20）电容充电电流为etS C R U U t u C i τ--==0d d这就是一阶RC 电路的全响应。

图5-20分别描述了s U ，0U 均大于零时，在0U U s >、0=s U 、0U U s <三种情况下c u 与i 的波形。

(a) (b)图5-20C u ，i 的波形图将式（5-20）重新调整后，得)1(0ττtS tC e U eU u ---+=从上式可以看出，右端第一项正是电路的零输入响应，第二项则是电路的零状态响应。

显然，RC 电路的全响应是零输入响应与零状态响应的叠加，即 全响应 = 零输入响应 + 零状态响应研究表明，线性电路的叠加定理不仅适用于RC 电路，在RC 电路的分析过程中同样适用，同时，对于n 阶电路也可应用叠加定理进行分析。

一阶电路的全响应一阶电路的全响应一、全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应，称为一阶电路的全响应（complete response）。

图5.5-1（a）所示的一阶RC电路，直流电压源Us是外加激励，时开关S处于断开状态，电容的初始电压。

时开关闭合，现讨论时电路响应的变化规律。

时，响应的初始值为时，响应的稳态值为用叠加定理计算全响应：开关闭合后，电容电压的全响应，等于初始状态U0单独作用时产生的零输入响应和电压源Us单独作用时产生的零状态响应的代数和，如图5.5-1（b）、（c）所示。

图5.5-1（b）中，零输入响应为图5.5-1（c）中，零状态响应为根据叠加定理，图5.5-1（a）电路的全响应为用表示全响应，表示响应的初始值，表示稳态值。

全响应的变化规律1、当时，即初始值大于稳态值，则全响应由初始值开始按指数规律逐渐衰减到稳态值，这是动态元件C或L对电路放电。

2、当时，即初始值小于稳态值，则全响应由初始值开始按指数规律逐渐增加到稳态值，这是电路对动态元件C或L充电。

3、当时，即初始值等于稳态值，则全响应。

电路换路后无过渡过程，直接进入稳态，动态元件C或L既不对电路放电，也不充电。

二、全响应的三要素计算方法全响应的三要素初始值稳态值时间常数例5.5-1 图5.5-2（a）所示电路，已知C=5uF，t<0时开关S处于断开状态，电路处于稳态， t=0时开关S闭合，求时的电容电流。

解：欲求电容电流，只要求出电容电压即可。

1、确定初始状态。

作时刻的电路，如图5.5-2（b）所示，这时电路已处于稳态，电容相当于开路，则。

由换路定则得初始状态2、确定电容电压的稳态值。

作t→∞时的电路，如图5.5-2（c）所示，这时电路也处于稳态，电容也相当于开路，则3KΩ电阻两端的电压则电容电压的稳态值为3、求时间常数τ。

求从电容C两端看进去的戴维南等效电阻R的电路如图5.5-2（d）所示，这时将15V和5V电压源都视为短路，等效电阻为6KΩ和3KΩ电阻的并联，即R=6K∥3K=2KΩ所以，时间常数为4、求全响应。

关于求解一阶电路的全响应的方法
求解一阶电路的全响应的方法有两种：时域方法和复频域方法。

1. 时域方法：
(a) 首先可以根据电路中的元件参数和初始条件，建立电路的微分方程。

(b) 对电路的微分方程进行求解，得到电路中的电流或电压关于时间的函数表达式。

(c) 根据实际问题中的初始条件，确定积分常数，并代入求解得到的函数表达式中。

(d) 通过得到的电流或电压函数表达式，可以确定电路的全响应。

2. 复频域方法：
(a) 将电路中的元件参数和初始条件通过拉普拉斯变换转换为复频域（s域）。

(b) 对电路的复频域方程进行代数求解，得到电路中的电流或电压的复频域表达式。

(c) 使用拉普拉斯反变换将复频域表达式变换回时域，得到电路中的电流或电压关于时间的函数表达式。

(d) 根据实际问题中的初始条件，确定积分常数，并代入求解得到的函数表达式中。

(e) 通过得到的电流或电压函数表达式，可以确定电路的全响应。

无论是使用时域方法还是复频域方法，求解一阶电路的全响应都需要根据实际情
况确定初始条件，例如电容器或电感器的初始电压或电流，以及连接电路的信号源等。

三元素法分析一阶电路的全响应电路论文学院：电子信息工程学院班级：电气091502班姓名：***学号：************三元素法分析一阶电路的全响应摘要：本文主要介绍用三元素法分析解决一阶电路问题。

用三元素法求一阶电路问题首先要求出三元素：初始值，稳态值，时间常数，用三元素法可以直接代入公式求解，求解过程简单。

关键词：一阶电路 三元素法一、 全响应定义当一个非零初始状态的一阶电路受到激励时，电路的响应称为一阶电路全响应。

全响应总是由初始值、特解和时间常数三个要素决定的。

二、 三元素法的基本原理一阶电路的数学模型是一阶线性微分方程： 其解答一般形式为：令 t = 0+ 全响应f （t ）的三要素求解公式为f （t ）=f （∞）＋[f （0+）－f （∞）]e －t/τ其中，f （0+）为t=0+时刻的初始值，f （∞）为t →∞时的特解稳态值，τ为t ≥0时的时间常数。

f （0+）、f （∞）和τ称为三要素。

只要知道f （0+）、f （∞）和τ这三个要素，就可以根据上述公式直接写出直流激励下一阶电路的全响应，这种方法称为三要素法。

三、 三元素法的解题步骤⒈ 求初始值 ⑴ 初始值定义t=0+时电路中电压与电流的值称为初始值。

⑵ 初始值的求解① 由换路前电路（稳定状态）求u C (0－)和i L (0－)； ② 由换路定律得 u C (0+) 和 i L (0+)。

③ 画0+等效电路。

c bf tfa=+d d τteA t f t f -+'=)()(a.换路后的电路b.电容（电感）用电压源（电流源）替代。

（取0+时刻值，方向与原假定的电容电压、电感电流方向相同）。

④由0+电路求所需各变量的0+值。

⒉求稳态值⑴稳态值的定义t=∞时电路中电压与电流的值称为稳态值。

⑵稳态值的求解稳态时，电容C视为开路，电感L视为短路，稳态值即求直流电阻性电路中的电压和电源。

⒊求时间常数τ⑴时间常数τ的定义当电阻的单位为Ω，电容的单位为F时，乘积RC的单位为s，称为RC电路的时间常数，用τ表示。

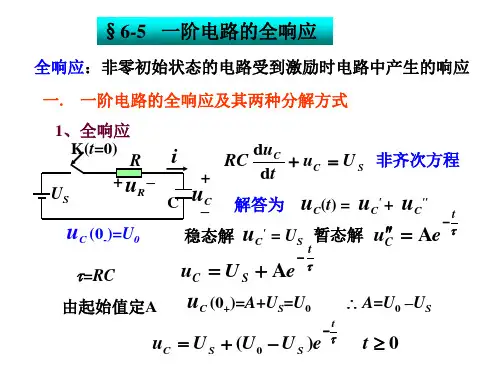
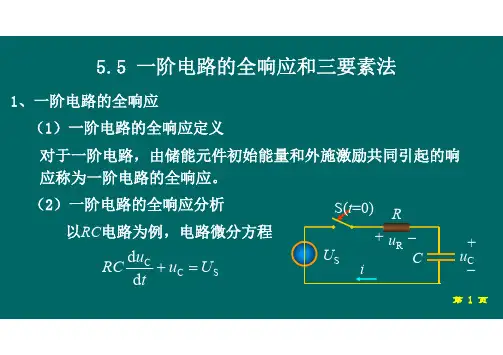
一阶电路全响应公式一阶电路全响应公式，这可是电学里相当重要的一部分知识呢！咱先来说说啥是一阶电路。

想象一下，电路里就那么几个元件，电阻、电容或者电感啥的，而且它们的关系比较简单，这就构成了一阶电路。

比如说，一个电阻和一个电容串联的电路，或者一个电阻和一个电感串联的电路，这都算一阶电路。

那啥又是全响应呢？简单说，就是电路在电源激励和初始储能共同作用下产生的响应。

一阶电路全响应公式，就像是打开这个神秘电学世界的一把钥匙。

比如说，对于一个包含电阻 R 和电容 C 的串联一阶电路，在电源电压U 作用下，电容初始电压为 U0，其全响应公式就是：u(t) = U + (U0 - U) e^(-t/RC) 。

这里的 e 是自然对数的底数，RC 叫做时间常数。

咱来举个例子感受感受。

有一次我在实验室里做实验，就是研究一个一阶 RC 串联电路的全响应。

我小心翼翼地连接好电路，打开电源，然后用示波器观察电压的变化。

一开始，电压的变化特别快，就像个调皮的孩子上蹿下跳。

随着时间推移，它慢慢变得稳定，就像那个调皮孩子终于累了，安静了下来。

这个过程中，全响应公式就像是一个幕后的指挥家，精准地预测着电压的每一步变化。

再来说说这公式的用处。

它能帮我们计算电路中电压或者电流在不同时刻的值，让我们对电路的行为了如指掌。

比如说，在设计电子设备的时候，我们得知道电路的响应速度有多快，能不能满足我们的要求。

这时候，一阶电路全响应公式就能大显身手啦。

还有啊，学习一阶电路全响应公式也不是一帆风顺的。

有时候，那些符号和参数会让人眼花缭乱，脑袋都大了。

但是，只要咱静下心来，多做几道题，多想想其中的道理，慢慢地也就搞明白了。

总的来说，一阶电路全响应公式虽然有点复杂，但只要我们用心去学，去理解，它就能成为我们解决电学问题的有力工具。

就像我们在生活中遇到困难，只要勇敢面对，找到方法，就能迎刃而解。

希望大家都能掌握好这个神奇的公式，在电学的世界里畅游无阻！。

一阶电路全响应的三要素公式好的，以下是为您生成的关于“一阶电路全响应的三要素公式”的文章：在学习电路知识的过程中，一阶电路全响应的三要素公式就像是一把神奇的钥匙，能帮我们轻松打开电路世界的神秘大门。

咱们先来说说这一阶电路全响应到底是啥。

简单来讲，它就是在电源激励和初始储能共同作用下，电路中产生的响应。

这就好比你有一笔存款（初始储能），然后每个月还有固定的工资收入（电源激励），加起来就是你的总财富变化情况（全响应）。

那这三要素公式到底是哪三个要素呢？它们分别是初始值、稳态值和时间常数。

初始值就是电路在初始时刻的状态，就像你刚出发时站的那个起点；稳态值呢，是经过足够长时间后电路稳定下来的状态，就好比你经过长途跋涉最终到达的那个目的地；时间常数则反映了电路从初始状态过渡到稳态的快慢，就像是你到达目的地所花的时间。

给大家讲讲我曾经碰到的一个小例子吧。

有一次，我在实验室里调试一个一阶电路，怎么都弄不对。

我盯着那些电阻、电容和电感，脑袋都大了。

后来我静下心来，仔细分析了初始值、稳态值和时间常数，发现原来是我把一个电阻的阻值算错了，导致整个计算都出了偏差。

经过这次教训，我更加深刻地理解了三要素公式的重要性。

那这三要素公式具体怎么用呢？比如说，我们已知一个一阶 RC 电路，电容的初始电压为 U0，电源电压为 US，电阻为 R，电容为 C。

那么，电路中的电压响应 u(t) 就可以用三要素公式表示为：u(t) = U∞ + [U0 - U∞] e^(-t/τ) ，其中U∞ 就是稳态值，等于 US；τ 就是时间常数，等于 RC 。

再比如说一阶 RL 电路，电感的初始电流为 I0，电源电流为 IS，电阻为 R，电感为 L。

那么，电路中的电流响应 i(t) 就可以表示为：i(t) = I∞ + [I0 - I∞] e^(-t/τ) ，这里的I∞ 等于 IS ，时间常数τ 等于 L/R 。

总之，一阶电路全响应的三要素公式是我们解决一阶电路问题的得力工具。