第七章 单 元 选 择_ 非线性分析
- 格式:ppt
- 大小:191.50 KB
- 文档页数:34


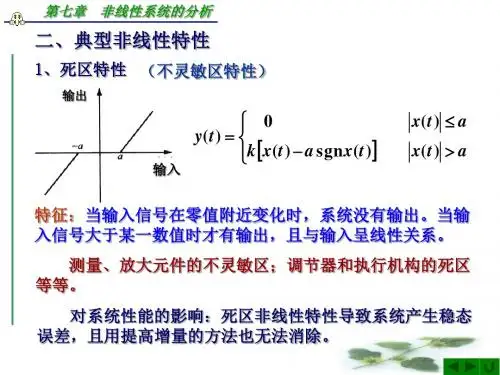


非线性分析简介非线性分析是数学中一个重要的分支,研究的对象是非线性系统。
在实际生活和科学研究中,许多系统都是非线性的,因此非线性分析具有广泛的应用价值。
本文将简要介绍非线性分析的基本概念、方法和应用。
一、非线性系统的特点在介绍非线性分析之前,首先需要了解非线性系统的特点。
与线性系统相比,非线性系统具有以下几个显著的特点:1. 非线性系统的响应与输入之间不满足叠加原理,即系统的输出不是输入的简单线性组合。
2. 非线性系统的行为复杂多样,可能出现周期性运动、混沌现象等。
3. 非线性系统的稳定性分析更加困难,存在更多的稳定性条件和现象。
二、非线性分析的基本概念1. 非线性方程:非线性系统的数学模型通常由非线性方程描述,如非线性微分方程、非线性差分方程等。
2. 非线性动力学:研究非线性系统随时间演化的规律,包括稳定性、周期性、混沌等性质。
3. 非线性控制:设计能够有效控制非线性系统的控制器,使系统达到期望的状态或性能。
三、非线性分析的方法1. 线性化方法:将非线性系统在某一工作点附近进行泰勒展开,得到近似的线性系统,然后应用线性系统的方法进行分析。
2. 相图分析:通过构建相空间中的相图,观察系统在相空间中的轨迹和稳定性,揭示系统的动力学行为。
3. 数值模拟:利用计算机进行数值模拟,求解非线性系统的数值解,研究系统的演化过程和特性。
4. 非线性优化:通过优化方法寻找非线性系统的最优控制策略或参数配置,使系统达到最佳性能。
四、非线性分析的应用1. 混沌理论:非线性分析在混沌理论中有重要应用,揭示了一些看似混乱的系统背后的规律和特性。
2. 生物系统:生物系统中存在许多非线性现象,如神经元网络、生物钟等,非线性分析有助于理解和模拟这些系统。
3. 控制工程:许多实际控制系统是非线性的,非线性分析为设计高效的控制器提供了理论支持和方法指导。
4. 物理学:非线性分析在物理学中有广泛应用,如流体力学、光学等领域,帮助揭示复杂系统的行为规律。






非线性分析非线性分析是一种数学方法,用于研究无法通过简单关系描述的现象。
它以非线性方程为基础,通过数值方法和解析方法来研究非线性系统的行为和性质。
非线性分析是在传统的线性分析基础上发展起来的,它对于探索和揭示复杂系统中的混沌现象、奇异现象和稳定性问题具有重要意义。
非线性分析的发展历程可以追溯到20世纪初,当时科学家们开始意识到很多自然现象无法被简单的线性模型描述。
随着计算机技术的发展和数值方法的提出,非线性分析得以快速发展。
它被广泛应用于自然科学、工程科学和社会科学等各个领域。
在非线性分析中,最基本的问题是确定非线性系统的解析解或数值解。
对于一些简单的非线性方程,可以通过代数方法或函数逼近法来找到解析解。
然而,对于更复杂的非线性系统,只能通过数值计算方法来获得近似解。
数值计算方法包括迭代法、有限元法、有限差分法等,它们利用计算机进行大量的数值计算,逼近非线性系统的解。
除了确定解析解或数值解外,非线性分析还包括对非线性系统的性质和行为的研究。
这包括稳定性分析、周期解的存在性和唯一性、混沌行为等。
稳定性分析是非线性分析中非常重要的一个方面,它研究系统在微小扰动下的行为。
周期解的存在性和唯一性研究系统是否存在周期解以及这些解的唯一性。
混沌行为是非线性系统中非常有趣和复杂的现象,它表现为对微小扰动极其敏感的系统行为。
非线性分析的应用非常广泛。
在物理学中,非线性分析常用于研究混沌现象、量子力学和天体物理学等问题。
在工程学中,非线性分析被用于研究结构的破坏、流体的流动和控制系统等。
在经济学和社会科学中,非线性分析常用于研究市场的波动、人口增长和社会网络等问题。
总之,非线性分析是一种研究复杂系统行为和性质的数学方法。
它适用于各种学科和领域,对于揭示系统的混沌现象和稳定性问题具有重要意义。
非线性分析的发展和应用为我们理解自然界和人类社会提供了独特的视角和方法。
非线性分析简介非线性分析是一种研究非线性系统行为的方法。
在许多实际问题中,线性模型无法准确描述系统的行为,因此需要使用非线性分析方法来研究系统的动力学特性。
本文将介绍非线性分析的基本概念、方法和应用领域。
一、非线性系统的特点非线性系统与线性系统相比,具有以下几个特点:1. 非线性关系:系统的输入和输出之间存在非线性的关系,即系统的响应不是简单的比例关系。
2. 多稳态性:非线性系统可以存在多个稳定的平衡点,系统的行为取决于初始条件。
3. 非周期性:非线性系统的响应可以是非周期性的,即系统的输出不会在一定时间内重复。
4. 非线性耦合:非线性系统的各个部分之间存在相互耦合的关系,一个部分的变化会影响其他部分的行为。
二、非线性分析的方法非线性分析的方法主要包括数值模拟和解析方法两种。
1. 数值模拟:数值模拟是通过计算机模拟非线性系统的行为。
常用的数值模拟方法包括有限元法、有限差分法和有限体积法等。
数值模拟可以得到系统的时间响应、相图和频谱等信息,对于复杂的非线性系统分析非常有用。
2. 解析方法:解析方法是通过数学分析推导非线性系统的解析解。
常用的解析方法包括平衡点分析、线性化分析和变分法等。
解析方法可以得到系统的稳定性、周期解和分岔等信息,对于简单的非线性系统分析较为方便。
三、非线性分析的应用领域非线性分析在许多领域都有广泛的应用,以下列举几个典型的应用领域:1. 力学系统:非线性分析在力学系统中的应用非常广泛,如弹性力学、振动力学和流体力学等。
通过非线性分析可以研究系统的稳定性、共振和混沌等现象。
2. 电子系统:非线性分析在电子系统中的应用主要包括电路和通信系统。
通过非线性分析可以研究电路的稳定性、非线性振荡和混沌现象,对于电子系统的设计和优化具有重要意义。
3. 生物系统:非线性分析在生物系统中的应用主要包括神经网络和生物钟等。
通过非线性分析可以研究生物系统的稳定性、同步和异步等现象,对于理解生物系统的行为具有重要意义。