(word完整版)初二数学反比例函数测试题

反比例函数的图象与性质练习题一、填空题（每小题3分，共30分）1、近视眼镜的度数y （度）与镜片焦距x 成反比例.已知400度近视眼镜片的焦距为0.25米，则眼镜度数y 与镜片焦距x 之间的函数关系式是 .2、如果反比例函数xk y =的图象过点（2，-3），那么k = . 3、已知y 与x 成反比例，并且当x=2时，y=-1，则当y=3时，x 的值是 .4、已知y 与（2x+1）成反比例，且当x=1时，y=2，那么当x=0，y 的值是 .5、若点A （6，y 1）和B （5，y 2）在反比例函数x y 4-=的图象上，则y 1与y 2的大小关系是 . 6、已知函数xy 3=，当x ＜0时，函数图象在第 象限，y 随x 的增大而 . 7、若函数12)1(---=m m x m y 是反比例函数，则m 的值是 .8、直线y=-5x+b 与双曲线xy 2-=相交于 点P （-2，m ），则b= .9、如图1，点A 在反比例函数图象上，过点A 作AB 垂直于x 轴，垂足为B ，若S △AOB =2，则这个反比例函数的解析式为. 图 110、如图2，函数y=-kx(k≠0)与xy 4-=的图 象交于点A 、B ，过点A 作AC 垂直于y 轴，垂足为C ，则△BOC 的面积为 . 图 2二、选择题（每小题3分，共30分）1、如果反比例函数的图象经过点P （-2，-1），那么这个反比例函数的表达式为（ ）A 、x y 21=B 、x y 21-=C 、xy 2= D 、x y 2-= 2、已知y 与x 成反比例，当x=3时，y=4，那么当y=3时，x 的值等于（ ）A 、4B 、-4C 、3D 、-33、若点A （-1，y 1）,B(2,y 2)，C （3，y 3）都在反比例函数xy 5=的图象上，则下列关系式正确的是（ ） A 、y 1＜y 2＜y 3 B 、y 2＜y 1＜y 3 C 、y 3＜y 2＜y 1 D 、y 1＜y 3＜y 24、反比例函数xm y 5-=的图象的两个分支分别在第二、四象限内，那么m 的取值范围是（ ） A 、m ＜0 B 、m ＞0 C 、m ＜5 D 、m ＞55、已知反比例函数的图象经过点（1，2），则它的图象也一定经过（ ）A 、（-1，-2）B 、（-1，2）C 、（1，-2）D 、（-2，1）6、若一次函数b kx y +=与反比例函数x k y =的图象都经过点（-2，1），则b 的值是（ ） A 、3 B 、-3 C 、5 D 、-57、若直线y=k 1x(k 1≠0)和双曲线xk y 2=（k 2≠0）在同一坐标系内的图象无交点，则k 1、k 2的关系是（ ） A 、k 1与k 2异号 B 、k 1与k 2同号 C 、k 1与k 2互为倒数 D 、k 1与k 2的值相等8、已知点A 是反比例函数图象上一点，它到原点的距离为5，到x 轴的距离为3，若点A 在第二象限内，则这个反比例函数的表达式为（ ）A 、x y 12=B 、x y 12-=C 、x y 121=D 、xy 121-= 9、如果点P 为反比例函数x y 6=的图像上的一点，PQ 垂直于x 轴，垂足为Q ，那么 △POQ 的面积为（ ）A 、12B 、6C 、3D 、1.510、已知反比例函数xk y =(k≠0),当x ＞0时，y 随x 的增大而增大，那么一次函数y=kx-k 的图象经过（ ）A 、第一、第二、三象限B 、第一、二、三象限C 、第一、三、四象限D 、第二、三、四象限三、解答题1、（７分）如图３，点Ａ是双曲线x k y =与直线y=-x-(k+1)在第二象限内的交点， ＡＢ⊥x 轴于B ，且Ｓ△ABO ＝23. （１）求这两个函数的解析式；（２）求直线与双曲线的两个交点Ａ、Ｃ的坐标和△AOC 的面积.2、（７分）已知反比例函数xk y 2=和一次函数y=2x-1，其中一次函数的图象经过（a,b ），（a+1，b+k ）两点.（1）求反比例函数的解析式；（2）如图4，已知点A 在第一象限，且同时在上述两个函数的图象上，求点A 的坐标；（3）利用（2）的结果，请问：在x 轴上是否存在点P ，使△AOP 为等腰三角形？若存在，把符合条件的P 点坐标都求出来；若不存在，请说明理由.。

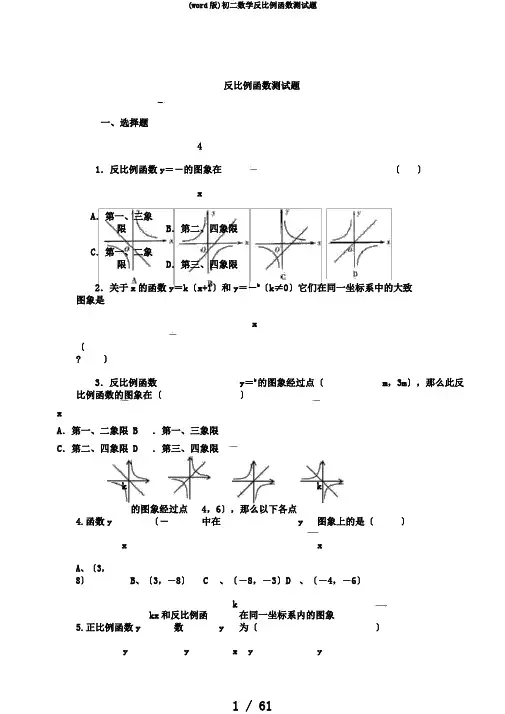
反比例函数测试题一、选择题4〔〕1．反比例函数y＝－的图象在xA．第一、三象限B．第二、四象限C．第一、二象限D．第三、四象限2．关于x的函数y＝k〔x+1〕和y＝－k〔k≠0〕它们在同一坐标系中的大致图象是x〔?〕3．反比例函数y＝k的图象经过点〔m，3m〕，那么此反比例函数的图象在〔〕xA．第一、二象限 B ．第一、三象限C．第二、四象限 D ．第三、四象限4.函数y k4，6〕，那么以下各点中在yk〕的图象经过点〔－图象上的是〔x xA、〔3，8〕B、〔3，－8〕C、〔－8，－3〕D、〔－4，－6〕5.正比例函数y kx和反比例函数k在同一坐标系内的图象为〔〕yy y x y yo x ox o x o xA B C D6.在同一直角坐标平面内，如果直线y k1x与双曲线y k2没有交点，那么k1和k2的x关系一定是〔〕A、k1<0，k2>0B、k1>0，k2<0C、k1、k2同号D、k1、k2异号7.一次函数y=kx+b的图像经过第一二四象限那么反比例函数kby的图像在x〔〕A 第一二象限B第三四象限C第一三象限D第二三象限二、填空题：〔3分×10=30分〕1、y 与x 成反比例，且当 y ＝6时，x1；，这个函数解析式为32、当路程s 一定时，速度 v 与时间t 之间的函数关系是；〔填函数类型〕3、函数yx2的图象有 个交点；和函数y x24、反比例函数 yk的图象经过〔－ 3，5〕点、〔a ，－3〕及〔10，b 〕点，那么k ＝x，b ＝ 2，a ＝；5y 4m 1xm 4是正比例函数，那么m，图象经过象、假设函数限；6、y 与x-2成反比例，当 x=3时，y=1，那么y 与x 间的函数关系式为；7、右图3是反比例函数y k 2的图象，那么k 的取值范围是.x28、函数y的图象，在每一个象限内，y 随x 的增大x而；9、反比例函y 2M 是图象数x 在第一象限内的图象如图，点上一点，MP垂直x轴于点P，那么△MOP的面积为；y10、y m2x m25是y关于x的反比例函数，那么m值为；MO P x 〔三〕解答题1、一次函数y kxb与反比例函数y m的图像交于A〔—2，1〕B〔1，n〕x俩点。

第17章《反比例函数》测试题一、选择题：1.下列函数中，不属于y 与x 反比例函数的是（ ） A.1xy = B.11y x =+ C.1y x -=- D.13y x= 2.有以下判断：①圆面积公式2S r π=中，面积S 与半径r 成正比例；②运动的时间与速度成反比例；③当电压不变时，电流强度和电阻成反比例；④圆柱体的体积公式213V r h π=中，当体积V 不变时，圆柱的高h 与底面半径r 的平方成反比例，其中错误的有（ ）A.1个B.2个C.3个D.4个3.若y 与x 成反比例，x 与z 成正比例，则y 是z 的（ ） A. 正比例函数 B. 反比例函数 C. 一次函数 D. 不能确定4.如图，A 为反比例函数ky x=图象上一点，AB 垂直x 轴于B 点，若S △AOB ＝3，则k 的值为（ ） A 、6B 、3C 、+3或-3D 、+6或-65.（2009年娄底）市一小数学课外兴趣小组的同学每人制作一个面积为200cm 2的矩形学具进行展示. 设矩形的宽为x cm ，长为y cm ，那么这些同学所制作的矩形长y （cm ）与宽x （cm ）之间的函数关系的图象大致是 ( )6.在同一直角坐标平面内，如果直线1y x k =与双曲线2k y x=没有交点，那么1k 和2k 的关系一定是（ ）A.1k <0,2k >0B.1k >0，2k <0C.1k 、2k 同号D.1k 、2k 异号7.（09河池）如图5，A 、B 是函数2y x=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，△ABC 的面积记为S ，则（ ） A ． 2S = B ． 4S = C ．24S << D ．4S >8.（2009丽水市）如图，点P 在反比例函数1y x =(x > 0)的图象上，且横坐标为2. 若将点P 先向右平移两个单位，再向上平移一个单位后所得的像为点P '.则在第一象限内，经过点P '的反比例函数图象的解析式是( )A ．)0(5>-=x xy B .)0(5>=x x yC . )0(6>-=x x yD . )0(6>=x xy9.（09恩施市）一张正方形的纸片，剪去两个一样的小矩形得到一个“E ”图案，如图所示，设小矩形的长和宽分别为x 、y ，剪去部分的面积为20，若2≤x ≤10，则y 与x 的函数图象是（ ）10.在同一坐标系中，函数ky x=和3y kx =+的图象大致是二、填空题： 11．如果函数122--=m xm y 是反比例函数，那么=m ____________.12．已知y 与x 成反比例，且当2-=x 时，3=y ，则y 与x 的函数关系是_________，当3-=x 时，=y _____________。

反比例函数测试题（含答案）（时间90分钟 满分100分）班级 学号 姓名 得分一、选择题（每小题3分，共24分） 1．如果x 、y 之间的关系是10(0)ax y a -+=≠，那么y 是x 的 （ ）A ．正比例函数B ．反比例函数C ．一次函数D ．二次函数 2．函数y ＝－4x 的图象与x 轴的交点的个数是（ ）A ．零个B ．一个C ．两个D ．不能确定3．反比例函数y ＝－4x 的图象在（ ）A ．第一、三象限B ．第二、四象限C ．第一、二象限D ．第三、四象限 4．已知关于x 的函数y ＝k （x +1）和y ＝－kx（k ≠0）它们在同一坐标系中的大致图象是（• ）5．已知反比例函数y＝x k 的图象经过点（m ，3m ），则此反比例函数的图象在 （ ）A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限6．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （ kPa ） 是气体体积V （ m 3） 的反比例函数，其图象如图所示．当气球内的气压大于120 kPa 时，气球发将爆炸．为了安全起见，气球的体积应 （ ）A ．不小于54m 3B ．小于54m 3C ．不小于45m 3D ．小于45m 37．如果点P 为反比例函数x y 4=的图象上一点，PQ ⊥x 轴，垂足为Q ，那么△POQ的面积为 （ ）A ．2B ． 4C ．6D ． 8 8．已知：反比例函数x my 21-=的图象上两点A （x 1，y 1），B （x 2， y 2）当x 1＜0＜x 2时，y 1＜y 2，则m 的取值范围（ ）A ．m ＜0B ．m ＞0C ．m ＜21 D ．m ＞21二、填空题（每小题2分，共20分）9．有m 台完全相同的机器一起工作，需m 小时完成一项工作，当由x 台机器（x 为不大于m 的正整数）完成同一项工作时，所需的时间y 与机器台数x 的函数关系式是____.10．已知y 与x 成反比例，且当x 32=-时，y =5，则y 与x 的函数关系式为__________. 11．反比例函数xy 3=的图象在第一象限与第 象限. 3) 第6题12．某食堂现有煤炭500吨，这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 . 13．若nxm y ++=2)5(是反比例函数，则m 、n 的取值是 .14．两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数图象上任意一点到两坐标轴的距离的积都是3；乙同学说：这个反比例函数的图象与直线y =x 有两个交点，你认为这两位同学所描述的反比例函数的解析式是 .15．在ABC △的三个顶点A （2，－3）、B （－4，－5）、C （－3，2）中，可能在反比例函数(0)ky k x=>的图象上的点是 ．16．如果反比例函数4ny x-=的图象位于第二、四象限，则n 的取值范围是_______；如果图象在每个象限内，y 随x 的增大而减小，则n 的取值范围是 .17．如图，△P 1OA 1、△P 2A 1 A 2是等腰直角三角形，点P 1、P 2在函数4(0)y x x=>的图象上，斜边OA 1、A 1 A 2都在x 轴上，则点A 2的坐标是 .18．两个反比例函数k y x =和1y x=在第一象限内的图象如图所示，点P 在k y x =的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x =的图象于点B ，当点P 在ky x =的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等； ④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是 （把你认为正确结论的序号都填上，少填或错填不给分）．三、解答题（共56分） 19．（4分）反比例函数xky =的图象经过点A （2 ，3）. （1）求这个函数的解析式；（2）请判断点B （1 ，6）是否在这个反比例函数的图象上，并说明理由.20．（4分）已知三角形的一边为x ，这条边上的高为y ，三角形的面积为3，写出y 与x 的函数表达式，并画出函数的图象.OA 12第17题21．（4分）如图，一次函数y =kx ＋b 的图像与反比例函数xmy =的图像相交于A 、B 两点，（1）利用图中条件，求反比例函数和一次函数的解析式（2）根据图像写出使一次函数的值大于反比例函数的值的x 的取值范围.22．（6分）某蓄水池的排水管每时排水8 m 3，6h 可将满池水全部排空． （1）蓄水池的容积是多少？（2）如果增加排水管，使每时排水量达到Q （m 3），那么将满池水排空所需的时间t （h ）将如何变化？（3）写出t 与Q 之间的函数关系式．（4）如果准备在5小时之内将满水池排空，那么每时的排水量至少为多少？ （5）已知排水管的最大排水量为每时12m 3，那么最少多长时间可将满池水全部排空？23．（6分）双曲线5y x=在第一象限的一支上有一点C （1，5），过点C 的直线y =kx ＋b （k >0）与x 轴交于点A （a ，0）.（1）求点A 的横坐标a 与k 之间的函数关系式；（2）当该直线与双曲线在第一象限内的另一交点D 的横坐标是9时，求△COA 的面积.第23题图第21题图24．（6分）已知反比例函数xmy 3-=和一次函数1-=kx y 的图象都经过点m P (，)3m -（1）求点P 的坐标和这个一次函数的解析式；（2）若点M （a ，1y ）和点N （1+a ，2y ）都在这个一次函数的图象上．试通过计算或利用一次函数的性质，说明1y 大于2y25．（6分）近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知800度近视眼镜镜片的焦距为0.125米， （1）求y 与x 的函数关系；（2）若张华同学近视眼镜镜片的焦距为0.25米，你知道他的眼睛近视多少度吗？26．（6分）对于取消市场上使用的杆秤的呼声越来越高，原因在于一些不法商贩在卖货时将秤砣挖空，或更换较小称砣，使砣较轻，从而欺骗顾客. （1）如图，对于同一物体，哪个图用的是标准秤砣，哪个用的是较轻的秤砣？ （2）在称同一物体时，所称得的物体质量y （千克）与所用秤砣质量x （千克）之间满足 关系.（3）当砣较轻时，称得的物体变重，这正好符合哪个函数的哪些性质？图1图227．（6分）联想电脑公司新春期间搞活动，规定每台电脑0.7万元，交首付后剩余的钱数y 与时间t 的关系如图所示： （1）根据图象写出y 与t 的函数关系式. （2）求出首付的钱数.（3）如果要求每月支付的钱数不少于400元，那么还至少几个才能将所有的钱全部还清？28．（8分）如图，直线b kx y +=与反比例函数xk y '=（x ＜0）的图象相交于点A 、点B ，与x 轴交于点C ，其中点A 的坐标为（－2，4），点B 的横坐标为－4. （1）试确定反比例函数的关系式； （2）求△AOC 的面积.新人教八年级（下）第17章《反比例函数》答案一、选择题1．B ；2． A ；3． B ；4． A ；5． B ；6． C ；7．A ；8． C ．二、填空题9．y ＝x m 2 10．152y x=- 11．三 12．y ＝x 50013．m ≠－5 n ＝－3 14．y＝x315．B 16.n ＞4，n ＜4 17．（0） 18．①②④ 三、解答题19．（1）y ＝x6；（2）在 20． y ＝6x，图像略 21．（1）2y x=-，1y x =--;（2） 2x <-或0x <<122．（1）348m ；（2）t 将减小；（3）48t Q=；（4）4859.6Q Q==，；月)y (）（5）48412t ==23．（1）51a k=-+， （2） 25 24．（1）12--=x y ；（2）略 25．（1）100y x=，（2）400度 26．（1）图②是用与秤配套的秤砣，图①则使用较轻的秤砣.（2）反比例. （3）函数y =xk（k ＞0），当x 变小时，y 增大 27．（1）y ＝t 6000 ；（2）7000－6000＝1000（元）；（3）400＝t6000，t ＝1528．（1）8xy =-；（2）126。

完整版)反比例函数经典习题及答案反比例函数练题1.下列函数中，经过点(1.-1)的反比例函数解析式是（）A。

y = 1/xB。

y = -1/xC。

y = 2/xD。

y = -2/x2.反比例函数y = -(k/ x)（k为常数，k ≠ 0）的图象位于（）A。

第一、二象限B。

第一、三象限C。

第二、四象限D。

第三、四象限3.已知反比例函数y = (k - 2)/x的图象位于第一、第三象限，则k的取值范围是（）A。

k。

2B。

k ≥ 2C。

k ≤ 2D。

k < 24.反比例函数y = k/x的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果三角形MON 的面积是2，则k的值为（）A。

2B。

-2C。

4D。

-45.对于反比例函数y = 2/x，下列说法不正确的是（）A。

点(-2.-1)在它的图象上B。

它的图象在第一、三象限C。

当x。

0时，y随x的增大而增大D。

当x < 0时，y随x的增大而减小6.反比例函数y = (2m - 1)x/(m^2 - 2)，当x。

0时，y随x 的增大而增大，则m的值是（）A。

±1B。

小于1的实数C。

-1D。

1/27.如图，P1、P2、P3是双曲线上的三点，过这三点分别作y轴的垂线，得到三个三角形P1A1O、P2A2O、P3A3O，设它们的面积分别是S1、S2、S3，则（）。

A。

S1 < S2 < S3B。

S2 < S1 < S3C。

S3 < S1 < S2D。

S1 = S2 = S38.在同一直角坐标系中，函数y = -2与y = 2x的图象的交点个数为（）A。

3B。

2C。

1D。

09.已知甲、乙两地相距s（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（h）与行驶速度v（km/h）的函数关系图象大致是（）10.如图，直线y = mx与双曲线y = k/(x-2)交于A、B两点，过点A作AM⊥x轴，垂足为M，连结BM，若三角形ABM的面积为2，则k的值是（）A。

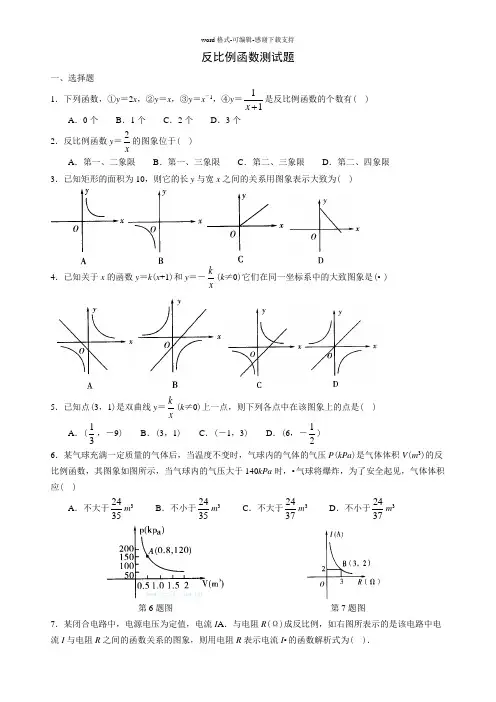
反比例函数测试题一、选择题1．下列函数，①y＝2x，②y＝x，③y＝x－1，④y＝11x是反比例函数的个数有()A．0个B．1个C．2个D．3个2．反比例函数y＝2x的图象位于()A．第一、二象限B．第一、三象限C．第二、三象限D．第二、四象限3．已知矩形的面积为10，则它的长y与宽x之间的关系用图象表示大致为()4．已知关于x的函数y＝k(x+1)和y＝－kx(k≠0)它们在同一坐标系中的大致图象是(• )5．已知点(3，1)是双曲线y＝kx(k≠0)上一点，则下列各点中在该图象上的点是()A．(13，－9)B．(3，1)C．(－1，3)D．(6，－12)6．某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数，其图象如图所示，当气球内的气压大于140kPa时，•气球将爆炸，为了安全起见，气体体积应()A．不大于2435m3B．不小于2435m3C．不大于2437m3D．不小于2437m3第6题图第7题图7．某闭合电路中，电源电压为定值，电流I A．与电阻R(Ω)成反比例，如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象，则用电阻R表示电流I•的函数解析式为()．A ．I ＝6R B ．I ＝－6R C ．I ＝3R D ．I ＝2R 8．函数y ＝1x与函数y ＝x 的图象在同一平面直角坐标系内的交点个数是( )．A ．1个B ．2个C ．3个D ．0个 9．若函数y ＝(m +2)|m |－3是反比例函数，则m 的值是( )．A ．2B ．－2C ．±2D ．×210．已知点A (－3，y 1)，B (－2，y 2)，C (3，y 3)都在反比例函数y ＝4x的图象上，则( )． A ．y 1＜y 2＜y 3 B ．y 3＜y 2＜y 1 C ．y 3＜y 1＜y 2 D ．y 2＜y 1＜y 3 二、填空题11．一个反比例函数y ＝kx(k ≠0)的图象经过点P (－2，－1)，则该反比例函数的解析式是________． 12．已知关于x 的一次函数y ＝kx +1和反比例函数y ＝6x的图象都经过点(2，m )，则一次函数的解析式是________．13．一批零件300个，一个工人每小时做15个，用关系式表示人数x •与完成任务所需的时间y 之间的函数关系式为________．14．正比例函数y ＝x 与反比例函数y ＝1x的图象相交于A 、C 两点，AB ⊥x 轴于B ，CD •⊥x 轴于D ，如图所示，则四边形ABCD 的为_______．第14题图 第15题图 第19题图15．如图，P 是反比例函数图象在第二象限上的一点，且矩形PEOF 的面积为8，则反比例函数的表达式是_________． 16．反比例函数y ＝21039n n x--的图象每一象限内，y 随x 的增大而增大，则n ＝_______．17．已知一次函数y ＝3x +m 与反比例函数y ＝3m x-的图象有两个交点，当m ＝_____时，有一个交点的纵坐标为6．18．若一次函数y ＝x +b 与反比例函数y ＝kx图象，在第二象限内有两个交点，•则k ______0，b _______0，(用“＞”、“＜”、“＝”填空)19．两个反比例函数y＝3x，y＝6x在第一象限内的图象如图所示，点P1，P2，P3……P2005，在反比例函数y＝6x的图象上，它们的横坐标分别是x1，x2，x3，…x2005，纵坐标分别是1，3，•5•……，•共2005年连续奇数，过点P1，P2，P3，…，P2005分别作y轴的平行线与y＝3x的图象交点依次是Q1(x1，y1)，Q2(x2，y2)，Q3(x3，y3)，…，Q2005(x2005，y2005)，则y2005＝________．20．当＞0时，两个函数值y，一个随x增大而增大，另一个随x的增大而减小的是( •)．A．y＝3x与y＝1xB．y＝－3x与y＝1xC．y＝－2x+6与y＝1xD．y＝3x－15与y＝－1x21．在y＝1x的图象中，阴影部分面积为1的有（）22．如图，已知一次函数y＝kx+b(k≠0)的图象与x轴、y轴分别交于A、B•两点，且与反比例函数y＝mx(m≠0)的图象在第一象限交于C点，CD垂直于x轴，垂足为D，•若OA＝OB＝OD＝1．(1)求点A、B、D的坐标；(2)求一次函数和反比例函数的解析式．第22题图23．如图，已知点A(4，m)，B(－1，n)在反比例函数y＝8x的图象上，直线AB•分别与x轴，y轴相交于C、D两点，(1)求直线AB的解析式．(2)C、D两点坐标．(3)S△AOC：S△BOD是多少？第23题图24．已知y＝y1－y2，y1与x成正比例，y与x成反比例，且当x＝1时，y＝－14，x＝4时，y＝3．求(1)y与x之间的函数关系式．(2)自变量x的取值范围．(3)当x＝14时，y的值．25．如图，一次函数y＝kx+b的图象与反比例函数y＝mx的图象交于A、B两点．(1)利用图中的条件，求反比例函数和一次函数的解析式．(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．第25题图26．如图，双曲线y＝5x在第一象限的一支上有一点C(1，5)，•过点C•的直线y＝kx+b(k＞0)与x轴交于点A(a，0)．(1)求点A的横坐标a与k的函数关系式(不写自变量取值范围)．(2)当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△COA•的面积．第26题图反比例函数测试题（一）答案1．B．；2．D．；3．A．；4．A．；5．B．；6．B．；7．A．；8．B．；9．A．；10．D．；11．y＝2x；12．y＝x+1；13．y＝20x；14．2；15．y＝－8x；16．n＝－3；17．m＝5；18．＜，＞；19．2004．5；20．A．；B．；；21．A．；C．；D．；22．解：(1)∵OA＝OB＝OD＝1，∴点A、B、D的坐标分别为A(－1，0)，B(0，1)，D(1，0)．(2)∵点AB在一次函数y＝kx+b(k≠0)的图象上，∴1k bb-+=⎧⎨=⎩解得11kb=⎧⎨=⎩∴一次函数的解析式为y ＝x +1，∵点C 在一次函数y ＝x +1的图象上，•且CD ⊥x 轴， ∴C 点的坐标为(1，2)，又∵点C 在反比例函数y ＝mx(m ≠0)的图象上， ∴m ＝2，•∴反比例函数的解析式为y ＝2x．；23．(1)y ＝2x －6；(2)C (3，0)，D (0，－6)；(3)S △AOC ：S △BOD ＝1：1．； 24．(1)y ＝216x 提示：设y ＝k－22k x，再代入求k 1，k 2的值． (2)自变量x 取值范围是x ＞0． (3)当x ＝14时，y ＝162＝255．；25．解：(1)由图中条件可知，双曲线经过点A (2，1)∴1＝2m ，∴m ＝2，∴反比例函数的解析式为y ＝2x． 又点B 也在双曲线上，∴n ＝21-＝－2，∴点B 的坐标为(－1，－2)．∵直线y ＝kx +b 经过点A 、B ．∴122k b k b =+⎧⎨-=-+⎩ 解得11k b =⎧⎨=-⎩∴一次函数的解析式为y ＝x －1．(2)根据图象可知，一次函数的图象在反比例函数的图象的上方时，•一次函数的值大于反比例函数的值，即x ＞2或－1＜x ＜0．；26．解：(1)∵点C (1，5)在直线y ＝－kx +b 上，∴5＝－k +b ， 又∵点A (a ，0)也在直线y ＝－kx +b 上，∴－ak +b ＝0，∴b ＝ak 将b ＝ak 代入5＝－k +a 中得5＝－k +ak ，∴a ＝5k+1． (2)由于D 点是反比例函数的图象与直线的交点∴599y y k ak⎧=⎪⎨⎪=-+⎩ ∵ak ＝5+k ，∴y ＝－8k +5 ③ 将①代入③得：59＝－8k +5，∴k ＝59，a ＝10． ∴A (10，0)，又知(1，5)，∴S △COA ＝12×10×5＝25．；。

反比例函数》测试题(含答案)1、选择题（每小题5分，共50分）1、若点（x1.-1）、(x2.-2)、(x3.1)都在反比例函数y= k/x 上，则它们之间的大小关系是（）A．x1<x3<x2B．x2<x1<x3C．x1<x2<x3D．x2<x3<x12、若反比例函数y=k/x的图象经过点(m，3m)，其中m≠0，则此反比例函数的图象在（）A．第一、二象限；B．第一、三象限；C．第二、四象限；D．第三、四象限3、在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线y=3/x上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是（）A。

0B。

1C。

2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点，设点A的坐标为（x1,y1），则边长分别为x1、y1的矩形面积和周长分别为（）A。

4，12B。

4，6C。

8，12D。

8，66、已知y1+y2=y，其中y1与x成反比例,且比例系数为k1，而y2与x2成正比例,且比例系数为k2，若x=-1时,y=0，则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是（）18、如图，直线y=mx与双曲线y=k/(x-1)交与A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=2，则k的值是（）A、2B、m-2C、mD、49、如图，点A在双曲线y=6/x上，且OA＝4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )A.47B.5C.27D.2210、如图，反比例函数y= k/x的图象经过点(1,2)，则k=（）。

二、填空题（每小题5分，共20分）11、若y=k/x是反比例函数，且x1y1=x2y2，则k=______。

完整版)反比例函数练习题含答案测试1 反比例函数的概念一、填空题1.一般的，形如 y=k/x 的函数称为反比例函数，其中x是自变量，y是因变量。

自变量x的取值范围是x≠0.2.写出下列各题中所要求的两个相关量之间的函数关系式，并指出函数的类别。

1) 商场推出分期付款购电脑活动，每台电脑元，首付4000元，以后每月付y元，x个月全部付清，则y=(8000+)/x，是反比例函数。

2) 某种灯的使用寿命为1000小时，它的使用天数y与平均每天使用的小时数x之间的关系式为 y=1000/x，是反比例函数。

3) 设三角形的底边、对应高、面积分别为a、h、S。

当a=10时，S与h的关系式为 S=10h/2，是正比例函数；当S=18时，a与h的关系式为 h=36/a，是反比例函数。

4) 某工人承包运输粮食的总数是w吨，每天运x吨，共运了y天，则 y=w/x，是反比例函数。

3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x和y=3x-1 中，是y关于x的反比例函数的有：①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。

4.若函数 y=m/(x-1) (m是常数) 是反比例函数，则 m=1，解析式为 y=1/(x-1)。

5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜片的焦距为0.25m，则 y=1000/x。

二、选择题6.已知函数 y=3x/(kx+1)，当x=1时，y=-3，那么这个函数的解析式是 y=3x/(3k+1)。

(解析：由 y=-3=3/(3k+1) 可得 k=-1/3，代入原式得 y=3x/(3x-1)。

)7.已知 y 与 x 成反比例，当 x=3 时，y=4，那么 y=3 时，x 的值等于 4/3.三、解答题8.已知 y 与 x 成反比例，当 x=2 时，y=3.1) 求y 与x 的函数关系式：y=k/x，代入已知条件得k=6，因此函数关系式为 y=6/x。

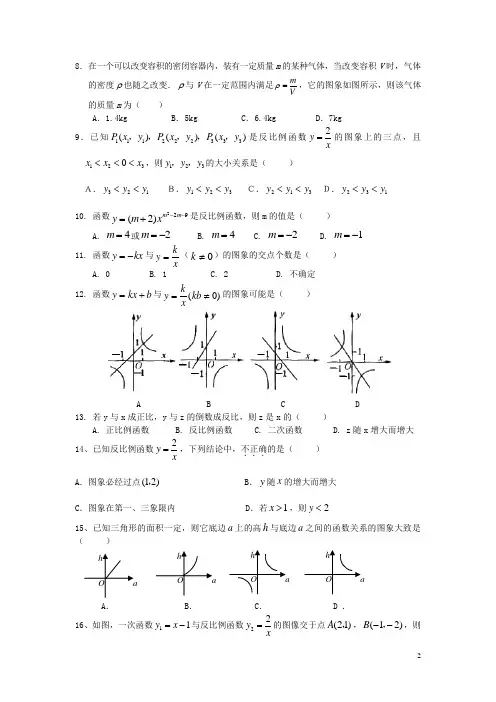
八年级数学《反比例函数》单元测试题学校 姓名一、选择题（每小题2分，共40分）1. 下列函数中，是反比例函数的是（ ）A. y x =-2 B. y x =-12 C. y x =-11 D. y x =122．已知函数y =3x（x ﹥0），那么（ ）A 、 函数图象在第一象限内，且y 随x 的增大而减小;B 、 函数图象在第一象限内，且y 随x 的增大而增大;C 、 函数图象在第二象限内，且y 随x 的增大而减小; D.函数图象在第二象限内，且y 随x 的增大而增大 3．正比例函数kx y 2=与反比例函数k y 1-=在同一坐标系中的图象不可能．．．是（ ） A B C D 4．已知点P 是反比例函数(0)ky k x=≠的图像上任一点，过P 点分别作x 轴，y 轴的平行线，若两平行线与坐标轴围成矩形的面积为2，则k 的值为（ ） A.2 B.-2 C.±2 D.45．函数y=xk（k ≠0）的图象过点（2，-2），则此函数的图象在平面直角坐标系中的（ ） A 、第一、三象限 B 、第三、四象限 C 、A 、第一、二象限 D 、第二、四象限 6．若双曲线6y x=-经过点A （m ，－2m ），则m 的值为（ ） 3± 7．如图，反比例函数ky x=与直线2y x =-相交于点A ，A 点的横坐标为－1，则此反比例函数的解析式为（ ） A ．2y x =B ．12y x =C ．2y x =-D ．12y x=-(第7题) (第8题)8．在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足mVρ=，它的图象如图所示，则该气体的质量m 为（ ） A ．1.4kg B ．5kg C ．6.4kg D ．7kg 9．已知111222333()()()P x y P x y P x y ，，，，，是反比例函数2y x=的图象上的三点，且1230x x x <<<，则123y y y ，，的大小关系是（ ）Ａ．321y y y << Ｂ．123y y y << Ｃ．213y y y << Ｄ．231y y y << 10. 函数y m x m m =+--()2229是反比例函数，则m 的值是（ ） A. m =4或m =-2 B. m =4 C. m =-2D. m =-111. 函数y kx =-与y k x=（k ≠0）的图象的交点个数是（ ） A. 0 B. 1 C. 2 D. 不确定 12. 函数y kx b =+与y kxkb =≠()0的图象可能是（ ）A B C D13. 若y 与x 成正比，y 与z 的倒数成反比，则z 是x 的（ ）A. 正比例函数B. 反比例函数C. 二次函数D. z 随x 增大而增大 14、已知反比例函数2y x=，下列结论中，不正确．．．的是（ ） A ．图象必经过点(12)， B ．y 随x 的增大而增大 C ．图象在第一、三象限内 D ．若1x >，则2y <15、已知三角形的面积一定，则它底边a 上的高h 与底边a 之间的函数关系的图象大致是（ ）A ．B ．C ．D ． 16、如图，一次函数11y x =-与反比例函数22y x=的图像交于点(21)A ，，(12)B --，，则使12y y > 的x 的取值范围是（ ） A ．2x > B ．2x >或10x -<< C ．12x -<<D ．2x >或1x <-17、已知120k k <<，则函数1y k x =和2k y x=的图象大致是（ ）18、已知函数5y x =-+，4y x=，它们的共同点是：①在每一个象限内，都是函数y 随x 的增大而 增大；②都有部分图象在第一象限；③都经过点(14)，，其中错误．．的有（ ） Ａ．0个Ｂ．1个Ｃ．2个Ｄ．3个19、平面直角坐标系中有六个点(15)A ，，533B ⎛⎫-- ⎪⎝⎭，，(51)C --，，522D ⎛⎫- ⎪⎝⎭，，533E ⎛⎫ ⎪⎝⎭， 522F ⎛⎫⎪⎝⎭，，其中有五个点在同一反比例函数图象上，不在这个反比例函数图象上的点（ ） A ．点CB ．点DC ．点ED ．点F20、在同一直角坐标平面内，如果直线1y x k =与双曲线2k y x=没有交点，那么1k 和2k 的关系一定是（ ）(A) 1k 、2k 异号 (B) 1k 、2k 同号 (C) 1k >0， 2k <0 (D) 1k <0， 2k >0 二、填空题（每小题3分，共18分）21．如图, 如果函数y=－x 与y=x4-的图像交于A 、B 两点, 过点A 作AC 垂直于y轴, 垂足为点C, 则△BOC 的面积为_________.22. 反比例函数y a x a a =---()3224的函数值为4时，自变量x 的值是_________。

反比例函数单元测试卷含答案一、选择题1. 反比例函数的一般形式是：A. y = kxB. y = ax + bC. y = k/xD. y = mx + c答案: C2. 当x为0时，反比例函数的值为：A. 0B. 1C. 无定义D. 任意值答案: C3. 若反比例函数的k值为正数，x趋近于无穷大，y会趋近于：A. 正无穷大B. 负无穷大C. 0D. 不存在极限答案: B4. 反比例函数的图像是一条：A. 直线B. 抛物线C. 余弦曲线D. 双曲线答案: D5. 若反比例函数的x值为正数，y值为负数，那么k值是：A. 正数B. 负数C. 零D. 无法确定答案: B二、计算题1. 已知反比例函数y = 5/x，当x = 2时，求y的值。

答案: 2.52. 已知反比例函数y = 3/x，当y = 6时，求x的值。

答案: 0.5三、简答题1. 什么是反比例函数？答案: 反比例函数是一种函数关系，当自变量x的值增大时，因变量y的值会减小，并且二者之间呈现出一种倒数关系。

它的一般形式为y = k/x，其中k为常数。

2. 反比例函数的图像有什么特点？答案: 反比例函数的图像是一条双曲线。

当x趋近于无穷大或无穷小时，函数的值趋近于零。

两支曲线的对称轴为y轴，并在y 轴上有一个渐近线。

3. 如何确定反比例函数的常数k的值？答案: 可以通过已知点的坐标进行求解。

将已知的x和y的值代入反比例函数的一般形式中，解方程得到k的值。

以上就是反比例函数单元测试卷的答案。

希望能对你的学习有所帮助！。

反比例函数综合复习题_、选择题1. 反比例函数y=—^阁象经过点（2, 3），则n 的位是（）•xA 、一2B 、一1C 、0D 、1Jr2. 茗反比例函数y=^ （k#））的图象经过点（一 1, 2），则这个函数的图象一定经过点（）.xA 、（2，一1）B 、（一— , 2）C 、（一2，一1）D 、（ — , 2）2 23. 己知甲、乙两地相距s （km ）,汽车从甲地匀速行驶到乙地，则汽车行驶的吋间/ （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4. 其y 与x 成正比例，x 与z 成反比例，则y 与z 之间的关系足（）.A 、成正比例B 、成反比例C 、不成il •:比例也不成反比例D 、无法确定b5. 一次函数丫=10<—1<:，y 随x 的增人而减小，那么反比例函数y=—满足（）.xB 、在每个象限内，y 随x 的增大而减小 D 、图象分布在第二、四象限6. 如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的■线PQ 交双曲线y=—于点Q ，违结OQ ：点 P 沿x 轴正方向运动时，RtAQOP 的面积（）.A 、逐渐增人B 、逐渐减小C 、保持不变D 、无法确定7. 在一个可以改变容积的密闭容器内，装有一定质量m 的菜种气体，当改变容积K 时，气体的密度p 也随之改变.p 与K 在一定范阑内满足，它的图象如图所示，则该气体的质景mA （)• A 、1.4kg B 、5kgC 、6.4kgD 、7kg 第7题图C.A 、当 x 〉0 时，y>0 C 、阁象分布在第一、三象限第6题阁8•若A （―3，y!），B （—2，y2），C （— h y3）三都在函数y=——的图象上，则yi，y2，乃的大小x关系是（ ）.C 、一l<x<0 或 x 〉2D 、x< —1 或 0<x<2二、填空题11. 某种灯的使用寿命为1000小吋，它的可使用天数与平均每天使川的小吋数x 之间的阁数关系式为 ____________________ .12. 已知反比例函数y = t 的图象分布在第二、四象限，则在一次函数j =+ 6十，y 随；v 的增人而（填“增大”或“减小”或“不变”）.114. 反比例函数y= （m+2） x m _1（）的图象分布在第二、|叫象限内，则m 的位为.15. 有一面积为S 的梯形，其上底是卜底长的一，若下底长为x,高为y,则y 与x 的W 数关系是 ____________16. 如图，点M 是反比例函数（6r#））的图象上一点，过M 点作x 轴、y 轴的平行线，若S TO = 5 则此反比例函数解析式为 ____________ .第19题图 第16题图 第20题图 17.使函数 y= (2m 1-7m-9) xm —9m+19 足反比例函数，且图象在每个象限内y 随x 的增人而减小，则 A 、yi>y 2>y3 9.已知反比例函数y:B 、yi<y 2<y31 - 2mC 、yi=y2=y3D 、yi<y 3<y 2的图象上有A （xp y0、B （x 2，y 2）两点，时，yi<y 2,则m的取值范围足（)•A 、m<0B 、m>0C 、D 、m>-10.如图，一次函数与反比例函数的图象相交丁• A 、B 两点，则图中使反比例函数 的值小于一次函数的值的x 的取值范围是（）.A 、x< — 1B 、x>2第10题图13.若反比例函数y:b-3和一次函数y=3x+b 的图象有两个交点，且有一个交点的纵坐标为6,则b可列方程（不等式组）为18.过双曲线y=i (VO)上任意一点引X轴和y轴的垂线，所得长方形的面积为 ____________________ .419.如图，直线y =kx(k〉O)与双曲线y =—交于A(x P yi)，B(x2，y2)两点，则2x^2—7x271= __________ .x2020.如罔，长方形AOCB的两边OC、OA分别位于x轴、y轴上，点B的坐标为B (- —,5)，D是3AB边上的一点，将AADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，荇点E在一反比例函数的图象上，那么该函数的解析式是___________ .三、解答题k21.如图，已知A (x P yi), B (x2, y2)是双曲线乂= 一迕第一象限内的分支上的两点，连结OA、OB.%(1)试说明yi<OA<y 1 + —；(2)过B作BC丄x轴于C,当m=4时，求ABOC的曲‘积.O22.如图，己知反比例函数丫=-一与一次闲数7=1«+15的图象交于A、B两点，且点A的横坐标和点B x 的纵坐标都是一2.求：(1) 一次函数的解析式;(2) AAOB的面积.23.如阁，一次函数7=狀+13的阁象与反比例函数y=—的阁象交于M、N两点.x(1)求反比例函数与一次函数的解析式；(2)根裾阁象写出使反比例函数的位人于一次函数的位的x的取位范k24.如图，已知反比例函数y=—的罔象与一次函数y=6/x+b的阁象交于M （2，m）和N （— 1，一4） x 两点.（1）求这两个函数的解析式；（2）求AMON的而积；（3）谘判断点P （4，1）是否在这个反比例蚋数的图象上，并说明理巾.3 k25.如閔，点P的坐标为（2,—），过点P作x轴的平行线交y轴于点A,交双曲线灭=—（x〉0）于点N;2 xk作PM丄AN交双曲线y二一（x〉0）于点M，连结AM.已知PN=4. x（1）求k的值.（2）求AAPM的血积.1 b26.如罔，已知直线;v = —x与双曲线jv = —（々〉0）交于儿B两点，且点d的横坐标为4.2 x（1）求々的值；（2）若双曲线;；=一（々〉0）上一点C的纵坐标为8,求A/JOC的則积；x（3）过原点0的另一条直线/交双曲线y二一（々〉（））于P, 两点（P点在第一象限），若山点xA，B，P，0为顶点组成的四边形面积为24,求点尸的坐标.k27.如图8，直线火=Ax + Z?与反比例函数J7 =——（x <0）的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为（一2, 4），点B的横坐标为一4. （1）试确定反比例函数的关系式；DACBD ； CDBDD. 100011、 y12、减小； 13、5 14、一3 ; 15、y:352x16、y:(2)求AAOC 的面积.k28. 已知：如阁，正比例函数少=似的阁象与反比例函数y =—的阁象交于点？1(3,2).x (1) 试确定上述正比例函数和反比例函数的表达式；(2) 根裾阁象回答，在第一象限内，当x 取何位时，反比例函数的位人于正比例函数的位？ (3) M (m, n)是反比例函数阁象上的一动;5、，其中0 < m < 3,过点作且线A/AM/JV 轴，交灭轴于点过点J 作直线/IC//y 轴交;c 轴于点C,交直线于点Z).当四边形的而积为6时，请判断线段的大小关系，并说明理由.参考答案21、解：（1）过点A 作AD 丄x 轴于D,则OD=x P AD = y P 因为点A （x P yi ）在双曲线）<=一上，故 xk Jrx, = —, 乂在 RtAOAD 小，AD<OA<AD+OD,所以力<0八<力+— ；（2） ABOC 的面积为 2.^1 J 6!1如图，对」.y =2x —2，y =0 时，x = 1» A （1» 0）, OA = 1» •••S2\MON =S AMOA +S/\NOA = — OA*MC+ -OAND= lx 1x2 + lx 1x4=3.2 2 242将点P （4，1）的坐标代入y=—，知两边相等，/.P 点在反比例函数图象上.%26.解:（1）.••当x =4吋，y =2.人点J 的坐标为（4, 2 ）.•••点d 是直线y 丄x 与双曲誇=2 （k>0）的交点，.•• 々 = 4x2 = 8.2 x （2）解法一：如阁12-1, •••点C 在双曲线上，当灭=8时，x =1 •••点C 的坐标为（1,8）.过点J 、C 分别做轴、y 轴的垂线，垂足为从、从得矩形S 矩形 ONDM =32 ， S AONC = 4 » S ACDA = 9, S AOAM = 4.S AAOC = S 矩形 ONDM - S AONC - S ACDA - S AOAM = 32-4-9-4 = 15. （3） V 反比例函数图象是关于原点（9的中心对称閔形.OP=OQ, OA=OB.:.四边形是平行四边形.. 1 1•• S APOA ~ S 平行四is 形 APB （^ X 24 = 6.m 1 2 3 4 5 — 9z?2 + 19 = —1 2m 2-7m-9>018、|k|; 19、 20；20、y:1222、 解••（1）山己知易得 A （―2, 4）, B （4, —2）,代入 y 二kx + b 中，求得 y=—x+2;（2） y —0 N't, x —2, WO y — —x+2 与 x 轴的交点 M （2，0），即|OM|=2，于足 S AAOB ^S^AOM + S ABOM =—|OM|-|y A |+ — |OM|-|y B |= — X 2M+ 丄 x2x2 = 6. 2k 423、 解：（1）将N （― 1，—4）代入y=—，得k=4. •••反比例函数的解析式为y=—.将M （2，m ）x x4代入 y=_，得 m=2.将 M （2，2），N （ —1，一4）代入 y=ax+b ，得 x2a + b = 2f -a + b = -4.解得a = 2,b = -2.—次函数的解析式为y=2x —2.（2）由图象可知，当x<_l 或0<x<2时，反比例函数的值大于•一次函数的值.b 4 24.解（1）巾己知，得一4= — , k=4, /.y= —.又*••图象过 M （2, m ）点， -1 x 4• • ITI = — = 2,2 •••y=ox+b 图象经过M 、N 两点，，解之得•••y=2x—2.设点尸的横平•标为m （州〉0且w关4），得尸（w，m过点P、//分别做x轴的垂线，基足为五、凡•••点P、■<4 件双曲线.1‘.，/.S^POE =S^AOF=4.若0</w<4，如图12-3，V S ^PEFA~S/IPOA-*-^AAOF>• • S 梯形PEFA =S APOA= 61 Q•••—（2H—）• （4 - AW）= 6 •2 m解得w = 2，zn = -8（舍去）.A P（2, 4）./w〉4，如阁12-4，•：S^AO/^ S W，AFEP =^AAOP^^APOE^^ S 悌形P£/?4 =^APOA = 6 . 1 8••• 7（2 + —）.（”卜4） = 6，解得，n =8，w =-2 （食去）••••尸（8, 1）.2 m•••点尸的坐标是尸（2, 4）或尸（8, 1）.6 228. （ 1 ） y= x ； y= 3 x ;（2） 0<x<3 ；（3 ） BM二DM ,••• =^AO4C =*^X W =3 ••• ••^MkMDC = + +^AO4C =3 + 3 + 6 = 12即（5CO12, •••003，£ o « 3 3即A m = — = —•••MB:—，A/D = 3— = 一 :n 2 2 2 2。

反比例函数练习一．选择题（共22小题）1．下列函数中，y是x的反比例函数的为（）A．y=2x+1 B．C．D．2y=x2．）函数y=k是反比例函数，则k的值是（）A．﹣1 B．2 C．±2D．±3．若y=（m﹣1）x|m|﹣2是反比例函数，则m的值为（）A．m=2 B．m=﹣1 C．m=1 D．m=04．若y与x成反比例，x与z成反比例，则y是z的（）A．正比例函数B．反比例函数C．一次函数D．不能确定5．反比例函数（m为常数）当x＜0时，y随x的增大而增大，则m的取值范围是（）A．m＜0 B．C．D．m≥6．已知k1＜0＜k2，则函数y=和y=k2x﹣1的图象大致是（）A．B．C．D．7．在同一直角坐标系中，函数y=kx+k与y=（k≠0）的图象大致为（）A． B．C．D．8．下列函数的图象中，与坐标轴没有公共点的是（）A．B．y=2x+1 C．y=﹣x D．y=﹣x2+19．若ab＞0，则函数y=ax+b与函数在同一坐标系中的大致图象可能是（）A．B．C．D．10．若方程=x+1的解x0满足1＜x0＜2，则k可能是（）A．1 B．2 C．3 D．611．如图，有反比例函数y=，y=﹣的图象和一个圆，则图中阴影部分的面积是（）第11题图第12题图A．πB．2πC．4πD．条件不足，无法求12．如图所示，点P（3a，a）是反比例函数y=（k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）A．y=B．y=C．y=D．y=13．关于反比例函数y=的图象，下列说法正确的是（）A．图象经过点（1，1）B．两个分支分布在第二、四象限C．两个分支关于x轴成轴对称D．当x＜0时，y随x的增大而减小14．如图是反比例函数y=（k为常数，k≠0）的图象，则一次函数y=kx﹣k的图象大致是（）A B C D15．已知函数y=的图象如图，以下结论：①m＜0；分支上y随x的增大而增大；③若点A（﹣1，a）、点B（2，b）在图象上，则a＜b；④若点P（x，y）在图象上，则点P1（﹣x，﹣y）也在图象上．其中正确的个数是（）A．4个 B．3个C．2个D．1个16．函数的自变量x满足≤x≤2时，函数值y满足≤y≤1，则这个函数可以是（）A．y=B．y=C．y=D．y=17．反比例函数y=在每个象限内的函数值y随x的增大而增大，则m的取值范围是（）A．m＜0 B．m＞0 C．m＞﹣1 D．m＜﹣118．以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐标系，双曲线y=经过点D，则正方形ABCD的面积是（）第18题图第19题图A．10 B．11 C．12 D．1319．如图，A、B是双曲线y=上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C．若△ADO的面积为1，D为OB的中点，则k的值为（）A．B．C．3 D．420．如图，过点O作直线与双曲线y=（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S1，△EOF的面积为S2，则S1、S2的数量关系是（）第20题图第21题图A．S1=S2B．2S1=S2C．3S1=S2D．4S1=S221．如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线y=（x＞0）上的一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小22．如图，反比例函数y=﹣在第二象限的图象上有两点A、B，它们的横坐标分别为﹣1，﹣3，直线AB 与x轴交于点C，则△AOC的面积为（）A．8 B．10 C．12 D．24二．填空题（共4小题）23．已知y=（a﹣1）是反比例函数，则a= ．24．已知反比例函数的解析式为y=，则最小整数k= ．25．函数y=，当y≥﹣2时，x的取值范围是（可结合图象求解）．26．若反比例函数的图象在其每个象限内，y随x的增大而增大，则k的值可以是．（写出一个符合条件的值即可）三．解答题（共4小题）27．已知反比例函数y=﹣（1）说出这个函数的比例系数；（2）求当x=﹣10时函数y的值；（3）求当y=6时自变量x的值．28．已知函数y=（5m﹣3）x2﹣n+（n+m），（1）当m，n为何值时是一次函数？（2）当m，n为何值时，为正比例函数？（3）当m，n为何值时，为反比例函数？29．如图，是反比例函数y=的图象的一支．根据给出的图象回答下列问题：（1）该函数的图象位于哪几个象限？请确定m的取值范围；（2）在这个函数图象的某一支上取点A（x1，y1）、B（x2，y2）．如果y1＜y2，那么x1与x2有怎样的大小关系？30．如图，已知函数y=（x＞0）的图象经过点A、B，点A的坐标为（1，2），过点A作AC∥y轴，AC=1（点C位于点A的下方），过点C作CD∥x轴，与函数的图象交于点D，过点B作BE⊥CD，垂足E在线段CD上，连接OC、OD．（1）求△OCD的面积；（2）当BE=AC时，求CE的长．答案：一．选择题（共22小题）1．C 2．D 3．B 4．A 5．C 6．C 7．B 8．A 9．C 10．C 11．B 12．D 13．D 14．B 15．B 16．A 17．D 18．C 19．B 20．B 21．C 22．C二．填空题（共4小题）23．-1 24．1 25．x≤-2或x＞0 26．-1（答案不唯一）三．解答题（共4小题）27． 28． 29． 30．。

反比例函数一、选择题1．（2016·黑龙江大庆）已知A（x1，y1）、B（x2，y2）、C（x3，y3）是反比例函数y=上的三点，若x1＜x2＜x3，y2＜y1＜y3，则下列关系式不正确的是（ ）A．x1•x2＜0 B．x1•x3＜0 C．x2•x3＜0 D．x1+x2＜0【考点】反比例函数图象上点的坐标特征．【分析】根据反比例函数y=和x1＜x2＜x3，y2＜y1＜y3，可得点A，B在第三象限，点C在第一象限，得出x1＜x2＜0＜x3，再选择即可．【解答】解：∵反比例函数y=中，2＞0，∴在每一象限内，y随x的增大而减小，∵x1＜x2＜x3，y2＜y1＜y3，∴点A，B在第三象限，点C在第一象限，∴x1＜x2＜0＜x3，∴x1•x2＜0，故选A．【点评】本题考查了反比例函数图象上点的坐标特征，解答此题的关键是熟知反比例函数的增减性，本题是逆用，难度有点大．2．（2016·湖北十堰）如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C 是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y=上（k＞0，x＞0），则k的值为（ ）A．25B．18C．9D．9【考点】反比例函数图象上点的坐标特征；平行线的性质；等边三角形的性质．【分析】过点A作AE⊥OB于点E，根据正三角形的性质以及三角形的边长可找出点A、B、E 的坐标，再由CD⊥OB，AE⊥OB可找出CD∥AE，即得出，令该比例=n，根据比例关系找出点D、C的坐标，利用反比例函数图象上点的坐标特征即可得出关于k、n的二元一次方程组，解方程组即可得出结论．【解答】解：过点A作AE⊥OB于点E，如图所示．∵△OAB为边长为10的正三角形，∴点A的坐标为（10，0）、点B的坐标为（5，5），点E的坐标为（，）．∵CD⊥OB，AE⊥OB，∴CD∥AE，∴．设=n（0＜n＜1），∴点D的坐标为（，），点C的坐标为（5+5n，5﹣5n）．∵点C、D均在反比例函数y=图象上，∴，解得：．故选C．【点评】本题考查了反比例函数图象上点的坐标特征、平行线的性质以及等边三角形的性质，解题的关键是找出点D、C的坐标．本题属于中档题，稍显繁琐，解决该题型题目时，巧妙的借助了比例来表示点的坐标，根据反比例函数图象上点的坐标特征找出方程组是关键．3. (2016·新疆)已知A（x1，y1），B（x2，y2）是反比例函数y=（k≠0）图象上的两个点，当x1＜x2＜0时，y1＞y2，那么一次函数y=kx﹣k的图象不经过（ ）A．第一象限B．第二象限C．第三象限D．第四象限【考点】反比例函数图象上点的坐标特征；一次函数图象与系数的关系．【分析】首先根据x1＜x2＜0时，y1＞y2，确定反比例函数y=（k≠0）中k的符号，然后再确定一次函数y=kx﹣k的图象所在象限．【解答】解：∵当x1＜x2＜0时，y1＞y2，∴k＞0，∴﹣k＜0，∴一次函数y=kx﹣k的图象经过第一、三、四象限，∴不经过第二象限，故选：B．【点评】此题主要考查了反比例函数图象上点的坐标特征以及一次函数图象与系数的关系，解决此题的关键是确定k的符号．4. (2016·云南)位于第一象限的点E在反比例函数y=的图象上，点F在x轴的正半轴上，O是坐标原点．若EO=EF，△EOF的面积等于2，则k=（ ）A．4 B．2 C．1 D．﹣2【考点】反比例函数系数k的几何意义．【分析】此题应先由三角形的面积公式，再求解k即可．【解答】解：因为位于第一象限的点E在反比例函数y=的图象上，点F在x轴的正半轴上，O 是坐标原点．若EO=EF，△EOF的面积等于2，所以，解得：xy=2，所以：k=2，故选：B【点评】主要考查了反比例函数系数k的几何意义问题，关键是由三角形的面积公式，再求解k．5. （2016·四川达州·3分）下列说法中不正确的是（ ）A．函数y=2x的图象经过原点B．函数y=的图象位于第一、三象限C ．函数y=3x ﹣1的图象不经过第二象限D ．函数y=﹣的值随x 的值的增大而增大【考点】正比例函数的性质；一次函数的性质；反比例函数的性质．【分析】分别利用正比例函数以及反比例函数的定义分析得出答案．【解答】解：A 、函数y=2x 的图象经过原点，正确，不合题意；B 、函数y=的图象位于第一、三象限，正确，不合题意；C 、函数y=3x ﹣1的图象不经过第二象限，正确，不合题意；D 、函数y=﹣的值，在每个象限内，y 随x 的值的增大而增大，故错误，符合题意．故选：D ．6. （2016·四川乐山·3动时，点C 图象上运动，若tan ()A 2()C 6答案：D解析：连结CO 所以，CO ⊥AB ，因为tan 作AE ⊥x 轴，CD ⊥x 轴于则有△OCD ∽△OEA 设C （m ，n ），则有A 所以，k n m =解①②得：k ＝87. （2016·四川凉山州·4分）二次函数y=ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是（ ）A．B．C．D．【考点】反比例函数的图象；一次函数的图象；二次函数的图象．【分析】根据二次函数的图象找出a、b、c的正负，再结合反比例函数、一次函数系数与图象的关系即可得出结论．【解答】解：观察二次函数图象可知：开口向上，a＞0；对称轴大于0，﹣＞0，b＜0；二次函数图象与y轴交点在y轴的正半轴，c ＞0．∵反比例函数中k=﹣a＜0，∴反比例函数图象在第二、四象限内；∵一次函数y=bx﹣c中，b＜0，﹣c＜0，∴一次函数图象经过第二、三、四象限．故选C．8. （2016,湖北宜昌，15，3分）函数y=的图象可能是（ ）A．B．C．D．【考点】反比例函数的图象．【分析】函数y=是反比例y=的图象向左移动一个单位，根据反比例函数的图象特点判断即可．【解答】解：函数y=是反比例y=的图象向左移动一个单位，即函数y=是图象是反比例y=的图象双曲线向左移动一个单位．故选C【点评】此题是反比例函数的图象，主要考查了反比例函数的图象是双曲线，掌握函数图象的平移是解本题的关键．9. （2016吉林长春，8，3分）如图，在平面直角坐标系中，点P（1，4）、Q（m，n）在函数y=（x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（ ）A．减小B．增大C．先减小后增大D．先增大后减小【考点】反比例函数系数k的几何意义．【分析】首先利用m和n表示出AC和AQ的长，则四边形ACQE的面积即可利用m、n表示，然后根据函数的性质判断．【解答】解：AC=m﹣1，CQ=n，则S四边形ACQE=AC•CQ=（m﹣1）n=mn﹣n．∵P （1，4）、Q （m ，n ）在函数y=（x ＞0）的图象上，∴mn=k=4（常数）．∴S 四边形ACQE =AC •CQ=4﹣n ，∵当m ＞1时，n 随m 的增大而减小，∴S 四边形ACQE =4﹣n 随m 的增大而增大．故选B ．【点评】本题考查了二次函数的性质以及矩形的面积的计算，利用n 表示出四边形ACQE 的面积是关键．10. (2016兰州，2,4分)反比例函数的图像在（）。

八年级下册数学《反比例函数》测试题（一）（一）填空题（每题3分共30分）1、已知反比例函数y=xkd 的图像经过点（3 ，—2） 则此函数的解析式为____________当x>0时 y 随x 的增大而____________2、写出一个具有性质“在每个象限内y 随x 的增大而减小”的反比例函数的表达式为_______3、反比例函数422)1(---=m m x m y 当x <0时 y 随x 的增大而增大 则 m 的值是________4、已知 正比例函数y=ax 和 反比例函数xby = 在同一坐标系中 两图像无交点， 则 a 和 b 的关系式是___________5、在函数x a y 12--= （a 为常数）的图像上三点 （—1 ，1y ） （41-2y ） （213y ） 则 函数值1y 2y 3y 的大小关系是__________________.6、若一个三角形的面积是82cm 则其底边长y(cm) 与这边上的高x(cm)之间的关系是____________7、直线b x y +-=5与双曲线xy 2-= 相交于点p (—2 ，m ) 则 b=____________8、已知 反比例函数)0(≠=k xk y 当x>0 时 y 随x 增大而增大 那么 一次函数 y=kx —kd 的图像经过_______________象限。

9、有一面积为120的梯形 其上底是下底长的32若上底长为x 高为y 则y 与 x 的函数关系式为____________ 当高为10时x=___________.10、反比例函数xy 6=的图像上 横坐标和纵坐标都是整数的点的个数是_____________（二）选择题（每题3分共30分）1、下列函数中 y 是x 的反比例函数的是（ ）A 21xy =B xy=8C 52+=x yD 53+=x y 2、当x>0时 四个函数 y= —x y=2x+1 x y 1-= xy 2= 其中y随x 的增大而增大的函数有（ ）A 1 个B 2 个C 3 个D 4个3、设A( 1x 1y ) B (2x 2y )是反比例函数xy 2-= 图像上的两点 若1x <2x <0 则1y 与 2y 之间的关系是（ ）A 1y <2y <0B 2y <1y <0C 2y >1y >0D 1y >2y >0 4、一次函数y=kx —1 与 反比例函数)0(≠=k xky 的图像的形状大致是（ ）A B C D5、已知 一次函数y=kx+b 的图像经过第一二四象限 则反比例函数xkby =的图像在（ ） A 第一二象限 B 第三 四象限 C 第一三象限 D 第二三象限6、如果点P 为反比例函数xy 6=的图像上的一点 ， PQ 垂直与x 轴， 垂足为Q ， 那么po ∆Q 的面积为（ ）A 12B 6C 3D 1.57、已知函数22-=m mx y 是反比例函数 且图像的两个分支在第二，四象限则m 的值是（ ）A 1B —1C 1±D 不能确定 8、反比例函数bky =与直线y=—2x 相交与点A ， A 点的横坐标为—1， 则此反比例函数的解析式为（ ）A xy 2=B x y 21=C x y 2-=D x y 21-=9、若反比例函数y =xk 3-的图像在每一个象限内，y 随x 的增大而增大，则有（ ）A K 0≠B K 3≠C K<3D K>310、已知XF 所做的功是15焦，则XF 与物体在力的方向上通过的距离S 的图像大致是下图中的（ ）A B C D（三）解答题1、已知一次函数b kx y +=与反比例函数xmy =的图像交于A （—2 ，1） B （1 ，n ）俩点求 ⑴ 反比例函数和一次函数的表达式？ ⑵ 求△AOB 的面积？2、已知 21y y y +=若1y 与2x成正比例关系 2y 与231+x 成反比例关系 且当X=-1时，，ｙ＝３．由ｘ＝１时，ｙ＝－３时， 求ｙ与ｘ的函数关系式？３ 如图所示：已知直线ｙ＝x 21与双曲线ｙ＝)0(>k xk 交于Ａ Ｂ两点，且点Ａ的横坐标为４ ⑴ 求ｋ的值？⑵ 若双曲线ｙ＝)0(>k xk 上的一点C 的纵坐标为8，求△AOC 的面积？4 已知反比例函数y=xm的图像经过点A （10 ，—3），一次函数y=kx+b 的图像经过点A 与点C (0. —4)，且与反比例函数的图像相交于另一点B⑴ 试确定这两个函数的表达式？ ⑵ 求点B 的坐标？参考答案㈠ 填空题1. y= —x6 增大 2. y=x3(答案不唯一) 3. —1 4. 异号5. 3y <1y <2y 6 y=x167. —9 8.一 二 四9 ｙ＝x96９.６ １０． ８个 ㈡选择题１Ｂ ２Ａ ３Ｃ ４Ｃ ５Ｄ ６Ｃ ７Ｂ ８Ｃ ９Ｃ １０Ｂ㈢解答题１⑴ ｙ＝—x —1 ⑵ 23=s 2 2322--=x x y 3⑴ k=8⑵15=∆COA s 4 ⑴ y=x —4 ⑵ （3 —1） 希望以上资料对你有所帮助，附励志名言3条： 1、宁可辛苦一阵子，不要苦一辈子。

反比例函数练习题集锦（含答案）1、综合题1、如图，已知直线与双曲线交于两点，且点的横坐标为．（1）求的值；（2）若双曲线上一点的纵坐标为8，求的面积；（3）过原点的另一条直线交双曲线于两点（点在第一象限），若由点为顶点组成的四边形面积为，求点的坐标．2、已知一次函数与双曲线在第一象限交于A、Ｂ两点，A点横坐标为1．B点横坐标为４(1)求一次函数的解析式;(2)根据图象指出不等式的解集；(2) 点P是x轴正半轴上一个动点，过P点作x轴的垂线分别交直线和双曲线于M、N，设P点的横坐标是t(t>0),△OMN的面积为S,求S和t的函数关系式，并指出t的取值范围。

二、简答题3、．已知：如图，在平面直角坐标系中，直线AB 分别与轴交于点B、A，与反比例函数的图象分别交（1）求该反比例函数的解析式；（2）求直线AB的解析式．4、如图，已知正比例函数与反比例函数的图象交于两点．（1）求出两点的坐标；的范围；（2）根据图象求使正比例函数值大于反比例函数值的三、计算题5、为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒。

已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t 的函数关系为（为常数）。

如下图所示，据图中提供的信息，解答下列问题：（1）写出从药物释放开始，y与t之间的两个函数关系式及相应的自变量取值范围；（2）据测定，当空气中每立方米和含药量降低到0.25毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？6、如图，在直角坐标系xOy中，一次函数y＝k1x＋b 的图象与反比例函数的图象交于A(1，4).B(3，m)两点。

(1)求一次函数的解析式；的面积。

(2)求△AOB7、如图,一次函数y=kx+b的图象与反比例函数y=图象交于A(－2,1)、B(1,n)两点.(1) 求反比例函数和一次函数的解析式.(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.（1）试确定上述反比例函数和一次函数的表达式；（2）求△AOB的面积。

反比例函数综合测试题一、选择题(每小题3分，共24分)1.已知点M (- 2，3 )在反比例函数xky=的图象上，下列各点也在该函数图象上的是( ).AA. (3，- 2)B. (- 2，- 3)C. (2，3)D. (3，2)2. 反比例函数(0)ky kx=≠的图象经过点(- 4，5)，则该反比例函数的图象位于( ).BA. 第一、三象限B. 第二、四象限C. 第二、三象限D. 第一、二象限3. 在同一平面直角坐标系中，函数xy2-=与xy2=的图象的交点个数为( ). DA. 3个B. 2个C. 1个D. 0个4. 如图1，点A是y轴正半轴上的一个定点，点B是反比例函数y = 2 x(x> 0)图象上的一个动点，当点B的纵坐标逐渐减小时，△OAB的面积将( ). AA．逐渐增大B．逐渐减小C．不变D．先增大后减小5. (2009年恩施市)如图2，一张正方形的纸片，剪去两个一样的小矩形得到一个“E”图案，设小矩形的长和宽分别为x，y，剪去部分的面积为20，若2 ≤x≤ 10，则y与x的函数图象是( ). A6. 已知点A(x1，y1)，B(x2，y2)是反比例函数xky=(k > 0)的图象上的两点，若x1 < 0 < x2，则( ).AA. y1 < 0 < y2B. y2 < 0 < y1C. y1 < y2 < 0D. y2 < y1 < 07. 如图3，反比例函数3yx=的图象与一次函数y = x + 2的图象交于A，B两点，那么△AOB 的面积是( ).CA. 2B. 3C. 4D. 68. 如图4，等腰直角三角形ABC位于第一象限，AB= AC = 2，直角顶点A在直线y = x上，1212图2图4A B C Dy xOP 1P 2P 3P 4 P 5A 1 A 2 A 3 A 4 A 5 图7其中点A 的横坐标为1，且两条直角边AB ，AC 分别平行于x 轴、y 轴，若反比例函数k y x=的图象与△ABC 有交点，则k 的取值范围是( ). C A.1 < k < 2B.1 ≤ k ≤ 3C.1 ≤ k ≤ 4D.1≤ k < 4二、填空题(每小题4分，共24分) 9. 已知反比例函数k y x =的图象经过点(23)，，则此函数的关系式是 ．6y x= 10. 在对物体做功一定的情况下，力F (N)与此物体在 力的方向上移动的距离s (m)成反比例函数关系，其图 象如图5所示，点P (5，1)在图象上，则当力达到10 N 时，物体在力的方向上移动的距离是 m. 0. 511. 反比例函数xky =)0(<k 的图象与经过原点的直线l 相交于A ，B 两点，若点A 坐标为(-2，1)，则点B 的坐标为 . (2，-1).12.一次函数y = x + 1与反比例函数ky x=的图象都经过点(1，m )，则使这两个函数值都小于0时x 的取值范围是___________. x < - 113. (2009年兰州市)如图6，若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 反比例函数1y x=(x > 0)的图象上，则点E 的坐标是_________. (215+，215-)14. (2009年莆田市)如图7，在x 轴的正半轴上依次截取OA 1 = A 1A 2 = A 2A 3 = A 3A 4 = A 4A 5，过点A 1，A 2，A 3，A 4，A 5，分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点P 1，P 2，P 3，P 4，P 5，得直角三角形OP 1A 1，A 1P 2A 2，A 1P 2A 2，A 2P 3A 3，A 3P 4A 4，A 4P 5A 5，并设其面积分别为S 1，S 2，S 3，S 4，S 5，则S 5的值为 . 三、解答题(共30分)15.(6分) 已知点P (2，2)在反比例函数xky =(k ≠ 0)的图象上. （1）当x = - 3时，求y 的值； （2）当1 < x < 3时，求y 的取值范围．F / N图5s / mO图616.(8分)已知图8中的曲线是反比例函数5myx-=(m为常数)图象的一支. 若该函数的图象与正比例函数y = 2x的图象在第一象内限的交于点A，过点A作x轴的垂线，垂足为点B，当△OAB的面积为4时，求点A的坐标及反比例函数的解析式.17.(8分)如图9，点P的坐标为322⎛⎫⎪⎝⎭，，过点P作x轴的平行线交y轴于点A，交反比例函数kyx=(x > 0)于点点N，作PM ⊥AN交反比例函数kyx=(x > 0)的图象于点M，连接AM.若PN = 4，求：（1）k的值.（2）△APM的面积.18.(8分)为预防“手足口病”，某校对教室进行“药熏消毒”. 已知药物燃烧阶段，室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例；燃烧后，y与x成反比例(如图10所示). 现测得药物10 min燃烧完，此时教室内每立方米空气含药量为8 mg. 根据以上信息，解答下列问题：（1）求药物燃烧时y与x的函数关系式；（2）求药物燃烧后y与x的函数关系式；（3）当每立方米空气中含药量低于1.6 mg时，对人体无毒害作用. 那么从消毒开始，经多长时间学生才可以返回教室？四、探究题(共22分)19.(10分) 我们学习了利用函数图象求方程的近似解，例如，把方程2x – 1 = 3 - x 的解看成函数y = 2 x - 1的图象与函数y = 3 - x 的图象交点的横坐标. 如图11，已画出反比例函数1y x=在第一象限内的图象，请你按照上述方法，利用此图象求方程x 2 – x – 1 = 0的正数解(要求画出相应函数的图象，求出的解精确到0.1）.20.(12分)一次函数y = ax + b 的图象分别与x 轴、y 轴交于点M ，N ，与反比例函数k y x=的图象相交于点A ，B ．过点A 分别作AC ⊥x 轴，AE ⊥y 轴，垂足分别为点C ，E ；过点B 分别作BF ⊥x 轴，BD ⊥y 轴，垂足分别为点F ，D ，AC 与BC 相交于点K ，连接CD ． （1）如图12，若点A ，B 在反比例函数ky x=的图象的同一分支上，试证明： ①A E D K C F B K S S =四边形四边形；②A N B M =． （2）若点AB ，分别在反比例函数ky x=的图象的不同分支上，如图13，则AN 与BM 还相等吗？试证明你的结论．反比例函数综合测试题参考答案一、选择题 1. A. 2. B. 3. D.4. A.5. A.6. A.7. C.8. C.二、填空题 9. 6y x=. 10. 0. 5. 11. (2，-1).12. x < - 1. 13. (215+，215-). 14.15. 三、解答题 15.（1）34-=y ；（2）y 的取值范围为434<<y ． 16.∵第一象限内的点A 在正比例函数y = 2x 的图象上，∴设点A 的坐标为(m ，2m )(m > 0)，则点B 的坐标为(m ，0). ∵S △OAB = 4，∴12m • 2m = 4. 解得m 1 = 2，m 2 = - 2(不符合题意，舍去).∴点A 的坐标为(2，4).又∵点A 在反比例函数5m y x -=的图象上，∴542m -=，即m – 5 = 8. ∴反比例函数的解析式为8y x=.17.（1）∵点P 的坐标为322⎛⎫ ⎪⎝⎭，，∴AP = 2，OA =32. ∵PN = 4，∴AN = 6. ∴点N 的坐标为362⎛⎫ ⎪⎝⎭，. 把点362N ⎛⎫ ⎪⎝⎭，代入ky x=中，得k = 9. （2）由（1）知k = 9，∴9y x =. 当x = 2时，92y =. ∴93322M P =-=. ∴12332A P MS =⨯⨯=△. 18.（1）设药物燃烧阶段函数关系式为y = k 1x (k 1 ≠ 0).根据题意，得8 = 10k 1，k 1 = 45. ∴此阶段函数关系式为45y x =(0 ≤ x < 10).（2）设药物燃烧结束后函数关系式为22(0)ky k x=≠.根据题意，得2810k=，280k =. ∴此阶段函数关系式为80y x=(x ≥ 10).（3）当y < 1.6时，801.6x<. ∵0x >，∴1.680x >，50x >. ∴从消毒开始经过50 min 学生才返可回教室. 四、探究题19. 方程x 2 – x – 1 = 0的正数解约为1.6.提示：∵x ≠ 0，将x 2 – x – 1 = 0两边同除以x ，得110x x --=．即11x x=-． 把x 2 – x – 1 = 0的正根视为由函数1y x=与函数y = x - 1的图象在第一象限交点的横坐标． 20.（1）①A C x ⊥轴，A E y ⊥轴，∴四边形AE O C 为矩形． BF x ⊥轴，B D y ⊥轴，∴四边形BD O F 为矩形．A C x ⊥轴，B D y ⊥轴，∴四边形A E D K D OC K C F B K ，，均为矩形．1111O C x A C y x y k ===，，，∴11A E O CS O C A C x y k ===矩形2222O F x F B y x yk ===，，，∴22B D O F S O F F B x y k ===矩形．∴A E O C B D O F S S =矩形矩形．A E D K A E O C D O C K S S S =-矩形矩形矩形，C FB K B D O F D OC K S S S =-矩形矩形矩形，∴A ED K C F B K S S =矩形矩形． ②由（1）知，AE D K CF B KS S =矩形矩形．∴A K D K B K C K =．∴AK BKCK DK=． 90A K B C K D ∠=∠=°，∴A K B C K D △∽△．∴C D K A B K ∠=∠．∴A B C D∥．A C y ∥轴，∴四边形AC D N 是平行四边形．∴A N C D =．同理可得B M C D =．A N B M∴=． （2）AN 与BM 仍然相等．A E D K A E O C O D K C S S S =+矩形矩形矩形，B KC F BD O F O D K CS S S =+矩形矩形矩形， 又A E O CB D O F S S k ==矩形矩形，∴A E D K B KC FS S =矩形矩形． ∴A K D K B K C K=．∴CK DKAK BK=． K K ∠=∠，∴C D K A B K △∽△．∴C D K A B K ∠=∠．∴A B C D∥．A C y ∥轴，∴四边形AN D C 是平行四边形．∴A N C D =．同理B M C D =．∴A N B M =【教学标题】反比例函数 【教学目标】1、 提高学生对反比例函数的学习兴趣2、 使学生掌握反比例函数基础知识3、让学生熟练地运用反比例知识【重点难点】图像及性质 【教学内容】反比例函数一、基础知识1. 定义：一般地，形如xk y =（k 为常数，o k ≠）的函数称为反比例函数。