河北省中考数学复习 第六单元 圆 第25讲 与圆相关的计

最新K12教育

教案试题 第24讲 与圆相关的计算

重难点 弧长、扇形面积的计算

(2017·枣庄改编)如图，在▱ABCD中，AB为⊙O的直径，⊙O与DC相切于点E，与AD相交于点F，已知AB＝12.

(1)⊙O内接正三角形的边长为63；

(2)以⊙O的下半圆制作一个无底的圆锥，则圆锥的高为33；

(3)若∠C＝60°.

①求EF︵的长；

②求阴影部分的面积．

【自主解答】 解：①连接OE，OF.

∵CD是⊙O的切线，

∴OE⊥CD.

∵AB∥CD，∴OE⊥AB，即∠AOE＝90°.

∵四边形ABCD是平行四边形，∠C＝60°，

∴∠A＝∠C＝60°.

∵OA＝OF，

∴∠A＝∠OFA＝60°.

∴∠AOF＝60°.

∴∠EOF＝∠AOE－∠AOF＝30°.

∴EF︵的长为30π×6180＝π.

②根据①可知，OE是▱ABCD的高，S▱ABCD＝12×6＝72，

∴S△AOF＝34×62＝93，S扇形BOF＝120π×62360＝12π.

∴S阴影＝S▱ABCD－S△AOF－S扇形BOF＝72－93－12π.

例题剖析(1)已知圆的直径的情况下，要求圆内接正三角形的边长，只需在含120°的等腰三角形中解出GH即可．含120°的等腰三角形三边之比为1∶1∶3；

(2)考查圆锥的高线的计算，h＝R2－r2；(其中R表示圆锥的母线长，即半圆的半径，r表示圆锥底面圆的半径)

(3)①求弧长的关键是求圆心角的度数，在求圆心角的度数时，涉及切线的性质，平行四边形的性质等等知识点； 最新K12教育

教案试题 ②求阴影部分的面积关键是要转化成规则图形的面积，然后再进行计算．

方法指导求阴影部分面积的常用方法：

(1)公式法：如果所求图形的面积是规则图形，如扇形、特殊四边形等，可直接利用公式计算；

(2)和差法：所求图形的面积是不规则的图形，可通过转化成规则图形的面积的和或差；

(3)等积变换法：直接求面积较麻烦或根本求不出时，通过对图形的平移、旋转、割补等，为公式法或和差法创造条件．

百度文库，精选试题

试题习题，尽在百度 与圆有关的位置关系

1．已知⊙O的半径是6 cm、点O到同一平面内直线l的距离为5 cm、则直线l与⊙O的位置关系是(A )

A．相交 B．相切 C．相离 D．无法判断

2．(2016·泉州)如图、AB和⊙O相切于点B、∠AOB＝60°、则∠A的大小为( B )

A．15° B．30° C．45° D．60°

3．(2015·泸州)如图、PA、PB分别与⊙O相切于A、B两点、若∠C＝65°、则∠P的度数为( C )

A．65° B．130° C．50° D．100°

4．(2016·同安区一模)在Rt△ABC中、∠A＝90°、BC＝10、D为BC的中点、当⊙A半径为6时、则D点与⊙A位置关系为( B )

A．圆上 B．圆内 C．圆外 D．以上三种都有可能

5．(2016·潍坊)如图、在平面直角坐标系中、⊙M与x轴相切于点A(8、0)、与y轴分别交于点B(0、4)和点C(0、16)、则圆心M到坐标原点O的距离是( D )

A．10 B．82 C．413 D．241

6．(2016·荆州)如图、过⊙O外一点P引⊙O的两条切线PA、PB、切点分别是A、B、OP交⊙O于点C、点D是优弧ABC︵上不与点A、点C重合的一个动点、连接AD、CD、若∠APB＝80°、则∠ADC的度数是( C )

A．15° B．20° C. 25° D．30°

7．(2016·合肥高新区一模)如图、在⊙O中、AB为直径、BC为弦、CD为切线、连接OC.若∠BCD＝50°、则∠AOC的度数为80°．

第25讲 点、线与圆的位置关系

知识梳理

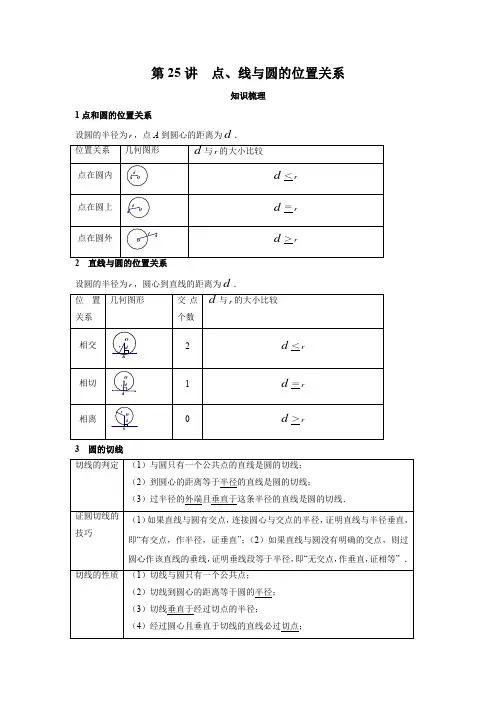
1点和圆的位置关系

设圆的半径为r，点A到圆心的距离为d．

位置关系 几何图形 d与r的大小比较

点在圆内

d＜r

点在圆上

d＝r

点在圆外

d＞r

2 直线与圆的位置关系

设圆的半径为r，圆心到直线的距离为d．

位置关系 几何图形 交点个数 d与r的大小比较

相交

2 d＜r

相切

1 d＝r

相离

0 d＞r

3 圆的切线

切线的判定 （1）与圆只有一个公共点的直线是圆的切线；

（2）到圆心的距离等于半径的直线是圆的切线；

（3）过半径的外端且垂直于这条半径的直线是圆的切线．

证圆切线的技巧 （1）如果直线与圆有交点，连接圆心与交点的半径，证明直线与半径垂直，即“有交点，作半径，证垂直”；（2）如果直线与圆没有明确的交点，则过圆心作该直线的垂线，证明垂线段等于半径，即“无交点，作垂直，证相等” ．

切线的性质 （1）切线与圆只有一个公共点；

（2）切线到圆心的距离等于圆的半径；

（3）切线垂直于经过切点的半径；

（4）经过圆心且垂直于切线的直线必过切点； dOAdOAdOAdrOAdrOAdrOA（5）经过切点且垂直于切线的直线必过圆心．

切线长 在经过圆外一点的切线上，这点和切点之间 线段的长叫做这点到圆的切线长

*切线长定理 从圆外一点引圆的两条切线，它们的切线长相等，并且圆心和这一点的连线平分两条切线的夹角．

4三角形与圆

确定圆的条件 不在同一直线上的三点确定一个圆

三角形的外接圆 （1）经过三角形各顶点的圆叫做三角形的外接圆；外接圆的圆心叫做三角形的外心，这个三角形叫做这个圆的内接三角形；（2）外心是三角形三条边垂直平分线的交点，它到三角形三个顶点的距离相等．

三角形的内切圆 （1）与三角形的各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．

（2）内心是三角形三内角平分线的交点，到三角形各边的距离相等．

浙江省2018年中考数学复习 第一部分 考点研究 第六单元 圆 第25课时 圆的基本性质（含近9年中考真题）试题

1 / 171 浙江省2018年中考数学复习 第一部分 考点研究 第六单元 圆 第25课时

圆的基本性质（含近9年中考真题）试题

编辑整理：

尊敬的读者朋友们：

这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（浙江省2018年中考数学复习 第一部分 考点研究 第六单元 圆 第25课时 圆的基本性质（含近9年中考真题）试题）的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快 业绩进步，以下为浙江省2018年中考数学复习 第一部分 考点研究 第六单元 圆 第25课时 圆的基本性质（含近9年中考真题）试题的全部内容。

浙江省2018年中考数学复习 第一部分 考点研究 第六单元 圆 第25课时 圆的基本性质（含近9年中考真题）试题

2 / 172 第一部分 考点研究

第六单元 圆

第25课时 圆的基本性质

浙江近9年中考真题精选(2009~2017）)，）

命题点1 与圆的基本性质有关的计算(杭州2考,绍兴2015.12）

1. (2016舟山8题3分）把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕,则错误!的度数是( )

A。 120° B。 135° C。 150° D。 165°

第1题图

2。 (2016杭州8题3分）如图，已知AC是⊙O的直径，点B在圆周上（不与A，C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB＝3∠ADB，则（ ）

第2题图

A. DE＝EB B.

2DE＝EB

C。 错误!DE＝DO D. DE＝OB

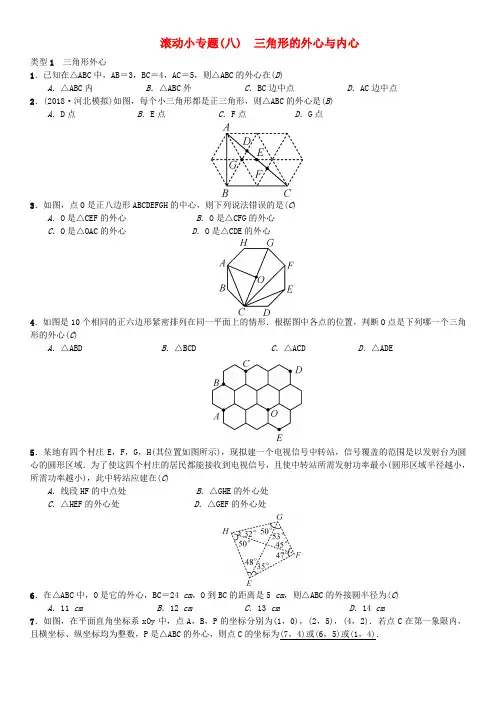
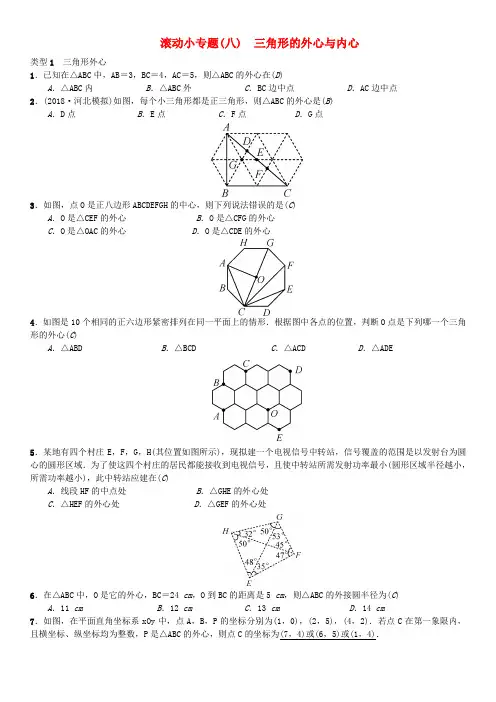
滚动小专题(八) 三角形的外心与内心

类型1 三角形外心

1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)

A．△ABC内 B．△ABC外 C．BC边中点 D．AC边中点

2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)

A．D点 B．E点 C．F点 D．G点

3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)

A．O是△CEF的外心 B．O是△CFG的外心

C．O是△OAC的外心 D．O是△CDE的外心

4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)

A．△ABD B．△BCD C．△ACD D．△ADE

5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)

A．线段HF的中点处 B．△GHE的外心处

C．△HEF的外心处 D．△GEF的外心处

6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C)

A．11 cm B．12 cm C．13 cm D．14 cm

7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．

第六章 圆

第二十三讲 圆的有关概念及性质

【基础知识回顾】

一、 圆的定义及性质：

1、 圆的定义：

⑴形成性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转形成的图形叫做圆，固定的端点叫 线段OA叫做

⑵描述性定义：圆是到定点的距离等于 的点的集合

2、弦与弧：

弦：连接圆上任意两点的 叫做弦

弧：圆上任意两点间的 叫做弧，弧可分为 、 、 三类

3、圆的对称性：

⑴轴对称性：圆是轴对称图形，有 条对称轴， 的直线都是它的对称轴

⑵中心对称性：圆是中心对称图形，对称中心是

【名师提醒：1、在一个圆中，圆心决定圆的 半径决定圆的

2、直径是圆中 的弦，弦不一定是直径；3、圆不仅是中心对称图形，而且具有旋转 性，即绕圆心旋转任意角度都被与原来的图形重合】

二、 垂径定理及推论：

1、垂径定理：垂直于弦的直径 ，并且平分弦所对的 。

2、推论：平分弦（ ）的直径 ，并且平分弦所对的 。

【名师提醒：1、垂径定理及其推论实质是指一条直线满足：⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个，那么可推出其余三个，注意解题过程中的灵活运用 2、圆中常作的辅助线是过圆心作弦的 线（即弦心距）。3、垂径定理常用作计算，在半径r、弦a、弦心d和弓高h中已知其中两个量可求另外两个量。】

三、圆心角、弧、弦之间的关系：

1、圆心角定义：顶点在 的角叫做圆心角

2、定理：在 中，两个圆心角、两条弧、两条弦中有一组量 它们所对应的其余各组量也分别

第25讲 直线与圆的位置关系

陕西《中考说明》 陕西2012～2014年中考试题分析

考点归纳 考试要求 年份 题型 题号 分值 考查内容 分值

比重

直线与圆的位置关系 1.了解并探索直线与圆的位置关系；2.了解切线的概念，知道切线与过切点的半径互相垂直，会过圆上一点画圆的切线；3.能判定一条直线是否为圆的切线；4.探索切线与过切点的半径之间的关系

2014 解答题 23 8 考查切线的性质，涉及相似三角形的判定与性质

2013 解答题 23 8 根据切线的性质，进行相关证明计算

2012 解答题 23 8 根据切线的性质，进行相关证明计算 6.7%

从上表和近几年陕西中考试题来看，陕西中考对本节内容的考查主要是切线的判定与性质，且都以解答题的形式出现，稳定在第23题，分值为8分，预计2015年切线的判定与性质仍会在解答题中出现，且题位为23题，但对于选择或填空题中涉及的此节考查内容，也要引起重视，多加练习．

1．直线和圆的位置关系

(1)设r是⊙O的半径，d是圆心O到直线l的距离．

直线和

圆的位置 图形 公共

点个

数 圆心到直线的

距离d与半

径r的关系 公共点

名称 直线

名称

相交

2 d＜r 交点 割线

相切

1 d＝r 切点 切线

相离

0 d＞r 无 无

(2)切线的性质：

①切线的性质定理：圆的切线__垂直于__经过切点的半径．

②推论1：经过切点且垂直于切线的直线必经过__圆心__．

③推论2：经过圆心且垂直于切线的直线必经过__切点__．

④切线长定理：从圆外一点可以引圆的两条切线，它们的切线长__相等__，这一点和圆心的连线__平分__两条切线的夹角．

(3)切线的判定定理：经过半径的外端并且__垂直于__这条半径的直线是圆的切线．

(4)三角形的外接圆与内接圆：

word

1 / 15 第29讲 圆的基本性质

1. (2012，某某)如图，CD是⊙O的直径，AB是弦(不是直径)，AB⊥CD于点E，则下列结论正确的是(D)

第1题图

A. AE>BE B. 弧AD＝弧BC C. ∠D＝12∠AEC D. △ADE∽△CBE

【解析】 ∵CD是⊙O的直径，AB是弦(不是直径)，AB⊥CD于点E，∴AE＝BE，弧AC＝弧BC.∴A，B两选项错误．∵∠AEC不是圆心角，∴∠D≠12∠AEC. ∴C选项错误．∵∠AED＝∠CEB＝90°，∠DAE＝∠BCE，∴△ADE∽△CBE.∴D选项正确．

2. (2015，某某)如图，AC，BE是⊙O的直径，弦AD与BE相交于点F.下列三角形中，外心不是点O的是(B)

第2题图

A. △ABE B. △ACF C. △ABD D. △ADE

【解析】 只有△ACF的三个顶点不都在⊙O上，故外心不是点O的是△ACF.

3. (2016，某某)如图所示的为4×4的网格图，A，B，C，D，O均在格点上，点O是(B)

第3题图

A. △ACD的外心 B. △ABC的外心 C. △ACD的内心 D. △ABC的内心

【解析】 由网格图，知点O是边AC，BC的垂直平分线的交点．根据三角形外心的定义，知点O是 △ABC的外心．

圆的有关概念 word 2 / 15 例1 下列语句正确的是(D)

A. 长度相等的两条弧是等弧 B. 平分弦的直径垂直于弦

C. 相等的圆心角所对的弧相等 D. 经过圆心的每一条直线都是圆的对称轴

【解析】 能完全重合的两条弧是等弧，所以A选项错误．平分弦(不是直径)的直径垂直于弦，所以B选项错误．在同圆或等圆中，相等的圆心角所对的弧相等，所以C选项错误．经过圆心的每一条直线都是圆的对称轴，所以D选项正确.

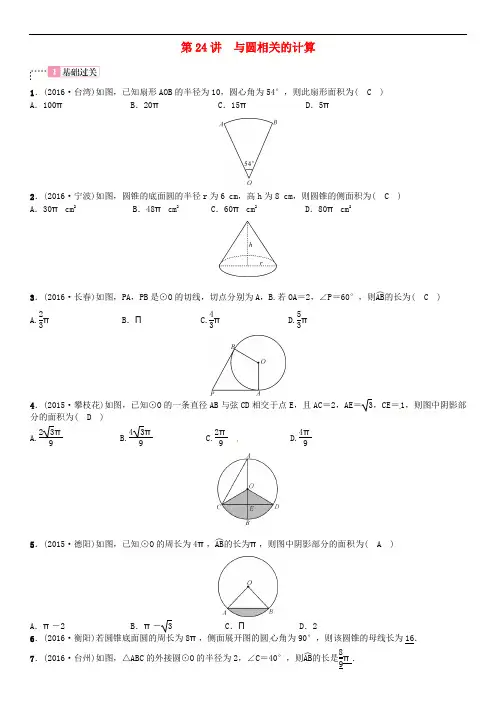
第24讲 与圆相关的计算

1．(2016·台湾)如图，已知扇形AOB的半径为10，圆心角为54°，则此扇形面积为( C )

A．100π B．20π C．15π D．5π

2．(2016·宁波)如图，圆锥的底面圆的半径r为6 cm，高h为8 cm，则圆锥的侧面积为( C )

A．30π cm2 B．48π cm2 C．60π cm2 D．80π cm2

3．(2016·长春)如图，PA，PB是⊙O的切线，切点分别为A，B.若OA＝2，∠P＝60°，则AB︵的长为( C )

A.23π B．Π C.43π D.53π

4．(2015·攀枝花)如图，已知⊙O的一条直径AB与弦CD相交于点E，且AC＝2，AE＝3，CE＝1，则图中阴影部分的面积为( D )

A.23π9 B.43π9 C.2π9 D.4π9

5．(2015·德阳)如图，已知⊙O的周长为4π，AB︵的长为π，则图中阴影部分的面积为( A )

A．π－2 B．π－3 C．Π D．2

6．(2016·衡阳)若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为16．

7．(2016·台州)如图，△ABC的外接圆⊙O的半径为2，∠C＝40°，则AB︵的长是89π．

8．(2016·德阳中江模拟四)如图，⊙O的半径为1 cm，正六边形ABCDEF内接于⊙O，则图中阴影部分的面积为π6cm2.

9．(2016·毕节)如图，分别以边长等于1的正方形的四边为直径作半圆，则图中阴影部分的面积为π2－1．

精选25道最新圆填空题专选培优练习

1．（2019•雨湖区一模）如图，点A、B、C、D在圆O上，∠A＝140°，则∠C＝

．

2．（2019•吴兴区校级一模）如图，一个圆形硬币刚好和一块三角尺的两边相切，其中与AB边的切点为D，若∠C＝30°，BC＝6，BD＝，则圆形硬币的半径为 ．

3．（2019•简阳市模拟）如图，△ABC内接于⊙O．AB为⊙O的直径，BC＝3，AB＝5，D、E分别是边AB、BC上的两个动点（不与端点A、B、C重合），将△BDE沿DE折叠，点B的对应点B′恰好落在线段AC上（包含端点A、C），若△ADB′为等腰三角形，则AD的长为 ．

4．（2019•宝山区二模）如果圆O的半径为3，圆P的半径为2，且OP＝5，那么圆O和圆P的位置关系是 ．

5．（2019•天桥区一模）如图，在3×3的方格纸中，每个小方格都是边长为l的正方形，点O，A，B均为格点，则的长等于 ．

6．（2019•青羊区模拟）如图，矩形ABCD中，AB＝8，BC＝4，以CD为直径的半圆O与AB相切于点E，连接BD，则阴影部分的面积为

．（结果保留π）

7．（2019•江北区模拟）如图，在直角三角形△ABC中，∠BAC＝90°，点E是斜边BC的中点，⊙O经过A、C、E三点，F是弧EC上的一个点，且∠B＝24°，则∠AFC＝ ．

8．（2019•延庆区一模）如图，⊙O的直径AB垂直于弦CD，垂足是E，已知∠A＝22.5°，OC＝2，则CD的长为 ．

9．（2019•金山区二模）一个正多边形的对称轴共有10条，且该正多边形的半径等于4，那么该正多边形的边长等于 ．

10．（2019•路桥区一模）如图，点B，C，F在⊙O上，∠C＝18°，BE是⊙O的切线，B为切点，OF的延长线交BE于点E，则∠BEO＝ 度．

11．（2019•香坊区一模）如图，AB是⊙O的直径，AT是⊙O的切线，∠ABT＝50°，BT交⊙O于点C，E是AB上一点，延长CE交⊙O于点D，则∠CDB的度数是

滚动小专题(八) 三角形的外心与内心

类型1 三角形外心

1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)

A．△ABC内 B．△ABC外 C．BC边中点 D．AC边中点

2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)

A．D点 B．E点 C．F点 D．G点

3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)

A．O是△CEF的外心 B．O是△CFG的外心

C．O是△OAC的外心 D．O是△CDE的外心

4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)

A．△ABD B．△BCD C．△ACD D．△ADE

5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)

A．线段HF的中点处 B．△GHE的外心处

C．△HEF的外心处 D．△GEF的外心处

6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C)

A．11 cm B．12 cm C．13 cm D．14 cm

7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．

39第7章圆之三角形的内切圆

一、单项选择题

1．假设RtABC的外接圆半径为R,内切圆半径为r,那么其内切圆的面积与RtABC的面积比为〔 〕

A．22rrRB．2rRrC．42rRrD．4rRr

【答案】B

【分析】画好符合题意的图形,由切线长定理可得：,,,CECFrAEAGmBFBGn结合勾股定理可得：22,mnRrr再求解直角三角形的面积21==22ACBSmrnrRrr,从而可得直角三角形的内切圆的面积与直角三角形的面积之比．

【详解】解：如图,由题意得：902ACBABR，，

111OEOFOGr,

由切线长定理可得：

,,,CECFrAEAGBFBG

设,,AEAGmBFBGn

222mrnrmn,2,mnR

2mnmnrr,

22,mnRrr

而211=+22ACBSmrnrmnmrnrr 221=222RrrRrr

2=2Rrr

122.22OABCSrrSRrrRr

应选B．

【点评】此题考查的是三角形的内切圆与三角形的外接圆,切线长定理,勾股定理的应用,掌握以上知识是解题的关键．

2．如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是DF上一点,那么∠EPF的度数是〔 〕

A．65°B．60°C．58°D．50°

【答案】B

【分析】连接OE,OF．求出∠EOF的度数即可解决问题．

【详解】解：如图,连接OE,OF． ∵⊙O是△ABC的内切圆,E,F是切点,

∴OE⊥AB,OF⊥BC,

∴∠OEB=∠OFB=90°,

∵△ABC是等边三角形,

∴∠B=60°,

∴∠EOF=120°,

∴∠EPF=12∠EOF=60°,

应选：B．

【点评】此题考查三角形的内切圆与内心,切线的性质,圆周角定理等知识,解题的关键是熟练掌握根本知识,属于中考常考题型．

初三数学复习计划精选10篇

时间的脚步是无声的，它在不经意间流逝，我们又将续写新的诗篇，展开新的旅程，此时此刻需要制定一个详细的计划了。拟起计划来就毫无头绪？下面是美丽的小编帮大家整理的初三数学复习计划精选10篇。

初三数学复习计划 篇一

中考的数学复习分为五轮进行。

一轮：(3月1日——4月1日)分册复习

1、在认真研究20__年考试复习大纲，摸清初中数学内容的脉络，开展基础知识系统复习。主要以课本分册复习，一章一单元过关，使知识系统化，练习专题化，专题规律化。通过典型的实例、习题讲解让学生掌握学习方法，对例、习题能举一反三，触类旁通。同时并定期检测，定期检查学生完成的作业。对于作业、练习、测验中的问题，采用集中讲授和个别辅导相结合，因材施教，全面提高复习效率。

第二轮：(4月2日——5月1日)按复习资料复习

按照所订的复习资料复习，从数与代数、空间与图形、统计与概率、实践与综合应用等25讲的内容进行系统的复习。如在复习统计与概率时，将统计与概率的有关知识按照课本要求中的识记、理解、运用整理出来，然后以课本进行基础知识系统复习。

第三轮：(5月2日——5月28日)专题复习

专题复习的主要目的是为了将一轮、第二轮复习知识点、线结合，交织成知识网，注重与现实的联系，以达到能力的培养和提高。“专题复习”我们按照中考题型分为“填空、选择题”、“商品经济问题”“阅读材料题”、“开放性题”等。同时还要根据历年中考试卷命题的特点，精心选择一些新颖的、有代表性的题型进行专题训练。

第四轮：(5月29日——6月14日)强化练习

从近年来的中考卷中选题，编制与中考数学试题完全接轨的、符合新课改标准及命题特点和规律的、高质量的模拟试卷进行训练，每份的练习要求学生独立完成，老师要及时批改，重点讲评，讲解时要善于引导学生自己去发现规律、问题，使学生在主动学习中去体会，感悟概念、定理和规律。

最新教案、学案、试题、试卷精选资料

第20讲:直角三角形与勾股定理

一、复习目标

（1）掌握判定直角三角形全等的条件和直角三角形的性质。

（2）掌握角平分线性质的逆定理。

（3）掌握勾股定理及其逆定理。

二、课时安排

1课时

三、复习重难点

直角三角形的性质和判定，勾股定理及其逆定理，直角三角形全等的判定及其应用。

四、教学过程

（一）知识梳理

直角三角形的概念、性质与判定

定义 有一个角是________的三角形叫做直角三角形

性质 (1)直角三角形的两个锐角互余

(2)在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于___________

(3)在直角三角形中，斜边上的中线等于________________

判定 (1)两个内角互余的三角形是直角三角形

(2)一边上的中线等于这边的一半的三角形是直角三角形

拓展 (1)SRt△ABC＝12ch＝12ab，其中a、b为两直角边，c为斜边，h为斜边上的高；(2)Rt△ABC内切圆半径r＝a＋b－c2，外接圆半径R＝c2，即等于斜边的一半

勾股定理及逆定理

勾股定理 直角三角形两直角边a、b的平方和，等于斜边c的平方．即：________ 最新教案、学案、试题、试卷精选资料

勾股定理

的逆定理 逆定理

如果三角形的三边长a、b、c有关系： ________ ，那么这个三角形是直角三角形

用途 (1)判断某三角形是否为直角三角形；

(2)证明两条线段垂直；

(3)解决生活实际问题

互逆命题

互逆命题 如果两个命题的题设和结论正好相反，我们把这样的两个命题叫做互逆命题，如果我们把其中一个叫做______，那么另一个叫做它的______

互逆定理 若一个定理的逆定理是正确的，那么它就是这个定理的________，称这两个定理为互逆定理

命题、定义、定理、公理

定义 在日常生活中，为了交流方便，我们就要对名称和术语的含义加以描述，作出明确的规定，也就是给他们下定义

襄垣县五阳矿中学九年级数学中考复习（教）学案

课题 第29讲 图形的轴对称 班级 姓名 组别

1．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做__轴对称图形__，这条直线就是它的__对称轴__．把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做__对称轴__，折叠后重合的点是对应点．

2．图形轴对称的性质

如果两个图形关于某条直线对称，那么对称轴是任意一对对应点所连线段的__垂直平分线__．轴对称图形的对称轴，是任意一对对应点所连线段的__垂直平分线__．对应线段、对应角__相等__．

3．由一个平面图形可以得到它关于一条直线l对称的图形，这个图形与原图形的形状、大小完全一样；新图形上的每一点，都是原图形上的某一点关于直线l的对称点；连接任意一对对应点的线段被对称轴__垂直平分__．这样，由一个平面图形得到它的轴对称图形叫做__轴对称变换__．一个轴对称图形可以看作以它的一部分为基础，经轴对称变换而成．

4．几何图形都可以看作由点组成，只要分别作出这些点关于对称轴的对应点，再连接这些对应点，就可以得到原图形的轴对称图形；对于一些由直线、线段或射线组成的图形，只要作出图形中的一些特殊点(如线段的端点)，连接这些对称点，就可以得到原图形的轴对称图形．

5．常见的轴对称图形：等腰三角形，等边三角形，矩形，菱形，正方形，正多边形，圆等． 轴对称与轴对称图形

轴对称图形和图形的轴对称之间的的区别是：轴对称图形是一个具有特殊性质的图形，而图形的轴对称是说两个图形之间的位置关系；两者之间的联系是：若把轴对称的两个图形视为一个整体，则它就是一个轴对称图形；若把轴对称图形在对称轴两旁的部分视为两个图形，则这两个图形就形成轴对称的位置关系．因此，它们是部分与整体、形状与位置的关系，是可以辩证地互相转化的．

失误与防范

(1)判断图形是否是轴对称图形，关键是理解、应用轴对称图形的定义，看是否能找到至少1条合适的直线，使该图形沿着这条直线对折后，两旁能够完全重合；若能找到，则是轴对称图形，若找不到则不是．

2

3

图形的性质——圆1

一．选择题（共8小题）

1．如图，正方形ABCD的边AB=1，和都是以1为半径的圆弧，则无阴影两部分的面积之差是（ ）

A． B．1﹣ C．﹣1 D．1﹣

2．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（ ）

A．cm B．cm C．cm或cm D．cm或cm

3．如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ）

A．2 B．4 C．6 D．8

4．如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（ ）

A．4 B． C． D． 2

3 5．已知⊙O的面积为2π，则其内接正三角形的面积为（ ）

A．3 B．3 C． D．

6．如图，半径为3的⊙O内有一点A，OA=，点P在⊙O上，当∠OPA最大时，PA的长等于（ ）

A． B． C．3 D．2

7．在△ABC中，AB=AC=5，sinB=，⊙O过点B、C两点，且⊙O半径r=，则OA的长为（ ）

A．3或5 B．5 C．4或5 D．4

8．如图，B，C，D是半径为6的⊙O上的三点，已知的长为2π，且OD∥BC，则BD的长为（ ）

A．3 B．6 C．6 D．12

二．填空题（共7小题）

9．如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面积是 _________ ．

10．正六边形的中心角等于

_________ 度．

11．如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A=65°，则∠DOE= _________ ． 2

3

12．如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为