中考数学复习讲义课件 中考考点解读 第六单元 圆 第25讲 与圆有关的计算

百度文库，精选试题

试题习题，尽在百度 与圆有关的位置关系

1．已知⊙O的半径是6 cm、点O到同一平面内直线l的距离为5 cm、则直线l与⊙O的位置关系是(A )

A．相交 B．相切 C．相离 D．无法判断

2．(2016·泉州)如图、AB和⊙O相切于点B、∠AOB＝60°、则∠A的大小为( B )

A．15° B．30° C．45° D．60°

3．(2015·泸州)如图、PA、PB分别与⊙O相切于A、B两点、若∠C＝65°、则∠P的度数为( C )

A．65° B．130° C．50° D．100°

4．(2016·同安区一模)在Rt△ABC中、∠A＝90°、BC＝10、D为BC的中点、当⊙A半径为6时、则D点与⊙A位置关系为( B )

A．圆上 B．圆内 C．圆外 D．以上三种都有可能

5．(2016·潍坊)如图、在平面直角坐标系中、⊙M与x轴相切于点A(8、0)、与y轴分别交于点B(0、4)和点C(0、16)、则圆心M到坐标原点O的距离是( D )

A．10 B．82 C．413 D．241

6．(2016·荆州)如图、过⊙O外一点P引⊙O的两条切线PA、PB、切点分别是A、B、OP交⊙O于点C、点D是优弧ABC︵上不与点A、点C重合的一个动点、连接AD、CD、若∠APB＝80°、则∠ADC的度数是( C )

A．15° B．20° C. 25° D．30°

7．(2016·合肥高新区一模)如图、在⊙O中、AB为直径、BC为弦、CD为切线、连接OC.若∠BCD＝50°、则∠AOC的度数为80°．

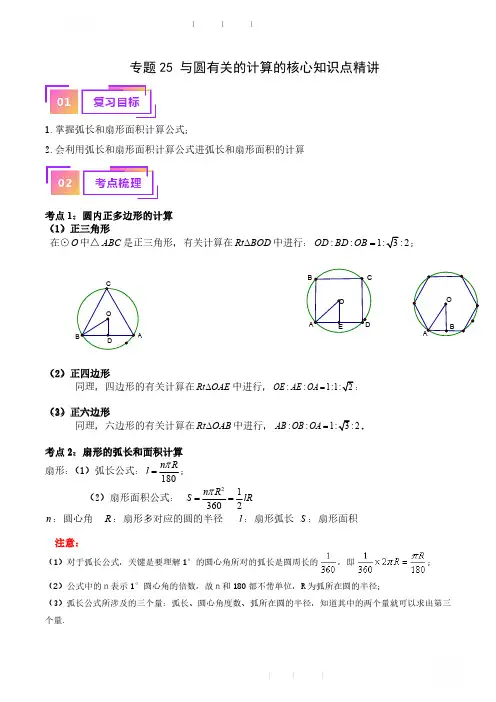
专题25 与圆有关的计算的核心知识点精讲

1.掌握弧长和扇形面积计算公式；

2.会利用弧长和扇形面积计算公式进弧长和扇形面积的计算考点1：圆内正多边形的计算（1）正三角形

在⊙O中△ABC是正三角形，有关计算在RtBODD

中进行：::1:3:2ODBDOB=；（2）正四边形

同理，四边形的有关计算在

RtOAED

中进行，

::1:1:2OEAEOA=：（3）正六边形

同理，六边形的有关计算在RtOABD

中进行，

::1:3:2ABOBOA=.考点2：扇形的弧长和面积计算

扇形：（1）弧长公式：

180nR

lp

=； （2）扇形面积公式：2

1

3602nR

SlRp

==

n：圆心角 R：扇形多对应的圆的半径 l：扇形弧长S：扇形面积

注意：

（1）对于弧长公式，关键是要理解1°的圆心角所对的弧长是圆周长的；　

（2）公式中的ｎ表示1°圆心角的倍数，故ｎ和180都不带单位，R为弧所在圆的半径；

（

3

）弧长公式所涉及的三个量：弧长、圆心角度数、弧所在圆的半径，知道其中的两个量就可以求出第三

个量

.

长的

，即即；

DC

BAO

EC

B

ADO

B

AO

(4)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的

(5)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就

可以求出第三个量.考点3：扇形与圆柱、圆锥之间联系

1、圆柱：

（1）圆柱侧面展开图

2SSS=+

侧表底=2

22rhrpp

+

（2）圆柱的体积：2

Vrhp

=

2、圆锥侧面展开图

（1）SSS=+

侧表底=2

Rrrpp

+

（2）圆锥的体积：21

3Vrhp

=

注意：圆锥的底周长

=扇形的弧长（

180r2RnΠ

Π=

）【题型1：正多边形和圆的有关计算】

【典例1】（2023•福建）我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆

的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少．割之又割，以至于不可割，则

与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率π的近似值为

九种题型答题模板

1.线段、角的计算与证明问题 中考的解答题一般是分两到三部分的。

第一部分基本上都是一些简单题或者中档题，目的在于考察基础。

第二部分往往就是开始拉分的中难题了。对这些题轻松掌握的意义不仅仅在于获得分数，更重要的是对于整个做题过程中士气，军心的影响。

线段与角的计算和证明，一般来说难度不会很大，只要找到关键“题眼”，后面的路子自己就“通”了。

2.图形位置关系中学数学当中，图形位置关系主要包括点、线、三角形、矩形/正方形以及圆这么几类图形之间的关系。

在中考中会包含在函数，坐标系以及几何问题当中，但主要还是通过圆与其他图形的关系来考察，这其中最重要的就是圆与三角形的各种问题。

3.动态几何从历年中考来看，动态问题经常作为压轴题目出现，得分率也是最低的。

动态问题一般分两类，一类是代数综合方面，在坐标系中有动点，动直线，一般是利用多种函数交叉求解。

另一类就是几何综合题，在梯形，矩形，三角形中设立动点、线以及整体平移翻转，对考生的综合分析能力进行考察。

所以说，动态问题是中考数学当中的重中之重，只有完全掌握，才有机会拼高分。

4.一元二次方程与二次函数在这一类问题当中，尤以涉及的动态几何问题最为艰难。几何问题的难点在于想象，构造，往往有时候一条辅助线没有想到，整个一道题就卡壳了。01相比几何综合题来说，代数综合题倒不需要太多巧妙的方法，但是对考生的计算能力以及代数功底有了比较高的要求。

中考数学当中，代数问题往往是以一元二次方程与二次函数为主体，多种其他知识点辅助的形式出现的。一元二次方程与二次函数问题当中，纯粹的一元二次方程解法通常会以简单解答题的方式考察。

但是在后面的中难档大题当中，通常会和根的判别式，整数根和抛物线等知识点结合。

5.多种函数交叉综合问题初中数学所涉及的函数就一次函数，反比例函数以及二次函数。这类题目本身并不会太难，很少作为压轴题出现，一般都是作为一道中档次题目来考察考生对于一次函数以及反比例函数的掌握。所以在中考中面对这类问题，一定要做到避免失分。

人教版六年级数学上册第六单元教案

六年级数学上册第六单元教案1

教学目标

1、使学生理解圆的周长和圆周率的意义，理解并掌握圆的周长公式，并能

正确计算圆周长。

2、培养学生的观察、比较、概括和动手操作的能力。

3、对学生进行爱国主义教育。

教学重难点

圆的周长和圆周率的意义，圆周长公式的推导过程。

教学工具

课件

教学过程

一、创设情境，导入新课。

1、出示花坛图。

问：你能量出花坛外沿的长度吗?

2、出示大树图。

问：你有办法量出大树干一圈的长度吗?

3、出示飞机图。

问：这个圆的周长如何测量呢?

二、圆周长的公式推导。

1、探索学习。

(1)你可以用什么办法知道一个圆的周长是多少?

(2)学生各抒己见，分别讨论说出自己的方法：

A、“滚动”--把实物圆沿直尺滚动一周;

B、“缠绕”--用绸带缠绕实物圆一周并打开;

C、“折叠”--把圆形纸片对折几次，再进行测量和计算; 用滚动，绳测的方法可测量出圆的周长，但是有局限性。今天我们来探讨出一种求圆周长的普遍规律。

2、动手实践。

(1)4人小组，分别测量学具圆，报出自己量得的直径，周长，并计算周长和直径的比值。

(2)引生看表，问你们看周长与直径的比值有什么关系?

(3)你有办法验证圆的周长总是直径的3倍多一点吗?

(4)阅读课本P63,介绍圆周率，及介绍祖冲之。

3、解决新问题。

(1)教学例1:圆形花坛的直径是20m,它的周长是多少米?小自行车车轮的直径是50m,绕花坛一周车轮 大约转动多少周?

第一个问题： 已知 d = 20米 求：C = ?

第 1 页 共 8 页

六年级数学上第一单元圆教案教学的反思（通用14篇）

六年级数学上第一单元圆教案教学的反思 1

本单元是在学生已经直观地认识了圆的基础上，进一步了解圆各部分的名称，认识圆的轴对称特征，然后继续探究圆的周长计算公式及圆的面积计算公式，为今后圆柱和圆锥的认识、圆柱的表面积与体积计算、圆锥的体积计算打下基础。

圆是小学阶段要学习的最后一个平面图形，与之前学习的由线段围成的平面图形有所不同，在探究周长计算公式的过程中，渗透着“化曲为直”的数学转换思想；在探究圆的面积计算公式的过程中，除了渗透转换的数学思想外，还涉及了极限的数学思想的渗透。

同时“圆周率的历史”的介绍是很好的德育教材，有助于增强学生的民族自豪感，要充分发挥学科的整合教育功能。本单元学习的'内容主要是圆的认识（一）、圆的认识（二）、欣赏与设计、圆的周长、圆周率的历史、圆的面积。

六年级数学上第一单元圆教案教学的反思 2

教材分析

圆的面积是在初步认识了圆，学习了圆的周长，以及学过几种常见直线几何图形面积的基础上进行的。学生从学习直线图形的面积，到学习曲线图形的面积，不论是内容本身还是研究方法，都是一次质的飞跃。学生掌握了圆面积的计算，不仅能解决简单的实际问题，因为以后学习圆柱、圆锥的知识打下基础。学生已有了平面几何图形的经验，知道运用转化的思想研究新的图形的面积，在学习中要鼓励学生大胆现象、勇于实践。在操作中将圆转化为已学过的平面图形，从中找到圆的.面积与半径、直径的关系。

学情分析

学生从认识直线图形发展到认识曲线图形，是一次飞跃，但是从学生思维特点的角度看，六年级学生以抽象思维为主，已具有一定的逻辑思维能力，已经有了许多机会接触到数与计算、空间图形等较丰富的数学内容，已经具备了初步的归纳、类比、推理的数学经验，并具有了转化的数学思想。所以在教学中应注意联系现实生活，组织学生利用学具开展探究性的数学活动，注重知识

第63页第11讲圆的面积【知识要点】【例题精讲】例题1：在一个边长为10厘米的正方形纸板里剪出一个最大的圆，剩下的面积是多少平方厘米？【举一反三】1.一只羊被拴在草地中央的一棵树上，已知拴羊的绳子长5米，这只羊最多能吃到多少平方米范围内的草？2.一张长方形纸片，长60厘米，宽40厘米。用这张纸剪下一个尽可能大的圆。这个圆的面积是多少平方厘米？剩下的面积是多少平方厘米？例题2：将一个圆剪拼成一个近似长方形（如下图），已知这个近似长方形的周长是16.56分米，求圆的面积。【举一反三】1.某小区沿着一面墙修建一个花坛（如图），量得围花坛的护栏长28.26

米，求圆的面积，首先要明确的圆的面积的计算公式如果用S表示圆的面积，则圆的面积为2rS（其中≈3.14，r是圆的半径），对于一些比较复杂的组合图形，有时直接分解有一定的困难，这时，可以通过把其中的部分图形进行平移、翻折或旋转，化难为易。第64

页这个花坛的占地面积是多少平方米？（得数保留一位小数）2.在草地中央有一个长20米，宽10米的建筑物。在建筑物的一角拴着一只羊（如图）。已知拴羊的绳子长30米，这只羊最多能吃到多少平方米范围内的草？例题3：已知正方形的面积为12平方厘米，求下图阴影部分的面积。【举一反三】1.求下面图形的阴影部分面积。（单位：分米）2.图中ABCD是边长为4米的正方形，分别以AB、BC、CD、AD为直径画半圆，求这四个半圆弧所围成的阴影部分的面积。例题4：一根铁丝长37.68米，在一根圆形木棒上正好绕200圈，木棒横截面的面积是多少平方厘米？第65页【举一反三】1.一根绳子长64.8米，在一棵大树的树干上绕了10圈后还余2米。这棵树树干的横截面面积是多少？2.把一只羊拴在一块长8m，宽6m的长方形草地上，拴羊的绳长2m，那么这只羊吃到草的最大面积是多少平方米？如果要使羊吃草的面积最小，应该将羊拴在这个长方形草地的什么位置？例题5：两个圆的周长之比是3∶2，面积之差是10平方厘米，两个圆的面积之和是多少？【举一反三】1.已知甲圆的半径长等于乙圆的直径长，且它们的面积之和是100平方厘米，那么甲圆的面积是多少？2.大小两个圆的面积之比是9：1，周长相差25.12厘米，大小两个圆的面积之和是多少平方厘米？例题6：在一个圆形喷水池的周长是62.8米，绕着这个水池修一条宽2米的水泥路。求路面的面积。【举一反三】1.校园内要修建一个直径是8米的圆形花坛，在花坛的外面铺设一条宽2米的第66

九种题型答题模板

1.线段、角的计算与证明问题

中考的解答题一般是分两到三部分的。

第一部分基本上都是一些简单题或者中档题，目的在于考察基础。

第二部分往往就是开始拉分的中难题了。对这些题轻松掌握的意义不仅仅在于获得分数，更重要

的是对于整个做题过程中士气，军心的影响。

线段与角的计算和证明，一般来说难度不会很大，只要找到关键“题眼”，后面的路子自己就“通”

了。

2.图形位置关系

中学数学当中，图形位置关系主要包括点、线、三角形、矩形/正方形以及圆这么几类图形之间的

关系。

在中考中会包含在函数，坐标系以及几何问题当中，但主要还是通过圆与其他图形的关系来考

察，这其中最重要的就是圆与三角形的各种问题。

3.动态几何

从历年中考来看，动态问题经常作为压轴题目出现，得分率也是最低的。

动态问题一般分两类，一类是代数综合方面，在坐标系中有动点，动直线，一般是利用多种函数

交叉求解。

另一类就是几何综合题，在梯形，矩形，三角形中设立动点、线以及整体平移翻转，对考生的综

合分析能力进行考察。

所以说，动态问题是中考数学当中的重中之重，只有完全掌握，才有机会拼高分。

4.一元二次方程与二次函数

在这一类问题当中，尤以涉及的动态几何问题最为艰难。几何问题的难点在于想象，构造，往往

有时候一条辅助线没有想到，整个一道题就卡壳了。

相比几何综合题来说，代数综合题倒不需要太多巧妙的方法，但是对考生的计算能力以及代数功

底有了比较高的要求。

中考数学当中，代数问题往往是以一元二次方程与二次函数为主体，多种其他知识点辅助的形式

出现的。一元二次方程与二次函数问题当中，纯粹的一元二次方程解法通常会以简单解答题的方

式考察。

但是在后面的中难档大题当中，通常会和根的判别式，整数根和抛物线等知识点结合。

5.多种函数交叉综合问题01

初中数学所涉及的函数就一次函数，反比例函数以及二次函数。这类题目本身并不会太难，很少

作为压轴题出现，一般都是作为一道中档次题目来考察考生对于一次函数以及反比例函数的掌

【 导语】中考数学即使数学成绩⾮常好的同学也有这样的担忧，害怕在中考数学之中会遇到偏题，怪题。很多同学，数学成绩也不差，可就是“虚”。⽣怕在中考之中会出现⾃⼰解答不了的题型，⾃⼰还没有认真摸透的数学知识点。下⾯⽆忧考整理了初⼀数学所有题型的考试技巧，⼀起看看吧。

⼀、选择题的解法

1、直接法：根据选择题的题设条件，通过计算、推理或判断，，最后得到题⽬的所求。

2、特殊值法：（特殊值淘汰法）有些选择题所涉及的数学命题与字母的取值范围有关；

在解这类选择题时，可以考虑从取值范围内选取某⼏个特殊值，代⼊原命题进⾏验证，然后淘汰错误的，保留正确的。

3、淘汰法：把题⽬所给的四个结论逐⼀代回原题的题⼲中进⾏验证，把错误的淘汰掉，直⾄找到正确的答案。

4、逐步淘汰法：如果我们在计算或推导的过程中不是⼀步到位，⽽是逐步进⾏，既采⽤“⾛⼀⾛、瞧⼀瞧”的策略；

每⾛⼀步都与四个结论⽐较⼀次，淘汰掉不可能的，这样也许⾛不到最后⼀步，三个错误的结论就被全部淘汰掉了。

5、数形结合法：根据数学问题的条件和结论之间的内在联系，既分析其代数含义，⼜揭⽰其⼏何意义；

使数量关系和图形巧妙和谐地结合起来，并充分利⽤这种结合，寻求解题思路，使问题得到解决。

⼆、常⽤的数学思想⽅法

1、数形结合思想：就是根据数学问题的条件和结论之间的内在联系，既分析其代数含义，⼜揭⽰其⼏何意义；

使数量关系和图形巧妙和谐地结合起来，并充分利⽤这种结合，寻求解体思路，使问题得到解决。

2、联系与转化的思想：事物之间是相互联系、相互制约的，是可以相互转化的。数学学科的各部分之间也是相互联系，可以相互转化的。

在解题时，如果能恰当处理它们之间的相互转化，往往可以化难为易，化繁为简。

如：代换转化、已知与未知的转化、特殊与⼀般的转化、具体与抽象的转化、部分与整体的转化、动与静的转化等等。 3、分类讨论的思想：在数学中，我们常常需要根据研究对象性质的差异，分各种不同情况予以考查；

第五单元 圆

【例1】一个圆的半径增加1厘米，它的周长就增加（ ）。 A.1厘米 B.2厘米 C.6.28厘

米 D.3.14厘米 解析：本题考查的知识点是圆的半径变化引起圆的周长变化的规律。解答时，根

据圆的周长公式为计算出圆的半径增加1厘米，

则，它的周长会增加厘米， 即6.28厘米，所以选C。

解答：C 【例2】妈妈要买一块台布盖住家中一张直径1米的圆形桌面，你认为选（ ）比较合适。 A.120厘米×120厘米 B.3140平方厘米 C.120厘米×80厘米 D.785平方厘

米

解析：本题考查的知识点是利用圆的知识解决实际问题。因为是一张直径1米的

圆形桌面，所以台布的边长应大于1米。选项中只有120厘米×120厘米的桌布符合要求，该题错误的做法是计算桌面的面积。

解答：A 【例3】计算下图的周长和面积。

要点提示 圆的半径增加a厘米，则圆的周长增加2a厘米。 解析：本题考查的知识点是利用“转化法”解答不规则图形的周长和面积。解答不

规则图形的周长时，可以把不规则的图形转化为大圆的周长的一半+小圆的周长，

这样根据圆的周长计算方法列式计算为3.14×10+3.14×10=20×3.14=62.8（厘米）；计算不规则图形的面积时，可以把不规则图形通过翻转、平移转化为一个

半圆，这样不规则图形的面积列式计算为3.14×102÷2=157（平方厘米）。 解答:

周长:3.14×10+3.14×10=20×3.14=62.8（厘米）

面积：3.14×102÷2=157（平方厘米） 【例4】有一个面积为700平方米的圆形草坪，要为它安装自动旋转喷灌装置进

行喷灌。现有射程为20米、15米、10米的三种装置，你认为选哪种比较合适？安装在什么位置？

解析：本题考查的知识点是圆的认识和面积计算。解答时，先要明确射程的含义，

即为圆的半径。已知的半径长度，分别求出可以喷灌的面积，再和给出的圆的面

积相比较得出结果。

解答：1256（平方米），（平方米），（平方米），706.5平方米最接近圆形草坪的面积。

初中数学广东卷复习重点资料(总5页)

-CAL-FENGHAI.-(YICAI)-Company One1

-CAL-本页仅作为文档封面，使用请直接删除 广东省中考知识点分析

一、珠海卷和省卷的题型区别

题型 题量 分值 总分值

珠海卷 省卷 珠海卷 省卷 珠海卷 省卷

选择题 1——5（5） 1——10（10） 3分/题 3分/题 15 30

填空题 6——10（5） 11——16（6） 4分/题 4分/题 20 24

解答题（一） 11——15（5） 17——19（3） 6分/题 6分/题 30 18

解答题（二） 16——19（4） 20——22（3） 7分/题 7分/题 28 21

解答题（三） 20——22（3） 22——25（3） 9分/题 9分/题 27 27

二、历年考点分值分析

三、中考题型分析 2011 2012 2013 2014 2015

数与式 29 代数61 33 代数66 22 代数53 29 代数55 25 代数54

方程与不等式 13 17 19 14 13

函数 19 16 12 12 16

图形的认识 37 几何49 23 几何42 25 几何56 32 几何55 38 几何59

图形的变换 12 19 31 23 21

统计与概率 10 12 11 10 7

11 12 13 14 15

选择题（每小题3分） 1 倒数 绝对值 相反数 有理数的大小比较 绝对值

2 科学记法 科学记数法 三视图 轴对称图形和中心对称图形 科学计数法

3 图形的缩小 众数 科学记数法 合并同类项 中位数

4 概率 三视图 不等式的性质 分解因式 平行线，三角形外角

5 正八边形内角 三角形的三边关系 中位数 多边形的内角与外角 轴对称图形和中心对称图形

6 平行线的性质 概率公式 幂的乘方和积的乘方

7 负整数指数幂;同底数幂平行四边形的性质 有理数的大小比较

2021中考考点必杀500题

专练12（几何压轴题）（30道）

1．（2021·上海九年级二模）如图，在矩形ABCD中，4AB，8BC，点P在边BC上（点P与端点B、C不重合），以P为圆心，PB为半径作圆，圆P与射线BD的另一个交点为点E，直线CE与射线AD交于点G．点M为线段BE的中点，联结PM．设,BPxBMy．

（1）求y关于x的函数解析式，并写出该函数的定义域；

（2）联结AP，当//APCE时，求x的值；

（3）如果射线EC与圆P的另一个公共点为点F，当CPF为直角三角形时，求CPF的面积．

【答案】（1）255852yxx；（2）2144；（3）6

【分析】

（1）勾股定理求出BD长，利用三角函数求解析式，根据点P和点G的位置确定该函数的定义域；

(2) 设4EHk，则8,8,BHkPHkxPEx，根据勾股定理列方程即可；

(3)根据哪个角是直角分类讨论，利用勾股定理或相似三角形的性质列方程，求出直角边长即可．

【详解】

解：(1)由勾股定理，228445BD，

∵点M为线段BE的中点，

∵PM∵BE，

RtBMP中，8cos45BMCBDBP，解得255yx，

点P与端点C不重合，所以8x，当直线CE恰好经过A点时，

BE=12BD=25，5BM，52x，该函数的定义域为：582x．

（2）过点E作EHBC于点H，若CE//AP，可知ABEHBPHC

设4EHk，则8,8,BHkPHkxPEx

由勾股定理，可得222(4)(8)xkkx，解得5xk

所以44588kkk，解得42145k（负根舍去）

所以52144BPxk

（3）①若90PFC，由垂径定理，可知E、F重合，不符合题意；

②90PCF时，此时E与D重合，2224(8)xx，解得5x

所以13,4,3462CPFCPCFCDS

吉林省长春市2020年中考数学试卷

一、单选题（共8题；共16分）

1.如图，数轴上被墨水遮盖的数可能为（ ）

A. =1 B. -1.5 C. -3 D. -4.2

【答案】 C

【考点】数轴及有理数在数轴上的表示

【解析】【解答】解：根据题意可知，墨水遮盖区域的数在-4和-2之间

∴数字可能为-3.

故答案为：C.

【分析】根据数轴上有理数的大小和顺序进行判断即可。

2.为了增加青少年的校外教育活动场所，长春市将建成面积约为79000平方米的新少年宫，预计2020年12月正式投入使用．79000这个数用科学记数法表示为（ ）

A. 79×103 B. 7.9×104 C. 0.79×105 D. 4𝑎𝑏

【答案】 B

【考点】科学记数法—表示绝对值较大的数

【解析】【解答】解：79000用科学记数法表示为7.9×104

故答案为：B.

【分析】根据科学记数法的含义，表示得到数字即可。

3.下列图形是四棱柱的侧面展开图的是（ ）

A. B.

C. D.

【答案】 A

【考点】几何体的展开图

【解析】【解答】解：由分析知：四棱柱的侧面展开图是四个矩形组成的图形．

故选：A．

【分析】根据四棱柱的侧面展开图是矩形图进行解答即可．

4.不等式 𝑥+2≥3 的解集在数轴上表示正确的是（ ） A. B.

六年级数学上册《圆》的单元教学设计方案

一、单元整体教学意图

单元整合教学是以学生的认知基础和认知经验为基础，同时依据知识之间的内在关系，突出知识联系的主线和核心结构，将既定的教学内容或教学序列进行强调和整合，使教学内容更具有整体性和结构性，从而提高学生的学习效率和学习主动性，更好地促进学生数学能力发展和数学素养提高的教学方式。单元整体教学有助于培养学生的数学思维和数学能力，因为学生的学习不仅是理解、建构某一个知识，更主要的是发现与建立知识之间的联系，打通知识板块之间的壁垒，构建知识的群组及其脉络，更好地落实核心素养的培养，当下，单元整体教学设计是一种创新型研究教学，新课标一颁布，基于核心素养实施单元教学是新时代的必然趋势。当今的教育要聚焦中国学生发展核心素养，培养学生适应未来发展的正确价值观、必备品格和关键能力。对于数学这门学科，在形成人的理性思维、科学精神和促进个人智力发展中发挥着不可替代的作用，数学素养是现代社会每一个公民应当具备的基本素养，那么数学的核心素养就是培养学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。单元整合教学符合当今时代的创新教育方向，建立学生知识的贯通性、结构化，突出知识之间的本质联系和发展脉络，更有利于学生发现并感受数学知识的多维度关联和多角度解析。

二、单元内容

这一单元安排了“圆的认识”、“圆的周长”“圆的面积”、“扇形的认识”及综合实践活动“确定起跑线”，这四个内容由易到难，层层深入。圆是在学生认识了长方形、正方形、三角形等多种平面图形的基础上展开的，也是小学阶段认识的最后一种常见的平面图形。低年级教学中出现过圆，只是直观认识。从教材的编排体系可以看出，圆是一种曲线图形，而前面学习的是直线图形，圆的教学是学生认识曲线图形的开始。教材通过对圆的研究，渗透了曲线图形与直线图形的内在联系，体现了“化圆为方”、“化曲为直”的转化思想，“无限逼近”的极限思想，以及“等积变形”“对应”“转化”的数学思想。通过对圆的研究教学，让学生掌握圆的一些基础知识，感悟数学思想方法，加强学生的动手操作能力，培养学生良好的数学核心素养。

2020北京中考数学必备学科知识及高频考点

一、初中数学基本内容

1.“数与代数”的主要内容有：数的认识，数的表示，数的大小，数的运算，数量的估计；字母表示数，代数式及其运算；方程、方程组、不等式、函数等。

2.“图形与几何”的主要内容有：空间和平面基本图形的认识，图形的性质、分类和度量；图形的平移、旋转、轴对称、相似和投影；平面图形基本性质的证明；运用坐标描述图形的位置和运动。

3.“统计与概率”的主要内容有：收集、整理和描述数据，包括简单抽样、整理调查数据、绘制统计图表等；处理数据，包括计算平均数、中位数、众数、极差、方差等；从数据中提取信息并进行简单的推断；简单随机事件及其发生的概率。

4.“综合与实践”是一类以问题为载体、以学生自主参与为主的学习活动。在学习活动中，学生将综合运用“数与代数”“图形与几何”“统计与概率”等知识和方法解决问题。“综合与实践”的教学活动应当保证每学期至少一次，可以在课堂上完成，也可以课内外相结合。

二、《2019北京中考说明》中提出的初中学段目标要求

1.知识技能

（1）体验从具体情境中抽象出数学符号的过程，理解有理数、实数、代数式、方程、不等式、函数；掌握必要的运算（包括估算）技能；探索具体问题中的数量关系和变化规律，掌握用代数式、方程、不等式、函数进行表述的方法。

（2）探索并掌握相交线、平行线、三角形、四边形和圆的基本性质与判定，掌握基本的证明方法和基本的作图技能；探索并理解平面图形的平移、旋转、轴对称；认识投影与视图；探索并理解平面直角坐标系，能确定位置。

（3）体验数据收集、处理、分析和推断过程，理解抽样方法，体验用样本估计总体的过程；进一步认识随机现象，能计算一些简单事件的概率。

2.数学思考

（1）通过用代数式、方程、不等式、函数等表述数量关系的过程，体会模型的思想，建立符号意识；在研究图形性质和运动、确定物体位置等过程中，进一步发展空间观念；经历借助图形思考问题的过程，初步建立几何直观。

1 人教版六年级数学上册第五单元

《圆》教学设计

一、单元教学目标

1、使学生认识圆，知道圆各部分的名称；掌握圆的特征，理解直径和半径的相互关系。初步学会用圆规画圆。

2、通过分组学习，动手操作，主动探索等活动，初步培养学生的合作意识和创新意识，以及抽象、概括等能力，进一步发展学生的空间观念。

3、通过学习，提高学生对数学的好奇心与求知欲，认识数学与人类生活的密切联系，体验数学活动的意义和作用，感受数学的魅力。

二、单元重难点

教学重点：圆的各部分名称和特征，让学生初步学会用圆规画圆。

教学难点：使学生在推导圆的周长与面积的计算公式过程中体会和掌握转化、极限等数学思想，进一步发展数学思维能力和问题解决的能力。

三、教具学具

教具准备：圆规，三角板，课件，圆片。

学生学具：圆规，尺子，白纸，圆片等。

四、单元课时安排

本单元计划课时数：（12课时）

1.圆的认识……………………………………………2课时左右

2.圆的周长……………………………………………2课时左右

3.圆的面积……………………………………………5课时左右

4.扇形 ……………………………………………… 1课时左右

整理和复习……………………………………………2课时

确定起跑线……………………………………………1课时

第 1 课时 圆的认识

教学内容：教材第57—59页。

教学目标：

1.通过动手操作、观察、思考等教学活动,认识圆并掌握圆的特征。 2 2.让学生理解在同一圆内直径与半径的关系,学会用圆规画圆。

3.初步渗透化曲为直的数学方法和极限的数学思想。

教学重点:直观地认识圆的特征,学会用圆规画圆。

教学难点:明确圆心与圆的位置之间的关系,半径与圆的大小的关系。

教学过程 ：

一、创设情景，导入新课

1.介绍“神奇的圆”。

老师可以查阅一些资料。例如:圆是一种看来简单实际上却很神奇的图形。古代人最早是从太阳,阴历十五的月亮得到圆的概念。约一万八千年前的山顶洞人在兽牙上打的孔是圆的,他们还发现圆圆的木头可以滚动,搬动重物时可以省力;大约六千年前,美索不达米亚人制成了第一个轮子;大约四千年前,人们发明了车子。古埃及人认为圆是神赐予的。我国古代伟大的思想家墨子在描述圆时说到“一中同长也”,也就是说圆有一个圆心,圆心到圆周的长都相等。

2021年广东省中考数学试卷分析

发布时间：2022-01-13T05:49:16.164Z 来源：《中小学教育》2021年11月31期 作者： 陈海祥

[导读] 2021年的广东省中考数学考试全卷满分120分，考试时间为90分钟

陈海祥

广东省博罗县园洲中学 516123

一、试卷整体评析

2021年的广东省中考数学考试全卷满分120分，考试时间为90分钟，共25题。题型分为10道选择题（每小题3分，共30分），7道填空题（每小题4分，共28分），3道解答题（一）（每小题6分，共18分），3道解答题（二）（每小题8分，共24分），2道解答题（三）（每小

题10分，共20分）。

试卷总体保持稳定，稳中有变，变中有新。中等难度题目增加，计算量加大，注重初高中衔接，对学生的动手作图能力和综合能力要求增大，知识面覆盖广，试题难易区分度明显，试卷难度总体有所提升。试卷突出特点是在考查知识与技能、过程与方法的同时，重视对

学生的数学素养的考查，注重了考查学生对数学思想方法的领悟和数学思维能力的达成水平，考试内容上更体现了基础性、开放性、新颖

性、应用性、探究性和综合性。命题实现了由“知识立意”向“能力立意”的过渡，体现了中考作为升学和选拔的双重功能，对初中数学教与

学有较强的导向性。

二、2021年广东省中考数学知识板块分布

三、近三年广东省中考数学知识模块分值对比

四、近三年广东省中考数学知识考点对比

年

份

题目2019年2020年2021年

第1题绝对值相反数实数比较大小第2题科学记数法中位数科学记数法

第3题三视图关于x轴、y轴对称的点的坐标概率计算

第4题整式运算多边形内角与外角幂的运算性质

第5题对称图形（轴对称、中心对称）二次根式有意义的条件绝对值与二次根式的非负性

第6题中位数三角形中位线定理正方形展开图

第7题实数（绝对值、数轴）二次函数图象与几何变换圆的简单计算

第8题二次根式解一元一次不等式组实数的小数部分和整数部分