节点电压法

09379090 葛佳音一、节点电压：指独立节点对非独立节点的电压。

二、基本指导思想用未知的节点电压代替未知的支路电压来建立电路方程，以减少联立方程的元数。

三、步骤应用基尔霍夫电流定律建立节点电流方程，然后用节点电压去表示支路电流，最后求解节点电压。

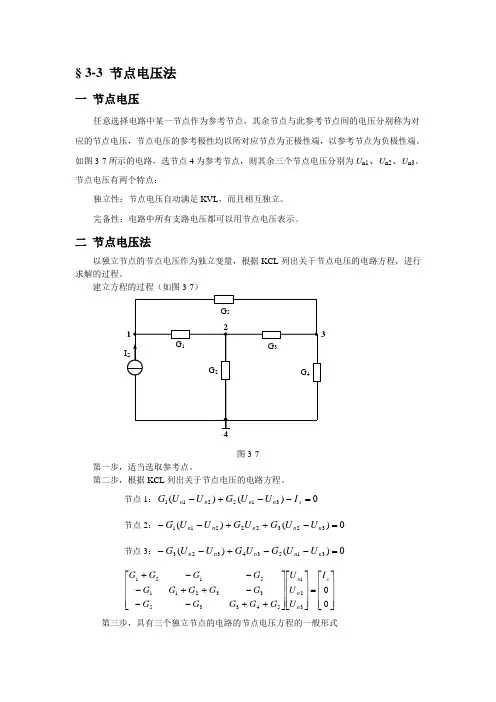
具体如下：1、选择参考节点，设独立节点电位选定参考节点和各支路电流的参考方向，并对独立节点分别应用基尔霍夫电流定律列出电流方程2、根据基尔霍夫电压定律和欧姆定律，建立用节点电位和已知的支路电阻表示支路电流的支路方程3、将支路方程和节点方程相结合，消去节点方程中的支路电流变量，代之以节点电位变量，经移项整理后，获得以两节点电位为变量的节点方程4、解方程得节点电位5、由节点电位求支路电压，进而求支路电流四、P74 例3.1应注意的细节：1、假设参考节点的原因：电压是指电路中两点A、B之间的电位差。

所以，由选取节点的电位可以表示支路电压。

2、不用考虑V1、V2谁大谁小。

可任意设一个电流方向。

但为减少出错，R2上的电流若写成（V1-V2）/R2，则默认R2上的电流朝向节点2。

3、不用考虑串并联。

这也是节点电压法的一大优势。

4、电路图中是电流源（不是电流表）。

***电流源（符号如下图）：R→∞电流源的内阻相对负载阻抗很大，负载阻抗波动不会改变电流大小。

在电流源回路中串联电阻无意义，因为它不会改变负载的电流，也不会改变负载上的电压。

在原理图上这类电阻应简化掉。

负载阻抗只有并联在电流源上才有意义，与内阻是分流关系。

***电压源（如下图）：R→0稳博电压源电压源就是给定的电压，随着你的负载增大，电流增大，理想状态下电压不变，实际会在传送路径上消耗，你的负载增大，消耗增多。

电压源的内阻相对负载阻抗很小，负载阻抗波动不会改变电压高低。

在电压源回路中串联电阻才有意义，并联在电压源的电阻因为它不能改变负载的电流，也不能改变负载上的电压，这个电阻在原理图上是多余的，应删去。

负载阻抗只有串联在电压源回路中才有意义，与内阻是分压关系。

节点电压法.一、节点电压方程出发点进一步减少方程数，用未知的节点电压代替未知的支路电压来建立方程。

图3.2-1电路共有4个节点、 6条支路（把电流源和电导并联的电路看成是一条支路）。

用支路电流法计算，需列写6个独立的方程选取节点d为参考点，d点的电位为，则节点a、b、c为独立的节点，它们与d 点之间的电压称为各节点的节点电压（node voltage），实际上就是各点的电位。

这样a、b、c的节点电压是。

各电导支路的支路电流也就可用节点电压来表示结论：用3个节点电压表示了6个支路电压。

进一步减少了方程数。

1、节点电压方程根据KCL，可得图3.2-1电路的节点电压方程节点电压方程的一般形式自电导×本节点电压－Σ（互电导×相邻节点电压）= 流入本节点的所有电流源的电流的代数和自电导（self conductance）是指与每个节点相连的所有电导之和，互电导（mutual conductance）是指连接两个节点之间的支路电导。

节点电压法分析电路的一般步骤确定参考节点，并给其他独立节点编号。

列写节点电压方程，并求解方程，求得各节点电压。

由求得的节点电压，再求其他的电路变量，如支路电流、电压等。

例3.2-1 图3.2-1所示电路中，G1=G2=G3=2S，G4=G5=G6=1S，，，求各支路电流。

解：1. 电路共有4个节点，选取d为参考点，。

其他三个独立节点的节点电压分别为。

2. 列写节点电压方程节点a：节点b：节点c：代入参数，并整理，得到解方程，得3. 求各支路电流特别注意：节点电压方程的本质是KCL，即Σ(流出电流) =Σ(流入电流)，在节点电压方程中，方程的左边是与节点相连的电导上流出的电流之和，方程的右边则是与节点相连的电流源流入该节点的电流之和。

如果某个电流源上还串联有一个电导，那么该电导就不应再计入自电导和互电导之中，因为该电导上的电流（与它串联的电流源的电流）已经计入方程右边了。

第二章电阻电路§2-4 节点电压法一、节点电压法（一）节点电压的概念任意选择电路中某一节点为参考节点，其他节点称为独立节点，各独立节点与参考节点之间的电压称为节点电压。

节点电压的参考方向一般选择为独立节点指向参考节点，因此节点电压就是节点电位。

一旦选定节点电压，各支路电压均可用节点电压表示，连在独立节点与参考节点之间的支路电压等于相应节点的节点电压。

连在独立节点之间的支路电压等于两个相关节点的节点电压之差。

电路中所有支路电压都可以用节点电压表示。

（二）节点电压方程⎪⎭⎪⎬⎫=++=++=++333332321312232322212111313212111s n n n s n n n s n n n i u G u G u G i u G u G u G i u G u G u G ⎪⎪⎭⎪⎪⎬⎫=+++=+++=+++snn nn nn n n n n s nn n n n s nn n n n i u G u G u G i u G u G u G i u G u G u G 2211222222121111212111（三）节点电压法的解题步骤（1）指定参考节点，其余节点独立节点与参考节点之间的电压即为节点电压，其参考方向时由独立节点指向参考节点。

（2）求出各节点的自电导、各相邻节点间的互电导、各节点电源电流，按式（2-14）方法列写节点方程。

（3）求解节点电压方程，得出各节点电压值。

（4）指定支路电流的参考方向，根据支路电流与节点电压的关系，求出各支路电流。

（5）如果电路中含有电压源与电阻的串联组合时，先将其等效变换为电流源与电阻并联的组合，然后再列写节点电压方程，进行计算。

（6）如果电路中含有电压源并没有电阻与之串联，可用下列方法：①尽可能选用电压源支路的负极性端作为参考节点，这时该支路另一端的节点电压就已知（节点电压等于电压源电压），该节点方程也就不用列写了，其余节点方程仍按一般方法列写；②假设流过电压源的电流为，增加了一个变量，同时补充一个节点电压与电压源电压关系的方程，这样就能可以解出节点电压。

关于节点电压法关于节点电压法： 场到路已经讲了，被冠以阳春白雪。

现在来个俗的节点电压法，不象场路之说，这在任何一本《电路》书中都有提及。

 从场中得到了KVL、KCL、I = U/R、I = C dU / dt 和U = L dI / dt，接下来如何玩呢?自然是解方程，但如何能充分利用上面的条件来列出方程来呢?答案是，节点电压法和网孔电流法。

下面简单介绍节点电压法： 所谓节点电压法，首先得标定电压：选定一个参考节点，令其为零电压(通常是地线)。

然后标定所有的节点电压Uk(注意，节点电压的标定实际上就用到了KVL条件。

为何?自己想)。

标定完节点电压后，就可以利用KCL写方程了。

原则上，一个节点对应于一个方程(∑Ij = 0)，其形式为： ∑(Uk - Uj)/Rj + ∑Cj d(Uk - Uj)/dt + ∑[(1/Lj)∫(Uk - Uj)dt + I0j] = 0 其中Uk 为此方程对应的那个节点电压，Uj 为邻近诸节点的电压(j 为求和变量)，Rj、Cj 和Lj 为连接此节点到邻近节点的电阻、电容和电感参数，I0j 为电感上电流的初始值。

 这显然是个微分-积分方程。

若要解纯微分方程的话，上述方程再对时间求导一次便可，这时I0j 将消失。

由于除参考节点外，每个节点存在一个方程，而且是相互独立的，所以可以解出每个节点的电压。

这就是节点电压法。

 关于节点电压法的具体描述和特殊用法(如超级节点的选择)，建议找本《电路》仔细领会。

在此只是想说明，电路的分析及其解是有章可循的，而这些章法就那幺几条，没什幺特殊玄妙之处。

 扩展阅读：高手讲解信号与系统。

图2-5-1首先介绍节点电压的概念。

在电路中，当选取任一节点作为参考节点时，其余节点与此参考节点之间的电压称为对应节点的节点电压。

在图2-5-1所示电路中，当选择c点作为参考节点时，a点与c点间的电压称为a点的节点电压，同理b点的节点电压为，常简写为。

以节点电压作为未知量，对个独立节点列写KCL方程，从而求出各节点电压继而进一步求解其他电量的电路分析方法，称为节点电压法。

下面以图2-5-1所示电路为例，推导节点电压方程。

假设已知。

以节点c为参考节点，选择各支路电流参考方向如图所示，对独立节点a、b 列写KCL方程，得到：其中：（式2-5-3）（式2-5-4）（式2-5-5）（式2-5-6）（式2-5-7）（式2-5-8）将（式2-5-3）~（式2-5-8）代入（式2-5-1）、（式2-5-2）中，整理得到：联立求解可得，再代入（式2-5-3）~（式2-5-8）即得到各支路电流。

（式2-5-9）（式2-5-10）可写成如下形式：式中：称为节点a的自电导，它等于与节点相连的各支路导纳之和，总取正；称为节点的自电导，它等于与节点相连的各支路导纳之和，总取正；称为节点之间（之间）的互电导，它等于两节点间各支路电导之和，总取负。

当电路只含两个节点时，选择一个节点作为参考节点，只剩下一个独立节点，因而只有一个节点电压方程：（式2-5-15）（式2-5-15）就是米尔曼定理，也称为米尔曼公式。

例2-5-1 已知，，利用节点法求图2-5-2所示电路中各支路电流。

图2-5-2 例2-5-1附图解：以c点作为参考节点，对独立节点a、b列写节点电压方程：节点a：节点b：代入数据得到：，，，，图2-5-3 例2-5-2附图例2-5-2 图2-5-3所示电路含有两个受控源，电路参数和电源值已在图中注明，求各节点电压。

解：以节点d作为参考节点，对独立节点a、b、c列写节点电压方程：节点a ：节点b：节点c：附加方程：，联立求解得：，，。

节点电压法节点电压法是一种基本的电路分析方法，它是基于基尔霍夫电压法和欧姆定律的原理而得出的。

该方法适用于解决复杂电路中的节点电压，可以用来求解电路中各个分支的电流以及电路中任意两个节点之间的电势差。

以下详细介绍节点电压法的原理及应用：节点电压法的基本思想是将电路中任意两个节点之间的电势差表示为各个电源电压和各个分支电阻的乘积之和，从而构建一个节点电压方程组，通过解这个方程组可以得出电路中各个节点的电压值。

具体来说，节点电压法分为以下步骤：1、虚设一个参考节点，假设它为电路中的0V点，这样就可以把电路中的所有节点的电压值都表示为相对于此参考节点的电势差。

2、对于每个非参考节点，用一个未知数表示它相对于参考节点的电势差。

3、对于每个电源和每个电阻，用欧姆定律来表示节点电势差与通过它们的电流之间的关系，即U=IR。

4、对于每个节点，应用基尔霍夫电流定律，即该节点的所有进出电流之和为0。

5、将上述电压和电流方程整合在一起，形成一个以未知数节点电压值为变量的方程组。

6、解方程组，就可以得出电路中各个节点的电压值。

下面通过一个例子来演示节点电压法的应用。

如图所示，已知电路中各个电阻的阻值、电源电压的大小和极性，请用节点电压法计算电路中各个节点的电压值。

接下来，根据欧姆定律，可得：VA/3 + (VA- VB)/4 + VA/2 - 30 = 0同时，由于A和B节点处的电流之和为0，因此可得：将上述式子整理后，可以得出以下节点电压方程组：1、7VA - 3VB = 180通过解这个方程组，即可以得到VA = 90V和VB = 30V。

由此可知，节点电压法可以有效地解决电路中各个节点的电压值，为电路设计和分析提供了便利。

值得注意的是，节点电压法要求对电路中的每一个节点都给定一个未知变量，因此对于大型电路来说，方程组的规模较大，计算量也较大。

因此，在实际应用中，需要综合考虑计算效率和精度问题，选择合适的电路分析方法。