节点电压法的MATLAB实现

电力系统潮流计算matlab程序电力系统潮流计算是电力系统运行和规划中的重要环节，它用于计算电力系统中各节点的电压、功率和电流等参数。

随着电力系统规模的不断扩大和复杂性的增加，传统的手工计算方法已经无法满足需求，因此，利用计算机编程进行潮流计算成为了一种必要的选择。

Matlab是一种功能强大的科学计算软件，它提供了丰富的数学函数和工具箱，可以方便地进行电力系统潮流计算。

下面我将介绍一下如何使用Matlab编写电力系统潮流计算程序。

首先，我们需要建立电力系统的节点模型。

节点模型是电力系统中各节点的电压、功率和电流等参数的数学表示。

在Matlab中，我们可以使用矩阵来表示节点模型。

假设电力系统有n个节点，我们可以定义一个n×n的复数矩阵Y来表示节点之间的导纳关系，其中Y(i,j)表示节点i和节点j之间的导纳。

同时，我们还需要定义一个n×1的复数向量V来表示各节点的电压，其中V(i)表示节点i的电压。

接下来，我们需要编写潮流计算的主程序。

主程序的主要功能是根据节点模型和潮流计算算法，计算出各节点的电压、功率和电流等参数。

在Matlab中，我们可以使用循环语句和矩阵运算来实现潮流计算。

具体的计算过程可以参考电力系统潮流计算的算法。

在编写主程序之前，我们还需要定义一些输入参数，如电力系统的节点数、发电机节点和负荷节点等。

这些参数可以通过用户输入或者读取文件的方式获取。

同时，我们还需要定义一些输出参数，如各节点的电压、功率和电流等。

这些参数可以通过矩阵运算和循环语句计算得到，并输出到文件或者显示在屏幕上。

最后，我们需要进行程序的测试和调试。

可以通过输入一些测试数据，运行程序并检查输出结果是否正确。

如果发现程序有错误或者结果不准确，可以通过调试工具和打印调试信息的方式进行调试。

总之，利用Matlab编写电力系统潮流计算程序可以提高计算效率和准确性，为电力系统的运行和规划提供有力的支持。

当然，编写一个完整的潮流计算程序需要考虑很多细节和特殊情况，这需要有一定的电力系统和编程知识。

1. Matlab3节点牛顿拉夫逊潮流计算简介Matlab是一种高度灵活的编程语言和数学工具，被广泛应用于科学计算和工程领域。

3节点牛顿拉夫逊潮流计算是一种电力系统分析方法，用于计算电力系统中各节点的电压和相角。

在本文中，我们将介绍如何使用Matlab进行3节点牛顿拉夫逊潮流计算，以及该方法的原理和应用。

2. 3节点牛顿拉夫逊潮流计算原理3节点牛顿拉夫逊潮流计算是一种基于潮流方程的迭代算法。

它通过不断迭代求解节点电压和相角，以达到系统在给定负荷下的稳态。

其核心原理是利用牛顿拉夫逊法迭代求解潮流方程，即功率平衡方程和节点电压方程，直至收敛得到结果。

3. Matlab在3节点牛顿拉夫逊潮流计算中的应用Matlab提供了丰富的数学工具和函数库，使其成为进行电力系统分析的理想工具。

在3节点牛顿拉夫逊潮流计算中，我们可以利用Matlab编写相应的算法和程序，对实际电力系统进行分析和计算。

通过Matlab的矩阵运算和迭代算法，可以高效地求解潮流方程，得到系统各节点的电压和相角。

4. 3节点牛顿拉夫逊潮流计算的应用3节点牛顿拉夫逊潮流计算在电力系统规划、运行和故障分析中具有重要的应用价值。

通过计算系统各节点的电压和相角，可以评估系统的电压稳定性和潮流分布，指导电力系统的规划和调度。

在系统发生故障时，可以利用3节点牛顿拉夫逊潮流计算分析系统的稳定性和可靠性，为故障处理提供依据。

5. 结语3节点牛顿拉夫逊潮流计算是一种重要的电力系统分析方法，Matlab作为一种强大的数学工具，为其提供了理想的支持和实现。

通过Matlab进行3节点牛顿拉夫逊潮流计算，可以高效地进行电力系统分析和计算，为电力系统的规划和运行提供科学依据。

希望本文可以帮助读者更加深入地了解3节点牛顿拉夫逊潮流计算及其在Matlab 中的应用。

6. Matlab3节点牛顿拉夫逊潮流计算的优势利用Matlab进行3节点牛顿拉夫逊潮流计算具有许多优势。

Matlab提供了丰富的数学函数和工具，能够快速高效地进行矩阵运算、迭代求解等操作，极大地简化了算法的实现。

节点电压法的计算机编程实现1. 建立电路方程在电路分析中，节点电压法是一种常用的分析方法。

首先，我们需要建立电路方程。

在电路中，任意选取一个节点作为参考节点，其他节点相对于参考节点的电压即为节点电压。

假设电路中有n个节点和b 条支路，那么我们可以建立如下方程组：(E/Z) * Vref + Σ(E/Z) * Vin = Σ(I/Z)，其中E是独立电源，Z是支路阻抗，Vref是参考节点电压，Vin是其他节点电压，I是支路电流。

2. 确定节点电压节点电压是指电路中其他节点相对于参考节点的电压。

对于任意一个节点i，其电压Vi可以表示为：Vi = Vref + (E/Z) * (1/in) * Σ(E/Z) * Vin -Σ(I/Z)，其中in是节点i的电导。

3. 选择参考节点选择参考节点是节点电压法中的重要步骤。

通常，我们选择便于求解的节点作为参考节点。

在实际应用中，如果没有特殊要求，可以选择任意一个节点作为参考节点。

4. 计算其他节点电压根据上述公式，我们可以计算出其他节点的电压。

具体来说，我们可以先求出每个节点的电导in，然后代入公式计算出该节点的电压。

5. 求解方程组求解方程组是节点电压法的核心步骤。

在实际应用中，我们需要使用计算机编程语言来实现求解方程组的过程。

通常，我们可以采用迭代法或直接法来求解方程组。

其中，迭代法是指通过不断迭代来逼近方程的解，而直接法是指通过一定的算法直接求出方程的解。

6. 处理复杂电路对于一些复杂的电路，我们需要采用一些特殊的方法来处理。

例如，对于含有多个电源的电路，我们需要对每个电源进行单独处理；对于含有受控源的电路，我们需要将受控源转化为独立源后再进行处理。

此外，对于一些非线性电路，我们需要采用一些非线性分析方法进行处理。

7. 优化算法性能在节点电压法的计算机编程实现中，我们需要优化算法性能以提高计算速度和精度。

具体来说，我们可以采用以下方法来优化算法性能：减少迭代次数、采用并行计算技术、使用稀疏矩阵存储方法等。

matlab结课论⽂—matlab在电⽓⼯程中的应⽤Matlab结课论⽂MATLAB在电路原理中的应⽤2014/11/29⼀、matlab 在节点电压法中的应⽤节点分析法是电路理论中最常⽤的⽅法，相⽐于⽀路分析法和回路电流法它的计算量和需要考虑的因素都相对较少，所以在电路理论中被⼴泛使⽤。

但是随着节点数量的增多，实现⼈⼯计算的可能性就变得相当的低，因为每⼀个独⽴节点需要列出⼀个节点电压⽅程，多个线性⽅程的求解并不容易。

利⽤MATLAB 就可以很好地解决这个问题。

⽅法是：做出电路模型写出节点导纳矩阵列写节点电流矩阵写出节点分析法的矩阵形式利⽤MATLAB 进⾏求解例：列写混合⽅程，编写Matlab 程序求解节点1、2、3、4的电压；解：（1）混合⽅程矩阵形式（要求写出考虑不同⽀路情况时的步骤）-+--++---++--+010000010100032222222211111µµG G G G G jwc gjwc g jwc jwc jwL jwc jwc jwc jwc G=??00014321S S k I G U I U U U U （2）matlab 程序：G1=0.2,G2=0.1,G3=0.5,C1=10e-6,C2=22e-6,L=1e-4,miu=0.5,g=1.5; Is=10*exp(20/180*pi*j); Us=100*exp(50/180*pi*j);w=10000;Y=[G1+j*w*C1,-j*w*C1,0,0,0;-j*w*C1,j*w*C1+1/(j*w*L)+j*w*C2,-j*w*C2,0,1; -g,- j*w*C2+g,j*w*C2+G2,-G2,0;0,0,-G2,G2+G3,0;0,1,miu,-miu,0];I=[Us*G1;0;0;Is;0];U=inv(Y)*IUabs=abs(U)Uang=angle(U)*180/pi（3）结果（写出时域表达式）G1 =0.2000G2 =0.1000G3 =0.5000C1 =1.0000e-005C2 =2.2000e-005L =1.0000e-004miu =0.5000U =1.0e+002 *0.5536 + 0.5926i 0.2068 + 0.7710i -0.3083 - 1.7819i 0.1052 - 0.2400i -0.1915 + 0.1281i Uabs =79.8204180.837126.203823.0413Uang =46.948874.9868-99.8162-66.3225146.2121时域U1=81.0982sin（10000t+46.9488）；U2=79.8204sin（10000t+74.9868）；U3=180.8371sin（10000t-99.8162）；U4=26.2038sin(10000t-66.3225);Ik=23.0413sin(10000t+146.2121)(4) 绘制出各节点电压及Ik的波形图⼆、Matlab在⼆端⼝⽹络中的应⽤：⼆端⼝⽹络在电⽓中应⽤⼴泛，研究⼆端⼝⽹络也极具意义，因为⼆端⼝⽹络应⽤较普遍；⼆端⼝的分析⽅法易推⼴应⽤于n 端⼝⽹络络可以分割成许多⼦⽹络（⼆端⼝）进⾏分析；仅研究端⼝特性时，可以⽤等效⼆端⼝电路模型进⾏分析。

·实验教学·节点电压法的编程实现及其拓展应用教学设计与实施沈 瑶，赵彦珍，高昕悦，王 超（西安交通大学 电工电子教学实验中心，西安 710049）摘要：为达到新工科人才的培养目标，西安交通大学电工电子教学实验中心积极进行教学改革。

该文介绍了近年进行的教学改革工作，并总结了实验教学中存在的问题。

针对这些问题，结合计算机专业学生的专业特点，开展新一轮教学改革试点工作，详细讨论了教学改革的具体实施过程和实施效果。

实践证明，此次改革有助于计算机专业学生加深对电路理论知识的理解，提高学生编程能力，分层次的实验任务激发了学生潜能，有效提高学生应用计算机编程手段解决实际电路问题的能力。

关　键　词：结点电压法；教学改革；创新能力；编程能力中图分类号：G420 文献标志码：A DOI: 10.12179/1672-4550.20190500Teaching Design and Implementation of Programming Realization ofNode Voltage Method and Its Extended ApplicationSHEN Yao, ZHAO Yanzhen, GAO Xinyue, WANG Chao（Electrical and Electronic Teaching Experiment Center, Xi’an Jiaotong University, Xi’an 710049, China ）Abstract: To train new engineering talents, the Electrical and Electronic Teaching Experimental Center of Xi’an Jiaotong University actively carried out teaching reforms. This paper introduced the teaching reform in recent years, and summarized the issues in the experimental teaching. Given the professional characteristics of students majoring in computer, and in response to these issues, a new round of teaching reform pilot work was carried out, and the specific implementation process and effect of teaching reform are discussed in detail. It has been proved that the reform can deepen students’ understanding of circuit theoretical knowledge, improve their programming ability, stimulate students’ potential through hierarchical experimental tasks, and effectively improve their ability to solve practical circuit problems through computer programming.Key words: node voltage method; teaching reform; creativity; programming ability实验是理论联系实际的重要手段。

电力系统仿真作业—-—-——--—-—-三机九节点电力系统暂态仿真学院：能源与动力工程学院专业:电力系统及其自动化学号：姓名：于永生导师：授课教师：目录一、概述 (1)二、课程主要任务 (1)1.系统数据 (1)2.潮流计算 (3)3.负荷等效和支路简化 (4)4.求解电磁功率 (5)5.求解运动方程 (5)6.程序清单 (8)(1).主程序： (8)(2).极坐标转换成直角坐标函数pol2rect(V,del) (17)(3).直角坐标转换成极坐标函数rect2pol(Z) (17)(4).求解微分方程所用的得到微分量的函数Gen_fw(t,X,Y_Gen,E,Pm0,Tj) (17)三、课程总结及心得体会 (17)四、参考文献 (18)于永生电力系统仿真作业一、概述在动态稳定分析中，系统由线性化的微分方程组和代数方程组描写，并用经典的或现代的线性系统理论来进行稳定分析,分析可以在时域或频域进行。

当用计算机和现代线性系统理论分析时,常把系统线性化的微分方程组和代数方程组消去代数变量,化为状态方程形式，并广泛采用特征分析进行稳定分析.电力系统是由不同类型的发电机组、多种电力负荷、不同电压等级的电力网络等组成的十分庞大复杂的动力学系统。

其暂态过渡过程不仅包括电磁方面的过渡过程，而且还有机电方面的过渡过程。

由此可见,电力系统的数学模型是一个强非线性的高维状态方程组。

在动态稳定仿真中使用简单的电力系统模型，发电机用三阶模型表示。

二、课程主要任务本次课程主要应用P。

M. Anderson and A. A. Fouad编写的《Power System Control and Stability》一书中所引用的Western System Coordinated Council (WSCC）三机九节点系统模型。

1.系统数据其中，节点数据如下：％节点数据％节点电压电压发电机发电机负荷负荷节点％号幅值相角有功无功有功无功类型（1PQ 2PV 3平衡)N=［ 1 1。

实验3 MATLAB在电路中的应用【实验目的】掌握MATLAB对电路系统的描述方法，会求解并表达结果。

1、加深对直流电路的节点电压法和网孔电流法的分析理解，学习Matlab的矩阵运算方法。

2、加深多戴维南定律，等效变换等的了解，进一步了解matlab在直流电路中的作用。

3、学习正弦交流电路的分析方法，学习matlab复数的运算方法。

4、学习动态电路的分析方法，学习动态电路的matlab计算方法。

5、学习有关频率响应的相关概念，学习matlab的频率计算。

【实验内容】1、练习书上部分例题，每一小节选一道例题进行验证2、课后5.3，5.9,5.12,5.13,5.15的编程求解3、总结MATLAB对直流电路，正弦稳态电路，动态电路分析的步骤，注明其中涉及到的关键函数和通用语句，并写出求解电路频率响应的关键语句。

1、练习书上部分例题5.1电阻电路例5.1 电阻电路的计算①⑴以压缩空格显示；给定元件赋值相当于是罗列题目的已知条件。

这是做题的第一步，包括了解题的初始化。

⑵以上模块是根据建模所列的方程而写出来的，是求解整个问题的方法和核心所在。

方程是根据电路的知识列出的，而编程是根据matlab的知识编出的。

从网孔方程中抽离出来的矩阵可以描述为A和B两个矩阵，而us是要求用户输入的。

数字方程列完后，用I=A\B*us求出电流，注意用到左除还是右除。

求出的三个电流分别放在ia、ib、ic中。

⑶上面这块是根据具体的题目要求所罗列的，往往题目要求不是只要矩阵的解，而是要用矩阵的解作为中间变量去求其他的解。

这时要根据电路中的定理如欧姆定律等去求。

当然，这也可以看做是结果的显示（末尾不加分号）。

运行结果：例5.3 戴维宁定理⑴程序初始化以及已知条件输入⑵根据方程列出数字矩阵。

方法是节点电压法。

⑶根据题目求出最终解，把需要显示的结果不加分号；并用plot 画出图像。

运行结果5.2动态电路例5.4 一阶动态电路，三要素公式⑴解题的初始化以及已知条件输入⑵对时间的设置。

基于Matlab的电路节点分析法王小增，杨久红(嘉应学院电子信息工程系广东梅州514015)摘要：在用计算机求解大规模电路时，多采用节点法分析。

M atlab具有强大的矩阵运算功能，在电子技术中应用广泛。

对用Matlab分析大规模电路时的模型建立方法进行了研究，并编写了相应的程序用于求解大规模电路中的电流和电压。

结合一个实例，说明用Matlab分析大规模电路的方法。

关键词：电路；节点法；Matlab；建模Nodal Analysis Method of Circuits Based on MatlabWANG Xiaozeng，YANG Jiuhong(Department of Electronics and Information Engineering，Jiaying University，Meizhou，514015，China)Abstract：Analysis of large scale circuit often makes use of the node method.Matlab has large ability of matrix arithmetic and was widely u sed in the electronic technology. The article discusses the method of modeling in analysis of large scale circuit with Matlab. The article makes a lot of prog ram to analyze the voltage and the current of the circuit, and gives an exa mple to account for the method which analyzes large scale circuit with MatlabKeywords：circuit；nodal analysis method；Matlab; module对于简单的电路分析，可以采用观察的方法列出所需要的独立方程，手算得出答案。

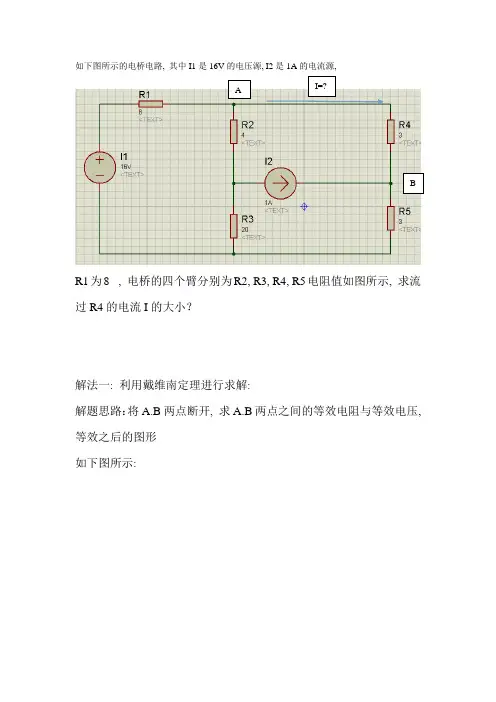
如下图所示的电桥电路, 其中I1是16V 的电压源, I2是1A 的电流源,R1为8 , 电桥的四个臂分别为R2, R3, R4, R5电阻值如图所示, 求流过R4的电流I 的大小？解法一: 利用戴维南定理进行求解:解题思路：将A.B 两点断开, 求A.B 两点之间的等效电阻与等效电压, 等效之后的图形 如下图所示:I=? ABAB其中R6是等效电阻, I3是等效电压。

①求解等效电阻:求解等效电阻时把所有的电流源开路, 电压源短路, 得到如下所示的电路：AB则AB两端的电阻值即等效电阻R6=(R2+R3)//R1+R5②求解等效电压可以利用叠加法求解AB 两端的电压值, 先不看电压源（即电压源相当于短路）, 计算电流源对AB 两端的电压值, 再不看电流源（即电流源相当于断路）, 再计算AB 两端的电压值, 然后将俩种情况下的电压值叠加即得到AB 两端的等效电压。

不看电压源的电路图如下:则UCB+I2*R5+I2*（R1+R2）//R3=0 可以得到:UCB =-[I2*R5+I2*（R1+R2）//R3]U AB1 =-I2*R5-I2*3213)21(R R R R R R ++•++I2*R2*3213R R R R ++不看电流源的电路图如下:ABC很容易的知道AB 两端的电压值为:U AB2=321)32(*1R R R R R I +++所以UAB=UAB1+UAB2则经过戴维南等效之后的电路图如下:可以很简单的求解出II=64R R U AB+ABMatlab求解程序如下:(程序代码如下)R1=8;R2=4;R3=20;R4=3;R5=3;I1=16;I2=1;R6=R5+(R2+R3)*R1/(R1+R2+R3);UAB1=-I2*R5-I2*(R1+R2)*R3/(R1+R2+R3)+I2*R2*R3/(R1+R2+R3); UAB2=I1*(R2+R3)/(R1+R2+R3);UAB=UAB1+UAB2;I=UAB/(R4+R6);解法二: 运用叠加定理直接求解①先考虑电压源对AB两点的电流影响, 此时不看电流源, 电流源相当于断路, 电路图如下：根据电路图, 容易知道: AB 之间的电流I1 为I 1=543232)54//()32(11R R R R R R R R R R R I ++++•+++②再考虑电流源对AB 端电流源的影响, 此时不看电压源, 即将电压源短路, 电路图如下所示:根据电路图, 分析容易知道: 可以根据三角形与Y 形电路之间的转换, 将三角形电阻ACD 转换为Y 形电阻, 公式为：ABI 1BCD形电阻之和相邻电阻的乘积形电阻∆∆Y转换之后的电路图如下:可以得到:R12=32121R R R R R ++•R13=32131R R R R R ++•由于是电流源, 电流一定, 可以忽略与电流源串联的电阻R23 所以I 2=-I2*541312513R R R R R R ++++综上知道:I=I 1+I 2Matlab 求解程序如下: (程序代码如下) R1=8 R2=4;I 2R3=20; R4=3; R5=3; I1=16; I2=1;i1=[(R2+R3)/(R2+R3+R4+R5)]*I1/[R1+(R2+R3)*(R4+R5)/(R2+R3+R4+R5)];R12=R1*R2/(R1+R2+R3); R13=R1*R3/(R1+R2+R3);i2=-I2*(R13+R5)/(R12+R13+R4+R5); I=i1+i2解法三: 利用回路电流法进行求解 实验电路图如下:将无伴电流源的支路作为一个回路电流, 可以有电路图结合回路电i1i2流法列出如下方程:i1=I2I*（R2+R3+R4+R5）+i1*(R3+R5)-i2*（R2+R3）=0 -I*(R2+R3)-i1*R3+i2*(R1+R2+R3)=I1解方程可以很容易解的I 的值。

电路仿真MATLAB实验报告班级：学号：姓名：学院：实验一直流电路（1）一、实验目的1、加深对直流电路的节点电压法和网孔电流法的理解2、学习使用MATLAB的矩阵运算的方法二、实验示例1、节点分析电路如图所示（见书本12页），求节点电压V1,V2,V3.根据电路图得到矩阵方程，根据矩阵方程使用matlab命令为Y =0.1500 -0.1000 -0.0500-0.1000 0.1450 -0.0250-0.0500 -0.0250 0.0750节点v1，v2和v3：v =404.2857350.0000412.85712、回路分析电路如图所示（见书本13页），使用解析分析得到同过电阻RB的电流，另外求10V电压源的输出功率。

分析电路得到节点方程，根据节点方程得到矩阵方程，根据矩阵方程，使用matlab的命令为z=[40,-10,-30;-10,30,-5;-30,-5,65];v=[10,0,0]';I=inv(z)*v;IRB=I(3)-I(2);fprintf('the current through R is %8.3f Amps \n',IRB)ps=I(1)*10;fprintf('the power supplied by 10v source is %8.4f watts\n',ps)结果为：the current through R is 0.037 Ampsthe power supplied by 10V source is 4.7531 watts三、实验内容1 根据书本15页电路图，求解电阻电路，已知：R1=2Ω,R2=6Ω,R3=12Ω,R4=8Ω,R5=12Ω,R6=4Ω,R7=2Ω如果Us=10V,求i3,u4,u7如果U4=4V,求Us,i3,i7使用matlab命令为clear% 初始化阻抗矩阵Z=[20 -12 0;-12 32 -12;0 -12 18];% 初始化电压矩阵V=[10 0 0]';% 解答回路电流I=inv(Z)*V;% I3的计算I3=I(1)-I(2);fprintf('the current I3 is %8.2f Amps\n',I3) % U4的计算U4=8*I(2);fprintf('the voltage U4 is %8.2f Vmps\n',U4) % U7的计算U7=2*I(3);fprintf('the voltage U7 is %8.2f Vmps\n',U7)结果the current I3 is 0.36 Ampsthe voltage U4 is 2.86 Vmpsthe voltage U7 is 0.48 Vmpsclear% 初始化矩阵XX=[20 -1 0;-12 0 -12;0 0 18];% 初始化矩阵YY=[6 -16 6]';% 进行解答A=inv(X)*Y;% 计算各要求量Us=A(2)I3=A(1)-0.5I7=A(3)结果Us = 14.0000I3 = 0.5000I7 =0.33332 求解电路里的电压如图1-4（书本16页），求解V1,V2,V3,V4,V5使用matlab命令为clear% 初始化节点电压方程矩阵Z=[0.725 -0.125 -0.1 -5 -1.25;-0.1 -0.2 0.55 0 0;-0.125 0.325 -0.2 0 1.25;1 0 -1 -1 0;0 0.2 -0.2 0 1];I=[0 6 5 0 0]';% 解答节点电压U1，U3，U4与Vb，IaA=inv(Z)*I;% 最终各电压计算V1=A(1)V2=A(1)-10*A(5)V3=A(2)V4=A(3)V5=24结果V1 =117.4792V2 = 299.7708V3 =193.9375V4 =102.7917V5 = 243、如图1-5（书本16页），已知R1=R2=R3=4Ω,R4=2Ω,控制常数k1=0.5，k2=4，is=2A，求i1和i2.使用matlab命令为clear% 初始化节点电压方程矩阵Z=[0.5 -0.25 0 -0.5;-0.25 1 -1 0.5;0 0.5 0 -1;1 -1 -4 0];I=[2 0 0 0]';% 解答节点电压V1，V2及电流I1，I2A=inv(Z)*I;% 计算未知数V1=A(1)V2=A(2)I1=A(3)I2=A(4)结果如下：V1 =6V2 =2I1 = 1I2 =1实验二直流电路（2）一、实验目的1、加深多戴维南定律，等效变换等的了解2、进一步了解matlab在直流电路中的作用二、实验示例如图所示（图见书本17页2-1），分析并使用matlab命令求解为clear,format compactR1=4;R2=2;R3=4;R4=8;is1=2;is2=0.5;a11=1/R1+1/R4;a12=-1/R1;a13=-1/R4;a21=-1/R1;a22=1/R1+1/R2+1/R3;a23=-1/R3;a31=-1/R4;a32=-1/R3;a33=1/R3+1/R4;A=[a11,a12,a13;a21,a22,a23;a31,a32,a33];B=[1,1,0;0,0,0;0,-1,1];X1=A\B*[is1;is2;0];uoc=X1(3);X2=A\B*[0;0;1];Req=X2(3);RL=Req;P=uoc^2*RL/(Req+RL)^2;RL=0:10,p=(RL*uoc./(Req+RL)).*uoc./(Req+RL),figure(1),plot(RL,p),gridfor k=1:21ia(k)=(k-1)*0.1;X=A\B*[is1;is2;ia(k)];u(k)=X(3);endfigure(2),plot(ia,u,'x'),gridc=polyfit(ia,u,1);%ua=c(2)*ia=c(1) , 用拟合函数术,c(1),c(2)uoc=c(1),Req=c(2) RL =0 1 2 3 4 5 6 7 8 9 10 p =Columns 1 through 70 0.6944 1.0204 1.1719 1.2346 1.2500 1.2397Columns 8 through 111.2153 1.1834 1.1480 1.1111A 、功率随负载变化曲线 B.电路对负载的输出特性0123456789100.20.40.60.811.21.400.20.40.60.81 1.2 1.4 1.6 1.82三、实验内容1、图见书本19页2-3，当RL从0改变到50kΩ，校验RL为10kΩ的时候的最大功率损耗使用matlab命令为clear% 定义电压源和电阻值Us=10;Rs=10000;RL=0:20000;p=(Us^2.*RL)./(RL+Rs).^2;plot(RL,p);输出结果为Maximum power occur at 10000.00hmsMaximum power dissipation is 0.0025Watts2、在图示电路里(书本20页2-4)，当R1取0，2，4，6，10，18，24，42，90和186Ω时，求RL 的电压UL,电流IL 和RL 消耗的功率。