第五章 三元合金相图(习题)

第五章 三元合金相图1 根据Fe －C －Si 的3.5%Si 变温截面图（5－1），写出含0.8%C 的Fe-C-Si 三元合金在平衡冷却时的相变过程和1100℃时的平衡组织。

图5－12 图5－2为Cu-Zn-Al 合金室温下的等温截面和2%Al 的垂直截面图，回答下列问题：1） 在图中标出X 合金（Cu-30%Zn-10%Al ）的成分点。

2） 计算Cu-20%Zn-8%Al 和 Cu-25%Zn-6%Al 合金中室温下各相的百分含量，其中α相成分点为Cu-22.5%Zn-3.45%Al ，γ相成分点为Cu-18%Zn-11.5%Al 。

3） 分析图中Y 合金的凝固过程。

Y％图5－23 如图5－3是A-B-C 三元系合金凝固时各相区，界面的投影图，A 、B 、C 分别形成固溶体α、β、γ。

1） 写出P p ''，P E '1和P E '2单变量线的三相平衡反应式。

2） 写出图中的四相平衡反应式。

3） 说明O 合金凝固平衡凝固所发生的相变。

图5－3 图5－44 图5－4为Fe-W-C三元系的液相面投影图。

写出e1→1085℃，P1→1335℃，P2→1380℃单变量线的三相平衡反应和1700℃，1200℃，1085℃的四相平衡反应式。

I，II，III三个合金结晶过程及室温组织，选择一个合金成分其组织只有三元共晶。

5 如图5－5为Fe-Cr-C系含13%Cr的变温截面１）大致估计2Cr13不锈钢的淬火加热温度（不锈钢含碳量０.２％, 含Cr量13％）２）指出Cr13模具钢平衡凝固时的凝固过程和室温下的平衡组织（Cr13钢含碳量2%）３）写出（１）区的三相反应及７９５ 时的四相平衡反应式。

图5－5 图5－66 如图5－6所示，固态有限溶解的三元共晶相图的浓度三角形上的投影图，试分析IV区及VI区中合金之凝固过程。

写出这个三元相图中四相反应式。

图5－77 分析如图5－7所示的三元相图，该合金中E 点成分为27Pb18Sn55Bi ，γ相成分取100％Bi 。

第一章 原子排列与晶体结构1. fcc 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,晶胞中原子数为 ，把原子视为刚性球时，原子的半径r 与点阵常数a 的关系是 ；bcc 结构的密排方向是 ，密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为 ，原子的半径r 与点阵常数a 的关系是 ；hcp 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,，晶胞中原子数为 ，原子的半径r 与点阵常数a的关系是 。

2. Al 的点阵常数为0.4049nm ，其结构原子体积是 ，每个晶胞中八面体间隙数为 ，四面体间隙数为 。

3. 纯铁冷却时在912ε 发生同素异晶转变是从 结构转变为 结构，配位数 ，致密度降低 ，晶体体积 ，原子半径发生 。

4. 在面心立方晶胞中画出）（211晶面和]211[晶向，指出﹤110﹥中位于（111）平面上的方向。

在hcp 晶胞的（0001）面上标出）（0121晶面和]0121[晶向。

5. 求]111[和]120[两晶向所决定的晶面。

6 在铅的（100）平面上，1mm 2有多少原子？已知铅为fcc 面心立方结构，其原子半径R=0.175×10-6mm 。

第二章 合金相结构一、 填空1） 随着溶质浓度的增大，单相固溶体合金的强度 ，塑性 ，导电性 ，形成间隙固溶体时，固溶体的点阵常数 。

2） 影响置换固溶体溶解度大小的主要因素是（1） ；（2） ；（3） ；（4） 和环境因素。

3） 置换式固溶体的不均匀性主要表现为 和 。

4） 按照溶质原子进入溶剂点阵的位置区分，固溶体可分为 和 。

5） 无序固溶体转变为有序固溶体时，合金性能变化的一般规律是强度和硬度 ，塑性 ，导电性 。

6）间隙固溶体是 ，间隙化合物是 。

二、 问答1、 分析氢，氮，碳，硼在α-Fe 和γ-Fe 中形成固溶体的类型，进入点阵中的位置和固溶度大小。

已知元素的原子半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，α-Fe ：0.124nm ，γ-Fe ：0.126nm 。

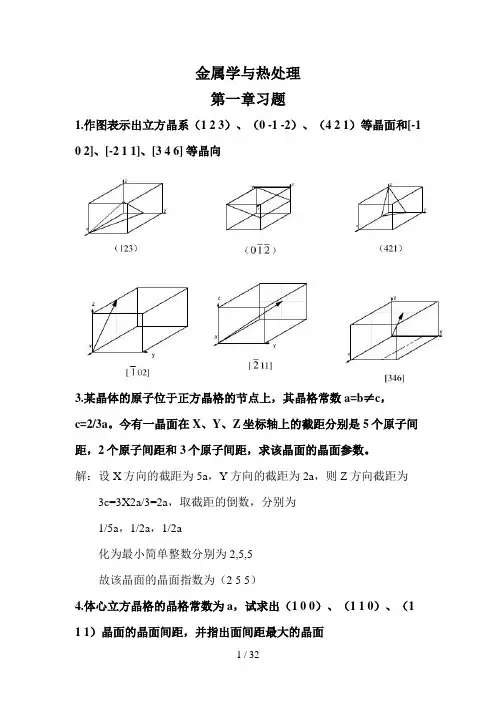
金属学与热处理第一章习题1.作图表示出立方晶系（1 2 3）、（0 -1 -2）、（4 2 1）等晶面和[-1 0 2]、[-2 1 1]、[3 4 6] 等晶向3.某晶体的原子位于正方晶格的节点上，其晶格常数a=b≠c，c=2/3a。

今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距，2个原子间距和3个原子间距，求该晶面的晶面参数。

解：设X方向的截距为5a，Y方向的截距为2a，则Z方向截距为3c=3X2a/3=2a，取截距的倒数，分别为1/5a，1/2a，1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为（2 5 5）4.体心立方晶格的晶格常数为a，试求出（1 0 0）、（1 1 0）、（1 1 1）晶面的晶面间距，并指出面间距最大的晶面解：（1 0 0）面间距为a/2，（1 1 0）面间距为√2a/2，（1 1 1）面间距为√3a/3三个晶面晶面中面间距最大的晶面为（1 1 0）7.证明理想密排六方晶胞中的轴比c/a=1.633证明：理想密排六方晶格配位数为12，即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切，成正四面体，如图所示则OD=c/2，AB=BC=CA=CD=a因△ABC是等边三角形，所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2则有(CD)2=(OC)2+(1/2c)2，即因此c/a=√8/3=1.6338.试证明面心立方晶格的八面体间隙半径为r=0.414R解：面心立方八面体间隙半径r=a/2-√2a/4=0.146a面心立方原子半径R=√2a/4，则a=4R/√2，代入上式有R=0.146X4R/√2=0.414R9.a）设有一刚球模型，球的直径不变，当由面心立方晶格转变为体心立方晶格时，试计算其体积膨胀。

b）经X射线测定，在912℃时γ-Fe的晶格常数为0.3633nm，α-Fe的晶格常数为0.2892nm，当由γ-Fe转化为α-Fe时，求其体积膨胀，并与a）比较，说明其差别的原因。

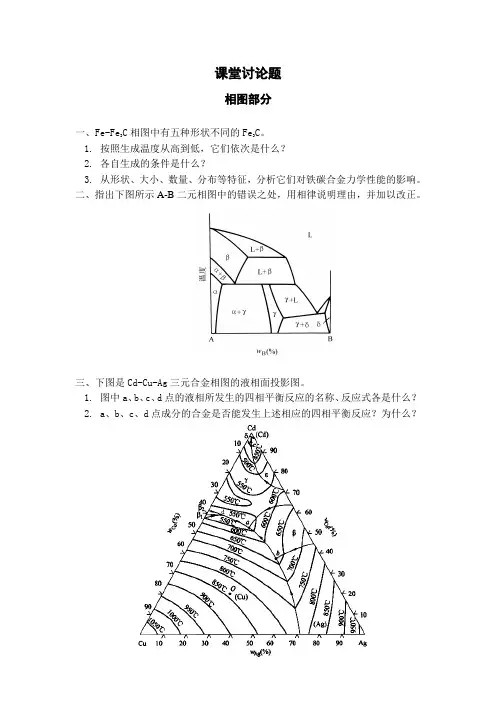
课堂讨论题相图部分一、Fe-Fe3C相图中有五种形状不同的Fe3C。

1.按照生成温度从高到低，它们依次是什么？2.各自生成的条件是什么？3.从形状、大小、数量、分布等特征，分析它们对铁碳合金力学性能的影响。

二、指出下图所示A-B二元相图中的错误之处，用相律说明理由，并加以改正。

三、下图是Cd-Cu-Ag三元合金相图的液相面投影图。

1.图中a、b、c、d点的液相所发生的四相平衡反应的名称、反应式各是什么？2.a、b、c、d点成分的合金是否能发生上述相应的四相平衡反应？为什么？四、下图是Cd-Ag-Zn三元系400℃的等温截面图。

1. 如何确定图中F点合金在该温度平衡相的成分？所用方法的依据是什么？2. 对于上题，教材中所介绍的“连线法则”实用吗？为什么？你有什么更好的方法吗？3.图中O点合金在该温度的平衡相的成分是什么？五、Co-Sb平衡相图如下图所示。

1. 写出图中1118℃、～1065℃、936℃、874℃、629℃、422℃、～377℃水平线的名称；2. 写出图中固态单相的相结构类型，并写出其中化合物的化学式；=90%的合金在200℃时的平衡相，并计算相组成物的相对量；3. 写出WSb4. 写出W=90%的合金在200℃时的平衡组织，并计算组织组成物的相对量。

Sb六、某三元合金相图的四相平衡平面如下图所示。

1. 计算A合金在该四相反应过程中．．．．．．．所生成的β相在合金中所占的质量分数。

2. 能使该四相反应中反应相耗尽的是哪些成分的合金？Array C合金系中各相的自由能-成分曲线，并以此图阐述七、示意画出750℃时Fe-Fe3该温度时合金系中的相平衡状态。

八、根据下图所示的投影图（教材中图5-114a），示意画出其立体图。

中南大学材料科学基础课后习题答案(总12页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 原子排列与晶体结构1. [110]， (111)， ABCABC…， ， 12 , 4 ， a r 42=； [111]， (110) , , 8 , 2 ， a r 43= ； ]0211[， (0001) ， ABAB ， ， 12 ， 6 ， 2a r =。

2.， 4 ， 8 。

3.FCC ， BCC ，减少 ，降低 ，膨胀 ，收缩 。

4.解答：见图1－1 5. 解答：设所决定的晶面为（hkl ），晶面指数与面上的直线[uvw]之间有hu+kv+lw=0，故有：h+k-l=0,2h-l=0。

可以求得（hkl ）＝（112）。

6 解答：Pb 为fcc 结构，原子半径R 与点阵常数a 的关系为a r 42=，故可求得a ＝×10-6mm 。

则（100）平面的面积S ＝a 2＝×0-12mm 2，每个（100）面上的原子个数为2。

所以1 mm 2上的原子个数s n 1=＝×1012。

第二章 合金相结构一、 填空1） 提高，降低，变差，变大。

2） （1）晶体结构；（2）元素之间电负性差；（3）电子浓度 ；（4）元素之间尺寸差别3） 存在溶质原子偏聚 和短程有序 。

4） 置换固溶体 和间隙固溶体 。

5） 提高 ，降低 ，降低 。

6） 溶质原子溶入点阵原子溶入溶剂点阵间隙中形成的固溶体，非金属原子与金属原子半径的比值大于时形成的复杂结构的化合物。

二、 问答1、 解答： -Fe 为bcc 结构，致密度虽然较小，但是它的间隙数目多且分散，间隙半径很小，四面体间隙半径为，即R ＝，八面体间隙半径为，即R ＝。

氢，氮，碳，硼由于与-Fe 的尺寸差别较大，在-Fe 中形成间隙固溶体，固溶度很小。

-Fe 的八面体间隙的[110]方向R= Ra ，间隙元素溶入时只引起一个方向上的点阵畸变，故多数处于-Fe 的八面体间隙中心。

第一章 原子排列与晶体结构1.[110]， (111)， ABCABC…， 0.74 ， 12 , 4 ， a r 42=； [111]， (110) , 0.68 , 8 , 2 ， a r 43= ；]0211[， (0001) ， ABAB ， 0.74 ， 12 ， 6 ， 2a r =。

2. 0.01659nm 3 ， 4 ， 8 。

3. FCC ， BCC ，减少 ，降低 ，膨胀 ，收缩 。

4. 解答：见图1－15.解答：设所决定的晶面为（hkl ），晶面指数与面上的直线[uvw]之间有hu+kv+lw=0，故有： h+k-l=0,2h-l=0。

可以求得（hkl ）＝（112）。

6 解答：Pb 为fcc 结构，原子半径R 与点阵常数a 的关系为ar 42=，故可求得a ＝0.4949×10-6mm 。

则（100）平面的面积S ＝a 2＝0.244926011×0-12mm 2，每个（100）面上的原子个数为2。

所以1 mm 2上的原子个数s n 1=＝4.08×1012。

第二章合金相结构一、 填空1） 提高，降低，变差，变大。

2） （1）晶体结构；（2）元素之间电负性差；（3）电子浓度 ；（4）元素之间尺寸差别 3） 存在溶质原子偏聚 和短程有序 。

4） 置换固溶体 和间隙固溶体 。

5） 提高 ，降低 ，降低 。

6） 溶质原子溶入点阵原子溶入溶剂点阵间隙中形成的固溶体，非金属原子与金属原子半径的比值大于0.59时形成的复杂结构的化合物。

二、 问答1、 解答： α-Fe 为bcc 结构，致密度虽然较小，但是它的间隙数目多且分散，间隙半径很小，四面体间隙半径为0.291Ra ，即R ＝0.0361nm ，八面体间隙半径为0.154Ra ，即R ＝0.0191nm 。

氢，氮，碳，硼由于与α-Fe 的尺寸差别较大，在α-Fe 中形成间隙固溶体，固溶度很小。

材料科学与⼯程基础习题第⼀章原⼦排列与晶体结构1. fcc 结构的密排⽅向是，密排⾯是，密排⾯的堆垛顺序是，致密度为，配位数是 ,晶胞中原⼦数为，把原⼦视为刚性球时，原⼦的半径r 与点阵常数a 的关系是；bcc 结构的密排⽅向是，密排⾯是 ,致密度为 ,配位数是 ,晶胞中原⼦数为，原⼦的半径r 与点阵常数a 的关系是；hcp 结构的密排⽅向是，密排⾯是，密排⾯的堆垛顺序是，致密度为，配位数是 ,，晶胞中原⼦数为，原⼦的半径r 与点阵常数a 的关系是。

2. Al 的点阵常数为0.4049nm ，其结构原⼦体积是，每个晶胞中⼋⾯体间隙数为，四⾯体间隙数为。

3. 纯铁冷却时在912℃发⽣同素异晶转变是从结构转变为结构，配位数，致密度，晶体体积，原⼦半径发⽣。

4. 在⾯⼼⽴⽅晶胞中画出）（211晶⾯和]211[晶向，指出﹤110﹥中位于（111）平⾯上的⽅向。

在hcp 晶胞的（0001）⾯上标出）（0121晶⾯和]0121[晶向。

5. 求]111[和]120[两晶向所决定的晶⾯。

6 在铅的（100）平⾯上，1mm 2有多少原⼦？已知铅为fcc ⾯⼼⽴⽅结构，其原⼦半径R=0.175×10-6mm 。

第⼆章合⾦相结构⼀、填空1）随着溶质浓度的增⼤，单相固溶体合⾦的强度，塑性，导电性，形成间隙固溶体时，固溶体的点阵常数。

2）影响置换固溶体溶解度⼤⼩的主要因素是（1）；（2）；（3）；（4）和环境因素。

3）置换式固溶体的不均匀性主要表现为和。

4）按照溶质原⼦进⼊溶剂点阵的位置区分，固溶体可分为和。

5）⽆序固溶体转变为有序固溶体时，合⾦性能变化的⼀般规律是强度和硬度，塑性，导电性。

6）间隙固溶体是，间隙化合物是。

⼆、问答1、分析氢，氮，碳，硼在α-Fe 和γ-Fe 中形成固溶体的类型，进⼊点阵中的位置和固溶度⼤⼩。

已知元素的原⼦半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，α-Fe ：0.124nm ，γ-Fe ：0.126nm 。

金属学与热处理第一章习题1.作图表示出立方晶系（1 2 3）、（0 -1 -2）、（4 2 1）等晶面和[-1 0 2]、[-2 1 1]、[3 4 6] 等晶向3.某晶体的原子位于正方晶格的节点上，其晶格常数a=b≠c，c=2/3a。

今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距，2个原子间距和3个原子间距，求该晶面的晶面参数。

解：设X方向的截距为5a，Y方向的截距为2a，则Z方向截距为3c=3X2a/3=2a，取截距的倒数，分别为1/5a，1/2a，1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为（2 5 5）4.体心立方晶格的晶格常数为a，试求出（1 0 0）、（1 1 0）、（1 1 1）晶面的晶面间距，并指出面间距最大的晶面解：（1 0 0）面间距为a/2，（1 1 0）面间距为√2a/2，（1 1 1）面间距为√3a/3三个晶面晶面中面间距最大的晶面为（1 1 0）7.证明理想密排六方晶胞中的轴比c/a=1.633证明：理想密排六方晶格配位数为12，即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切，成正四面体，如图所示则OD=c/2，AB=BC=CA=CD=a因△ABC是等边三角形，所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2则有(CD)2=(OC)2+(1/2c)2，即因此c/a=√8/3=1.6338.试证明面心立方晶格的八面体间隙半径为r=0.414R解：面心立方八面体间隙半径r=a/2-√2a/4=0.146a面心立方原子半径R=√2a/4，则a=4R/√2，代入上式有R=0.146X4R/√2=0.414R9.a）设有一刚球模型，球的直径不变，当由面心立方晶格转变为体心立方晶格时，试计算其体积膨胀。

b）经X射线测定，在912℃时γ-Fe的晶格常数为0.3633nm，α-Fe的晶格常数为0.2892nm，当由γ-Fe转化为α-Fe时，求其体积膨胀，并与a）比较，说明其差别的原因。

三元相图练习题三元相图练习题1⼀、在如图所⽰的相图中完成下⾯各个问题。

（25分）1. 直接在给定图中划分副三⾓形；2. 直接在给定图中⽤箭头标出界线上温度下降的⽅向及界线的性质；3. 判断化合物D 和M 的性质；4. 写出各⽆变量点的性质及反应式；5. G 点的析晶路程；6. 组成为H 的液相在完全平衡条件下进⾏冷却，写出结晶结束时各物质的百分含量（⽤线段⽐表⽰）。

解：1、见图；2、见图；3、 D ，⼀致熔融⼆元化合物，⾼温稳定、低温分解；M ，不⼀致熔融三元化合物；4、 E1，单转熔点，M C A L +?+E2，低共熔点，M B C L ++?E3，单转熔点，M B A L +?+E4，过渡点，B A D L +?→←5、6、过H 点做副三⾓形BCM 的两条边CM 、BM 的平⾏线HH 1、HH 2，C%=BH 2/BC ×100%，B%=CH 1/BC ×100%，C%=H 1H 2/BC ×100%1 没有⼼脏我还可以思念你没有下体我还可以燃烧你■■■■■■■■■■■■■张为政整理■■■■■■■■■■■■■勿删■■■■■■■■■■■■■■ L ? A f=2 熔体G L f=3 G[B ，(B)] 1[B,B+(A)] L ?A ＋B f=1 E 3[2,A+B+(M)] L ＋A ?B ＋M f=0 E 3[3,A 消失+B ＋M] L ? B ＋M f=2 E 2[4, B ＋M +(C)] L ?M ＋C ＋B f=0 E 2(L 消失)[G,M+B+C]⼆（20分）下图为CaO-A12O3-SiO2系统的富钙部分相图，对于硅酸盐⽔泥的⽣产有⼀定的参考价值。

试：1、画出有意义的付三⾓形；2、⽤单、双箭头表⽰界线的性质；3、说明F、H、K三个化合物的性质和写出各点的相平衡式；4、写出M熔体的冷却平衡结晶过程；5、为何在缓慢冷却到⽆变量点K（1455℃）时再要急剧冷却到室温？解：⼆1、画出有意义的付三⾓形；（如图所⽰）；（4分）2、⽤单、双箭头表⽰界线的性质；（如图所⽰）；（4分）3、说明F 、H 、K 三个化合物的性质和写出各点的相平衡式；（4分） F 点低共熔点，LF →C 3A+C 12A 7+C 2SH 点单转熔点，LH+CaO →C 3A+C 3SK 点单转熔点，LK+C 3S →C 3A+C 2S4、分析M #熔体的冷却平衡结晶过程并写出相变式；（4分） M 点：5、为何在缓慢冷却到⽆变量点K （1455℃）时再要急剧冷却到室温？（4分）因为缓慢冷却到K 点，可以通过转熔反应L+C2S →C3S 得到尽可能多的C3S 。

三元合金相图工业上使用的各种材料大多数是多元合金。

多元合金相图的测定比较复杂，所得到的相图也很少，应用较多的多元相图是三元相图。

三元合金相图由两个独立的成分变量，再加上温度变量应该用立体图形来表示;由一些空间曲面构成相图。

但是实际所用的三元相图主要是它们的各种截面图或投影图。

本章除了学习一些典型的立体相图以外，着重进行各种截面图或投影图分析。

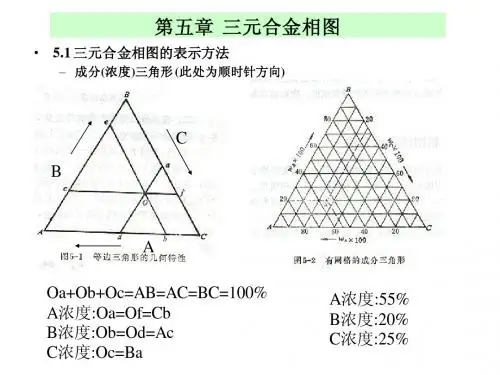
§3－1 三元相图的基本知识一．浓度的表示方法三元合金有两个组元的浓度是可以独立变化的，成分常用三角形中的一个点来表示，称为浓度三角形。

三个顶点代表三个纯组元，每个边是一个二元合金系的成分轴。

1.等边三角形在★图9－1浓度三角形中的任意一点（例如Ｏ点）均代表一个三元合金。

三个组元的含量按如下规则确定。

过0点作A组元对边平行线交于AＣ或AB边于b、e两点，bC％或Be％分别表示合金0中的含A％；同理可以求出含B％和含C％。

三元合金0的成分：A%＝Cb％= Be％B％＝Ac％ =Cf%C％＝Ba％=Ad%（或1－A%－B％）２．其它三角形当三元合金中各组元含量相差较大时，可以采用其它形式的三角形，否则，合金成分点可能非常靠近一边或某一顶点。

当某一个组元含量远大于其它二组元时，可以采用直角三角形，例如★图9－２直角三角形ABC。

一般把含量最高的组元放在直角位置，两直角边则代表其它两组元的含量。

例如01点所代表的三元合金成分C％＝Ac1％B％＝Ab1%A％＝1－A％－B％当某一个组元含量远小于其它二组元时，可以采用★图9－３等腰三角形。

一般把含量最高的组元放在底边位置，两腰则代表其它两组元的含量。

例如ｘ点所代表的三元合金成分C％＝Ac％B％＝Ab%A％＝Ba％3.成分三角形中两条特殊线浓度三角形中有两条特殊性质的直线（1）过三角形顶点的直线，两个组元浓度之比为定值。

如★图9-4b中CE线上的任意一个三元合金含A%/B%为定值。

(A%/B%=BE/AE)（2）平行于三角形任意一边的直线，一个组元的浓度为定值。