当前位置：文档之家 › 第5章 三元相图

第5章 三元相图

  • 格式：ppt
  • 大小：518.00 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

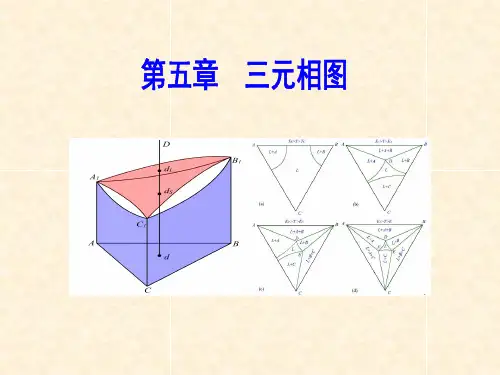
第五章 三元相图

第五章 三元相图

B
B%
C%
A
← A% C% →
C
b c
a
图 部分浓度三角形
§5.1.2 浓度三角形中具有特定意义的线
1）与某一边平行的直线
C
含对角组元浓度相等
A% d C% c
Bc C% 100% BC
A
B B% 图 平行于浓度三角形某一条边的直线
确定O点的成分 1）过O作A角对边的平行线 2）求平行线与A坐标的截距 得组元A的含量 3）同理求组元B、C的含量
三元系中如果任意两个组 元都可以无限互溶,那么它们 所组成的三元合金也可以形 成无限固溶体,这样的三元合 金相图,叫三元匀晶相图。
相图概况
[1] 特征点： ta, tb, tc- 三个纯组 元的熔点； [2]特征面：液相面、固相面； [3]相区：L, α, L+α。
图 三元匀晶相图
§5.3.1 相图分析
( A B )
Ax nE nA Ee
( A B C )
Ax ne nA Ee
§5.4.2 组元在固态下有限溶解，具有共晶转变的三 元相图
1.相图分析
从占有空间的角度看,固态有限互溶三元共晶相图比固态 完全不互溶三元共晶相图要多三个单相区(α、 β、 γ)和三个 固态两相区(α+β、 β+ γ、 α+ γ)。
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程，了解合金在 平衡冷却过程中发生相变的临界温度，以及可以了解合金在 一定温度下所处的平衡状态。 但是，用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用

三元合金相图

三元合金相图

图5.3 直角成分三角形
如图 5.3 所示，当三元系成分以某一组元为主，其他两个组元含量很少时，合金成分点 将靠近等边三角形某一顶点。若采用直角坐标表示成分，则可使该部分相图更为清楚的表示 出来，一般用坐标原点代表高含量组元，而两个互相垂直的坐标轴代表其他两个组元的成分。 5.1.3 成分三角形中特殊的点和线
接。
三相平衡区的特点：直边三角形；两相区与之线接；单相区与之点接。
图 5.24 组元在固态有限互溶的三元相图的等温截面示意图 （3）变温截面
图 5.25 是组元在固态有限互溶的三元相图的变等温截面示意图。
图 5.8 三元相图中的重心定律
如图 5.8 所示，R 合金的重量与三个相的重量有如下关系
WR ⋅ Rd = Wα ⋅αd
Wα
= S∆Rβγ S ∆αβγ
= Rd αd
WR ⋅ Re = Wβ ⋅ βe
Wβ
= S∆Rαγ S ∆αβγ
= Re βe
WR ⋅ Rf = Wγ ⋅ γd
Wγ
= S∆Rαβ S ∆αβγ
以图 5.19 中合金 O 为例，可定量 计算其室温平衡组织的各组织组成物 的相对含量。
WA
=
oq Aq
×100%
WL
=
Ao Aq
×100%
W( A+C) = Eq × Ao ×100% W0 Ef Aq
W( A+B+C) = qf × Ao ×100%
W0
Ef Aq
图 5.20 是合金 o 的室温组织示意
(A+B+C)
5.3.2 固态有限互溶的三元共晶相图 固态下有限互溶的三元相图是由三对在液态无限互溶，而在固态有限互溶的二元共晶相

第5章三元共晶相图

第5章三元共晶相图

A+B+C
A+B+C A+B+C A+B+C A+B+C
A初+( A+B+C ) B初+( A+B+C ) C初+( A+B+C )
( A+B+C )
e1
三元 简单共晶相图 平衡结晶产物 小结
A e
e3
B
e2
C
课堂练习
如图所示，已知A,B,C三组元固态完全不互溶，A，B，C的质量分数 分别为80％，10％，10％的O合金在冷却过程中将进行二元共晶反应和三 元共晶反应，在二元共晶反应开始时，该合金液相的质量分数成分（a点） A为60％，B为20％，C为20％，而三元共晶反应开始时的液相成分（E点） A为50％，B为10％，C为40％。 （1）试计算A(初)％，（A+B）％和 （A+B+C)％为多少？ （2）写出图中Ⅰ和P合金的室温平衡组织。
投影图
A-e-B B-e-C
相变类型
L A+B L B+C L C+A L A+B+C
E1
相 区 L+C+A 四 相 L+A+B+C 区
A+B+C
C-e-A A-B-C A-B-C
A1-B1-C1
A3 A2 A1
TB B3 B2
E3
TC E
E2
B1
A e
BA
C3 C2 C1
B
C
A
e1
A
B
C1
C
液 相 面

第五章 三元相图

第五章 三元相图

B1
AБайду номын сангаас
B
C
（二）等温截面及其投影
L+C L
L+C L
L+A
L+A+C L+A L+C L
L+A+C L L+B
L+B
L+A+C L+A+B+C
C B
A+B+C
A
L+A+C L+A+B+C L+A+C L L+B
1.等温截面上的三相平衡区都是直边三角形，与 三角形相邻接的是两相平衡区 2.三角形的顶点与单相区相接，分别表示该温度 下三个平衡相的成分
LA+ C
TA C1 A3 A2 A1
E
L B + C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
——
TB E1 B3 B2 E2 E B1
A
E3
TC
B
C3 C2 C1
C
中 转平 间 变衡 开 共 三面
始晶相
A3
A2 A1
E1
B2
B1
LA+ B
——
TA
A3 A2 A1
E TB E1 E3 TC E2 B3 B2 B1 B3 E2 B1 E C2 C1
B 10 20 30 40
50
C% 60 70 80 90
50 40 ← A%
30
20 10
C
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60

第五章 三元合金相图

第五章 三元合金相图

二元共晶
三元共晶
第四节三元共晶相图
通过成分三角形 顶点的变温截面
第四节三元共晶相图
(四) 投影图 1. 投影图分析
2. 合金O结晶过程 L----L+A------------L+A+(A+B)---------------A+(A+B)+(A+B+C)
二元共晶 三元共晶
第四节三元共晶相图
3.合金O在室温下的相和 组织含量
第一节三元合金相图的表示方法
B （1）确定O点的成分 1）过O作A角对边的平行线 B% C% 2）求平行线与A坐标的截距 得组元A的含量 3）同理求组元B、C的含量 O A C
← A%
第一节三元合金相图的表示方法
C B
A
Oa+Ob+Oc=AB=AC=BC=100% A浓度:Oa=Of=Cb B浓度:Ob=Od=Ac C浓度:Oc=Ba A浓度:55% B浓度:20% C浓度:25%
90 • 标出 50%A+20%B+30%C 的合金 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
80
70
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
第一节三元合金相图的表示方法
二、在成分三角形中具有特定意义的直线 B 成分三角形中特殊的点和线
第五章 三元合金相图
三元系相图简介
相图基本知识
三元相图的主要特点——立体图形，主要由曲面构成
三元系相图简介
垂直轴表示温度。 成分表示在棱柱底，通常是 一等边三角形。 棱柱的每个侧面表示三个二 元系统，如AB，BC，AC。

第5章-三元相图PPT课件

第5章-三元相图PPT课件
•20
2、结晶过程分析 O 自液态缓冷至于液互
相相交时，开始从液相中结晶出 α 固溶体，此时液相的成分l1即为合金成分， 而固相的成分为固相面某一点 s。
α 相越来 越多，固相的成分由s1点沿固相面移至s2 点，液相成分自l1点移至 l2点，由直线法则可知，合金的成分点必落 在l2和s2的连线上。
Ca＝WA＝30％ Ac＝WC＝60％ Ab＝WB＝10％。
中都有应用，但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金，它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律： a、 当温度一定时，若已知两平衡相的 成分，则合金的成分必位于两平衡相成分 的连线上； b、 当温度一定时，若已知一相的成分 及合金的成分，则另一平衡相的成分必位 于两已知成分点的连线的延长线上； c、 当温度变化时，两平衡相的成分变 化时，其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较，组元数增加 了1个,即成分变量是两个，故表示成分的坐 标轴应为2个,需要用一个平面表示，再加上 垂直于该平面的温度轴，这样三元相图就 演变成一个在三维空间的立体图形，分隔 相区的是一系列空间曲面，而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金

第5章 三元合金相图

第5章 三元合金相图
相对应成分点的连接直线称为连接线， 或称共轭连线；
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时，三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定，三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2， α相的成分变到mp线上的α2 ， α2在 L2和 x 两点连线的延长线上，根据杠杆定律可 算出此时两相相对量为：
L2 %

x 2 L2 2
100 %
2%

L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中，就得到三元相图的投影图， 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中，并在每一条投影上标注 相应的温度，就得到等温线投影图；类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上，包晶反应结束而进入α＋β两相区。反应结束 时α和β两相的相对量为

第五章 三元相图

第五章 三元相图

5.1
三元相图的成分表示法
C
二元系的成分可用一条 直线上的点来表示；三元 系合金有两个独立的成分 参数，所以必须用一个平 面三角形来表示，这个三 角形叫做成分三角形或浓 度三角形。常用的成分三 角形是等边三角形，有时 也用直角三角形或等腰三 角形。 A
A%
C%
B%
B
浓度三角形
5.1.1 浓度三角形 1. 等边三角形 三角形的三个顶点A，B， C分别表示3个纯组元， 三角形的边AB，BC， CA分别表示3个二元系 的成分坐标，三角形内 的任一点都代表一定成 分的三元合金. A 一般按顺时针(或逆时针) 标注组元浓度。
L(三元) ΔT α(三元)
自由度：f=c-P+1=3-2+1=2 故三元匀晶转变区可有两个自由度： 温度和相成分。
5.3.1 相图分析
1 画图 (1) 先画一成份三角形 (应为正三角形) (2) 画温度轴 (3) 画二元匀晶相图(每 两个合金上存在一个二 元相图) ---三元系立体图可视为三 个二元系在空间的延伸 液相面----三个二元系的液相线 所围成的面. 固相面----三个二元系的固相线 所围成的面.
5.4
三元共晶相图
TA A2 A3 A1 E3 E C2 C3 C1 C TB
5.4.1 组元在固态互不溶,具有共晶转变的相图
一、相图分析
1. 画图 (1) 先画一成份三角形
(2) 画温度轴
(3) 画二元共晶相图
E1 TC E2
B2 B3
B1 B
三个二元共晶相图向空间 A 延伸 (4) 画出四相平衡共晶转变平 面A1B1C1 (5) 三个二元系共晶点向空间 延伸为三条共晶沟线，交 A1B1C1面于E点，称为共晶点

5.1_三元合金相图

5.1_三元合金相图
34
本节要点
概念：成分三角形、截面图、水平截面、垂直截 面、等温线投影图、直线法则、重心定律
三元合金成分的确定 截面图和投影图 杠杆定律和中心法则
下节内容：固态互不溶解的三元共晶相图
35
思考题
1 下图的成分三角形中有P、R、S、T 四个材料点， 问哪个点的材料，其成分为： A=20%， B=10%，C=70%
B
B%
C%
A
← A%
C
6
浓度确定
确定O点的成分
B
1）过S作A角对边的平行线
2）求平行线与A坐标的截距
得组元A的含量
B%
3）同理求组元B、C的含量 O
A
← A%
C%
C
7
课堂练习
B
1 确定合金I、II、
90
III、IV的成分
80
I 点：
A%=60% B%=30% C%=10%
70
60 B% 50
40 30 I
(BM BN) BO BN
BO BN BM BN
N O M N
NO MN
1
1
NO MN
OM MN
ON OM
推论：当给定材料在一定温度下处于两相平衡状态时，若其
中一相的成分给定，另一相的成分点必在两已知成分点连线
的延长线上；若两个平衡相的成分点已知，材料的成分点必
然位于此两个成分点的连线上。
19
其它浓度三角形
1） 等腰浓度三角形
组元B的含量很少
B
成分点靠近AC边
按比例放大AB、BC边
A
C
20
2） 直角浓度三角形
组元A占绝大多数时
原点为基体组元A

第五章 三元相图

第五章 三元相图

三 一 组元在固态互不相溶的共晶相图
元 相
（1）相图分析
图
点：熔点；二相共晶点；三相共晶点。
两相共晶线
第
液相面交线
三
线：EnE 两相共晶面交线
液相单变量线
节
液相区与两相共晶面交线 共
晶
相
图
11
第 五
第三节 三元共晶相图
章 一 组元在固态互不相溶的共晶相图
三
（1）相图分析
元
液相面
相
固相面
图
面： 两相共晶面 三相共晶面
三 （1）相图分析
元
点：熔点；二元共晶点；三元共晶点。
相
两相共晶线 液相面交线
图
线：EnE 两相共晶面交线
液相单变量线
液相区与两相共晶面交线
第
固相单变量线
三
液相面
固相面(组成)
节 面： 二相共晶面
共
三相共晶面
晶
溶解度曲面：6个
相
两相区：6个
图
区： 单相区：4个
三相区：4个
四相区：1个
16
第 五
第三节 三元共晶相图
三 5 共线法则与杠杆定律
元 两条推论
相
（1）给定合金在一定温度下处于两相平衡时，若其中一个
图 相的成分给定，另一个相的成分点必然位于已知成分点连线
的延长线上。
第
（2）若两个平衡相的成分点已知，合金的成分点必然位于
一 两个已知成分点的连线上。
节
基 本 知 识
5
第 五
第一节 相图基本知识
章 6 重心法则
7
第 五
第二节 三元匀晶相图
章 3 等温截面（水平截面）

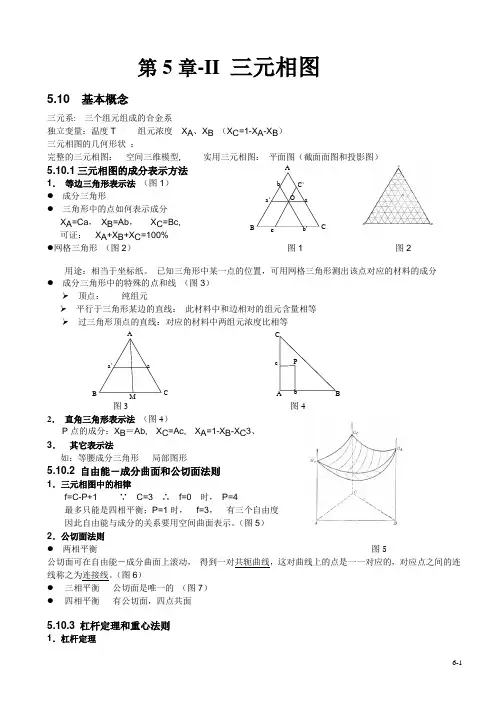
东南材料科学基础 第5章-II 三元相图提纲

东南材料科学基础 第5章-II 三元相图提纲

A B C O b b' c C ’a a ’ 第5章-II 三元相图5.10 基本概念三元系: 三个组元组成的合金系独立变量：温度T 组元浓度 X A 、X B （X C =1-X A -X B ）三元相图的几何形状 ：完整的三元相图： 空间三维模型,实用三元相图： 平面图（截面面图和投影图）5.10.1三元相图的成分表示方法1． 等边三角形表示法 （图1） ● 成分三角形 ● 三角形中的点如何表示成分 X A =Ca ， X B =Ab ， X C =Bc, 可证： X A +X B +X C =100% ●网格三角形 （图2）图1图2用途：相当于坐标纸。

已知三角形中某一点的位置，可用网格三角形测出该点对应的材料的成分 ● 成分三角形中的特殊的点和线 （图3） ➢ 顶点： 纯组元➢ 平行于三角形某边的直线： 此材料中和边相对的组元含量相等 ➢ 过三角形顶点的直线：对应的材料中两组元浓度比相等ABCaa ’CPb图3 图4 2． 直角三角形表示法 （图4）P 点的成分：X B ＝Ab, X C =Ac, X A =1-X B -X C 3、 3． 其它表示法如：等腰成分三角形 局部图形5.10.2 自由能－成分曲面和公切面法则1．三元相图中的相律f=C-P+1 ∵ C=3 ∴ f=0 时， P=4最多只能是四相平衡；P=1时， f=3， 有三个自由度 因此自由能与成分的关系要用空间曲面表示。

（图5） 2．公切面法则 ● 两相平衡图5公切面可在自由能－成分曲面上滚动， 得到一对共轭曲线，这对曲线上的点是一一对应的，对应点之间的连线称之为连接线。

（图6）● 三相平衡 公切面是唯一的 （图7） ● 四相平衡 有公切面，四点共面5.10.3 杠杆定理和重心法则1．杠杆定理aboaabob==%%βα%100⨯=PMOMWα%100⨯=QRORWβ%100⨯=STOTWγA BCabo .图6 图7（1）共线法则当三元系处于两相平衡时，此两相的成分点和材料的成分点位于成分三角形的同一直线上。

第5章 三元合金相图

第5章 三元合金相图

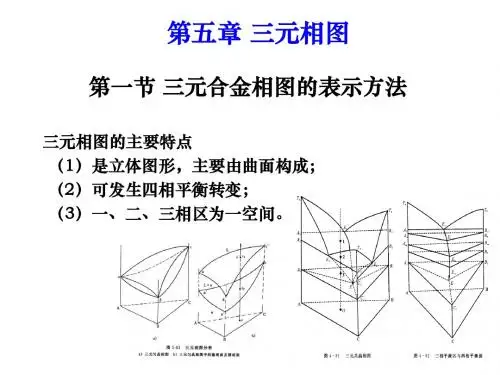
第5章 三元合金相图由A-B-C 三组元组成的合金称三元合金，其相图称三元相图。

要确定三元合金的成分，必须给出其中两个组元的成分。

所以，在三元相图中表示成分的坐标轴有两个。

5-1 三元相图成分表示方法在三元相图中表示成分的两个坐标轴原则上可以交成任何角度，但一般采用等边三角形的三个边表示。

设P 为等边三角形内任意点，从P 点分别做三条边的平行线，交三条边于a 、b 、c 点。

根据等边三角形的几何性质：%100==++=++AB Ba Ac Cb Pc Pb Pa 因此，可用Cb 、Ac 、Ba 表示A 、B 、C 的成分。

这样，三角形中每一点都表示一个三元合金的成分。

该三角形称浓度三角形，或成分三角形。

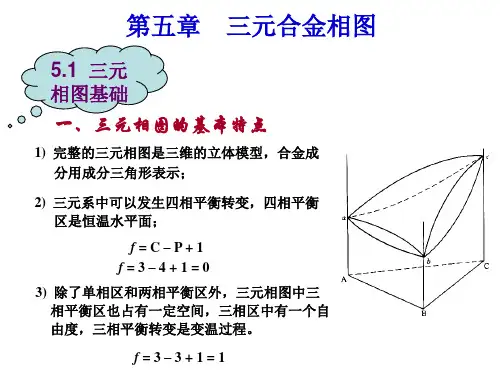
5-2 三元相图中的定量法则一、直线法则二元合金处于两相平衡时，自由度f =2-2+1=1，温度和成分两个变量中只有一个可以独立改变，如当温度一定时，两个平衡相的成分是确定的。

三元合金处于两相平衡时，f =3-2+1=2，当温度一定时，两个平衡相中，只有一个相的成分可独立改变。

当温度和其中一个相的成分一定时，剩余相的成分是确定的。

假设某三元合金的成分点为P ，在某一温度下，该合金处于α、β两相平衡，两相的成分点为a 、b （P133图4）。

可以证明（P133），此时，a 、b 、P 三成分点在一条直线上，且P 点位于a 、b 之间。

这一规律称直线法则。

二、杠杆定律三元相图中的杠杆定律与二元相图中的类似，即同样也只适用于两相区，但形式上略有不同，在直线法则的基础上：%100%⨯=ab Pbα， %100%⨯=ab Paβ三、重心法则三元合金处于α、β、γ三相平衡时，f =3-3+1=1。

当温度一定时，三个平衡相的成分是确定的，其成分点a 、b 、c 构成一个三角形。

若将成分比喻成重量，则合金的成分点P 一定落在成分点a 、b 、c三角形的重心处，这一规律称重心法则。

其数学表达式为（证明见P135）%100%⨯''=a a a P α %100%⨯''=b b b P β %100%⨯''=c c c P γ 其实，重心法则可看作是直线法则和杠杆定律的变形。

材料学基础第5章三元相图

材料学基础第5章三元相图

材料科学基础
第五章
5.6三元相图小结
材料科学基础
第五章
一、单相状态 f＝3－1＋1＝3，而一个温度变量和两个成分变量之间没有任何
相互制约的关系，因此，不论是等温截面还是变温截面，单相区可能具 有多种多样的形状。 二、两相平衡 立体图：共轭曲面。 成分变化：蝶形规则。 等温图：共轭曲线（可用杠杆定律） 变温截面：判定转变温度范围和相转变过程，不能用杠杆定律。 三、三相平衡 立体图：三棱柱，棱边是三个平衡相单变量线。
二、投影图
材料科学基础
第五章
投影图的作用：合金结晶过程分析、相组成物相对量计算、组织组成 物相对量计算。
图8.17 三元共晶相图的投影区
表8.2 各典型区域合金的凝固组织过程及室温组织
材料科学基础
第五章
区
凝固过程
室温组织
Ⅰ
L→α
α
Ⅱ
L→α ，α→βⅡ
α＋βⅡ
Ⅲ
L→α ，α→βⅡ，α β
α＋βⅡ＋γⅡ
(1)当给定合金在一定温度下处于两相平衡状态时，若其中一相的成分 给定，则根据直线法则，另一相的成分点必位于两已知成分点连线的 延长线上。 (2)如果两个平衡相的成分点已知，则合金的成分点必然位于两平衡相 成分点的连线上，根据两平衡相的成分，可用杠杆定律求出合金的成 分。
5.2.2重心定律
x，y，z分别为α，β，γ成分点，则
材料科学基础
第五章
投影图有两种。一种是把空间相图中所有相区间的交线部投影到浓度 三角形中，借助对立体图空间构造的了解，可以用投影图来分析合 金的冷却和加热过程。另一种是把一系列水平截面中的相界线投影 到浓度三角形中。每一条线上注明相应的温度，这样的投影图叫等 温线投影图。等温线可反映空间相图中各种相界面的变化趋势，等 温线越密，表示这个相面越陡。

第5章-2---三元相图1

第5章-2---三元相图1

5.13 四相平衡共晶系
5.13.4 综合投影图
冷却过程中有 四相反应
L-a+b+
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系 L
L－a
合金 o
L－a+b
L－a+b+
a+a + b+a+b++b+
L
合金 o’
L－b
L－a+b
a+b
b+a+b+a+
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.3、垂直截面
5.13 四相平衡共晶系
5.13.4 综合投影图
1、作法：将立体图中 各空间曲面、曲线投 影到成分三角形
2、用途： a、可得到各个面的投影 b、可得到各相区的投影 c、各种成分的平衡冷却
过程 d、组织分区图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
I a; II a + bII ; III a + bII + II ; IV a + (a + b ) + bII ; V a + (a + b ) + bII + II ; VI a + (a + b ) + (a + b + ) + bII + II
用杠杆定理
5.12 三相平衡三元
5.12.2 几种典型的三相平衡三元系
5.12 三相平衡三元系

大学材料科学基础第五章三元相图(3)

大学材料科学基础第五章三元相图(3)
第五节 三元相图和类型
生产中使用的合金除了二元之外，还有三元、 甚至多元，即使是二元合金，由于杂质元素的 存在，在偏析区它们也不能看成是二元的。三 元合金的性质不同于二元，也不能简单的从二 元相图来推断，必须使用三元相图进行研究。 本章重点是建立三元相图的空间概念，三元相 图的识别和使用。 三元相图比二元相图复杂，但基础还是二元相 图。
C
连接线法则 1) 在等温截面上，通过给出的 合金成分点，只能有唯一的 一条共轭连线。 温度不变时，给定成分的合金 处于两相平衡时其成分不能 随意变动。当合金成分沿共 轭连线变化时，两平衡相的 成分是不变化的 2) 共轭连线不可能位于从三角 形顶点引出的直线上 (图中 所示的Af线)。
选分结晶原理 液、固两相平衡共存时，液相中低 熔点组元与高熔点组元含量的比 值，应大于与之共存的固相中低、 高熔点组元含量的比值：
2．三相平衡及三相平衡反应
由相律可知，恒温下的 三相平衡，三个共存相 的成分任意一相都不可 变动，即在等温截面上 是满足热力学平衡条件 的三个成分点 三相平衡时，三个相也两两平衡，按两相平衡时的直线法 则，两两平衡相间可做出三条共轭连线 (图5—90b)，这三条 共轭连线在等温截面上围成一直边三角形，称为共轭三角形。 位于共轭三角形内的合金，其成分在共轭三角形内变动时三 个平衡相成分固定不变。 • 三相区的三条棱边线，分别表示了三相平衡共存时每一相 的成分随温 度的变化迹线，故称为成分变温线；又因为三相 共存时各相的成分和 温度只有一个独立变量，所以又称为单 变量线。
A
注意该图与二元相图的区别，两者只是在 形式上相似。在变温截面图上不能使用杠杆定 律，也不能确定多相平衡时各相的成分，因为 在图上无法确定连接线。
垂直截面图的用途：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1）3个液相面以上：L； 2）3个液相面与6个二元空间曲面间：L+A,L+B,L+C; 3）6个二元共晶曲面和1个三元共晶面之间构成的3个空间三 棱曲面柱体:L+A+B, L+A+C,L+B+C; 4)1个三元共晶面（固相面）： L+A+B+C； 5）三元共晶面（固相面）以下：A+B+C。 成分变化线：随温度降低，空间三棱曲面柱体中三个相 的成分变化的轨迹。 等温三角形：固定温度下三个平衡相的成分点连线（直 线）f=0
五、三元相图分析法总结
1．两相平衡
等温截面
成分变化：蝶形规则 共轭线：可杠杆定律
变温截面
判定转变温度范围， 不能用杠杆定律。 2．三相平衡 等温截面：直边 三角形，三顶点为 相成分点，可用重 心法则
变温截面： 曲边三角形或多边形 三相反应的判定： 1) 变温截面上
2)投影图判断三相反应 液相单变量线穿 过两旁固相成分点连 线的为二元共晶型， 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应，且靠近单变线 的为生成相
3．浓度三角形中特殊线： 平行浓度三角形任一边的直线 从浓度三角形的一个顶点到 对边的任意直线 4. 其它成分三角形的形式：
二、杠杆定律及重心法则
单相平衡勿须计算，四相平衡无从计算 两相平衡：杠杆定律 1．三元相图中杠杆定律 共线法则：三元合金中两相平衡时合金 成分点与两平衡相成分点在浓度三角形 的同一直线上 杠杆定律表达式：α%=EO/DE×100%，β=OD/DE×100% 注意：当一个合金O在液相的凝固过程中，析出α相成分不变时， 液相成分一定沿α相成分点与O点连线延长线变化。 2．三相平衡重心法则（重量三角形重心） x,y,z分别为α,β,γ成分点，则 α%=oa/ax×100%， β=ob/by×100%， γ%=oc/cz×100% 为什么三角形是直线而不是曲线连接？
三、匀晶三元相图
1． 立体模型 液相区，固相区，液、固两相区
2． 合金凝固过程及组织 a.平衡凝固 b.蝶形法则：如图 匀晶合金凝固中相成分变化 凝固中固、液相成分沿固相面、液相面呈曲线变化，每一个 温度下的固、液相成分连线在浓度三角形中投影呈蝴蝶状
3．等温截面 匀晶三元系的等温截面（实验方法测定，而非立体截取） 两相区内， f=3-2+1=2, T一定时,f=1, 只有一个平 衡相的成分 可以独立改 变。对于一 定的合金， 连接线唯一。 等温截面作用： 1. 该温度下三元系中各合金的相态 2．杠杆定律计算平衡相的相对量 3．反映液相面、固相面走向和坡度，确定熔点、凝固点
4、变温截面（实验测试而得）
变温截面的能与不能： 能分析某合金不同温度下状态分析合金的相变过程； 变温截面上的液相线和固相线不能表示平衡相的成分， 不能根据这些线应用杠杆元共晶相图模型（教材图5－12）
3个初晶液相面； 3条二元共晶线(共晶转变，三相平衡，f=1)； 1个三元共晶点(四相平衡,f=0);1个三元共晶面(固相面) 6个二元共晶曲面 每3条成分变化线（单变量线）构成1个空间三棱曲面柱体 9个相区如下：
2． 简单三元共晶中合金的凝固过程和组织
投影图
如图x合金 L→A，L→A+B，L→A+B+C
4． 简单三元共晶的等温截面 二相区： 三相区：三角形，三个顶点代表成分点
5．变温截面： 平行于浓度三角形一边的变温截面cd 分析合金x的结晶过程：L→B，L→A+B，L→A+B+C 分析合金O的结晶过程 通过顶点的变温截面 注意：不能用杠杆定律，
第五章
三元相图
必要性：工业材料为多元合金 本章主要内容： 1. 三元相图的表达方式，使用方法 2．几种基本的三元相图立体模型 3．各种等温截面，变温截面及各相区在浓 度三角形上的投影图 4．典型合金的凝固过程及组织，各种相变 过程及相平衡关系。
一、三元相图的成分表示法
1．浓度等边三角形：
三个顶点为纯组元， 三条边为二元合金， 三角形内任一点为三元合金 2．三元合金成分确定 浓度等边三角形
3．四相平衡
反应类型判断 液相面投影图： 指向结点单变量线数为产物数 变温截面：根据水平线上、下方三相区判断
4．三元相图截面图上相区接触法则
相数差为1的两相邻相区线段为界 差大小1或等于零的为点接触
等温截面上 单相区边界线走向