当前位置：文档之家 › 第五章 三元合金相图

第五章 三元合金相图

  • 格式：ppt
  • 大小：6.49 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

第五章 三元相图

第五章 三元相图
F B% A ← A% C%
D a2 a1
C
课堂练习
• 绘出C / B ＝1/3的合金
C 1 25% B 3 75%
B
90 10 20 30 40
80
70
60 • 绘出A / C ＝ B% 50 1/4的合金 40 30 20 10 A 90 80 70 60 50 40 ← A%
50
C%
B
10 20 30 40
80
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
课堂练习
• 确定合金I、II、 III、IV的成分
II点： A%=20% B%=50% C%=30% 70 60 B% 50 40 30 20 10 A 90 80 70 60 90
B
10 20 30 40 II
课堂练习
90 • 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
课堂练习
90 • 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
2. 浓度三角形中具有特定意义的直线
90 80 70
B 10 20 30 40 50

三元合金相图

三元合金相图

三元合金相图第五章三元合金相图内容提要：本章介绍三元相图的基本知识。

三元相图是由一系列空间（相区）组成的三维立体图形，其成分用浓度三角形表示。

一些二元相图的规则，如相区相邻规则、杠杆定律、在三元相图也适用。

为了便于分析，常采用相图的某些投影图和截面图。

三元相图是三元系相平衡关系的图解。

因此根据三元相图可确定该三元系任一成分的合金随温度变化发生的相平衡转变及相平衡点温度，同时也可确定任一给定温度下，该合金处于平衡状态下的相组成和组织组成物，并可利用直线法则（杠杆定律）或重心法则在其等温截面图上计算各平衡相的相对量。

本章采用三元匀晶相图和三元共晶相图为例介绍了三元相图的基本结构特点以及进行上述分析的具体步骤和方法。

通过三元匀晶相图的分析，介绍了三元系两相平衡转变特点、蝴蝶形变化规律及如何在两相区利用杠杆定律计算平衡相相对量。

通过三元共晶相图的分析，介绍了三元系中的三相共晶平衡转变和共晶平衡转变特点及三相区和四相区的特征。

着重介绍了利用投影图，等温截面和垂直截面分析给定合金相平衡和相转变的步骤与方法：以及杠杆定律和重心法则在平衡相相对量计算中的应用。

本章专门分出一节对三元相图中相平衡特点进行了总结，为进一步分析复杂三元相图打下基础。

最后结合三个实用相图分析，力图使初学者初步掌握分析复杂三元相图的能力。

基本要求：1. 三元系的相平衡和相平衡转变的特征：以及不同相区的基本结构特征。

2. 灵活运用三元相图的投影图、垂直截面图和等温截面图分析三元合金随温度变化发生的相平衡转变及形成的组织组成物。

3. 在等温截面图上熟练运用直线法则（杠杆定律）和重心法则计算合金各平衡相的相对量。

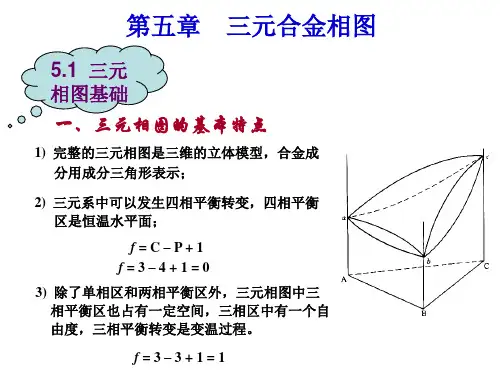
第一节三元相图的表示方法相律：f=c-p+1（对凝聚态体系）。

对二元系（Binary System）：令p=1（一个体系中至少有一个相），则，f2=2-1+1=2。

用T-x图表示，二维、平面图。

对三元系（T ernary System）：令p=1（一个体系中至少有一个相），则f3=3-1+1=3。

三元合金相图

三元合金相图

图5.3 直角成分三角形
如图 5.3 所示，当三元系成分以某一组元为主，其他两个组元含量很少时，合金成分点 将靠近等边三角形某一顶点。若采用直角坐标表示成分，则可使该部分相图更为清楚的表示 出来，一般用坐标原点代表高含量组元，而两个互相垂直的坐标轴代表其他两个组元的成分。 5.1.3 成分三角形中特殊的点和线
接。
三相平衡区的特点：直边三角形；两相区与之线接；单相区与之点接。
图 5.24 组元在固态有限互溶的三元相图的等温截面示意图 （3）变温截面
图 5.25 是组元在固态有限互溶的三元相图的变等温截面示意图。
图 5.8 三元相图中的重心定律
如图 5.8 所示，R 合金的重量与三个相的重量有如下关系
WR ⋅ Rd = Wα ⋅αd
Wα
= S∆Rβγ S ∆αβγ
= Rd αd
WR ⋅ Re = Wβ ⋅ βe
Wβ
= S∆Rαγ S ∆αβγ
= Re βe
WR ⋅ Rf = Wγ ⋅ γd
Wγ
= S∆Rαβ S ∆αβγ
以图 5.19 中合金 O 为例，可定量 计算其室温平衡组织的各组织组成物 的相对含量。
WA
=
oq Aq
×100%
WL
=
Ao Aq
×100%
W( A+C) = Eq × Ao ×100% W0 Ef Aq
W( A+B+C) = qf × Ao ×100%
W0
Ef Aq
图 5.20 是合金 o 的室温组织示意
(A+B+C)
5.3.2 固态有限互溶的三元共晶相图 固态下有限互溶的三元相图是由三对在液态无限互溶，而在固态有限互溶的二元共晶相

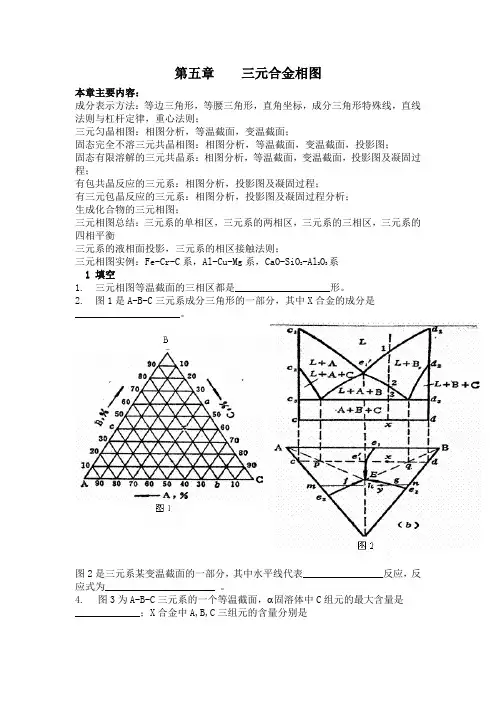
第五章 三元合金相图

第五章 三元合金相图

第五章三元合金相图本章主要内容：成分表示方法：等边三角形，等腰三角形，直角坐标，成分三角形特殊线，直线法则与杠杆定律，重心法则；三元匀晶相图：相图分析，等温截面，变温截面；固态完全不溶三元共晶相图：相图分析，等温截面，变温截面，投影图；固态有限溶解的三元共晶系：相图分析，等温截面，变温截面，投影图及凝固过程；有包共晶反应的三元系：相图分析，投影图及凝固过程；有三元包晶反应的三元系：相图分析，投影图及凝固过程分析；生成化合物的三元相图；三元相图总结：三元系的单相区，三元系的两相区，三元系的三相区，三元系的四相平衡三元系的液相面投影，三元系的相区接触法则；三元相图实例：Fe-Cr-C系，Al-Cu-Mg系，CaO-SiO2-Al2O3系1 填空1. 三元相图等温截面的三相区都是___________________形。

2. 图1是A-B-C三元系成分三角形的一部分，其中X合金的成分是_____________________。

图2是三元系某变温截面的一部分，其中水平线代表________________反应，反应式为______________________ 。

4.图3为A-B-C三元系的一个等温截面， 固溶体中C组元的最大含量是_____________；X合金中A,B,C三组元的含量分别是_____________________________；在X合金的相组成物中，α相的百分含量是______，δ相的百分含量是____________。

图4图315图4是Cu-Zn-Al三元相图2%Al的一个变温截面，合金凝固时，L+α+β三相区将发生____________反应。

图中X合金的化学成分是______________________。

6图5是某三元系变温截面的一部分，合金凝固时，L+M＋C将发生_________________反应。

7 三元相图的成分用__________________________表示。

第五章 三元合金相图

第五章 三元合金相图

第五章 三元合金相图1 根据Fe －C －Si 的3.5%Si 变温截面图（5－1），写出含0.8%C 的Fe-C-Si 三元合金在平衡冷却时的相变过程和1100℃时的平衡组织。

图5－12 图5－2为Cu-Zn-Al 合金室温下的等温截面和2%Al 的垂直截面图，回答下列问题：1） 在图中标出X 合金（Cu-30%Zn-10%Al ）的成分点。

2） 计算Cu-20%Zn-8%Al 和 Cu-25%Zn-6%Al 合金中室温下各相的百分含量，其中α相成分点为Cu-22.5%Zn-3.45%Al ，γ相成分点为Cu-18%Zn-11.5%Al 。

3） 分析图中Y 合金的凝固过程。

Y％图5－23 如图5－3是A-B-C 三元系合金凝固时各相区，界面的投影图，A 、B 、C 分别形成固溶体α、β、γ。

1） 写出P p ''，P E '1和P E '2单变量线的三相平衡反应式。

2） 写出图中的四相平衡反应式。

3） 说明O 合金凝固平衡凝固所发生的相变。

图5－3 图5－44 图5－4为Fe-W-C三元系的液相面投影图。

写出e1→1085℃，P1→1335℃，P2→1380℃单变量线的三相平衡反应和1700℃，1200℃，1085℃的四相平衡反应式。

I，II，III三个合金结晶过程及室温组织，选择一个合金成分其组织只有三元共晶。

5 如图5－5为Fe-Cr-C系含13%Cr的变温截面１）大致估计2Cr13不锈钢的淬火加热温度（不锈钢含碳量０.２％, 含Cr量13％）２）指出Cr13模具钢平衡凝固时的凝固过程和室温下的平衡组织（Cr13钢含碳量2%）３）写出（１）区的三相反应及７９５ 时的四相平衡反应式。

图5－5 图5－66 如图5－6所示，固态有限溶解的三元共晶相图的浓度三角形上的投影图，试分析IV区及VI区中合金之凝固过程。

写出这个三元相图中四相反应式。

图5－77 分析如图5－7所示的三元相图，该合金中E 点成分为27Pb18Sn55Bi ，γ相成分取100％Bi 。

5 三元合金相图

5 三元合金相图

等边成分三角形中具有特定意义的点和线平行于三角形某一条边的直线：凡成分位于该线上的合金，它们所含的、由这条边对应顶点所代表的组元的含量为一定——等含量规则通过三角形某顶点的任一直线：凡成分位于该直线上的所有合金，它们所含的由另两个顶点所代表的两组元的含量之比为一——定比规则单相、两相和三相区为一空间。

w Om w Onαβ=平衡相含量的计算：所计算相的成分点、合金成分点和二者连线的延长线与对边的交点组成一个杠杆。

合金成分点为支点。

计算方法'100%'OF w FF γ=×'100%'OD w DD α=×'100%'OE w EE β=×3) 结晶过程分析成分轴的两端不一定是纯组元；注意：液、固相线不一定相交；液、固相线不是成分变化线，不能运用杠杆定律。

(3) 变温截面(平行于浓度三角形AB边的变温截面)合金x的结晶过程：L→BL→A+BL→A+B+C化，不能应用杠杆定律。

计算室温组织组成物含量100%,100%A L oqw Aq Ao w Aq =×=×。

()()100%100%A C A B C Eq Ao w Ef Aq qf Ao w Ef Aq+++=××=××个5.4 其他形式的三元合金相图两个共晶型二元系与一个匀晶型二元系构成的三元相图5.4.2L+α→β+4个液相面5条单变量线三相平衡反应开始面与结束面结束与四相面重合5.4.3 具有四相平衡包晶转变的相图三个液相面三个单相固相面(2) 两相平衡(f=2)立体图：以一对共轭曲面为边界与其两个组成相的单相区相接；等温截面和变温截面：以一对曲线作为两相区和两个组成相的单相区的分界线。

(3) 三相平衡立体图：三棱柱体，棱边是三个平衡相成分的单变量线。

棱边与3个组成相的单相区相接，柱面与组成相两两组成的两相区相连。

第五章 三元合金相图

第五章 三元合金相图
两种变温截面; 单相区, 两相区, 相线; 两种变温截面 单相区 两相区 液(固)相线 凝固过程 固 相线 凝固过程.
变温截面同二元相图的区别: 变温截面同二元相图的区别
根据三元固溶体合金结晶时的蝴蝶形规律,在两相平衡时 根据三元固溶体合金结晶时的蝴蝶形规律 在两相平衡时, 平衡相的成分点 在两相平衡时 不是落在一个垂直面上. 因此,变温截面的液 变温截面的液(固 相线不能表示平衡相的成分 相线不能表示平衡相的成分, 不是落在一个垂直面上 因此 变温截面的液 固)相线不能表示平衡相的成分 不能应用杠杆定律计算相的相对含量. 不能应用杠杆定律计算相的相对含量
五.投影图 投影图
5.4 三元共晶相图 一.组元在固态完全不溶的共晶相图 组元在固态完全不溶的共晶相图 (一).相图分析 一 相图分析
液相面（ 个）；固相面 个）；二元共晶点 固相面（ 二元共晶点(线 条）；二元共晶面 个 二元共晶面（ 液相面（3个）；固相面（1个）；二元共晶点 线3条）；二元共晶面（6个）； 三元共晶点(面 个 三元共晶点 面1个).
注意:在同一温度下 尽管三元合金的液相和固相成分的连接线是条水平线, 注意 在同一温度下, 尽管三元合金的液相和固相成分的连接线是条水平线 在同一温度下 但是,液相和固相成分的变化轨迹不在同一个平面上 液相和固相成分的变化轨迹不在同一个平面上. 但是 液相和固相成分的变化轨迹不在同一个平面上
等温截面(水平截面 三.等温截面 水平截面 在某一温度下的状态 等温截面 水平截面): 在某一温度下的状态. 单相区, 两相区, 相等温线(或者称 相线). 单相区 两相区 液(固)相等温线 或者称 液(固)相线 固 相等温线 或者称:液 固 相线
三个液相面、六个二元功晶面、 三个液相面、六个二元功晶面、一个三元 共晶面将相图分成九个相区： 共晶面将相图分成九个相区： 液相区： L 液相区： 两相区：（ ：（L+A、L+B、L+C） 两相区：（ 、 、 ） 三相区：（ ：（L+A+B、L+B+C、L+C+A） 三相区：（ 、 、 ） 三相区：（ ：（A+B+C） 三相区：（ ） 四相区：（ ：（L+A+B+C） 四相区：（ ）

第五章 三元合金相图

第五章 三元合金相图

二元共晶
三元共晶
第四节三元共晶相图
通过成分三角形 顶点的变温截面
第四节三元共晶相图
(四) 投影图 1. 投影图分析
2. 合金O结晶过程 L----L+A------------L+A+(A+B)---------------A+(A+B)+(A+B+C)
二元共晶 三元共晶
第四节三元共晶相图
3.合金O在室温下的相和 组织含量
第一节三元合金相图的表示方法
B （1）确定O点的成分 1）过O作A角对边的平行线 B% C% 2）求平行线与A坐标的截距 得组元A的含量 3）同理求组元B、C的含量 O A C
← A%
第一节三元合金相图的表示方法
C B
A
Oa+Ob+Oc=AB=AC=BC=100% A浓度:Oa=Of=Cb B浓度:Ob=Od=Ac C浓度:Oc=Ba A浓度:55% B浓度:20% C浓度:25%
90 • 标出 50%A+20%B+30%C 的合金 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
80
70
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
第一节三元合金相图的表示方法
二、在成分三角形中具有特定意义的直线 B 成分三角形中特殊的点和线
第五章 三元合金相图
三元系相图简介
相图基本知识
三元相图的主要特点——立体图形，主要由曲面构成
三元系相图简介
垂直轴表示温度。 成分表示在棱柱底，通常是 一等边三角形。 棱柱的每个侧面表示三个二 元系统，如AB，BC，AC。

第5章 三元合金相图

第5章 三元合金相图
相对应成分点的连接直线称为连接线， 或称共轭连线；
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时，三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定，三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2， α相的成分变到mp线上的α2 ， α2在 L2和 x 两点连线的延长线上，根据杠杆定律可 算出此时两相相对量为：
L2 %

x 2 L2 2
100 %
2%

L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中，就得到三元相图的投影图， 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中，并在每一条投影上标注 相应的温度，就得到等温线投影图；类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上，包晶反应结束而进入α＋β两相区。反应结束 时α和β两相的相对量为

三元合金相图

三元合金相图
成 分 三 角 形 （ 又 称 浓 度 三 角 形 ） (Concentration/ Composition Triangle) （等边、等腰、直角坐标）
（1）已知点确定成分； （2）已知成分确定点。
如图 5.1 所示，浓度三角形的三个顶 点代表 A，B，C 三个纯组元，各边表示 二冗合金的成分，AB 边代表 A-B 二元合 金的成分，BC，AC 边分别代表 B－C， A－C 二元合金的成分。三角形内任一点 O，代表一定成分的三元合金。
图 5.21 组元在固态有限互溶的三元相图
图 5.22 固态有限互溶三元共晶相图中 空间各相区示意图。
图 5.23 三元共晶相图中的三相平衡区和两相共晶面
（2）等温截面 图 5.24 是组元在固态有限互溶的三元相图的等温截面示意图。 应用：可确定平衡相及其成分；可运用杠杆定律和重心定律。 相区接触法则：相邻相区的相数差 1；单相区/两相区曲线相接；两相区/三相区直线相
第五章 三元合金相图 工业上所使用的金属材料，如各种合金钢和有色合金，大多由两种以上的组元构成，这 些材料的组织、性能和相应的加工、处理工艺等通常不同于二元合金，因为在二元合金中加 入第三组元后，会改变原合金组元间的溶解度，甚至会出现新的相变，产生新的组成相。 因此，为了更好地了解和掌握金属材料，除了使用二元合金相图外，还需掌握三元甚至 多元合金相图，由于多元合金相图的复杂性，在测定和分析等方面受到限制，因此，用的较 多的是三元合金相图，简称三元相图(Ternary Phase Diagram）。 5.1 三元相图基础 5.1.1 三元相图的主要特点 （1）是立体图形，主要由曲面构成； （2）可发生四相平衡转变； （3）一、二、三相区均占有一定空间，是变温转变，四相区为恒温水平面。 5.1.2 三元合金相图的成分表示法

第五章 三元相图

第五章 三元相图

5.1
三元相图的成分表示法
C
二元系的成分可用一条 直线上的点来表示；三元 系合金有两个独立的成分 参数，所以必须用一个平 面三角形来表示，这个三 角形叫做成分三角形或浓 度三角形。常用的成分三 角形是等边三角形，有时 也用直角三角形或等腰三 角形。 A
A%
C%
B%
B
浓度三角形
5.1.1 浓度三角形 1. 等边三角形 三角形的三个顶点A，B， C分别表示3个纯组元， 三角形的边AB，BC， CA分别表示3个二元系 的成分坐标，三角形内 的任一点都代表一定成 分的三元合金. A 一般按顺时针(或逆时针) 标注组元浓度。
L(三元) ΔT α(三元)
自由度：f=c-P+1=3-2+1=2 故三元匀晶转变区可有两个自由度： 温度和相成分。
5.3.1 相图分析
1 画图 (1) 先画一成份三角形 (应为正三角形) (2) 画温度轴 (3) 画二元匀晶相图(每 两个合金上存在一个二 元相图) ---三元系立体图可视为三 个二元系在空间的延伸 液相面----三个二元系的液相线 所围成的面. 固相面----三个二元系的固相线 所围成的面.
5.4
三元共晶相图
TA A2 A3 A1 E3 E C2 C3 C1 C TB
5.4.1 组元在固态互不溶,具有共晶转变的相图
一、相图分析
1. 画图 (1) 先画一成份三角形
(2) 画温度轴
(3) 画二元共晶相图
E1 TC E2
B2 B3
B1 B
三个二元共晶相图向空间 A 延伸 (4) 画出四相平衡共晶转变平 面A1B1C1 (5) 三个二元系共晶点向空间 延伸为三条共晶沟线，交 A1B1C1面于E点，称为共晶点

三元相图

三元相图

三元匀晶体系合金的结晶
（1）根据Gibbs相率，C-P+1，三元系两相区自由度为2。如果温度 固定，例如T2温度，则自由度为1。进一步如果合金成分固定，则自 由度为0。这意味着合金O结晶，在每一温度下的平衡相成分L1-L4 和S1-S4都是固定不变的。 （2）在各温度下连接液固相成分，例如L2S2，则其物理意义是T2温 度下液固两相平衡的一条共轭线。根据直线法则，其必过合金成分 点O。因此从T1到T4温度，我们得到四条共轭线L1(O)S1，L2OS2， L3OS3，L4S4(O)。来自——典型的质量守恒问题 O
重心法则
三元合金N处于α、β和γ三相平 衡，三相平衡成分为D、E和F， 质量为Ｗα、Ｗβ 和Ｗγ，则合金 N的成分点必落在三角形DEF的 质量重心上。 Ｗα ＝ Nd / Dd × WN Ｗβ ＝ Ne / Ee × WN Ｗγ = Nf / Ff × WN DEF称连接三角形(共轭三角形)
5.3 三元匀晶相图
三元恒压相图是个正三 棱柱。
三元匀晶相图的特点是 三个边二元系均为二元 匀晶系统，没有合成与 分解反应。
液相面、固相面； 液相区、固相区和两相
区。
Fe-Cu-Al phase diagram
三元匀晶体系合金的结晶
O合金在t1温度开始结晶 析出成分为S1的固相，液 固 两 相 平 衡 成分 为 L1/S1 。 温度降至t2时，固相成 分 沿 固 相 曲 面 由 S1 变 为 S2，液相成分沿着液相曲 面由L1变为L2，相平衡为 L2/S2。 冷至t4时，结晶终了， 此时固相成分S4为合金成 分。
应用杠杆定律确定三元新合金成分
母合金P
20 wt.% Co
20 wt.% Ni 母合金Q 30 wt.% Co 50 wt.% Ni WP/WQ=3:1

5.1_三元合金相图

5.1_三元合金相图
34
本节要点
概念：成分三角形、截面图、水平截面、垂直截 面、等温线投影图、直线法则、重心定律
三元合金成分的确定 截面图和投影图 杠杆定律和中心法则
下节内容：固态互不溶解的三元共晶相图
35
思考题
1 下图的成分三角形中有P、R、S、T 四个材料点， 问哪个点的材料，其成分为： A=20%， B=10%，C=70%
B
B%
C%
A
← A%
C
6
浓度确定
确定O点的成分
B
1）过S作A角对边的平行线
2）求平行线与A坐标的截距
得组元A的含量
B%
3）同理求组元B、C的含量 O
A
← A%
C%
C
7
课堂练习
B
1 确定合金I、II、
90
III、IV的成分
80
I 点：
A%=60% B%=30% C%=10%
70
60 B% 50
40 30 I
(BM BN) BO BN
BO BN BM BN
N O M N
NO MN
1
1
NO MN
OM MN
ON OM
推论：当给定材料在一定温度下处于两相平衡状态时，若其
中一相的成分给定，另一相的成分点必在两已知成分点连线
的延长线上；若两个平衡相的成分点已知，材料的成分点必
然位于此两个成分点的连线上。
19
其它浓度三角形
1） 等腰浓度三角形
组元B的含量很少
B
成分点靠近AC边
按比例放大AB、BC边
A
C
20
2） 直角浓度三角形
组元A占绝大多数时
原点为基体组元A

第5章 三元合金相图

第5章 三元合金相图

第5章 三元合金相图由A-B-C 三组元组成的合金称三元合金，其相图称三元相图。

要确定三元合金的成分，必须给出其中两个组元的成分。

所以，在三元相图中表示成分的坐标轴有两个。

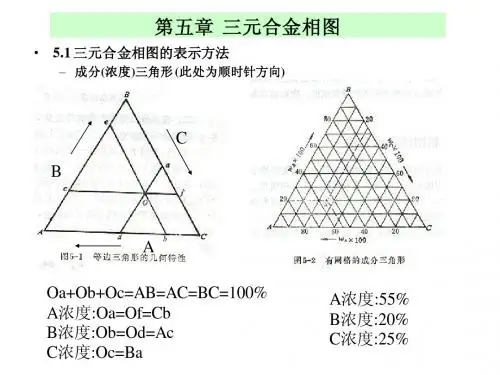
5-1 三元相图成分表示方法在三元相图中表示成分的两个坐标轴原则上可以交成任何角度，但一般采用等边三角形的三个边表示。

设P 为等边三角形内任意点，从P 点分别做三条边的平行线，交三条边于a 、b 、c 点。

根据等边三角形的几何性质：%100==++=++AB Ba Ac Cb Pc Pb Pa 因此，可用Cb 、Ac 、Ba 表示A 、B 、C 的成分。

这样，三角形中每一点都表示一个三元合金的成分。

该三角形称浓度三角形，或成分三角形。

5-2 三元相图中的定量法则一、直线法则二元合金处于两相平衡时，自由度f =2-2+1=1，温度和成分两个变量中只有一个可以独立改变，如当温度一定时，两个平衡相的成分是确定的。

三元合金处于两相平衡时，f =3-2+1=2，当温度一定时，两个平衡相中，只有一个相的成分可独立改变。

当温度和其中一个相的成分一定时，剩余相的成分是确定的。

假设某三元合金的成分点为P ，在某一温度下，该合金处于α、β两相平衡，两相的成分点为a 、b （P133图4）。

可以证明（P133），此时，a 、b 、P 三成分点在一条直线上，且P 点位于a 、b 之间。

这一规律称直线法则。

二、杠杆定律三元相图中的杠杆定律与二元相图中的类似，即同样也只适用于两相区，但形式上略有不同，在直线法则的基础上：%100%⨯=ab Pbα， %100%⨯=ab Paβ三、重心法则三元合金处于α、β、γ三相平衡时，f =3-3+1=1。

当温度一定时，三个平衡相的成分是确定的，其成分点a 、b 、c 构成一个三角形。

若将成分比喻成重量，则合金的成分点P 一定落在成分点a 、b 、c三角形的重心处，这一规律称重心法则。

其数学表达式为（证明见P135）%100%⨯''=a a a P α %100%⨯''=b b b P β %100%⨯''=c c c P γ 其实，重心法则可看作是直线法则和杠杆定律的变形。

《金属学与热处理》教学课件：第五章 三元合金相图

《金属学与热处理》教学课件：第五章 三元合金相图
、Q成分分别为： P：WA=60%，WB=20%， WC=20%； Q： WA=20%，WB=40%， WC=40%； P合金质量占新合金R的75%。
解答： RQ/PQ=75% RQ/PQ=R1/Q1 R1/Q1=（R1C-20）/（60-20）=0。 75 R1C=50% 同理：R2A=25% R合金成分： WA=50%，WB=25%， WC=25%；
L----L+A----------L+A+(A+C)-----------A+(A+C)+(A+B+C)
通过成分三角形顶点的变温截面
(四) 投影图 1. 投影图分析
2. 合金O结晶过程
L----L+A------------L+A+(A+B)---------------A+(A+B)+(A+B+C)
注意:a ao 、bbo、cco为溶解度曲面的交线, 也是 、、三相的成分变温线(单变量曲线).
5.相区
4个单相区:
6个两相区: 4个三相区: 1个四相区:
(二) 等温截面
二元相图中的相区接触法则 对三元相图也适用.
(三) 变温截面
三元共晶的典型特征 (a)截到四相平衡平面:
水平线上：3个三相平衡区； 水平线下：一个三相平衡区。 (b)截到三相共晶转变的开始面和结束面: 顶点朝上的曲边三角形。
B
C
A
WA/Wc=Ba1/Bc1=Ba2/Bc2=Ba/Bc=EC/AE
5.2 三元系平衡相的定量法则 问题: 如果将两个已知成分的合金熔配到一起,那么, 所得到的新的合金 的成分是多少?
一.直线法则和杠杆定律 •直线法则(共线法则): 三元合金在两相平衡时,合金的成分点和两个 平衡相的成分点,必须在同一条直线上. •利用直线法则和杠杆定律可以计算三元合金中两相平衡时相对的含量. 如图所示: W/W=Ob/Oa

材料学基础第5章三元相图

材料学基础第5章三元相图

材料科学基础
第五章
5.6三元相图小结
材料科学基础
第五章
一、单相状态 f＝3－1＋1＝3，而一个温度变量和两个成分变量之间没有任何
相互制约的关系，因此，不论是等温截面还是变温截面，单相区可能具 有多种多样的形状。 二、两相平衡 立体图：共轭曲面。 成分变化：蝶形规则。 等温图：共轭曲线（可用杠杆定律） 变温截面：判定转变温度范围和相转变过程，不能用杠杆定律。 三、三相平衡 立体图：三棱柱，棱边是三个平衡相单变量线。
二、投影图
材料科学基础
第五章
投影图的作用：合金结晶过程分析、相组成物相对量计算、组织组成 物相对量计算。
图8.17 三元共晶相图的投影区
表8.2 各典型区域合金的凝固组织过程及室温组织
材料科学基础
第五章
区
凝固过程
室温组织
Ⅰ
L→α
α
Ⅱ
L→α ，α→βⅡ
α＋βⅡ
Ⅲ
L→α ，α→βⅡ，α β
α＋βⅡ＋γⅡ
(1)当给定合金在一定温度下处于两相平衡状态时，若其中一相的成分 给定，则根据直线法则，另一相的成分点必位于两已知成分点连线的 延长线上。 (2)如果两个平衡相的成分点已知，则合金的成分点必然位于两平衡相 成分点的连线上，根据两平衡相的成分，可用杠杆定律求出合金的成 分。
5.2.2重心定律
x，y，z分别为α，β，γ成分点，则
材料科学基础
第五章
投影图有两种。一种是把空间相图中所有相区间的交线部投影到浓度 三角形中，借助对立体图空间构造的了解，可以用投影图来分析合 金的冷却和加热过程。另一种是把一系列水平截面中的相界线投影 到浓度三角形中。每一条线上注明相应的温度，这样的投影图叫等 温线投影图。等温线可反映空间相图中各种相界面的变化趋势，等 温线越密，表示这个相面越陡。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

E2
B1
A
B
C3 C2
C1
C
TA
A3 A2 A1 TB E1 E3 TC E2 B3 B2 B1
LA
L B
A
B
E
C3 C2 C1
C L C
LA+ B
TA A3 A2 A1 TB E1 B3 B2 E2 E C3 C2 C1
A
E3
TC
B1
B
LA+ C
C L B +C
TA
A3 A2 A1 TB E1 E3 TC E2 B3 B2 B1
LA+ C
LA+ B
A
L A+B
e
B
C
L B +C
TA A3 A2 A1 TB E1 E3 TC E C3 C2 E2 B3 B2 B1
A
B
A+B +C
C1
LA+B +C
C
A+B +C
A LA+ B +C A+B +C
B
LA+B +C
C
A E1
TB E1 E3 E TA A3 A2 A1 TC E E2 E2
E2 B1
LB
LA
A
E3
TC
E e1
B
e2
e3
C3 C2 C1
e
C LC
E1
LB
B
e2 E2
LA
A
LA
e1
LB
e
e3 E3
LC
C LC
LA+ B
TA A3 A2 A1 TB E1 B3 B2 E2 E e3 C3 C2 C1 e e1 e2
A
E3
TC
B1
B
LA+ C
C L B +C
D a2 a 1
C
练习
6. 绘出C / B ＝1/3的合金
C 1 25% B 3 75%
B 90 80 70 60 B% 50 40 30 20 10 A 90 80 70 60 50 40 ← A% 30 20 10 10 20 30 40
7. 绘出A / C ＝1/4的合金
50
C%
60 70 80 90 C
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
练习
1. 确定合金I、II、 III、IV的成分
II点： A%=20% B%=50% C%=30% 70 60 B% 50 40 30 20 10 A 90 80 70 60 90 80
B 10 20 30 40 II
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
2. 浓度三角形中具有特定意义的直线 90 II点：20%A- 50%B- 30%C III 点：20%A- 20%B- 60%C IV 点：40%A- 0%B- 60%C 80 70
B 10 20 30
60 B% 50
40 30 20
40
II 50
C% 60
III IV
70 80
10 A
90 80 70 60
90
50 40 ← A% 30 20 10 C
1）与某一边平行的直线
B
含对角组元浓度相等
B% C%
P A
Q ← A% C
练习
4. 绘出A ＝40%的 合金
5. 绘出C ＝30%的 合金
40 30 20 10 A 90 80 70 60 70 60 90 80

L+
L


用与成分三角形平行的平面与立体图在某温度相截，将其截线投影到成分三角形 平面上所得到的图形。 水平面与液相面的截痕线是液相面等温线，凸向于低熔点组元方向； 水平面与固相面的截痕线是固相面等温线，凸向于高熔点组元方向；
通过分析不同温度的等温截面图，可以分析合金 状态随温度的变化情况： 合金X：
5、等温投影图：将一系列等温截面中的相界线投 影到成分三角形中，在每一条线上标明相应的温 度； ------可以反映空间相图中各种相界面的变 化趋势；
第四节 三元共晶相图
三元共晶相图
共晶转变：
一个液相 ，同时结晶出两个（或三个）固相 —— 共同结晶
共晶线：
M-E-N
T（℃） TA
L
L＋
M 183℃ E
A A+B +C
B
E
C3 C2 C1
LA+ B + C C
单相区： 一个
L
TA A3 A2 A1 TB E1
双相区： 三个
L + A、L + B、L + C
B3 B2
E2 B1
A
E3
TC E C3 C2 C1
B
三相区：四个
L + A + B、L + B +C、 L + A + C、A + B + C
液相线：
线：
TA——E——TS

L＋
N
TS

固相线：
TA—M—E—N—TS
＋
F Pb G Sn
固溶度曲线：
MF、NG
共晶点：
点：
E
最大溶解度点：
M、N
简单共晶：
T（℃）
A
B
1. 简单三元共晶相图分析
A
B
B
C
A
C
A
B
C
A
B
C
立体图：
相区的立体图 曲面的立体图 曲线的立体图 点
TA A3 A2 A1 TB E1 E3 TC E B3 B2
第二节
三元系平衡相的定量法则
直线法则与重心法则
1）直线法则
—— 适用于两相平衡的情况
B
投影到任何一边上，按二 元杠杆定律计算
C% B% g’ R
fg f ' g ' R W ef e' f ' R W
e’ A
f’
e
f
g
← A% C
直线法则和杠杆定律的应用：
（1）某温度下，成分确定的三元合金处于两相 平衡时，若其中一相成分已知，则可确定另一相 成分,它必位于两已知成分点的延长线上；
E2
B1
A
B
C3 C2
C1
C
固 相 面
A1
LA+ B LA+ B + C
B1
LA+ C
TA C1 A3 A2 A1
E
L B + C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
——
TB E1
B3 B2 E2 E B1
A
E3
TC
B
C3 C2
C1
C
中 转平 间 变衡 开 共 三面
始晶相
A3

将它们投影到浓度三角形上，得到蝴蝶形的图 形。更清楚地表明了两相在结晶过程中的成分 变化情况。
结晶过程中，固相成分、合金成分、液相成分遵循 直线法则。
3. 等温截面及其投影
B
C
A
B
L+
C
L
A
利用等温截面图可知： 1、所截温度下，三元系中 各种合金所存在的相态； 2、合金状态随温度的变化 情况； 3、各平衡相的相成分和相 对量（单相区不需计算； 两相区用直线法则和杠杆 定律确定和计算；三相区 用重心法则计算）。
B
B%
C%
f

R d

e

← A% C
A
第三节
三元匀晶相图
—— 匀晶转变： 由液相直接结晶出单相固溶体的转变（相变） —— 形成匀晶相图的条件 组元在液相、固相均可完全互溶 组元晶体结构相同、原子尺寸、电负性相似
液相线
T （℃）
L
固相线
单相区 双相区
L ＋

A B
1. 三元匀晶 相图
B C
E
B1
固 相 面
LA+ C
L B +C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束

在t1温度为液相和固相共存，且液相的相对量多，固相 的相对量少。 在t2 温度仍为液相和固相共存，但液相的相对量减少 ，固相的相对量增多。 在t3 温度为单相的固相。
4. 垂直截面
类型一：
B
C
C
A
类型二：
B
C
A
从变温截面图可知： （1）合金冷却过程中的相变次序； （2）转变温度范围； （3）不同温度下的相组成。 但必须指出： 变温截面图不能用来确定某一温度时平衡相的成 分和计算相的相对量。 因为： 根据三元合金结晶时的蝴蝶形规律，在两相平衡 时，平衡相的成分不是都落在一个垂直截面上 ；
练习
90 2. 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60