2015年上海中考数学二模24-25题

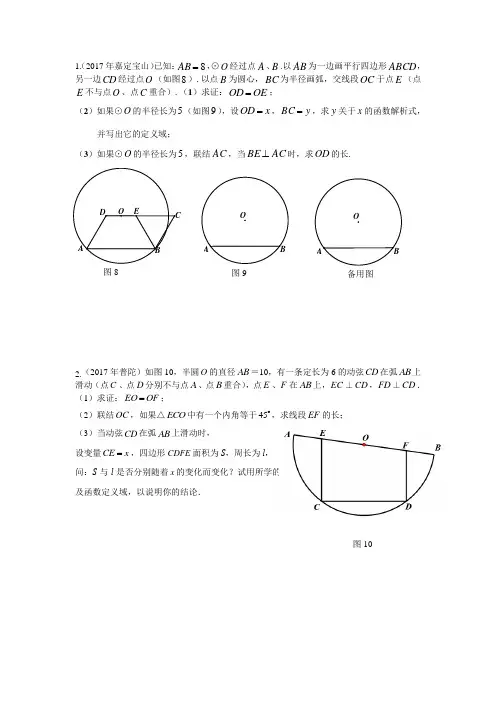
1.（2017年嘉定宝山）已知：8=AB ，⊙O 经过点A 、B .以AB 为一边画平行四边形ABCD ，另一边CD 经过点O （如图8）.以点B 为圆心，BC 为半径画弧，交线段OC 于点E （点E 不与点O 、点C 重合）.（1）求证：OE OD =；（2）如果⊙O 的半径长为5（如图9），设x OD =，y BC =，求y 关于x 的函数解析式，并写出它的定义域；（3）如果⊙O 的半径长为5，联结AC ，当AC BE ⊥时，求OD 的长.2.（2017年普陀）如图10，半圆O 的直径AB ＝10，有一条定长为6的动弦CD 在弧AB 上滑动（点C 、点D 分别不与点A 、点B 重合），点E 、F 在AB 上，EC ⊥CD ，FD ⊥CD ． （1）求证：EO OF =；（2）联结OC ，如果△ECO 中有一个内角等于45 ，求线段EF 的长； （3）当动弦CD 在弧AB 上滑动时，设变量CE x =，四边形CDFE 面积为S ，周长为l ，问：S 与l 是否分别随着x 的变化而变化？试用所学的函数知识直接写出它们的函数解析式及函数定义域，以说明你的结论．图9 B O A 备用图 B OA 图8 E CB A O D 图103.（2017年崇明）如图，梯形ABCD 中，AB CD ∥，90ABC ∠=︒，6AB =，8BC =，tan 2D =，点E 是射线CD 上一动点（不与点C 重合），将BCE ∆沿着BE 进行翻折，点C 的对应点记为点F ． （1）如图1，当点F 落在梯形ABCD 的中位线MN 上时，求CE 的长；（2）如图2，当点E 在线段CD 上时，设CE x =，BFC EFCS y S ∆∆=，求y 与x 之间的函数关系式，并写出定义域；（3）如图3，联结AC ，线段BF 与射线CA 交于点G ，当CBG ∆是等腰三角形时，求CE 的长．ABCDEFM NEDCFABEDC FAB GD CAB（第25题图1）（第25题图2）（第25题图3）（第25题备用图）4.（2017年杨浦）已知：以O 为圆心的扇形AOB 中，∠AOB =90°，点C 为»AB 上一动点，射线AC 交射线OB 于点D ，过点D 作OD 的垂线交射线OC 于点E ，联结AE . （1） 如图1，当四边形AODE 为矩形时，求∠ADO 的度数； （2） 当扇形的半径长为5，且AC =6时，求线段DE 的长；（3） 联结BC ，试问：在点C 运动的过程中，∠BCD 的大小是否确定？若是，请求出它 的度数；若不是，请说明理由.5.（2017年奉贤）已知：如图9，线段AB =4，以AB 为直径作半圆O ，点C 为弧AB 的中点，点P 为直径AB 上一点，联结PC ，过点C 作CD //AB ，且CD =PC ，过点D 作DE//PC ，交射线PB 于点E ，PD 与CE 相交于点Q ． （1）若点P 与点A 重合，求BE 的长； （2）设PC = x ，y CEPD，当点P 在线段AO 上时，求y 与x 的函数关系式及定义域； （3）当点Q 在半圆O 上时，求PC 的长．图9ACPOBD E Q备用图AO BCA OBCD E（备用图） A O B CD E （图1）6.（2017年闵行）如图，在梯形ABCD 中，AD // BC ，∠B = 90°，AB = 4，BC = 9，AD = 6．点E 、F 分别在边AD 、BC 上，且BF = 2DE ，联结FE ．FE 的延长线与CD 的延长线相交于点P ．设DE = x ，PEy EF ． （1）求y 关于x 的函数解析式，并写出函数的定义域；（2）当以ED 为半径的⊙E 与以FB 为半径的⊙F 外切时，求x 的值；（3）当△AEF ∽△PED 时，求x 的值．7.（2017年长宁金山）如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知AC =6 cm ，BC =8 cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，BQ =k ·AP （k >0），连接PC 、PQ ． （1）求⊙O 的半径长； （2）当k =2时，设AP =x ，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域； （3）如果△CPQ ∽△ABC ，且∠ACB =∠CPQ ，求k 的值.第25题图A B CDE F P （第25题图）A B C D （备用图）EP 第25题图 C AB D8.（2017年虹口）如图，在△ABC 中，AB=AC =5，cos B =45，点P 为边BC 上一动点，过点P 作射线PE 交射线BA 于点D ，∠BPD=∠BAC ．以点P 为圆心，PC 长为半径作⊙P 交射线PD 于点E ，联结CE ，设BD=x ，CE=y ． （1）当⊙P 与AB 相切时，求⊙P 的半径；（2）当点D 在BA 的延长线上时，求y 关于x 的函数解析式，并写出定义域； （3）如果⊙O 与⊙P 相交于点C 、E ，且⊙O 经过点B ，当OP=54时，求AD 的长．9.（2017年浦东新区）如图所示，︒=∠45MON ，点P 是MON ∠内一点，过点P 作OM PA ⊥于点A 、ON PB ⊥于点B ，且22=PB ．取OP 的中点C ，联结AC 并延长，交OB 于点D ．（1）求证：OPB ADB ∠=∠；（2）设x PA =，y OD =，求y 关于x 的函数解析式；（3）分别联结AB 、BC ，当ABD △与CPB △相似时，求PA 的长．（第25题图）（备用图）10.（2016年崇明）如图，已知BC 是半圆O 的直径，8BC =，过线段BO 上一动点D ，作AD BC ⊥交半圆O 于点A ，联结AO ，过点B 作BH AO ⊥，垂足为点H ，BH 的延长线交半圆O 于点F ． （1）求证：AH BD =；（2）设BD x =，BE BF y ⋅=，求y 关于x 的函数关系式；（3）如图2，若联结FA 并延长交CB 的延长线于点G ，当FAE ∆与FBG ∆相似时，求BD 的长度．11.（2016年宝山嘉定）如图8，⊙O 与过点O 的⊙P 相交于AB ，D 是⊙P 的劣弧OB 上一点，射线OD 交⊙O 于点E ，交AB 的延长线于点C .如果AB =24，32tan =∠AOP . (1) 求⊙P 的半径长；(2) 当△AOC 为直角三角形时，求线段OD 的长； (3) 设线段OD 的长度为x ，线段CE 的长度为y ，求y 与x 之间的函数关系式及其定义域．（第25题图1）ABDOE HFC（第25题图2） CO D B G A F H E 图8_C _ E _B _O_P_A_ D12.（2016年长宁金山）如图, 已知在Rt △ABC 中, ∠ACB =90°, AB =5, 4sin 5A, P 是边BC 上的一点, PE ⊥AB , 垂足为E , 以点P 为圆心, PC 为半径的圆与射线PE 相交于点Q , 线段CQ 与边AB 交于点D . （1）求AD 的长;（2）设CP =x , △PCQ 的面积为y , 求y 关于x 的函数解析式, 并写出定义域;（3）过点C 作CF ⊥AB , 垂足为F , 联结PF 、QF , 如果△PQF 是以PF 为腰的等腰三角形, 求CP 的长.13.（2016年闸北）如图，在△ABC 中，AB=AC=6，BC=4，⊙B 与边AB 相交于点D ，与边BC 相交于点E ，设⊙B 的半径为x ． （1）当⊙B 与直线AC 相切时，求x 的值；（2）设DC 的长为y ，求y 关于x 的函数解析式，并写出定义域； （3）若以AC 为直径的⊙P 经过点E ，求⊙P 与⊙B 公共弦的长．BCAP EQDBCACB ADE （第25题图）14.（2016年闵行）如图，已知在△ABC 中，AB = AC = 6，AH ⊥BC ，垂足为点H ．点D 在边AB 上，且AD = 2，联结CD 交AH 于点E ．（1）如图1，如果AE = AD ，求AH 的长；（2）如图2，⊙A 是以点A 为圆心，AD 为半径的圆，交线段AH 于点F ．设点P 为边BC 上一点，如果以点P 为圆心，BP 为半径的圆与⊙A 外切，以点P 为圆心，CP 为半径的圆与⊙A 内切，求边BC 的长；（3）如图3，联结DF ．设DF = x ，△ABC 的面积为y ，求y 关于x 的函数解析式，并写出自变量x 的取值范围．15.（2016年松江）已知：如图1，在梯形ABCD 中，AD //BC ，∠BCD =90º， BC=11，CD=6，tan ∠ABC =2，点E 在AD 边上，且AE=3ED ，EF //AB 交BC 于点F ，点M 、N 分别在射线FE 和线段CD 上．（1）求线段CF 的长； （2）如图2，当点M 在线段FE 上，且AM ⊥MN ，设FM ·cos ∠EFC =x ，CN =y ，求y 关于x 的函数解析式，并写出它的定义域；（3）如果△AMN 为等腰直角三角形，求线段FM 的长．AB C H D （第25题图1) E AB C H D E（第25题图3) F P AB C H D E（第25题图2) F （第25题图1）AC B DE F（第25题图2）AC B DE FNM （备用图）A CBDE F16.（2016年黄埔）如图7，在Rt △ABC 中，90ACB ∠=︒，1AC =，BC =7，点D 是边CA 延长线上的一点，AE ⊥BD ，垂足为点E ，AE 的延长线交CA 的平行线BF 于点F ，联结CE 交AB 于点G ．（1）当点E 是BD 的中点时，求tan AFB ∠的值；（2）CE AF 的值是否随线段AD 长度的改变而变化，如果不变，求出CE AF 的值；如果变化，请说明理由；（3）当BGE ∆与BAF ∆相似时，求线段AF 的长．19.（2016年杨浦）已知：半圆O 的直径AB =6，点C 在半圆O 上，且tan 22ABC ∠=，点D 为AC 上一点，联结DC （如图）．（1）求BC 的长；（2）若射线DC 交射线AB 于点M ，且△MBC 与△MOC 相似，求CD 的长； （3）联结OD ，当OD//BC 时，作∠DOB 的平分线交线段DC 于点N ，求ON 的长．图7AB C DEF G （第25题备用图） A B O C A B O C D（第25题图）20.（2016年奉贤） 已知：如图，在边长为5的菱形ABCD 中，cos A =35，点P 为边AB 上一点，以A 为圆心、AP 为半径的⊙A 与边AD 交于点E ，射线CE 与⊙A 另一个交点为点F ． （1）当点E 与点D 重合时，求EF 的长；（2）设AP =x ，CE =y ，求y 关于x 的函数关系式及定义域；（3）是否存在一点P ，使得 2EF PE =⋅，若存在，求AP 的长，若不存在，请说明理由．21.（2016年普陀）如图9，在Rt △ABC 中，90C ∠= ，14AC =，3tan 4A =，点D 是边AC 上的一点，8AD =．点E 是边AB 上一点，以点E 为圆心，EA 为半径作圆，经过点D ．点F 是边AC 上一动点（点F 不与A 、C 重合），作FG EF ⊥，交射线BC 于点G ． （1）用直尺圆规作出圆心E ，并求圆E 的半径长（保留作图痕迹）；（2）当点G 在边BC 上时，设AF x =，CG y =，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EG ，当△EFG 与△FCG 相似时，推理判断以点G 为圆心、CG 为半径的圆G 与圆E 可能产生的各种位置关系．DCBA E F第25题图P DCBA备用图DCBA图9DCBA图9备用图22.(2016年浦东）如图，Rt △ABC 中，90ACB ∠= ，6BC =，点D 为斜边AB 的中点，点E 为边AC 上的一个动点．联结DE ，过点E 作DE 的垂线与边BC 交于点F ，以,DE EF 为邻边作矩形DEFG ．（1）如图1，当8AC =，点G 在边AB 上时，求DE 和EF 的长； （2）如图2，若12DE EF =，设AC x =，矩形DEFG 的面积为y ，求y 关于x 的函数解析式； （3）若23DE EF =，且点G 恰好落在Rt △ABC 的边上，求AC 的长．23.(2015年黄埔）如图8，Rt △ABC 中，90C ︒∠=，30A ︒∠=，BC =2，CD 是斜边AB 上的高，点E 为边AC 上一点（点E 不与点A 、C 重合），联结DE ，作CF ⊥DE ，CF 与边AB 、线段DE 分别交于点F 、G ．（1）求线段CD 、AD 的长；（2）设CE x =，DF y =，求y 关于x 的函数解析式，并写出它的定义域； （3）联结EF ，当△EFG 与△CDG 相似时，求线段CE 的长．GFED C BA 第25题 图2A BC D EFG 第25题 图1 ABCD备用图DCBA(备用图）图8GFDCB A E23.(2015年奉贤）已知：如图，线段AB =8，以A 为圆心，5为半径作圆A ，点C 在⊙A 上，过点C 作CD //AB 交⊙A 于点D （点D 在C 右侧），联结BC 、AD ． （1）若CD=6，求四边形ABCD 的面积；（2）设CD =x ，BC =y ，求y 与x 的函数关系式及自变量x 的取值范围；（3）设BC 的中点为M ，AD 的中点为N ，线段MN 交⊙A 于点E ，联结CE ，当CD 取何值时，CE //AD ．23.(2015年松江区）如图，已知在直角梯形ABCD 中，AD ∥BC ，∠ABC =90º，AB =4，AD=3，552sin =∠BCD ，点P 是对角线BD 上一动点，过点P 作PH ⊥CD ，垂足为H ． （1）求证：∠BCD =∠BDC ；（2）如图1，若以P 为圆心、PB 为半径的圆和以H 为圆心、HD 为半径的圆外切时，求DP 的长；（3）如图2，点E 在BC 延长线上，且满足DP =CE ，PE 交DC 于点F ，若△ADH 和△ECF 相似，求DP 的长．DCB （第25题图）AB（备用图）AABCHPD （第25题图1）ABCHPD EF（第25题图2）23.(2015年闵行区）如图，已知在梯形ABCD 中，AD // BC ，AB = DC = 5，AD = 4．M 、N 分别是边AD 、BC 上的任意一点，联结AN 、DN ．点E 、F 分别在线段AN 、DN 上，且ME // DN ，MF // AN ，联结EF ．（1）如图1，如果EF // BC ，求EF 的长；（2）如果四边形MENF 的面积是△ADN 的面积的38，求AM 的长；（3）如果BC = 10，试探索△ABN 、△AND 、△DNC 能否两两相似？如果能，求AN 的长；如果不能，请说明理由．23.(2015年嘉定）在Rt △ABC 中，︒=∠90C ，2=BC ，Rt △ABC 绕着点B 按顺时针方向旋转，使点C 落在斜边AB 上的点D ，设点A 旋转后与点E 重合，联结AE ，过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合如图10，求BAE ∠cot 的值；（2）若点M 在边BC 上如图11，设边长x AC =，y BM =，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围； （3）若EBM BAE ∠=∠，求斜边AB 的长．A B C D M N E F（图1）A B C D M NE F （第25题图）A CB (M )ED 图10ACBMED图11。

2015年上海市初中毕业统一学业考试数学试卷考生注意：1 •本试卷含三个大题，共 25题；2 •答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3•除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤. -、选择题： （本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置1.下列实数中，是有理数的为（）A. 2 ;B . 34 ;C .;D . 0 .2.当a0时, 卞万【【辛二P 宴白&踪皆 TT 槁白&旦 （)下列天于幂的运算正确的是（A.a 1 ;B . a 1a ;22C . aa ;D . a 22.a3.下列 y 关于x 的函数中，是正比例函数的为（ )A.2y x厂 2 ;B . y -;xx C . y2 ;x 1D . y24.如果一个正多边形的中心角为 72°，那么这个正多边形的边数是（）A . 4;B . 5;C . 6;D . 7.6. 如图，已知在O O 中，AB 是弦，半径OC AB ，垂足为点D ，要使四边形 一个条件，这个条件可以是（ ）A . AD BD ;B . OD CD ;C . CAD CBD ; D . OCA OCB .二、填空题：（本大题共12题，每题4分，满分48分） 【请将结果直接填入答题纸的相应位置】 7.计算：| 22 ___________ & 方程• 3x 22的解是 __________9.___________________________________________________ 如果分式有意义，那么x 的取值范围是x 310._______________________________________________________________________________ 如果关于x 的一元二次方程x 24x m 0没有实数根，那么 m 的取值范围是 _________________________________________11.___________________________________ 同一温度的华氏度数y （o F ）与摄氏度数x （o c ）之间的函数关系是y |x 32 .5.下列各统计量中，表示一组数据波动程度的量是（) A .平均数； B .众数； C .方差;D .频率.如果某一温度的摄氏度数是25o C，那么它的华氏度数是°F .12•如果将抛物线y x22x 1向上平移，使它经过点A （0, 3）,那么所得新抛物线的表达式是___________________13•某校学生会提倡双休日到养老院参加服务活动，首次活动需要7位同学参加，现有包括小杰在内的50位同学报名，因此学生会将从这50位同学中随机抽取7位，小杰被抽到参加此次活动的概率是 _______________ •14年龄（岁）1112131415人数55161512那么“科技创新社团”成员年龄的中位数是______________ 岁.uun IT UULT15址如图T，已知在△ ABC中，D、E分别是边AB、边AC的中点，AB m , AC 量m、n表示为______________________ •16•已知E是正方形ABCD的对角线AC上一点，AE AD，过点E作AC的垂线，交边CD于点F，那么FAD_________________ 度.17•在矩形ABCD中，AB 5 , BC 12，点A在O B上•如果O D与O B相交，且点B在O D内，那么O D的半径长可以等于_______________________ •（只需写出一个符号要求的数）18.已知在厶ABC中，AB AC 8 , BAC 30°•将△ ABC绕点A旋转，使点B落在原△ ABC的点C 处，此时点C落在点D处•延长线段AD，交原△ ABC的边BC的延长线于点E，那么线段DE的长等于三、解答题：（本大题共7题，满分78分）19. （本题满分10分）2先化简，再求值：丁必X口，其中xx 4x 4 x 2 x 220. （本题满分10分）4x 2x 6解不等式组：x ! x !，并把解集在数轴上表示出来.3 921. （本题满分10分，第（1）小题满分4分，第（2）小题满分6分）4已知，如图，在平面直角坐标系 xOy 中，正比例函数y —x 的图像经过点 A ，点A 的纵坐标为4,反比3例函数y m 的图像也经过点A ，第一象限内的点x轴于点C ，且AC AB .求：（1）这个反比例函数的解析式；（2）直线AB 的表达式.22. （本题满分10分，第（1）小题满分4分，第（2）小题满分6分）如图，MN 表示一段笔直的高架道路，线段 AB 表示高架道路旁的一排居民楼.已知点 A 到MN 的距离为 15米，BA 的延长线与MN 相交于点D ，且 BDN 30°，假设汽车在高速道路上行驶时，周围 39米以内会 受到噪音的影响.（1） 过点A 作MN 的垂线，垂足为点 H .如果汽车沿着从 M 到N 的方向在MN 上行驶，当汽车到达点 P 处 时，噪音开始影响这一排的居民楼，那么此时汽车与点 H 的距离为多少米？（2） 降低噪音的一种方法是在高架道路旁安装隔音板，当汽车行驶到点 Q 时，它与这一排居民楼的距离 QC为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？（精确到 1米）（参考数据：・.3 1.7）B 在这个反比例函数的图像上，过点 B 作BC // x 轴，交y23. （本题满分12分，第（1）小题满分6分，第（2）小题满分6分）已知：如图，平行四边形ABCD的对角线相交于点0，点E在边BC的延长线上，且0E 0B，联结DE .(1) 求证：DE BE ;(2) 如果OE CD，求证：BD CE CD DE .图24. （本题满分12分，第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分4分）已知在平面直角坐标系xOy中（如图），抛物线y ax2 4与x轴的负半轴相交于点A，与y轴相交于点B , AB 2 5 •点P在抛物线上，线段AP与y轴的正半轴相交于点C，线段BP与x轴相交于点D •设点P的横坐标为m .x（1）求这条抛物线的解析式；（2）用含m的代数式表示线段CO的长度；3（3）当tan ODC 时，求PAD的正弦值.225. （本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）已知：如图，AB是半圆0的直径，弦CD // AB,动点P、Q分别在线段0C、CD上，且DQ 4cos AOC .设OP x , △ CPF 的面积为y.5（1）求证：AP OQ ;（2）求y关于x的函数关系式，并写出它的定义域；（3）当厶OPE是直角三角形时，求线段OP的长. OP ,AP的延长线与射线0Q相交于点E，与弦CD相交于点F（点F与点C、D不重合），AB 20 ,图7备用图2015年上海市初中毕业统一学业考试数学试卷参考答案一、选择题1、D ；2、A;3、C ；4、B;5、C ；6、B二、填空题7、4 ；8、：2；9、x 3 ；10、m 4 ；1 Lr 1 r14、14；m n ; 16、22.5 ；17、1422三、解答题2x x 2x 119.解：原式= ' 2(X 2)x x 2x x 1x 2x 227 11、77；12、y x 2x 3 ；13、；50（大于13且小于18的数）；18、^3 4 .当lx1时，原式11f—J; 2 1 2 2 120•解：由4x 2x6，得x3x 1 x 1 口由，得x239原不等式组的解集是3x 2.1 1J L IA-3 -2-1 01 2 3x4 一21.解：（1 ）•••正比例函数y X的图像经过点A，点A的纵坐标为4,344 — x 二x 3 •••点A 的坐标是（3,4）3•••反比例函数的图像经过点A,12 yx (2)••• AC AB ，•点A 在线段BC 的中垂线上.•/ BC // X 轴，点C 在y 轴上，点A 的坐标是(3,4)，•点B 的横坐标为6. •••点B 在反比例函数的图像上，.••点 B 的坐标是(6,2). 22•解：(1)联结 AP.由题意得 AH MN , AH 15(m), AP 39(m).在 Rt APH 中，得 PH 36(m).答：此时汽车与点 H 的距离为36米.(2)由题意可知，PQ 段高架道路旁需要安装隔音板， QC AB ,QDC 30 ,QC 39(m).在 Rt DCQ 中，DQ 2QC 78(m).在 Rt ADH 中，DH AH cot30 15、、3(m),• PQ PH DH DQ 114 15 1.7 88.5 89(m). 答：高架道路旁安装的隔音板至少需要 89米长.23•证明：(1 )••• OE OB, OBE OEB .T 平行四边形 ABCD 的对角线相交于点 0,「.OB OD .• OE OD • ODE OED .在 BDE 中, OBE OEB OED ODE 180 • OEB 0ED BE 90, 即DE BE .(2)T OE CD ,••• CDE DEO 90 .又••• CEO DEO 90 , CDE CEO.m 12•直线AB 的表达式为y 2x 6.3 b 6•••反比例函数的解析式为 设直线AB 的表达式为y kx b ，将点A 、B 代入表达式得:4 3k b 2 6k b k 解得Q OBE OEB, OBE 在 DBE 和 CDE 中：OBE CDEBED DECDBE s CDE.点A 在x 轴的负半轴上，AB 2、. 5，2 抛物线y ax 4与x 轴相交于点A ,这条抛物线的表达式为 y x 24 2 (2)：点P 在抛物线上，它的横坐标为m ,「.点P的坐标为(m, m 4) 2由题意，得点P 在第一象限内，因此 m 0,m4 0过点P 作PH 丄x 轴，垂足为H CO AO•/ CO // PH ,PH AHCO 2m 2 4 m 2解得CO 2m 4(3)过点P 作PG 丄y 轴， 垂足为点 G OD BO•/ OD // D G , •PG BG OD 4 口 42,即 ODm m m CO 3在 Rt A ODC 中， •/ ODCOD 2 • 2(2m4) 3 -,解得m 3或m 1 (舍去)。

2021 年度初三上海各区二模18-24-25〔2021 宝山、嘉定〕18．如图，点 M 的坐标为 (3,2) ，动点 P 从点 O 出发，沿y 轴以每秒 1 个单位的速度向上移动，且过点P 的直线 l ： y＝－ x＋ b 也随之移动，如果点M 关于上，设点 P 的移动时间为t，那么 t 的值可以是．l的对称点落在坐标轴24．〔此题总分值 12 分，第(1)、第 (2) 、第 (3) 小题总分值各4 分〕如图，对称轴为直线 x 1 的抛物线y ax2bx3与 x 轴交于 A 、 B 两点，与y 轴交于C点，其中A(1,0).〔1〕求点 B 的坐标及此抛物线的表达式；〔2〕点 D 为y 轴上一点，假设直线BD和直线BC的夹角为 15o，求线段CD的长度；〔3〕设点P为抛物线的对称轴当BPC 为直角三角形时，求点x 1 上的一个动点，P的坐标.第 24题图25．〔此题总分值14 分，第 (1)、第(2)小题总分值各4 分 ,第 (3) 小题总分值如图：AB 是圆 O 的直径， AB=10 ，点 C 为圆 O 上异于点BC 的中点．6 分〕A 、B 的一点，点M 为弦（1〕如果 AM 交 OC 于点 E，求 OE： CE 的值；（2〕如果 AM ⊥OC 于点 E，求∠ ABC 的正弦值；（3〕如果 AB ： BC=5 ： 4，D 为 BC 上一动点，过 D 作 DF⊥ OC，交 OC 于点 H ，与射线BO 交于圆内点 F ，请完成以下探究．探究一：设BD=x ， FO=y ，求 y 关于 x 的函数解析式及其定义域．探究二：如果点 D 在以 O 为圆心， OF 为半径的圆上，写出此时BD 的长度．A AFO OE1/ 14HPB BM C D C2021 年度初三上海各区二模18-24-25崇明18．如图 4，在△ABC中，AB AC ， BAC 30 ，将△ABC 绕着点A逆时针旋转 30 ，记点 C 的对应点为点D，AD 、BC 的延长线相交于点 E. 如果线段DE 的长为 2 ，那么边AB的长为▲．24．〔此题总分值12 分，每题总分值各 4 分〕如图 8，抛物线y x2bx c 交 x 轴于点A (1, 0)和点 B，交y轴于点C (0, 3)．（1〕求抛物线的解析式；（2〕在抛物线上找出点 P，使PC PO，求点 P 的坐标；〔3〕将直线AC 沿 x 轴的正方向平移，平移后的直线交y 轴于点M，交抛物线于点N．当四边形 ACMN 为等腰梯形时，求点M、 N 的坐标．y yC CO A B x O A B x备用图图 825．〔此题总分值14 分，其中第 (1) 、 (2) 小题总分值各 4 分，第 (3) 小题总分值 6 分〕如图 9，在梯形 ABCD 中，AD∥BC，AB DC8， BC 12 ， cosC 3，点 E为5AB 边上一点，且BE 2 ．点F是BC边上的一个动点〔与点B、点 C 不重合〕，点 G 在射线 CD 上，且EFG B ．设 BF 的长为 x，CG 的长为．y〔1〕当点 G 在线段DC 上时，求y与 x 之间的函数关系式，并写出自变量x 的取值范围；（2〕当以点 B 为圆心， BF 长为半径的⊙ B 与以点 C 为圆心， CG 长为半径的⊙ C 相切时，求线段 BF 的长；〔3〕当△CFG为等腰三角形时，直接写出线段BF 的长．A DGE2/14 B F图9C18． 如图 5，矩形 ABCD ，AD= a ，将矩形 ABCD 绕着顶点B 顺时针旋转， 得到矩形 EBGF ，顶点 A 、D 、 C 分别与点 E 、F 、 G 对应〔点 D 与点 F 不重合〕．如果点D 、E 、F 在同一条直线上，那么线段DF 的长是 ▲ ．〔用含 a 的代数式表示 〕D CAB24．〔此题总分值 12 分，每题总分值各 4 分〕图 5如图 9，平面直角坐标系 xOy ，抛物线 y = ax 2 + bx + 2 与 x 轴交于点 A(- 2，0)和点 B(4， 0) ．〔 1〕求这条抛物线的表达式和对称轴；〔 2〕点 C 在线段 OB 上，过点 C 作 CD ⊥ x 轴，垂足为点C ，交抛物线与点D ，E 是 BD中点，联结 CE 并延长，与 y 轴交于点 F ．①当 D 恰好是抛物线的顶点时，求点F 的坐标；y②联结 BF ，当△ DBC 的面积是△ BCF 面积的 3时，2求点 C 的坐标．A OB x图 925．〔此题总分值 14 分，第 (1)小题总分值 4 分，第 (2) 小题总分值 5 分，第 (3)小题总分值 5 分〕如图 10 ABC ， AB= 2 ，BC= 3，∠ B=45° D 在边 BC 上，联结AD， 以 ，△，点 点 A 为圆心， AD 为半径画圆，与边 AC 交于点 E ，点 F 在圆 A 上，且 AF ⊥ AD ．〔1〕设 BD 为 x ，点 D 、 F 之间的距离为 y ，求 y 关于 x 的函数解析式，并写出定义域；〔2〕如果 ?E 是 DF 的中点，求 BD : CD 的值；〔3〕联结 CF ，如果四边形ADCF 是梯形，求 BD 的长 ．FAAEBD CCB图 10备用图3/1418．如图，在矩形 ABCD 中，AB=6，点 E 在边 AD 上且 AE=4，点 F 是边 BC 上的一个动点，将四边形 ABFE 沿 EF 翻折， A、B 的对应点 A1、B1与点 C 在同一直线上， A1B1与边 AD 交于点 G，如果 DG =3，那么 BF 的长为▲．EA DB题图C第 1824．如图，在平面直角坐标系xOy 中，抛物线 y ax2 + bx 8 与x轴相交于点A〔- 2，0〕和点 B〔 4， 0〕，与 y 轴相交于点C，顶点为点P．点 D 〔0， 4〕在 OC 上，联结BC、 BD ．〔1〕求抛物线的表达式并直接写出点P 的坐标；〔2〕点 E 为第一象限内抛物线上一点，如果△COE 与△ BCD 的面积相等，求点 E 的坐标；〔3〕点 Q 在抛物线对称轴上，如果△BCD ∽△ CPQ，求点 Q 的坐标．yPCDA OB x第24题图25．〔此题总分值14 分，第〔 1〕小题 5 分，第〔 2〕小题 5 分，第〔 3〕小题 4 分〕如图， AD∥ BC，∠ ABC=90 °，AD =3，AB=4 ，点 P 为射线 BC 上一动点，以 P 为圆心，BP 长为半径作⊙ P，交射线 BC 于点 Q，联结 BD 、AQ 相交于点 G，⊙ P 与线段 BD 、AQ 分别相交于点 E、 F．〔 1〕如果 BE=FQ ，求⊙ P 的半径；〔 2〕设 BP=x ， FQ=y ，求 y 关于 x 的函数关系式，并写出x 的取值范围；〔 3〕联结 PE、 PF，如果四边形EGFP 是梯形，求BE 的长．A DGE FBP Q C4 /14第25题图黄浦A318．如图 3，在 ABC 中，ACB 90 ，sin B ABC 绕顶点1，将A5C 顺时针旋转，得到A1B1C，点 A、B 分别与点A1、B1对应，边 A1B1DBD分别交边 AB 、 BC 于点 D 、E，如果点 E 是边A1B1的中点，那么B1C▲ ．C BE图 3B124．〔此题总分值 12 分〕如图 7，抛物线 y ax 2bx cy经过原点 O 0,0 、 A 2,0 ，直线y2x经过抛物B线的顶点 B ，点C是抛物线上一点，且位于对称C轴的右侧，联结 BC 、OC 、AB，过点 C 作 CE ∥x E F轴，分别交线段OB、AB于点E、F.〔1〕求抛物线的表达式；〔2〕当BC CE 时，求证：BCE ∽ ABO ；〔3〕当CBA BOC 时，求点C的坐标.AO x图 725．〔此题总分值 14 分〕四边形 ABCD 中， AD ∥ BC，ABC 2 C，点E是射线AD上一点，点 F 是射线 DC 上一点，且满足BEFA.（1〕如图 8，当点 E 在线段 AD 上时，假设 AB=AD ，在线段 AB 上截取 AG=AE ，联结 GE.求证： GE=DF ；〔2〕如图 9，当点 E 在线段 AD 的延长线上时，假设AB=3 ， AD=4 ，cos A 1x ，，设 AE3DF y ，求y关于x的函数关系式及其定义域；〔3〕记 BE 与 CD 交于点 M，在〔 2〕的条件下，假设△EMF 与△ ABE 相似，求线段 AE 的长 .A ED A D EG F FB C B C图 85/14图 9静安y18．如图4，在平面直角坐标系 xOy 中， A〔 2 3 ，0〕，Q B〔 0， 6〕， M〔 0， 2〕．点 Q 在直线 AB 上，把△ BMQ B沿着直线 MQ 翻折，点 B 落在点 P 处，联结 PQ．如果直线 PQ 与直线 AB 所构成的夹角为60°，那么点 P 的坐M﹒标是▲．AO xQ图 424．在平面直角坐标系xOy 中〔如图 7〕，抛物线y ax2bx c( a 0) 经过原点，与x 轴的另一个交点为A，顶点为 P〔3， 4〕．y 〔 1〕求这条抛物线表达式；〔 2〕将该抛物线向右平移，平移后的新抛P·物线顶点为 Q，它与 y 轴交点为 B，联结 PB、PQ．设点 B 的纵坐标为 m，用含 m 的代数式1表示∠BPQ 的正切值；O 1x 〔 3〕联结 AP，在〔 2〕的条件下，射线 PB平分∠ APQ，求点 B 到直线 AP 的距离．图 725．〔此题总分值 14 分，第〔 1〕小题总分值 3 分，第〔 2〕小题总分值 6 分，第〔 3〕小题总分值 5分〕：如图 8，梯形 ABCD 中， AD∥ BC，AD= 2，AB=BC=CD =6．动点 P 在射线 BA 上，以 BP 为半径的⊙ P 交边 BC 于点 E〔点 E 与点 C 不重合〕，A D联结 PE、 PC．设 BP= x，PC= y．〔 1〕求证： PE∥ DC；〔 2〕求 y 关于 x 的函数解析式，并写出定义域；〔 3〕联结 PD ，当∠ PDC =∠B 时，以 D 为圆心P半径为 R 的⊙D与⊙P相交，求 R 的取值范围．CB E图 86/14闵行18．如图，在△ABC中，AB = AC =5， BC 2 5，D为边AC上一点〔点 D 与点A、 C不重合〕．将△ ABC 沿直线 BD 翻折，使点 A 落在点 E 处，联结 CE．如果 CE // AB，那么C AD︰CD =▲．A B〔第 18 题图〕24．此题共 3 小题，每题各 4 分，总分值 12 分〕〔抛物线 yx2 b x c 经过点 A〔 1， 0〕、 B〔 3， 0〕，且与 y 轴的公共点为点C．〔1〕求抛物线的解析式，并求出点 C 的坐标；y〔 2〕求∠ ACB 的正切值；〔 3〕点 E 为线段 AC 上一点，过点 E 作 EF⊥BC，1垂足为点 F ．如果EF1，求△ BCE 的面积．BF4-1O1x-1〔第 24 题图〕25．〔此题共 3 小题，其中第〔1〕小题各 4 分，第〔 2〕、〔 3〕小题各5分，总分值14 分〕如图 1，点 P 为∠ MAN 的内部一点．过点 P 分别作 PB⊥ AM 、PC⊥AN，垂足分别为点B、C．过点 B 作 BD ⊥ CP，与 CP 的延长线相交于点 D ．BE⊥AP ，垂足为点 E．（1〕求证：∠ BPD =∠ MAN ；〔 2〕如果 sin MAN 3 10，AB 2 10 ， BE = BD，求 BD 的长；10〔 3〕如图 2，设点 Q 是线段 BP 的中点．联结QC、CE，QC 交 AP 于点 F．如果∠MAN = 45 °，且 BE // QC，求SPQF的值．SCEFMMB D B DQPPEF EAC N ACN〔图 1〕7〔图 2〕/ 14浦东18. 定义：如果 P 是圆 O 所在平面内的一点， Q 是射线 OP 上一点，且线段 OP 、 OQ 的比例中项等于圆 O 的半径， 那么我们称点P 与点 Q 为这个圆的一对反演点， 点 M 、 N 为圆 O 的一对反演点，且点 M 、 N 到圆心 O 的距离分别为 4 和 9，那么圆 O 上任意一点 A 到点M 、N 的距离之比AMAN24. 抛物线 y 1 x 2 bx c 经过点 M (3, 4) ，与 x 轴相交于点 A( 3,0) 和点 B ，与 y 轴相交于点 C .3〔1〕求这条抛物线的表达式；〔2〕如果 P 是这条抛物线对称轴上一点， PC BC ，求点 P 的坐标；〔3〕在第〔 2〕小题的条件下，当点P 在 x 轴上方时，求 PCB 的正弦值 .25. AB 是圆 O 的一条弦， P 是圆 O 上的一点，过点 O 作MNAP ，垂足为点 M ，并交射线 AB 于点 N ，圆 O 的半径为 5， AB 8 .〔1〕当 P 是优弧 AB 的中点时〔如图〕，求弦AP 的长；〔2〕当点 N 与点 B 重合时， 试判断： 以点 O 为圆心， 3为半径的圆与直线AP 的位置关系，并说明理由； 2〔3〕当 BNOBON ，且圆 N 与圆 O 相切时，求圆 N 的半径的长 .8/14度初三上海各区二模1824252021 年度初三上海各区二模18-24-25普陀A18.如图 7，AD是△ABC的中线，点E在边AB上，且DE⊥AD，将△ BDE 绕着点 D 旋转，使得点 B与点C重合，点 E 落在点 F处，联结 AF 交BC于点G，如果AE5，那么GF的值等于EBE2AB B D C▲．图 7224．在平面直角坐标系xOy 中，直线y x4m (m 0) 与x轴、y轴分别交于点A、 B3如图 11 所示，点C在线段AB的延长线上，且AB 2BC ．〔1〕用含字母m的代数式表示点C的坐标；y〔2〕抛物线y 1 x2bx 10 经过点A、 C ，求此抛物线3的表达式；〔3〕在第〔 2〕题的条件下，位于第四象限的抛物线上，是B否存在这样的点P ：使S△PAB2S△OBC，如果存在，求出点1P的坐标，如果不存在，试说明理由．O1A x 25．如图 12，在 Rt △ABC中，ACB 90，AB 5，cos BAC 4，点 O 是边 AC 上一个动点〔不与A、C重5图 11合〕，以点 O 为圆心， AO 为半径作⊙O ，⊙O 与射线AB交于点D；以点 C 为圆心， CD 为半径作⊙C ，设OA x．〔1〕如图13，当点D与点B重合时，求x的值；〔2〕当点D在线段AB上，如果⊙C与AB的另一个交点 E 在线段 AD 上时，设AE y ，试求 y 与x之间的函数解析式，并写出x 的取值范围；〔 3〕在点O的运动的过程中，如果⊙ C 与线段AB只有一个公共点，请直接写出x 的取值范围．B D B〔D〕C O A C O A9/14B图12图1318． 我们把满足某种条件的所有点组成的图形，叫做符合这个条件的点的轨迹．如图6，在Rt △ ABC 中，∠ C =90°， AC =8， BC =12，动点 P 从点 A 开始沿射线 AC 方向以 1 个单位 / 秒的速度向点 C 运动，动点 Q 从点 C 开始沿射线 CB 方向以 2 个单位 /秒的速度向点 B 运动，P 、 Q 两点分别从点 A 、 C 同时出发，当其中一点到达端点时，另一点也随之停止运动，在整个运动过程中，线段PQ 的中点 M 运动的轨迹长为▲． BQM24. 〔此题总分值 12 分，每题总分值各4 分〕CP A：如图 10，在平面直角坐标系 xOy 中，抛物线〔〕经过点图 6A 〔 6， - 3〕，对称轴是直线 x=4 ，顶点为 B ， OA 与其对称轴交于点 M ， M 、 N 关于点 B 对称．〔 1〕求这条抛物线的表达式和点B 的坐标；y〔 2〕联结 ON 、 AN ，求△ OAN 的面积；〔 3〕点 Q 在 x 轴上，且在直线x=4 右侧，OMx当∠ ANQ=45°时，求点Q 的坐标．AB N图 1025. 〔此题总分值 14 分，第〔 1〕小题 4 分，第〔 2〕小题 5 分，第〔 3〕小题 5 分〕：在 Rt △ ABC 中，∠ ACB =90°，AC=1 ，D 是 AB 的中点 . 以 CD 为直径的⊙ Q 分别交 BC 、 BA 于点 F 、 E ，点 E 位于点 D 下方，联结 EF 交 CD 于点 G ．（ 1〕如图 11，如果 BC=2 ，求 DE 的长；（ 2〕如图 12，设 BC=x ，GD=y ，求 y 关于 x 的函数关系式及其定义域； GQ（ 3〕如图 13，联结 CE ，如果 CG=CE ，求 BC 的长．BBBDFDFDFGGGQQQEE18． Rt△ ABC 中，∠ ACB= 90°，AC=8，BC=6．将△ ABC 绕点 B 旋转得到△ DBE ，点 A的对应点 D 落在射线 BC 上．直线AC 交 DE 于点 F，那么 CF 的长为 ________．24．〔此题总分值12分，第〔 1〕小题 3分，第〔 2〕小题 4 分，第〔 3〕小题 5 分〕如图，抛物线y ax24x c 过点A〔6，0〕、B〔3，3〕，与 y 轴交于点 C．联结 AB 2并延长，交 y 轴于点 D ．y〔 1〕求该抛物线的表达式；D（2〕求△ ADC 的面积；（3〕点 P 在线段 AC 上，如果△ OAP 和△ DCA 相似，求点 P 的坐标．BO A x C〔第 24 题图〕25．〔此题总分值14 分，第〔 1〕小题 4 分，第〔 2〕小题 5 分，第〔 3〕小题 5 分〕如图，Rt△ ABC 中，∠ ACB= 90°，AC= 42 ，BC= 16．点O在边BC上，以O为圆心， OB 为半径的弧经过点A． P 是弧 AB 上的一个动点．（1〕求半径 OB 的长；（2〕如果点 P 是弧 AB 的中点，联结 PC，求∠ PCB 的正切值；（3〕如果 BA 平分∠ PBC，延长 BP 、CA 交于点 D，求线段 DP 的长．A AC·B C·B O O〔第 25 题图〕〔备用图〕徐汇18．如图，在 Rt △ABC 中，∠ ACB=90 °， AB=6， cosB=2，先将△ ACBB3绕着顶点 C 顺时针旋转 90°，然后再将旋转后的三角形进行放大或缩小得到△ A'CB' 〔点 A'、 C 、B'的对应点分别是点 A 、 C 、B 〕，联结 A'A 、B'B ，如果△ AA'B 和△ AA'B' 相似，那么 A C 的长是▲．A C〔第 18 题图〕24 ． 如 图 ， 在 平 面 直 角 坐 标 系 xOy 中 ， 抛 物 线y1x 2 bx c 与直线 y1x 3 分别交于 x 轴、 y4 2轴上的 B 、C 两点，设该抛物线与x 轴的另一个交点为点 A ，顶点为点 D ，联结 CD 交 x 轴于点 E ．O〔 1〕求该抛物线的表达式及点 D 的坐标；（ 2〕求∠ DCB 的正切值；（ 3〕如果点 F 在 y 轴上，且∠ FBC= ∠ DBA +∠DCB ，求点 F 的坐标．25.如图，在 △ ABC 中， AC=BC= 10， cosC3，点 P 是 AC 边上一动点〔不与点A 、 C 重5合〕，以 PA 长为半径的 ⊙P 与边 AB 的另一个交点为D ，作 DE ⊥CB 于 E.BBEDCPAAC〔第 25 题图〕备用图（ 1〕当 ⊙ P 与边 BC 相切时，求 ⊙P 的半径；（ 2〕联结 BP 交 DE 于点 F ，设 AP 的长为 x ，PF 的长为 y ，求 y 关于 x 的函数解析式，并直接写出 x 的取值范围；（ 3〕在〔 2〕的条件下，当以 PE 长为直径的 ⊙Q 与 ⊙P 相交于 AC 上边的点 G 时，求相交所得的公共弦的长 .杨浦A FD18．如图，在矩形ABCD 中，过点 A 的圆 O 交边 AB 于点 E，交边AD 于点 F ， AD =5， AE=2 ， AF=4. 如果以点 D 为圆心， r E 为半径的圆 D 与圆 O 有两个公共点，那么r的取值范围是▲ .B24．〔此题总分值12 分，第〔 1〕小题 4 分，第〔 2〕小题 4 分，第〔 3〕小题 4 分〕开口向下的抛物线y = ax2 - 2ax + 2 与y轴的交点为A，顶点为B，对称轴与的交点为 C，点 A 与点 D 关于对称轴对称，直线BD 与 x 轴交于点M，直线 AB 与直线Cx轴OD交于点 N.y〔 1〕求点 D 的坐标；〔 2〕求点 M 的坐标〔用含 a 的代数式表示〕；5〔 3〕当点 N 在第一象限，且∠OMB =∠ ONA 时，求 a 的值 .4321-3 -2 -1 O 1 2 3 4x-1-2-3〔第24题图〕25．〔此题总分值 14 分，第〔 1〕小题 4 分，第〔 2〕小题 5 分，第〔 3〕小题 5 分〕圆 O 的半径长为 2，点 A、 B、C 为圆 O 上三点，弦 BC=AO，点 D 为 BC 的中点 .〔 1〕如图 1，联结 AC、 OD，设∠ OAC=，请用表示∠ AOD；?A、 D 之间的距离；〔 2〕如图 2，当点 B 为AC的中点时，求点（3〕如果 AD 的延长线与圆 O 交于点 E，以 O 为圆心， AD 为半径的圆与以 BC 为直径的圆相切，求弦 AE 的长 .B B.CD C DA O A O A O〔图 1〕〔图2〕〔备用图〕〔第 25 题图〕2021 年度初三上海各区二模18-24-25长宁18.如图 3，在ABC 中， AB AC 5 ， BC 8 ，将ABC 绕着点 C 旋转，点 A、 B 的对应点分别是点A' 、 B' ，假设点 B' 恰好在线段 AA' 的延长线上，A 那么 AA'的长等于▲．B图 3交于点 A ，点 A 的横坐标为 6 ，抛物线顶点为点B．〔1〕求这条抛物线的表达式和顶点 B 的坐标；〔2〕过点O作OP // AB，在直线OP上点取一点Q，使得QAB OBA ，求点 Q 的坐标；〔 3〕将该抛物线向左平移m(m0) 个单位，所得新抛物线与y 轴负半轴相交于点 C 且顶y 点仍然在第四象限，此时点A移动到点 D 的位置，CB : DB 3 : 4 ，求m的值．1O1ACB 90 ， AC 图 625.如图 7，在Rt ABC 中，3，BC4，点P在边 AC上〔点 P与点 A 不重合〕，以点 P 为圆心， PA 为半径作⊙ P 交边 AB 于另一点 D ， ED DP ，交边BC于点 E．(1)求证： BE DE ；(2)假设BE x ， AD y ，求 y 关于 x 的函数关系式并写出定义域；(3)延长 ED 交 CA 的延长线于点F ，联结 BP ，假设BDP 与DAF相似，求线段AD 的长．BB BEDCx。

cm18.如图，等边ABC △中，D 是BC 边上的一点，且:1:3BD DC =，把ABC ∆折叠，使点A 落在BC 边上的点D 处.那么AMAN的值为 ▲ .cm23.如图1，ABC △中，90ACB ∠=︒，CD AB ⊥，垂足为D .（1）求证：ACD △∽CBD △；（2）如图2，延长DC 至点G ，联结BG ，过点A 作AF BG ⊥，垂足为F ，AF 交CD 于点E .求证：2CD DE DG =⋅.第18题图ZCM8ABCDMNACDBAC DGFEcm24.如图，在直角坐标系中，一条抛物线与x 轴交于A 、B 两点，与y 轴交于C 点，其中(3,0)B ， (0,4)C ，点A 在x 轴的负半轴上，4OC OA =.（1）求这条抛物线的解析式，并求出它的顶点坐标；（2）联结AC 、BC ，点P 是x 轴正半轴上一个动点，过点P 作PM BC ∥交射线AC 于点M ，联结CP ，若CPM △的面积为2，则请求出点P 的坐标.cm25 如图，已知矩形ABCD 中，6AB =，8BC =，E 是BC 边上一点（不与B 、C 重合），过点E 作EF AE ⊥交AC 、CD 于点M 、F ，过点B 作BG AC ⊥，垂足为G ，BG 交AE 于点H .（1）求证：ABH △∽ECM △；（2）设BE x =，EHy EM=，求y 关于x 的函数解析式，并写出定义域； （3）当BHE △为等腰三角形时，求BE 的长.AB DFCMG HEABDCGhk 18.如图，在矩形ABCD 中，AB =6，AD =10，点E 是边BC 的中点，联结AE ，若将△ABE沿AE 翻折，点B 落在点F 处，联结FC ，则cos ECF ∠= ▲ .hk23.如图，点E 是四边形ABCD 的对角线BD 上的一点，∠BAE=∠CBD=∠DAC . （1）求证：DE AB BC AE ⋅=⋅； （2）求证：∠AED +∠ADC =180°.hk24.在平面直角坐标系xOy 中，抛物线23y ax bx =++与x 轴分别交于点A (2，0)、点B （点B 在点A 的右侧），与y 轴交于点C ，1tan 2CBA ∠=. （1）求该抛物线的表达式；（2）设该抛物线的顶点为D ，求四边形ACBD 的面积；（3）设抛物线上的点E 在第一象限，△BCE 是以BC 为一条直角边的直角三角形，请直接写出点E 的坐标.第24题图 ZHK11hk25.如图，在□ABCD 中，E 为边BC 的中点，F 为线段AE 上一点，联结BF 并延长交边AD 于点G ，过点G 作AE 的平行线，交射线DC 于点H .设AD EFx AB AF==.（1）当1x =时，求:AG AB 的值；（2）设GDH EBASy S =△△，求y 关于x 的函数关系式，并写出x 的取值围；（3）当3DH HC =时，求x 的值.sj18.已知在△ABC 中，∠C =90°, BC =3,AC =4，点D 是AB 边上一点，将△ABC 沿着直线CD翻折，点A 落在直线AB 上的点A ′处，则sin A CD ∠' = ▲ .23.已知如图，在△ABC 中，BD 平分∠ABC 交AC 于点D ，点E 在AB 上，且BC BE BD ⋅=2。

2024年4月上海市中考数学二模题型分类汇编5---二次函数压轴题（24题）【2024.4月奉贤区二模】24.（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图9，在直角坐标平面xOy 中，抛物线22y ax ax c =-+与x 轴交于点A 、B ，与y 轴正半轴交于点C ，顶点为P ，点A 坐标为（-1，0）.（1）写出这条抛物线的开口方向，并求顶点P 的坐标（用a 的代数式表示）；（2）将抛物线向下平移后经过点（0，1），顶点P 平移至P'.如果锐角∠CP'P 的正切值为12，求a 的值；（3）设抛物线对称轴与x 轴交于点D ，射线PC 与x 轴交于点E ，如果∠EDC =∠BPE ，求此抛物线的表达式.图9xyO11-124．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）新定义：已知抛物线2y ax bx c =++（其中abc ≠0），我们把抛物线2y cx ax b =++称为2y ax bx c =++的“轮换抛物线”．例如：抛物线y ＝2x 2+3x +1的“轮换抛物线”为y ＝x 2+2x +3．已知抛物线C 1：24(45)y mx m x m =+-+的“轮换抛物线”为C 2，抛物线C 1、C 2与y 轴分别交于点E 、F ，点E 在点F 的上方，抛物线C 2的顶点为P ．（1）如果点E 的坐标为（0，1），求抛物线C 2的表达式；（2）设抛物线C 2的对称轴与直线38y x =+相交于点Q ，如果四边形PQEF 为平行四边形，求点E 的坐标；（3）已知点M （-4，n ）在抛物线C 2上，点N 坐标为（-2，172-），当△PMN ∽△PEF 时，求m 的值．备用图Oy xyOx24．（本题满分12分）问题：已知抛物线L ：22y x x =-．抛物线W 的顶点在抛物线L 上（非抛物线L 的顶点）且经过抛物线L 的顶点．请求出一个满足条件的抛物线W 的表达式．（1）解这个问题的思路如下：先在抛物线L 上任取一点（非顶点），你所取的点是①；再将该点作为抛物线W 的顶点，可设抛物线W 的表达式是②；然后求出抛物线L 的顶点是③；再将抛物线L 的顶点代入所设抛物线W 的表达式，求得其中待定系数的值为④；最后写出抛物线W 的表达式是⑤．（2）用同样的方法，你还可以获得其他满足条件的抛物线W ，请再写出一个抛物线W的表达式．（3）如果问题中抛物线L 和W 在x 轴上所截得的线段长相等，求抛物线W 的表达式．24.（本题满分12分,第（1）小题4分，第（2）小题中①②题各4分）已知：抛物线2y x bx c =++经过点A （3，0）、B （0，-3），顶点为P ．（1）求抛物线的解析式及顶点P 的坐标；（2）平移抛物线，使得平移后的抛物线顶点Q 在直线AB 上，且点Q 在y 轴右侧．①若点B 平移后得到的点C 在x 轴上，求此时抛物线的解析式；②若平移后的抛物线与y 轴相交于点D ，且△BDQ 是直角三角形，求此时抛物线的解析式．yxO24．（本题满分12分）如图，在平面直角坐标系xOy 中，已知抛物线关于直线25=x 对称，且经过点A （0，3）和点B （3，0），横坐标为4的点C 在此抛物线上．（1）求该抛物线的表达式；（2）联结AB 、BC 、AC ，求tan BAC ∠的值；（3）如果点P 在对称轴右方的抛物线上，且∠PAC =45°，过点P 作PQ ⊥y 轴，垂足为Q ，请说明∠APQ =∠BAC ，并求点P 的坐标．24．（满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）在平面直角坐标系xOy 中，已知抛物线212y x bx c =++与x 轴相交于A （1-，0）、B两点，且与y 轴交于点C （0，2-）．（1）求抛物线的表达式；（2）如果点D 是x 正半轴上一点，∠ADC=2∠ACO ，且四边形AQCD 是菱形，请直接写出点D 和点Q 的坐标（不需要说明理由）；（3）由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形，对于平面内的一个多边形，画出它的任意一边所在的直线，如果其余各边都在这条直线的一侧，那么这个多边形叫做“凸多边形”；否则叫做“凹多边形”．如果点E 是抛物线对称轴上的一个动点，纵坐标为t ，且四边形ACBE 是凹四边形（线段AE 与线段BC 不相交），求t 的取值范围．yxO（第24题图）24．（本题满分12分，其中每小题各4分）在平面直角坐标系xOy 中，已知直线+2y x =-与x 轴、y 轴分别交于点A 、点B ，抛物线C 1：2y x bx c =-++经过点A 、B 两点，顶点为点C ．（1）求b 、c 的值；（2）如果点D 在抛物线C 1的对称轴上，射线AB 平分∠CAD ，求点D 的坐标；（3）将抛物线C 1平移，使得新抛物线C 2的顶点E 在射线BA 上，抛物线C 2与y 轴交于点F ，如果△BEF 是等腰三角形，求抛物线C 2的表达式．（第24题图）11OxyAB24．（本题满分12分）在平面直角坐标系xOy 中（如图8），已知抛物线()()20y a x m n a =-+≠与x 轴交于点A 、B ，抛物线的顶点P 在第一象限，且90APB ∠=︒．（1）当点P 的坐标为()4,3时，求这个抛物线的表达式；（2）抛物线()()20y a x m n a =-+≠表达式中有三个待定系数，求待定系数a 与n 之间的数量关系；（3）以点P 为圆心，PA 为半径作P ，P 与直线2ny x =+相交于点M 、N ．当点P 在直线12y x =上时，用含a 的代数式表示MN 的长．图8yxOPAB24.（本题满分12分，每小题满分各4分）在平面直角坐标系xOy 中，抛物线23y axbx =+-的图像与x 轴交于点A （-3，0）和点B （1，0），与y 轴交于点C ，D 是线段OA 上一点．（1）求这条抛物线的表达式和点C 的坐标；（2）如图，过点D 作DG ⊥x 轴，交该抛物线于点G ，当DGA ＝DGC 时，求△GAC 的面积；（3）点P 为该抛物线上第三象限内一点，当OD ＝1，且∠DCB +∠PBC ＝45°时，求点P 的坐标．第24题图24.（本题满分12分，第（1）小题4分，第（2）小题第①问4分，第（2）小题第②问4分）如图8,在平面直角坐标系xOy 中，已知点A （2，0）、点B （0，2），抛物线2y x bx c =-++经过点A ，且顶点C 在线段AB 上（与点A 、B 不重合）．（1）求b 、c 的值；（2）将抛物线向右平移m （0m >）个单位，顶点落在点P 处,新抛物线与原抛物线的对称轴交于点D ，联结PD ，交x 轴于点E ．①如果m =2,求△ODP 的面积；②如果EC =EP ,求m 的值.(图8)11OxyA B24．（本题满分12分）如图，在平面直角坐标系xOy 中，抛物线)0(442>+-=a ax ax y 与x 轴交于点)0,1(A 和点B ，与y 轴交于点C ．（1）求该抛物线的表达式及点B 的坐标；（2）已知点),0(m M ，联结BC ，过点M 作BC MG ⊥，垂足为G ，点D 是x 轴上的动点，分别联结GD 、MD ，以GD 、MD 为边作平行四边形GDMN ．①当23=m 时，且□GDMN 的顶点N 正好落在y 轴上，求点D 的坐标；②当0≥m 时，且点D 在运动过程中存在唯一的位置，使得□GDMN 是矩形，求m 的值．（第24题图）A O xyB C24．（本题满分12分，第（1）小题3分，第（2）小题9分）定义：我们把平面内经过已知直线外一点并且与这条直线相切的圆叫做这个点与已知直线的点切圆．如图1，已知直线l外有一点H，圆Q经过点H且与直线l相切，则称圆Q 是点H与直线l的点切圆．阅读以上材料，解决问题：已知直线OA外有一点P，PA⊥OA，OA=4，AP=2，圆M是点P与直线OA的点切圆．（1）如果圆心M在线段OP上，那么圆M的半径长是▲(直接写出答案)．（2）如图2，以O为坐标原点、OA为x轴的正半轴建立平面直角坐标系xOy，点P在第一象限，设圆心M的坐标是（x，y）．①求y关于x的函数解析式；②点B是①中所求函数图像上的一点，联结BP并延长交此函数图像于另一点C．如果CP：BP=1：4，求点B的坐标．lH Q第24题图1PyxAO第24题图224．（本题满分12分，每小题满分各4分）在平面直角坐标系xOy （如图8）中，已知抛物线32++=bx ax y 经过点)0,1(A 、)3,2-(B 两点，与y 轴的交点为C 点，对称轴为直线l ．（1）求此抛物线的表达式；（2）已知以点C 为圆心，半径为CB 的圆记作圆C ，以点A 为圆心的圆记作圆A ，如果圆A 与圆C 外切，试判断对称轴直线l 与圆A 的位置关系，请说明理由；（3）已知点D 在y 轴的正半轴上，且在点C 的上方，如果BAC BDC ∠=∠，请求出点D 的坐标．图8O 11xy-1-1。

12015年上海市初中毕业统一学业考试数学试卷考生注意：1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效； 3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】 1． 下列实数中，是有理数的为（ ）． A ．2；B ．34；C ．π；D ．0．2． 当0>a 时，下列关于幂的运算正确的是（ ）． A ．10=a ；B ．a a -=-1； C ．22)(a a -=-； D ．2211aa =． 3． 下列y 关于x 的函数中，是正比例函数的为（ ）． A ．2x y =；B ．x y 2=； C ．2xy =； D ．21+=x y ． 4． 如果一个正多边形的中心角为︒72，那么这个正多边形的边数是（ ）． A ．4； B ．5；C ．6；D ．7．5． 下列各统计量中，表示一组数据波动程度的量是（ ）．A ．平均数；B ．众数；C ．方差；D ．频率．6． 如图1，已知在⊙O 中，AB 是弦，半径AB OC ⊥，垂足为点D ，要使 四边形OACB 为菱形，还需要添加一个条件，这个条件可以是（ ）． A ．BD AD =； B ．CD OD =； C ．CBD CAD ∠=∠； D ．OCB OCA ∠=∠．二、填空题：（本大题共12题，每题4分，满分48分） 【请将结果直接填入答题纸的相应位置】 7． 计算：=+-22 ． 8． 方程223=-x 的解是 ． 9． 如果分式32+x x有意义，那么x 的取值范围是 ． 10．如果关于x 的一元二次方程042=-+m x x 没有实数根，那么m 的取值范围是 ． 11．同一温度的华氏度数)(F y ︒与摄氏度数)(C x ︒之间的函数关系是3259+=x y ．如果某一温度的摄氏度数是C ︒25，那么它的华氏度数是 F ︒．图1图212．如果将抛物线122-+=x x y 向上平移，使它经过点)3,0(A ，那么所得新抛物线的表达式是 ． 13．某校学生会提倡双休日到养老院参加服务活动，首次活动需要7位同学参加，现有包括小杰在内的50位同学报名，因此学生会将从这50位同学中随机抽取7位，小杰被抽到参加此次活动的概率是 ． 14．已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示：那么“科技创新社团”成员年龄的中位数是 岁． 15．如图2，已知在ABC ∆中，D 、E 分别是边AB 、边AC 的中点， m AB =，n AC =，那么向量DE 用向量m 、n 表示为 ． 16．已知E 是正方形ABCD 的对角线AC 上一点，AD AE =，过点E 作AC 的 垂线，交边CD 于点F ，那么=∠FAD 度．17．在矩形ABCD 中，5=AB ，12=BC ，点A 在⊙B 上．如果⊙D 与⊙B 相交，且点B 在⊙D 内，那么⊙D 的半径长可以等于 ． （只需写出一个符号要求的数）18．已知在ABC ∆中，8==AC AB ，︒=∠30BAC ．将ABC ∆绕点A 旋转，使点B 落在原ABC ∆的点C处，此时点C 落在点D 处．延长线段AD ，交原ABC ∆的边BC 的延长线于点E ，那么线段DE 的长等于 ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）先化简，再求值：2124422+--+÷++x x x x x x x ，其中12-=x ．3图320．（本题满分10分）解不等式组：⎪⎩⎪⎨⎧+≤-->9131624x x x x ，并把解集在数轴上表示出来．21．（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）已知，如图3，在平面直角坐标系xOy 中，正比例函数x y 34=的图像经过点A ，点A 的纵坐标为4，反比例函数xmy =的图像也经过点A ，第一象限内的点B 在这个反比例函数的图像上，过点B 作BC ∥x 轴，交y 轴于点C ，且AB AC =．求：（1）这个反比例函数的解析式； （2）直线AB 的表达式．图422．（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）如图4，MN 表示一段笔直的高架道路，线段AB 表示高架道路旁的一排居民楼．已知点A 到MN 的距离为15米，BA 的延长线与MN 相交于点D ，且︒=∠30BDN ，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．（1）过点A 作MN 的垂线，垂足为点H ．如果汽车沿着从M 到N 的方向在MN 上行驶，当汽车到达点P 处时，噪音开始影响这一排的居民楼，那么此时汽车与点H 的距离为多少米？（2）降低噪音的一种方法是在高架道路旁安装隔音板，当汽车行驶到点Q 时，它与这一排居民楼的距离QC 为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？（精确到1米） （参考数据：7.13≈）5图5已知：如图5，平行四边形ABCD 的对角线相交于点O ，点E 在边BC 的延长线上，且OB OE =，联结DE ．（1）求证：BE DE ⊥；（2）如果CD OE ⊥，求证：DE CD CE BD ⋅=⋅．图6已知在平面直角坐标系xOy 中（如图6），抛物线42-=ax y 与x 轴的负半轴相交于点A ，与y 轴相 交于点B ，52=AB ．点P 在抛物线上，线段AP 与y 轴的正半轴相交于点C ，线段BP 与x 轴相交于点D ．设点P 的横坐标为m ．（1）求这条抛物线的解析式；（2）用含m 的代数式表示线段CO 的长度； （3）当23tan =∠ODC 时，求PAD ∠的正弦值．7图7 备用图25．（本题满分14分，其中第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）已知：如图7，AB 是半圆O 的直径，弦CD ∥AB ，动点P 、Q 分别在线段OC 、CD 上，且OP DQ =，AP 的延长线与射线OQ 相交于点E ，与弦CD 相交于点F （点F 与点C 、D 不重合），20=AB ，54cos =∠AOC ．设x OP =，CPF ∆的面积为y ． （1）求证：OQ AP =；（2）求y 关于x 的函数关系式，并写出它的定义域； （3）当OPE ∆是直角三角形时，求线段OP 的长．911。

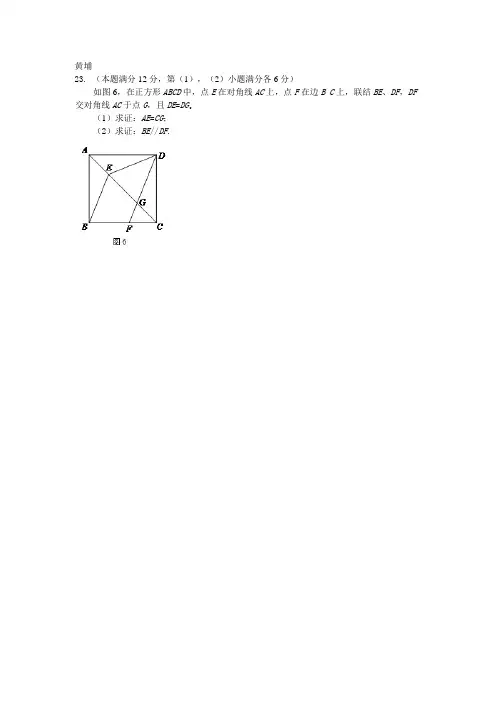
黄埔23. （本题满分12分，第（1），（2）小题满分各6分）如图6，在正方形ABCD中，点E在对角线AC上，点F在边B C上，联结BE、DF，DF 交对角线AC于点G，且DE=DG．（1）求证：AE=CG；（2）求证：BE//DF.24. （本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）如图7，在平面直角坐标系xOy中，已知点A的坐标为（，3）（其中>4)，射线OA与反比例函数的图像交于点P，点B、C分别在函数的图像上，且AB//x轴，AC//y 轴．（1）当点P横坐标为6，求直线AO的表达式；（2）联结BO，当时，求点A坐标；（3）联结BP、CP，试猜想：的值是否随的变化而变化？如果不变，求出的值；如果变化，请说明理由．奉贤区23．（本题满分12分，每小题满分各6分）已知：如图，在四边形ABCD中，AB//CD，点E是对角线A C上一点，∠DEC=∠ABC，且．（1）求证：四边形ABCD是平行四边形；（2）分别过点E、B作AB和AC的平行线交于点F，联结CF，若∠FCE= ∠DCE，求证：四边形EFCD是菱形．24．（本题满分12分，第（1）小题4分，第（2）小题8分）已知：在平面直角坐标系中，抛物线的对称轴为直线x=2，顶点为A．（1）求抛物线的表达式及顶点A的坐标；（2）点P为抛物线对称轴上一点，联结OA、OP．①当O A⊥OP时，求O P的长；②过点P作OP的垂线交对称轴右侧的抛物线于点B，联结OB，当∠OAP=∠OBP时求点B的坐标．23．已知：如图，正方形ABCD，BM、DN分别是正方形的两个外角平分线，∠MAN=45°，将∠MAN绕着正方形的顶点A旋转，边AM、AN分别交两条角平分线于点M、N，联结MN．（1）求证：；（2）联结BD，当∠BAM的度数为多少时，四边形BMND为矩形，并加以证明．24．如图，在平面直角坐标系中，O为坐标原点，开口向上的抛物线与x轴交于点A（－1，0）和点B（3，0），D为抛物线的顶点，直线AC与抛物线交于点C（5，6）．（1）求抛物线的解析式；（2）点E在x轴上，且和相似，求点E的坐标；（3）若直角坐标平面中的点F和点A、C、D构成直角梯形，且面积为16，试求点F的坐标．静安、青浦区23.（本题满分12分，第小题满分6分）如图，在梯形ABCD中，AB//CD，AD＝BC，E是CD的中点，BE交AC于F，过点F作FG∥AB，交AE于点G．(1)求证：AG=BF；(2)当时，求证：．24．（本题满分12分，第（1）小题满分8分，第（2）小题满分4分）如图，在直角坐标系中，抛物线与轴的正半轴相交于点A、与轴的正半轴相交于点B，它的对称轴与轴相交于点C，且∠OBC=∠OAB，AC=3．（1）求此抛物线的表达式；（2）如果点D在此抛物线上，DF⊥OA，垂足为F，DF与线段AB相交于点G，且，求点D的坐标．宝山嘉定23．（本题满分12分，每小题满分各6分)如图8，已知△和△都是等边三角形，点在边上，点在边的右侧，联结．（1）求证：；（2）在边上取一点，使，联结、．求证：四边形是等腰梯形．24．（本题满分12分，每小题满分各4分）已知平面直角坐标系（图9），双曲线与直线都经过点．（1）求与的值；（2）此双曲线又经过点，过点的直线与直线平行交轴于点，联结、，求△的面积；（3）在（2）的条件下，设直线与轴交于点，在射线上有一点，如果以点、、所组成的三角形与△相似，且相似比不为，求点的坐标．松江区23.（本题满分12分，每小题各6分）如图，已知在正方形ABCD中，点E在CD边上，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交AF于点G，联结B G.（1）求证：△ADG≌△CDF；（2）如果E为CD的中点，求证：BG⊥AF.24．（本题满分12分，每小题各4分）如图，二次函数的图像与轴的正半轴交于点A（4，0），过A点的直线与y轴的正半轴交于点B，与二次函数的图像交于另一点C，过点C作CH⊥x轴，垂足为H．设二次函数图像的顶点为D，其对称轴与直线AB及轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．长宁23．（本题满分12分）如图，正方形ABCD中，点E、F分别在边BC、CD上，AE=AF，AC和EF交于点O，延长AC至点G，使得AO=OG，联结EG、FG.（1）求证: BE=DF；（2）求证:四边形AEGF是菱形.24．（本题满分12分）如图，已知抛物线的顶点A在第四象限，过点A作AB⊥y轴于点B，C是线段AB上一点(不与A、B重合)，过点C作CD⊥x轴于点D，并交抛物线于点P. （1）若点C的横坐标为1，且是线段AB的中点，求点P的坐标；（2）若直线AP交y轴负半轴于点E，且AC=CP，求四边形OEP D的面积S关于t的函数解析式，并写出定义域；（3）在（2）的条件下，当△ADE的面积等于2S时，求t的值.崇明县23．（本题满分12分，每小题各6分）如图，中，，点D、E分别是BC、AC的中点，过点A作交线段DE的延长线于点F，取AF的中点G，联结DG，GD与AE交于点H．（1）求证：四边形是菱形；（2）求证：．24．（本题满分12分，每小题各6分）如图，已知抛物线经过点，点，点．（1）求这个抛物线的解析式，并写出顶点坐标；（2）已知点在轴上，，求点的坐标．闵行区23．（本题满分12分，其中每小题各6分）如图，已知在梯形ABCD中，AD // BC，∠A = 90º，AB = AD．点E在边AB上，且DE ⊥CD，DF平分∠EDC，交BC于点F，联结CE、EF．（1）求证：DE = DC；（2）如果，求证：∠BEF =∠CEF．24．（本题满分12分，其中每小题各4分）如图，已知在平面直角坐标系xOy中，抛物线与x轴相交于A、B两点，与y轴相交于点C，其中点A的坐标为（-3，0）．点D在线段AB上，AD = AC．（1）求这条抛物线的关系式，并求出抛物线的对称轴；（2）如果以DB为半径的圆D与圆C外切，求圆C的半径；（3）设点M在线段AB上，点N在线段BC上．如果线段MN被直线CD垂直平分，求的值．浦东新区23．（本题满分12分，其中每小题各6分）如图，已知在平行四边形ABCD中，AE⊥BC，垂足为点E，AF⊥CD，垂足为点F．（1）如果AB=AD，求证：EF∥BD；（2）如果EF∥BD，求证：AB=AD．24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）已知：如图，直线y=kx+2与x轴的正半轴相交于点A（t,0）、与y轴相交于点B，抛物线经过点A和点B，点C在第三象限内，且AC⊥AB，tan∠ACB=．（1）当t=1时，求抛物线的表达式；（2）试用含t的代数式表示点C的坐标；（3）如果点C在这条抛物线的对称轴上，求t的值．普陀区23．（本题满分12分）如图9，在△中，点、分别在边、上，、相交于点，∥交于点，且，联结．（1）求证：∥；（2）设，求证：四边形是菱形．24．（本题满分12分）如图10，在平面直角坐标系中，二次函数的图像经过点，，．点是点关于原点的对称点，联结，点是x轴上的一个动点，设点的坐标为(m, 0)，过点作x轴的垂线l交抛物线于点．（1）求这个二次函数的解析式；（2）当点在线段OB上运动时，直线l交BD于点．当四边形是平行四边形时，求m的值；（3）是否存在点，使△是不以为斜边的直角三角形，如果存在，请直接写出点的坐标；如果不存在，请说明理由．杨浦区23．(本题满分12分)已知：如图，Rt△ABC和Rt△CDE中，∠AB C=∠CDE =，且BC与CD共线，联结AE，点M为AE中点，联结BM，交AC于点G，联结MD，交CE于点H。

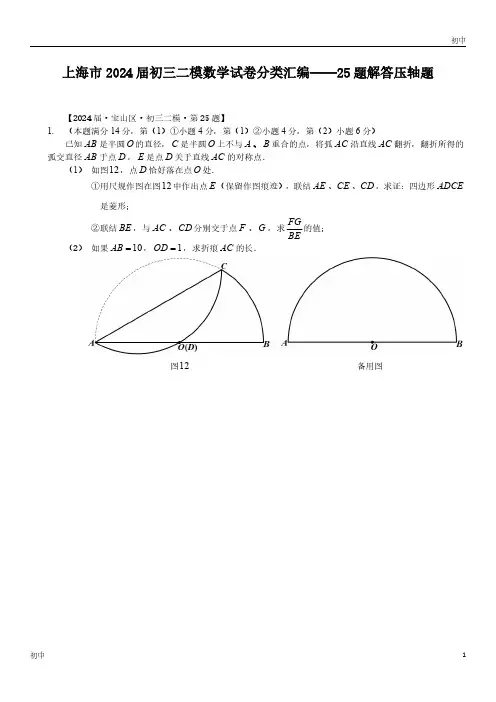
图12备用图上海市2024届初三二模数学试卷分类汇编——25题解答压轴题【2024届·宝山区·初三二模·第25题】1.（本题满分14分，第（1）①小题4分，第（1）②小题4分，第（2）小题6分）已知AB 是半圆O 的直径，C 是半圆O 上不与A 、B 重合的点，将弧AC 沿直线AC 翻折，翻折所得的弧交直径AB 于点D ，E 是点D 关于直线AC 的对称点．（1）如图12，点D 恰好落在点O 处．①用尺规作图在图12中作出点E （保留作图痕迹），联结AE 、CE 、CD ，求证：四边形ADCE 是菱形；②联结BE ，与AC 、CD 分别交于点F 、G ，求FGBE的值；（2）如果10AB =，1OD =，求折痕AC 的长．备用图2【2024届·崇明区·初三二模·第25题】2.（本题满分14分，第（1）①小题4分，第（1）②小题5分，第（2）小题5分）如图，已知Rt ABC ∆中，90ACB ∠=︒，6AC =，3sin 5B =，点D 是射线BA 上一动点（不与A 、B 重合），过点D 作//DE AC ，交射线BC 于点E ，点Q 为DE 中点，联结AQ 并延长，交射线BC 于点P ．（1）如图1，当点D 在线段AB 上时．①若2AD =，求PC 的长；②当ADQ ∆与ABP ∆相似时，求AD 的长；（2）当ADQ ∆是以AD 为腰的等腰三角形时，试判断以点A 为圆心、AD 为半径的⊙A 与以点C 为圆心、CE 为半径的⊙C 的位置关系，并说明理由．第25题图1备用图1图10备用图【2024届·奉贤区·初三二模·第25题】3.（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图10，已知半圆O 的直径为MN ，点A 在半径OM 上，B 为 MN 的中点，点C 在 BN 上，以AB 、BC为邻边作矩形ABCD ，边CD 交MN 于点E ．（1）如果6MN =，2AM =，求边BC 的长；（2）联结CN ，当CEN ∆是以CN 为腰的等腰三角形时，求BAN ∠的度数；（3）联结DO 并延长，交AB 于点P ，如果2BP AP =，求BCAB的值．【2024届·虹口区·初三二模·第25题】4.（本题满分14分，第（1）小题4分，第（2）①小题5分，第（2）②小题5分）在梯形ABCD 中，//AD BC ，点E 在射线DA 上，点F 在射线AB 上，联结CE 、DF 相交于点P ，EPF ABC ∠=∠．（1）如图10①，如果AB CD =，点E 、F 分别在边AD 、AB 上．求证：AF DFDE CE=；（2）如图10②，如果AD CD ⊥，5AB =，10BC =，3cos 5ABC ∠=．在射线DA 的下方，以DE 为直径作半圆O ，半圆O 与CE 的另一个交点为点G ．设DF 与弧EG 的交点为Q ．①当6DE =时，求EG 和AF 的长；②当点Q 为弧EG 的中点时，求AF 的长．图10①图10②图10②备用图图10备用图【2024届·黄浦区·初三二模·第25题】5.（本题满分14分）已知：如图10，ABC ∆是圆O 的内接三角形，AB AC =，弧 AB 、AC 的中点分别为M 、N ，MN 与AB 、OA 、AC 分别交于点P 、T 、Q ．（1）求证：OA MN ⊥；（2）当ABC ∆是等边三角形时，求ATOT的值；（3）如果圆心O 到弦BC 、MN 的距离分别为7和15，求线段PQ 的长．图9图10备用图在菱形ABCD 中，60DAB ∠=︒，点E 在射线AB 上，联结CE 、BD ．（1）如图9，当点E 是边AB 的中点，求ECD ∠的正切值；（2）如图10，当点E 在线段AB 的延长线上，联结DE 与边BC 交于点F ，如果6AD =，EFC ∆的面积等于33EF 的长；（3）当点E 在边AB 上，CE 与BD 交于点H ，联结DE 并延长DE 与CB 的延长线交于点G ，如果6AD =，BCH ∆与以点E 、G 、B 所组成的三角形相似，求AE 的长．第25题图1第25题图2如图，已知：等腰梯形ABCD 中，//AD BC ，AB DC =，以A 为圆心，AB 为半径的圆与BC 相交于点E ，与CD 相交于点F ，联结AE 、AC 、BF ，设AE 、AC 分别与BF 相交于点G 、H ，其中H 是AC 的中点．（1）求证：四边形AECD 为平行四边形；（2）如图1，如果AE BF ⊥，求ABBC的值；（3）如图2，如果BG GH =，求ABC ∠的余弦值．=第25题图1第25题图2如图1，ABC ∆中，已知6AB =，9BC =，B ∠为锐角，1cos 3ABC ∠=．（1）求sin C 的值；（2）如图2，点P 在边AB 上，点Q 是边BC 的中点，⊙P 经过点A ，⊙P 与⊙Q 外切，且⊙Q 的直径不大于BC ，设⊙P 的半径为x ，⊙Q 的半径为y ，求y 关于x 的函数解析式，并写出定义域；（3）在第（2）小题条件下，联结PQ ，如果BPQ ∆是等腰三角形，求AP 的长．第25题图1第25题图2备用图【2024届·闵行区·初三二模·第25题】9.（本题满分14分，第（1）①小题4分，第（1）②小题5分，第（2）小题5分）如图，OB 是⊙O 的半径，弦AB 垂直于弦BC ，点M 是弦BC 的中点，过点M 作OB 的平行线，交⊙O 于点E 和点F ．（1）如图1，当AB BC =时．①求ABO ∠的度数；②联结OE ，求证：30OEF ∠=︒；（2）如图2，联结OE ，当AB BC ≤时，tan OEF x ∠=，ABy BC=，求y 关于x 的函数关系式并直接写出定义域．第25题图1第25题图2第25题图3【2024届·浦东新区·初三二模·第25题】10.（本题满分14分，第（1）小题5分，第（2）小题4分，第（3）小题5分）已知：⊙1O 和⊙2O 相交于A 、B 两点，线段12O O 的延长线交⊙2O 于点C ，CA 、CB 的延长线分别交⊙1O 于点D 、E ．（1）联结AB 、DE ，AB 、DE 分别与连心线12O O 相交于点H 、点G ．如图1，求证：//AB DE ；（2）如果125O O ．①如图2，当点G 与1O 重合，⊙1O 的半径为4时，求⊙2O 的半径；②联结2AO 、BD ，BD 与连心线12O O 相交于点F ，如图3，当2//BD AO ，且⊙2O 的半径为2时，求1O G 的长．11.（本题满分14分）如图9，在梯形ABCD 中，//AD BC （AD BC <），90A ∠=︒，6BC CD ==．将梯形ABCD 绕点C 按顺时针方向旋转，使点B 与点D 重合，此时点A 、D 的对应点分别是点E 、F ．（1）当点F 正好落在AD 的延长线上时，求BCD ∠的度数；（2）联结AE ，设AD x =，AE y =．①求y 关于x 的函数解析式；②定义：同中心同边数的两个正多边形称为双同正多边形．设BCF ∠是一个正多边形的中心角，联结BD ，请说明以线段BD 、AE 为边的正多边形是双同正多边形的理由．当这两个正多边形的面积比是4:5时，求双同正多边形的边数．图9第25题（1）图第25题（2）图12.（本题满分14分，第（1）①小题4分，第（1）②小题5分，第（2）小题5分）在ABC ∆中，2AB AC ==，以C 为圆心、CB 为半径的弧分别与射线BA 、射线CA 相交于点D 、E ，直线ED 与射线CB 相交于点F ．（1）如图，当点D 在线段AB 上时．①设ABC α∠=，求BDF ∠；（用含α的式子表示）②当1BF =时，求cos ABC ∠的值；（2）如图，当点D 在BA 的延长线上时，点M 、N 分别为BC 、DF 的中点，联结MN ，如果//MN CE ，求CB 的长．图9备用图13.（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图9，已知矩形ABCD 中，1AB =，2BC =，点P 是边AD 上一动点，过点P 作PE AC ⊥，垂足为点E ，联结BE ，过点E 作EF BE ⊥，交边AD 于点F （点F 与点A 不重合）．（1）当F 是AP 的中点时，求证：BA BE =；（2）当AP 的长度取不同值时，在PEF ∆中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由；（3）延长PE 交边BC 于点G ，联结FG ，EFG ∆与AEF ∆能否相似？若能相似，求出此时AP 的长；若不能相似，请说明理由．第25题图14.（本题满分14分，第（1）①小题2分，第（1）②小题3分，第（2）①小题5分，第（2）②小题4分）如图，在扇形OAB 中，62OA OB ==90AOB ∠=︒，点C 、D 是弧AB 上的动点（点C 在点D 的上方，点C 不与点A 重合，点D 不与点B 重合），且45COD ∠=︒．（1）①请直接写出弧AC 、弧CD 和弧BD 之间的数量关系；②分别联结AC 、CD 和BD ，试比较AC BD +和CD 的大小关系，并证明你的结论；（2）联结AB 分别交OC 、OD 于点M 、N ．①当点C 在弧AB 上运动过程中，AN BM ⋅的值是否变化？若变化，请说明理由；若不变，请求AN BM ⋅的值；②当5MN =时，求圆心角DOB ∠的正切值．第25题图1备用图15.（本题满分14分，第（1）小题4分，第（2）小题10分）已知以AB 为直径的半圆O 上有一点C ，CD OA ⊥，垂足为点D ，点E 是半径OC 上一点（不与点O 、C 重合），作EF OC ⊥交弧BC 于点F ，联结OF ．（1）如图1，当FE 的延长线经过点A 时，求CD AF的值；（2）如图2，作FG AB ⊥，垂足为点G ，联结EG ．①试判断EG 与CD 的大小关系，并证明你的结论；②当EFG ∆是等腰三角形，且4sin 5COD ∠=，求OE OD 的值．第25题图1备用图备用图16.（本题满分14分，第（1）小题4分，第（2）①小题5分，第（2）②小题5分）已知在ABC ∆中，CA CB =，6AB =，3cos 5CAB ∠=，点O 为边AB 上一点，以点O 为圆心，OA 为半径作⊙O ，交边AC 于点D （点D 不与点A 、C 重合）．（1）当4AD =时，判断点B 与⊙O 的位置关系，并说明理由；（2）过点C 作CE OD ⊥，交OD 延长线于点E ．以点E 为圆心，EC 为半径作⊙E ，延长CE ，交⊙E 于点'C ．①如图1，如果⊙O 与⊙E 的公共弦恰好经过线段EO 的中点，求CD 的长；②联结'AC 、OC ，如果'AC 与BOC ∆的一条边平行，求⊙E 的半径长．。

押上海卷第24-25题押题方向一：二次函数综合题5年上海真题考点命题趋势2023年上海卷第24题二次函数综合题从近5年上海中考命题来看，二次函数五年五考，难度较难。

预计2024年上海卷还将继续考查二次函数综合体，为避免丢分，学生应扎实掌握。

2022年上海卷第24题二次函数综合题2021年上海卷第24题二次函数综合题2020年上海卷第24题二次函数综合题2019年上海卷第24题二次函数综合题1．（2023.上海）在平面直角坐标系xOy 中，已知直线364y x =+与x 轴交于点A ，y 轴交于点B ，点C 在线段AB 上，以点C 为顶点的抛物线2:M y ax bx c =++经过点B ，点C 不与点B 重合．（1）求点A ，B 的坐标；（2）求b ，c 的值；（3）平移抛物线M 至N ，点C ，B 分别平移至点P ，D ，联结CD ，且//CD x 轴，如果点P 在x 轴上，且新抛物线过点B ，求抛物线N 的函数解析式．2.（2022•上海）在平面直角坐标系xOy 中，抛物线212y x bx c =++过点(2,1)A --，(0,3)B -．（1）求抛物线的解析式；（2）平移抛物线，平移后的顶点为(P m ，)(0)n m >．ⅰ．如果3OBP S ∆=，设直线x k =，在这条直线的右侧原抛物线和新抛物线均呈上升趋势，求k 的取值范围；ⅱ．点P 在原抛物线上，新抛物线交y 轴于点Q ，且120BPQ ∠=︒，求点P 的坐标．3．（2021•上海）已知抛物线2(0)y ax c a =+≠经过点(3,0)P 、(1,4)Q ．（1）求抛物线的解析式；（2）若点A 在直线PQ 上，过点A 作AB x ⊥轴于点B ，以AB 为斜边在其左侧作等腰直角三角形ABC ．①当Q 与A 重合时，求C 到抛物线对称轴的距离；②若C 在抛物线上，求C 的坐标．4．（2020•上海）在平面直角坐标系xOy 中，直线152y x =-+与x 轴、y 轴分别交于点A 、B （如图）．抛物线2(0)y ax bx a =+≠经过点A ．（1）求线段AB 的长；（2）如果抛物线2y ax bx =+经过线段AB 上的另一点C ，且BC =，求这条抛物线的表达式；（3）如果抛物线2y ax bx =+的顶点D 位于AOB ∆内，求a 的取值范围．5.（2019•上海）在平面直角坐标系xOy 中（如图），已知抛物线22y x x =-，其顶点为A ．（1）写出这条抛物线的开口方向、顶点A 的坐标，并说明它的变化情况；（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”．①试求抛物线22y x x =-的“不动点”的坐标；②平移抛物线22y x x =-，使所得新抛物线的顶点B 是该抛物线的“不动点”，其对称轴与x 轴交于点C ，且四边形OABC 是梯形，求新抛物线的表达式．（1）二次函数图象与其他函数图象相结合问题解决此类问题时，先根据给定的函数或函数图象判断出系数的符号，然后判断新的函数关系式中系数的符号，再根据系数与图象的位置关系判断出图象特征，则符合所有特征的图象即为正确选项．（2）二次函数与方程、几何知识的综合应用将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．（3）二次函数在实际生活中的应用题从实际问题中分析变量之间的关系，建立二次函数模型．关键在于观察、分析、创建，建立直角坐标系下的二次函数图象，然后数形结合解决问题，需要我们注意的是自变量及函数的取值范围要使实际问题有意义．1．如图，已知在平面直角坐标系xOy 中，直线33y x =+与x 轴相交于点A ，与y 轴相交于点B ，抛物线211:3C y x bx c =++经过点B 和点(1,0)C ，顶点为D ．（1）求抛物线1C 的表达式及顶点D 的坐标；（2）设抛物线与x 轴的另一个交点为E ，若点P 在y 轴上，当90PED ∠=︒时，求点P 的坐标；（3）将抛物线1C 平移，得到抛物线2C ．平移后抛物线1C 的顶点D 落在x 轴上的点M 处，将MAB ∆沿直线AB 翻折，得到QAB ∆，如果点Q 恰好落在抛物线2C 的图象上，求平移后的抛物线2C 的表达式．2．已知二次函数222(1)23y x k x k k =-++--与x 轴有两个交点．（Ⅰ）求k 取值范围；（Ⅱ）当k 取最小整数时，此二次函数的对称轴和顶点坐标；（Ⅲ）将（Ⅱ）中求得的抛物线在x 轴下方的部分沿x 轴翻折到x 轴上方，图象的其余部分不变，得到一个新图象．请你求出新图象与直线y x m =+有三个不同公共点时m 的值．3．在平面直角坐标系xOy 中（如图），已知开口向下的抛物线224y ax x =-+经过点(0,4)P ，顶点为A ．（1）求直线PA 的表达式；（2）如果将POA ∆绕点O 逆时针旋转90︒，点A 落在抛物线上的点Q 处，求抛物线的表达式；（3）将（2）中得到的抛物线沿射线PA 平移，平移后抛物线的顶点为B ，与y 轴交于点C ．如果PC =，求tan PBC ∠的值．4．在平面直角坐标系xOy （如图）中，已知抛物线23y ax bx =++经过点(1,0)A 、(2,3)B -两点，与y 轴的交点为C 点，对称轴为直线l ．（1）求此抛物线的表达式；（2）已知以点C 为圆心，半径为CB 的圆记作圆C ，以点A 为圆心的圆记作圆A ，如果圆A 与圆C 外切，试判断对称轴直线l 与圆A 的位置关系，请说明理由；（3）已知点D 在y 轴的正半轴上，且在点C 的上方，如果BDC BAC ∠=∠，请求出点D 的坐标．5．如图，在平面直角坐标系xOy 中，抛物线244(0)y ax ax a =-+>与x 轴交于点(1,0)A 和点B ，与y 轴交于点C ．（1）求该抛物线的表达式及点B 的坐标；（2）已知点(0,)M m ，联结BC ，过点M 作MG BC ⊥，垂足为G ，点D 是x 轴上的动点，分别联结GD 、MD ，以GD 、MD 为边作平行四边形GDMN ．①当32m =时，且GDMN 的顶点N 正好落在y 轴上，求点D 的坐标；②当0m 时，且点D 在运动过程中存在唯一的位置，使得GDMN 是矩形，求m 的值．6．若二次函数21111y a x b x c =++与22222y a x b x c =++的图象关于点(1,0)P 成中心对称图形，我们称1y 与2y 互为“中心对称”函数．（1）求二次函数263y x x =++的“中心对称”函数的解析式；（2）若二次函数22(0)y ax ax c a =++>的顶点在它的“中心对称”函数图象上，且当24c a a cxa a+-时，y 最大值为2，求此二次函数解析式；（3）二次函数21(0)y ax bx c a =++<的图象顶点为M ，与x 轴负半轴的交点为A 、B ，它的“中心对称”函数2y 的顶点为N ，与x 轴的交点为C 、D ，从左往右依次是A 、B 、C 、D ，若2AB BP =，且四边形AMDN 为矩形，求24b ac -的值．7．小聪同学在解决抛物线2y x bx c =++平移问题时，发现了一些几何结论：如图1，抛物线2y x bx c =++的顶点为A ，沿右上方平移后，所得抛物线的顶点B 落在原抛物线上，且与原抛物线的对称轴交于点C ，连结BA ，BC ，延长BC 交原抛物线于点D ，则BA BC =．（1）如图2，当0b c ==时，请说明该结论成立．（2）当0b =，3c =-，ABC ∠=︒时，求点D 的坐标．（3）过点D 作//DE x 轴，交原抛物线的对称轴于点E ，若2ABC S ∆=，直接写出CDE ∆的面积．8．已知抛物线22(y mx mx n m =++，n 为常数，0)m >与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交点C ，顶点为D ，4AB =．（1）求3m n +的值；（2）如图，连接BD 交AC 于点E ，求证：2BE DE =；（3）设M 是x 轴下方抛物线上的动点（不与C 重合），过点M 作//MN x 轴，交直线AC 于点N ．由线段MN 长的不同取值，试探究符合条件的点M 的个数．9．如图，已知抛物线2y ax =，点(2,1)A -，(8,)B m 在此函数图象上，动点P 位于点O 、B 之间的抛物线上（不与点O ，B 重合），过点B 作直线AP 的垂线，垂足为Q ．（1）如图1，求该二次函数的解析式；（2）尺规作图：当AQ BQ ⋅最大时，在图2中作出此时的点P ；（3）如图3，连接OB ，交直线AP 于点M ，直接写出QMAM的最大值．10．如图，二次函数2(1)y x m x m =-+-+（其中1)m >的图象与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C ，连接AC 、BC ，点D 为ABC ∆的外心．（1）填空：点A 的坐标为，ABC ∠=︒；（2）记ACD ∆的面积为1S ，ABD ∆的面积为2S ，试探究12S S -是否为定值？如果是，求出这个定值；（3）若在第一象限内的抛物线上存在一点E ，使得以B 、D 、C 、E 为顶点的四边形是菱形，则m =．押题方向二：几何综合1．（2023.上海）如图（1）所示，已知在ABC ∆中，AB AC =，O 在边AB 上，点F 是边OB 中点，以O 为圆心，BO 为半径的圆分别交CB ，AC 于点D ，E ，连接EF 交OD 于点G ．（1）如果OG DG=，求证：四边形CEGD为平行四边形；（2）如图（2）所示，连接OE，如果90BAC∠=︒，OFE DOE∠=∠，4AO=，求边OB的长；（3）连接BG，如果OBG∆是以OB为腰的等腰三角形，且AO OF=，求OGOD的值．2．（2022•上海）如图，在 中，P是线段BC中点，联结BD交AP于点E，联结CE．（1）如果AE CE=．ⅰ．求证：ABCD为菱形；ⅱ．若5AB=，3CE=，求线段BD的长；（2）分别以AE，BE为半径，点A，B为圆心作圆，两圆交于点E，F，点F恰好在射线CE上，如果CE=，求ABBC的值．3．（2021•上海）如图，在四边形ABCD中，//AD BC，90ABC∠=︒，AD CD=，O是对角线AC的中点，联结BO并延长交边CD或边AD于点E．（1）当点E在CD上，①求证：DAC OBC∆∆∽；②若BE CD⊥，求ADBC的值；（2）若2DE=，3OE=，求CD的长．4．（2020•上海）如图，ABC∆中，AB AC=，O是ABC∆的外接圆，BO的延长线交边AC于点D．（1）求证：2BAC ABD∠=∠；（2）当BCD∆是等腰三角形时，求BCD∠的大小；（3）当2AD=，3CD=时，求边BC的长．5．（2019•上海）如图1，AD、BD分别是ABC∆的内角BAC∠、ABC∠的平分线，过点A作AE AD⊥，交BD的延长线于点E．（1）求证：12E C ∠=∠；（2）如图2，如果AE AB =，且:2:3BD DE =，求cos ABC ∠的值；（3）如果ABC ∠是锐角，且ABC ∆与ADE ∆相似，求ABC ∠的度数，并直接写出ADE ABC S S ∆∆的值．1．三角形综合题涉及到的知识点比较多，如全等三角形的证明，三角形的相似、解直角三角形，锐角三角函数以及与四边形的综合考查2．四边形综合题涉及到的知识点比较多，主要考查平行四边形、菱形、矩形、正方形，经常与二次函数和圆一起出现，综合性比较强．3．圆的综合题考查的知识点比较多，一般考查垂径定理、圆周角定理、切线长定理、扇形的面积和弧长，经常与四边形一起，难度比较大．4．相似形综合题主要考查相似三角形的判定与性质，其中穿插全等三角形的判定和性质、平行线分线段成比例等知识，难度大．1．如图1，在Rt ABC∆中，90C∠=︒，6AC=，60BAC∠=︒，点D在线段BC上，将ACD∆沿AD折叠使得点C落在AB上C点处．（1）则CD的长为；（2）过点D作//DE AC交AB于点E，点M是线段AD上的动点，连结BM并延长分别交DE，AC于点F、G．①如图2，若点M是线段AD的中点，求EFDF的值；②请问当DM的长满足什么条件时，在线段DE上恰好只有一点P，使得60CPG∠=︒？请说明理由．2．定义：如果一个三角形一条边上的高与这条边的比值是4:5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（1）如图1，在ABC ∆中，8AC =，5BC =，30ACB ∠=︒，试判断ABC ∆是否是“准黄金”三角形，请说明理由．（2）如图2，ABC ∆是“准黄金”三角形，BC 是“金底”，把ABC ∆沿BC 翻折得到DBC ∆，AD 交BC 的延长线于点E ，若点C 恰好是ABD ∆的重心，求AB BC的值．（3）如图3，12//l l ，且直线1l 与2l 之间的距离为4，“准黄金”ABC ∆的“金底”BC 在直线2l 上，点A在直线1l 上，AB BC =ABC ∠是钝角，将ABC ∆绕点C 按顺时针方向旋转得到△A B C ''，线段A C '交1l 于点D ．当点B '落在直线1l 上时，则AD CD 的值为．3．【问题发现】如图1所示，将ABC∆绕点A逆时针旋转90︒得ADE∆，连接CE、DB，根据条件填空：①ACE∠的度数为︒；②若2CE=，则CA的值为；【类比探究】如图2所示，在正方形ABCD中，点E在边BC上，点F在边CD上，且满足45EAF∠=︒，1BE=，2DF=，求正方形ABCD的边长；【拓展延伸】如图3所示，在四边形ABCD中，CD CB=，90BAD BCD∠+∠=︒，AC、BD为对角线，且满足32AC CD=，若3AD=，4AB=，请直接写出BD的值．4．在ABC∆中，10BC=，以BC为直径的O交AC于点D，过点D作//DE AB，交BC于点E．（1）如图1，若90ABC∠=︒，2:3EC=，求DE的长．（2）如图2，若90ABC∠<︒，AB与O相交于点F，连接FD，当点E与圆心O重合时，①求证：FD DC=；②四边形FBCD的周长有最大值吗？请说明理由．5．综合与实践【模型探究】（1）如图1，在ABC⊥于点N．求∆中，点O为边BC的中点，作射线AO，CM AO⊥于点M，BN AO证：OM ON=．【尝试建构】（2）如图2，在ABC∆中，点O为边BC的中点，点P在边BC上（不与点B，C，O重合），作射线AP，⊥于点N．连接OM，ON．猜想OM与ON的数量关系，并证明你的猜想．CM AP⊥于点M，BN AP【迁移应用】（3）如图3，在ABC⊥∆中，点D，E在边BC上，2⊥于点M，BN AD==，作射线AD，CM ADBD DE EC于点N．连接EM，EN．若1EM=，EN=tan CDA∠的值．6．如图，ABC∠=∠．上，连结AD，AO，分别交BC于点E，F，CAD BAO ∆内接于O，点D在O（1）如图1，求证：AD BC ⊥．（2）如图1，若//AO CD ，求证：CA CF =．（3）如图2，在（2）的条件下，①若5,CD BF ==，求BC 的长．②若CF k FB=，求tan ACE ∠的值．7．如图，在ABCD 中，B ∠是锐角，AB =，10BC =．在射线BA 上取一点P ，过P 作PE BC ⊥于点E ，过P ，E ，C 三点作O ．（1）当3cos 5B =时，①如图1，若AB 与O 相切于点P ，连结CP ，求CP 的长；②如图2，若O 经过点D ，求O 的半径长．（2）如图3，已知O 与射线BA F ，将BEF ∆沿EF 所在的直线翻折，点B 的对应点记为B '，且B '恰好同时落在O 和边AD 上，求此时PA 的长．8．四边形ABCD 内接于O ，AC 是O 的直径，连结BD 交AC 于点G ，AF BD ⊥，垂足为E ．（1）如图1，若AF交BC于点F．①求证：BAF CAD∠=∠；②若O的直径为10，4cos5BCA∠=，:3:5BF CG=，求AF的长．（2）如图2，若AF交CD于点F，连结OD，若//OD AB，AE=2DF CF=，求O的直径．9．定义：我们把对角线相等的四边形叫作伪矩形，对角线的交点称作伪矩形的中心．（1）①写出一种你学过的伪矩形：．②顺次连接伪矩形各边中点所得的四边形是．A．正方形B．矩形C．菱形D．无法确定（2）如图1，在伪矩形ABCD中，90BCD∠=︒，3AC=，2CD=，求BC的长．（3）如图2，在伪矩形ABCD 中，90ABC ∠=︒，60BAC ∠=︒，2AB =，AC CD =，求这个伪矩形的面积．。

一、解答题：1.(2015.上海市，第24题，12分) (本题满分12分，每小题满分各4分)已知在平面直角坐标系xOy 中（如图），抛物线24y ax =-与x 轴的负半轴相交于点A ，与y 轴相交于点B ，25AB =．点P 在抛物线上，线段AP 与y 轴的正半轴交于点C ，线段BP 与x 轴相交于点D ．设点P 的横坐标为m ．（1）求这条抛物线的解析式；（2）用含m 的代数式表示线段CO 的长； （3）当3tan 2ODC ∠=时，求PAD ∠的正弦值．11xyO2.(2015.上海市，第25题，14分) (本题满分14分，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分5分)已知：如图，AB 是半圆O 的直径，弦//CD AB ，动点P 、Q 分别在线段OC 、CD 上，且DQ OP =，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），20AB =，4cos 5AOC ∠=．设OP x =，CPF ∆的面积为y ． （1）求证：AP OQ =；（2）求y 关于x 的函数关系式，并写出它的定义域； （3）当OPE ∆是直角三角形时，求线段OP 的长．OPQ F EDCBA备用图O DCBA【答案】（1）通过证明AOP ∆≌ODQ ∆，过程略；（2）236030050(10)13x x y x x -+=<<；（3）8OP =∴2360300x x y x-+=，考点：1.三角形全等的判定及性质；2.锐角三角函数的综合应用；3.圆的综合应用.3. （2015.河南省，第23题，11分）（11分）如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F.点D 、E 的坐标分别为（0，6），（-4，0），连接PD ，PE ，DE. （1）请直接写出抛物线的解析式；（2）小明探究点P 的位置发现：当点P 与点A 或点C 重合时，PD 与PF 的差为定值. 进而猜想：对于任意一点P ，PD 与PF 的差为定值. 请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE 的面积为整数”的点P 记作“好点”，则存在多个“好点”，且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE 的周长最小时“好点”的坐标.PE OF C DBA 图xy∴PD=812x +2， ∴PD-PF=812x +2－812x =2，∴猜想正确.4. （2015.重庆市A 卷，第26题，12分）如图1，在平面直角坐标系中，抛物线233334y x x =-++交x 轴于A ，B 两点（点A 在点B 的左侧），交y 轴于点W ，顶点为C ，抛物线的对称轴与x 轴的交点为D 。