(完整版)上海市2019年初三下学期数学中考二模汇编：24题二次函数专题

青浦区2019学年九年级第二次学业质量调研测试数 学 试 卷（时间100分钟，满分150分） Q2020.05考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本调研卷上答题一律无效．2．除第一、二大题外,其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂] 1． (0)a a ≠的倒数是（ ▲ ）（A ）a ； （B ）a -； （C ）1a ； （D ）1a-． 2．计算2(2)x -的结果，正确的是（ ▲ ）（A ）22x ； （B ）22x -； （C ）24x ； （D ）24x -． 3．如果反比例函数ky x=的图像分布在第二、四象限，那么k 的取值范围是（ ▲ ） （A ）0k >； （B ）0k <； （C ）0k ≥； （D ）0k ≤． 4．下列方程中，没有实数根的是（ ▲ ）（A ）； （B ）；（C ）；（D ）． 5． 为了解某校初三400名学生的体重情况，从中抽取50名学生的体重进行分析．在这项调查220x x -=2210x x --=2210x x -+=2220x x -+=中，下列说法正确的是（ ▲ ）（A ）400名学生中每位学生是个体； （B ）400名学生是总体； （C ）被抽取的50名学生是总体的一个样本； （D ）样本的容量是50． 6．如图1，点G 是ABC ∆的重心，联结AG 并延长交BC 边于点D ．设a AB =u u u r r ，b GD =u u u r r ，那么向量BC u u u r 用向量a r 、b r表示为（ ▲（A ）32BC b a =-u u u rr r； （B ）32BC b a =+u u u rr r；（C ）62BC b a =-u u u r r r；（D ）62BC b a =+u u u rr r．二、填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案] 7． 计算：3a a ÷= ▲ ．8． 在实数范围内因式分解：22m -= ▲ ． 9． 函数y 的定义域是 ▲ ．10．不等式组1020.x x +≥⎧⎨->⎩，的解集是 ▲ ．11．如果将直线3y x =平移，使其经过点（0,-1），那么平移后的直线表达式是 ▲ ． 12．从2，3，4，5，6这五个数中任选一个数，选出的这个数是素数的概率是 ▲ ． 13．如果点D 、E 分别是ABC ∆的AB 、AC 边的中点，那么ADE ∆与ABC ∆的周长之比是 ▲ ．图114．已知点C 在线段AB 上，且012AC AB <<．如果⊙C 经过点A ，那么点B 与⊙C 的位置关系是 ▲ ．15．随机选取50粒种子在适宜的温度下做发芽天数的试验，试验的结果如右表所示．估计该作物种子发芽的天数的平均数约为 ▲ 天．16．在ABC ∆中，3AB AC ==，2BC =，将ABC ∆绕着点B 顺时针旋转，如果点A 落在射线BC 上的点A '处．那么=AA ' ▲ ．17．在Rt ABC ∆中，90oACB ∠=，3AC =，4BC =．分别以A 、B 为圆心画圆，如果⊙A 经过点C ，⊙B 与⊙A 相交，那么⊙B 的半径r 的取值范围是 ▲ ． 18．小明学习完《相似三角形》一章后，发现了一个有趣的结论：在两个不相似的直角三角形中，分别存在经过直角顶点的一条直线，把直角三角形分成两个小三角形后，如果第一个直角三角形分割 出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似，那么分割出来的另外两个小三角形也相似．他把这样的 两条直线称为这两个直角三角形的相似．．分割线．．．． 如图2、图3，直线CG 、DH 分别是两个不相似的Rt ABC ∆ 和Rt DEF ∆的相似分割线，CG 、DH 分别与斜边AB 、EF 交于 点G 、 H ，如果BCG ∆与DFH ∆相似，3AC =，5AB =，4DE =，8DF =，那么AG = ▲ ．三、解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答题纸的相应位置上]GCA图2HFED图319．（本题满分10分）计算：2121182-⎛⎫- ⎪⎝⎭．20．（本题满分10分）解方程：24211422x x x x -=---+. 21.（本题满分10分，第（1）小题5分，第（2）小题5分）如图4，在Rt ABC ∆中，90ACB ∠=o，4AC BC ==， 点D 在边BC 上，且3BD CD =，DE AB ⊥，垂足为点E ，联结CE .（1）求线段AE 的长； （2）求ACE ∠的余切值．22．（本题满分10分，第（1）小题3分，第（2）小题7分）某湖边健身步道全长1500米，甲、乙两人同时从同一起 点匀速向终点步行．甲先到达终点后立刻返回，在整个步行过 程中，甲、乙两人间的距离y （米）与出发的时间x的关系如图5中OA —AB 折线所示．（1）用文字语言描述点A 的实际意义； （2）求甲、乙两人的速度及两人相遇时x 的值． 23．（本题满分12分，第（1）小题7分，第（2）小题5分）如图6，在平行四边形ABCD 中，BE 、DF 分别是平行四边形的ABCDE 图4GBA图5两个外角的平分线，12EAF BAD ∠=∠，边AE 、AF 分别交两条角平分线于点E 、F ．（1）求证：ABE ∆∽FDA ∆；（2）联结BD 、EF ，如果2DF AD AB =⋅，求证：BD EF =．24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图7，在平面直角坐标系xOy 中，二次函数243y a x a x =-+ 的图像与x 轴正半轴交于点A 、B ，与y 轴相交于点C ，顶点为D ，且tan 3∠=CAO ．（1）求这个二次函数的解析式；（2）点P 是对称轴右侧抛物线上的点，联结CP ，交对称轴于点F ，当:2:3CDF FDP S S =V V 时，求点P 的坐标；（3）在（2）的条件下，将△PCD 沿直线MN 翻折，当点P 恰好与点O 重合时，折痕MN 交轴于点M ，交轴于点N ，求OM ON的值．x y 图7备用图25.（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）如图8，已知AB 是半圆O 的直径，6AB =，点C 在半圆O 上.过点A 作AD ⊥OC ，垂足为点D ，AD 的延长线与弦BC 交于点E ，与半圆O 交于点F （点F 不与点B 重合）.（1）当点F 为»BC的中点时，求弦BC 的长； （2）设OD x =，DE AEy =，求与的函数关系式；（3）当△AOD 与△CDE 相似时，求线段OD 的长.y x OABCDE FOABCDE F备用图图8青浦区2019学年九年级第二次学业质量调研测试评分参考 202005一、选择题：1．C ； 2．C ； 3．B ； 4．D ； 5．D ； 6．C ．二、填空题：7．2a ； 8．(m m ； 9．3x ≥-；10．12x -≤<； 11．31y x =-； 12．35；13．1:2； 14．点B 在⊙C 外； 15．1.8；16． 17．2＜r ＜8； 18．3．三、解答题：19．解：原式4+． ····················································· （8分）=3． ············································································· （2分）20．解：两边同乘以(2)(2)x x +-，得242(2)4(2)x x x x -+=--- ································································ （4分）2320x x -+=．·················································································· （2分） 解得121,2x x ==． ·············································································· （2分） 经检验，11x =是原方程的根，22x =是原方程的增根，舍去． ······················· （1分）所以，原方程的根是1x =．······································································· （1分） 21．证明：（1）∵4BC =，3BD CD =， ∴3BD =． ······································ （1分）∵AB=BC ， ∠ACB =90°∴∠A =∠B =45°．································· （1分）∵DE ⊥AB ， ∴在Rt △DEB 中，cos 2BE B BD==．∴BE =·· （2分）在Rt △ACB 中，AB ==AE =·············· （1分）（2）∵过点E 作EH ⊥AC 于点H.∴在Rt △AHE 中，cos AH A AE ==，AH=cos45AE ⋅︒= 52············· （1分） ∴53422CH AC AH =-=-=，∴EH= AH=52···································· （2分） ∴在Rt △CHE 中，cot ∠ECB =35CH EH=，即∠ECB 的余切值是35············· （2分）22．解：（1）20分钟时，甲乙两人相距500米． ··············································· （3分）（2）1500==7520V 米分甲，1000==5020V 米乙分··································· （4分）依题意，可列方程：75（x -20）+50(x -20)=500 ······································· （1分） 解这个方程，得 x =24 ····································································· （1分）答：甲的速度是每分钟75米，乙的速度是每分钟50米，两人相遇时x 的值为24． ·· （1分）23．证明：（1）∵∠EAF=12∠BAD．∴∠DAF+∠BAE=12∠BAD ·························（1分）∵DF平分∠HDC，∴∠HDF=12∠HDC．····································（1分）又∵ABCD是平行四边形，∴AB∥CD．∴∠BAD=∠CDH．∴∠HDF =∠DAF+∠BAE．·······················································（1分）又∵∠HDF =∠DAF+∠F， ·······················································（1分）∴∠BAE=∠F． ······································································（1分）同理：∠DAF=∠E···································································（1分）∴△ABE∽△FDA ····································································（1分）（2）作AP平分∠DAB交CD∴∠DAP=12∠BAD，∵∠HDF=12∠CDH，且∠BAD=∠CDH∴DF∥AP ·······················································································（1分）同理：BE∥AP，∴DF∥BE∵△ABE∽△FDA ∴AD DFBE AB=，即BE DF AD AB⋅=⋅···························（1分）又∵2DF AD AB =⋅∴BE =DF ························································································ （1分） ∴四边形DFEB 是平行四边形 ····························································· （1分） ∴BD =EF ························································································ （1分）24．解：（1）∵二次函数243y ax ax =-+的图像与y 轴交于点C ，∴点C 的坐标为(0，3) ∴OC =3 ·························································· （1分）联结AC ，在Rt △AOC 中，tan ∠CA O=OC OA=3∴OA =1 ·························· （1分） 将点A （1，0）代入243y ax ax =-+，得430a a -+=, ······················· （1分） 解得： 1a =．所以，这个二次函数的解析式为 243y x x =-+． ································· （1分） （2）过点C 作CG ⊥DF ，过点P 作PQ ⊥DF ，垂足分别为点G 、Q ．∵抛物线243y x x =-+的对称轴为直线2x =，∴2CG =．····················· （1分）∵23CDF FDP CG PQ S S ∆∆==，∴3PQ =． ························································· （1分） ∴点P 的横坐标为5． ······································································· （1分） ∴把5x =代入 243y x x =-+，得 8y =∴点P 的坐标为（5，8） ········· （1分）（3）过点P 作PH ⊥OM ，垂足分别为点H∵点P 的坐标为（5，8） ∴OH=5，PH=8． ··············································· （1分） ∵将△PCD 沿直线MN 翻折，点P 恰好与点O 重合，∴MN OP ⊥，∴∠ONM +∠NOP=90°． ···················································· （1分） 又∵∠POH +∠NOP=90°，∴∠ONM =∠POH ． ········································································ （1分） ∴85tan tan OMPHONM POM ON OH ∠=∠===．············································ （1分） 25．解：（1）联结OF ，交BC 于点H ．∵F 是»BC 中点，∴OF ⊥BC ，BC =2BH ． ····················································· （1分）∴∠BOF =∠COF ．∵OA =OF 且OC ⊥AF ，∴∠AOC=∠COF∴∠AOC =∠COF =∠BOF =60° ·································································· （1分）在Rt BOH ∆中，Sin ∠BOH =BHOB =2························································ （1分）∴BH BC =·········································································· （1分） （2）联结BF ．∵AF ⊥OC ，垂足为点=D ，∴AD =DF ． ······················································· （1分） 又∵OA = OB ，∴OD ∥BF ，22BF OD x ==． ································································· （1分）∴32DECDxEF BF x -==， ············································································· （1分）∴33DEx DFx -=+ 即33DE x AD x -=+ ·································································· （1分） ∴36DEx AE -=， ····················································································· （1分） ∴36x y -=． ······················································································· （1分） （3）AOD ∆∽CDE ∆，分两种情况：①当DOA DCE ∠=∠时,CB AB //，不符合题意，舍去． （1分） ②当DAO DCE ∠=∠时，联结OF ．∵,OA OF OB OC ==，∴,OAF OFA OCB OBC ∠=∠∠=∠．DAO DCE ∠=∠ΘOBC OCB OFA OAF ∠=∠=∠=∠∴． （1分） ∵2AOD OCB OBC OAF ∠=∠+∠=∠， （1分）30OAF ∴∠=︒ ，2321==∴OA OD ． （1分） 即，线段OD 的长为32。

2019年上海市徐汇区中考数学二模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）【四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．（4分）下列计算正确的是（）A．a2•a3=a6B．a+a=a2C．（a2）3=a6D．a8÷a2=a4考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．分析：根据同底数幂相乘，底数不变指数相加；合并同类项法则；幂的乘方，底数不变指数相乘；同底数幂相乘，底数不变指数相减；对各选项分析判断后利用排除法求解．解答：解：A、a2•a3=a2+3=a5，故本选项错误；B、a+a=2a，故本选项错误；C、（a2）3=a2×3=a6，故本选项正确；D、a8÷a2=a8﹣2=a6，故本选项错误．故选C．点评：本题考查了同底数幂的乘法，同底数幂的除法，幂的乘方的性质，熟练掌握运算性质，理清指数的变化是解题的关键．2．（4分）一次函数y=2x+1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限考点：一次函数图象与系数的关系．分析：根据k，b的取值范围来确定图象在坐标平面内的位置．解答：解：∵一次函数y=2x+1中的2＞0，∴该直线经过第一、三象限．又∵一次函数y=2x+1中的1＞0，∴该直线与y轴交于正半轴，∴该直线经过第一、二、三象限，即不经过第四象限．故选：D．点评：本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．3．（4分）如图，AF是∠BAC的平分线，EF∥AC交AB于点E．若∠1=25°，则∠BAF的度数为（）A．15°B．50°C．25°D．12.5°考点：平行线的性质；角平分线的定义．分析：根据两直线平行，同位角相等求出∠2，再根据角平分线的定义解答．解答：解：∵EF∥AC，∠1=25°，∴∠2=∠1=25°，∵AF是∠BAC的平分线，∴∠BAF=∠2=25°．故选C．点评：本题考查了平行线的性质，角平分线的定义，是基础题，熟记性质并准确识图是解题的关键．4．（4分）在△ABC中，∠A、∠B都是锐角，且sinA=cosB=，那么△ABC的形状是（）A．钝角三角形B．直角三角形C．锐角三角形D．无法确定考点：特殊角的三角函数值．分析：根据∠A、∠B都是锐角，且sinA=cosB=，可得出∠A和∠B的度数，继而可得出三角形ABC的形状．解答：解：在△ABC中，∵∠A、∠B都是锐角，且sinA=cosB=，∴∠A=30°，∠B=60°，则∠A=180°﹣30°﹣60°=90°．故△ABC为直角三角形．故选B．点评：本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．5．（4分）“大衣哥”朱之文是从“我是大明星”这个舞台走出来的民间艺人．受此影响，卖豆腐的老张也来参加节目的海选，当天共有15位选手参加决逐争取8个晋级名额．已知他们的分数互不相同，老张要判断自己是否能够晋级，只要知道下列15名选手成绩统计量中的（）A．众数B．方差C．中位数D．平均数考点：统计量的选择．分析：由于比赛设置了8个获奖名额，共有15名选手参加，故应根据中位数的意义分析．解答：解：因为6位获奖者的分数肯定是15名参赛选手中最高的，而且15个不同的分数按从小到大排序后，中位数及中位数之后的共有8个数，故只要知道自己的分数和中位数就可以知道是否获奖了．故选C．点评：此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的统计量有平均数、中位数、众数、方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．6．（4分）如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，联结BC，若∠A=36°，则∠C 等于（）A．36°B．54°C．60°D．27°考点：切线的性质．分析：根据题目条件易求∠BOA，根据圆周角定理求出∠C=∠BOA，即可求出答案．解答：∵AB与⊙O相切于点B，∴∠ABO=90°，∵∠A=36°，∴∠BOA=54°，∴由圆周角定理得：∠C=∠BOA=27°，故选D．点评：本题考查了三角形内角和定理，切线的性质，圆周角定理的应用，关键是求出∠BOA度数．二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】7．（4分）函数y=的定义域是x≥﹣1．考点：函数自变量的取值范围．分析：根据被开方数大于等于0列式计算即可得解．解答：解：由题意得，x+1≥0，解得x≥﹣1．故答案为：x≥﹣1．点评：本题考查的知识点为：二次根式的被开方数是非负数．8．（4分）分解因式：a3﹣ab2=a（a+b）（a﹣b）．考点：提公因式法与公式法的综合运用．专题：因式分解．分析：观察原式a3﹣ab2，找到公因式a，提出公因式后发现a2﹣b2是平方差公式，利用平方差公式继续分解可得．解答：解：a3﹣ab2=a（a2﹣b2）=a（a+b）（a﹣b）．点评：本题是一道典型的中考题型的因式分解：先提取公因式，然后再应用一次公式．本题考点：因式分解（提取公因式法、应用公式法）．9．（4分）如果反比例函数的图象经过点（1，﹣2），那么这个函数的解析式是y=﹣．考点：待定系数法求反比例函数解析式．分析：设反比例函数解析式为（k≠0），把点（1，﹣2）代入函数解析式（k≠0），即可求得k的值．解答：解：设反比例函数的解析式为（k≠0）．由图象可知，函数经过点（1，﹣2），∴﹣2=，得k=﹣2．∴反比例函数解析式为y=﹣．故答案为：y=﹣．点评：此题比较简单，考查的是用待定系数法求反比例函数的解析式，是中学阶段的重点．10．（4分）2019年政府报告中安排财政赤字约为13500亿元，13500亿用科学记数法表示为 1.35×104亿．考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n是负数．解答：解：将13500用科学记数法表示为：1.35×104．故答案为：1.35×104．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a的值以及n的值．11．（4分）不等式组的解集是＜x≤2．考点：解一元一次不等式组．专题：计算题．分析：分别求出不等式组中两不等式的解集，找出解集的公共部分即可确定出不等式组的解集．解答：解：，由①得：x＞；由②得：x≤2，则不等式组的解集为＜x≤2．故答案为：点评：此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键．12．（4分）若关于x的方程ax2﹣4x+3=0有两个相等的实数根，则常数a的值是．考点：根的判别式．分析：根据判别式的意义得到△=（﹣4）2﹣4a×3=0，然后求解即可．解答：解：根据题意得△=（﹣4）2﹣4a×3=0，解得a=．故答案为．点评：本题考查了一元二次方程根的判别式，当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．13．（4分）掷一个材质均匀的骰子，向上一面的点数是3的倍数的概率是．考点：概率公式．分析：由掷一个材质均匀的骰子，共有6种等可能的结果，其中向上一面的点数是3的倍数的有，3和6；直接利用概率公式求解即可求得答案．解答：解：∵掷一个材质均匀的骰子，共有6种等可能的结果，其中向上一面的点数是3的倍数的有，3和6；∴掷一个材质均匀的骰子，向上一面的点数是3的倍数的概率是：=．故答案为：．点评：此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．14．（4分）如图，在△ABC中，D是BC的中点，设=，=，则=﹣．考点：*平面向量．分析：由=，=，利用三角形法则可求得，又由在△ABC中，D是BC的中点，即可求得答案．解答：解：∵=，=，∴=﹣=﹣，∵在△ABC中，D是BC的中点，∴==（﹣）=﹣．故答案为：﹣．点评：此题考查了平面向量的知识．此题难度不大，注意掌握三角形法则的应用，注意掌握数形结合思想的应用．15．（4分）解放军某部承担一段长1500米的清除公路冰雪任务．为尽快清除冰雪，该部官兵每小时比原计划多清除20米，结果提前24小时完成任务．若设原计划每小时清除公路冰雪x米，则可列出方程﹣=24．考点：由实际问题抽象出分式方程．分析：设原计划每小时清除公路冰雪x米，则实际每小时清除（x+20）米，根据提前24小时完成任务，列出方程即可．解答：解：设原计划每小时清除公路冰雪x米，则实际每小时清除（x+20）米，由题意得，﹣=24．故答案为：﹣=24．点评：本题考查了由实际问题抽象出分式方程，解答本题的关键是设出未知数，找出合适的等量关系列方程．16．（4分）如图，△ABC中，AC、BC上的中线交于点O，且BE⊥AD．若BD=5，BO=4，则AO 的长为6．考点：三角形的重心；勾股定理．分析：先根据勾股定理得到OD的长，再根据重心的性质即可得到AO的长．解答：解：∵BE⊥AD，BD=5，BO=4，∴OD==3，∵AC、BC上的中线交于点O，∴AO=2OD=6．故答案为：6．点评：此题主要考查了勾股定理的应用以及重心的性质，根据已知得出各边之间的关系进而求出是解题关键．17．（4分）如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2﹣2x﹣3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为3+．考点：二次函数综合题．分析：连接AC，BC，有抛物线的解析式可求出A，B，C的坐标，进而求出AO，BO，DO的长，在直角三角形ACB中，利用射影定理可求出CO的长，进而可求出CD的长．解答：解：连接AC，BC，∵抛物线的解析式为y=x2﹣2x﹣3，∴点D的坐标为（0，﹣3），∴OD的长为3，设y=0，则0=x2﹣2x﹣3，解得：x=﹣1或3，∴A（﹣1，0），B（3，0）∴AO=1，BO=3，∵AB为半圆的直径，∴∠ACB=90°，∵CO⊥AB，∴CO2=AO•BO=3，∴CO=，∴CD=CO+OD=3+，故答案为：3+．点评：本题是二次函数综合题型，主要考查了抛物线与坐标轴的交点问题、解一元二次方程、圆周角定理、射影定理，读懂题目信息，理解“果圆”的定义是解题的关键．18．（4分）如图，已知△ABC中，∠B=90°，BC=3，AB=4，D是边AB上一点，DE∥BC交AC于点E，将△ADE沿DE翻折得到△A′DE，若△A′EC是直角三角形，则AD长为．考点：翻折变换（折叠问题）．分析：先根据勾股定理得到AC=5，再根据平行线分线段成比例得到AD：AE=AB：AC=4：5，设AD=x，则AE=A′E=x，EC=5﹣x，A′B=2x﹣4，在Rt△A′BC中，根据勾股定理得到A′C，再根据△A′EC是直角三角形，根据勾股定理得到关于x的方程，解方程即可求解．解答：解：在△ABC中，∠B=90°，BC=3，AB=4，∴AC=5，∵DE∥BC，∴AD：AB=AE：AC，即AD：AE=AB：AC=4：5，设AD=x，则AE=A′E=x，EC=5﹣x，A′B=2x﹣4，在Rt△A′BC中，A′C=，∵△A′EC是直角三角形，∴（）2+（5﹣x）2=（x）2，解得x1=4（不合题意舍去），x2=．故AD长为．故答案为：．点评：此题主要考查了图形的翻折变换，以及勾股定理的应用，关键是掌握翻折后哪些线段是对应相等的．三、解答题：（本大题共7题，满分78分）19．（10分）计算：÷+（2﹣）0﹣（﹣1）2019+|﹣2|+（﹣）﹣1．考点：实数的运算；零指数幂；负整数指数幂．分析：分别进行零指数幂、绝对值的化简、负整数指数幂等运算，然后合并．解答：解：原式=2+1﹣1+2﹣﹣2=2﹣．点评：本题考查了实数的运算，涉及了零指数幂、绝对值的化简、负整数指数幂等知识，属于基础题．20．（10分）先化简，再求值：（1+）÷（x﹣），其中x=．考点：分式的化简求值．专题：计算题．分析：原式括号中两项通分并利用同分母分式的加减法则计算，同时利用除法法则变形，约分得到最简结果，将x的值代入计算即可求出值．解答：解：原式=÷=•=，当x=时，原式==．点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．21．（10分）如图，在△ABC中，AB=AC=10，sinC=，点D是BC上一点，且DC=AC．（1）求BD的长；（2）求tan∠BAD．考点：解直角三角形．分析：（1）过点A作AE⊥BC于点E，求出CE，BE，再由CD=AC，可求出BD的长度．（2）过点D作DF⊥AB于点F，在Rt△BDF中求出DF，BF，继而可得AF，从而可求tan∠BAD．解答：解：（1）过点A作AE⊥BC于点E，∵AB=AC，∴BE=CE，在Rt△ACE中，AC=10，sin∠C=，∴AE=6，∴CE==8，∴CD=2CE=16，∴BD=BC﹣BD=BC﹣AC=6．（2）过点D作DF⊥AB于点F，在Rt△BDF中，BD=6，sin∠B=sin∠C=，∴DF=，∴BF==，∴AF=AB﹣BF=，∴tan∠BAD==．点评：本题考查了解直角三角形的知识，解答本题的关键是作出辅助线，构造直角三角形，注意熟练掌握锐角三角函数的定义．22．（10分）春季流感爆发，某校为了解全体学生患流感情况，随机抽取部分班级对患流感人数的进行调查，发现被抽查各班级患流感人数只有1名、2名、3名、4名、5名、6名这六种情况，并制成如下两幅不完整的统计图：（1）抽查了20个班级，并将该条形统计图（图2）补充完整；（2）扇形图（图1）中患流感人数为4名所在扇形的圆心角的度数为72°；（3）若该校有45个班级，请估计该校此次患流感的人数．考点：条形统计图；用样本估计总体；扇形统计图．分析：（1）根据患流感人数有6名的班级有4个，占20%，可求得抽查的班级数，再减去其它班级数，即可补全统计图；（2）用患流感人数为4名的班级4个除以抽查的班级数，再乘以360°即可；（3）先求出该校平均每班患流感的人数，再利用样本估计总体的思想，用这个平均数乘以45即可．解答：解：（1）抽查的班级个数为4÷20%=20（个），患流感人数只有2名的班级个数为：20﹣（2+3+4+5+4）=2（个），补图如下：（2）×360°=72°；（3）∵该校平均每班患流感的人数为：（1×2+2×2+3×3+4×4+5×5+6×4）÷20=4，∴若该校有45个班级，则此次患流感的人数为：4×45=180．点评：本题考查了条形统计图和扇形统计图以及利用样本估计总体的思想，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．23．（12分）已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E是BC的中点、F是CD上的点，联结AE、EF、AC．（1）求证：AO•OF=OC•OE；（2）若点F是DC的中点，联结BD交AE于点G，求证：四边形EFDG是菱形．考点：相似三角形的判定与性质；菱形的判定；梯形．分析：（1）由BC=2AD，点E是BC的中点，可得AD=CE，又由AD∥BC，可得四边形AECD 是平行四边形，即可得AE∥CD，继而证得△AOE∽△COF，即可判定AO•OF=OC•OE；（2）易得EF是△BCD的中位线，则可判定四边形EFDG是平行四边形，又由直角三角形斜边上的中线的性质，证得DG=EG，继而证得四边形EFDG是菱形．解答：证明：（1）∵BC=2AD，点E是BC的中点，∴AD=EC=BC，∵在梯形ABCD中，AD∥BC，∴四边形AECD是平行四边形，∴AE∥CD，∴△AOE∽△COF，∴OA：OC=OE：OF，∴AO•OF=OC•OE；（2）∵E是BC的中点，F是CD的中点，∴EF是△BCD的中位线，∴EF∥BD，∵AE∥CD，∴四边形EFDG是平行四边形，∵AD∥BC，∴△ADG∽△EBG，∴DG：BG=AD：EB=AG：EG，∵AD=BE=BC，∴AG=EG，DG=BG，∵∠ABC=90°，∴BG=GE=AE，∴EG=DG，∴四边形EFDG是菱形．点评：此题考查了相似三角形的判定与性质、平行四边形的判定与性质、三角形中位线的性质以及直角三角形的性质．此题难度适中，注意掌握数形结合思想的应用．24．（12分）如图，直线y=4x+4与x轴、y轴相交于B、C两点，抛物线y=ax2﹣2ax+c（a≠0）过点B、C，且与x轴另一个交点为A，以OC、OA为边作矩形OADC，CD交抛物线于点G．（1）求抛物线的解析式以及点A的坐标；（2）已知直线x=m交OA于点E，交CD于点F，交AC于点M，交抛物线（CD上方部分）于点P，请用含m的代数式表示PM的长；（3）在（2）的条件下，联结PC，若△PCF和△AEM相似，求m的值．考点：二次函数综合题．分析：（1）根据直线的解析式易求B，C的坐标将，再把其坐标分别代入y=ax2﹣2ax+c，即可求出抛物线的解析式，设y=0，解方程即可求出A的坐标；（2）先根据A、C的坐标，用待定系数法求出直线AC的解析式，进而根据抛物线和直线AC的解析式分别表示出点P、点M的坐标，即可得到PM的长；（3）由于∠PFC和∠AEM都是直角，F和E对应，则若以P、C、F为顶点的三角形和△AEM相似时，分两种情况进行讨论：①△PFC∽△AEM，②△CFP∽△AEM；可分别用含m的代数式表示出AE、EM、CF、PF的长，根据相似三角形对应边的比相等列出比例式，求出m的值．解答：解：（1）∵直线y=4x+4与x轴、y轴相交于B、C两点，∴C坐标为（0，4），设y=0，则x=﹣1，∴B坐标为（﹣1，0），∵抛物线y=ax2﹣2ax+c（a≠0）过点B、C，∴，解得：，∴抛物线的解析式为y=﹣x2+x+4，设y=0，0=﹣x2+x+4，解得：x=﹣1或3，∴A的坐标为：（3，0）；（2）设直线AC的解析式为y=kx+b，∵A（3，0），点C（0，4），∴，解得，∴直线AC的解析式为y=﹣x+4．∵点M的横坐标为m，点M在AC上，∴M点的坐标为（m，﹣m+4），∵点P的横坐标为m，点P在抛物线y=﹣x2+x+4上，∴点P的坐标为（m，﹣m2+m+4），∴PM=PE﹣ME=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+4m，即PM=﹣m2+4m（0＜m＜3）；（3）在（2）的条件下，连结PC，在CD上方的抛物线部分存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似．理由如下：由题意，可得AE=3﹣m，EM=﹣m+4，CF=m，PF=﹣m2+m+4﹣4=﹣m2+m．若以P、C、F为顶点的三角形和△AEM相似，分两种情况：①若△PFC∽△AEM，则PF：AE=FC：EM，即（﹣m2+m）：（3﹣m）=m：（﹣m+4），∵m≠0且m≠3，∴m=．②若△CFP∽△AEM，则CF：AE=PF：EM，即m：（3﹣m）=（﹣m2+m）：（﹣m+4），∵m≠0且m≠3，∴m=1．综上所述，存在这样的点P使△PFC与△AEM相似．此时m的值为或1．点评：此题是二次函数的综合题，其中涉及到运用待定系数法求二次函数、一次函数的解析式，矩形的性质，相似三角形的判定和性质，直角三角形、等腰三角形的判定，难度适中．要注意的是当相似三角形的对应边和对应角不明确时，要分类讨论，以免漏解．25．（14分）如图，已知∠MON两边分别为OM、ON，sin∠O=且OA=5，点D为线段OA上的动点（不与O重合），以A为圆心、AD为半径作⊙A，设OD=x．（1）若⊙A交∠O 的边OM于B、C两点，BC=y，求y关于x的函数解析式，并写出函数的定义域；（2）将⊙A沿直线OM翻折后得到⊙A′．①若⊙A′与直线OA相切，求x的值；②若⊙A′与以D为圆心、DO为半径的⊙D相切，求x的值．考点：圆的综合题．专题：综合题．分析：（1）作AH⊥OM于H，如图1，在Rt△OAH中，根据正弦的定义求出AH=3，根据垂径定理由AH⊥BC得CH=BH=BC=y，由于OD=x，则AD=5﹣x，然后在Rt△ACH中利用勾股定理得到（y）2=（5﹣x）2﹣32，再整理即可得到y与x的函数关系；（2）作A′E⊥OA于E，根据折叠的性质得A′H=AH=3，⊙A′的半径为5﹣x，在Rt△OAH中，利用勾股定理计算出OH=4；由于⊙A′与直线OA相切，根据切线的性质得A′E=5﹣x，再证明Rt△OAH∽Rt△A′AE，利用相似比得到5：6=4：（5﹣x），然后解方程可得到x的值；（3）作A′G⊥OA于G，连结A′D，根据两圆相切的性质得A′D=x+5﹣x=5，再证明Rt△OAH∽Rt△A′AG，利用相似比可计算出AG=，A′G=，则DG=AG﹣AD=x﹣，然后在Rt△A′GD中，根据勾股定理得到（）2+（x﹣）2=52，整理得x2﹣x=0，然后解方程即可．解答：解：（1）作AH⊥OM于H，如图1，在Rt△OAH中，OA=5，sin∠AOH==，∴AH=3，∵AH⊥BC，∴CH=BH=BC=y，∵OD=x，∴AD=5﹣x，在Rt△ACH中，AC=5﹣x，AH=3，CH=y，∴（y）2=（5﹣x）2﹣32，∴y=2（0＜x＜5）；（2）作A′E⊥OA于E，如图，∵⊙A沿直线OM翻折后得到⊙A′，∴A′H=AH=3，⊙A′的半径为5﹣x，在Rt△OAH中，OH==4，∵⊙A′与直线OA相切，∴A′E=5﹣x，∵∠HAO=∠EAA′，∴Rt△OAH∽Rt△A′AE，∴OA：AA′=OH：A′E，即5：6=4：（5﹣x），∴x=；（3）作A′G⊥OA于G，连结A′D，如图3，∵⊙A′与以D为圆心、DO为半径的⊙D相切，∴A′D=x+5﹣x=5，∵∠HAO=∠GAA′，∴Rt△OAH∽Rt△A′AG，∴==，即==，∴AG=，A′G=，∴DG=AG﹣AD=﹣（5﹣x）=x﹣，在Rt△A′GD中，∵A′G2+GD2=A′D2，∴（）2+（x﹣）2=52，整理得x2﹣x=0，解得x1=0（舍去），x2=，∴x的值为．点评：本题考查了圆的综合题：熟练掌握垂径定理、切线的性质和两圆相切的性质；会运用锐角三角函数、相似比和勾股定理进行几何计算．。

3
（2）过点 O 作 OH⊥AB，垂足为点 H，则由（1）可得 AH=4，OH=3 ∵AC=x，∴ CH | x 4 | 在 Rt△HOC 中， CHO 90 ，AO=5， ∴ CO HO2 HC 2 32 | x 4 |2 x2 8x 25 ，
（1 分）
易知△CDA∽△BCA，又 AC BC2 AB2 x2 4 ，
则 AD CA 1 x2 4 x 1 17 （舍负）—————（2
AC CB
x2 4
x
2
分）
易知∠ACE<90°.
8
所以边 BC 的长为 2 或 1 17 .——————————————————（1 2
海C B 图9
C B
图 10
上
25.（1）证明：∵ AO 、 BO 是圆 O 的半径 ∴ AO BO …………1 分 ∴ OAB B …………1 分 ∵ AC ∥ OB ∴ BAC B …………1 分 ∴ OAB BAC ∴ AB 平分 OAC …………1 分
A
O
C B
升 （2）如果点 Q 在线段 AD 上（与点 A、D 不重合），设△APQ 的面积为 y，
求 y 关于 x 的函数关系式，并写出定义域； （3）如果△QED 与△QAP 相似，求 BP 的长．
E
B
AQ P
海D CB
A
D C
上图9
备用图
25．解：（1）在⊙P 中，PA=PQ，∴∠PAQ ＝∠PQA，……………………………（1 分） ∵AD∥BC，∴∠PAQ ＝∠APB，∠PQA ＝∠QPC，∴∠APB ＝∠EPC，……（1 分） ∵梯形 ABCD 中，AD∥BC，AB=DC，∴∠B ＝∠C，…………………………（1 分） ∴△APB∽△ECP．…………………………………………………………（1 分）

上海市2019届一模提升题汇编第24题（二次函数综合）含2019上海中考试题中考【2019届一模徐汇】24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ，AO =OB =2，120AOB ∠=．（1）求该抛物线的表达式； （2）联结AM ，求AOMS；（3）将抛物线C 1向上平移得到抛物线C 2，抛物线C 2与x 轴分别交于点E 、F （点E 在点F 的左侧），如果△MBF 与△AOM 相似，求所有符合条件的抛物线C 2的表达式．【24．解：（1）过A 作AH ⊥x 轴，垂足为H ，∵OB=2，∴B （2,0）………………………………（1分） ∵120AOB ∠=︒∴60,30AOH HAO ∠=︒∠=︒．∵OA=2，∴112OH OA ==．∵222Rt AHO OH AH OA +=在中，，∴22213AH =-=．∴(1,3)A --……………………………………（1分）（第24题图）∵抛物线21:C y ax bx A B=+经过点、，∴可得：42033a a b a b b ⎧=-⎪+=⎧⎪⎪⎨⎨-=⎪⎩⎪=⎪⎩………………………………………………（1分）∴这条抛物线的表达式为233y x x =-+…………………………………………（1分）（2）过M 作MG ⊥x 轴，垂足为G，∵2y x x =+∴顶点M是⎛ ⎝⎭，得3MG = ……………………………………………………（1分）∵(1,A -，M⎛ ⎝⎭． ∴得：直线AM为33y x =- …………………………………………………（1分）∴直线AM 与x 轴的交点N 为1,02⎛⎫⎪⎝⎭……………………………………………………（1分）∴1122AOM S ON MG ON AH ∆=⋅+⋅111122322=⨯⨯+⨯=…………………………………………………………………………（1分）（3）∵）33，1（M 、)0,2(B ，∴3MG Rt BGM MBG BG ∆∠=在中，tan =，∴MBG ∠︒=30．∴MBF 150∠=︒．由抛物线的轴对称性得：MO=MB ，∴MBO MOB=150∠=∠︒． ∵OB=120A ∠︒，∴OM=150A ∠︒ ∴OM=MBF A ∠∠．∴BM BFOA OM 或BF BM OA OM 相似时，有：AOM 与MBF 当==∆∆ 即332BF 2332或BF 3322332==，∴32BF 或2BF ==． ∴）0，38）或（0，4（F ………………………………………………（2分）设向上平移后的抛物线k x x y ++-=33233:为C 22，当）0，4（F 时，338=k ，∴抛物线33833233:为C 22++-=x x y …（1分）当）0，38（F 时，27316=k ，抛物线22:3327C y x x =-++……．（1分）】【2019届一模浦东】24. （本题满分12分，其中每小题各4分）已知：如图9，在平面直角坐标系xOy 中，直线12y x b=-+与x 轴相交于点A ，与y 轴相交于点B. 抛物线（1）求抛物线的表达式; （2）求证: △BOD ∽△AOB;（3）如果点P 在线段AB 上，且∠BCP=∠DBO求点P 的坐标.【24、（1）211482y x x =-++；（2）证明略；（3）1612,55⎛⎫ ⎪⎝⎭】【2019届一模杨浦】24．（本题满分12分，每小题各4分） 在平面直角坐标系xOy 中，抛物线2(0)yax bx c a与y 轴交于点C （0,2），它的顶点为D （1,m ），且1tan 3COD.（1）求m 的值及抛物线的表达式；（2）将此抛物线向上平移后与x 轴正半轴交于点A ，与y 轴交于点B ，且OA=OB.若点A 是由原抛物线上的点E 平移所得，求点E 的坐标；（3）在（2）的条件下，点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°.求P 点的坐标.Oxy1 2 3 4 1 23 4 5-1 -2 -3-1 -2 -3 （第24题图）【24．解：（1）作DH ⊥y 轴，垂足为H ，∵D （1,m ）（0m），∴DH= m ，HO=1.∵1tan 3COD，∴13OH DH ，∴m=3. ····················································· （1分）∴抛物线2y ax bx c 的顶点为D （1,3）. 又∵抛物线2yax bxc 与y 轴交于点C （0,2）， ∴3,1,22.ab c ba c （2分）∴1,2,2.a b c∴抛物线的表达式为222y x x.······ （1分）（2）∵将此抛物线向上平移， ∴设平移后的抛物线表达式为222(0)y x x k k，. ···························· （1分）则它与y 轴交点B （0,2+k ）.∵平移后的抛物线与x 轴正半轴交于点A ，且OA=OB ，∴A 点的坐标为（2+k,0）. .（1分） ∴20(2)2(2)2k k k .∴122,1k k .∵0k，∴1k.∴A （3,0），抛物线222y x x向上平移了1个单位. . ······························ （1分）∵点A 由点E 向上平移了1个单位所得，∴E （3,-1）. . ··································· （1分） （3）由（2）得A （3,0），B （0, 3），∴32AB.∵点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°,原顶点D （1,3）, ∴设P （1,y ），设对称轴与AB 的交点为M ，与x 轴的交点为H ，则H （1,0）. ∵A （3,0），B （0, 3），∴∠OAB=45°, ∴∠AMH=45°. ∴M （1,2）. ∴2BM.∵∠BMP=∠AMH, ∴∠BMP=45°. ∵∠APB=45°, ∴∠BMP=∠APB.∵∠B=∠B ，∴△BMP ∽△BPA. ·································································· （2分）B APy OM H∴BP BABMBP .∴23226BPBA BM∴221(3)6BPy .∴123535y y ，（舍）.. ···························· （1分）∴(1,35)P . . ····················································································· （1分）】【2019届一模普陀】 24．（本题满分12分） 如图10，在平面直角坐标系中，抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ，且3OB OA =，与y 轴交于点C ，此抛物线顶点为点D ．（1）求抛物线的表达式及点D 的坐标；（2）如果点E 是y 轴上的一点（点E 与点C 不重合），当BE DE ⊥时，求点E 的坐标； （3）如果点F 是抛物线上的一点，且，求点F 的坐标．135FBD ∠=xOy图10【24．解：（1）∵抛物线与x 轴交于点A ()1,0-和点，且3OB OA =，∴点的坐标是()3,0． ··········································································· （1分）解法一：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 得03,093 3.a b a b =--⎧⎨=+-⎩ 解得1,2.a b =⎧⎨=-⎩ ······························································ （1分）∴抛物线的表达式是223y x x =--． ······················································ （1分）点D 的坐标是()1,4-． ············································································· （1分）解法二：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 可设抛物线的表达式为(1)(3)y a x x =+-， 由抛物线与y 轴的交点C 的坐标是()0,3-，得3(01)(03)a -=+-，解得1a =． ······························································ （1分）∴抛物线的表达式是223y x x =--． ························································ （1分）点D 的坐标是()1,4-． ············································································· （1分）（2）过点D 作DH OC ⊥，H 为垂足． ∴90DHO ∠=．∴90DEH EDH ∠+∠=． ∵BE DE ⊥，∴90DEH BEO ∠+∠=． ∴BEO EDH ∠=∠．又∵BOE EHD ∠=∠，∴△BOE ∽△EHD ． ········································· （1分）∴BO OEEH HD =．∵点D 的坐标是()1,4-，∴1DH =，4OH =．B B∵点的坐标是()3,0，∴3OB =．∴341OEOE =-． ·············································································· （1分）∴1OE =或3OE =． ················································································ （1分） ∵点E 与点C 不重合，∴1OE =． ∴点E 的坐标是()0,1-． ··········································································· （1分）（3）过点F 作FG x ⊥轴，G 为垂足．作45DBM ∠=，由第（2）题可得，点M 与点E 重合． ∵1OE =，1DH =，∴OE DH =． 可得△BOE ≌△EHD ． ∴BE ED =． ∵90BED ∠=，∴45DBE ∠=． ∵135FBD ∠=，∴90FBE ∠=． ················································································ （1分） ∴OBE GFB ∠=∠．∴在Rt △BOE 中，90BOE ∠=，∴cot 3OBE ∠=∴cot 3GFB ∠=． ·········· （1分） ∴3FG BG =．设点F 点的坐标为()2,23m mm --．∴223FG m m =--,3BG m =-．∴2233(3)m m m --=-． ··································································· （1分）解得3m =，4m =-． ∵3m =不合题意舍去，∴4m =-． 点F 的坐标是()4,21-． ·········································································· （1分）】【2019届一模奉贤】24．（本题满分12分，每小题满分6分）B如图10，在平面直角坐标系中，直线AB 与抛物线2yax bx 交于点A(6，0)和点B(1，－5)．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且∠BOC 的正切值是32，求点C 的坐标．【24．解：（1）由题意得，抛物线2yax bx 经过点A(6，0)和点B(1，－5)，代入得3660,5.a b a b 解得1,6.ab∴抛物线的表达式是26y x x =-. ······ （4分）由题意得，设直线AB 的表达式为ykxb ，它经过点A(6，0)和点B(1，－5)，代入得60,5.k bk b解得1,6.k b∴直线AB 的表达式是6y x =-. ········ （2分）（2）过点O 作OH AB ，垂足为点H ．设直线AB 与y 轴交点为点D ，则点D 坐标为()0,6-.∴45ODA OAD，cos45DH OH OD ==•︒= ∵2BD，∴22BH.在Rt △OBH 中，90OHB ，3tan 2OHOBHBH． ······························· （2分）∵∠BOC 的正切值是32，∴BOCCBO . ··············································· （1分） ①当点C 在点B 上方时，BOCCBO .∴COCB ． 设点C(,6)x x -，2222(6)(1)(65)x x xxOy图10ABxyo解得174x，1776644x .--------------------------------------------------------------------（2分）所以点D坐标为177,44⎛⎫-⎪⎝⎭. ②当点C 在点B 下方，BOC CBO 时，OC//AB. 点C 不在直线AB 上. ········ （1分）综上所述，如果∠BOC 的正切值是32，点C 的坐标是177,44⎛⎫-⎪⎝⎭．】【2019届一模松江】24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线cbx x y ++-=221经过点A （﹣2，0），点B （0，4）.（1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果∠PBO=∠BAO ，求点P 的坐标； （3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作DE∥x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果EO=2OF ，求m 的值.【24．解：（1）∵抛物线经过点A （﹣2，0），点B （0，4）∴⎩⎨⎧==+--4022c c b …………（1分）， 解得14b c =⎧⎨=⎩………………………（1分） ∴抛物线解析式为2142y x x =-++ …………………………………………（1分）(第24题图)y xOBA（2）()2912142122+--=++-=xxxy…………………………………（1分）∴对称轴为直线x=1，过点P作PG ⊥y轴，垂足为G ∵∠PBO=∠BAO，∴tan∠PBO=tan∠BAO，∴PG BOBG AO=……………………………………………（1分）∴121BG=，∴12BG=…………………………………（1分）∴72OG=，∴P（1，27）………………………………（1分）（3）设新抛物线的表达式为2142y x x m=-++-…（1分）则()0,4D m-,()2,4E m-，DE=2……………………（1分）过点F作FH⊥y轴，垂足为H，∵DE∥FH，EO=2OF∴2=1DE EO DOFH OF OH==，∴FH=1……………………………………………（1分）点D在y轴的正半轴上，则51,2F m⎛⎫--⎪⎝⎭，∴52OH m=-∴42512DO mOH m-==-，∴m=3……………………………………………………（1分）点D在y轴的负半轴上，则91,2F m⎛⎫-⎪⎝⎭，∴92OH m=-∴42912DO mOH m-==-，∴m=5……………………………………………………（1分）∴综上所述m的值为3或5.】(第24题图)yx OBAEDF H【2019届一模嘉定】24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ，与y 轴的交点为C ．（1）试求这个抛物线的表达式；（2）如果这个抛物线的顶点为M ，求△AMC 的面积； （3）如果这个抛物线的对称轴与直线BC 交于点D ，点E 在线段AB 上，且︒=∠45DOE ，求点E 的坐标．【24. 解：（1）∵抛物线22++=bx ax y 点经过)0,4(A 、)2,2(B ∴⎩⎨⎧=++=++222402416b a b a ……………………1分 ∴⎪⎪⎩⎪⎪⎨⎧=-=2141b a …………2分 ∴抛物线的表达式是221412++-=x x y …………1分 （2）由（1）得：抛物线221412++-=x x y 的顶点M 的坐标为)49,1(……1分图7O 11-1 -1∴点C 的坐标为)0,2(， ……………………1分 过点M 作y MH ⊥轴，垂足为点H ∴AOCMHC AOHM AMC S S S S ∆∆∆--= …………1分∴42211412149)41(21⨯⨯-⨯⨯-⨯+⨯=∆AMC S∴23=∆AMC S …………1分（3）联结OB过点B 作x BG ⊥轴，垂足为点G∵点B 的坐标为)2,2(，点A 的坐标为)0,4(∴2=BG ，2=GA ∴△BGA 是等腰直角三角形∴︒=∠45BAO 同理：︒=∠45BOA∵点C 的坐标为)0,2(∴2=BC ，2=OC 由题意得，△OCB 是等腰直角三角形 ∴︒=∠45DBO ,22=BO ∴DBO BAO ∠=∠∵︒=∠45DOE ∴︒=∠+∠45BOE DOB ∵︒=∠+∠45EOA BOE ∴DOB EOA ∠=∠ ∴△AOE ∽△BOD∴BO AOBD AE =…………1分 ∵抛物线221412++-=x x y 的对称轴是直线1=x ，∴点D 的坐标为)2,1(∴1=BD …………1分∴2241=AE ∴2=AE …………1分过点E 作x EF ⊥轴，垂足为点F 易得，△AFE 是等腰直角三角形 ∴1==AF EF∴点E 的坐标为)1,3( …………1分】 【2019届一模青浦】24．（本题满分12分， 其中第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，将抛物线2y x =-平移后经过点A （-1，0）、B （4，0），且平移后的抛物线与y 轴交于点C （如图）． （1）求平移后的抛物线的表达式；（2）如果点D 在线段CB 上，且CAD 的正弦值；（3）点E 在y 轴上且位于点C 的上方，点P 在直线BC 上，点Q 在平移后的抛物线上，如果四边形ECPQ 是菱形，求点Q 的坐标．【24．解：（1）设平移后的抛物线的解析式为2+=-+y x bx c ． ······················· （1分）将A （-1，0）、B （4，0），代入得（第24题图）（备用图）101640.，--+=⎧⎨-++=⎩b c b c ··············································································· （1分） 解得：34.，=⎧⎨=⎩b c所以，2+34=-+y x x ． ·········································································· （1分）（2）∵2+34=-+y x x ，∴点C 的坐标为（0，4） ····································· （1分）．设直线BC 的解析式为y= kx+4，将B （4，0），代入得kx+4=0，解得k=-1，∴y= -x+4． ········································································································ 设点D 的坐标为（m ，4- m ）．∵，∴22=2m ，解得=1m 或=1-m （舍去），∴点D 的坐标为（1，3）． ········································································· （1分） 过点D 作DM ⊥AC ，过点B 作BN ⊥AC ，垂足分别为点M 、N ．∵1122⋅=⋅AC BN AB OC54=⨯BN，∴17=BN ． ········ （1分） ∵DM ∥BN ，∴=DM CD BN CB，∴=DM BN，∴17=DM ． ···················· （1分）∴sin =17221∠==DM CAD AD ． ············································· （1分）（3）设点Q 的坐标为（n ，2+34-+n n ）．如果四边形ECPQ 是菱形，则0>n ，PQ ∥y 轴，PQ=PC ，点P 的坐标为（n ，4-+n ）．∵22+3444=-++-=-PQ n n n n n，=PC ， ····································· （2分）∴24-n n，解得=4n 或=0n （舍）． ·········································· （1分） ∴点Q的坐标为（4，2）． ···················································· （1分）】【2019届一模静安】24．（本题满分12分，其中第（1）小题4分，第（2）小题3分，第（3）小题5分）在平面直角坐标系xOy 中（如图10），已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ，、(53)D ，，设它与x 轴的另一个交点为A （点A 在点B 的左侧），且ABD ∆的面积是3．（1）求该抛物线的表达式； （2）求ADB ∠的正切值；（3）若抛物线与y 轴交于点C ，直线CD 交x 轴于点E ，点P 在射线AD 上，当APE ∆与 ABD ∆相似时，求点P 的坐标．【24．解：（1）过点D 作DH ⊥x 轴，交x 轴于点H ．∵132ABD S AB DH ∆=⋅=，又∵(5,3)D∴2AB =．····························································································· （1分） ∵(4,0)B ，点A 在点B 的左侧，∴(2,0)A ． ····························································································· （1分）把(2,0)A ，(4,0)B ，(5,3)D 分别代入2y ax bx c =++， 得04201643255a b ca b c a b c =++⎧⎪=++⎨⎪=++⎩解得168a b c =⎧⎪=-⎨⎪=⎩． ···························································· （1分）∴抛物线解析式是268y x x =-+． ······························································ （1分）（2）过点B 作BG AD ⊥，交AD 于点G ． ··················································· （1分）BD O图10xy﹒ ﹒由(2,0)A ，(5,0)H ，(5,3)D ，得ADH ∆是等腰直角三角形，且45HAD ∠=∵3AH DH ==，∴AD = ································································ （1分） ∴在等腰直角AGB ∆中，由2AB =，得AG BG ==，∴DG AD AG =-=∴在Rt DGB ∆中，1tan 2BG ADB DG ∠==． ·················································· （1分）（3）∵抛物线268y x x =-+与y 轴交于点(0,8)C ，又(5,3)D ，∴直线CD 的解析式为8y x =-+，∴(8,0)E ． ···························································································· （1分） 当点P 在线段AD 上时，APE ∆∽ABD ∆，点,,A P E 分别与点,,A B D 对应，则AP AE AB AD =，即AB AE AP AD ⨯===．………………………………………（1分）··························································································································· 过点P 作PQ ⊥∴2AQ PQ ==，即(4,2)P ． ····································································· （1分） ②当点P 在线段AD 延长线上时，APE ADB ∠=∠， ·················································· ∴EP //DB过点P 作PR x ⊥轴于点R ， ··················································································13AH AD AB AR AP AE ===，∴9AR PR ==， ······················································································ （1分） 即(11,9)P ． ···························································································· （1分） ∴APE ∆与ABD ∆相似时，点P 的坐标为 (4,2)或 (11,9)．】 【2019届一模宝山】24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分） 如图9，已知：二次函数的图像交x 轴正半轴于点A ，顶点为P,一次函数2y x bx=+。

上海市黄浦区2019届初三数学二模试卷一、选择题（本大题共6小题，共24.0分） 1、下列自然数中，素数是（ ）A. 1B. 2C. 4D. 92、下列运算正确的是（ ）A. (a 2)3=a 5B. a 2⋅a 3=a 5C. (2a)2=4aD. a 6÷a 3=a 23、反比例函数y =mx 的图象在第二、四象限内，则点（m ，-1）在（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限4、为了了解某校九年级400名学生的体重情况，从中抽取50名学生的体重进行统计分析，在这个问题中，样本是指（ ）A. 400B. 被抽取的50名学生C. 400名学生D. 被抽取的50名学生的体重5、下列等式成立的是（ ）A. −(−a ⃗ )=a ⃗B. a ⃗ +(−a ⃗ )=0C. a ⃗ −b ⃗ =b ⃗ −a ⃗D. 0⃗ −a ⃗ =a ⃗ 6、半径分别为1和5的两个圆相交，它们的圆心距可以是（ ）A. 3B. 4C. 5D. 6二、填空题（本大题共12小题，共48.0分） 7、√4=______．8、因式分解：a 2-9=______．9、方程√x +1=3的根是x =______． 10、直线y =2x -3的截距是______． 11、不等式组{x −3<02x>5,的解集是______．12、若关于x 的方程x 2-（2m -1）x +m 2=0没有实数根，则m 的取值范围是______．13、掷一枚质地均匀的正方体骰子，骰子的六个面分别标有1到6的点数，向上的一面出现的点数是2的倍数的概率是______． 14、秋季新学期开学时，某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了不完整的图表（如表所示），图表中c =______．15、正九边形的中心角等于______度．16、如图，点O 是△ABC 的重心，过点O 作DE ∥AB ，分别交AC 、BC于点D 、E ，如果AB ⃗⃗⃗⃗⃗ =a ⃗ ，那么DO⃗⃗⃗⃗⃗⃗ =______（结果用a ⃗ 表示）．17、如图，函数y =12x （x ＞0）的图象经过△OAB 的顶点B 和边AB 的中点C ，如果点B 的横坐标为3，则点分 数 段 频数 频率 60≤x ＜70 6 a70≤x ＜80 20 0.4 80≤x ＜90 15 b 90≤x ≤100c0.18第18题图第16题图 第17题图18、如图，在△ABC 中，∠ACB =90°，sin B =35，将△ABC 绕顶点C 顺时针旋转，得到△A 1B 1C ，点A 、B 分别与点A 1、B 1对应，边A 1B 1分别交边AB 、BC 于点D 、E ，如果点E 是边A 1B 1的中点，那么BDB 1C =______．三、计算题（本大题共1小题，共10.0分） 19、解分式方程：x+2x−2−16x 2−4=1x+2．四、解答题（本大题共6小题，共68.0分） 20、计算：√3tan60°−cos30°-（27）13+|1-√3|-（√2019）0．21、如图，已知⊙O 是△ABC 的外接圆，圆心O 在△ABC 的外部，AB =AC =4，BC =4√3，求⊙O 的半径．22、A 、B 两地相距30千米，已知甲、乙两人分别骑自行车和摩托车从A 地出发前往B 地，途中乙因修车耽误了些时间，然后又继续赶路．图中的线段OM 和折线OCDE 分别反映了甲、乙两人所行的路程y （千米）与时间x （分）的函数关系，根据图象提供的信息回答下列问题： （1）甲骑自行车的速度是______千米/分钟； （2）两人第二次相遇时距离A 地______千米；（3）线段DE 反映了乙修好车后所行的路程y （千米）与时间x （分）的函数关系．请求出线段DE 的表达式及其定义域．23、如图，已知四边形ABCD，AD∥BC，对角线AC、BD交于点O，DO=BO，过点C作CE⊥AC，交BD 的延长线于点E，交AD的延长线于点F，且满足∠DCE=∠ACB．（1）求证：四边形ABCD是矩形；（2）求证：DEEF =ADCD．24、如图，已知抛物线y=ax2+bx+c经过原点O（0，0）、A（2，0），直线y=2x经过抛物线的顶点B，点C是抛物线上一点，且位于对称轴的右侧，联结BC、OC、AB，过点C作CE∥x轴，分别交线段OB、AB 于点E、F．（1）求抛物线的表达式；（2）当BC=CE时，求证：△BCE∽△ABO；（3）当∠CBA=∠BOC时，求点C的坐标．25、已知四边形ABCD中，AD∥BC，∠ABC=2∠C，点E是射线AD上一点，点F是射线DC上一点，且满足∠BEF=∠A．（1）如图1，当点E在线段AD上时，若AB=AD，在线段AB上截取AG=AE，联结GE．求证：GE=DF；（2）如图2，当点E在线段AD的延长线上时，若AB=3，AD=4，cos A=13，设AE=x，DF=y，求y关于x的函数关系式及其定义域；（3）记BE与CD交于点M，在（2）的条件下，若△EMF与△ABE相似，求线段AE的长．上海市黄浦区2019届初三数学二模试卷答案和解析1.【答案】B【解析】解：素数是2，故选：B．根据素数的概念判断即可．此题考查有理数，关键是根据素数的概念解答．2.【答案】B【解析】解：A、（a2）3=a6，错误；B、a2•a3=a5，正确；C、（2a）2=4a2，错误；D、a6÷a3=a3，错误；故选：B．分别根据同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减，对各选项计算后利用排除法求解．本题考查了同底数幂的乘法，幂的乘方，同底数幂的除法，熟练掌握运算性质是解题的关键．3.【答案】C【解析】解：∵反比例函数y=的图象在第二、四象限内，∴m＜0，∴点（m，-1）的横纵坐标都为负，∴点M在第三象限，故选：C．根据反比例函数的性质，结合反比例函数图象所在象限，求出m的取值范围，再由点的坐标特点，确定点所在象限．本题主要考查了反比例函数的性质，象限内点的坐标特征，关键是根据反比例函数图象的位置确定m的取值范围．4.【答案】D【解析】解：样本是抽取50名学生的体重，故选：D．总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．5.【答案】A【解析】解：（B）原式=，故B错误；（C）-≠-，故C错误；（D）原式=-，故D错误；故选：A．根据平面向量的线性运算法则即可求出答案．本题考查平面向量，解题的关键是熟练运用平面向量的运算法则，本题属于基础题型．6.【答案】C【解析】解：∵5-1=4，1+5=9，∴相交时，4＜圆心距＜9，∴只有C中5满足．故选：C．根据两圆相交时圆心距与两圆半径之间的数量关系进行解答．本题利用两圆相交时，圆心距与两圆半径之间的数量关系进行判断．7.【答案】2【解析】解：∵22=4，∴=2．故答案为：2如果一个数x的平方等于a，那么x是a的算术平方根，由此即可求解．此题主要考查了学生开平方的运算能力，比较简单．8.【答案】（a+3）（a-3）【解析】解：a2-9=（a+3）（a-3）．a2-9可以写成a2-32，符合平方差公式的特点，利用平方差公式分解即可．本题考查了公式法分解因式，熟记平方差公式的结构特点是解题的关键．9.【答案】8【解析】解：方程两边平方得：x+1=9，解得：x=8，经检验：x=8是方程的解．故答案是：8．把方程两边平方去根号后求解．本题考查了无理方程的解法，在解无理方程是最常用的方法是两边平方法及换元法，本题用了平方法．10.【答案】-3【解析】解：∵在一次函数y=2x-3中，b=-3，∴一次函数y=2x-3在y轴上的截距b=-3．故答案是：-3．由一次函数y=kx+b在y轴上的截距是b，可求解．本题考查了一次函数图象上点的坐标特征．一次函数图象上的点的坐标，一定满足该函数的关系式．＜x＜311.【答案】52【解析】解：，解①得x＞，解②得x＜3，所以不等式组的解集为＜x＜3．故答案为＜x＜3．分别解两个不等式得到x＞和x＜3，然后根据大小小大中间找确定不等式组的解集．本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．12.【答案】m＞14【解析】解：根据题意△=（2m-1）2-4m2＜0，整理得-4m+1＜0，解得m＞．故答案为m＞．根据根的判别式的意义得到△=（2m-1）2-4m2＜0，然后解不等式即可．本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．13.【答案】12【解析】解：掷一次骰子，向上的一面出现的点数是2的倍数的有2、4，6，故骰子向上的一面出现的点数是2的倍数的概率是：=．故答案为：．共有6种等可能的结果数，其中点数是2的倍数有2、4和6，从而利用概率公式可求出向上的一面出现的点数是2的倍数的概率．本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．14.【答案】9【解析】解：，c=50-6-20-15=9，故答案为：9根据表格中的数据可以求得抽查的学生数，从而可以求得c的值．本题考查频数分布表，解题的关键是明确题意，利用表格中的数据，求出所求问题的答案．15.【答案】40【解析】解：正九边形的中心角等于：=40°．故答案是：40．利用360度除以边数9，即可求解．本题考查了正多边形的计算，理解正多边形的中心角相等是关键．a．16.【答案】13【解析】解：如图，连接CO并延长交AB于点M，∵点O是△ABC的重心，∴M是AB的中点，∵DE∥AB，∴△CDO∽△CAM，∴，∴DO=AM=×a=a．故答案为：a．连接CO并延长交AB于点M，因为点O是△ABC的重心，可得M是AB的中点，由DE∥AB，可得△CDO∽△CAM，即，即可得出DO的长．本题考查三角形重心的概念和性质，相似三角形的判定和性质．解题的关键是掌握三角形重心的概念和性质．17.【答案】（6，2）【解析】解：把x=3代入y=（x＞0）中，得y=4，∴B（3，4），∵C点是AB的中点，A点在x轴上，∴C点的纵坐标为：4÷2=2，把B点的横坐标代入反比例函数的解析式求得B点的纵坐标，再根据C点AB的中点求得C点的纵坐标，进而代入反比例函数的解析式中求得其横坐标便可．本题主要考查了反比例函数图象上点的坐标特征，中点坐标公式，关键是由B点纵坐标求出C点的纵坐标．18.【答案】35【解析】解：∵∠ACB=90°，sinB==，∴设AC=3x，AB=5x，∴BC==4x，∵将△ABC绕顶点C顺时针旋转，得到△A1B1C，∴CB1=BC=4x，A1B1=5x，∠ACB=∠A1CB1，∵点E是A1B1的中点，∴CE=A1B1=2.5x=B1E，∴BE=BC-CE=1.5x，∵∠B=∠B1，∠CEB1=∠BED∴△CEB1∽△DEB ∴=故答案为：设AC=3x，AB=5x，可求BC=4x，由旋转的性质可得CB1=BC=4x，A1B1=5x，∠ACB=∠A1CB1，由题意可证△CEB1∽△DEB，可得=，即可求解．本题考查了旋转的性质，解直角三角形，相似三角形的判定和性质，证△CEB1∽△DEB是本题的关键．19.【答案】解：去分母得：（x+2）2-16=x-2，整理得：x2+3x-10=0，即（x-2）（x+5）=0，解得：x=2或x=-5，经检验x=2是增根，分式方程的解为x=-5．【解析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．20.【答案】解：原式=√3√3−√32−3+√3−1−1=2−3+√3−2=−3+√3．【解析】直接利用特殊角的三角函数值以及零指数幂的性质和绝对值的性质、分数指数幂的性质分别化简得出答案．此题主要考查了特殊角的三角函数值以及零指数幂的性质和绝对值的性质、分数指数幂的性质，正确化简各数是解题关键．21.【答案】解：如图，连接AO，交BC于点D，连接BO∵AB=AC，∴AB⏜=AC⏜又AO是半径，∴AO⊥BC，BD=CD∵BC=4√3，∴BD=2√3∴在Rt△ABD中，∠ADB=90°，∴BD2+AD2=AB2又∵AB=4，∴AD=2设半径为r．在Rt△BDO中，∵BD2+DO2=BO2∴(2√3)2+(r−2)2=r2∴r=4∴⊙O的半径为4．【解析】连接AO，交BC于点D，连接BO，由垂径可求AO⊥BC，BD=CD，即可求BD=2，由勾股定理可求AD的长，圆的半径．本题考查了三角形的外接圆与外心，等腰三角形的性质，勾股定理，熟练运用勾股定理求线段的长是本题的关键．22.【答案】1420【解析】解：（1）由图可得，甲骑自行车的速度是：30÷120=千米/分钟，故答案为：；（2）两人第二次相遇时距离A地：×80=20千米，故答案为：20；（3）设线段DE的表达式为y=kx+b（k≠0），∵线段DE经过点D（50，10）和（80，20），∴，解得，，∴y=x-，当y=30时，x=110，∴．（1）根据函数图象中的数据可以求得甲骑自行车的速度；（2）根据（1）中的答案和函数图象中的数据可以求得两人第二次相遇时距离A地的距离；（3）根据（2）中的答案和一次函数的性质可以求得线段DE的表达式及其定义域．本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．23.【答案】解：（1）证明∵AD∥BC，∴ADBC =DOBO，∵DO=BO，∴AD=BC，∴四边形ABCD是平行四边形，∵CE⊥AC，∴∠ACD+∠DCE=90°，∵∠DCE=∠ACB，∴∠ACB+∠ACD=90°，即∠BCD=90°，∴四边形ABCD是矩形；（2）∵四边形ABCD是矩形，∴AC=BD，∠ADC=90°，∵AD∥BC，∴DEBD =EFFC，∴DEAC =EFFC∴DEEF =ACFC，∵∠ADC=∠ACF=90°，∴cot∠DAC=ACFC =ADCD，∴DEEF =ADCD．【解析】（1）先证明四边形ABCD是平行四边形，再证明∠BCD=90°，即可求解；（2）由AD∥BC，得：，，即可求解．本题主要考查对矩形的性质，成比例的线段性质的理解和掌握，此题难度不大．24.【答案】解：（1）∵抛物线y=ax2+bx+c经过原点O（0，0）、A（2，0），∴对称轴为x=1，∵直线y=2x经过抛物线的顶点B，∴B（1，2），设y=a（x-1）2+2，∵抛物线经过原点O（0，0），∴a=-2，∴y=-2x2+4x．（2）∵BC=CE，∴∠BEF=∠CBE，∴∠BEF=∠BOA，∵B（1，2），A（2，0），∴OB=AB=√5，∴∠BOA=∠BAO，∴∠CBE=∠BEF=∠BOA=∠BAO，∴△BCE∽△ABO；（3）记CE与y轴交于点M，过点B作BN⊥CE，垂足为点N．设C（m，-2m2+4m）．∵∠BEF=∠BOC+∠ECO，∠BFE=∠CBA+∠BCE，又∠CBA=∠BOC，∠BEF=∠BFE，∴∠ECO=∠BCE，∴tan∠ECO=tan∠BCE．∵CE∥x轴，x轴⊥y轴，∴∠OMC=∠BNC=90°，∴OMCM =BNCN，∴−2m2+4mm =2+2m2−4mm−1，∴m1=1（舍），m2=32，∴C(32，32)．【解析】（1）先根据题意得出抛物线的顶点坐标，设其顶点式，再将原点代入计算可得；（2）由BC=CE知∠BEF=∠CBE，再由CE∥x轴知∠BEF=∠BOA，根据知∠BOA=∠BAO，从而得∠CBE=∠BEF=∠BOA=∠BAO，据此即可得证；（3）记CE与y轴交于点M，作BN⊥CE，设C（m，-2m2+4m）．由∠BEF=∠BOC+∠ECO，∠BFE=∠CBA+∠BCE知∠ECO=∠BCE，据此得tan∠ECO=tan∠BCE．结合∠OMC=∠BNC=90°得，据此得出关于m的方程，解之可得．本题是二次函数的综合问题，解题的关键是熟练掌握待定系数法求函数解析式，相似三角形的判定与性质、平行线的判定与性质、三角形外角的性质等知识点．25.【答案】解：（1）∵AG=AE，∴∠AGE=180°−∠A2．∵AD∥BC，∴∠A+∠ABC=180°，∵∠ABC=2∠C，∴∠C=180°−∠A2，∴∠AGE=∠C，∵AD∥BC，∴∠D+∠C=180°，又∠BGE+∠AGE=180°，∴∠BGE=∠D，∵∠BEF+∠FED=∠A+∠GBE，∵∠BEF=∠A，∴∠FED=∠GBE，又AB=AD，AG=AE，∴BG=ED，∴△GBE≌△DEF（ASA），∴GE=DF；（2）在射线AB上截取AH=AE，联结EH，∵∠HBE=∠A+∠AEB，∠DEF=∠BEF+∠AEB，又∠BEF=∠A，∴∠HBE=∠DEF．∴∠EDC=∠C，∠A+∠ABC=180°．∵AH=AE，∴∠H=180°−∠A2，又∠ABC=2∠C，∴∠H=∠C，∴∠H=∠EDC，∴△BHE∽△EDF，∴BHED =EHDF．过点H作HP⊥AE，垂足为点P．∵cosA=13，AE=AH=x，∴AP=13x，PH=2√23x，PE=23x，∴EH=2√33x，∵AB=3，AD=4，AE=x，DF=y，∴x−3x−4=2√3x3y，∴y=2√3x2−8√3x3x−9(x＞4)；（3）记EH与BC相交于点N．∵△EMF∽△ABE，∠BEF=∠A，∴∠AEB=∠EMF，或∠AEB=∠EFM，若∠AEB=∠EMF，又∠AEB＜∠EMF，矛盾，∴此情况不存在，若∠AEB=∠EFM，∵△BHE∽△EDF，∴∠BEH=∠EFM，∴∠AEB=∠BEH，∵AD∥BC，∴∠AEB=∠EBC，∴∠BEH=∠EBC，∴BN=EN=BH=x-3，∵AD∥BC，∴ABAH =ENEH，∴3x=2√3x3，∴x=2√3+3，∴线段AE的长为2√3+3．【解析】（1）根据全等三角形的判定和性质解答即可；（2）在射线AB上截取AH=AE，联结EH，根据相似三角形的判定和性质以及勾股定理解答即可；（3）记EH与BC相交于点N，分∠AEB=∠EMF或∠AEB=∠EFM两种情况进行解答即可．本题属于相似三角形综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

2019年上海市徐汇区中考数学二模试卷一．选择题（本大题共6题，每题4分，满分24分）B．、与被开方数不同，故不是同类二次根式；与与被开方数相同，故是同类二次根式．23．（4分）（2019•徐汇区二模）如果关于x的一元二次方程x2﹣2x+m﹣1=0有两个不相等的实数根，那么和﹣））[的平均数为=﹣））﹣6．（4分）（2019•徐汇区二模）在△ABC中，AB=AC=2，∠A=150°，那么半径长为1的⊙B和直线AC的分析：过B作BD⊥AC交CA的延长线于D，求出BD，和⊙B的半径比较，即可得出答案．BD=AB=二．填空题（本大题共12题，每题4分，满分48分）7．（4分）（2019•徐汇区二模）计算：=﹣1．数学试卷解：=8．（4分）（2019•徐汇区二模）计算：2a（3a﹣1）=6a2﹣2a．9．（4分）（2019•徐汇区二模）方程x﹣1=的解是x 1=1或x2=2．，10．（4分）（2019•市中区二模）已知函数f（x）=，那么f（﹣1）=．=．故答案为：．11．（4分）（2019•徐汇区二模）如图，点A在反比例函数的图象上，那么该反比例函数的解析式是．，将即可得到y=，y=12．（4分）（2019•徐汇区二模）如图，在△ABC中，中线AD和BE相交于点G，如果=，=，那么向量=．，，利用三角形法则，即可求得的长，又由在，可求得的长，继而求得解：∵=﹣=﹣==（﹣=﹣=+=）+，==（+=数学试卷故答案为：．13．（4分）（2019•徐汇区二模）如图，AB∥CD，CB平分∠ACD，如果∠BAC=120°，那么cosB=．BCD=．故答案为：．14．（4分）（2019•徐汇区二模）在形状、大小、颜色都一样的卡片上，分别画有线段、直角三角形、等腰三角形、等边三角形、平行四边形、菱形、等腰梯形、正五边形、正六边形、圆等10个图形，小杰随机抽取一张卡片，抽得图形既是轴对称图形，又是中心对称图形的概率是．=．故答案为：．=15．（4分）（2019•徐汇区二模）为了解某校初三年级学生一次数学测试成绩的情况，从近450名九年级学生中，随机抽取50名学生这次数学测试的成绩，通过数据整理，绘制如下统计表（给出部分数据，除[90，分以上）约为38%（填百分数）．=0.516．（4分）（2019•徐汇区二模）如图，⊙O半径为5，△ABC的顶点在⊙O上，AB=AC，AD⊥BC，垂足是D，cotB=2，那么AD的长为2．cotB==2数学试卷17．（4分）（2000•安徽）一个二元一次方程和一个二元二次方程组成的二元二次方程组的解是和，试写出符合要求的方程组（只要填写一个即可）．．18．（4分）（2019•徐汇区二模）在Rt△ABC中，∠C=90°，sinA=，将△ABC绕点A旋转后，点C落在射线BA上，点B落到点D处，那么sin∠ADB的值等于或．，AC==4ABD===2BE=BD=a==2ADB==的值为或故答案为：或三．（本大题共7题，第19-22题每题10分；第23、24题每题12分；第25题14分；满分78分）19．（10分）（2019•徐汇区二模）计算：（）0﹣cos30°+﹣（）2．+﹣，然后合并即可．﹣+﹣++20．（10分）（2019•徐汇区二模）解不等式组：；并将解集在数轴上表示出来．数学试卷解：21．（10分）（2019•徐汇区二模）销售某种商品，根据经验，销售单价不少于30元∕件，但不超过50元∕件时，销售数量N（件）与商品单价M（元∕件）的函数关系的图象如图所示中的线段AB．（1）求y关于x的函数关系式；（2）如果计划每天的销售额为2400元时，那么该商品的单价应该定多少元？由题意，得解得22．（10分）（2019•徐汇区二模）如图，梯形ABCD中，AB∥CD，AC和BD相交于点O，BD⊥AB，AB=3，BD=4，CD=2．求：（1）tan∠CAB的值；（2）△AOD的面积．CAB=即可得出答案．===，BO=CAB==；﹣，××=．23．（12分）（2019•徐汇区二模）如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE=AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N．（1）求证：四边形DBEC是平行四边形；（2）如果AD2=AB•AF，求证：CM•AB=DM•CN．数学试卷，所以，，，24．（12分）（2019•徐汇区二模）抛物线y=ax2+bx（a≠0）经过点A（1，），对称轴是直线x=2，顶点是D，与x轴正半轴的交点为点B．（1）求抛物线y=ax2+bx（a≠0）的解析式和顶点D的坐标；（2）过点D作y轴的垂线交y轴于点C，点M在射线BO上，当以DC为直径的⊙N和以MB为半径的⊙M相切时，求点M的坐标．，解得：）的解析式，顶点解得．解得．相切时，25．（14分）（2019•徐汇区二模）如图1，在Rt△ABC中，∠CAB=90°，AC=3，AB=4，点P是边AB上任意一点，过点P作PQ⊥AB交BC于点E，截取PQ=AP，联结AQ，线段AQ交BC于点D，设AP=x，DQ=y．（1）求y关于x的函数解析式及定义域；（2）如图2，联结CQ，当△CDQ和△ADB相似时，求x的值；（3）当以点C为圆心，CQ为半径的⊙C和以点B为圆心，BQ为半径的⊙B相交的另一个交点在边AB 上时，求AP的长．数学试卷；a=，．定义域是：≤，）的解法，可得，，，解得．，；；又∵解得．。

上海松江区2019年中考二模数学试题数学试卷〔总分值150分，完卷时间100分钟〕 2018.4考生注意：1、本试卷含三个大题，共25题；2、答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3、除第【一】二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤、 【一】选择题：〔本大题共6题，每题4分，总分值24分〕 【以下各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1、以下各运算中，正确的运算是 〔A 〕523=+； 〔B 〕6234)2(a a =-；〔C 〕326a a a =÷； 〔D 〕9-)3-(22a a =、2、用换元法解方程1323=---x xx x 时，可以设x x y 3-=，那么原方程可以化为〔A 〕02y 2=-+y ； 〔B 〕012=-+y y ；〔C 〕0122=--y y ； 〔D 〕022=--y y 、 3、数据10、5、7、12、10、8的众数和中位数分别是〔A 〕10，9； 〔B 〕10，8； 〔C 〕8，10； 〔D 〕10，10、 4、a >b ，以下关系式中一定正确的选项是〔A 〕a ->b -； 〔B 〕a 2<b 2； 〔C 〕a -2<b -2； 〔D 〕2a >ab 、5、现有两根木棒，它们的长度分别是5dm 和8dm 、如果不改变木棒的长度，要钉成一个三角形的木架，那么在以下四根木棒中应选取〔A 〕3dm 长的木棒；〔B 〕8dm 长的木棒； 〔C 〕13dm 长的木棒；〔D 〕16dm 长的木棒、 〔A 〕一组对边平行且另一组对边相等的四边形是平行四边形； 〔B 〕两条对角线相等的四边形是矩形；〔C 〕顺次联结等腰梯形各边中点所得的四边形是菱形； 〔D 〕四条边相等的四边形是正方形、 【二】填空题：〔本大题共12题，每题4分，总分值48分〕 【请将结果直接填入答题纸的相应位置上】 7.计算：23-=▲、8.因式分解：=-24a ▲、 9.方程112=-x 的根是▲、10.在函数x y 3=的图像所在的每个象限中，y 的值随x 的值增大而▲、〔增大或减小〕11.如果关于x 的一元二次方程02=-+m x x 有两个不相等的实数根，那么m 的取值范围是___▲、 12.将抛物线2x y =向右平移1个单位，所得新的抛物线的表达式为▲、13.一个不透明的口袋中，装有红球4个，白球8个，黑球3个，这些球除颜色不同外没有任何区别，从中任意摸出一个球，那么摸到黑球的概率为▲、14.为了解九年级学生体能情况，随机抽查了其中的40名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，那么仰卧起坐的次数在20～25次之间的频率是▲、 15.斜坡的坡度为5:1=i ，如果这一斜坡的高度为2米，那么这一斜坡的水平距离为▲米、 16.⊙O 1和⊙O 2外切，O 1O 2=8，⊙O 1的半径分别为5，那么⊙O 2的半径为▲、 17.如图，在梯形ABCD 中，AD ∥BC ，点E 、F 分别是AB 、DC 的中点，a AD =，=，那么=▲、〔用、表示〕、18.三角形的三条高或其延长线相交于一点，这点称为三角形的垂心、边长为2的等边三角形的垂心到这个三角形各顶点之间的距离之和为___________、【三】解答题：〔本大题共7题，总分值78分〕 19、〔此题总分值10分〕先化简，再求值：)111(4422--÷-+-a aa a a ，其中2=a 、 20、〔此题总分值10分〕解方程组：⎩⎨⎧=--=026-222y xy x y x 21、(此题总分值10分，第〔1〕小题4分，第〔2〕小题6分) 如图，在△ABC 中，AC ＝15，AB =25，sin ∠CAB =54，以CA 为半径的⊙C 与AB 、BC 分别交于点D 、E ，联结AE ，DE 、 〔1〕求BC 的长；〔2〕求△AED 的面积、(1) 当∠ABC =60°时，求CD 的长；(2) 如果AC=x ，AD=y ，求y 关于x(3) 联结CG ，如果∠ACB=∠CGB ，求AC 的长、2018年松江区初中毕业生学业模拟考试2018.4【一】选择题1、B ；2、D ；3、A ；4、C ；5、B ；6、C 、 【二】填空题7、91；8、()()a a -+22；9、1=x ；10、减小；11、m ＞41-；12、2)1(-=x y ； 13、51；14、103；15、10；16、3；17、a b -2；18、32、(第17题图)（第21题图）【三】解答题19、解:原式=12)1()2(2--÷--a a a a a ……………………………………………………………6分 =21)1(22--⋅--a a a a a ）（……………………………………………………………1分=a a 2-………………………………………………………………………1分当2=a 时，212222-=-=-a a ………………………………………2分 20、解：由②得0,02=+=-y x y x …………………………………………………………4分原方程组化为⎩⎨⎧=-=-0262y x y x ，⎩⎨⎧=+=-062y x y x …………………………………………2分解得⎩⎨⎧-==⎩⎨⎧==22242211y x y x ……………………………………………………4分 21、解：〔1〕过点C 作CH ⊥AB ，垂足为H ，在Rt △CHA 中，sin ∠CAB =54=AC CH …………………………………………………1分 ∵AC =15，∴CH =12………………………………………………………………………1分 ∴AH =9…………………………………………………………………………………1分∵AB =25，∴HB =16，∴BC =2022=+HB CH …………………………………………1分 (2)过点E 作EF ⊥AB ，垂足为F ，∵EF ⊥AB ,CH ⊥AB ，∴EF ∥CH ………………………………………………………………1分∴BC BECHEF =………………………………………………………………………………1分 ∵BE =BC -CE =20-15=5，∴20512=EF ，∴EF =3……………………………………………1分 在⊙C 中，CH ⊥AB ，CH 过圆心，∴AD =2AH =18………………………………………2分∴273182121=⨯⨯=⋅⋅=∆EF AD S AED ………………………………………………1分22.解：〔1〕设一次函数的关系式为y =kx +b (k ≠0)…………………………………1分 ∵一次函数的图像过点〔5，334〕，〔10，337〕∴解得⎪⎩⎪⎨⎧==33153b k ………………………………………………………4分∴33153+=x y ………………………………………………………………………………1分〔2〕由题意得：7.5035.1)33153(=⨯+x (2)分[来源:]解得x =8…………………………………………………………………………………1分 答：此时的气温为8℃、………………………………………………………………………1分 23.证明：(1)∵∠BAC =90°，∴∠BAD+∠DAC=90°………………………………1分 ∵四边形ADEF 是正方形，∴∠DAF =90°，AD =AF ………………………………………1分 ∴∠DAC+∠CAF=90°,∴∠BAD=∠CAF ……………………………………………1分 ∵AB =AC ，∴△ABD ≌△ACF …………………………………………………………1分 ∴∠B=∠ACF …………………………………………………………………………1分 ∵∠B+∠ACB=90°，∴∠ACF+∠ACB=90°，即∠BCF=900∴FC ⊥BC …………………………………………………………………………………1分 (2)∵△ABD ≌△ACF ,∴BD =FC ………………………………………………………1分 又∵BD =AC ,∴AC =FC ………………………………………………………………1分∴∠CAF =∠CFA ………………………………………………………………………………1分 ∵∠DAF =∠EFA =90°，∴∠DAC=∠EFC ……………………………………………………1分 又∵AD =FE ，∴△ADC ≌△FEC ………………………………………………………………1分∴CD=CE ………………………………………………………………………………………1分24.解：〔1〕∵抛物线c bx x y ++-=2经过点A 〔0，1)，B (4，3).所以⎩⎨⎧=++-=34161c b c …………………………………………………………………1分 解得⎪⎩⎪⎨⎧==129c b ………………………………………………………………………1分∴抛物线的解析式为1292++-=x x y ……………………………………………1分(2)过点B 作y 轴的垂线，垂足为H ，过点A 作AG ⊥BO ，垂足为G∵A 〔0，1)，B (4，3)，∴OA =1,OB =5………………………………………………………1分∵BH AO AG BO S ABO ⋅⋅=⋅⋅=∆2121，∴4121521⨯⨯=⨯⨯AG ，∴AG=54………1分⎩⎨⎧=+=+337103345b k b k∴OG=53，∴BG=522……………………………………………………………………1分∴tan ∠ABO=112=BG AG …………………………………………………………………1分 〔3〕∵设直线AB 的解析式为)0(≠'+=k b kx y将A 〔0，1)，B (4，3)代入得解得⎪⎩⎪⎨⎧==121/b k ，∴直线AB 的解析式为121+=x y ……………………………………………………………1分设M)129,(2++-m m m ，N )121,(+m m ，MN =)121(1292+-++-m m m ……………1分∵四边形MNCB 为平行四边形，∴MN =BC =3，∴)121(1292+-++-m m m =3解得3,121==m m ……………………………………………………………………………1分∵抛物线的对称轴为直线49=x ，直线MN 在抛物线对称轴的左侧……………………1分∴1=m ，∴M )29,1(……………………………………………………………………………1分 25.解：〔1〕在Rt △ABC 中，∠BAC =90°,∠ABC =60°，∵AB =4，∴34=AC …………………………………………………………………………1分由翻折得∠ABD =30°，得334=AD ………………………………………………1分 ∴CD =338……………………………………………………………………………………1分 (2)由翻折得∠BED =∠BAD =90°，∴∠CED =90°，∴∠CED=∠CAB又∵∠DCE =∠DCE ，∴△CED ∽△CAB ………………………………………………1分 ∴CBCDAB DE =，∵y AD x AC ==,，∴y x DC -=，∵4=AB ⎪⎩⎪⎨⎧+==//431bk b216x BC +=…………………………………………………………………………………1分∵DE =AD =y ，2164xyx y +-=………………………………………………………………1分 ∴)0(161642>-+=x xx y …………………………………………………………2分(3)过点C 作CH ⊥BG ，垂足为H∵BG ∥AC ，∴∠ACB =∠CBG ，∵∠ACB =∠CGB ，∴∠CBG =∠CGB ，∴CB =CG ……………………………………………………………………………………1分 ∴BH =HG=AC=x ，∴BG =2x ，…………………………………………………………1分 ∵AE ⊥BD ，∴∠ADB +∠DAE =∠DAE +∠BAG =90°，∴∠ADB =∠BAG …………………………………………………………………1分 又∵∠BAC =∠ABG =90°,△ABD ∽△BGA∴BG ABAB AD =…………………………………………………………………………1分 ∴x y 244=，∴xy 8=…………………………………………………………………………1分 ∵xx y 161642-+=，∴x x x 1616482-+=，解得52=x 〔负值已舍〕即AC=52……………………………………………………………………………………1分。

初三数学 二次函数 知识点总结一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：三、二次函数图象的平移1. 平移步骤：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a<-时，y 随x 的增大而减小； 当2bx a>-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a -．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式（交点式）：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴．（同左异右 b 为0对称轴为y 轴） 3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．. ② 当0∆=时，图象与x 轴只有一个交点；③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2'当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <． 2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；二次函数对应练习试题一、选择题1. 二次函数247y x x =--的顶点坐标是( )A.(2,－11)B.（－2，7）C.（2，11）D. （2，－3） 2. 把抛物线22y x =-向上平移1个单位，得到的抛物线是（ ）A. 22(1)y x =-+ B. 22(1)y x =-- C. 221y x =-+ D. 221y x =-- 3.函数2y kx k =-和(0)ky k x=≠在同一直角坐标系中图象可能是图中的( )4.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个5.已知二次函数2(0)y ax bx c a =++≠的顶点坐标（-1，-3.2）及部分图象(如图),由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是121.3x x ==和（ ）Ａ．－１.３ B.-2.3 C.-0.3 D.-3.36. 已知二次函数2y ax bx c =++的图象如图所示，则点(,)ac bc 在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 7.方程222x x x-=的正根的个数为（ ） A.0个 B.1个 C.2个. 3 个8.已知抛物线过点A(2,0),B(-1,0),与y 轴交于点C,且OC=2.则这条抛物线的解析式为A. 22y x x =-- B. 22y x x =-++C. 22y x x =--或22y x x =-++ D. 22y x x =---或22y x x =++二、填空题9．二次函数23y x bx =++的对称轴是2x =，则b =_______。

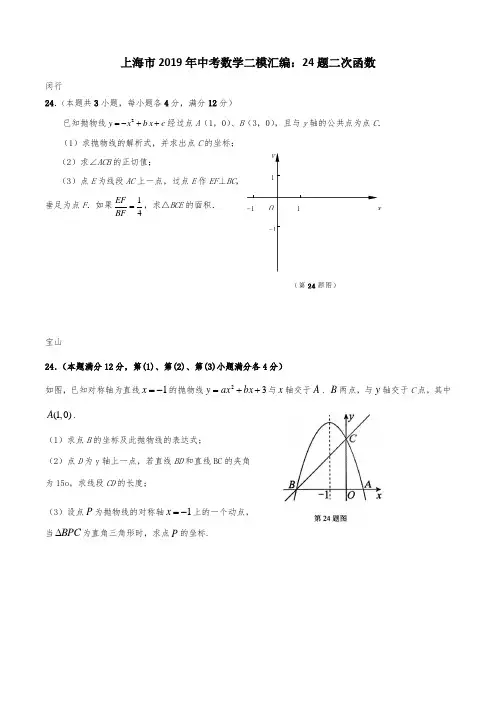
上海市2019年中考数学二模汇编：24题二次函数闵行24．（本题共3小题，每小题各4分，满分12分）已知抛物线2y x b x c =-++经过点A （1，0）、B （3，0），且与y 轴的公共点为点C ． （1）求抛物线的解析式，并求出点C 的坐标； （2）求∠ACB 的正切值；（3）点E 为线段AC 上一点，过点E 作EF ⊥BC ， 垂足为点F ．如果14EF BF =，求△BCE 的面积． 宝山24．（本题满分12分，第(1)、第(2)、第(3)小题满分各4分）如图，已知对称轴为直线1x =-的抛物线32++=bx ax y 与x 轴交于A 、B 两点，与y 轴交于C 点，其中(1,0)A .（1）求点B 的坐标及此抛物线的表达式；（2）点D 为y 轴上一点，若直线BD 和直线BC 的夹角 为15o ，求线段CD 的长度；（3）设点P 为抛物线的对称轴1x =-上的一个动点， 当BPC ∆为直角三角形时，求点P 的坐标.Oxy（第24题图）11-1-1崇明24．（本题满分12分，每小题满分各4分）如图8，抛物线2y x bx c =++交x 轴于点(1,0)A 和点B ，交y 轴于点(0,3)C ． （1）求抛物线的解析式；（2）在抛物线上找出点P ，使PC PO =，求点P 的坐标；（3）将直线AC 沿x 轴的正方向平移，平移后的直线交y 轴于点M ，交抛物线于点N ． 当四边形ACMN 为等腰梯形时，求点M 、N 的坐标． 奉贤24．（本题满分12分，每小题满分各4分） 如图9，已知平面直角坐标系，抛物线22y ax bx与轴交于点A (-2，0)和点B (4，0) ．（1）求这条抛物线的表达式和对称轴；（2）点C 在线段OB 上，过点C 作CD ⊥x 轴，垂足为点C ，交抛物线与点D ，E 是BD 中点，联结CE 并延长，与y 轴交于点F ．①当D 恰好是抛物线的顶点时，求点F 的坐标； ②联结BF ，当△DBC 的面积是△BCF 面积的32时，求点C 的坐标．xOy x 图8A BCOyx备用图y金山22. 已知：抛物线c bx x y ++-=2，经过点()2,1--A ，()10，B .（1）求抛物线的关系式及顶点P 的坐标.（2）若点B '与点B 关于x 轴对称，把（1）中的抛物线向左平移m 个单位，平移后的抛物线经过点B '，设此时抛物线顶点为点P '. ①求B B P ''∠的大小.②把线段B P ''以点B '为旋转中心顺时针旋转120，点P '落在点M 处，设点N 在（1）中的抛物线上，当B MN '∆的面积等于36时，求点N 的坐标.普陀24．（本题满分12分）在平面直角坐标系xOy 中，直线243y x m =-+(0)m >与x 轴、y 轴分别交于点A 、B 如图11所示，点C 在线段AB 的延长线上，且2AB BC =． （1）用含字母m 的代数式表示点C 的坐标；（2）抛物线21103y x bx =-++经过点A 、C ，求此抛物线的表达式；（3）在第（2）题的条件下，位于第四象限的抛物线上，是否存在这样的点P ：使2PAB OBC S S =△△，如果存在，求出点P 的坐标，如果不存在，试说明理由．xyO 第24题图杨浦24. 已知开口向下的抛物线222y ax ax =-+与y 轴的交点为A ，顶点为B ，对称轴与x 轴的交点为C ，点A 与点D 关于对称轴对称，直线BD 与x 轴交于点M ，直线AB 与直线OD 交于点N. （1）求点D 的坐标；（2）求点M 的坐标（用含a 的代数式表示）；（3）当点N 在第一象限，且∠OMB=∠ONA 时，求a 的值.长宁24.（本题满分12分，每小题4分）如图6，已知在平面直角坐标系xOy 中，抛物线c bx x y ++=294经过原点，且与x 轴相交于点A ，点A 的横坐标为6，抛物线顶点为点B ． （1）求这条抛物线的表达式和顶点B 的坐标；（2）过点O 作AB OP //，在直线OP 上点取一点Q ，使得OBA QAB ∠=∠，求点Q 的坐标；图11xyO AB11（3）将该抛物线向左平移)0(>m m 个单位，所得新抛物线与y 轴负半轴相交于点C 且顶点仍然在第四象限，此时点A 移动到点D 的位置，4:3:=DB CB ，求m 的值． 黄浦嘉定图61y1xO静安松江徐汇答案 闵行24．解：（1）由题意，得30,9330.a b a b +-=⎧⎨+-=⎩ ………………………………………………………（1分） 解得 1,4.a b =-⎧⎨=⎩…………………………………………………………（1分）所以，所求抛物线的解析式为 243y x x =-+-． ………………（1分） 由 x = 0，得 y = -3．∴ 点C 的坐标为（0，-3）．…………………………………………（1分） （2）联结AC 、BC ．过点A 作AH ⊥BC ，垂足为点H ．∵ B （3，0），C （0，3），∴ OB = OC = 3．BC =．……………………………………（1分）在Rt △BOC 和Rt △BHA 中，∠AHB =∠COB = 90°．∴ cos BH OB ABH AB BC ∠===．∴ BH ．………………（1分）即得AH =CH =． ………………………………………（1分） 在Rt △ACH 中，∠AHC = 90°， ∴ 1tan 2AH ACB CH ∠==．……………………………………………（1分） （3）联结BE ．设EF = a ．由14EF BF =，得 BF = 4a ．…………………（1分） 又∵ 1tan 2EF ACB CF ∠==，∴ CF = 2a ．…………………………（1分） ∴ BC = BF +FC = 6a ． ∴6a = 解得a =EF ．………………………………（1分） ∴113222BCE S BC EF ∆=⋅=． ………………………（1分） 宝山24.解：（1）依题意得：1203ba abc c ⎧-=-⎪⎪++=⎨⎪=⎪⎩，解之得：123a b c =-⎧⎪=-⎨⎪=⎩，……………………3分∴抛物线的解析式为223y x x =--+. …………………1分 （2）∵对称轴为1x =-，且抛物线经过(1,0)A ，∴(3,0)B -∴直线BC 的解析式为3y x =+. ∠CBA =45° …………………1分 ∵直线BD 和直线BC 的夹角为15o ， ∴∠DBA =30°或∠DBA =60° …………1分 在△BOD ，DBO BO DO ∠⋅=tan ，BO=3 …………………1分∴DO=33或33，∴CD=333-或333-. …………………1分 （3）设(1,)P t -，又(3,0)B -，(0,3)C ，∴218BC =，2222(13)4PB t t =-++=+，2222(1)(3)610PC t t t =-+-=-+， ①若点B 为直角顶点，则222BC PB PC +=即：22184610t t t ++=-+解之得：2t =-， ②若点C 为直角顶点，则222BC PC PB +=即：22186104t t t +-+=+解之得：4t =，③若点P 为直角顶点，则222PB PC BC +=即：22461018t t t ++-+=解之得：13172t +=，23172t -=. …………………4分 综上所述P 的坐标为(1,2)--或(1,4)-或317(1,)2+-或317(1,)2--. 崇明24．（本题满分12分，每小题满分各4分）解：（1）∵抛物线2y x bx c =++ 过点A （1，0）、C （0，3）∴013b cc =++⎧⎨=⎩………………………………………………………………（2分）解得43b c =-⎧⎨=⎩ ……………………………………………………………（1分）∴抛物线的解析式为243y x x =-+ ………………………………………（1分） （2）过P 作PH OC ⊥，垂足为H∵PO ＝OC ，PH OC ⊥∴CH ＝OH 32= ………………………………………………………………（1分） ∴ 23432x x -+=……………………………………………………………（1分）∴1022x =±………………………………………………………………（1分） 103103(2,)-2222P P +或（2，）………………………………………………（1分） （3）连接NA 并延长交OC 于G∵四边形ACMN 为等腰梯形，且AC ∥MN∴∠ANM ＝∠CMN ，∠ANM ＝∠GAC ，∠GCA ＝∠CMN ∴∠GAC ＝∠GCA ，∴GA ＝GC 设GA ＝x ，则GC ＝x ，OG ＝3－x 在Rt△OGA 中，OA2＋OG2＝AG2A BC OyxM NG∴12＋(3－x )2＝x 2，解得x ＝53∴OG ＝3－x ＝43，∴G （0，43）易得直线AG 的解析式为y ＝－43x ＋43令－43x ＋43＝x 2－4x ＋3，解得x 1＝1（舍去），x 2＝53∴N （53，－89）………………………………………………………………（2分）∴CM ＝AN ＝(1－53)2＋(89)2＝109∴OM ＝OC ＋CM ＝3＋109＝379∴M （0，379）…………………………………………………………………（2分）∴存在M （0，379）、N （53，－89）使四边形ACMN 为等腰梯形奉贤24．解：（1）由题意得，抛物线22yax bx 经过点A (－2，0)和点B (4，0)，代入得4220,16420.a b a b 解得1,41.2a b··············（2分）因此，这条抛物线的表达式是211242yx x . ···········（1分） 它的对称轴是直线1x.······················· （1分） （2）①由抛物线的表达式211242yx x ，得顶点D 的坐标是（1，94）. ·（1分） ∴9,1,4134DCOC BC .∵D 是抛物线顶点，CD ⊥x 轴，E 是BD 中点，∴CE BE . ∴EBC ECB .∵ECBOCF ，∴EBC OCF . ···············（1分） 在Rt △DCB 中，90DCB，34cot 934BCEBCDC ． 在Rt △OFC 中，90FOC ，cot OCOCFOF． ∴143OF =，34OF．∴点F 的坐标是（0，34）． ··········· （2分） ②∵12DBC S BC DC ∆=⋅⋅，12BCF S BC OF ∆=⋅⋅， ∴DBC BCF SDC S OF ． ····· （1分）∵△DBC 的面积是△BCF 面积的32， ∴32DCOF ． ············ （1分）由①得BDC OFC ，又90DCBFOC ，∴△DCB ∽△FOC ．∴DC CB OFOC=． ·················· （1分）又OB =4，∴342OC OC -=，∴85OC =．即点C 坐标是8(,0)5. （1分） 金山24.解：（1）把点()2,1--A ，()10，B 代入c bx x y ++-=2得⎩⎨⎧=+--=-c c b 112解得⎩⎨⎧==1c 2b∴抛物线的关系式为：122++-=x x y （2分） 得()212+--=x y ； （1分）∴顶点坐标为()21，P . （1分） （2）①设抛物线平移后为()2121++--=m x y ，代入点()1,0-'B 得()2112+--=-m ，解得131+=m ，132+-=m （舍去）；∴()2321++-=x y ，得顶点()2,3-'P （2分） 连结B P '，B P ''，作y H P ⊥'轴，垂足为H ，得3='H P ,1=HB ，213=+='B P∵3tan ='='∠BHHP BH P , （1分） ∴60='∠BH P , ∴12060180=-=''∠B B P . （1分） ②∵2='B B ,2='B P 即B P B B '=', ∴30=''∠=''∠B B P B P B ;∵线段B P ''以点B '为旋转中心顺时针旋转120，点P '落在点M 处; ∴90='∠M B O ,P B M B ''=' ∴x B M //'轴，32=''='P B M B ;设B MN '∆在M B '边上的高为h ，得：362=⋅'='∆hM B S B MN ，解得6=h ； ∴设()7-，a N 或()5，a N 分别代入122++-=x x y 得1272++-=-a a 解得：4=a 或2-=a ∴()74-，N 或()72--，N ，1252++-=a a 方程无实数根舍去，∴综上所述：当36='∆B MN S 时，点N 的坐标为()74-，N 或()72--，N . （2分+2分） 普陀 24．解：（1） 过点C 作CH ⊥OB ，垂足为点H ．∵直线243y x m =-+与x 轴、y 轴分别相交于点A 、B ，∴点A 的坐标是()6,0m ，点B 的坐标是()0,4m . ············ （2分） ∴6OA m =，4OB m =. ∵CH ⊥OB ，∴CH OACH BH BCOA OB AB==2AB BC =3CH m =2BH m =∴点C 的坐标是()3,6m m -. ··································· （1分） （2） ∵抛物线21103y x bx =-++经过点A 、点C ，可得 221(6)6100,31(3)3106.3m m b m m b m ⎧-⨯+⋅+=⎪⎪⎨⎪-⨯--⋅+=⎪⎩ ················ （2分）∵0m >，解得 1,13m b =⎧⎪⎨=⎪⎩.······················ （1分） ∴抛物线的表达式是2111033y x x =-++. ·············· （1分） （3）过点P 分别作PQ ⊥OA 、垂足为点Q ．设点P 的坐标为211(,10)33n n n -++．可得OQ n =，2111033PQ n n =--． ∵2PAB OBC S S =△△，2AB BC =．∴△PAB 与△OBC 等高，∴OP AB BAO POQ ∠=∠tan tan BAO POQ ∠=∠.∴211102333n n n --=. ························ （1分）解得1n =，2n =（舍去）． ············· （1分） ∴点P的坐标是⎝⎭. ················ （1分） 杨浦24.（1）D （2,2） （2）22,0M a ⎛⎫- ⎪⎝⎭（3）1 长宁24.（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）解：（1） 点)0,0(O 、)0,6(A 在抛物线c bx x y ++=294上 ∴⎪⎩⎪⎨⎧=++⨯=0636940c b c ，解得⎪⎩⎪⎨⎧=-=038c b （ 2分）∴抛物线的解析式为x x y 38942-=，顶点B 的坐标是)4,3(- （ 2分） （2）∵)0,6(A ，)4,3(-B ∴34AB =k ，∵AB OP // ∴34OP =k ， 设点)4,3(k k Q ，因为 OAB OBA ∠>∠ ，所以 0>k （ 1分）∵OP 平行于AB ， QA 不平行于 OB ∴四边形OQAP 为梯形又∵OBA QAB ∠=∠ ∴四边形OQAP 为等腰梯形 ∴OA QB = （1分）∴36)44(3322=++-k k ）（ ∴2511=k 或1-=k （舍去） （1分） ∴)2544,2533(Q （ 1分） （3）由（1）知4)3(94389422--=-=x x x y 设抛物线向左平移)0(>m m 个单位后的新抛物线表达式为4)3(942-+-=m x y 因为新抛物线与y 轴负半轴相交于点C 且顶点仍然在第四象限，设点C 的坐标为),0(c C所以30<<m ，04<<-c ，过点B 分别做作x 、y 轴垂线，垂足分别为点E 、F∴43==BE BF BD BC︒=∠=∠90BED BFC ∴BCF ∆∽BDE ∆∴43==BD BC DE CF ∴433=-m CF ∴)3(43m CF -=∴ )3(4344m CF OC --=-= （2分） 又∵4)3(942-+-=m x y ∴ 2)3(944m OC --= （1分） ∴ 2)3(944)3(434m m --=--∴16211=m 或者 32=m （舍去） ∴ 1621=m （1分）黄浦嘉定静安松江徐汇。

九年级中考二模数学试卷精选汇编 函数综合运用专题宝山区、嘉定区22、有一座抛物线拱型桥，在正常水位时，水面BC 的宽为10米，拱桥的最高点D 到水面BC 的距离DO 为4米，点O 是BC 的中点，如图5，以点O 为原点，直线BC 为x 轴，建立直角坐标系xOy .（1）求该抛物线的表达式；（2）如果水面BC 上升3米（即3=OA ）至水面EF ，点E 在点F 的左侧， 求水面宽度EF 的长.22.解：（1）根据题意：该抛物线的表达式为：b ax y +=2………………1分 ∵该抛物线最高点D 在y 轴上，4=DO ，∴点D 的坐标为)4,0(………1分 ∵10=BC ,点O 是BC 的中点 ∴点B 的坐标为)0,5(- ∴254-=a ，4=b …2分 ∴抛物线的表达式为：42542+-=x y …………………1分（2）根据题意可知点E 、点F 在抛物线42542+-=x y 上，EF ∥BC ……1分 ∵3=OA ∴点E 、点F 的横坐标都是3，…1分 ∴点E 坐标为)3,25(-……………1分 ， 点F 坐标为)3,25(……1分 ∴5=EF （米）……………1分 答水面宽度EF 的长为5米.长宁区22．（本题满分10分，第（1）小题5分，第（2）小题5分）某旅游景点的年游客量y （万人）是门票价格x （元）的一次函数，其函数图像如下图． （1）求y 关于x 的函数解析式；（2）经过景点工作人员统计发现：每卖出一张门票所需成本为20元．那么要想获得年利润11500万元，且门票价格不得高于230元，该年的门票价格应该定为多少元？22．（本题满分10分，第（1）小题5分，第（2）小题5分）解：（1）设)0(≠+=k b kx y ，函数图像过点（200,100）， （50,250） （1分）代入解析式得：⎩⎨⎧=+=+25050100200b k b k （2分）解之得：⎩⎨⎧=-=3001b k （1分）所以y 关于x 的解析式为：300+-=x y （1分） （2）设门票价格定为x 元，依题意可得：11500)300)(20(=+--x x （2分） 整理得： 0175003202=+-x x 解之得：x=70或者x=250（舍去） （2分） 答：门票价格应该定为70元. （1分）第22题图崇明区22．（本题满分10分，第(1)、(2)小题满分各5分）温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y 与摄氏度数x 之间是一次函数关系，下表列出了部分华氏度与摄氏度之间的对应关系：（1）选用表格中给出的数据，求y 关于x 的函数解析式；（2）有一种温度计上有两个刻度，即测量某一温度时左边是摄氏度，右边是华氏度，那么在多少摄氏度时，温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56？ 22．（本题满分10分，每小题5分）（1）解：设(0)y kx b k =+≠ ………………………………………………1分把0x =，32y =；35x =，95y =代入，得323595b k b =⎧⎨+=⎩……………1分解得9532k b ⎧=⎪⎨⎪=⎩ ……………………………………………………………………2分∴y 关于x 的函数解析式为9325y x =+ ……………………………………1分 （2）由题意得：932565x x +=+ ………………………………………………4分 解得30x = …………………………………………………1分 ∴在30摄氏度时，温度计右边华氏度的刻度正好比左边摄氏度的刻度大56奉贤区22.（本题满分10分，第(1)小题满分4分，第(2)小题满分6分）某学校要印刷一批艺术节的宣传资料，在需要支付制版费100元和每份资料0.3元印刷费的前提下，甲、乙两个印刷厂分别提出了不同的优惠条件．甲印刷厂提出：所有资料的印刷费可按9折收费；乙印刷厂提出：凡印刷数量超过200份的，超过部分的印刷费可按8折收费． （1）设该学校需要印刷艺术节的宣传资料x 份，支付甲印刷厂的费用为y 元，写出y 关于x 的函数关系式，并写出它的定义域；（2）如果该学校需要印刷艺术节的宣传资料600份，那么应该选择哪家印刷厂比较优惠？22、（1）0.27100(0)y x x =+>； （2）乙；黄浦区22．（本题满分10分）今年1月25日，上海地区下了一场大雪.这天早上王大爷去买菜，他先去了超市，发现蔬菜普遍涨价了，青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜，所以他又去了菜市场，他花了30元买了一些新鲜菠菜，他跟卖菜阿姨说：“你今天的菠菜比昨天涨了5元/斤。

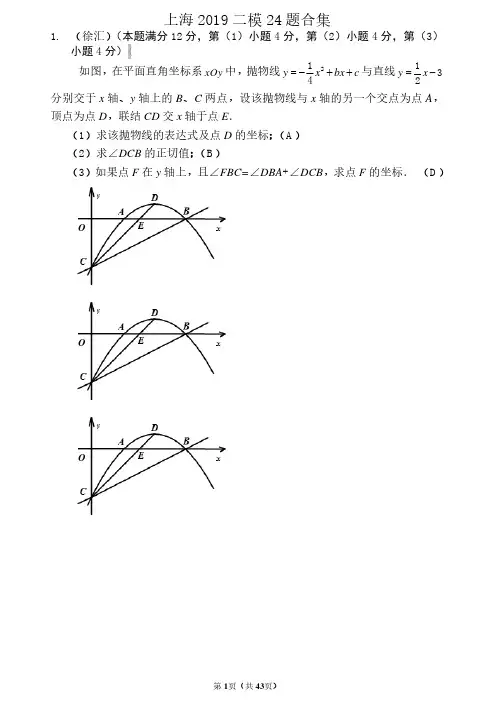
上海2019二模24题合集1.（徐汇）（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）(如图，在平面直角坐标系xOy 中，抛物线214y x bx c =-++与直线132y x =-分别交于x 轴、y 轴上的B 、C 两点，设该抛物线与x 轴的另一个交点为点A ，顶点为点D ，联结CD 交x 轴于点E ．（1）求该抛物线的表达式及点D 的坐标；（A ）（2）求∠DCB 的正切值；（B ）（3）如果点F 在y 轴上，且∠FBC=∠DBA +∠DCB ，求点F 的坐标．（D ）OOO2.(金山)已知：抛物线c bx x y ++-=2，经过点()2,1--A ，()10，B .（1）求抛物线的关系式及顶点P 的坐标.（2）若点B '与点B 关于x 轴对称，把（1）中的抛物线向左平移m 个单位，平移后的抛物线经过点B '，设此时抛物线顶点为点P '.①求B B P ''∠的大小.②把线段B P ''以点B '为旋转中心顺时针旋转 120，点P '落在点M 处，设点N 在（1）中的抛物线上，当B MN '∆的面积等于36时，求点N 的坐标.3.（奉贤）（本题满分12分，每小题满分各4分）如图9，已知平面直角坐标系xOy，抛物线22=++与x轴交于点A(-2，y ax bx0)和点B(4，0)．（1）求这条抛物线的表达式和对称轴；（A）（2）点C在线段OB上，过点C作CD⊥x轴，垂足为点C，交抛物线与点D，E是BD中点，联结CE并延长，与y轴交于点F．①当D恰好是抛物线的顶点时，求点F的坐标；（B）时，求点C的坐标．（C）②联结BF，当△DBC的面积是△BCF面积的324.（杨浦）（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）已知开口向下的抛物线222y ax ax=-+与y轴的交点为A，顶点为B，对称轴与x轴的交点为C，点A与点D关于对称轴对称，直线BD与x轴交于点M，直线AB与直线OD交于点N.（1）求点D的坐标；（B）（2）求点M的坐标（用含a的代数式表示）；（B））（3）当点N在第一象限，且∠OMB=∠ONA时，求a的值.（D5.（宝山）（本题满分12分，第(1)、第(2)、第(3)小题满分各4分）如图，已知对称轴为直线1x =-的抛物线32++=bx ax y 与x 轴交于A 、B 两点，与y 轴交于C 点，其中(1,0)A .（1）求点B 的坐标及此抛物线的表达式；（A ）（2）点D 为y 轴上一点，若直线BD 和直线BC 的夹角为15º，求线段CD 的长度；（B ）（3）设点P 为抛物线的对称轴1x =-上的一个动点，当BPC ∆为直角三角形时，求点P 的坐标.（C ）6.（崇明）（本题满分12分，每小题满分各4分）如图8，抛物线2y x bx c =++交x 轴于点(1,0)A 和点B ，交y 轴于点(0,3)C ．（1）求抛物线的解析式；（A ）（2）在抛物线上找出点P ，使PC PO =，求点P 的坐标；（B ）（3）将直线AC 沿x 轴的正方向平移，平移后的直线交y 轴于点M ，交抛物线于点N ．当四边形ACMN 为等腰梯形时，求点M 、N 的坐标．（D ）7.（松江）（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线24y ax x c =++过点A （6，0）、B （3，23），与y 轴交于点C ．联结AB 并延长，交y 轴于点D ．（1）求该抛物线的表达式；（A ）（2）求△ADC 的面积；（B ）（3）点P 在线段AC 上，如果△OAP 和△DCA 相似，求点P 的坐标．（C ）8.（闵行）（本题共3小题，每小题各4分，满分12分）已知抛物线2y x b x c =-++经过点A （1，0）、B （3，0），且与y 轴的公共点为点C ．（1）求抛物线的解析式，并求出点C 的坐标；（A ）（2）求∠ACB 的正切值；（B ）（3）点E 为线段AC 上一点，过点E 作EF ⊥BC ，垂足为点F ．如果14EF BF =，求△BCE 的面积．（C ）（第24题图）9.（长宁）（本题满分12分，每小题4分）如图6，已知在平面直角坐标系xOy 中，抛物线c bx x y ++=294经过原点，且与x 轴相交于点A ，点A 的横坐标为6，抛物线顶点为点B ．（1）求这条抛物线的表达式和顶点B 的坐标；（B ）（2）过点O 作AB OP //，在直线OP 上点取一点Q ，使得OBA QAB ∠=∠，求点Q 的坐标；（C ）（3）将该抛物线向左平移)0(>m m 个单位，所得新抛物线与y 轴负半轴相交于点C 且顶点仍然在第四象限，此时点A 移动到点D 的位置，4:3:=DB CB ，求m 的值．（D ）图610.（黄浦）（本题满分12分）如图7，已知抛物线2y ax bx c =++经过原点()0,0O 、()2,0A ，直线2y x =经过抛物线的顶点B ，点C 是抛物线上一点，且位于对称轴的右侧，联结BC 、OC 、AB ，过点C 作CE ∥x 轴，分别交线段OB 、AB 于点E 、F .（1）求抛物线的表达式；（B ）（2）当BC CE =时，求证：BCE ∆∽ABO ∆；（B ）（3）当CBA BOC ∠=∠时，求点C 的坐标.（D ）11.（普陀）（本题满分12分）在平面直角坐标系xOy 中，直线243y x m =-+(0)m >与x 轴、y 轴分别交于点A 、B 如图11所示，点C 在线段AB 的延长线上，且2AB BC =．（1）用含字母m 的代数式表示点C 的坐标；（A ）（2）抛物线21103y x bx =-++经过点A 、C ，求此抛物线的表达式；（B ）（3）在第（2）题的条件下，位于第四象限的抛物线上，是否存在这样的点P ：使2PAB OBC S S =△△，如果存在，求出点P 的坐标，如果不存在，试说明理由（C ）．图11第（3）小题满分4分）在平面直角坐标系xOy中（如图7），已知抛物线2(0)y ax bx c a=++≠经过原点，与x轴的另一个交点为A，顶点为P（3-，4）．（1）求这条抛物线表达式；（B）（2）将该抛物线向右平移，平移后的新抛物线顶点为Q，它与y轴交点为B，联结PB、PQ．设点B的纵坐标为m，用含m的代数式表示∠BPQ的正切值；（B）（3）联结AP，在（2）的条件下，射线PB平分∠APQ，求点B到直线AP的距离．（D）图7小题4分）如图，在平面直角坐标系xOy 中，抛物线2+8y ax bx =+与x 轴相交于点A （-2，0）和点B （4，0），与y 轴相交于点C ，顶点为点P ．点D （0，4）在OC 上，联结BC 、BD ．（1）求抛物线的表达式并直接写出点P 的坐标；（A ）（2）点E 为第一象限内抛物线上一点，如果△COE 与△BCD 的面积相等，求点E 的坐标；（B ）（3）点Q 在抛物线对称轴上，如果△BCD ∽△CPQ ，求点Q 的坐标．（C ，相似通解通法）第24题图x B O CDA P14.（青浦）（本题满分12分，每小题满分各4分）已知：如图10，在平面直角坐标系xOy 中，抛物线)0(2≠+=a bx ax y 经过点A （6，-3），对称轴是直线x =4，顶点为B ，OA 与其对称轴交于点M ，M 、N 关于点B 对称．（1）求这条抛物线的表达式和点B 的坐标；（B ）（2）联结ON 、AN ，求△OAN 的面积；（B ）（3）点Q 在x 轴上，且在直线x =4右侧，当∠ANQ =45°时，求点Q 的坐标．（C ）图1015.（2019•浦东新区二模）已知抛物线213y x bx c =++经过点(3,4)M -，与x 轴相交于点(3,0)A -和点B ，与y 轴相交于点C ．（1）求这条抛物线的表达式；（2）如果P 是这条抛物线对称轴上一点，PC BC =，求点P 的坐标；（3）在第（2）小题的条件下，当点P 在x 轴上方时，求PCB ∠的正弦值．。

上海市2019届一模提升题汇编第24题（二次函数综合）含2019上海中考试题中考【2019届一模徐汇】24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ，AO =OB =2，120AOB ∠=．（1）求该抛物线的表达式； （2）联结AM ，求AOMS；（3）将抛物线C 1向上平移得到抛物线C 2，抛物线C 2与x 轴分别交于点E 、F （点E 在点F 的左侧），如果△MBF 与△AOM 相似，求所有符合条件的抛物线C 2的表达式．【24．解：（1）过A 作AH ⊥x 轴，垂足为H ，∵OB=2，∴B （2,0）………………………………（1分） ∵120AOB ∠=︒∴60,30AOH HAO ∠=︒∠=︒．∵OA=2，∴112OH OA ==．∵222Rt AHO OH AH OA +=在中，，∴22213AH =-=．∴(1,3)A --……………………………………（1分）（第24题图）∵抛物线21:C y ax bx A B=+经过点、，∴可得：42033a a b a b b ⎧=-⎪+=⎧⎪⎪⎨⎨-=⎪⎩⎪=⎪⎩………………………………………………（1分）∴这条抛物线的表达式为233y x x =-+…………………………………………（1分）（2）过M 作MG ⊥x 轴，垂足为G，∵2y x x =+∴顶点M是⎛ ⎝⎭，得3MG = ……………………………………………………（1分）∵(1,A -，M⎛ ⎝⎭． ∴得：直线AM为33y x =- …………………………………………………（1分）∴直线AM 与x 轴的交点N 为1,02⎛⎫⎪⎝⎭……………………………………………………（1分）∴1122AOM S ON MG ON AH ∆=⋅+⋅111122322=⨯⨯+⨯=…………………………………………………………………………（1分）（3）∵）33，1（M 、)0,2(B ，∴3MG Rt BGM MBG BG ∆∠=在中，tan =，∴MBG ∠︒=30．∴MBF 150∠=︒．由抛物线的轴对称性得：MO=MB ，∴MBO MOB=150∠=∠︒． ∵OB=120A ∠︒，∴OM=150A ∠︒ ∴OM=MBF A ∠∠．∴BM BFOA OM 或BF BM OA OM 相似时，有：AOM 与MBF 当==∆∆ 即332BF 2332或BF 3322332==，∴32BF 或2BF ==． ∴）0，38）或（0，4（F ………………………………………………（2分）设向上平移后的抛物线k x x y ++-=33233:为C 22，当）0，4（F 时，338=k ，∴抛物线33833233:为C 22++-=x x y …（1分）当）0，38（F 时，27316=k ，抛物线22:3327C y x x =-++……．（1分）】【2019届一模浦东】24. （本题满分12分，其中每小题各4分）已知：如图9，在平面直角坐标系xOy 中，直线12y x b=-+与x 轴相交于点A ，与y 轴相交于点B. 抛物线（1）求抛物线的表达式; （2）求证: △BOD ∽△AOB;（3）如果点P 在线段AB 上，且∠BCP=∠DBO求点P 的坐标.【24、（1）211482y x x =-++；（2）证明略；（3）1612,55⎛⎫ ⎪⎝⎭】【2019届一模杨浦】24．（本题满分12分，每小题各4分） 在平面直角坐标系xOy 中，抛物线2(0)yax bx c a与y 轴交于点C （0,2），它的顶点为D （1,m ），且1tan 3COD.（1）求m 的值及抛物线的表达式；（2）将此抛物线向上平移后与x 轴正半轴交于点A ，与y 轴交于点B ，且OA=OB.若点A 是由原抛物线上的点E 平移所得，求点E 的坐标；（3）在（2）的条件下，点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°.求P 点的坐标.Oxy1 2 3 4 1 23 4 5-1 -2 -3-1 -2 -3 （第24题图）【24．解：（1）作DH ⊥y 轴，垂足为H ，∵D （1,m ）（0m），∴DH= m ，HO=1.∵1tan 3COD，∴13OH DH ，∴m=3. ····················································· （1分）∴抛物线2y ax bx c 的顶点为D （1,3）. 又∵抛物线2yax bxc 与y 轴交于点C （0,2）， ∴3,1,22.ab c ba c （2分）∴1,2,2.a b c∴抛物线的表达式为222y x x.······ （1分）（2）∵将此抛物线向上平移， ∴设平移后的抛物线表达式为222(0)y x x k k，. ···························· （1分）则它与y 轴交点B （0,2+k ）.∵平移后的抛物线与x 轴正半轴交于点A ，且OA=OB ，∴A 点的坐标为（2+k,0）. .（1分） ∴20(2)2(2)2k k k .∴122,1k k .∵0k，∴1k.∴A （3,0），抛物线222y x x向上平移了1个单位. . ······························ （1分）∵点A 由点E 向上平移了1个单位所得，∴E （3,-1）. . ··································· （1分） （3）由（2）得A （3,0），B （0, 3），∴32AB.∵点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB=45°,原顶点D （1,3）, ∴设P （1,y ），设对称轴与AB 的交点为M ，与x 轴的交点为H ，则H （1,0）. ∵A （3,0），B （0, 3），∴∠OAB=45°, ∴∠AMH=45°. ∴M （1,2）. ∴2BM.∵∠BMP=∠AMH, ∴∠BMP=45°. ∵∠APB=45°, ∴∠BMP=∠APB.∵∠B=∠B ，∴△BMP ∽△BPA. ·································································· （2分）B APy OM H∴BP BABMBP .∴23226BPBA BM∴221(3)6BPy .∴123535y y ，（舍）.. ···························· （1分）∴(1,35)P . . ····················································································· （1分）】【2019届一模普陀】 24．（本题满分12分） 如图10，在平面直角坐标系中，抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ，且3OB OA =，与y 轴交于点C ，此抛物线顶点为点D ．（1）求抛物线的表达式及点D 的坐标；（2）如果点E 是y 轴上的一点（点E 与点C 不重合），当BE DE ⊥时，求点E 的坐标； （3）如果点F 是抛物线上的一点，且，求点F 的坐标．135FBD ∠=xOy图10【24．解：（1）∵抛物线与x 轴交于点A ()1,0-和点，且3OB OA =，∴点的坐标是()3,0． ··········································································· （1分）解法一：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 得03,093 3.a b a b =--⎧⎨=+-⎩ 解得1,2.a b =⎧⎨=-⎩ ······························································ （1分）∴抛物线的表达式是223y x x =--． ······················································ （1分）点D 的坐标是()1,4-． ············································································· （1分）解法二：由抛物线23y ax bx =+-经过点()1,0-和()3,0． 可设抛物线的表达式为(1)(3)y a x x =+-， 由抛物线与y 轴的交点C 的坐标是()0,3-，得3(01)(03)a -=+-，解得1a =． ······························································ （1分）∴抛物线的表达式是223y x x =--． ························································ （1分）点D 的坐标是()1,4-． ············································································· （1分）（2）过点D 作DH OC ⊥，H 为垂足． ∴90DHO ∠=．∴90DEH EDH ∠+∠=． ∵BE DE ⊥，∴90DEH BEO ∠+∠=． ∴BEO EDH ∠=∠．又∵BOE EHD ∠=∠，∴△BOE ∽△EHD ． ········································· （1分）∴BO OEEH HD =．∵点D 的坐标是()1,4-，∴1DH =，4OH =．B B∵点的坐标是()3,0，∴3OB =．∴341OEOE =-． ·············································································· （1分）∴1OE =或3OE =． ················································································ （1分） ∵点E 与点C 不重合，∴1OE =． ∴点E 的坐标是()0,1-． ··········································································· （1分）（3）过点F 作FG x ⊥轴，G 为垂足．作45DBM ∠=，由第（2）题可得，点M 与点E 重合． ∵1OE =，1DH =，∴OE DH =． 可得△BOE ≌△EHD ． ∴BE ED =． ∵90BED ∠=，∴45DBE ∠=． ∵135FBD ∠=，∴90FBE ∠=． ················································································ （1分） ∴OBE GFB ∠=∠．∴在Rt △BOE 中，90BOE ∠=，∴cot 3OBE ∠=∴cot 3GFB ∠=． ·········· （1分） ∴3FG BG =．设点F 点的坐标为()2,23m mm --．∴223FG m m =--,3BG m =-．∴2233(3)m m m --=-． ··································································· （1分）解得3m =，4m =-． ∵3m =不合题意舍去，∴4m =-． 点F 的坐标是()4,21-． ·········································································· （1分）】【2019届一模奉贤】24．（本题满分12分，每小题满分6分）B如图10，在平面直角坐标系中，直线AB 与抛物线2yax bx 交于点A(6，0)和点B(1，－5)．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且∠BOC 的正切值是32，求点C 的坐标．【24．解：（1）由题意得，抛物线2yax bx 经过点A(6，0)和点B(1，－5)，代入得3660,5.a b a b 解得1,6.ab∴抛物线的表达式是26y x x =-. ······ （4分）由题意得，设直线AB 的表达式为ykxb ，它经过点A(6，0)和点B(1，－5)，代入得60,5.k bk b解得1,6.k b∴直线AB 的表达式是6y x =-. ········ （2分）（2）过点O 作OH AB ，垂足为点H ．设直线AB 与y 轴交点为点D ，则点D 坐标为()0,6-.∴45ODA OAD，cos45DH OH OD ==•︒= ∵2BD，∴22BH.在Rt △OBH 中，90OHB ，3tan 2OHOBHBH． ······························· （2分）∵∠BOC 的正切值是32，∴BOCCBO . ··············································· （1分） ①当点C 在点B 上方时，BOCCBO .∴COCB ． 设点C(,6)x x -，2222(6)(1)(65)x x xxOy图10ABxyo解得174x，1776644x .--------------------------------------------------------------------（2分）所以点D坐标为177,44⎛⎫-⎪⎝⎭. ②当点C 在点B 下方，BOC CBO 时，OC//AB. 点C 不在直线AB 上. ········ （1分）综上所述，如果∠BOC 的正切值是32，点C 的坐标是177,44⎛⎫-⎪⎝⎭．】【2019届一模松江】24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线cbx x y ++-=221经过点A （﹣2，0），点B （0，4）.（1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果∠PBO=∠BAO ，求点P 的坐标； （3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作DE∥x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果EO=2OF ，求m 的值.【24．解：（1）∵抛物线经过点A （﹣2，0），点B （0，4）∴⎩⎨⎧==+--4022c c b …………（1分）， 解得14b c =⎧⎨=⎩………………………（1分） ∴抛物线解析式为2142y x x =-++ …………………………………………（1分）(第24题图)y xOBA（2）()2912142122+--=++-=xxxy…………………………………（1分）∴对称轴为直线x=1，过点P作PG ⊥y轴，垂足为G ∵∠PBO=∠BAO，∴tan∠PBO=tan∠BAO，∴PG BOBG AO=……………………………………………（1分）∴121BG=，∴12BG=…………………………………（1分）∴72OG=，∴P（1，27）………………………………（1分）（3）设新抛物线的表达式为2142y x x m=-++-…（1分）则()0,4D m-,()2,4E m-，DE=2……………………（1分）过点F作FH⊥y轴，垂足为H，∵DE∥FH，EO=2OF∴2=1DE EO DOFH OF OH==，∴FH=1……………………………………………（1分）点D在y轴的正半轴上，则51,2F m⎛⎫--⎪⎝⎭，∴52OH m=-∴42512DO mOH m-==-，∴m=3……………………………………………………（1分）点D在y轴的负半轴上，则91,2F m⎛⎫-⎪⎝⎭，∴92OH m=-∴42912DO mOH m-==-，∴m=5……………………………………………………（1分）∴综上所述m的值为3或5.】(第24题图)yx OBAEDF H【2019届一模嘉定】24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ，与y 轴的交点为C ．（1）试求这个抛物线的表达式；（2）如果这个抛物线的顶点为M ，求△AMC 的面积； （3）如果这个抛物线的对称轴与直线BC 交于点D ，点E 在线段AB 上，且︒=∠45DOE ，求点E 的坐标．【24. 解：（1）∵抛物线22++=bx ax y 点经过)0,4(A 、)2,2(B ∴⎩⎨⎧=++=++222402416b a b a ……………………1分 ∴⎪⎪⎩⎪⎪⎨⎧=-=2141b a …………2分 ∴抛物线的表达式是221412++-=x x y …………1分 （2）由（1）得：抛物线221412++-=x x y 的顶点M 的坐标为)49,1(……1分图7O 11-1 -1∴点C 的坐标为)0,2(， ……………………1分 过点M 作y MH ⊥轴，垂足为点H ∴AOCMHC AOHM AMC S S S S ∆∆∆--= …………1分∴42211412149)41(21⨯⨯-⨯⨯-⨯+⨯=∆AMC S∴23=∆AMC S …………1分（3）联结OB过点B 作x BG ⊥轴，垂足为点G∵点B 的坐标为)2,2(，点A 的坐标为)0,4(∴2=BG ，2=GA ∴△BGA 是等腰直角三角形∴︒=∠45BAO 同理：︒=∠45BOA∵点C 的坐标为)0,2(∴2=BC ，2=OC 由题意得，△OCB 是等腰直角三角形 ∴︒=∠45DBO ,22=BO ∴DBO BAO ∠=∠∵︒=∠45DOE ∴︒=∠+∠45BOE DOB ∵︒=∠+∠45EOA BOE ∴DOB EOA ∠=∠ ∴△AOE ∽△BOD∴BO AOBD AE =…………1分 ∵抛物线221412++-=x x y 的对称轴是直线1=x ，∴点D 的坐标为)2,1(∴1=BD …………1分∴2241=AE ∴2=AE …………1分过点E 作x EF ⊥轴，垂足为点F 易得，△AFE 是等腰直角三角形 ∴1==AF EF∴点E 的坐标为)1,3( …………1分】 【2019届一模青浦】24．（本题满分12分， 其中第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，将抛物线2y x =-平移后经过点A （-1，0）、B （4，0），且平移后的抛物线与y 轴交于点C （如图）． （1）求平移后的抛物线的表达式；（2）如果点D 在线段CB 上，且CAD 的正弦值；（3）点E 在y 轴上且位于点C 的上方，点P 在直线BC 上，点Q 在平移后的抛物线上，如果四边形ECPQ 是菱形，求点Q 的坐标．【24．解：（1）设平移后的抛物线的解析式为2+=-+y x bx c ． ······················· （1分）将A （-1，0）、B （4，0），代入得（第24题图）（备用图）101640.，--+=⎧⎨-++=⎩b c b c ··············································································· （1分） 解得：34.，=⎧⎨=⎩b c所以，2+34=-+y x x ． ·········································································· （1分）（2）∵2+34=-+y x x ，∴点C 的坐标为（0，4） ····································· （1分）．设直线BC 的解析式为y= kx+4，将B （4，0），代入得kx+4=0，解得k=-1，∴y= -x+4． ········································································································ 设点D 的坐标为（m ，4- m ）．∵，∴22=2m ，解得=1m 或=1-m （舍去），∴点D 的坐标为（1，3）． ········································································· （1分） 过点D 作DM ⊥AC ，过点B 作BN ⊥AC ，垂足分别为点M 、N ．∵1122⋅=⋅AC BN AB OC54=⨯BN，∴17=BN ． ········ （1分） ∵DM ∥BN ，∴=DM CD BN CB，∴=DM BN，∴17=DM ． ···················· （1分）∴sin =17221∠==DM CAD AD ． ············································· （1分）（3）设点Q 的坐标为（n ，2+34-+n n ）．如果四边形ECPQ 是菱形，则0>n ，PQ ∥y 轴，PQ=PC ，点P 的坐标为（n ，4-+n ）．∵22+3444=-++-=-PQ n n n n n，=PC ， ····································· （2分）∴24-n n，解得=4n 或=0n （舍）． ·········································· （1分） ∴点Q的坐标为（4，2）． ···················································· （1分）】【2019届一模静安】24．（本题满分12分，其中第（1）小题4分，第（2）小题3分，第（3）小题5分）在平面直角坐标系xOy 中（如图10），已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ，、(53)D ，，设它与x 轴的另一个交点为A （点A 在点B 的左侧），且ABD ∆的面积是3．（1）求该抛物线的表达式； （2）求ADB ∠的正切值；（3）若抛物线与y 轴交于点C ，直线CD 交x 轴于点E ，点P 在射线AD 上，当APE ∆与 ABD ∆相似时，求点P 的坐标．【24．解：（1）过点D 作DH ⊥x 轴，交x 轴于点H ．∵132ABD S AB DH ∆=⋅=，又∵(5,3)D∴2AB =．····························································································· （1分） ∵(4,0)B ，点A 在点B 的左侧，∴(2,0)A ． ····························································································· （1分）把(2,0)A ，(4,0)B ，(5,3)D 分别代入2y ax bx c =++， 得04201643255a b ca b c a b c =++⎧⎪=++⎨⎪=++⎩解得168a b c =⎧⎪=-⎨⎪=⎩． ···························································· （1分）∴抛物线解析式是268y x x =-+． ······························································ （1分）（2）过点B 作BG AD ⊥，交AD 于点G ． ··················································· （1分）BD O图10xy﹒ ﹒由(2,0)A ，(5,0)H ，(5,3)D ，得ADH ∆是等腰直角三角形，且45HAD ∠=∵3AH DH ==，∴AD = ································································ （1分） ∴在等腰直角AGB ∆中，由2AB =，得AG BG ==，∴DG AD AG =-=∴在Rt DGB ∆中，1tan 2BG ADB DG ∠==． ·················································· （1分）（3）∵抛物线268y x x =-+与y 轴交于点(0,8)C ，又(5,3)D ，∴直线CD 的解析式为8y x =-+，∴(8,0)E ． ···························································································· （1分） 当点P 在线段AD 上时，APE ∆∽ABD ∆，点,,A P E 分别与点,,A B D 对应，则AP AE AB AD =，即AB AE AP AD ⨯===．………………………………………（1分）··························································································································· 过点P 作PQ ⊥∴2AQ PQ ==，即(4,2)P ． ····································································· （1分） ②当点P 在线段AD 延长线上时，APE ADB ∠=∠， ·················································· ∴EP //DB过点P 作PR x ⊥轴于点R ， ··················································································13AH AD AB AR AP AE ===，∴9AR PR ==， ······················································································ （1分） 即(11,9)P ． ···························································································· （1分） ∴APE ∆与ABD ∆相似时，点P 的坐标为 (4,2)或 (11,9)．】 【2019届一模宝山】24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分） 如图9，已知：二次函数的图像交x 轴正半轴于点A ，顶点为P,一次函数2y x bx=+。

2019年上海市虹口区中考数学二模试卷一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．]1．（4分）计算（a3）2的结果是（）A．a5B．a6C．a8D．a92．（4分）方程的解为（）A．x＝4B．x＝7C．x＝8D．x＝10．3．（4分）已知一次函数y＝（3﹣a）x+3，如果y随自变量x的增大而增大，那么a的取值范围为（）A．a＜3B．a＞3C．a＜﹣3D．a＞﹣3．4．（4分）下列事件中，必然事件是（）A．在体育中考中，小明考了满分B．经过有交通信号灯的路口，遇到红灯C．抛掷两枚正方体骰子，点数和大于1D．四边形的外角和为180度．5．（4分）正六边形的半径与边心距之比为（）A．B．C．D．6．（4分）如图，在△ABC中，AB＝AC，BC＝4，tan B＝2，以AB的中点D为圆心，r为半径作⊙D，如果点B在⊙D内，点C在⊙D外，那么r可以取（）A．2B．3C．4D．5二、填空题：（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．（4分）计算：2﹣1＝．8．（4分）在数轴上，实数2﹣对应的点在原点的侧．（填“左”、“右”）9．（4分）不等式﹣2x＞﹣4的正整数解为．10．（4分）如果关于x的方程kx2﹣6x+9＝0有两个相等的实数根，那么k的值为．11．（4分）已知反比例函数的图象经过点A（1，3），那么这个反比例函数的解析式是．12．（4分）如果将抛物线y＝2x2向左平移3个单位，那么所得新抛物线的表达式为．13．（4分）一个不透明的袋中装有4个白球和若干个红球，这些球除颜色外其他都相同，摇匀后随机摸出一个球，如果摸到白球的概率为0.4，那么红球有个．14．（4分）为了了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，共分成4组，频率分布表（不完整）如下表所示．如果次数在110次（含110次）以上为达标，那么估计该校初三毕业生一分钟跳绳次数的达标率约为．组别分组（含最小值，不含最大值）频数频率190～10030.062100～1101a3110～120240.484120～130b c15．（4分）已知两圆外切，圆心距为7，其中一个圆的半径为3，那么另一个圆的半径长为．16．（4分）如图，AD∥BC，BC＝2AD，AC与BD相交于点O，如果，，那么用、表示向量是．17．（4分）我们知道，四边形不具有稳定性，容易变形．一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把的值叫做这个平行四边形的变形度．如图，矩形ABCD的面积为5，如果变形后的平行四边形A1B1C1D1的面积为3，那么这个平行四边形的变形度为．18．（4分）如图，在矩形ABCD中，AB＝6，点E在边AD上且AE＝4，点F是边BC上的一个动点，将四边形ABFE沿EF翻折，A、B的对应点A1、B1与点C在同一直线上，A1B1与边AD交于点G，如果DG＝3，那么BF的长为．三、解答题（本大题共7题，满分78分）19．（10分）先化简，再求值：，m＝﹣3．20．（10分）解方程组：21．（10分）如图，在锐角△ABC中，小明进行了如下的尺规作图：①分别以点A、B为圆心，以大于AB的长为半径作弧，两弧分别相交于点P、Q；②作直线PQ分别交边AB、BC于点E、D．（1）小明所求作的直线DE是线段AB的；（2）联结AD，AD＝7，sin∠DAC＝，BC＝9，求AC的长．22．（10分）甲、乙两组同时加工某种零件，甲组每小时加工80件，乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，部分数据如下表所示．x（小时）246y（件）50150250（1）求y与x之间的函数关系式；（2）甲、乙两组同时生产，加工的零件合在一起装箱，每满340件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？23．（12分）如图，在▱ABCD中，AC与BD相交于点O，过点B作BE∥AC，联结OE交BC于点F，点F为BC的中点．（1）求证：四边形AOEB是平行四边形；（2）如果∠OBC＝∠E，求证：BO•OC＝AB•FC．24．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+8与x轴相交于点A（﹣2，0）和点B（4，0），与y轴相交于点C，顶点为点P．点D（0，4）在OC上，联结BC、BD．（1）求抛物线的表达式并直接写出点P的坐标；（2）点E为第一象限内抛物线上一点，如果△COE与△BCD的面积相等，求点E的坐标；（3）点Q在抛物线对称轴上，如果△BCD∽△CPQ，求点Q的坐标．25．（14分）如图，AD∥BC，∠ABC＝90°，AD＝3，AB＝4，点P为射线BC上一动点，以P为圆心，BP长为半径作⊙P，交射线BC于点Q，联结BD、AQ相交于点G，⊙P 与线段BD、AQ分别相交于点E、F．（1）如果BE＝FQ，求⊙P的半径；（2）设BP＝x，FQ＝y，求y关于x的函数关系式，并写出x的取值范围；（3）联结PE、PF，如果四边形EGFP是梯形，求BE的长．2019年上海市虹口区中考数学二模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．]1．（4分）计算（a3）2的结果是（）A．a5B．a6C．a8D．a9【分析】根据幂的乘方，底数不变，指数相乘即可求．【解答】解：（a3）2＝a6，故选：B．【点评】本题考查了幂的乘方，解题的关键是熟练掌握幂的乘方公式．2．（4分）方程的解为（）A．x＝4B．x＝7C．x＝8D．x＝10．【分析】将方程两边平方求解可得．【解答】解：将方程两边平方得x﹣1＝9，解得：x＝10，经检验：x＝10是原无理方程的解，故选：D．【点评】本题考查解无理方程，解无理方程的基本思想是把无理方程转化为有理方程来解，在变形时要注意根据方程的结构特征选择解题方法．常用的方法有：乘方法，配方法，因式分解法，设辅助元素法，利用比例性质法等．3．（4分）已知一次函数y＝（3﹣a）x+3，如果y随自变量x的增大而增大，那么a的取值范围为（）A．a＜3B．a＞3C．a＜﹣3D．a＞﹣3．【分析】先根据一次函数的性质得出关于a的不等式，再解不等式即可求出a的取值范围．【解答】解：∵一次函数y＝（3﹣a）x+3，函数值y随自变量x的增大而增大，∴3﹣a＞0，解得a＜3．故选：A．【点评】本题考查的是一次函数的图象与系数的关系，熟知一次函数的增减性是解答此题的关键．4．（4分）下列事件中，必然事件是（）A．在体育中考中，小明考了满分B．经过有交通信号灯的路口，遇到红灯C．抛掷两枚正方体骰子，点数和大于1D．四边形的外角和为180度．【分析】根据事件发生的可能性大小判断相应事件的类型即可．【解答】解：A、在体育中考中，小明考了满分是随机事件；B、经过有交通信号灯的路口，遇到红灯是随机事件；C、抛掷两枚正方体骰子，点数和大于1是必然事件；D、四边形的外角和为180度是不可能事件，故选：C．【点评】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．5．（4分）正六边形的半径与边心距之比为（）A．B．C．D．【分析】求出正六边形的边心距（用R表示），根据“接近度”的定义即可解决问题．【解答】解：∵正六边形的半径为R，∴边心距r＝R，∴R：r＝1：＝2：，故选：D．【点评】本题考查正多边形与圆的知识，等边三角形高的计算，记住等边三角形的高h ＝a（a是等边三角形的边长），理解题意是解题的关键，属于中考常考题型．6．（4分）如图，在△ABC中，AB＝AC，BC＝4，tan B＝2，以AB的中点D为圆心，r为半径作⊙D，如果点B在⊙D内，点C在⊙D外，那么r可以取（）A．2B．3C．4D．5【分析】先求出DB和DC的长，根据点B在⊙D内，点C在⊙D外，确定r的取值范围，从而确定r可以取的值．【解答】解：如图，过点A作AF⊥BC于点F，连接CD交AF于点G，∵AB＝AC，BC＝4，∴BF＝CF＝2，∵tan B＝2，∴，即AF＝4，∴AB＝，∵D为AB的中点，∴BD＝，G是△ABC的重心，∴GF＝AF＝，∴CG＝，∴CD＝CG＝，∵点B在⊙D内，点C在⊙D外，∴＜r＜，故选：B．【点评】本题考查点与圆的位置关系，锐角三角函数的定义，等腰三角形的性质，解题的关键是掌握点与圆的位置关系的判别方法．二、填空题：（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．（4分）计算：2﹣1＝．【分析】根据幂的负整数指数运算法则进行计算即可．【解答】解：2﹣1＝．故答案为．【点评】本题考查负整数指数幂的运算．幂的负整数指数运算，先把底数化成其倒数，然后将负整数指数幂当成正的进行计算．8．（4分）在数轴上，实数2﹣对应的点在原点的左侧．（填“左”、“右”）【分析】根据2＜＜3，可知2﹣＜0，所以2﹣在原点的左侧．【解答】解：根据题意可知：2﹣＜0，∴2﹣对应的点在原点的左侧．故填：左【点评】本题考查实数与数轴上点的对应关系，掌握了实数与数轴上的点的一一对应关系，很容易得出正确答案．9．（4分）不等式﹣2x＞﹣4的正整数解为x＝1．【分析】由题意可求一元一次不等式的解，即可得正整数解．【解答】解：∵﹣2x＞﹣4∴x＜2∴正整数解为：x＝1故答案为：x＝1【点评】本题考查了一元一次不等式的整数解，熟练运用解不等式的方法是本题的关键．10．（4分）如果关于x的方程kx2﹣6x+9＝0有两个相等的实数根，那么k的值为1．【分析】根据根的判别式和已知得出△＝（﹣6）2﹣4k×9＝0且k≠0，求出即可．【解答】解：∵关于x的方程kx2﹣6x+9＝0有两个相等的实数根，∴△＝（﹣6）2﹣4k×9＝0且k≠0，解得：k＝1，故答案为：1．【点评】本题考查了一元二次方程的定义和根的判别式，能根据已知得出△＝（﹣6）2﹣4k×9＝0且k≠0是解此题的关键．11．（4分）已知反比例函数的图象经过点A（1，3），那么这个反比例函数的解析式是y ＝．【分析】把（1，3）代入函数y＝中可先求出k的值，那么就可求出函数解析式．【解答】解：由题意知，k＝1×3＝3．则反比例函数的解析式为：y＝．故答案为：y＝．【点评】本题考查了待定系数法求解反比例函数解析式，此为近几年中考的热点问题，同学们要熟练掌握．12．（4分）如果将抛物线y＝2x2向左平移3个单位，那么所得新抛物线的表达式为y＝2（x+3）2．【分析】根据“左加右减，上加下减”的规律解题．【解答】解：将抛物线y＝2x2向左平移3个单位，所得新抛物线的表达式为y＝2（x+3）2，故答案为：y＝2（x+3）2．【点评】主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．13．（4分）一个不透明的袋中装有4个白球和若干个红球，这些球除颜色外其他都相同，摇匀后随机摸出一个球，如果摸到白球的概率为0.4，那么红球有6个．【分析】设红球有x个，根据摸到白球的概率为0.4列出方程，求出x的值即可．【解答】解：设红球有x个，根据题意得：＝0.4，解得：x＝6，答：红球有6个；故答案为：6．【点评】本题考查了概率公式，设出未知数，列出方程是解题的关键．用到的知识点为：概率＝所求情况数与总情况数之比．14．（4分）为了了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，共分成4组，频率分布表（不完整）如下表所示．如果次数在110次（含110次）以上为达标，那么估计该校初三毕业生一分钟跳绳次数的达标率约为92%．组别分组（含最小值，不含最大值）频数频率190～10030.062100～1101a3110～120240.484120～130b c【分析】根据抽取的学生一分钟跳绳的达标率，即可估计该校初三毕业生一分钟跳绳的达标率．【解答】解：∵样本容量为：3÷0.06＝50，∴该校初三毕业生一分钟跳绳次数的达标率约为×100%＝92%，故答案为：92%【点评】本题考查的是频数分布表的知识，准确读表、从中获取准确的信息是解题的关键，注意用样本估计总体的运用．15．（4分）已知两圆外切，圆心距为7，其中一个圆的半径为3，那么另一个圆的半径长为4．【分析】根据两圆外切时圆心距等于两圆的半径的和，即可求解．【解答】解：∵两圆外切，圆心距为7，若其中一个圆的半径为3，∴另一个圆的半径＝7﹣3＝4．故答案为：4．【点评】本题考查了圆与圆的位置关系与数量关系间的联系．此类题为中考热点，需重点掌握．16．（4分）如图，AD∥BC，BC＝2AD，AC与BD相交于点O，如果，，那么用、表示向量是﹣2．【分析】根据平面向量的线性运算法则即可求出答案．【解答】解：∵AD∥BC，∴△ADO∽△CBO，∴，∴＝+＝++3＝+﹣3＝﹣2，故答案为：．【点评】本题考查平面向量，解题的关键是熟练运用平面向量的运算法则，本题属于基础题型．17．（4分）我们知道，四边形不具有稳定性，容易变形．一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把的值叫做这个平行四边形的变形度．如图，矩形ABCD的面积为5，如果变形后的平行四边形A1B1C1D1的面积为3，那么这个平行四边形的变形度为．【分析】设矩形的长和宽分别为a，b，变形后的平行四边形的高为h，根据平行四边形和矩形的面积公式即可得到结论．【解答】解：过A1作A1D⊥B1C1，设矩形的长和宽分别为a，b，变形后的平行四边形的高为h，∴ab＝5，3＝ah，∴b＝，h＝，∴B1D＝＝，∴＝＝，故答案为：．【点评】本题考查了平行四边形的性质，矩形的性质，三角函数的定义，正确的理解题意是解题的关键．18．（4分）如图，在矩形ABCD中，AB＝6，点E在边AD上且AE＝4，点F是边BC上的一个动点，将四边形ABFE沿EF翻折，A、B的对应点A1、B1与点C在同一直线上，A1B1与边AD交于点G，如果DG＝3，那么BF的长为．【分析】由DG＝3，CD＝6可知△CDG的三角函数关系，由△CDG分别与△A'EG，△B'FC相似，可求得CG，CB'，由勾股定理△CFB'可求得BF长度．【解答】解：∵△CDG∽△A'EG，A'E＝4∴A'G＝2∴B'G＝4由勾股定理可知CG'＝则CB'＝由△CDG∽△CFB'设BF＝x∴解得x＝故答案为【点评】本题考查了翻折的性质与相似，通过寻找等角关系，确定相似关系是本题的关键．三、解答题（本大题共7题，满分78分）19．（10分）先化简，再求值：，m＝﹣3．【分析】先把分式化简，再将m的值代入求解．【解答】解：原式＝÷＝×＝﹣当m＝﹣3时，原式＝﹣．【点评】本题主要考查了分式的化简求值这一知识点，要求把式子化到最简，然后代值．20．（10分）解方程组：【分析】对于第1个方程利用因式分解法可得x﹣6y＝0或x+y＝0，再将它们与方程②分别组成方程组，分别求解可得．【解答】解：由①得，x﹣6y＝0或x+y＝0，将它们与方程②分别组成方程组，得：或分别解这两个方程组，得原方程组的解为．【点评】本题是考查高次方程，高次方程的解法思想：通过适当的方法，把高次方程化为次数较低的方程求解．所以解高次方程一般要降次，即把它转化成二次方程或一次方程．也有的通过因式分解来解．21．（10分）如图，在锐角△ABC中，小明进行了如下的尺规作图：①分别以点A、B为圆心，以大于AB的长为半径作弧，两弧分别相交于点P、Q；②作直线PQ分别交边AB、BC于点E、D．（1）小明所求作的直线DE是线段AB的线段AB的垂直平分线（或中垂线）；（2）联结AD，AD＝7，sin∠DAC＝，BC＝9，求AC的长．【分析】（1）利用基本作法进行判断；（2）过点D作DF⊥AC，垂足为点F，如图，根据线段垂直平分线的性质得到AD＝BD ＝7，则CD＝2，在Rt△ADF中先利用正弦的定义可计算出DF，再利用勾股定理可计算出AF，接着在Rt△CDF中利用勾股定理可计算出CF，然后计算AF+CF．【解答】解：（1）小明所求作的直线DE是线段AB的垂直平分线（或中垂线）；故答案为线段AB的垂直平分线（或中垂线）；（2）过点D作DF⊥AC，垂足为点F，如图，∵DE是线段AB的垂直平分线，∴AD＝BD＝7∴CD＝BC﹣BD＝2，在Rt△ADF中，∵sin∠DAC＝＝，∴DF＝1，在Rt△ADF中，AF＝＝4，在Rt△CDF中，CF＝＝，∴AC＝AF+CF＝4+＝5．【点评】本题考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了解直角三角形．22．（10分）甲、乙两组同时加工某种零件，甲组每小时加工80件，乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，部分数据如下表所示．x（小时）246y（件）50150250（1）求y与x之间的函数关系式；（2）甲、乙两组同时生产，加工的零件合在一起装箱，每满340件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？【分析】（1）运用待定系数法解答即可；（2）设经过x小时恰好装满第1箱，可得方程80x+50x﹣50＝340，解方程即可解答．【解答】解：（1）设y与x之间的函数关系式为y＝kx+b（k≠0）把（2，50）（4，150）代入，得解得∴y与x之间的函数关系式为y＝50x﹣50；（2）设经过x小时恰好装满第1箱，根据题意得80x+50x﹣50＝340，∴x＝3，答：经过3小时恰好装满第1箱．【点评】本题考查一次函数的应用，解答本题的关键是明确题意，运用待定系数法求出y 与x之间的函数关系式．23．（12分）如图，在▱ABCD中，AC与BD相交于点O，过点B作BE∥AC，联结OE交BC于点F，点F为BC的中点．（1）求证：四边形AOEB是平行四边形；（2）如果∠OBC＝∠E，求证：BO•OC＝AB•FC．【分析】（1）根据平行四边形的性质和判定以及平行线分线段成比例解答即可；（2）根据平行四边形的性质和相似三角形的判定和性质解答即可．【解答】证明：（1）∵BE∥AC，∴∵点F为BC的中点，∴CF＝BF，∴OC＝BE∵四边形ABCD是平行四边形，∴AO＝CO∴AO＝BE∵BE∥AC，∴四边形AOEB是平行四边形（2）∵四边形AOEB是平行四边形，∴∠BAO＝∠E∵∠OBC＝∠E，∴∠BAO＝∠OBC∵∠ACB＝∠BCO，∴△COB∽△CBA∴∵四边形ABCD是平行四边形，∴AC＝2OC∵点F为BC的中点，∴BC＝2FC∴即BO•OC＝AB•FC【点评】此题考查相似三角形的判定和性质，关键是根据平行四边形的性质和相似三角形的判定和性质解答．24．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+8与x轴相交于点A（﹣2，0）和点B（4，0），与y轴相交于点C，顶点为点P．点D（0，4）在OC上，联结BC、BD．（1）求抛物线的表达式并直接写出点P的坐标；（2）点E为第一象限内抛物线上一点，如果△COE与△BCD的面积相等，求点E的坐标；（3）点Q在抛物线对称轴上，如果△BCD∽△CPQ，求点Q的坐标．【分析】（1）由点A，B的坐标，利用待定系数法可求出抛物线的表达式，再利用配方法可求出抛物线顶点P的坐标；（2）利用二次函数图象上点的坐标特征可求出点C的坐标，设点E的坐标为（x，﹣x2+2x+8）（0＜x＜4），由三角形的面积公式结合S△COE ＝S△BCD可得出关于x的一元一次方程，解之即可得出x的值，再将其代入点E的坐标中即可求出结论；（3）过点C作CM∥x轴，交抛物线对称轴于点M，由点C，P，B，D的坐标可得出∠CPQ＝∠CDB＝135°及CP，BD，CD的长度，由△BCD∽△CPQ可得出＝或＝，代入CP，BD，CD的长可求出PQ的长，再结合点P的坐标即可得出点Q的坐标．【解答】解：（1）将点A（﹣2，0），B（4，0）代入y＝ax2+bx+8，得：，解得：，∴抛物线的表达式为y＝﹣x2+2x+8．∵y ＝﹣x 2+2x +8＝﹣（x ﹣1）2+9， ∴点P 的坐标为（1，9）．（2）当x ＝0时，y ＝﹣x 2+2x +8＝8， ∴点C 的坐标为（0，8）．设点E 的坐标为（x ，﹣x 2+2x +8）（0＜x ＜4）， ∵S △COE ＝S △BCD ， ∴×8•x ＝×4×4， 解得：x ＝2，∴点E 的坐标为（2，8）．（3）过点C 作CM ∥x 轴，交抛物线对称轴于点M ，如图所示． ∵点B （4，0），点D （0，4）， ∴OB ＝OD ＝4， ∴∠ODB ＝45°，BD ＝4，∴∠BDC ＝135°．∵点C （0，8），点P （1，9）， ∴点M 的坐标为（1，8）， ∴CM ＝PM ＝1， ∴∠CPM ＝45°，CP ＝， ∴点Q 在抛物线对称轴上且在点P 的上方， ∴∠CPQ ＝∠CDB ＝135°． ∵△BCD ∽△CPQ ， ∴＝或＝．①当＝时，，解得：PQ ＝2，∴点Q 的坐标为（1，11）； ②当＝时，，解得：PQ ＝1，∴点Q 的坐标为（1，10）．综上所述，点Q的坐标为（1，11）或（1，10）．【点评】本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数图象上点的坐标特征、三角形的面积以及相似三角形的性质，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用三角形的面积公式，找出关于x的一元一次方程；（3）分＝或＝两种情况，求出PQ的长度．25．（14分）如图，AD∥BC，∠ABC＝90°，AD＝3，AB＝4，点P为射线BC上一动点，以P为圆心，BP长为半径作⊙P，交射线BC于点Q，联结BD、AQ相交于点G，⊙P 与线段BD、AQ分别相交于点E、F．（1）如果BE＝FQ，求⊙P的半径；（2）设BP＝x，FQ＝y，求y关于x的函数关系式，并写出x的取值范围；（3）联结PE、PF，如果四边形EGFP是梯形，求BE的长．【分析】（1）证出∠FQP＝∠ADB，由三角函数得出tan∠FQP＝＝，得出＝，即可得出结果；（2）过点P作PM⊥FQ，垂足为点M，在Rt△ABQ中，由三角函数得出cos∠AQB＝＝，在Rt△PQM中，QM＝PQ cos∠AQB＝，进一步求出，当圆与D点相交时，x最大，作DH⊥BC于H，则PD＝PB＝x，DH＝AB＝4，BH＝AD＝3，则PH＝BP﹣BH＝x﹣3，在Rt△PDH中，由勾股定理得出方程，解方程求出x的值，即可得出x的取值范围；（3）设BP＝x，分两种情况：①EP∥AQ时，求出QG＝QB＝2x，同理：AG＝AD＝3，在Rt△ABQ中，由勾股定理得出方程，解方程得出x＝，QG＝QB＝2x＝，由平行线得出＝，求出BG＝，即可得出结果；②PF∥BD时，同①得：BG＝BQ＝2x，DG＝AD＝3，在Rt△ABD中，由勾股定理得出方程，解方程求出BQ＝2，BP＝1，作PN⊥BG于N，由垂径定理得出BE＝2BN，由三角函数得出cos∠PBN＝cos∠ADB＝，求出BN＝，即可得出结果．【解答】解：（1）∵BE＝FQ，∴∠BPE＝∠FPQ，∵PE＝PB，∴∠EBP＝（180°﹣∠EPB），同理∠FQP＝（180°﹣∠FPQ），∴∠EBP＝∠FQP，∵AD∥BC，∴∠ADB＝∠EBP，∴∠FQP＝∠ADB，∴tan∠FQP＝tan∠ADB＝，设⊙P的半径为r，则tan∠FQP＝＝，∴＝，解得：r＝，∴⊙P的半径为；（2）过点P作PM⊥FQ，垂足为点M，如图1所示：在Rt△ABQ中，cos∠AQB＝＝＝＝，在Rt△PQM中，QM＝PQ cos∠AQB＝，∵PM⊥FQ，PF＝PQ，∴FQ＝2QM＝，∴，当圆与D点相交时，x最大，作DH⊥BC于H，如图2所示：则PD＝PB＝x，DH＝AB＝4，BH＝AD＝3，则PH＝BP﹣BH＝x﹣3，在Rt△PDH中，由勾股定理得：42+（x﹣3）2＝x2，解得：x＝，∴x的取值范围为：；（3）设BP＝x，分两种情况：①EP∥AQ时，∴∠BEP＝∠BGQ，∵PB＝PE，∴∠PBE＝∠BEP，∴∠BGQ＝∠PBE，∴QG＝QB＝2x，同理：AG＝AD＝3，在Rt△ABQ中，由勾股定理得：42+（2x）2＝（3+2x）2，解得：x＝，∴QG＝QB＝2x＝，∵EP∥AQ，PB＝PQ，∴BE＝EG，∵AD∥BC，∴＝，即＝，解得：BG＝，∴BE＝BG＝；②PF∥BD时，同①得：BG＝BQ＝2x，DG＝AD＝3，在Rt△ABD中，由勾股定理得：42+32＝（3+2x）2，解得：x＝1或x＝﹣4（舍去），∴BQ＝2，∴BP＝1，作PN⊥BG于N，则BE＝2BN，如图3所示：∵AD∥BC，∴∠PBN＝∠ADB，∴cos∠PBN＝cos∠ADB＝，即＝，∴BN＝，∴BE＝2BN＝；综上所述，或．【点评】本题是圆的综合题目，考查了等腰三角形的判定与性质、平行线的性质、三角函数、垂径定理、勾股定理等知识；本题综合性强，熟练掌握等腰三角形的性质，由勾股定理得出方程是解题关键．。

由△DPH与△AOB相似，易知∠AOB=∠PHD=90°，
所以 或 ，————————————（2分）
解得： 或 ，
所以点P的坐标为（5,8）， .————————————————（1分）
金山区
24．（本题满分12分，每小题4分）
平面直角坐标系xOy中（如图8），已知抛物线 经过点A（1,0）和B（3,0），
（2）当CB平分∠DCO时，求 的值．
黄浦区
24．（本题满分12分）
已知抛物线 经过点A（1,0）和B（0,3），其顶点为D.
（1）求此抛物线的表达式；
（2）求△ABD的面积；
（3）设P为该抛物线上一点，且位于抛物线对称轴
右侧，作PH⊥对称轴，垂足为H，若△DPH与△AOB相
似，求点P的坐标.
24.解：（1）由题意得： ，———————————————————（2分）
奉贤区
24．（本题满分12分，每小题满分各4分）
已知平面直角坐标系 （如图8），抛物线 与 轴交于点A、B（点A在点B左侧），与 轴交于点C，顶点为D，对称轴
为直线，过点C作直线的垂线，垂足为点E，联结DC、BC．
（1）当点C（0，3）时，
①求这条抛物线的表达式和顶点坐标；
②求证：∠DCE=∠BCE；
24.解：（1）∵直线 的经过点
∴ ……………………1分
∴ ………………………………1分
∵直线 的经过点
∴ ……………………1分
∴ …………………………………………1分
（2）由可知点 的坐标为
∵抛物线 经过点 、
∴
∴ ，
∴抛物线 的表达式为 …………………1分
∴抛物线 的顶点坐标为 ……………1分

2019年上海市虹口区中考数学二模试卷一、选择题：（本大题共6题，每题4分，满分24分）1.计算(a3)2的结果是( )A. a5B. a6C. a8D. a9【答案】B【解析】试题分析：（a3）2=a6，故选B．考点：幂的乘方与积的乘方．=的解为（ ）2.3A. x＝4B. x＝7C. x＝8D. x＝10．【答案】D【解析】【分析】将等式两边同时平方得到一元一次方程x﹣1＝9，解方程并检验即可解题.【详解】将方程两边平方得x﹣1＝9解得：x＝10经检验：x＝10是原无理方程的解故选：D．【点睛】本题考查了无理方程及一元一次方程的解法，解本题的关键是注意解出方程之后一定要进行检验，确保式子有意义.3.已知一次函数y＝（3﹣a）x+3，如果y随自变量x的增大而增大，那么a的取值范围为（ ）A. a＜3B. a＞3C. a＜﹣3D. a＞﹣3．【答案】A【解析】【分析】根据题意一次函数y随自变量x的增大而增大，即可得出3﹣a＞0，从而求得a的取值范围.【详解】∵一次函数y＝（3﹣a）x+3，函数值y随自变量x的增大而增大∴3﹣a＞0解得a＜3故选：A．【点睛】本题考查了一次函数图像增减性问题，解决此类问题只要牢固掌握一次函数k>0，函数图像递增，k<0函数图像递减，反过来亦适用.4.下列事件中，必然事件是（ ）A. 体育中考中，小明考了满分B. 经过有交通信号灯的路口，遇到红灯C. 抛掷两枚正方体骰子，点数和大于1D. 四边形的外角和为180度．【答案】C【解析】【分析】必然事件：，在一定的条件下重复进行试验时，有的事件在每次试验中必然会发生，这样的事件叫必然发生的事件随机事件：可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件，【详解】A、在体育中考中，小明考了满分是随机事件；B、经过有交通信号灯的路口，遇到红灯是随机事件；C、抛掷两枚正方体骰子，点数和大于1是必然事件；D、四边形的外角和为180度是不可能事件，故选：C．【点睛】本题考查了必然事件和随机事件的定义，解决本类题目的关键是掌握一定会发生的，和一定不会发生的都是必然事件.5.正六边形的半径与边心距之比为（ ）A. 1B. 1C. 2D. 2在【答案】D【解析】【分析】边心距：是指正多边形的每条边到其外接圆的圆心的距离,正六边形的边长就等于其外接圆的半径.它的边心倍..正多边形的边心距就是其内切圆的半径.【详解】∵正六边形的半径为R，∴边心距r，∴R：r＝12，故选：D．【点睛】本题主要考查了正多边形的半径与边心距之比，解决本题的关键是掌握边心距的求法.6.如图，在△ABC中，AB＝AC，BC＝4，tan B＝2，以AB的中点D为圆心，r为半径作⊙D，如果点B在⊙D内，点C在⊙D外，那么r可以取（ ）A. 2B. 3C. 4D. 5【答案】B【解析】【分析】已知等腰三角形ABC中tan B＝2，根据题意可求得△ABC中过顶点A的高AF的长度，进而求得AB的长度，以及得到；因为AF和CD均为中线，故交点为重心，通过重心到顶点的距离与重心到对边中点的距离之比为2：1，可求出CD，所以要满足B点在⊙D内，即满足r大于BD长度；要满足点C在⊙D外即r小于CD长度.【详解】如图，过点A作AF⊥BC于点F，连接CD交AF于点G，∵AB＝AC，BC＝4，∴BF ＝CF ＝2，∵tan B ＝2，∴2AFBF=，即AF ＝4，∴AB ∵D 为AB 的中点，∴BD G 是△ABC 的重心，∴GF ＝13AF ＝43，∴CG ，∴CD ＝32CG ，∵点B 在⊙D 内，点C 在⊙D 外，＜r ，故选：B ．【点睛】本题考查了等腰三角形的性质，三角函数求线段长度，三角形重心，点与圆的位置关系；解答本题的关键是发现BC 边上的高和CD 的交点是三角形的重心，重心到顶点的距离与重心到对边中点的距离之比为2：1，即可求出CD 的长度.二、填空题：（本大题共12题，每题4分，满分48分）7.计算：2﹣1＝_____．【答案】12．【解析】【分析】负整数指数幂：:任何不为零的数的 -n(n 为正整数)次幂等于这个数n 次幂的倒数.【详解】2﹣1＝111=22．故答案为12．【点睛】本题考查了负整数指数幂的运算，掌握运算法则即可解题.8.在数轴上，实数2_____侧．（填“左”、“右”）【答案】左【解析】【分析】2可得到2＜0，判断出2.【详解】根据题意可知：20∴2故填：左大小比较即可解题.9.不等式﹣2x ＞﹣4的正整数解为_____．【答案】x ＝1．【解析】【分析】将不等式两边同时除以-2，即可解题【详解】∵﹣2x ＞-4∴x ＜2∴正整数解为：x ＝1故答案为：x ＝1．【点睛】本题考查解不等式，掌握不等式的基本性质即可解题.10.如果关于x 的方程kx 2﹣6x +9＝0有两个相等的实数根，那么k 的值为_____．【答案】1．【解析】分析】根据题意方程有两个相等实根可知△=0，代入求值即可解题.【详解】∵关于x 的方程kx 2﹣6x +9＝0有两个相等的实数根，∴△＝（﹣6）2﹣4k ×9＝0且k ≠0，解得：k ＝1，故答案为：1．【点睛】本题考查了一元二次方程根的判别式，本题解题关键是根据题意得到根的情况，代值到判别式即可解题.11.已知反比例函数的图象经过点()1,3A ，那么这个反比例函数的解析式是________．【答案】3y x=【解析】【分析】把(1,3)代入函数y=kx中可先求出k 的值,那么就可求出函数解析式.【详解】解:由题意知,k=1´3=3.则反比例函数的解析式为:y=3x故答案为:y=3x.【点睛】本题考查了待定系数法求解反比例函数解析式,此为近几年中考的热点问题,同学们要熟练掌握.12.如果将抛物线y ＝2x 2向左平移3个单位，那么所得新抛物线的表达式为____．【答案】y ＝2（x +3）2．【解析】【分析】根据“左加右减”原则可知向左平移3各单位函数表达式变y ＝2（x +3）2.【详解】将抛物线y ＝2x 2向左平移3个单位，所得新抛物线的表达式为y ＝2（x +3）2，故答案为：y ＝2（x +3）2．【点睛】本题考查了二次函数图像的平移，本题的解题关键是牢记“上加下减，左加右减”的原则.【为13.一个不透明的袋中装有4个白球和若干个红球，这些球除颜色外其他都相同，摇匀后随机摸出一个球，如果摸到白球的概率为0.4，那么红球有____个．【答案】6．【解析】【分析】通过概率的求法：P（A）=满足条件的可能性/所有的可能性，代值44x+=0.4，即可求得红球数量.【详解】设红球有x个，根据题意得：44x+＝0.4解得：x＝6答：红球有6个；故答案为：6．【点睛】本题考查了概率的应用，掌握随机事件概率的求法即可解题.14.为了了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，共分成4组，频率分布表（不完整）如下表所示．如果次数在110次（含110次）以上为达标，那么估计该校初三毕业生一分钟跳绳次数的达标率约为__________．组别分组（含最小值，不含最大值）频数频率190～10030.06 2100～1101a3110～120240.48 4120～130b c【答案】92%【解析】【分析】根据第一组数据，频数÷频率=抽查的学生人数（样本容量），进而算出第四组的频数b，要求初三毕业生一分钟跳绳次数的达标率即为第三、四组频数和÷样本容量，即可求得答案.【详解】∵样本容量为：3÷0.06＝50，∴该校初三毕业生一分钟跳绳次数的达标率约为503150--×100%＝92%，故答案为：92%【点睛】本题考查了随机抽样调查中样本容量，频数以及频率的求法，牢固掌握即可解题.15.已知两圆外切，圆心距为7，其中一个圆的半径为3，那么另一个圆的半径长为___．【答案】4．【解析】【分析】根据题意，两圆外切，故圆心距为两圆半径和，已知一个圆半径为3，可求得另一圆的半径.【详解】∵两圆外切，圆心距为7，若其中一个圆的半径为3∴另一个圆的半径＝7﹣3＝4．故答案为：4．【点睛】本题考查了圆与圆位置关系，本题的解题关键是掌握当两圆外切时圆心距为两圆半径之和，两圆内切时，圆心距为大圆半径-小圆半径.16.如图，AD ∥BC ，BC ＝2AD ，AC 与BD 相交于点O ，如果AO a =uuu v v ，OD b =uuu r r，那么用a r 、b r 表示向量ABuuu r 是___．【答案】a r -2b r【解析】【分析】根据题意可知△ADO ∽△CBO ，根据相似三角形对应边成比例可得12AD OD BC OB ==，即OD=13DB ，通过转化AB AD DB =+uuu vuuu v uuu v =3AO OD DO ++uuu r uuu ruuur =2a b -rr【详解】∵AD ∥BC ，∴△ADO ∽△CBO ，的∴12AD OD BC OB == ，∴AB AD DB =+uuu v uuu v uuu v ＝3AO OD DO++uuu r uuu r uuur ＝3a b b +-r r r＝2a b -rr，故答案为：2a b -r r．【点睛】本题考查了平面向量的相关计算，解决本题的关键是将要求的进行转化为与已知向量相关的两条线段.17.我们知道，四边形不具有稳定性，容易变形．一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把αcos 1的值叫做这个平行四边形的变形度．如图，矩形ABCD 的面积为5，如果变形后的平行四边形A 1B 1C 1D 1的面积为3，那么这个平行四边形的变形度为___．【答案】54．【解析】【分析】根据变形前后底边不变，可根据面积算的变形后的平行四边形的高.根据题意，变形度即为求∠B 1的余弦，及转化为求B 1D 的长度，利用勾股定理可求得B 1D ，最终求得1cos α.【详解】过A 1作A 1D ⊥B 1C 1，设矩形的长和宽分别为a ，b ，变形后的平行四边形的高为h ，∴ab ＝5，3＝ah ，∴b ＝5a ，h ＝3a，∴B 1D 4a=，∴14551()cos 4a a α=¸¸=故答案为：54．【点睛】本题考查了平行四边形与矩形的性质，勾股定理，三角函数的求法，解决本题的关键即为求变形后平行四边形的高，即可解题.18.如图，在矩形ABCD 中，AB ＝6，点E 在边AD 上且AE ＝4，点F 是边BC 上的一个动点，将四边形ABFE 沿EF 翻折，A 、B 的对应点A 1、B 1与点C 在同一直线上，A 1B 1与边AD 交于点G ，如果DG ＝3，那么BF 的长为____．【答案】8-.【解析】【分析】根据题意可得到△CDG ∽△A'EG ，利用对应边成比例可求得A'G 、B'G 的长，进而可求得CG'、CB'，再利用△CDG ∽△CFB'，根据比例关系''CB GDB F CD=代值求得B ’F 即BF 的长度.详解】∵△CDG ∽△EA'G ，A'E ＝4∴A'G ＝2∴B'G ＝4由勾股定理可知CG'＝则CB'＝-4由△CDG ∽△CFB'设BF ＝x''CB GDB F CD=36【解得x＝8-故答案为8-【点睛】本题考查了图形的三大变化之轴对称，解答本类题的关键是找到轴对称前后相等的边和角，可进一步得到全等三角形或相似三角形，进而解题.三、解答题（本大题共7题，满分78分）19.先化简，再求值：35(2)242mmm m-¸+---，m﹣3．【答案】【解析】【分析】根据题意将括号部分进行通分整理，再利用除法法则转化为乘法进行运算，进而约分化简即可，最后代值算的结果.【详解】解：原式＝(3)(3)(3) 2(2)2m m mm m--+-¸--＝(3)22(2)(3)(3) m mm m m---´-+-＝12(3)m-+当m﹣3时，原式＝12(3)m-+=．【点睛】本题考查了分式的化简求值，掌握相关的运算法则即可解题.20.解方程组：22560312x xy yx yì--=í-=î①②【答案】11244x y =ìí=î，2233x y =ìí=-î.【解析】【分析】将①式进行因式分解的（x ﹣6y ）（x+y ）=0，故将式子拆分为两个式子与②式组成两个二元一次方程组进行求解，求得的两组解即为原方程组的解.【详解】由①得，x ﹣6y ＝0或x+y ＝0，将它们与方程②分别组成方程组，得：60312x y x y -=ìí-=î或0312x y x y +=ìí-=î分别解这两个方程组，得原方程组的解为11244x y =ìí=î或2233x y =ìí=-î．【点睛】此题本质考查二元一次方程组的运算，解本题的关键是将①式化为两个二元一次方程进行计算即可.21.如图，在锐角△ABC 中，小明进行了如下的尺规作图：①分别以点A 、B 为圆心，以大于12AB 的长为半径作弧，两弧分别相交于点P 、Q ；②作直线PQ 分别交边AB 、BC 于点E 、D ．（1）小明所求作的直线DE 是线段AB 的 ；（2）联结AD ，AD ＝7，sin ∠DAC ＝17，BC ＝9，求AC 的长．【答案】（1）线段AB 的垂直平分线（或中垂线）；（2）AC ＝．【解析】【分析】（1）垂直平分线：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（2）根据题意垂直平分线定理可得AD＝BD，得到CD＝2，又因为已知sin∠DAC=17，故可过点D作AC垂线，求得DF=1，利用勾股定理可求得AF，CF，即可求出AC长.【详解】（1）小明所求作的直线DE是线段AB的垂直平分线（或中垂线）；故答案为线段AB的垂直平分线（或中垂线）；（2）过点D作DF⊥AC，垂足为点F，如图，∵DE是线段AB的垂直平分线，∴AD＝BD＝7∴CD＝BC﹣BD＝2，在Rt△ADF中，∵sin∠DAC＝17 DFAD=，∴DF＝1，在Rt△ADF中，AF=，在Rt△CDF中，CF=，∴AC＝AF+CF＝=．【点睛】本题考查了垂直平分线的尺规作图方法，三角函数和勾股定理求线段长度，解本题的关键是充分利用中垂线，将已知条件与未知条件结合起来解题.22.甲、乙两组同时加工某种零件，甲组每小时加工80件，乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，部分数据如下表所示．x（小时）246y（件）50150250（1）求y与x之间的函数关系式；（2）甲、乙两组同时生产，加工的零件合在一起装箱，每满340件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？【答案】（1）y＝50x﹣50；（2）经过3小时恰好装满第1箱．【解析】【分析】（1）根据已知条件乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，利用待定系数法代入两对x、y值即可求函数解析式；（2）根据题意甲生产零件+乙生产零件=340件（1箱），时间相同，故设时间为x小时恰好装满第1箱可列式80x+50x﹣50＝340，解得的x即为所求.【详解】（1）设y与x之间的函数关系式为y＝kx+b（k≠0）把（2，50）（4，150）代入，得50=21504k bk b+ìí=+î解得5050kb=ìí=-î∴y与x之间的函数关系式为y＝50x﹣50；（2）设经过x小时恰好装满第1箱，根据题意得80x+50x﹣50＝340，∴x＝3，答：经过3小时恰好装满第1箱．【点睛】本题考查了一次函数的应用，解本题的关键为乙装箱的数量可用时间表示，明确这个隐藏条件即可解题.23.如图，在□ABCD中，AC与BD相交于点O，过点B作BE∥AC，联结OE交BC于点F，点F为BC的中点．（1）求证：四边形AOEB是平行四边形；（2）如果∠OBC＝∠E，求证：BO•OC＝AB•FC．【答案】（1）见解析；（2）见解析.【解析】【分析】（1）根据BE∥AC，△COF∽△BEF，又因为F为BC的中点可得CF=BF，所以BE=OC=OA，结合BE∥AC，即可证得AOEB是平行四边形.（2）根据题意可证得△COB∽△CBA，即BO BCAB AC=，在依据AC＝2OC，BC＝2FC，可得BO FCAB OC=，即可证得BO•OC＝AB•FC 【详解】（1）∵BE∥AC，∴△COF∽△BEF∴OC CF BE BF=∵点F为BC的中点，∴CF＝BF，∴OC＝BE∵四边形ABCD是平行四边形，∴AO＝CO∴AO＝BE∵BE∥AC，∴四边形AOEB是平行四边形（2）∵四边形AOEB是平行四边形，∴∠BAO＝∠E∵∠OBC＝∠E，∴∠BAO＝∠OBC∵∠ACB＝∠BCO，∴△COB∽△CBA∴BO BC AB AC=∵四边形ABCD是平行四边形，∴AC＝2OC∵点F为BC的中点，∴BC＝2FC∴BO FC AB OC=即BO•OC ＝AB•FC.【点睛】本题考查了平行四边形性质与判定的综合应用，本题的关键是通过平行得到几组相似三角形来解题.24.如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx +8与x 轴相交于点A （﹣2，0）和点B （4，0），与y 轴相交于点C ，顶点为点P ．点D （0，4）在OC 上，联结BC 、BD ．（1）求抛物线的表达式并直接写出点P 的坐标；（2）点E 为第一象限内抛物线上一点，如果△COE 与△BCD 的面积相等，求点E 的坐标；（3）点Q 在抛物线对称轴上，如果△BCD ∽△CPQ ，求点Q 的坐标．【答案】（1）点P 的坐标为（1，9）；（2）点E 的坐标为（2，8）；（3）点Q 的坐标为（1，11）或（1，10）．【解析】【分析】（1）通过待定系数法代入A 、B 坐标即可求得解析式；（2）根据解析式可求得点C 坐标（0，8），根据点E 为第一象限内抛物线上一点设点E （（x ，﹣x 2+2x+8）再根据S △COE ＝S △BCD ，可求得E 点坐标.（3）根据点B 、D 的坐标可得到∠BDC ＝135°，要满足△BCD ∽△CPQ ，∠CPQ=135°或者∠PCQ=135°，通过点C 、P 的坐标可得，∠PCM ＝45°，所以∠MCQ=90°，Q 在对称轴上，此情况不成立，所以要满足△BCD ∽△CPQ ，仅∠CPQ=135°，即Q 在P 点上方，可分两类讨论，CP PQ CD DB =或CP PQ BD DC=代值即可求出Q 点坐标.【详解】（1）将点A （﹣2，0），B （4，0）代入y ＝ax 2+bx+8，得：428016480a b a b -+=ìí++=î解得：12ab=-ìí=î，∴抛物线的表达式为y＝﹣x2+2x+8．∵y＝﹣x2+2x+8＝﹣（x﹣1）2+9，∴点P的坐标为（1，9）．（2）当x＝0时，y＝﹣x2+2x+8＝8，∴点C的坐标为（0，8）．设点E的坐标为（x，﹣x2+2x+8）（0＜x＜4），∵S△COE＝S△BCD，∴12×8•x＝12×4×4，解得：x＝2，∴点E的坐标为（2，8）．（3）过点C作CM∥x轴，交抛物线对称轴于点M，如图所示．∵点B（4，0），点D（0，4），∴OB＝OD＝4，∴∠ODB＝45°，BD＝，∴∠BDC＝135°．∵点C（0，8），点P（1，9），∴点M的坐标为（1，8），∴CM＝PM＝1，∴∠CPM＝45°，CP，∴点Q在抛物线对称轴上且在点P的上方，∴∠CPQ＝∠CDB＝135°．∵△BCD∽△CPQ，∴CP PQCD DB=或CP PQBD DC=．①当CP PQCD DB==，解得：PQ＝2，∴点Q 的坐标为（1，11）；②当CP PQ BD DC =4PQ =，解得：PQ ＝1，∴点Q 的坐标为（1，10）．综上所述，点Q 的坐标为（1，11）或（1，10）．【点睛】本题前两问考查了二次函数常考的求解析式和点的坐标，最后一问考查了二次函数与相似三角形的结合，解答本类型题重点是发现成相似的两个三角形有什么特点，是否有隐藏条件已知角度的对应或者边的对应.25.如图，AD ∥BC ，∠ABC ＝90°，AD ＝3，AB ＝4，点P 为射线BC 上一动点，以P 为圆心，BP 长为半径作⊙P ，交射线BC 于点Q ，联结BD 、AQ 相交于点G ，⊙P 与线段BD 、AQ 分别相交于点E 、F ．（1）如果BE ＝FQ ，求⊙P 的半径；（2）设BP ＝x ，FQ ＝y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结PE 、PF ，如果四边形EGFP 是梯形，求BE 的长．【答案】（1）⊙P 的半径为32；（2）x 的取值范围为2506x <£；（3）BE ＝710或65．【解析】【分析】（1）由题意BE＝FQ可得∠BPE＝∠FPQ，进而可得∠EBP＝∠FQP.又AD∥BC，故∠ADB＝∠EBP，即∠FQP＝∠ADB，故两角的正切值相等即可求出半径.（2）要求y关于x的函数关系式即可通过过P点做垂线PM，将QM用含x的式子表示，利用QM＝PQcos∠AQB，而FQ=2QM，即y=D点相交时，x最大，可求出x的取值范围；（3）根据题意四边形EGFP是梯形，由于P点是动点所以产生两种情况，当GF∥EP时和GE∥FP时，故应进行分类讨论.①当GF∥EP时，可发现PE为△BGQ的中点，根据线段关系可求得BP的长度，因为△BGQ和△DGA相似，故有BG QGBD AQ=，可求得BG＝75，所以BE=12BG.②当GE∥FP时，过点P作PN⊥BG ，跟①同理，可求得BE＝2BN.【详解】（1）∵BE＝FQ，∴∠BPE＝∠FPQ，∵PE＝PB，∴∠EBP＝12（180°﹣∠EPB），同理∠FQP＝12（180°﹣∠FPQ），∴∠EBP＝∠FQP，∵AD∥BC，∴∠ADB＝∠EBP，∴∠FQP＝∠ADB，∴tan∠FQP＝tan∠ADB＝43，设⊙P的半径为r，则tan∠FQP＝42 ABBQ r=，∴44 32r =，解得：r＝32，∴⊙P的半径为32；（2）过点P 作PM ⊥FQ ，垂足为点M ，如图1所示：在Rt △ABQ 中，cos ∠AQB ＝BQ AQ ===在Rt △PQM 中，QM ＝PQcos ∠AQB ，∵PM ⊥FQ ，PF ＝PQ ，∴FQ ＝2QM∴y =当圆与D 点相交时，x 最大，作DH ⊥BC 于H ，如图2所示：则PD ＝PB ＝x ，DH ＝AB ＝4，BH ＝AD ＝3，则PH ＝BP ﹣BH ＝x ﹣3，在Rt △PDH 中，由勾股定理得：42+（x ﹣3）2＝x 2，解得：x ＝256，∴x 的取值范围为：0＜x ≤256；（3）设BP ＝x ，分两种情况：①EP ∥AQ 时，∴∠BEP＝∠BGQ，∵PB＝PE，∴∠PBE＝∠BEP，∴∠BGQ＝∠PBE，∴QG＝QB＝2x，同理：AG＝AD＝3，在Rt△ABQ中，由勾股定理得：42+（2x）2＝（3+2x）2，解得：x＝7 12，∴QG＝QB＝2x＝76，∵EP∥AQ，PB＝PQ，∴BE＝EG，∵AD∥BC，∴BG QG BD AQ=，即767 536 BG=+，解得：BG＝75，∴BE＝12BG＝710；②PF∥BD时，同①得：BG＝BQ＝2x，DG＝AD＝3，在Rt△ABD中，由勾股定理得：42+32＝（3+2x）2，解得：x＝1或x＝﹣4（舍去），∴BQ＝2，∴BP＝1，作PN⊥BG于N，则BE＝2BN，如图3所示：∵AD∥BC，∴∠PBN＝∠ADB，∴cos∠PBN＝cos∠ADB＝35，即BNBP＝35，∴BN＝3 5，∴BE＝2BN＝65；综上所述，BE=710或65．【点睛】本题考查了圆与函数，四边形的综合，已知条件较多，存在不确定的动点情况，难度较大，解决本类题目的关键因素有①找到动点问题的临界点或特殊位置来解题；②对已知条件充分把握和利用，准确进行分类讨论.。

2019年上海市金山区中考数学二模试卷一.选择题（每小题4分，共24分）1．（4分）下列实数中，是有理数的是（）A．πB．C．D．2．（4分）不等式组的解集是（）A．x＞﹣3B．x＜﹣3C．x＞1D．x＜13．（4分）用换元法解方程：﹣2＝0时，如果设＝y，那么将原方程变形后表示为一元二次方程一般形式的是（）A．y﹣﹣2＝0B．y﹣﹣1＝0C．y2﹣2y﹣1＝0D．y2﹣y﹣2＝04．（4分）数据2、1、0、﹣2、0、﹣1的中位数与众数分别是（）A．0和0B．﹣1和0C．0和1D．0和25．（4分）下列四边形中，是中心对称而不是轴对称图形的是（）A．平行四边形B．矩形C．菱形D．正方形6．（4分）已知⊙O1与⊙O2内切于点A，⊙O1的半径等于5，O1O2＝3，那么O2A的长等于（）A．2B．3C．8D．2或8二．填空题（每小题4分，共48分）7．（4分）计算：a2÷a﹣2＝．8．（4分）因式分解：a3+2a＝．9．（4分）方程＝2的解是．10．（4分）化简：（b≥0）的结果是．11．（4分）已知反比例函数的图象在第二、四象限内，那么k的取值范围是．12．（4分）已知关于x的一元二次方程x2+x+m＝0的一个根是x＝1，那么这个方程的另一个根是．13．（4分）从方程x2＝0，＝﹣1，x2﹣2x+4＝0中，任选一个方程，选出的这个方程无实数解的概率为．14．（4分）100克鱼肉中蛋白质的含量如图表，每100克草鱼、鲤鱼、花鲢鱼鱼肉的平均蛋白质含量为16.8克，那么100克鲤鱼肉的蛋白质含量是克．15．（4分）在△ABC中，AB＝AC，请你再添加一个条件使得△ABC成为等边三角形，这个条件可以是（只要写出一个即可）．16．（4分）如图，在▱ABCD中，E是边BC上的点，AE交BD于点F，＝，＝，＝，那么＝（用、表示）．17．（4分）如图，飞机于空中A处观测其正前方地面控制点C的俯角为30°，若飞机航向不变，继续向前飞行1000米至B处时，观测到其正前方地面控制点C的俯角为45°，那么该飞机与地面的高度是米（保留根号）．18．（4分）一个正多边形的对称轴共有10条，且该正多边形的半径等于4，那么该正多边形的边长等于．三．解答题（19-22题，每题10分，23-24题，每题12分，25题14分，共78分）19．（10分）计算：（）0（）+（）﹣1．20．（10分）解方程：＝1．21．（10分）已知：如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，CE＝CB，CD＝5，sin．求：（1）BC的长．（2）tan E的值．22．（10分）某演唱会购买门票的方式有两种．方式一：若单位赞助广告费10万元，则该单位所购门票的价格为每张0.02万元；方式二：如图所示．设购买门票x张，总费用为y万元，方式一中：总费用＝广告赞助费+门票费．（1）求方式一中y与x的函数关系式．（2）若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张，且乙单位购买超过100张，两单位共花费27.2万元，求甲、乙两单位各购买门票多少张？23．（12分）已知：如图，菱形ABCD的对角线AC与BD相交于点O，若∠CAD＝∠DBC．（1）求证：四边形ABCD是正方形．（2）E是OB上一点，DH⊥CE，垂足为H，DH与OC相交于点F，求证：OE＝OF．24．（12分）已知：抛物线y＝﹣x2+bx+c，经过点A（﹣1，﹣2），B（0，1）．（1）求抛物线的关系式及顶点P的坐标．（2）若点B′与点B关于x轴对称，把（1）中的抛物线向左平移m个单位，平移后的抛物线经过点B′，设此时抛物线顶点为点P′．①求∠P′BB′的大小．②把线段P′B′以点B′为旋转中心顺时针旋转120°，点P′落在点M处，设点N在（1）中的抛物线上，当△MNB′的面积等于6时，求点N的坐标．25．（14分）如图，在Rt△ABC中，∠C＝90°，AC＝16cm，AB＝20cm，动点D由点C向点A以每秒1cm速度在边AC上运动，动点E由点C向点B以每秒cm速度在边BC上运动，若点D，点E从点C同时出发，运动t 秒（t＞0），联结DE．（1）求证：△DCE∽△BCA．（2）设经过点D、C、E三点的圆为⊙P．①当⊙P与边AB相切时，求t的值．②在点D、点E运动过程中，若⊙P与边AB交于点F、G（点F在点G左侧），联结CP并延长CP交边AB于点M，当△PFM与△CDE相似时，求t的值．2019年上海市金山区中考数学二模试卷参考答案与试题解析一.选择题（每小题4分，共24分）1．【解答】解：有理数是整数和分数的集合，故选：D．2．【解答】解：解不等式﹣x＞3，得：x＜﹣3，解不等式x﹣1＜0，得：x＜1，则不等式组的解集为x＜﹣3．故选：B．3．【解答】解：设＝y，那么将原方程可化为：，去分得，y2﹣1﹣2y＝0，整理得y2﹣2y﹣1＝0故选：C．4．【解答】解：在这一组数据中2是出现次数最多的，故众数是0；将这组数据已从小到大的顺序排列，处于中间位置的数是0，那么由中位数的定义可知，这组数据的中位数是0；故选：A．5．【解答】解：A、平行四边形是中心对称图形，不是轴对称图形，故选项正确；B、矩形既是轴对称图形，又是中心对称图形，故选项错误；C、菱形既是轴对称图形，又是中心对称图形，故选项错误；D、正方形，矩形既是轴对称图形，又是中心对称图形，故选项错误．故选：A．6．【解答】解：设⊙O2的半径为r，∵⊙O1与⊙O2内切于点A，∴O2A＝r，O1A＝5，∴r﹣5＝3或5﹣r＝3，∴r＝8或r＝2，即O2A的长等于2或8．故选：D．二．填空题（每小题4分，共48分）7．【解答】解：a2÷a﹣2＝a2﹣（﹣2）＝a4，故答案为：a4．8．【解答】解：a3+2a＝a（a2+2），故答案为a（a2+2）．9．【解答】解：∵＝2，∴3x﹣2＝4，∴x＝2，当x＝2时，左边＝，右边＝2，∵左边＝右边，∴方程＝2的解是：x＝2．故答案为：x＝2．10．【解答】解：＝，故答案为：．11．【解答】解：由题意可得k﹣1＜0，则k＜1．故答案为：k＜1．12．【解答】解：设关于x的一元二次方程x2+x+m＝0的另一个实数根是α，∵关于x的一元二次方程x2+x+m＝0的一个实数根为1，∴α+1＝﹣1，∴α＝﹣2．故答案为﹣2．13．【解答】解：∵＝﹣1，x2﹣2x+4＝0无实数解，∴无实数解的概率为，故答案为：．14．【解答】解：∵每100克草鱼、鲤鱼、花鲢鱼鱼肉的平均蛋白质含量为16.8克，∴设100克鲤鱼肉的蛋白质含量是x克，由题意可得：（17.9+15.3+x）＝16.8，解得：x＝17.2．故答案为：17.2．15．【解答】解：在△ABC中，AB＝AC，再添加∠A＝60°可得△ABC是等边三角形，故答案为：∠A＝60°．16．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AC＝BC，∵BE：BC＝2：3，∴BE：AD＝2：3，∴AD＝BE，∵＝，∴＝，∵＝+，∴＝﹣，故答案为﹣．17．【解答】解：作CD⊥AB于点D．∴∠BDC＝90°，∵∠DBC＝45°，∴BD＝CD，∵∠DAC＝30°，∴tan30°＝＝＝＝，解得CD＝BD＝500+500（米）．答：飞机再向前飞行（500+500）米与地面控制点C的距离最近．故答案为：（500+500）．18．【解答】解：∵正多边形的对称轴共有10条，∴这个正多边形是正十边形，设这个正十边形的中心为O，则OA＝OB＝4，∠AOB＝＝36°，∵OA＝OB，∴∠OAB＝∠B＝72°，作AC平分∠OAB交OB于C，则∠OAC＝∠O，∠ACB＝∠B，∴OC＝CA＝AB，△ABC∽△OAB，∴＝，即AB2＝4×（4﹣AB），解得，AB1＝2﹣2，AB2＝﹣2﹣2（舍去），∴AB＝2﹣2，故答案为：2﹣2．三．解答题（19-22题，每题10分，23-24题，每题12分，25题14分，共78分）19．【解答】解：原式＝1++2﹣+＝1++2﹣+＝3+；20．【解答】解：去分母，得x+2﹣2x＝x2﹣4，整理，得x2+x﹣6＝0，∴（x+3）（x﹣2）＝0，∴x+3＝0或x﹣2＝0，∴x＝﹣3或x＝2，检验：x＝2时，分母x﹣2＝0，因此x＝2是原分式方程的增根，x＝﹣3时，左边＝1＝右边所以原方程的解为x＝﹣3．21．【解答】解：（1）∵在Rt△ABC中，∠ACB＝90，D是边AB的中点；∴CD＝AB，∵CD＝5，∴AB＝10，∵sin∠ABC＝＝，∴AC＝6∴；（2）作EH⊥BC，垂足为H，∴∠EHC＝∠EHB＝90°∵D是边AB的中点，∴BD＝CD＝AB，∠DCB＝∠ABC，∵∠ACB＝90°，∴∠EHC＝∠ACB，∴△EHC∽△ACB，∴由BC＝8，CE＝CB得CE＝8，∠CBE＝∠CEB，∴解得EH＝，CH＝，BH＝8﹣＝∴tan∠CBE＝＝3，即tan E＝3．22．【解答】解：（1）方案一：单位赞助广告费10万元，该单位所购门票的价格为每张0.02万元，则y＝10+0.02x；（2）方案二：当x＞100时，设解析式为y＝kx+b．将（100，10），（200，16）代入，得，解得，所以y＝0.06x+4．设乙单位购买了a张门票，则甲单位购买了（400﹣a）张门票，根据题意得0.06a+4+[10+0.02（400﹣a）]＝27.2，解得，a＝130，∴400﹣a＝270，答：甲、乙两单位购买门票分别为270张和130张．23．【解答】（1）证明：∵四边形ABCD是菱形，∴AD∥BC，∠BAD＝2∠DAC，∠ABC＝2∠DBC，∴∠BAD+∠ABC＝180°，∵∠CAD＝∠DBC，∴∠BAD＝∠ABC，∴2∠BAD＝180°，∴∠BAD＝90°，∴四边形ABCD是正方形；（2）证明：∵四边形ABCD是正方形，∴AC⊥BD，AC＝BD，CO＝AC，DO＝BO，∴∠COB＝∠DOC＝90°，CO＝DO，∵DH⊥CE，垂足为H，∴∠DHE＝90°，∠EDH+∠DEH＝90°，∵∠ECO+∠DEH＝90°，∴∠ECO＝∠EDH，在△ECO和△FDO中，，∴△ECO≌△FDO（ASA），∴OE＝OF．24．【解答】解：（1）把点A、B坐标代入抛物线表达式得：，解得：，则抛物线的表达式为：y＝﹣x2+2x+1＝﹣（x﹣1）2+2，故顶点P的坐标为（1，2）；（2）①设抛物线平移后为y＝﹣（x﹣1+m）2+2，代入点B′（0，﹣1）得：﹣1＝﹣（m﹣1）2+2，解得：m＝1（舍去负值），则y＝﹣（x+）2+2，则顶点P′（﹣，2），连结P′B、P′B′，作P′H⊥y轴交于点H，则：P′H＝，HB＝1，BP′＝＝2，∵tan∠P′BH＝＝，∴∠P′BH＝60°，∴∠P′BB′＝180°﹣60°＝120°，②∵BB′＝2，P′B＝2，即BB′＝P′B，∴∠BP′B′＝∠P′B′B＝30°；∵线段P′B′围绕B′旋转120°，点P′落在M处，∴∠OB′M＝90°，B′M＝B′P′，∴MB′∥x轴，MB′＝B′P′＝2，设：△MNB′在MB′边上的高为h，则S△MNB′＝×B′M•h＝6，解得：h＝6，设：N（a，﹣7）或（a，5）分别代入y＝﹣x2+2x+1得：﹣7＝﹣a2+2a+1，解得：a＝4或﹣2；5＝﹣a2+2a+1，△＝b2﹣4ac＜0，故方程无实数根，故：a＝4或﹣2，即点N（4，﹣7）或（﹣2，﹣7）．25．【解答】（1）证明：由题意得：CD＝t，CE＝t，由勾股定理得，BC＝＝12，＝，＝＝，∴＝，又∠C＝∠C，∴△DCE∽△BCA；（2）①连结CP并延长CP交AB于点H，∵∠ACB＝90°，∴DE是⊙P的直径，即P为DE中点，∴CP＝DP＝PE＝DE，∴∠PCE＝∠PEC，∵△DCE∽△BCA，∴∠CDE＝∠B，∵∠CDE+∠CED＝90°，∴∠B+∠HCB＝90°，即CH⊥AB，∵⊙P与边AB相切，∴点H为切点，CH为⊙P的直径，∵sin A＝＝，∴＝，解得，CH＝，∴DE＝，sin A＝sin∠CED＝＝，即＝，解得，CD＝，∴t＝；②由题意得，0＜t≤12，即0＜t≤9，∵CD＝t，CE＝t，∴DE＝＝t，由①得，CM＝，CP＝DE＝t，CM⊥AB，∴PM＝﹣t，PF＝CP＝t，∠PMF＝90°，当△FMP∽△DCE时，＝，即＝，解得，t＝；当△PMF∽△DCE时，＝，即＝，解得，t＝；∴综上所述：当△PFM与△CDE相似时．t＝或t＝．。