2015年上海中考数学二模24题整理

2015 年浦东新区中考二模试题数 学 卷 2015.4（满分150分，考试时间100分钟）考生注意：1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．】 1．化简32(3)x 所得的结果是（ ）．A ．99x B ．69x C ．66x D ．96x 2．若b a <，则下列各式中一定成立的是（ ） A ．33a b ->- B ．33a b< C ．33a b -<- D ．ac bc < 3．在平面直角坐标系中，下列直线中与直线23y x =-平行的是（ ）A ．3y x =-B ．23y x =-+C ．23y x =+D ．32y x =- 4．在平面直角坐标系中，将二次函数22x y =的图象向左平移3个单位，所得图象的解析式为（ ）A ．22(3)y x =+B ．22(3)y x =-C ．223y x =+D ．223y x =- 5．在正多边形中，外角和等于内角和的是（ ） A ．正六边形 B ．正五边形 C ．正四边形 D ．正三边形 6．已知半径分别是3和5的两个圆没有公共点，那么这两个圆的圆心距d 的取值范围是（ ） A ．8d > B ． 2d > C ．02d ≤< D ． 8d >或02d ≤<二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置】7．因式分解：22x x -= ． 8．如果方程()132x a -=的根是3x =，那么a = ．9．请你写一个大于2且小于3的无理数 ． 10．函数1()1f x x=-的定义域是 ． 11． ()322a b a --= ．12．在Rt △ABC 中，∠C =90°，13sinA =，BC =6，那么AB = ． 13．在一个不透明的布袋中装有2个白球和n 个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，摸到黄球的概率是45，则n =__________． 14．如图1，已知a ∥b ，140∠=，那么2∠的度数等于 ．15．两个相似三角形对应边上高的比是1∶4 ，那么它们的面积比是 ．16．在Rt △ABC 中，∠C =90°，∠A =30°，BC =6，以点C 为圆心的⊙C 与AB 相切，那么⊙C 的半径等于 ．17．在四边形ABCD 中，点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点，如果四边形EFGH 为菱形，那么四边形ABCD 可能是 （只要写一种）． 18．如图2，在△ABC 中，AD 是BC 上的中线，BC =4，∠ADC =30°，把△ADC 沿AD 所在直线翻折后 点C 落在点C ′ 的位置，那么点D 到直线BC ′ 的距离是 ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分） 解分式方程：212111xx x -=-- 20．（本题满分10分）一块长方形绿地的面积为2400平方米，并且长比宽多20米，那么这块绿地的长和宽分别为多少米？1 2a b图1C / BD CA图221．（本题满分10分，每小题满分各5分） 如图3，在△ABC 中，sin ∠B =45，∠C =30°，AB =10。

黄浦区2015年九年级学业考试数学试卷一. 选择题1. 下列分数中，可以化为有限小数的是（ ） A.115； B. 118； C. 315； D. 318； 2. 下列二次根式中最简根式是（ ）A.B. C. D.3. 下表是某地今年春节放假七天最低气温（C ︒）的统计结果A. 4，4；B. 4，5；C. 6，5；D. 6，6；4. 将抛物线2y x =向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（ ）A. 2(1)2y x =-+；B. 2(2)1y x =-+；C. 2(1)2y x =+-；D. 2(2)1y x =+-；5. 如果两圆的半径长分别为6与2，圆心距为4，那么这两个圆的位置关系是（ ） A. 内含； B. 内切； C. 外切； D. 相交；6. 下列命题中真命题是（ ）A. 对角线互相垂直的四边形是矩形；B. 对角线相等的四边形是矩形；C. 四条边都相等的四边形是矩形；D. 四个内角都相等的四边形是矩形；二. 填空题7. 计算：22()a = ；8. 因式分解：2288x x -+= ； 9. 计算：111x x x +=+- ；10. 1x =-的根是 ；11. 如果抛物线2(2)3y a x x a =-+-的开口向上，那么a 的取值范围是 ； 12. 某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为 ；13. 将一枚质地均匀的硬币抛掷2次，硬币证明均朝上的概率是 ； 14. 如果梯形的下底长为7，中位线长为5，那么其上底长为 ；15. 已知AB 是O e 的弦，如果O e 的半径长为5，AB 长为4，那么圆心O 到弦AB 的距离是 ；16. 如图，在平行四边形ABCD 中，点M 是边CD 中点，点N 是边BC 上的点，且12CN BN =，设AB a =uu u r r ，BC b =uu u r r ，那么MN uuu r 可用a r 、b r表示为 ；17. 如图，△ABC 是等边三角形，若点A 绕点C 顺时针旋转30°至点A '，联结A B '，则ABA '∠度数是 ；18. 如图，点P 是以r 为半径的圆O 外一点，点P '在线段OP 上，若满足2OP OP r '⋅=，则称点P '是点P 关于圆O 的反演点，如图，在Rt △ABO 中，90B ∠=︒，2AB =，4BO =，圆O 的半径为2，如果点A '、B '分别是点A 、B 关于圆O 的反演点，那么A B ''的长是 ；三. 解答题19.计算：1012481)|1-+-+；20. 解方程组：22221x y x y ⎧-=-⎨-=⎩①②；21. 温度通常有两种表示方法：华氏度（单位：F ︒）与摄氏度（单位：C ︒），已知华氏度数y 与摄氏度数x 之间是一次函数关系，下表列出了部分华氏度与摄氏度之间的对应关系：（2）已知某天的最低气温是-5C ︒，求与之对应的华氏度数；22. 如图，在梯形ABCD 中，AD ∥BC ，AB ⊥BC ，已知2AD =，4cot 3ACB ∠=，梯形ABCD 的面积是9； （1）求AB 的长； （2）求tan ACD ∠的值；23. 如图，在正方形ABCD 中，点E 在对角线AC 上，点F 在边BC 上，联结BE 、DF ，DF 交对角线AC 于点G ，且DE DG =；（1）求证：AE CG =； （2）求证：BE ∥DF ；24. 如图，在平面直角坐标系xOy 中，已知点A 的坐标为(,3)a （其中4a >），射线OA 与反比例函数12y x =的图像交于点P ，点B 、C 分别在函数12y x=的图像上，且AB ∥x 轴，AC ∥y 轴；（1）当点P 横坐标为6，求直线AO 的表达式； （2）联结BO ，当AB BO =时，求点A 坐标； （3）联结BP 、CP ，试猜想：ABP ACP S S ∆∆的值是否随a 的变化而变化？如果不变，求出ABPACPSS ∆∆的值；如果变化，请说明理由；25. 如图，Rt △ABC 中，90C ∠=︒，30A ∠=︒，2BC =，CD 是斜边AB 上的高，点E 为边AC 上一点（点E 不与点A 、C 重合），联结DE ，作CF ⊥DE ，CF 与边AB 、线段DE 分别交于点F 、G ； （1）求线段CD 、AD 的长；（2）设CE x =，DF y =，求y 关于x 的函数解析式，并写出它的定义域； （3）联结EF ，当△EFG 与△CDG 相似时，求线段CE 的长；2015年黄浦区初三二模数学参考答案一. 选择题1. C ；2. C ；3. B ；4. D ；5. B ；6. D ； 二. 填空题7. 4a ； 8. 22(2)x -； 9. 2211x x +-； 10. 3x =； 11. 2a <； 12. 40%；13. 14； 14. 3； 15. ； 16. 1123a b - ； 17. 15︒； 18.三. 解答题19. 解：原式12131)11=+-=-+=； 20. 解：由②得：1x y =+，代入①得：22(1)22y y +-=-，即2230y y --=， ∴(1)(3)0y y +-=，∴11y =-，23y =，∴10x =，24x =， ∴方程组的解为01x y =⎧⎨=-⎩或43x y =⎧⎨=⎩；21. 解：设y kx b =+，代入(0,32)和(35,95)，即0323595b k b +=⎧⎨+=⎩，∴32b =，95k =，∴9325y x =+， 当5x =-时，93223y =-+=；22. 解：（1）Rt ABC 中，4cot 3BC ACB AB ∠==，设4BC k =，3AB k =， ∴11()(24)3922ABCD S AD BC AB k k =⋅+⋅=+⋅=，∴1k =或32k =-（舍），∴3AB =，4BC =，5AC =；（2）作DH AC ⊥，∵AD ∥BC ，∴DAH ACB ∠=∠，∴Rt ADH ∽Rt CAB ，∴25DH AD AH AB AC BC ===， ∴65DH =，85AH =，∴175CH AC AH =-=，∴6tan 17DH ACD CH ∠==； 23. 解：（1）∵DE DG =，∴DEG DGE ∠=∠，∴AED CGD ∠=∠， 又∵AD CD =，45DAC DCA ∠=∠=︒，∴△ADE ≌△CDG ， ∴AE CG =（2）∵BC CD =，CE CE =，45BCE DCE ∠=∠=︒， ∴△BCE ≌△DCE ，∴BEC DEC DGE ∠=∠=∠， ∴BE ∥DF ；24. 解：（1）当6x =时，2y =，∴(6,2)P ，设:OA l y kx =，代入(6,2)P 得13k =，∴1:3OA l y x =； （2）当3y =时，4x =，∴(4,3)B ，∵AB BO =， ∴54a =-，即9a =，∴(9,3)A （3）3:OA l y x a =，联立12y x =，得P ，作PM AB ⊥，PN AC ⊥，当x a =时，12y a =，即12(,)C a a，当3y =时，4x =，即(4,3)B ，∴1(4)(32ABP S a =-，112()2ACP S a a =-- ，∴3121ABP ACP a S S --== ； 25. 解：（1）CD =，3AD =；（2）∵90CDE BFC DCF ∠=∠=︒-∠，60ECD B ∠=∠=︒， ∴△CDE ∽△BFC ，∴CE CD BC BF =，即21x y =+，∴1y x =-，（2x ≤<（3）90EGF CGD ∠=∠=︒① △EGF ∽△DGC 时，GEF GDC ∠=∠，∴EF ∥DC ，∴CE DF AC AD =133y x -==，解得x = ② △EGF ∽△CGD 时，∴GEF GCD GDF ∠=∠=∠，∴EF DF =，又∵CF DE ⊥，∴EG DG =，∴CD CE =综上，CE =3；。

2015 年初三数学教学质量检测试卷（考试时间 100 分钟，满分 150 分）2015.4考生注意 :1．本试卷含三个大题，共 25 题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤 ．一、单项选择题 :（本大题共 6 题，每题 4 分，满分 24 分）1.将抛物线 y x 2向右平移 3个单位得到的抛物线表达式是 ( )A.y x 3 2 ； B. y x 32； C.y x 23 ； D. y x 23 .2.下列各式中，与3 是同类二次根式的是 ()A.3 1 ； B.6 ；C.9 ；D. 12.3. 一组数据 : 5,7,4,9,7的中位数和众数分别是 ( )A. 4,7 ；B. 7,7 ；C. 4,4 ；D. 4,5 .4. 用换元法解方程 :yy 2 3 5y，那么原方程可化为 ( )3y2 时，如果设 xy 2y 2 3A. 2x25x 2 0 ；B. x25x 1 0 ；ADC. 2x 25x 2 0 ；D. 2x 25x 1 0 .OE5. 在下列图形中，①等边三角形，②正方形，③正五边形，④正六边形.其中既是轴对称图形又是中心对称的图形有 ()A. 1个；B. 2个；C. 3个；D. 4个.B C第6题图6. 如图，在四边形 ABCD 中，∠ ABC=9 0°，对角线 AC 、BD 交于点 O ， AO=CO ，∠ AOD =∠ADO ， E 是 DC 边的中点 .下列结论中，错误的是 ()1AD ； B. OE11 1 A. OEOB ； C.； OE2OC ； D. OEBC .2 22二、填空题 : （本大题共 12 题，每题 4 分，满分 48 分）17. 计算:9 2 = ▲．初三数学 共 4 页 第1页8. 计算 :m3 n 2=▲．9.方程 2x 3 1 的解是▲．10.若关于 x 的二次方程x2ax a 3 0 有两个相等的实数根，则实数 a =▲．11.从数字 1,2,3,4中，任意取两个数字组成一个两位数，这个数是素数的概率是▲．12. 2015年 1月份，某区体委组织“迎新春长跑活动”，现将报名的男选手分成 : 青年组、中年组、老年组 .各组人数所占比例如图所示，已知青年组 120人，则中年组的人数是▲．青年老年60%20%中年？13.已知b ka ，如果a 2，b 6 ，那么实数 k =▲．第 12题图A 14.已知⊙O1和⊙O2的半径分别是5和 3，若O1O2 =2，则两圆的位置关系是▲．15.已知在离地面 30米的高楼窗台 A 处测得地面花坛中心标志物 C 的俯角为60°，那么这一标志物 C 离此栋楼房的地面距离BC 为▲米．16.已知线段 AB=10 ，P 是线段 AB 的黄金分割点 (AP﹥ PB)，则 AP= ▲． C B17.请阅读下列内容 :第 15 题图2我们在平面直角坐标系中画出抛物线y x 2 1和双曲线，如图yyx所示，利用两图像的交点个数和位置来确定方程x2 1 2 有一个正x 实数根，这种方法称为利用函数图像判断方程根的情况.请用图像法判断方程x 3 2 4 2 的根的情况▲ （填写根的个数及正负）．x18.如图，△ ABC≌△ DEF （点 A 、 B 分别与点 D、 E 对应）， AB=AC=5 ，BC=6，△ ABC 固定不动，△ DEF 运动，并满足点E在BC边从B向 C 移动（点 E 不与 B、 C 重合）， DE 始终经过点A，EF 与 AC 边交于点 M，当△ AEM 是等腰三角形时， BE= ▲.O x第17题图DAF三、解答题 : （本大题共7 题，满分78 分）M 19．（本题满分 10 分）BE C 2( m 1.5) 5, 第 18 题图解不等式组5 m m ，并将解集在数轴上表示出来.32初三数学共4页第2页20．（本题满分10 分）先化简，再求代数式的值a 2 2 a:a 2 a 1，其中 a 1 1 a21．（本题满分10 分）在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回甲地 .设汽车从甲地出发 x（ h）时，汽车与甲地的距离为 y（ km）， y 与 x 的关系如图所示 . 根据图像回答下列问题 :（ 1）汽车在乙地卸货停留（h）；（ 2）求汽车返回甲城时y 与 x 的函数解析式，并写出定义域；（ 3）求这辆汽车从甲地出发 4 h 时与甲地的距离.3 1.y（km）120O2 2.5 5x（ h ）第 21题图22．（本题满分10 分）如图， AD 是等腰△ ABC 底边上的高，且AD=4，sin B4. 若 E 是 AC 边上的点，且满5足 AE:EC=2:3，联结 DE ，求cot ADE 的值. AEB D C第22题图23．（本题满分12 分）如图，正方形 ABCD 中，点 E、F 分别在边BC、CD 上， AE=AF，AC 和 EF 交于点 O，延长 AC 至点 G，使得 AO=OG，联结 EG、 FG . A D（ 1）求证 : BE =DF ；（ 2）求证 :四边形 AEGF 是菱形 . FOBE CG第23题图初三数学共4页第3页24．（本题满分 12 分）如图，已知抛物线y x2 2tx t 2 2 的顶点A在第四象限，过点 A 作 AB⊥ y 轴于点 B，C 是线段 AB 上一点 (不与 A、B 重合 )，过点 C 作 CD ⊥ x 轴于点 D，并交抛物线于点P.（ 1）若点 C 的横坐标为1，且是线段AB 的中点，求点P 的坐标；（ 2）若直线 AP 交 y 轴负半轴于点 E，且 AC=CP，求四边形 OEPD 的面积 S 关于 t 的函数解析式，并写出定义域；（ 3）在（ 2）的条件下，当△ADE 的面积等于2S 时，求 t 的值 .yDOEPBC Ax第24题图25．（本题满分14 分）如图，已知矩形ABCD ，AB =12 cm，AD =10 cm ，⊙ O 与 AD、AB、BC 三边都相切，与DC 交于点 E、 F 。

2015年上海市松江区中考数学二模试卷一、选择题（本大题共6题，每题4分，满分24分）（下列各题的四个选项中，有且只有一个选项是正确的）1．下列根式中与是同类二次根式的是（）A． B． C． D．2．如果关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根，那么k的取值范围是（）A． k＜4 B． k＞4 C． k＜0 D． k＞03．已知一次函数y=kx﹣1，若y随x的增大而增大，则它的图象经过（）A．第一、二、三象限 B．第一、二、四象限C．第一、三、四象限 D．第二、三、四象限4．一组数据：﹣1，1，3，4，a，若它们的平均数为2，则这组数据的众数为（）A． 1 B． 2 C． 3 D． 45．已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是（）A． AD=BC B． AC=BD C．∠A=∠C D．∠A=∠B6．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AB=c，∠a=α，则CD长为（）A． c•sin2α B． c•cos2α C． c•sinα•tanα D． c•sinα•cosα二、填空题：（本大题共12题，每题4分，满分48分）．7．计算：2﹣1= ．8．分解因式：a2﹣4b2= ．9．如果f（x）=，那么f（3）= ．10．已知正比例函数的图象经过点（﹣1，3），那么这个函数的解析式为．11．不等式组的解集是．12．用换元法解方程时，可设，则原方程可化为关于y的整式方程为．13．任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是．14．将抛物线y=2x2﹣1向上平移4个单位后，所得抛物线的解析式是．15．如图，在△ABC中，AD是BC边上的中线，如果，，那么= （用，表示）．16．如图，DE为△ABC的中位线，点F在DE上，且∠AFB为直角，若AB=8，BC=10，则EF 的长为．17．如图，当小明沿坡度i=1：3的坡面由A到B行走了100米，那么小明行走的水平距离AC= 米．（结果可以用根号表示）．18．如图，△ABC中，AB=AC=5cm，BC=6cm，BD平分∠ABC，BD交AC于点D，如果将△ABD 沿BD翻折，点A落在点A′处，那么△DA′C的面积为cm2．三、解答题：（本大题共7题，满分78分）19．计算：（1+）÷．20．解方程组：．21．某品牌电动车经销商一月份销售该品牌电动车100辆，二月份的销售量比一月份增加10%，二月份每辆电动车的售价比一月份每辆电动车的售价低80元，二月份的销售总额比一月份销售总额多12200元，问一月份每辆电动车的售价是多少？22．如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．23．如图，已知在正方形ABCD中，点E在CD边长，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交A于点G，联结BG．（1）求证：△ADG≌△CDF；（2）如果E为CD的中点，求证：BG⊥AF．24．如图，二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A（4，0），过A点的直线与y 轴的正半轴交于点B，与二次函数的图象交于另一点C，过点C作CH⊥x轴，垂足H，设二次函数图象的顶点为D，其对称轴与直线AB及x轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．25．如图，已知在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=3，sin∠BCD=，点P是对角线BD上一动点，过点P作PH⊥CD，重足为H．（1）求证：∠BCD=∠BDC；（2）如图1，若以P为圆心，PB为半径的圆和以H为圆心、HD为半径的圆外切时，DP的长；（3）如图2，点E在BC延长线上，且满足DP=CE，PE交DC于点F，若△ADH和△ECF相似，求DP的长．2015年上海市松江区中考数学二模试卷参考答案与试题解析一、选择题（本大题共6题，每题4分，满分24分）（下列各题的四个选项中，有且只有一个选项是正确的）1．下列根式中与是同类二次根式的是（）A． B． C． D．考点：同类二次根式．分析：先将各选项化简，再找到被开方数为6的选项即可．解答：解：因为=2；A、与2被开方数不同，故不是同类二次根式；B、与2被开方数不同，故不是同类二次根式；C、与2被开方数不同，故不是同类二次根式；D、与2被开方数相同，故是同类二次根式；故选D．点评：要判断几个根式是不是同类二次根式，须先化简根号里面的数，把非最简二次根式化成最简二次根式，然后判断．2．如果关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根，那么k的取值范围是（）A． k＜4 B． k＞4 C． k＜0 D． k＞0考点：根的判别式．分析：利用一元二次方程ax2+bx+c=0（a≠0）的根与△=b2﹣4ac有如下关系：方程有两个不相等的两个实数根，△＞0，进而求出即可．解答：解：∵关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根，∴b2﹣4ac=16﹣4k＞0，解得：k＜4．故选：A．点评：此题主要考查了根的判别式，正确记忆△与方程根的关系是解题关键．3．已知一次函数y=kx﹣1，若y随x的增大而增大，则它的图象经过（）A．第一、二、三象限 B．第一、二、四象限C．第一、三、四象限 D．第二、三、四象限考点：一次函数图象与系数的关系．专题：数形结合．分析：根据“一次函数y=kx﹣1且y随x的增大而增大”得到k＞0，再由k的符号确定该函数图象所经过的象限．解答：解：∵一次函数y=kx﹣1且y随x的增大而增大，∴k＞0，该直线与y轴交于y轴负半轴，∴该直线经过第一、三、四象限．故选：C．点评：本题考查了一次函数图象与系数的关系．函数值y随x的增大而减小⇔k＜0；函数值y随x的增大而增大⇔k＞0；一次函数y=kx+b图象与y轴的正半轴相交⇔b＞0，一次函数y=kx+b图象与y轴的负半轴相交⇔b＜0，一次函数y=kx+b图象过原点⇔b=0．4．一组数据：﹣1，1，3，4，a，若它们的平均数为2，则这组数据的众数为（）A． 1 B． 2 C． 3 D． 4考点：众数；算术平均数．分析：根据平均数的定义即可列方程求得a的值，然后根据众数的定义求解．解答：解：根据题意得：（﹣1+1+3+4+a）=2，解得：a=3．则组数据的众数是3．故选C．点评：本题考查了众数的定义以及平均数，正确依据平均数定义求得a的值是关键．5．已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是（）A． AD=BC B． AC=BD C．∠A=∠C D．∠A=∠B考点：平行四边形的判定．分析：利用平行线的判定与性质结合平行四边形的判定得出即可．解答：解：如图所示：∵AB∥CD，∴∠B+∠C=180°，当∠A=∠C时，则∠A+∠B=180°，故AD∥BC，则四边形ABCD是平行四边形．故选：C．点评：此题主要考查了平行线的判定与性质以及平行四边形的判定，得出AD∥BC是解题关键．6．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AB=c，∠a=α，则CD长为（）A． c•sin2α B． c•cos2α C． c•sinα•tanα D． c•sinα•cosα考点：解直角三角形．分析：根据已知条件在Rt△ABC中，用AB和α表示BC，在Rt△DCB中，根据余弦求出CD 的长，得到答案．解答：解：在Rt△ABC中，∠ACB=90°，AB=c，∠A=α，siα=，BC=c•sinα，∠A+∠B=90°，∠DCB+∠B=90°，∴∠DCB=∠A=α，在Rt△DCB中，∠CDB=90°，cos∠DCB=，CD=BC•cosα=c•sinα•cosα，故选：D．点评：本题考查的是解直角三角形的知识，掌握锐角三角函数的概念是解题的关键，把三角函数的概念看作是公式，在相应的直角三角形中，直接运用．二、填空题：（本大题共12题，每题4分，满分48分）．7．计算：2﹣1= ．考点：负整数指数幂．专题：计算题．分析：根据幂的负整数指数运算法则进行计算即可．解答：解：2﹣1=．故答案为．点评：本题考查负整数指数幂的运算．幂的负整数指数运算，先把底数化成其倒数，然后将负整数指数幂当成正的进行计算．8．分解因式：a2﹣4b2= （a+2b）（a﹣2b）．考点：因式分解-运用公式法．分析：直接用平方差公式进行分解．平方差公式：a2﹣b2=（a+b）（a﹣b）．解答：解：a2﹣4b2=（a+2b）（a﹣2b）．点评：本题考查运用平方差公式进行因式分解，熟记公式结构是解题的关键．9．如果f（x）=，那么f（3）= ．考点：函数值．分析：把x=3代入函数关系式计算即可得解．解答：解：x=3时，f（3）==．故答案为：．点评：本题考查了函数值求解，是基础题，准确计算是解题的关键．10．已知正比例函数的图象经过点（﹣1，3），那么这个函数的解析式为y=﹣3x ．考点：待定系数法求正比例函数解析式．分析：根据待定系数法，可得正比例函数的解析式．解答：解：设正比例函数的解析式为y=kx，图象经过点（﹣1，3），得3=﹣k，解得k=﹣3．正比例函数的解析式为y=﹣3x，故答案为：y=﹣3x．点评：本题考查了待定系数法求正比例函数解析式，八点的坐标代入函数解析式得出k值是解题关键．11．不等式组的解集是3＜x＜4 ．考点：解一元一次不等式组．分析：首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．解答：解：，解①得：x＜4，解②得：x＞3．则不等式组的解集是：3＜x＜4．故答案是：3＜x＜4．点评：本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．12．用换元法解方程时，可设，则原方程可化为关于y的整式方程为y2+2y+1=0 ．考点：换元法解分式方程．分析：换元法即是整体思想的考查，解题的关键是找到这个整体，此题的整体是，设，换元后整理即可求得．解答：解：∵，∴y++2=0，整理得：y2+2y+1=0．故答案为：y2+2y+1=0．点评：考查了换元法解分式方程，用换元法解一些复杂的分式方程是比较简单的一种方法，根据方程特点设出相应未知数，解方程能够使问题简单化．13．任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是．考点：概率公式．专题：常规题型．分析：根据概率的求法，找准两点：①全部情况的总数，②符合条件的情况数目；二者的比值就是其发生的概率．解答：解：∵投掷一次会出现1，2，3，4，5，6共六种情况，并且出现每种可能都是等可能的，∴朝上的面的数字大于2的概率是：=．故答案为：．点评：本题主要考查了概率公式：概率=所求情况数与总情况数之比，比较简单．14．将抛物线y=2x2﹣1向上平移4个单位后，所得抛物线的解析式是y=2x2+3 ．考点：二次函数图象与几何变换．分析：直接利用二次函数图象平移规律得出即可．解答：解：∵将抛物线y=2x2﹣1向上平移4个单位，∴平移后解析式为：y=2x2+3．故答案为：y=2x2+3．点评：此题主要考查了二次函数图象与几何变换，正确记忆平移规律是解题关键．15．如图，在△ABC中，AD是BC边上的中线，如果，，那么= （用，表示）．考点： *平面向量．分析：先求出，然后根据AD是BC边上的中线，可得出，继而可得出．解答：解：∵=，=，∴=﹣=﹣，则=﹣=﹣，∵AD是BC边上的中线，∴=2=2（﹣），则=+=+2（﹣）=2﹣．故答案为：2﹣．点评：本题考查了向量的知识，难度适中，解答本题的关键是熟练掌握用平行四边形法则求向量．16．如图，DE为△ABC的中位线，点F在DE上，且∠AFB为直角，若AB=8，BC=10，则EF 的长为 1 ．考点：三角形中位线定理；直角三角形斜边上的中线．分析：根据三角形的中位线定理求得DE的长，然后根据FD是直角△ABF斜边上的中线，求得FD的长，则EF即可求得．解答：解：∵DE为△ABC的中位线，∴DE=BC=×10=5，∵∠AFB为直角，D是AB的中点，即FD是直角△ABF的中线，∴FD=AB=×8=4．∴EF=DE﹣FD=5﹣4=1．故答案是：1．点评：本题考查了三角形的中位线定理以及直角三角形的性质，直角三角形斜边上的中线等于斜边的一半．17．如图，当小明沿坡度i=1：3的坡面由A到B行走了100米，那么小明行走的水平距离AC= 30米．（结果可以用根号表示）．考点：解直角三角形的应用-坡度坡角问题．分析：直接利用坡度的定义得出设BC=x，则AC=3x，进而利用勾股定理得出即可．解答：解：∵小明沿坡度i=1：3的坡面由A到B行走了100米，∴设BC=x，则AC=3x，故x2+（3x）2=1002，解得：x=10，那么小明行走的水平距离AC=30（m）．故答案为：30．点评：此题主要考查了坡度和坡角问题以及勾股定理，得出BC的长是解题关键．18．如图，△ABC中，AB=AC=5cm，BC=6cm，BD平分∠ABC，BD交AC于点D，如果将△ABD 沿BD翻折，点A落在点A′处，那么△DA′C的面积为cm2．考点：翻折变换（折叠问题）．分析：如图，作辅助线；首先运用勾股定理求出AE的长度，进而求出△ABC的面积；求出△DBA′、△CDA′的面积之比；证明△ABD、△A′BD的面积相等，即可解决问题．解答：解：如图，过点A作AE⊥BC于点E；∵AB=AC，∴BE=CE=3；由勾股定理得：AB2=AE2+BE2，而AB=5，∴AE=4，；由题意得：，A′B=AB=5，∴CA′=6﹣5=1，∴，∴若设=5λ，故λ+5λ+5λ=12，∴λ=（cm2），故答案为．点评：该题主要考查了翻折变换的性质、等腰三角形的性质、勾股定理等几何知识点及其应用问题；解题的方法是作辅助线，构造直角三角形；解题的关键是灵活运用翻折变换的性质来分析、判断、解答．三、解答题：（本大题共7题，满分78分）19．计算：（1+）÷．考点：分式的混合运算．分析：首先将括号里面通分，进而将能分解因式进行分解因式，进而化简求出即可．解答：解：（1+）÷=×=．点评：此题主要考查了分式的混合运算，正确运算顺序是解题关键．20．解方程组：．考点：高次方程．分析：先将方程组②变形为（x﹣5y）（x+y）=0，再重新构成二元一次方程组，解这两个二元一次方程组即可．解答：解：原方程变形为：，解得：．点评：本题考查了消元、降次的方法解二元二次方程组的运用，因式分解的运用，二元一次方程组的解法的运用，解答时将原方程转化为两个二元一次方程组是关键．21．某品牌电动车经销商一月份销售该品牌电动车100辆，二月份的销售量比一月份增加10%，二月份每辆电动车的售价比一月份每辆电动车的售价低80元，二月份的销售总额比一月份销售总额多12200元，问一月份每辆电动车的售价是多少？考点：一元一次方程的应用．分析：首先设一月份每辆电动车的售价是x元，利用二月份的销售总额比一月份销售总额多12200元，进而得出等式求出即可．解答：解：设一月份每辆电动车的售价是x元，根据题意可得：100x+12200=（x﹣80）×100×（1+10%）解得：x=2100，答：一月份每辆电动车的售价是2100元．点评：此题主要考查了一元一次方程的应用，根据题意结合两个月的销售金额得出等式是解题关键．22．如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．考点：垂径定理；勾股定理；圆周角定理．分析：（1）根据垂径定理求出DE的长，设出半径，根据勾股定理，列出方程求出半径；（2）根据OM=OB，证出∠M=∠B，根据∠M=∠D，求出∠D的度数，根据锐角三角函数求出OE的长．解答：解：（1）设⊙O的半径为x，则OE=x﹣8，∵CD=24，由垂径定理得，DE=12，在Rt△ODE中，OD2=DE2+OE2，x2=（x﹣8）2+122，解得：x=13．（2）∵OM=OB，∴∠M=∠B，∴∠DOE=2∠M，又∠M=∠D，∴∠D=30°，在Rt△OED中，∵DE=12，∠D=30°，∴OE=4．点评：本题考查的是垂径定理、勾股定理和圆周角定理的综合运用，灵活运用定理求出线段的长度、列出方程是解题的关键，本题综合性较强，锻炼学生的思维能力．23．如图，已知在正方形ABCD中，点E在CD边长，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交A于点G，联结BG．（1）求证：△ADG≌△CDF；（2）如果E为CD的中点，求证：BG⊥AF．考点：正方形的性质；全等三角形的判定与性质；相似三角形的判定与性质．分析：（1）根据正方形性质和垂直求出AD=CD，∠ADE=∠GDF=90°，求出∠ADG=∠CDF，∠DAG=∠DCF，根据ASA推出两三角形全等即可；（2）设正方形ABCD的边长为a，求出DE=EC=a，在Rt△ADE中，由勾股定理求出AE=a，证△ADE∽△CFE，求出CF=2EF，由勾股定理求出EF=a，CF=a，求出AG=CF=a，=，证△ABG∽△EAD，推出∠BGA=∠ADE即可．解答：证明：（1）∵四边形ABCD是正方形，DG⊥DF，∴AD=CD，∠ADE=∠GDF=90°，∴∠ADG=∠CDF=90°﹣∠GDE，∵AF⊥CF，∴∠EFC=∠ADE=90°，∵∠AED=∠CEF，∴由三角形内角和定理得：∠DAG=∠DCF，在△ADG和△CDF中∴△ADG≌△CDF；（2）设正方形ABCD的边长为a，∵E为CD的中点，∴DE=EC=a，在Rt△ADE中，由勾股定理得：AE==a，∵∠ADE=∠CFE，∠AED=∠FEC，∴△ADE∽△CFE，∴===2，∴CF=2EF，∵CE=a，∠EFC=90°，∴由勾股定理得：EF=a，CF=a，∵△ADG≌△CDF，∴AG=CF=a，即=，∵四边形ABCD是正方形，∴AB∥CD，∴∠BAG=∠AED，∴△ABG∽△EAD，∴∠BGA=∠ADE，∵∠ADE=90°，∴∠BGA=90°，∴BG⊥AF．点评：本题考查了正方形的性质，勾股定理，全等三角形的性质和判定，平行线的性质，相似三角形的性质和判定的应用，能综合运用性质进行推理是解此题的关键，此题综合性比较强，难度偏大．24．如图，二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A（4，0），过A点的直线与y 轴的正半轴交于点B，与二次函数的图象交于另一点C，过点C作CH⊥x轴，垂足H，设二次函数图象的顶点为D，其对称轴与直线AB及x轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．考点：二次函数综合题．分析：（1）直接利用待定系数求出二次函数解析式即可；（2）利用平行线分线段成比例定理得出HO=，CH=，进而得出BO的长即可得出答案；（3）利用等腰三角形的性质结合勾股定理得出EF的长即可得出答案．解答：解：（1）将A（4，0），代入y=﹣x2+bx得：0=﹣16+4b，解得：b=4，故y=﹣x2+4x；（2）∵y=﹣x2+4x=﹣（x﹣2）2+4，∴D（2，4），则FO=2，∵BO∥HC∥EF，∴==3，∴HO=，CH=，由=得，BO=2，则B（0，2）；（3）连接EH，DH，当△DHE是等腰三角形，DH为底，则HE=DE，设OH=a，CH=﹣a2+4a由=，即=，得：EF=2a，故DE=HE=4﹣2a，由EH2=EF2+FH2得，（4﹣2a）2=（2a）2+（2﹣a）2，解得：a=4﹣6（负数舍去），故E（2，8﹣12）．点评：此题主要考查了二次函数综合以及等腰三角形的性质以及勾股定理等知识，正确应用勾股定理以及数形结合求出是解题关键．25．如图，已知在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=3，sin∠BCD=，点P是对角线BD上一动点，过点P作PH⊥CD，重足为H．（1）求证：∠BCD=∠BDC；（2）如图1，若以P为圆心，PB为半径的圆和以H为圆心、HD为半径的圆外切时，DP的长；（3）如图2，点E在BC延长线上，且满足DP=CE，PE交DC于点F，若△ADH和△ECF相似，求DP的长．考点：四边形综合题．分析：（1）作DQ⊥BC，在直角△CDQ中利用三角函数即可求解；（2）设DP=x，当⊙P与⊙H外切时，PH=DH+BP，据此即可列方程求得；（3）作PM∥BE，分△ADH∽△FCE和△ADH∽△ECF两种情况进行讨论，依据相似三角形的对应边的比相等求解．解答：解：（1）作DQ⊥BC，∵BQ=AD=3，DQ=AB=4，∴CD==2，CQ=2，∴BC=5=BD，∴∠BCD=∠BDC；（2）设DP=x，则DH=x，PH=x，BP=5﹣x．当⊙P与⊙H外切时，PH=DH+BP，即x=x+5﹣x，解得：x=；（3）作PM∥BE．则PM=DP=x，DH=HM=x，由==1，CF=FM=﹣x，当△ADH∽△FCE时，，即=，解得：x=﹣10（舍去）．当△ADH∽△ECF时，=，即=，解得：x=．∴DP的长是．点评：本题考查了三角函数以及相似三角形的判定与性质和圆外切的性质，正确分成△ADH ∽△FCE和△ADH∽△ECF两种情况进行讨论，求得x的值是关键．。

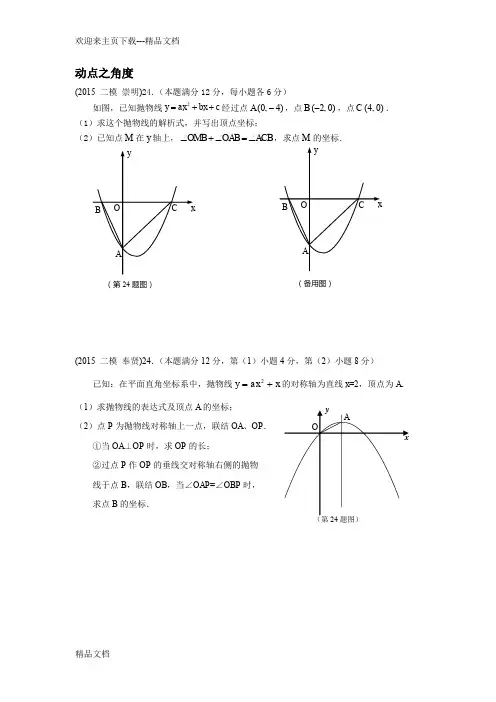
动点之角度(2015 二模 崇明)24．（本题满分12分，每小题各6分）如图，已知抛物线2y ax bx c =++经过点(0,4)A -，点(2,0)B -，点(4,0)C ． （1）求这个抛物线的解析式，并写出顶点坐标；（2）已知点M 在y 轴上，OMB OAB ACB ∠+∠=∠，求点M 的坐标．(2015 二模 奉贤)24．（本题满分12分，第（1）小题4分，第（2）小题8分）已知：在平面直角坐标系中，抛物线x ax y +=2的对称轴为直线x =2，顶点为A ． （1）求抛物线的表达式及顶点A 的坐标； （2）点P 为抛物线对称轴上一点，联结OA 、OP ．①当OA ⊥OP 时，求OP 的长；②过点P 作OP 的垂线交对称轴右侧的抛物 线于点B ，联结OB ，当∠OAP =∠OBP 时， 求点B 的坐标．（第24题图）（备用图）xyO (2015 二模 杨浦)24．(本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分，)已知：在直角坐标系中，直线y =x +1与x 轴交与点A ，与y 轴交与点B ，抛物线21()2y x m n =-+的顶点D 在直线AB 上，与y 轴的交点为C 。

（1）若点C （非顶点）与点B 重合，求抛物线的表达式；（2）若抛物线的对称轴在y 轴的右侧，且CD ⊥AB ，求∠CAD 的正切值； （3）在第（2）的条件下，在∠ACD 的内部作射线CP 交抛物线的对称 轴于点P ，使得∠DCP =∠CAD ，求点P 的坐标。

动点之相似(2015 二模 宝山嘉定) 24．（本题满分12分，每小题满分各4分）已知平面直角坐标系xOy （图9），双曲线)0(≠=k xky 与直线2+=x y 都经过点),2(m A ．（1）求k 与m 的值；（2）此双曲线又经过点)2,(n B ，过点B 的直线BC 与直线2+=x y 平行交y 轴于点C ，联结AB 、AC ，求△ABC 的面积；（3）在（2）的条件下，设直线2+=x y 与y 轴交于点D ，在射线CB 上有一点E ，如果以点A 、C 、E 所组成的三角形与△ACD 相似，且相似比不为1，求点E 的坐标． （第24题图） 图9(2015 二模 金山)24．（本题满分12分）已知抛物线)0(82≠-+=a bx ax y 经过)0,2(-A ，)0,4(B 两点，与y 轴交于点C ． （1） 求抛物线)0(82≠-+=a bx ax y 的解析式，并求出顶点P 的坐标； （2）求APB ∠的正弦值；（3）直线2+=kx y 与y 轴交于点N ，与直线AC 的交点为M ，当MN C ∆与AOC ∆相似时，求点M 的坐标．动点之面积(2015 二模 黄浦)24. （本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）如图7，在平面直角坐标系xOy 中，已知点A 的坐标为（a ，3）（其中a >4)，射线OA 与反比例函数12y x =的图像交于点P ，点B 、C 分别在函数12y x=的图像上，且AB //x 轴，AC //y 轴．Oxy(2015 二模 静安青浦)24．（本题满分12分，第（1）小题满分8分，第（2）小题满分4分）如图，在直角坐标系xOy 中，抛物线c ax ax y +-=22与x 轴的正半轴相交于点A 、与y 轴的正半轴相交于点B ，它的对称轴与x 轴相交于点C ，且∠OBC =∠OAB ，AC =3．（1） 求此抛物线的表达式；（2） 如果点D 在此抛物线上，DF ⊥OA ，垂足为F ，DF 与线段AB 相交于点G ，且2:3:=∆∆AFG ADG S S ，求点D(2015 二模 长宁)24．（本题满分12分）如图，已知抛物线2222-+-=t tx x y 的顶点A 在第四象限，过点A 作AB ⊥y 轴于点B ，C 是线段AB 上一点(不与A 、B 重合)，过点C 作CD ⊥x 轴于点D ，并交抛物线于点P . （1）若点C 的横坐标为1，且是线段AB 的中点，求点P 的坐标；（2）若直线AP 交y 轴负半轴于点E ，且AC =CP ，求四边形OEPD 的面积S 关于t 的函数解析式，并写出定义域；（3）在（2）的条件下，当△ADE 的面积等于2S 时 ，求t 的值.（第24题图）动点之直角、等腰三角形存在性(2015 二模 普陀) 如图10，在平面直角坐标系xOy 中，二次函数的图像经过点()1,0A -，()4,0B ，()0,2C ．点D 是点C 关于原点的对称点，联结BD ，点E 是x 轴上的一个动点，设点E 的坐标为(m , 0)，过点E 作x 轴的垂线l 交抛物线于点P ． （1）求这个二次函数的解析式；（2）当点E 在线段OB 上运动时，直线l 交BD 于点Q ．当四边形CDQP 是平行四边形时，求m 的值；（3）是否存在点P ，使△BDP 是不以BD 为斜边的直角三角形，如果存在，请直接写出点P 的坐标；如果不存在，请说明理由．(2015 二模 松江)24．（本题满分12分，每小题各4分）如图，二次函数bx x y +-=2的图像与x 轴的正半轴交于点A （4，0），过A 点的直线与y 轴的正半轴交于点B ，与二次函数的图像交于另一点C ，过点C 作CH ⊥x 轴，垂足为H ．设二次函数图像的顶点为D ，其对称轴与直线AB 及x 轴分别交于点E 和点F ． （1）求这个二次函数的解析式； （2）如果CE =3BC ，求点B 的坐标；（3）如果△DHE 是以DH 为底边的等腰三角形，求点E 的坐标．图10备用图x动点之梯形(2015 二模 徐汇)24． 如图，在平面直角坐标系中，O 为坐标原点，开口向上的抛物线与x 轴交于点A （－1，0）和点B （3，0），D 为抛物线的顶点， 直线AC 与抛物线交于点C （5，6）．（1）求抛物线的解析式；（2）点E 在x 轴上，且AEC ∆和AED ∆相似，求点E 的坐标；（3）若直角坐标平面中的点F 和点A 、C 、D 构成直角梯形，且面积为16，试求点F 的坐标．其他(2015 二模 闵行)24．（本题满分12分，其中每小题各4分）如图，已知在平面直角坐标系xOy 中，抛物线224y ax ax =--与x 轴相交于A 、B 两点，与y 轴相交于点C ，其中点A 的坐标为（-3，0）．点D 在线段AB 上，AD = AC ． （1）求这条抛物线的关系式，并求出抛物线的对称轴； （2）如果以DB 为半径的圆D 与圆C 外切，求圆C 的半径； （3）设点M 在线段AB 上，点N 在线段BC 上．如果线段MN 被直线CD 垂直平分，求BN CN的值．（第24题图）(2015 二模 浦东)24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分） 已知：如图，直线y =kx +2与x 轴的正半轴相交于点A （t ,0）、与y 轴相交于点B ，抛物线c bx x y ++-=2经过点A 和点B ，点C 在第三象限内，且AC ⊥AB ，tan ∠ACB =21． （1）当t =1时，求抛物线的表达式；（2）试用含t 的代数式表示点C 的坐标；（3）如果点C 在这条抛物线的对称轴上，求t 的值．（第24题图）。

2015年上海市松江区中考数学二模试卷一、选择题（本大题共6题，每题4分，满分24分）（下列各题的四个选项中，有且只有一个选项是正确的）1．（4分）下列根式中与是同类二次根式的是（）A ．B ．C ．D ．2．（4分）如果关于x 的一元二次方程x 2﹣4x+k=0有两个不相等的实数根，那么k 的取值范围是（）A ．k ＜4B ．k ＞4C ．k ＜0D ．k ＞03．（4分）已知一次函数y=kx ﹣1，若y 随x 的增大而增大，则它的图象经过（）A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限4．（4分）一组数据：﹣1，1，3，4，a ，若它们的平均数为2，则这组数据的众数为（）A ．1B ．2C ．3D ．45．（4分）已知在四边形ABCD 中，AB ∥CD ，添加下列一个条件后，一定能判定四边形ABCD 是平行四边形的是（）A ．AD=BCB ．AC=BDC ．∠A=∠CD ．∠A=∠B6．（4分）如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB ，垂足为D ，AB=c ，∠a=α，则CD 长为（）A ．c •sin 2αB ．c •cos 2αC ．c •sin α•tan αD ．c •sin α•cos α二、填空题：（本大题共12题，每题4分，满分48分）．7．（4分）计算：2﹣1=．8．（4分）分解因式：a 2﹣4b 2=．9．（4分）如果f （x ）=，那么f （3）=．10．（4分）已知正比例函数的图象经过点（﹣1，3），那么这个函数的解析式为．11．（4分）不等式组的解集是．12．（4分）用换元法解方程时，可设，则原方程可化为关于y的整式方程为．13．（4分）任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是．14．（4分）将抛物线y=2x2﹣1向上平移4个单位后，所得抛物线的解析式是．15．（4分）如图，在△ABC中，AD是BC边上的中线，如果，，那么=（用，表示）．16．（4分）如图，DE为△ABC的中位线，点F在DE上，且∠AFB为直角，若AB=8，BC=10，则EF的长为．17．（4分）如图，当小明沿坡度i=1：3的坡面由A到B行走了100米，那么小明行走的水平距离AC=米．（结果可以用根号表示）．18．（4分）如图，△ABC中，AB=AC=5cm，BC=6cm，BD平分∠ABC，BD交AC于点D，如果将△ABD沿BD翻折，点A落在点A′处，那么△DA′C的面积为cm2．三、解答题：（本大题共7题，满分78分）19．（10分）计算：（1+）÷．20．（10分）解方程组：．21．（10分）某品牌电动车经销商一月份销售该品牌电动车100辆，二月份的销售量比一月份增加10%，二月份每辆电动车的售价比一月份每辆电动车的售价低80元，二月份的销售总额比一月份销售总额多12200元，问一月份每辆电动车的售价是多少？22．（10分）如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．23．（12分）如图，已知在正方形ABCD中，点E在CD边长，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交A于点G，联结BG．（1）求证：△ADG≌△CDF；（2）如果E为CD的中点，求证：BG⊥AF．24．（12分）如图，二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A（4，0），过A点的直线与y轴的正半轴交于点B，与二次函数的图象交于另一点C，过点C作CH⊥x轴，垂足H，设二次函数图象的顶点为D，其对称轴与直线AB及x轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．25．（14分）如图，已知在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=3，sin∠BCD=，点P是对角线BD上一动点，过点P作PH⊥CD，重足为H．（1）求证：∠BCD=∠BDC；（2）如图1，若以P为圆心，PB为半径的圆和以H为圆心、HD为半径的圆外切时，DP 的长；（3）如图2，点E在BC延长线上，且满足DP=CE，PE交DC于点F，若△ADH和△ECF相似，求DP的长．2015年上海市松江区中考数学二模试卷参考答案与试题解析一、选择题（本大题共6题，每题4分，满分24分）（下列各题的四个选项中，有且只有一个选项是正确的）1．（4分）下列根式中与是同类二次根式的是（）A．B．C．D．【考点】同类二次根式．【分析】先将各选项化简，再找到被开方数为6的选项即可．【解答】解：因为=2；A、与2被开方数不同，故不是同类二次根式；B、与2被开方数不同，故不是同类二次根式；C、与2被开方数不同，故不是同类二次根式；D、与2被开方数相同，故是同类二次根式；故选D．【点评】要判断几个根式是不是同类二次根式，须先化简根号里面的数，把非最简二次根式化成最简二次根式，然后判断．2．（4分）如果关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根，那么k的取值范围是（）A．k＜4B．k＞4C．k＜0D．k＞0【考点】根的判别式．【分析】利用一元二次方程ax2+bx+c=0（a≠0）的根与△=b2﹣4ac有如下关系：方程有两个不相等的两个实数根，△＞0，进而求出即可．【解答】解：∵关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根，∴b2﹣4ac=16﹣4k＞0，解得：k＜4．故选：A．【点评】此题主要考查了根的判别式，正确记忆△与方程根的关系是解题关键．3．（4分）已知一次函数y=kx﹣1，若y随x的增大而增大，则它的图象经过（）A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限【考点】一次函数图象与系数的关系．【专题】数形结合．【分析】根据“一次函数y=kx﹣1且y随x的增大而增大”得到k＞0，再由k的符号确定该函数图象所经过的象限．【解答】解：∵一次函数y=kx﹣1且y随x的增大而增大，∴k＞0，该直线与y轴交于y轴负半轴，∴该直线经过第一、三、四象限．故选：C．【点评】本题考查了一次函数图象与系数的关系．函数值y随x的增大而减小⇔k＜0；函数值y随x的增大而增大⇔k＞0；一次函数y=kx+b图象与y轴的正半轴相交⇔b＞0，一次函数y=kx+b图象与y轴的负半轴相交⇔b＜0，一次函数y=kx+b图象过原点⇔b=0．4．（4分）一组数据：﹣1，1，3，4，a，若它们的平均数为2，则这组数据的众数为（）A．1B．2C．3D．4【考点】众数；算术平均数．【分析】根据平均数的定义即可列方程求得a的值，然后根据众数的定义求解．【解答】解：根据题意得：（﹣1+1+3+4+a）=2，解得：a=3．则组数据的众数是3．故选C．【点评】本题考查了众数的定义以及平均数，正确依据平均数定义求得a的值是关键．5．（4分）已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是（）A．AD=BC B．AC=BD C．∠A=∠C D．∠A=∠B【考点】平行四边形的判定．【分析】利用平行线的判定与性质结合平行四边形的判定得出即可．【解答】解：如图所示：∵AB∥CD，∴∠B+∠C=180°，当∠A=∠C时，则∠A+∠B=180°，故AD∥BC，则四边形ABCD是平行四边形．故选：C．【点评】此题主要考查了平行线的判定与性质以及平行四边形的判定，得出AD∥BC是解题关键．6．（4分）如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AB=c，∠a=α，则CD长为（）A．c•sin2αB．c•cos2αC．c•sinα•tanαD．c•sinα•cosα【考点】解直角三角形．【分析】根据已知条件在Rt△ABC中，用AB和α表示BC，在Rt△DCB中，根据余弦求出CD的长，得到答案．【解答】解：在Rt△ABC中，∠ACB=90°，AB=c，∠A=α，siα=，BC=c•sinα，∠A+∠B=90°，∠DCB+∠B=90°，∴∠DCB=∠A=α，在Rt△DCB中，∠CDB=90°，cos∠DCB=，CD=BC•cosα=c•sinα•cosα，故选：D．【点评】本题考查的是解直角三角形的知识，掌握锐角三角函数的概念是解题的关键，把三角函数的概念看作是公式，在相应的直角三角形中，直接运用．二、填空题：（本大题共12题，每题4分，满分48分）．7．（4分）计算：2﹣1=．【考点】负整数指数幂．【专题】计算题．【分析】根据幂的负整数指数运算法则进行计算即可．【解答】解：2﹣1=．故答案为．【点评】本题考查负整数指数幂的运算．幂的负整数指数运算，先把底数化成其倒数，然后将负整数指数幂当成正的进行计算．8．（4分）分解因式：a2﹣4b2=（a+2b）（a﹣2b）．【考点】因式分解-运用公式法．【分析】直接用平方差公式进行分解．平方差公式：a2﹣b2=（a+b）（a﹣b）．【解答】解：a2﹣4b2=（a+2b）（a﹣2b）．【点评】本题考查运用平方差公式进行因式分解，熟记公式结构是解题的关键．9．（4分）如果f（x）=，那么f（3）=．【考点】函数值．【分析】把x=3代入函数关系式计算即可得解．【解答】解：x=3时，f（3）==．故答案为：．【点评】本题考查了函数值求解，是基础题，准确计算是解题的关键．10．（4分）已知正比例函数的图象经过点（﹣1，3），那么这个函数的解析式为y=﹣3x．【考点】待定系数法求正比例函数解析式．【分析】根据待定系数法，可得正比例函数的解析式．【解答】解：设正比例函数的解析式为y=kx，图象经过点（﹣1，3），得3=﹣k，解得k=﹣3．正比例函数的解析式为y=﹣3x，故答案为：y=﹣3x．【点评】本题考查了待定系数法求正比例函数解析式，八点的坐标代入函数解析式得出k 值是解题关键．11．（4分）不等式组的解集是3＜x＜4．【考点】解一元一次不等式组．【分析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．【解答】解：，解①得：x＜4，解②得：x＞3．则不等式组的解集是：3＜x＜4．故答案是：3＜x＜4．【点评】本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．12．（4分）用换元法解方程时，可设，则原方程可化为关于y 的整式方程为y2+2y+1=0．【考点】换元法解分式方程．【分析】换元法即是整体思想的考查，解题的关键是找到这个整体，此题的整体是，设，换元后整理即可求得．【解答】解：∵，∴y++2=0，整理得：y2+2y+1=0．故答案为：y2+2y+1=0．【点评】考查了换元法解分式方程，用换元法解一些复杂的分式方程是比较简单的一种方法，根据方程特点设出相应未知数，解方程能够使问题简单化．13．（4分）任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是．【考点】概率公式．【专题】常规题型．【分析】根据概率的求法，找准两点：①全部情况的总数，②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：∵投掷一次会出现1，2，3，4，5，6共六种情况，并且出现每种可能都是等可能的，∴朝上的面的数字大于2的概率是：=．故答案为：．【点评】本题主要考查了概率公式：概率=所求情况数与总情况数之比，比较简单．14．（4分）将抛物线y=2x2﹣1向上平移4个单位后，所得抛物线的解析式是y=2x2+3．【考点】二次函数图象与几何变换．【分析】直接利用二次函数图象平移规律得出即可．【解答】解：∵将抛物线y=2x2﹣1向上平移4个单位，∴平移后解析式为：y=2x2+3．故答案为：y=2x2+3．【点评】此题主要考查了二次函数图象与几何变换，正确记忆平移规律是解题关键．15．（4分）如图，在△ABC中，AD是BC边上的中线，如果，，那么=（用，表示）．【考点】*平面向量．【分析】先求出，然后根据AD是BC边上的中线，可得出，继而可得出．【解答】解：∵=，=，∴=﹣=﹣，则=﹣=﹣，∵AD是BC边上的中线，∴=2=2（﹣），则=+=+2（﹣）=2﹣．故答案为：2﹣．【点评】本题考查了向量的知识，难度适中，解答本题的关键是熟练掌握用平行四边形法则求向量．16．（4分）如图，DE为△ABC的中位线，点F在DE上，且∠AFB为直角，若AB=8，BC=10，则EF的长为1．【考点】三角形中位线定理；直角三角形斜边上的中线．【分析】根据三角形的中位线定理求得DE的长，然后根据FD是直角△ABF斜边上的中线，求得FD的长，则EF即可求得．【解答】解：∵DE为△ABC的中位线，∴DE=BC=×10=5，∵∠AFB为直角，D是AB的中点，即FD是直角△ABF的中线，∴FD=AB=×8=4．∴EF=DE﹣FD=5﹣4=1．故答案是：1．【点评】本题考查了三角形的中位线定理以及直角三角形的性质，直角三角形斜边上的中线等于斜边的一半．17．（4分）如图，当小明沿坡度i=1：3的坡面由A到B行走了100米，那么小明行走的水平距离AC=30米．（结果可以用根号表示）．【考点】解直角三角形的应用-坡度坡角问题．【分析】直接利用坡度的定义得出设BC=x，则AC=3x，进而利用勾股定理得出即可．【解答】解：∵小明沿坡度i=1：3的坡面由A到B行走了100米，∴设BC=x，则AC=3x，故x2+（3x）2=1002，解得：x=10，那么小明行走的水平距离AC=30（m）．故答案为：30．【点评】此题主要考查了坡度和坡角问题以及勾股定理，得出BC的长是解题关键．18．（4分）如图，△ABC中，AB=AC=5cm，BC=6cm，BD平分∠ABC，BD交AC于点D，如果将△ABD沿BD翻折，点A落在点A′处，那么△DA′C的面积为cm2．【考点】翻折变换（折叠问题）．【分析】如图，作辅助线；首先运用勾股定理求出AE的长度，进而求出△ABC的面积；求出△DBA′、△CDA′的面积之比；证明△ABD、△A′BD的面积相等，即可解决问题．【解答】解：如图，过点A作AE⊥BC于点E；∵AB=AC，∴BE=CE=3；由勾股定理得：AB2=AE2+BE2，而AB=5，∴AE=4，；由题意得：，A′B=AB=5，∴CA′=6﹣5=1，∴，∴若设=5λ，故λ+5λ+5λ=12，∴λ=（cm2），故答案为．【点评】该题主要考查了翻折变换的性质、等腰三角形的性质、勾股定理等几何知识点及其应用问题；解题的方法是作辅助线，构造直角三角形；解题的关键是灵活运用翻折变换的性质来分析、判断、解答．三、解答题：（本大题共7题，满分78分）19．（10分）计算：（1+）÷．【考点】分式的混合运算．【分析】首先将括号里面通分，进而将能分解因式进行分解因式，进而化简求出即可．【解答】解：（1+）÷=×=．【点评】此题主要考查了分式的混合运算，正确运算顺序是解题关键．20．（10分）解方程组：．【考点】高次方程．【分析】先将方程组②变形为（x﹣5y）（x+y）=0，再重新构成二元一次方程组，解这两个二元一次方程组即可．【解答】解：原方程变形为：，解得：．【点评】本题考查了消元、降次的方法解二元二次方程组的运用，因式分解的运用，二元一次方程组的解法的运用，解答时将原方程转化为两个二元一次方程组是关键．21．（10分）某品牌电动车经销商一月份销售该品牌电动车100辆，二月份的销售量比一月份增加10%，二月份每辆电动车的售价比一月份每辆电动车的售价低80元，二月份的销售总额比一月份销售总额多12200元，问一月份每辆电动车的售价是多少？【考点】一元一次方程的应用．【分析】首先设一月份每辆电动车的售价是x元，利用二月份的销售总额比一月份销售总额多12200元，进而得出等式求出即可．【解答】解：设一月份每辆电动车的售价是x元，根据题意可得：100x+12200=（x﹣80）×100×（1+10%）解得：x=2100，答：一月份每辆电动车的售价是2100元．【点评】此题主要考查了一元一次方程的应用，根据题意结合两个月的销售金额得出等式是解题关键．22．（10分）如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．【考点】垂径定理；勾股定理；圆周角定理．【分析】（1）根据垂径定理求出DE的长，设出半径，根据勾股定理，列出方程求出半径；（2）根据OM=OB，证出∠M=∠B，根据∠M=∠D，求出∠D的度数，根据锐角三角函数求出OE的长．【解答】解：（1）设⊙O的半径为x，则OE=x﹣8，∵CD=24，由垂径定理得，DE=12，在Rt△ODE中，OD2=DE2+OE2，x2=（x﹣8）2+122，解得：x=13．（2）∵OM=OB，∴∠M=∠B，∴∠DOE=2∠M，又∠M=∠D，∴∠D=30°，在Rt△OED中，∵DE=12，∠D=30°，∴OE=4．【点评】本题考查的是垂径定理、勾股定理和圆周角定理的综合运用，灵活运用定理求出线段的长度、列出方程是解题的关键，本题综合性较强，锻炼学生的思维能力．23．（12分）如图，已知在正方形ABCD中，点E在CD边长，过C点作AE的垂线交于点F，联结DF，过点D作DF的垂线交A于点G，联结BG．（1）求证：△ADG≌△CDF；（2）如果E为CD的中点，求证：BG⊥AF．【考点】正方形的性质；全等三角形的判定与性质；相似三角形的判定与性质．【分析】（1）根据正方形性质和垂直求出AD=CD，∠ADE=∠GDF=90°，求出∠ADG=∠CDF，∠DAG=∠DCF，根据ASA推出两三角形全等即可；（2）设正方形ABCD的边长为a，求出DE=EC=a，在Rt△ADE中，由勾股定理求出AE=a，证△ADE∽△CFE，求出CF=2EF，由勾股定理求出EF=a，CF=a，求出AG=CF=a，=，证△ABG∽△EAD，推出∠BGA=∠ADE即可．【解答】证明：（1）∵四边形ABCD是正方形，DG⊥DF，∴AD=CD，∠ADE=∠GDF=90°，∴∠ADG=∠CDF=90°﹣∠GDE，∵AF⊥CF，∴∠EFC=∠ADE=90°，∵∠AED=∠CEF，∴由三角形内角和定理得：∠DAG=∠DCF，在△ADG和△CDF中∴△ADG≌△CDF；（2）设正方形ABCD的边长为a，∵E为CD的中点，∴DE=EC=a，在Rt△ADE中，由勾股定理得：AE==a，∵∠ADE=∠CFE，∠AED=∠FEC，∴△ADE∽△CFE，∴===2，∴CF=2EF，∵CE=a，∠EFC=90°，∴由勾股定理得：EF=a，CF=a，∵△ADG≌△CDF，∴AG=CF=a，即=，∵四边形ABCD是正方形，∴AB∥CD，∴∠BAG=∠AED，∴△ABG∽△EAD，∴∠BGA=∠ADE，∵∠ADE=90°，∴∠BGA=90°，∴BG⊥AF．【点评】本题考查了正方形的性质，勾股定理，全等三角形的性质和判定，平行线的性质，相似三角形的性质和判定的应用，能综合运用性质进行推理是解此题的关键，此题综合性比较强，难度偏大．24．（12分）如图，二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A（4，0），过A点的直线与y轴的正半轴交于点B，与二次函数的图象交于另一点C，过点C作CH⊥x轴，垂足H，设二次函数图象的顶点为D，其对称轴与直线AB及x轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．【考点】二次函数综合题．【分析】（1）直接利用待定系数求出二次函数解析式即可；（2）利用平行线分线段成比例定理得出HO=，CH=，进而得出BO的长即可得出答案；（3）利用等腰三角形的性质结合勾股定理得出EF的长即可得出答案．【解答】解：（1）将A（4，0），代入y=﹣x2+bx得：0=﹣16+4b，解得：b=4，故y=﹣x2+4x；（2）∵y=﹣x2+4x=﹣（x﹣2）2+4，∴D（2，4），则FO=2，∵BO∥HC∥EF，∴==3，∴HO=，CH=，由=得，BO=2，则B（0，2）；（3）连接EH，DH，当△DHE是等腰三角形，DH为底，则HE=DE，设OH=a，CH=﹣a2+4a由=，即=，得：EF=2a，故DE=HE=4﹣2a，由EH2=EF2+FH2得，（4﹣2a）2=（2a）2+（2﹣a）2，解得：a=4﹣6（负数舍去），故E（2，8﹣12）．【点评】此题主要考查了二次函数综合以及等腰三角形的性质以及勾股定理等知识，正确应用勾股定理以及数形结合求出是解题关键．25．（14分）如图，已知在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=3，sin∠BCD=，点P是对角线BD上一动点，过点P作PH⊥CD，重足为H．（1）求证：∠BCD=∠BDC；（2）如图1，若以P为圆心，PB为半径的圆和以H为圆心、HD为半径的圆外切时，DP 的长；（3）如图2，点E在BC延长线上，且满足DP=CE，PE交DC于点F，若△ADH和△ECF相似，求DP的长．【考点】四边形综合题．【分析】（1）作DQ⊥BC，在直角△CDQ中利用三角函数即可求解；（2）设DP=x，当⊙P与⊙H外切时，PH=DH+BP，据此即可列方程求得；（3）作PM∥BE，分△ADH∽△FCE和△ADH∽△ECF两种情况进行讨论，依据相似三角形的对应边的比相等求解．【解答】解：（1）作DQ⊥BC，∵BQ=AD=3，DQ=AB=4，∴CD==2，CQ=2，∴BC=5=BD，∴∠BCD=∠BDC；（2）设DP=x，则DH=x，PH=x，BP=5﹣x．当⊙P与⊙H外切时，PH=DH+BP，即x=x+5﹣x，解得：x=；（3）作PM∥BE．则PM=DP=x，DH=HM=x，由==1，CF=FM=﹣x，当△ADH∽△FCE时，，即=，解得：x=﹣10（舍去）．当△ADH∽△ECF时，=，即=，解得：x=．∴DP的长是．【点评】本题考查了三角函数以及相似三角形的判定与性质和圆外切的性质，正确分成△ADH∽△FCE和△ADH∽△ECF两种情况进行讨论，求得x的值是关键．2015年松江区初中毕业生学业模拟考试语文试卷（满分150分，考试时间100分钟）2015.4考生注意：本试卷共27题。

2015年上海市黄浦区中考数学二模试卷一、选择题（每题4分，共24分）1．（4分）（2015?黄浦区二模）下列分数中，可以化为有限小数的是（）A． B． C． D．2．（4分）（2015?黄浦区二模）下列二次根式中最简根式是（）A． B． C．D．3．（4分）（2015?黄浦区二模）如表是某地今年春节放假七天最低气温（℃）的统计结果日期除夕初一初二初三初四初五初六最低气温（℃）44561064这七天最低气温的众数和中位数分别是（）A．4，4 B．4，5 C．6，5 D．6，64．（4分）（2015?黄浦区二模）将抛物线y=x2向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x﹣2）2+1 C．y=（x+1）2﹣2 D．y=（x+2）2﹣1 5．（4分）（2015?黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4，那么这两个圆的位置关系是（）A．内含B．内切C．外切D．相交6．（4分）（2015?黄浦区二模）下列命题中真命题是（）A．对角线互相垂直的四边形是矩形B．对角线相等的四边形是矩形C．四条边都相等的四边形是矩形D．四个内角都相等的四边形是矩形二、填空题（每题4分，共48分）7．（4分）（2015?黄浦区二模）计算：（a2）2= ．8．（4分）（2015?房山区二模）分解因式：2x2﹣8x+8= ．9．（4分）（2015?黄浦区二模）计算：+= ．10．（4分）（2004?上海）方程=x﹣1的根是．11．（4分）（2015?黄浦区二模）如果抛物线y=（2﹣a）x2+3x﹣a的开口向上，那么a的取值范围是．12．（4分）（2015?黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为．13．（4分）（2015?黄浦区二模）将一枚质地均匀的硬币抛掷2次，硬币正面均朝上的概率是．14．（4分）（2015?黄浦区二模）如果梯形的下底长为7，中位线长为5，那么其上底长为．15．（4分）（2015?黄浦区二模）已知AB是⊙O的弦，如果⊙O的半径长为5，AB长为4，那么圆心O到弦AB的距离是．16．（4分）（2015?黄浦区二模）如图，在平行四边形ABCD中，点M是边CD中点，点N是边BC上的点，且=．设=，=，那么可用、表示为．17．（4分）（2015?黄浦区二模）如图，△ABC是等边三角形，若点A绕点C顺时针旋转30°至点A′，联结A′B，则∠ABA′度数是．18．（4分）（2015?黄浦区二模）如图1，点P是以r为半径的圆O外一点，点P′在线段OP上，若满足OP?OP′=r2，则称点P′是点P关于圆O的反演点．如图2，在Rt△ABO中，∠B=90°，AB=2，BO=4，圆O的半径为2，如果点A′、B′分别是点A、B关于圆O的反演点，那么A′B′的长是．三、解答题（48分）19．（6分）（2015?黄浦区二模）计算：40+﹣（﹣1）﹣1+|1﹣|．20．（6分）（2015?黄浦区二模）解方程组：．21．（6分）（2015?盘锦二模）温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：华氏度数x（℃）…0…35…100…摄氏度数y（℉）…32…95…212…（1）选用表格中给出的数据，求y关于x的函数解析式（不需要写出该函数的定义域）；（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数．22．（6分）（2015?黄浦区二模）如图，在梯形ABCD中，AD∥BC，AB⊥BC，已知AD=2，cot∠ACB=，梯形ABCD的面积是9；（1）求AB的长；（2）求tan∠ACD的值．23．（6分）（2015?黄浦区二模）如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；（1）求证：AE=CG；（2）求证：BE∥DF．24．（9分）（2015?黄浦区二模）如图，在平面直角坐标系xOy中，已知点A的坐标为（a，3）（其中a＞4），射线OA与反比例函数y=的图象交于点P，点B、C分别在函数y=的图象上，且AB∥x轴，AC∥y轴；（1）当点P横坐标为6，求直线AO的表达式；（2）联结BO，当AB=BO时，求点A坐标；（3）联结BP、CP，试猜想：的值是否随a的变化而变化？如果不变，求出的值；如果变化，请说明理由．25．（9分）（2015?黄浦区二模）如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF与边AB、线段DE分别交于点F、G；（1）求线段CD、AD的长；（2）设CE=x，DF=y，求y关于x的函数解析式，并写出它的定义域；（3）联结EF，当△EFG与△CDG相似时，求线段CE的长．2015年上海市黄浦区中考数学二模试卷参考答案与试题解析一、选择题（每题4分，共24分）1．（4分）（2015?黄浦区二模）下列分数中，可以化为有限小数的是（）A． B． C． D．【分析】根据分数与小数间的转化，可得答案．【解答】解：A、是无限循环小数，故A错误；B、是无限循环小数，故B错误；C、是有限小数，故C正确；D、是无限循环小数，故D错误；故选：C．2．（4分）（2015?黄浦区二模）下列二次根式中最简根式是（）A． B． C．D．【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【解答】解：A、被开方数含开的尽的因数，故A错误；B、被开方数含开的尽的因数，故B错误；C、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故C正确；D、被开方数含分母，故D错误；故选：C．3．（4分）（2015?黄浦区二模）如表是某地今年春节放假七天最低气温（℃）的统计结果日期除夕初一初二初三初四初五初六最低气温（℃）44561064这七天最低气温的众数和中位数分别是（）A．4，4 B．4，5 C．6，5 D．6，6【分析】众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据定义即可求解．【解答】解：将一周气温按从小到大的顺序排列为4，4，4，5，6，6，10，中位数为第四个数5；4出现了3次，故众数为4．故选B．4．（4分）（2015?黄浦区二模）将抛物线y=x2向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x﹣2）2+1 C．y=（x+1）2﹣2 D．y=（x+2）2﹣1【分析】把抛物线的平移问题转化为点平移的问题：先确定抛物线y=x2的顶点坐标为（0，0），再根据点平移的规律得到把向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（﹣2，﹣1），然后根据顶点式写出平移后的抛物线解析式．【解答】解：抛物线y=x2的顶点坐标为（0，0），把点（0，0）向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（﹣2，﹣1），所以所得抛物线的表达式是y=（x+2）2﹣1．故选：D．5．（4分）（2015?黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4，那么这两个圆的位置关系是（）A．内含B．内切C．外切D．相交【分析】根据数量关系来判断两圆的位置关系．设两圆的半径分别为R和r，且R≥r，圆心距为d：外离，则d＞R+r；外切，则d=R+r；相交，则R﹣r＜d＜R+r；内切，则d=R﹣r；内含，则d＜R﹣r．【解答】解：∵两圆半径之差=6﹣2=4=圆心距，∴两个圆的位置关系是内切．故选B．6．（4分）（2015?黄浦区二模）下列命题中真命题是（）A．对角线互相垂直的四边形是矩形B．对角线相等的四边形是矩形C．四条边都相等的四边形是矩形D．四个内角都相等的四边形是矩形【分析】根据矩形的判定方法对四个命题进行判断．【解答】解：A、对角线相等的平行四边形是矩形，所以A选项错误；B、对角线相等的平行四边形是矩形，所以B选项错误；C、四个角都相等的四边形是矩形，所以C选项错误；D、四个角都相等的四边形是矩形，所以D选项正确．故选D．二、填空题（每题4分，共48分）7．（4分）（2015?黄浦区二模）计算：（a2）2= a4．【分析】根据幂的乘方和积的乘方的运算法则求解．【解答】解：（a2）2=a4．故答案为：a4．8．（4分）（2015?房山区二模）分解因式：2x2﹣8x+8= 2（x﹣2）2．【分析】先提公因式2，再用完全平方公式进行因式分解即可．【解答】解：原式=2（x2﹣4x+4）=2（x﹣2）2．故答案为2（x﹣2）2．9．（4分）（2015?黄浦区二模）计算：+= ．【分析】原式通分并利用同分母分式的加法法则计算，即可得到结果．【解答】解：原式==，故答案为：10．（4分）（2004?上海）方程=x﹣1的根是x=3 ．【分析】把方程两边平方去根号后求解，注意检验．【解答】解：两边平方得7﹣x=（x﹣1）2，即（x+2）（x﹣3）=0，解得：x=﹣2或x=3，代入原方程，当x=﹣2时，左边==3，右边=﹣3，原方成不成立．当x=3时，左边=，右边=2，原方程成立．故方程=x﹣1的根是x=3，故本题答案为：x=3．11．（4分）（2015?黄浦区二模）如果抛物线y=（2﹣a）x2+3x﹣a的开口向上，那么a的取值范围是a＜2 ．【分析】根据二次函数的性质可知，当抛物线开口向上时，二次项系数2﹣a＞0，解不等式即可求得a的取值．【解答】解：因为抛物线y=（2﹣a）x2+3x﹣a的开口向上，所以2﹣a＞0，即a＜2．故答案为：a＜2．12．（4分）（2015?黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40% ．【分析】根据条形统计图给出的数据求出外出旅游学生的总人数，再用三班外出旅游学生人数除以总人数即可得出答案．【解答】解：三班外出旅游学生人数占全年级外出旅游学生人数的百分比为×100%=40%；故答案为：40%．13．（4分）（2015?黄浦区二模）将一枚质地均匀的硬币抛掷2次，硬币正面均朝上的概率是．【分析】列举出所有情况，看正面都朝上的情况数占总情况数的多少即可．【解答】解：如图所示：共4种情况，正面都朝上的情况数有1种，所以概率是．故答案是．14．（4分）（2015?黄浦区二模）如果梯形的下底长为7，中位线长为5，那么其上底长为 3 ．【分析】设出梯形的上底长，直接运用梯形的中位线定理列出关于上底λ的方程，求出λ即可解决问题．【解答】解：设梯形的上底长为λ；由题意得：，解得：λ=3，故答案为3．15．（4分）（2015?黄浦区二模）已知AB是⊙O的弦，如果⊙O的半径长为5，AB长为4，那么圆心O到弦AB的距离是．【分析】根据题意画出图形，过点O作OD⊥AB于点D，由垂径定理可得出AD的长，在Rt△OAD中，利用勾股定理及可求出OD的长．【解答】解：如图所示：过点O作OD⊥AB于点D，∵AB=4，∴AD=AB=×4=2，在Rt△OBD中，∵OA=5，AD=2，∴OD===．故答案为：．16．（4分）（2015?黄浦区二模）如图，在平行四边形ABCD中，点M是边CD中点，点N是边BC上的点，且=．设=，=，那么可用、表示为﹣．【分析】首先由四边形ABCD是平行四边形，求得==，又由点M是边CD中点，点N是边BC上的点，且=，求得与，再利用三角形法则求解即可求得答案．【解答】解：∵四边形ABCD是平行四边形，∴==，∵点M是边CD中点，点N是边BC上的点，且=，∴==，==，∴=﹣=﹣．故答案为：﹣．17．（4分）（2015?黄浦区二模）如图，△ABC是等边三角形，若点A绕点C顺时针旋转30°至点A′，联结A′B，则∠ABA′度数是15°．【分析】如图，首先运用旋转变换的性质得到AC=A′C，∠ACA′=30°；运用等腰三角形的性质得到，∠A′BC=45°，借助∠ABC=60°，即可解决问题．【解答】解：如图，由题意得：AC=A′C，∠ACA′=30°；∵△ABC为等边三角形，∴∠ACB=∠ABC=60°，AC=BC，∴BC=A′C，∠A′BC=∠BA′C==45°，∴∠ABA′=60°﹣45°=15°．18．（4分）（2015?黄浦区二模）如图1，点P是以r为半径的圆O外一点，点P′在线段OP上，若满足OP?OP′=r2，则称点P′是点P关于圆O的反演点．如图2，在Rt△ABO中，∠B=90°，AB=2，BO=4，圆O的半径为2，如果点A′、B′分别是点A、B关于圆O的反演点，那么A′B′的长是．【分析】先证明△AOB∽△B′OA′，然后根据相似三角形的对应角相等可以推知∠OA′B′=∠OBA=90°，根据勾股定理即可求得．【解答】解：∵A′、B′分别是点A、B关于圆O的反演点，∴=，又∵∠O=∠O，∴△AOB∽△B′OA′，∴∠OA′B′=∠OBA=90°，∵AB=2，BO=4，圆O的半径为2，∴OA=2，∴OA′==，OB′==1，∴A′B′==．故答案为：．三、解答题（48分）19．（6分）（2015?黄浦区二模）计算：40+﹣（﹣1）﹣1+|1﹣|．【分析】先根据0指数幂及负整数指数幂的计算法则、绝对值的性质及数的开方法则分别计算出各数，再根据实数混合运算的法则进行计算即可．【解答】解：原式=1+2﹣+﹣1=3﹣（+1）+﹣1=3﹣﹣1+﹣1=1．20．（6分）（2015?黄浦区二模）解方程组：．【分析】把x﹣y=1化为x=y+1，代入方程①，求出y，再把y值代入x=y+1，求出x 即可．【解答】解：由②得：x=y+1 ③，把③代入①得：（y+1）2﹣2y2=﹣2，即y2﹣2y﹣3=0，解得：y1=﹣1，y2=3，把y1=﹣1，y2=3代入③得x1=0，x2=4．故方程组的解为，．21．（6分）（2015?盘锦二模）温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：华氏度数x（℃）…0…35…100…摄氏度数y（℉）…32…95…212…（1）选用表格中给出的数据，求y关于x的函数解析式（不需要写出该函数的定义域）；（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数．【分析】（1）设一次函数的解析式为y=kx+b，由待定系数法求出其解即可；（2）当x=﹣5时代入（1）的解析式求出其解即可．【解答】解：（1）设y=kx+b，把（0，32）和（35，95）代入得：，解得：，∴y=．（2）当x=﹣5时，y=﹣9+32=23．∴某天的最低气温是﹣5℃，与之对应的华氏度数为23℉．22．（6分）（2015?黄浦区二模）如图，在梯形ABCD中，AD∥BC，AB⊥BC，已知AD=2，cot∠ACB=，梯形ABCD的面积是9；（1）求AB的长；（2）求tan∠ACD的值．【分析】（1）根据锐角三角函数设出边长，利用梯形的面积公式列方程即可；（2）作DH⊥AC于H，利用三角形相似，列比例式求出DH=，AH=，CH=AC﹣AH=，即可求出tan∠ACD==．【解答】解：（1）在R t ABC中，cot∠ACB==，设BC=4k，AB=3k，∴S梯形ABCD=（AD+BC）•AB=（2+4k）•3k=9，∴k=1或k=﹣（舍），∴AB=3；（2）作DH⊥AC于H，∵AD∥BC，∴∠DAH=∠ACB，∴△ADH∽△CAB，∴===，∴DH=，AH=，∴CH=AC﹣AH=，∴tan∠ACD==．23．（6分）（2015?黄浦区二模）如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；（1）求证：AE=CG；（2）求证：BE∥DF．【分析】（1）先证∠AED=∠CGD，再证明△ADE≌△CDG，根据全等三角形的对应边相等即可得出结论；（2）先证明△BCE≌△DCE，得出对应角相等∠BEC=∠DEG，得出∠BEC=∠DGE，即可证出平行线．【解答】证明：（1）∵DE=DG，∴∠DEG=∠DGE，∴∠AED=∠CGD，∵四边形ABCD是正方形，∴AD=CD=BC，∠DAC=∠BCE=∠DCA=45°，在△ADE和△CDG中，，∴△ADE≌△CDG（AAS），∴AE=CG；（2）在△B CE和△DCE中，，∴△BCE≌△DCE （SAS），∴∠BEC=∠DEG，∴∠BEC=∠DGE，∴BE∥DF．24．（9分）（2015?黄浦区二模）如图，在平面直角坐标系xOy中，已知点A的坐标为（a，3）（其中a＞4），射线OA与反比例函数y=的图象交于点P，点B、C分别在函数y=的图象上，且AB∥x轴，AC∥y轴；（1）当点P横坐标为6，求直线AO的表达式；（2）联结BO，当AB=BO时，求点A坐标；（3）联结BP、CP，试猜想：的值是否随a的变化而变化？如果不变，求出的值；如果变化，请说明理由．【分析】（1）根据自变量的值，可得函数值，根据待定系数法，可得函数解析式；（2）根据函数值，可得自变量的值，根据勾股定理，可得OB长，根据AB=OB，可得A点坐标；（3）联立函数解析式，可得方程组，根据解方程组，可得P点坐标，根据自变量与函数值的对应关系，可得B、C点坐标，根据三角形面积公式，可得答案．【解答】解：（1）当x=6时，y=2，∴P（6，2），设直线AO的解析式为y=kx，代入P（6，2）得k=，∴直线AO的解析式为y=x；（2）由AB∥x轴，得B点横坐标为4．当y=3时，x=4，∴B（4，3）．OB==5，∵AB=OB，∴5=a﹣4，即a=9，∴A（9，3）；（3）直线AO的解析式为y=x，联立y=，得，解得．∴P（2，），作PM⊥AB，PN⊥AC．当x=a时，y=，即C（a，），当y=3时，x=4，即B（4，3）．AC=3﹣，PN=a﹣2，AB=a﹣4，PM=3﹣，∴S △ABP=（a﹣4）（3﹣），S△ACP=（a﹣2）（3﹣），∴==1．25．（9分）（2015?黄浦区二模）如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF与边AB、线段DE分别交于点F、G；（1）求线段CD、AD的长；（2）设CE=x，DF=y，求y关于x的函数解析式，并写出它的定义域；（3）联结EF，当△EFG与△CDG相似时，求线段CE的长．【分析】（1）利用特殊角的三角函数可知sin∠B=，tan∠A=，由此求得线段CD、AD的长；（2）证得△CDE∽△BFC，得出=，整理得出答案即可；（3）分两种情况考虑：①当△EGF∽△DGC时；②当△FEG∽△CGD时；利用相似的性质探讨得出答案即可．【解答】解：（1）在Rt△BCD中，BC=2，∠B=90°﹣∠A=60°，sin∠B=，即CD=×2=，同理tan∠A=，AD==3；（2）∵∠CDE=∠BFC=90°﹣∠DCF，∠ECD=∠B=60°，∴△CDE∽△BFC，∴=，即=，∴y=﹣1，（≤x＜2）；（3）∠EGF=∠CGD=90°①当△EGF∽△DGC时，∠GEF=∠GDC，∴EF∥DC，∴=，即==，解得x=；②当△EG∽△CGD时，∴∠GEF=∠GCD=∠GDF，∴EF=DF，又∵CF⊥DE，∴EG=DG，∴CD=CE=；综上，CE=或；2020-2-8。

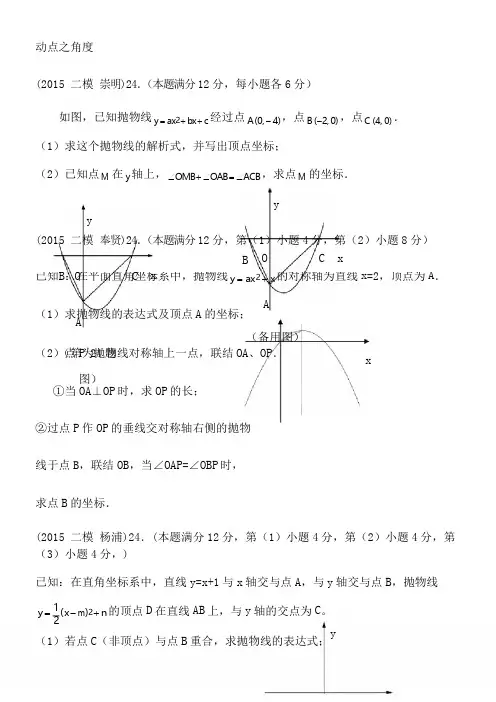
已知B ：在平面直角坐标系中，抛物线 y = ax 2 + x 的对称轴为直线 x =2，顶点为 A ．（1）求抛物线的表达式及顶点 A 的坐标； A点 P 24 题 y = ( x - m )2 + n 的顶点 D 在直线 AB 上，与 y 轴的交点为 C 。

动点之角度(2015 二模 崇明)24．（本题满分 12 分，每小题各 6 分）如图，已知抛物线 y = ax 2 + bx + c 经过点 A (0, - 4) ，点 B (-2, 0) ，点 C (4, 0) ．（1）求这个抛物线的解析式，并写出顶点坐标；（2）已知点 M 在 y 轴上， ∠OMB + ∠OAB = ∠ACB ，求点 M 的坐标．yy(2015 二模 奉贤)24．（本题满分 12 分，第（1）小题 4 分，第（2）小题 8 分）B OC x O C xA（备用图）（2）（第为抛物线对称轴上一点，联结 OA 、OP ．x图）①当 OA ⊥OP 时，求 OP 的长；②过点 P 作 OP 的垂线交对称轴右侧的抛物线于点 B ，联结 OB ，当∠OAP =∠OBP 时，求点 B 的坐标．(2015 二模 杨浦)24．(本题满分 12 分，第（1）小题 4 分，第（2）小题 4 分，第 （3）小题 4 分，)已知：在直角坐标系中，直线 y =x +1 与 x 轴交与点 A ，与 y 轴交与点 B ，抛物线12（1）若点 C （非顶点）与点 B 重合，求抛物线的表达式；y（2）若抛物线的对称轴在y轴的右侧，且CD⊥AB，求∠CAD的正切值；（3）在第（2）的条件下，在∠ACD的内部作射线CP交抛物线的对称轴于点P，使得∠DCP=∠CAD，求点P的坐标。

动点之相似(2015二模宝山嘉定)24．（本题满分12分，每小题满分各4分）已知平面直角坐标系xOy（图9），双曲线y=k(k≠0)与直线y=x+2都经过点xA(2,m)．（1）求k与m的值；（2）此双曲线又经过点B(n,2)，过点B的直线BC与直线y=x+2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）在（2）的条件下，设直线y=x+2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．y(2015二模金山)24．（本题满分12分）已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0)，B(4,0)两点，与y轴交于点C．（1）求抛物线y=ax2+bx-8(a≠0)的解析式，并求出顶点P的坐标；（2）求∠APB的正弦值；B A 如图，在直角坐标系 xOy 中，抛x 物线 y = ax O 2 - 2ax + c 与 x 轴的正半轴相x 交于点 A 、与 y 轴 （3）直线 y = kx + 2 与 y 轴交于点 N ，与直线 AC 的交点为 M ，当 ∆MNC 与 ∆AOC 相似时，求点 M 的坐标．动点之面积(2015 二模 黄浦)24. （本题满第（1）小题满分 3 分，第（2） 分 12 分，小题满分 4分，第（3）小题满分 5 分）如图 7，在平面直角坐标系xOy 中，已知点 A 的坐标为（a ，3）（其中a >4)，射线 OA与反比例函数y = 12 的图像交于点 P ，点 B 、C 分别在函数y = 12 的图像上，且 AB //x 轴，xxAC //y 轴．（1）当点 P 横坐标为 6，求直线 AO 的表达式；（2）联结 BO ，当 AB = BO 时，求点 A 坐标；（3）联结 BP 、CP ，试猜想：S ∆ABP 的值是否随 a 的变化而变化？如果不变，求出 S ∆ABP 的SS∆ACP∆ACP值；如果变化，请说明理由．(2015 二模 静安青浦)24．（本题满分 12 分，第（1）小题满分 8 分，第（2）小题满分 4 分）PCO 图7的正半轴相交于点 B ，它的对称轴与 x 轴相交于点 C ，且∠OBC =∠OAB ，AC =3．（1）求此抛物线的表达式；如图，已知抛物线 y = x 2 - 2tx + t 2 - 2 的顶点 A 在第四象限，过点 A 作 AB ⊥y 轴于点 B ，A (-1,0)，B (4,0 )，C (0,2 )．点D 是点 C 关于原点的对称C 点A ，联结 B D ，点E 是 x 轴上的E （2）如果点 D 在此抛物线上，DF ⊥OA ，垂足为 F ，DF 与线段 AB 相交于点G ，且 S∆ADG : S∆AFG= 3 : 2 ，求点 D 的坐标．y(2015 二模 长宁)24．（本题满分 12 分）BCC 是线段 AB 上一点(不与 A 、B 重合)，过点 C 作 CD ⊥x 轴于点 D ，并交抛物线于点 P .（1）若点 C 的横坐标为 1，且是线段 AB 的中点，求点 P 的坐标；（2）若直线 AP 交 y 轴负半轴于点 E ，且 AC =CP ，求四边形 OEPD 的面积 S 关于 t 的函数解析式，并写出定义域；（3）在（2）的条件下，当△ADE 的面积等于 2S 时 ，求 t 的值.y动点之直角、等腰三角形存在性DO x(2015 二模 普陀 ) 如图10，在平面直角坐标系xOy 中，二次函数的图像经过点 PB一个动点，设点 E 的坐标为(m , 0)，过点 E 作 x 轴的垂线 l 交抛物线于点 P ．第 24 题（1）求这个二次函数的解析式；图（2）当点E 在线段 OB 上运动时，直线 l 交 BD 于点 Q ．当四边形CDQP 是平行四边形时，求 m 的值；（3）是否存在点 P ，使△ B DP 是不以 BD 为斜边的直角三角形，如果存在，请直接写出点 P 的坐标；如果不存在，请说明理由．y y(2015二模松江)24．（本题满分12分，每小题各4分）C C如图，二次函数y=-x2+bx的图像与x轴的正半轴交于点A（4，0），过A点的直线与A OB x A O B xy轴的正半轴交于点B，与二次函数的图像交于另一点C，过点C作CH⊥x轴，垂足为H．设二次函数图像的顶点为D，其对称轴与直线AB及x轴分别交于点E和点F．（1）求这个二次函数的解析式；（2）如果CE=3BC，求点B的坐标；（3）如果△DHE是以DH为底边的等腰三角形，求点E的坐标．动点之梯形(2015二模徐汇)24．如图，在平面直角坐中，O为坐标原点，开口向上的抛物线与x点A（－1，0）和点B（3，0），D为抛物线的直线AC与抛物线交于点C（5，6）．（1）求抛物线的解析式；（2）点E在x轴上，且∆AEC和∆AED相似，求点E的坐标；标系轴交于顶点，（3）若直角坐标平面中的点F和点A、C、D构成求点F的坐标．其他直角梯形，且面积为16，试（(2015 二模 闵行)24．（本题满分 12 分，其中每小题各 4 分）如图，已知在平面直角坐标系 xOy 中，抛物线 y = ax 2 - 2ax - 4 与 x 轴相交于 A 、B 两点，与 y 轴相交于点 C ，其中点 A 的坐标为（-3，0）．点 D 在线段 AB 上，AD = AC ．（1）求这条抛物线的关系式，并求出抛物线的对称轴；（2）如果以 DB 为半径的圆 D 与圆 C 外切，求圆 C 的半径；（3）设点 M 在线段 AB 上，点 N 在线段 BC 上．如果线段 MN 被直线 CD 垂直平分，求BN 的值． CN(2015 二模 浦东)24． 本题满分 12 分，其中第（1）小题 3 分，第（2）小题 4 分，第（3）小题 5 分） 已知：如图，直线 y =kx +2 与 x 轴的正半轴相交于点 A（t ,0）、与 y 轴相交于点 B ，抛物线 y = - x 2 + bx + c 经过点 A 和点 B ，点 C 在第三象限内，且 AC ⊥AB ，tan∠ACB = 1 ．2（1）当 t =1 时，求抛物线的表达式；（2）试用含 t 的代数式表示点 C 的坐标；（3）如果点 C 在这条抛物线的对称轴上，求 t2020-2-8的值．。

《2015年上海各区中考数学二模压轴题图文解析》目录2015年上海各区中考数学二模第24、25题例1 2015年宝山区嘉定区中考数学二模第24、25题图文解析/2例2 2015年奉贤区中考数学二模第24、25题图文解析/6例3 2015年虹口区中考数学二模第24、25题图文解析/10例4 2015年黄浦区中考数学二模第24、25题图文解析14例5 2015年金山区中考数学二模第24、25题图文解析/18例6 2015年静安区青浦区中考数学二模第24、25题图文解析/22例7 2015年闵行区中考数学二模第24、25题图文解析/26例8 2015年浦东新区中考数学二模第24、25题图文解析/30例9 2015年普陀区中考数学二模第24、25题图文解析34例10 2015年松江区中考数学二模第24、25题图文解析38例11 2015年徐汇区中考数学二模第24、25题图文解析42例12 2015年杨浦区中考数学二模第24、25题图文解析/46例13 2015年长宁区中考数学二模第24、25题图文解析/50例14 2015年崇明县中考数学二模第24、25题图文解析/54例15 2015年闸北区中考数学二模第24、25题图文解析/592015年上海各区中考数学二模第18题例1 2015年宝山区嘉定区中考数学二模第18题图文解析/63例2 2015年奉贤区中考数学二模第18题图文解析/64例3 2015年虹口区中考数学二模第18题图文解析/615例4 2015年黄浦区中考数学二模第18题图文解析/66例5 2015年金山区中考数学二模第18题图文解析/67例6 2015年静安区青浦区中考数学二模第18题图文解析/68例7 2015年闵行区中考数学二模第18题图文解析/69例8 2015年浦东新区中考数学二模第18题图文解析/70例9 2015年普陀区中考数学二模第18题图文解析/71例10 2015年松江区中考数学二模第18题图文解析/72例11 2015年徐汇区中考数学二模第18题图文解析/73例12 2015年杨浦区中考数学二模第18题图文解析/74例13 2015年长宁区中考数学二模第18题图文解析/75例14 2015年崇明县中考数学二模第18题图文解析/76例15 2015年闸北区中考数学二模第18题图文解析/77例 2015年上海市宝山区嘉定区中考模拟第24题如图1，在平面直角坐标系中，双曲线kyx=（k≠0）与直线y＝x＋2都经过点A(2, m)．（1）求k与m的值；（2）此双曲线又经过点B(n, 2)，过点B的直线BC与直线y＝x＋2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）在（2）的条件下，设直线y＝x＋2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．图1动感体验请打开几何画板文件名“15宝山嘉定24”，拖动点E在射线CB上运动，可以体验到，△ACE与△ACD相似，存在两种情况．思路点拨1．直线AD//BC，与坐标轴的夹角为45°．2．求△ABC的面积，一般用割补法．3．讨论△ACE与△ACD相似，先寻找一组等角，再根据对应边成比例分两种情况列方程．满分解答（1）将点A(2, m)代入y＝x＋2，得m＝4．所以点A的坐标为(2, 4)．将点A(2, 4)代入kyx=，得k＝8．（2）将点B(n, 2)，代入8yx=，得n＝4．所以点B的坐标为(4, 2)．设直线BC为y＝x＋b，代入点B(4, 2)，得b＝－2．所以点C的坐标为(0,－2)．由A(2, 4) 、B(4, 2) 、C (0,－2)，可知A、B两点间的水平距离和竖直距离都是2，B、C两点间的水平距离和竖直距离都是4．所以AB＝22，BC＝42，∠ABC＝90°．图22所以S△ABC＝12BA BC⋅＝122422⨯⨯＝8．（3）由A(2, 4) 、D(0, 2) 、C (0,－2)，得AD＝22，AC＝210．由于∠DAC＋∠ACD＝45°，∠ACE＋∠ACD＝45°，所以∠DAC＝∠ACE．所以△ACE与△ACD相似，分两种情况：①如图3，当CE ADCA AC=时，CE＝AD＝22．此时△ACD≌△CAE，相似比为1．②如图4，当CE ACCA AD=时，21021022CE=．解得CE＝102．此时C、E两点间的水平距离和竖直距离都是10，所以E(10, 8)．图3 图4考点伸展第（2）题我们在计算△ABC的面积时，恰好△ABC是直角三角形．一般情况下，在坐标平面内计算图形的面积，用割补法．如图5，作△ABC的外接矩形HCNM，MN//y轴．由S矩形HCNM＝24，S△AHC＝6，S△AMB＝2，S△BCN＝8，得S△ABC＝8．图54例 2015年上海市宝山区嘉定区中考模拟第25题在Rt △ABC 中，∠C ＝90°，BC ＝2，Rt △ABC 绕着点B 按顺时针方向旋转，使点C 落在斜边AB 上的点D ，设点A 旋转后与点E 重合，联结AE ．过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合（如图1），求cot ∠BAE 的值；（2）若点M 在边BC 上（如图2），设边长AC ＝x ，BM ＝y ，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围；（3）若∠BAE ＝∠EBM ，求斜边AB 的长．图1 图2动感体验请打开几何画板文件名“15宝山嘉定25”，拖动点A 上下运动，可以体验到，△ABE 保持等腰三角形，∠BAE ＝∠EBM 按照点M 与点B 的位置关系存在两种情况． 思路点拨1．第（1）题的特殊性是∠DEB ＝∠CAB ＝∠EBD ，△EDB 是等腰直角三角形．2．第（1）题暗示了第（2）题中蕴含着三个等角，因此寻找相似三角形．3．第（3）题∠BAE ＝∠EBM 要分两种情况考虑，各有各的特殊性．满分解答（1）如图3，当点M 与点B 重合时，EB //AC ．所以∠CAB ＝∠EBD ．又因为旋转前后∠CAB ＝∠DEB ，所以∠EBD ＝∠DEB ．所以△EDB 和△ACB 是等腰直角三角形．已知BC ＝2，所以AC ＝2，AB ＝22． 在Rt △AED 中，ED ＝2，AD ＝222-，所以cot ∠BAE ＝AD ED＝2222-＝21-．图3 图4（2）在Rt △ABC 中，BC ＝2，AC ＝x ，所以AB ＝24x +． 如图4，设EM 与AB 交于点F ．由FM //AC ，得BM BF BC BA =，即224y BFx =+．所以BF ＝242y x +． 由于BD ＝BC ＝2，所以DF ＝2422y x +-． 由∠DEB ＝∠CAB ＝∠DFE ，∠EDB 是公共角，得△DEB ∽△DFE ．所以DE 2＝DF ·DB ，即2242(2)2y x x +=-．整理，得2244x y x -=+． 定义域是0＜x ＜2．（3）已知BA ＝BE ，所以∠BAE ＝∠BEA ．当∠BAE ＝∠EBM 时，∠BAE ＝∠BEA ＝∠EBM ．按照M 、B 的位置分两种情况： ①如图5，当M 在B 右侧时，由∠BEA ＝∠EBM ，得AE //CM ．此时∠BAE ＝∠ABC ．又已知∠ABC ＝∠EBD ，所以∠ABC ＝∠EBD ＝∠EBM ＝60°．在Rt △ABC 中，AB ＝2BC ＝4．②如图6，当M 在B 左侧时，在△BAE 中，∠BAE ＝∠BEA ＝2∠ABE ．所以∠ABE ＝36°，∠BAE ＝∠BEA ＝72°．延长EA 交BC 的延长线于G ，那么∠G ＝36°，AG ＝AB ，GE ＝GB ＝2CB ＝4． 由于点A 是GE 的黄金分割点，所以512AG GE -=．所以AB ＝AG ＝252-．图5 图6考点伸展第（3）题的第②种情况，我们直接应用了黄金分割数，也可以用相似比来解． 由∠BAE ＝∠BEA ＝∠MBE ，容易得到GB ＝GE ＝4，AG ＝AB ＝BE ．由△GBE ∽△BAE ，得到EB 2＝EA ·EG ．设AB ＝BE ＝m ．于是得到24(4)m m =-．整理，得m 2＋4m －16＝0．解得252m =．6例 2015年上海市奉贤区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2＋x 的对称轴为直线x ＝2，顶点为A ．（1）求抛物线的表达式及顶点A 的坐标；（2）点P 为抛物线对称轴上一点，联结OA 、OP ．①当OA ⊥OP 时，求OP 的长；②过点P 作OP 的垂线交对称轴右侧的抛物线于点B ，联结OB ，当∠OAP ＝∠OBP 时，求点B 的坐标．图1动感体验请打开几何画板文件名“15奉贤24”，拖动点P 在抛物线的对称轴上运动，可以体验到，△BNP ∽△PMO 保持不变，当∠OAP ＝∠OBP 时，△BOP ∽△AOH ． 思路点拨1．根据等角的余角相等，通过已知的等角寻找未知的等角．2．过直角顶点P 向坐标轴画垂线，可以构造相似的直角三角形，于是通过对应边成比例，可以列方程．满分解答（1）由抛物线的对称轴为122x a =-=，可得14a =-． 所以抛物线的表达式为2211(2)144y x x x =-+=--+． 顶点A 的坐标为(2, 1)．（2）①如图2，设AP 与x 轴交于点H ．由A (2, 1)，可得tan ∠OAH ＝2．当OA ⊥OP 时，∠POH ＝∠OAH ．所以tan ∠POH ＝PH OH＝2． 因此PH ＝2OH ＝4．所以OP ＝25． 图2②如图3，当∠OAP ＝∠OBP 时，tan ∠AOH ＝tan ∠BOP ．所以2PO HO PB HA==．如图4，过点P 作PM ⊥y 轴于M ，过点B 作x 轴的垂线交直线PM 于N ．由△OMP ∽△PNB ，得2OM MP PO PN NB BP===．所以OM ＝2PN ，MP ＝2NB ． 设21(,)4B x x x -+，P (2, n )，那么2(2)n x -=-，2122()4x x n =-+-． 将n ＝4－2x 代入2114x x n -+-=，整理，得x 2－12x ＋20＝0． 解得x ＝10，或x ＝2（B 与A 重合，舍去）．所以点B 的坐标为(10, －15)．图3 图4考点伸展如果应用四点共圆的知识，结合勾股定理，那么第（2）②题可以这样做：如图3，当∠OAP ＝∠OBP 时，A 、B 、P 、O 四点共圆．此时∠OAB ＝∠OPB ＝90°．所以OB 2＝OA 2＋AB 2．设21(,)4B x x x -+，那么22222211()5(2)(1)44x x x x x x ⎡⎤+-+=+-+-+-⎢⎥⎣⎦． 整理，得x 2－12x ＋20＝0．解得x ＝10，或x ＝2．所以B (10, －15)．例 2015年上海市奉贤区中考模拟第25题如图1，已知线段AB＝8，以A为圆心，5为半径作⊙A，点C在⊙A上，过点C作CD//AB 交⊙A于点D（点D在点C右侧），联结BC、AD．（1）若CD＝6，求四边形ABCD的面积；（2）设CD＝x，BC＝y，求y与x的函数关系式及自变量x的取值范围；（3）设BC的中点为M，AD的中点为N，线段MN交⊙A于点E，联结CE，当CD取何值时，CE//AD．图1 备用图动感体验请打开几何画板文件名“15奉贤25”，拖动点C在圆上运动，可以体验到，当CE//AD 时，四边形CEND是平行四边形，四边形CEAN是平行四边形，四边形CF AG是矩形．思路点拨1．已知△ABC的三边长分别为5，8，y，构造AB边上的高CK，那么CK为两个直角三角形的公共直角边，根据勾股定理列方程，可以得到y关于x的关系式．2．当CE//AD时，注意到CE与AN、DN的关系都是平行且相等．满分解答（1）如图2，过点A作AH⊥CD，垂足为H．在△ACD中，AC＝AD＝5，CD＝6，所以CH＝DH＝3．所以AH＝4．所以S梯形ABCD＝1()2CD AB AH+⨯＝1(68)42+⨯＝28．图2 图3（2）如图3，作CK⊥AB，垂足为K，那么四边形CKAH为矩形．在△ACD中，AC＝AD＝5，CH＝DH＝12 x．8在△ABC 中，BC ＝y ，AC ＝5，AK ＝12x ，BK ＝182x -． 由CK 2＝BC 2－BK 2＝AC 2－AK 2，得222211(8)5()22y x x --=-． 整理，得898y x =-．自变量x 的取值范围是0＜x ＜10．（3）如图4，已知MN 是梯形ABCD 的中位线，MN //CD ，当CE //AD 时，四边形CEND 是平行四边形，此时CE ＝DN ＝12AD ＝52． 由CE //NA ，CE ＝NA ，得四边形CEAN 是平行四边形．所以CN ＝EA ＝CA ＝5．作CG ⊥AN 于G ，那么AG ＝12AN ＝14AD ＝54．所以DG ＝515544-=． 在Rt △CAG 中，AG ＝54，CA ＝5，由勾股定理，得CG ＝5154． 在Rt △CDG 中，CG ＝5154，DG ＝154，由勾股定理，得CD ＝562．图4 图5考点伸展第（3）题还可以用相似比来解：如图5，设直线AE 与DC 的延长线交于点P ，与⊙A 交于点Q ，那么CE 是△P AD 的中位线，因此PC ＝CD ＝x ，PE ＝EA ＝AQ ＝5．由CE //DA ，得∠1＝∠3，∠2＝∠4．又因为∠1＝∠2，所以∠3＝∠4．于是可得∠Q ＝∠5＝∠6．由△PCE ∽△PQD ，得PC PQ PE PD =．所以1552x x =．解得562x = 由△PDA ∽△PQD ，得PD PQ PA PD =．所以215102x x =．解得562x =例 2015年上海市虹口区中考模拟第24题如图1，在平面直角坐标系中，抛物线y＝ax2＋bx＋c过A(－1,0)、B(3,0)、C(2, 3)三点，与y轴交于点D．（1）求该抛物线的解析式，并写出该抛物线的对称轴；（2）分别联结AD、DC、CB，直线y＝4x＋m与线段DC交于点E，当此直线将四边形ABCD的面积平分时，求m的值；（3）设点F为该抛物线对称轴上一点，当以A、B、C、F为顶点的四边形是梯形时，请直接写出所有满足条件的点F的坐标．图1动感体验请打开几何画板文件名“15虹口24”，拖动点P运动，可以体验到，经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．拖动点F在抛物线的对称轴上运动，可以体验到，以A、B、C、F为顶点的梯形有3个．思路点拨1．已知抛物线与x轴的两个交点，设两点式比较简便．2．经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．3．过△ABC的3个顶点分别画对边的平行线，三条直线与抛物线的对称轴的3个交点，就是符合条件的点F．满分解答（1）因为抛物线与x轴交于A(－1,0)、B(3,0)两点，设y＝a(x＋1)(x－3)．将点C(2, 3)代入，得3＝－3a．解得a＝－1．所以抛物线的解析式为y＝－(x＋1)(x－3)＝－x2＋2x＋3.对称轴是直线x＝1．（2）如图2，由C(2, 3)、D(0, 3)，得CD//x轴．所以四边形ABCD是梯形．经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．梯形ABCD的中位线的中点为3(1,)2，将点3(1,)2代入y＝4x＋m，得m＝52．（3）符合条件的点F有3个，坐标分别为(1, 3)，(1,－2)，(1,－6)．10图2 图3考点伸展第（3）题这样解：过△ABC的3个顶点分别画对边的平行线，三条直线与抛物线的对称轴的3个交点，就是符合条件的点F．①如图3，当CF//AB时，点F的坐标是(1, 3)．②如图4，当BF//AC时，由tan∠CAM＝tan∠FBH，得CM FHAM BH=．所以332FH=．解得FH＝2．此时点F的坐标为(1,－2)．③如图5，当AF//CB时，由tan∠CBM＝tan∠F AH，得CM FHBM AH=．所以312FH=．解得FH＝6．此时点F的坐标为(1,－6)．图4 图512例 2015年上海市虹口区中考模拟第25题如图1，在Rt △ABC 中，∠ACB ＝90°，AB ＝13，CD //AB ，点E 为射线CD 上一动点（不与点C 重合），联结AE 交边BC 于F ，∠BAE 的平分线交BC 于点G ．（1）当CE ＝3时，求S △CEF ∶S △CAF 的值；（2）设CE ＝x ，AE ＝y ，当CG ＝2GB 时，求y 与x 之间的函数关系式；（3）当AC ＝5时，联结EG ，若△AEG 为直角三角形，求BG 的长．图1动感体验请打开几何画板文件名“15虹口25”，拖动直角顶点C 运动，可以体验到，CG ＝2GB 保持不变，△ABC 的形状在改变，EA ＝EM 保持不变．点击屏幕左下角的按钮“第（3）题”，拖动E 在射线CD 上运动，可以体验到，△AEG 可以两次成为直角三角形． 思路点拨1．第（1）题中的△CEF 和△CAF 是同高三角形，面积比等于底边的比．2．第（2）题中的△ABC 是斜边为定值的形状不确定的直角三角形．3．第（3）题中的直角三角形AEG 分两种情况讨论．满分解答（1）如图2，由CE //AB ，得313EF CE AF BA ==． 由于△CEF 与△CAF 是同高三角形，所以S △CEF ∶S △CAF ＝3∶13．（2）如图3，延长AG 交射线CD 于M ． 图2由CM //AB ，得2CM CG AB BG==．所以CM ＝2AB ＝26． 由CM //AB ，得∠EMA ＝∠BAM ．又因为AM 平分∠BAE ，所以∠BAM ＝∠EAM ．所以∠EMA ＝∠EAM ．所以y ＝EA ＝EM ＝26－x ．图3 图4（3）在Rt△ABC中，AB＝13，AC＝5，所以BC＝12．①如图4，当∠AGE＝90°时，延长EG交AB于N，那么△AGE≌△AGN．所以G是EN的中点．所以G是BC的中点，BG＝6．②如图5，当∠AEG＝90°时，由△CAF∽△EGF，得FC FA FE FG=．由CE//AB，得FC FB FE FA=．所以FA FBFG FA=．又因为∠AFG＝∠BF A，所以△AFG∽△BF A．所以∠F AG＝∠B．所以∠GAB＝∠B．所以GA＝GB．作GH⊥AH，那么BH＝AH＝132．在Rt△GBH中，由cos∠B＝BHBG，得BG＝132÷1213＝16924．图5 图6考点伸展第（3）题的第②种情况，当∠AEG＝90°时的核心问题是说理GA＝GB．如果用四点共圆，那么很容易．如图6，由A、C、E、G四点共圆，直接得到∠2＝∠4．上海版教材不学习四点共圆，比较麻烦一点的思路还有：如图7，当∠AEG＝90°时，设AG的中点为P，那么PC和PE分别是Rt△ACG和Rt △AEG斜边上的中线，所以PC＝PE＝P A＝PG．所以∠1＝2∠2，∠3＝2∠5．如图8，在等腰△PCE中，∠CPE＝180°－2(∠4＋∠5)，又因为∠CPE＝180°－(∠1＋∠3)，所以∠1＋∠3＝2(∠4＋∠5)．所以∠1＝2∠4．所以∠2＝∠4＝∠B．所以∠GAB＝∠B．所以GA＝GB．图7 图814例 2015年上海市黄浦区中考模拟第24题如图1，在平面直角坐标系中，已知点A 的坐标为(a , 3)（其中a ＞4），射线OA 与反比例函数12y x =的图像交于点P ，点B 、C 分别在函数12y x =的图像上，且AB //x 轴，AC //y 轴．（1）当点P 的横坐标为6时，求直线AO 的表达式；（2）联结BO ，当AB ＝BO 时，求点A 的坐标；（3）联结BP 、CP ，试猜想ABP ACP S S △△的值是否随a 的变化而变化？如果不变，求出ABPACPS S △△的值；如果变化，请说明理由．图1 备用图动感体验请打开几何画板文件名“15黄浦24”，拖动点A 在点B 右侧运动，观察度量值，可以体验到，△ABP 与△ACP 的面积保持相等．事实上，四边形ABDC 是矩形，△ABP 与△ACP 是同底等高的两个三角形．思路点拨1．点B 是确定的，点C 、P 随点A 的改变而改变．2．已知a ＞4隐含了点A 在点B 的右侧这个条件．满分解答（1）如图1，当x ＝6时，12y x=＝2．所以点P 的坐标为(6, 2)． 由O (0, 0)、P (6, 2)，得直线AO 的解析式为13y x =． （2）如图2，因为AB //x 轴，A (a , 3)，所以点B 的纵坐标为3．又因为点B 在反比例函数12y x=的图像上，所以B (4, 3)．因此OB ＝5． 所以当AB ＝BO ＝5时，点A 的坐标为(9, 3)．（3）如图3，过点B 向x 轴作垂线交OA 于点D ，联结CD ．由于直线OA 的解析式为3y x a =，所以点D 的坐标为12(4)a，．由于AC //y 轴，所以点C 的坐标为12()a a ，． 所以CD //x 轴．因此四边形ABDC 是矩形． 所以点B 、C 到对角线AP 的距离相等．因此△ABP 与△ACP 是同底等高的两个三角形，它们的面积相等．所以ABP ACPS S △△＝1．图2 图3考点伸展第（3）题也可以这样说理：如图3，ABP ABD S S △△＝AP AD ，ACP ACD S S △△＝AP AD，而S △ABD ＝S △ACD ，所以ABP ACP S S △△＝1． 第（3）题还可以计算说理：如图4，作PM ⊥AB 于M ，作PN ⊥AC 于N ．设点P 的坐标为12()m m ，．将点P 12()m m，代入直线OA 的解析式3y x a=，可以得到24m a =． 于是，由A (a , 3)、B (4, 3)、C 12()a a ，、P 12()m m，，可得 S △ABP ＝12AB PM ⋅＝112(4)(3)2a m --＝3416(4)2a a m m--+＝2316(4)24m m m --+， S △ACP ＝12AC PN ⋅＝112(3)()2a m a --＝34(4)2m a m a--+＝2316(4)24m m m --+． 所以S △ABP ＝S △ACP ．而事实上，如图5，由于S 1＝S 2，所以S △ABO ＝S △ACO ．所以B 、C 到AO 的距离相等．于是△ABP 与△ACP 就是同底等高的三角形．图4 图5例 2015年上海市黄浦区中考模拟第25题如图1，Rt△ABC中，∠C＝90°，∠A＝30°，BC＝2，CD是斜边AB上的高，点E 为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF与边AB、线段DE 分别交于点F、G．（1）求线段CD、AD的长；（2）设CE＝x，DF＝y，求y关于x的函数解析式，并写出它的定义域；（3）联结EF，当△EFG与△CDG相似时，求线段CE的长．图1动感体验请打开几何画板文件名“15黄浦25”，拖动点E在AC边上运动，可以体验到，△EFG 与△CDG相似存在两种情况．一种情况是FC垂直平分DE，另一种情况是EF⊥AB．思路点拨1．图形中的垂直关系较多，因此互余的角较多，相等的角较多．把相等的角都标注出来，便于分析题意．2．求y关于x的函数关系式，设法构造相似三角形．3．△EFG与△CDG都是直角三角形，分两种情况讨论相似．按照对应的锐角相等，可以推出相似时的特殊的位置关系．满分解答（1）在Rt△ABC中，∠A＝30°，BC＝2，所以AB＝4，AC＝23．在Rt△ACD中，∠A ＝30°，AC＝23，所以CD＝3，AD＝3．（2）如图2，∠CDE与∠BFC都是∠EDF的余角，所以∠CDE＝∠BFC．又因为∠DCE＝∠B＝60°，所以△CDE∽△BFD．所以CD BFCE BC=，即312yx+=．整理，得23xyx-=．定义域是32≤x＜23．图2（3）△EFG与△CDG都是直角三角形，分两种情况讨论相似：①如图3，当∠FEG＝∠DCG时，由于∠FDG＝∠DCG，所以∠FEG＝∠FDG．因此FE＝FD．所以FC垂直平分DE．此时CE＝CD＝3．16②如图4，当∠FEG＝∠CDG时，EF//CD．此时EF⊥AB．作EH⊥CD于H，那么四边形EFDH是矩形，DF＝HE．所以y＝32x．解2332xxx-=，得3393x-±=．此时3933CE-=．图3 图4考点伸展第（2）题也可以这样思考：如图5，过点E作EH⊥CD，垂足为H．在Rt△CEH中，∠CEH＝30°，CE＝x，所以CH＝12x，EH＝32x．如图6，由tan∠DEH＝tan∠DCF，得13(3)::322x x y-=．整理，得23xyx-=．图5 图6 图7 第（2）题还可以如图6这样，过点C作AB的平行线交DE的延长线于M．由tan∠M＝tan∠DCF，得CD DFCM DC=．所以CM＝23CDDF y=．由MC//AD，得CM CEAD AE=．所以323xCMx=-．由3323xy x=-，得23xyx-=．定义域的两个临界值，如图8，CE＝12CD＝32；如图9，CE＝CA＝23．图8 图9例 2015年上海市金山区中考模拟第24题已知抛物线y＝ax2＋bx－8（a≠0）经过A(－2,0)、B(4, 0)两点，与y轴交于点C．（1）求抛物线y＝ax2＋bx－8（a≠0）的解析式，并求出顶点P的坐标；（2）求∠APB的正弦值；（3）直线y＝kx＋2 与y轴交于点N，与直线AC的交点为M，当△MNC与△AOC相似时，求点M的坐标．图1动感体验请打开几何画板文件名“15金山24”，拖动点M在AC上运动，可以体验到，△MNC 与△AOC相似存在两种情况．思路点拨1．用面积法求等腰三角形P AB的腰上的高，进而可以求顶角的正弦值．2．探求△MNC与△AOC相似，可以转化为探求直角三角形MNC．满分解答（1）因为抛物线y＝ax2＋bx－8与x轴交于A(－2,0)、B(4, 0)两点，设y＝a(x＋2)(x－4)＝ax2－2ax－8a．所以－8a＝－8．解得a＝1．所以y＝x2－2x－8＝(x－1)2－9．所以顶点P的坐标为(1,－9)．（2）如图2，由A(－2,0)、B(4, 0)、P(1,－9)，得AB＝6，PB＝P A＝310．作PG⊥AB，AH⊥PB，垂足分别为G、H．由S△P AB＝1122AB PG PB AH⋅=⋅，得699105310AB PGAHPB⋅⨯===．在Rt△APH中，sin∠APB＝910331055AHPA=÷=．图2 （3）由y＝kx＋2，得点N的坐标为(0, 2)．由A(－2,0)、C(0, －8)，得直线AC的解析式为y＝－4x－8．因为△MNC与△AOC有公共的锐角∠ACO，所以分两种情况讨论相似：18①如图3，当∠MNC＝90°时，14NM OANC OC==．所以1105442NM NC===．此时点M的坐标为5(,2)2-．②如图4，当∠NMC＝90°时，过点M作x轴的垂线，过点N、C分别作y轴的垂线，构造直角三角形NEM和直角三角形MFC，那么△NEM∽△MFC．所以EN FM EM FC=．设点M的坐标为(x, －4x－8)，那么(48)(8)2(48)x xx x-----=----．解得4017x=-．此时点M的坐标为4024(,)1717-．图3 图4 图5考点伸展第（3）题也可以这样解：①如图3，当∠MNC＝90°时，MN//x轴，所以y M＝2．解方程－4x－8＝2，得52x=-．此时点M的坐标为5(,2)2-．②如图5，当∠NMC＝90°时，设直线NM交x轴于K，那么△NOK≌△AOC．所以OK＝OC＝8．所以直线NM的解析式为124y x=+．联立y＝－4x－8和124y x=+，解得4017x=-，2417y=．此时M4024(,)1717-．例 2015年上海市金山区中考模拟第25题如图1，已知在△ABC中，AB＝AC＝10，tan∠B＝43．（1）求BC的长；（2）点D、E 分别是AB、AC的中点，不重合的两动点M、N在边BC上（点M、N不与点B、C重合），且点N始终在点M的右边，联结DN、EM交于点O．设MN＝x，四边形ADOE的面积为y．①求y与x的函数关系式，并写出定义域；②当△OMN是等腰三角形且BM＝1时，求MN的长．图1动感体验请打开几何画板文件名“15金山25”，拖动点N在MC上运动，可以体验到，等腰三角形OMN存在两种情况．思路点拨1．把四边形ADOE分割为△ADE和△DOE，△DOE与△NOM是相似的．2．分三种情况讨论等腰三角形OMN，其中NM＝NO是不存在的．满分解答（1）如图2，作AF⊥BC，垂足为F．在Rt△ABF中，AB＝10，tan∠B＝43，设BF＝3m，AF＝4m，那么AB＝5m．所以5m＝10．解得m＝2．所以BF＝6，AF＝8．因为AB＝AC，AF⊥BC，所以BC＝2BF＝12．图2（2）①如图3，S△ABC＝1112848 22BC AF⋅=⨯⨯=．因为DE是△ABC的中位线，所以DE＝12BC＝6，S△ADE＝14S△ABC＝12．过点O作BC的垂线，垂足为H，交DE于G，那么GH＝12AF＝4．由DE//BC，得DE GONM HO=，即64GOx GO=-．所以246GOx=+．因此S△DOE＝11247262266 DE GOx x⋅=⨯⨯=++．所以y＝S四边形ADOE＝S△ADE＋S△DOE＝7212144 1266xx x++=++．定义域是0＜x＜12．②如图4，作EQ⊥BC，垂足为Q．在Rt△ECQ中，EC＝5，所以EQ＝4，CQ＝3．20在Rt△EMQ中，MQ＝11－3＝8，EQ＝4，所以EM＝45．如图5，在Rt△DMP中，DP＝4，MP＝3－1＝2，所以DM＝25．图3 图4 图5 因为△OMN∽△OED，所以讨论等腰△OMN可以转化为讨论等腰△OED．（I）如图6，当OM＝ON时，OE＝OD．此时点O在ED的垂直平分线上．所以BN＝CM＝11．此时MN＝22－12＝10．．（II）如图7，当MO＝MN时，EO＝ED＝6．此时MN＝MO＝45x（III）如果NM＝NO，那么DO＝DE＝6．如图8，因为DM＝25＜6，所以以D为圆心，DE为半径的⊙D与线段ME只有一个交点E，因此不存在NM＝NO的情况．图6 图7 图8考点伸展我们把图8局部放大，如图9，⊙D与直线ME的两个交点为E、O，此时点O在EM的延长线上，点N与点B重合，在点M的左侧，NO＝NM．图922例 2015年上海市静安区青浦区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2－2ax ＋c 与x 轴正半轴交于点A ，与y 轴正半轴交于点B ，它的对称轴与x 轴交于点C ，且∠OBC ＝∠OAB ，AC ＝3．（1）求此抛物线的表达式；（2）如果点D 在此抛物线上，DF ⊥OA ，垂足为F ，DF 与线段AB 相交于点G ，且32ADG AFG S S =△△，求点D 的坐标．图1动感体验请打开几何画板文件名“15静安青浦24”，拖动点D 在抛物线上运动，观察度量值，可以体验到，DG 与GF 的比值可以等于1.5，此时点D 的横坐标为3．思路点拨1．抛物线的解析式中待定两个系数，需要代入A 、B 两点的坐标列方程组．2．△ADG 与△AFG 是同高三角形，面积比等于对应的底边的比．3．把DG ∶GF ＝3∶2转化为GF ∶DF ＝2∶5，运算就简便一些．满分解答（1）由y ＝ax 2－2ax ＋c ，得抛物线的对称轴是直线x ＝1．因为AC ＝3，所以点A 的坐标为(4,0)．如图2，由∠OBC ＝∠OAB ，∠BOC ＝∠AOB ，得△BOC ∽△AOB ．于是可得OB 2＝OC ·OA ＝4．所以OB ＝2，B (0, 2)．将A (4,0)、B (0, 2)分别代入y ＝ax 2－2ax ＋c ，得1680,2.a a c c -+=⎧⎨=⎩ 解得14a =-，c ＝2．所以抛物线的表达式是211242y x x =-++．图2 图3（2）如图3，因为△ADG 与△AFG 是同高三角形，所以32ADG AFG S DG S GF ==△△． 所以25GF DF =． 由A (4,0)、B (0, 2)，得直线AB 的解析式为122y x =-+． 设D 211(,2)42x x x -++，G 1(,2)2x x -+，那么21222115242x x x -+=-++ 解得x ＝3，或x ＝4（与A 重合，舍去）．所以点D 的坐标是5(3,)4． 考点伸展第（2）题凭直觉，△ADG 的面积总要比△AFG 的面积小，但是32ADG AFG S S =△△确实是有解的． 我们分析一下方程21222115242x x x -+=-++，等号左边是可以化简、约分的． 因为1(4)222125(2)(4)4x x x x --==+-+-，所以原分式方程总有一个增根x ＝4，另一个就是一元一次方程的根．24例 2015年上海市静安区青浦区中考模拟第25题 在⊙O 中，OC ⊥弦AB ，垂足为C ，点D 在⊙O 上．（1）如图1，已知OA ＝5，AB ＝6，如果OD //AB ，CD 与半径OB 相交于点E ，求DE 的长；（2）已知OA ＝5，AB ＝6（如图2），如果射线OD 与AB 的延长线相交于点F ，且 △OCD 是等腰三角形，求AF 的长；（3）如果OD //AB ，CD ⊥OB ，垂足为E ，求sin ∠ODC 的值．图1 备用图动感体验请打开几何画板文件名“15静安青浦25”，拖动点C 运动，观察度量值，可以体验到，当CD ⊥OB 时，sin ∠ODC 的值就是黄金分割数啊．思路点拨1．反反复复的勾股定理和三角比的运算，要仔细哦．2．第（2）题等腰三角形OCD 只存在两种情况，因为OC ＜OD ．3．第（3）题中的所有直角三角形都是相似的．怎样简化错综复杂的线段间的关系呢？设⊙的半径为1，设sin ∠ODC ＝x ，然后把其他线段用x 表示出来．这个设法不多见哦． 满分解答（1）如图2，因为弦心距OC ⊥弦AB ，所以OC 平分AB ．在Rt △OAC 中，OA ＝5，AC ＝3，所以OC ＝4．在Rt △OCD 中，OC ＝4，OD ＝5，所以DC ＝224541+=．由OD//CB ，得53DE OD CE BC ==．所以554188DE DC ==．图2 图3 图4（2）因为OC ＜OD ，所以等腰三角形OCD 存在两种情况：①如图3，当DO ＝DC 时，作DH ⊥OC ，那么DH 是△OCF 的中位线．在Rt △ODH 中，OD ＝5，OH ＝2，所以DH ＝225221-=． 所以FC ＝2DH ＝221．此时AF ＝AC ＋FC ＝3221+．②如图4，当CO ＝CD 时，作CM ⊥OD ，那么CM 平分OD ．在Rt △OCM 中，OC ＝4，OM ＝12OD ＝52，所以CM ＝22539422⎛⎫-= ⎪⎝⎭． 由tan ∠COF ＝CM FC OM OC=，得3954394225CM OC FC OM ⋅==⨯÷=． 此时AF ＝AC ＋FC ＝43935+． （3）设⊙O 的半径为1，设sin ∠ODC ＝x ．如果OD //AB ，CD ⊥OB ，那么∠COD ＝90°，∠ODC ＝∠BOC ．如图5，在Rt △ODE 中，由sin ∠ODC ＝OE OD＝x ，得OE ＝x ． 如图6，在Rt △OBC 中，由sin ∠BOC ＝BC OB＝x ，得BC ＝x ． 如图7，由OD //CB ，得OD OE BC BE =．所以11x x x =-． 整理，得x 2＋x －1＝0．解得152x -±=．所以sin ∠ODC ＝512-．图5 图6 图7考点伸展看到第（3）题的结果，不由得想起了黄金分割数，那么图形中的黄金分割点在哪里？ 如图7，因为51DE OE OE DC OB OD -===，所以点E 是线段OB 的黄金分割点，点E 也是线段CD 的黄金分割点．26例 2015年上海市闵行区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2－2ax －4与x 轴交于A 、B 两点，与y 轴交于点C ，其中点A 的坐标为(－3,0)，点D 在线段AB 上，AD ＝AC ．（1）求这条抛物线的解析式，并求出抛物线的对称轴；（2）如果以DB 为半径的⊙D 与⊙C 外切，求⊙C 的半径；（3）设点M 在线段AB 上，点N 在线段BC 上，如果线段MN 被直线CD 垂直平分，求BN CN的值．图1动感体验请打开几何画板文件名“15闵行24”，拖动点N 在BC 上运动，可以体验到，当DC 垂直平分MN 时，∠NDC ＝∠ADC ＝∠ACD ，此时DN //AC ．思路点拨1．准确描绘A 、B 、C 、D 的位置，把相等的角标注出来，利于寻找等量关系．2．第（3）题在图形中模拟比划MN 的位置，近似DC 垂直平分MN 时，把新产生的等角与前面存在的等角对比，思路就有了．满分解答（1）将点A (－3,0)代入y ＝ax 2－2ax －4，得15a －4＝0．解得415a =．所以抛物线的解析式为24841515y x x =--． 抛物线的对称轴为直线x ＝1． （2）由24844(3)(5)151515y x x x x =--=+-，得B (5, 0)，C (0,－4)． 由A (－3,0)、B (5, 0)、C (0,－4)，得 AB ＝8，AC ＝5．当AD ＝AC ＝5时，⊙D 的半径DB ＝3．由D (2, 0)、C (0,－4)，得DC ＝25因此当⊙D 与⊙C 外切时，⊙C 的半径为253（如图2所示）．（3）如图3，因为AD ＝AC ，所以∠ACD ＝∠ADC ．如果线段MN 被直线CD 垂直平分，那么∠ADC ＝∠NDC ．这时∠ACD＝∠NDC．所以DN//AC．于是35BN BDCN AD==．图2 图3考点伸展解第（3）题画示意图的时候，容易误入歧途，以为M就是点O．这是为什么呢？我们反过来计算：当DN//AC，35BNCN=时，38DNAC=，因此DM＝DN＝31588AC=．而DO＝2，你看M、O相距是多么的近啊．放大还原事实的真相，如图4所示．图4例 2015年上海市闵行区中考模拟第25题如图1，已知梯形ABCD中，AD//BC，AB＝DC＝5，AD＝4．M、N分别是边AD、BC 上的任意一点，联结AN、DN．点E、F分别在线段AN、DN上，且ME//DN，MF//AN，联结EF．（1）如图2，如果EF//BC，求EF的长；（2）如果四边形MENF的面积是△AND 面积的38，求AM的长；（3）如果BC＝10，试探求△ABN、△AND、△DNC能否两两相似？如果能，求AN的长；如果不能，请说明理由．图1 图2动感体验请打开几何画板文件名“15闵行25”，拖动点M在AD上运动，可以体验到，当EF//BC 时，EF是△AND的中位线．还可以体验到，当N是BC的中点时，△ABN、△AND和△DNC 是三个底角相等的等腰三角形．思路点拨1．由平行四边形MENF和平行四边形AEFM，可以得到E是AN的中点．2．第（2）题把四边形MENF与△AND的面积比，转化为△AEM与△MFD的和与△AND的面积比．再根据相似三角形的面积比等于对应边的比的平方列方程．3．第（3）题先探求两个三角形相似，再验证是否与第三个三角形相似．满分解答（1）如图3，由ME//DN，MF//AN，得四边形MENF是平行四边形．所以MF＝EN．如果EF//BC，那么四边形AEFM是平行四边形．所以MF＝AE．所以E是AN的中点．同理F是DN的中点．所以EF是△AND的中位线，此时EF＝12AD＝2．图3 图4 （2）如图4，设AM的长为x．28由ME //DF ，得224AEM AND S AM x S AD ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭△△． 由MF //AN ，得2244MFD AND S DM x S AD -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭△△． 所以22(4)16AEM MFD AND S S x x S ++-=△△△． 如果四边形MENF 的面积是△AND 面积的38，那么22(4)5=168x x +-． 整理，得x 2－4x ＋3＝0．解得x ＝1，或x ＝3．（3）如图5，在等腰梯形ABCD 中，保持AB ＝DC ，∠B ＝∠C ，∠1＝∠2，∠3＝∠4． 在△ABN 、△AND 、△DNC 中，保持不变的是∠B ＝∠C ．因此△ABN 与△DCN 相似时，存在两种可能：①如果=BA CD BN CN，那么BN ＝CN ．所以N 是BC 的中点． ②如果=BA CN BN CD ，那么510=5BN BN -．解得BN ＝5．所以N 也是BC 的中点． 当点N 是BC 的中点时，△ABN 与△DCN 是两个全等的等腰三角形．此时△AND 也是等腰三角形，∠1＝∠2＝∠4＝∠3．因此△ABN 、△AND 、△DNC 两两相似．由=AB AN AN AD ，得5=4AN AN ．所以=25AN ．图5考点伸展有一种传说叫做数学典型题．这道题目里的3个题目，都是典型图，都有典型结论． 如图3，联结三角形三边中点得到的三角形与原三角形相似，而且与其它三个小三角形全等．第（3）题可以推广为：如果等腰梯形ABCD 的下底BC 等于腰长的2倍，N 是下底BC 的中点，那么△ABN ∽△NCD ∽AND ．。

2015年上海市黄浦区中考数学二模试卷、选择题（每题4分，共24 分）1. （4分）（2015?黄浦区二模）下列分数中，可以化为有限小数的是（）A. —B. —C. 一D.—15 18 15 182. （4分）（2015?黄浦区二模）下列二次根式中最简根式是（3这七天最低气温的众数和中位数分别是（）A . 4, 4B . 4, 5 C. 6, 5 D . 6, 624. （4分）（2015?黄浦区二模）将抛物线y=x2向下平移1个单位，再向左平移2个单位后, 所得新抛物线的表达式是（）2 2 2 2A . y= （x- 1）+2B . y= （x - 2）+1 C. y= （x+1 ）- 2 D . y= （x+2 ）- 15. （4分）（2015?黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4,那么这两个圆的位置关系是（）A .内含B.内切C.外切D.相交6. （4分）（2015?黄浦区二模）下列命题中真命题是（）A •对角线互相垂直的四边形是矩形B. 对角线相等的四边形是矩形C. 四条边都相等的四边形是矩形D .四个内角都相等的四边形是矩形二、填空题（每题4分，共48分）2 27. （4分）（2015?黄浦区二模）计算：（a ）= ____2& （4分）（2015?房山区二模）分解因式：2x - 8x+8=9. （4分）（2015?黄浦区二模）计算：：，+ =—x+l X - 110. （4分）（2004?上海）方程寸—,=x - 1的根是 __________________ .211 . （4分）（2015?黄浦区二模）如果抛物线y= （2- a）x +3x - a的开口向上，那么a的取值范围是_______________ .12 . （4分）（2015?黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为______________ .20. （6分）（2015?黄浦区二模）解方程组:x 2-Sy^-2® K -y=l@人数（人）2012S10E -0 E 三四班’班级13.（4分）（2015?黄浦区二模）将一枚质地均匀的硬币抛掷 2次，硬币正面均朝上的概率是 ______________ .14.（4分）（2015?黄浦区二模）如果梯形的下底长为7,中位线长为5，那么其上底长为 ______________ .15. （4分）（2015?黄浦区二模）已知 AB 是O O 的弦，如果O O 的半径长为5, AB 长为4,那么圆心O 到弦AB 的距离是 ___________________ .16. （4分）（2015?黄浦区二模）如图，在平行四边形 ABCD 中，点M 是边CD 中点，点N是边BC 上的点，且 ='•设小=于=】，那么川可用I 、【表示为.BN 2D________ C17. （4分）（2015?黄浦区二模）如图， △ ABC 是等边三角形，若点 A 绕点C 顺时针旋转 30°至点A ；联结 A B ，则/ ABA 度数是 ___________________ .18. （4分）（2015?黄浦区二模）如图1，点P 是以r 为半径的圆O 外一点，点P 在线段OP 上，若满足OP?OP=r 2，则称点P 是点P 关于圆O 的反演点.如图2,在Rt △ ABO 中，/ B=90 °,AB=2 , BO=4 ,圆O 的半径为2,如果点A '、B 分别是点A 、B 关于圆O 的反演点，那么A B ' 的长是 .三、解答题（48分）119. （6分）（2015?黄浦区二模）计算：4°+ -（ ■- 1） -1 +|1 - _：|.21. (6分)(2015?盘锦二模)温度通常有两种表示方法：华氏度(单位：T)与摄氏度(单位：C)，已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：华氏度数x (C)035100摄氏度数y (T)3295212(1 )选用表格中给出的数据，求y关于x的函数解析式(不需要写出该函数的定义域) (2)已知某天的最低气温是- 5 C,求与之对应的华氏度数.22. (6分)(2015?黄浦区二模)如图，在梯形ABCD中，AD // BC, AB丄BC ,已知AD=2 , cot/ ACB= •，梯形ABCD的面积是9;3(1 )求AB的长；(2)求tan/ ACD 的值.23. (6分)(2015?黄浦区二模)如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF, DF交对角线AC于点G,且DE=DG ;(1)求证：AE=CG ;(2)求证：BE // DF .xOy中，已知点A的坐标为(a,12 123)(其中a> 4),射线OA与反比例函数y=——的图象交于点P,点B、C分别在函数y=——的图象上，且AB // x轴，AC // y轴；(1)当点P横坐标为6,求直线AO的表达式；(2)联结BO,当AB=BO时，求点A坐标；(3)联结BP、CP,试猜想："「的值是否随a的变化而变化？如果不变,S AACP求出■ 的S AACP 值；如果变化，请说明理由.25. （9 分）（2015?黄浦区二模）如图，Rt△ ABC 中，/ C=90 ° / A=30 ° BC=2 , CD 是斜边AB 上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF丄DE, CF 与边AB、线段DE分别交于点F、G ;（1）求线段CD、AD的长；（2 ）设CE=x, DF=y，求y关于x的函数解析式，并写出它的定义域；（3）联结EF，当△ EFG与厶CDG相似时，求线段CE的长.B2015年上海市黄浦区中考数学二模试卷参考答案与试题解析一、选择题（每题4分，共24分）1. （4分）（2015?黄浦区二模）下列分数中，可以化为有限小数的是（）A . B. C.三D .上15 1S 15 13【分析】根据分数与小数间的转化，可得答案.【解答】解：A、亠是无限循环小数，故A错误；15B、.是无限循环小数，故B错误；1SC、亠是有限小数，故C正确；15D、士是无限循环小数，故D错误；故选：C.2. （4分）（2015?黄浦区二模）下列二次根式中最简根式是B . ■: C. S D .【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是.【解答】解：A、被开方数含开的尽的因数，故A错误；B、被开方数含开的尽的因数，故B错误；C、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故C正确;D、被开方数含分母，故D错误；故选：C.3日期除夕初一初二初三初四初五初六最低气温（C）44561064这七天最低气温的众数和中位数分别是（）A . 4, 4B . 4, 5 C. 6, 5 D . 6, 6【分析】众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据定义即可求解.【解答】解：将一周气温按从小到大的顺序排列为4, 4, 4, 5, 6, 6, 10,中位数为第四个数5；4出现了3次，故众数为4.故选B .24. （4分）（2015?黄浦区二模）将抛物线y=x向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）2 2 2 2A . y= （x- 1）+2B . y= （x - 2）+1 C. y= （x+1 ） - 2 D . y= （x+2 ） - 1【分析】把抛物线的平移问题转化为点平移的问题：先确定抛物线y=x2 3的顶点坐标为（0, 0）,再根据点平移的规律得到把向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（-2,- 1）,然后根据顶点式写出平移后的抛物线解析式.2【解答】解：抛物线y=x的顶点坐标为（0, 0）,把点（0, 0）向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（- 2, - 1）,所以所得抛物线的表达式是y= （x+2）2- 1.故选：D.5. （4分）（2015?黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4,那么这两个圆的位置关系是（）A .内含B.内切C.外切D.相交【分析】根据数量关系来判断两圆的位置关系•设两圆的半径分别为R和r,且R才，圆心距为d:外离，贝U d> R+r;外切，则d=R+r;相交，则R- r v d v R+r;内切，贝U d=R - r; 内含，贝U d v R - r.【解答】解：•••两圆半径之差=6 - 2=4=圆心距，•••两个圆的位置关系是内切.故选B .6. （4分）（2015?黄浦区二模）下列命题中真命题是（）A •对角线互相垂直的四边形是矩形B. 对角线相等的四边形是矩形C. 四条边都相等的四边形是矩形D .四个内角都相等的四边形是矩形【分析】根据矩形的判定方法对四个命题进行判断.【解答】解：A、对角线相等的平行四边形是矩形，所以A选项错误；B、对角线相等的平行四边形是矩形，所以B选项错误；C、四个角都相等的四边形是矩形，所以C选项错误；D、四个角都相等的四边形是矩形，所以D选项正确.故选D .二、填空题（每题4分，共48分）2 2 47. （4分）（2015?黄浦区二模）计算：（a ）= a .【分析】根据幕的乘方和积的乘方的运算法则求解.【解答】解：（a2）2=a4.2 2& （ 4分）（2015?房山区二模）分解因式：2x - 8x+8= 2 （x - 2）【分析】先提公因式2,再用完全平方公式进行因式分解即可.【解答】解：原式=2 （x2- 4x+4）=2 ( x- 2)故答案为2 （x - 2）故答案为：a4.9. （4分）（2015?黄浦区二模）计算：”+—•_,—x+1 X - 1 —- 1 —【分析】原式通分并利用同分母分式的加法法则计算，即可得到结果.【解答】解：原式故答案为:10. （4分）（2004?上海）方程寸■—・：=x - 1的根是x=3 .【分析】把方程两边平方去根号后求解，注意检验.【解答】解：两边平方得7 - x= （x - 1）2,即（x+2）（x - 3）=0,解得：x= - 2或x=3 ,代入原方程，当x= - 2时，左边=.「二=3，右边=-3，原方成不成立. 当x=3时，左边=:，右边=2，原方程成立.故方程亍_、.=x - 1的根是x=3 ,故本题答案为：x=3 .211. （4分）（2015?黄浦区二模）如果抛物线y= （2- a）x +3x - a的开口向上，那么a的取值范围是a v 2 .【分析】根据二次函数的性质可知，当抛物线开口向上时，二次项系数 2 - a>0,解不等式即可求得a的取值.【解答】解：因为抛物线y= （2 - a）x2+3x - a的开口向上，所以2- a>0，即a v 2.故答案为：a v 2.12. （4分）（2015?黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%4</鐵（人）【分析】根据条形统计图给出的数据求出外出旅游学生的总人数，再用三班外出旅游学生人数除以总人数即可得出答案.【解答】解：三班外出旅游学生人数占全年级外出旅游学生人数的百分比为20------ ----------- X100%=40% ;12+8+20+10故答案为：40%.13. （4分）（2015?黄浦区二模）将一枚质地均匀的硬币抛掷2次，硬币正面均朝上的概率是：.一4—【分析】列举出所有情况，看正面都朝上的情况数占总情况数的多少即可.【解答】解：如图所示：正反A A正反正反共4种情况，正面都朝上的情况数有1种，所以概率是 .4故答案是■.414. （4分）（2015?黄浦区二模）如果梯形的下底长为7中位线长为5,那么其上底长为3 . 【分析】设出梯形的上底长，直接运用梯形的中位线定理列出关于上底入的方程，求出入即可解决问题.【解答】解：设梯形的上底长为入由题意得：-,,2解得：*3,故答案为3.15. （4分）（2015?黄浦区二模）已匸AB是O O的弦，如果O O的半径长为5, AB长为4, 那么圆心O到弦AB的距离是_ f二1【分析】根据题意画出图形，过点O作OD丄AB于点D,由垂径定理可得出AD的长，在Rt A OAD中，利用勾股定理及可求出OD的长.【解答】解：如图所示：过点O作OD丄AB于点D,•/ AB=4 ,••• AD= AB= >4=2,2 2在Rt△ OBD 中，•/ OA=5 , AD=2 ,•OD=二-，匸.=•「：：：'=:-.故答案为：二7.16. （4分）（2015?黄浦区二模）如图，在平行四边形ABCD中，点M是边CD中点，点N 是边BC上的点，且卜.设小―，那么讪用表示为—匚―【分析】首先由四边形ABCD是平行四边形，求得「'=.•「=；，又由点M是边CD中点，点N是边BC上的点，且侯1,求得宀J再利用三角形法则求解即可求得答案.【解答】解：：•四边形ABCD是平行四边形,•••点M是边CD中点，点N是边BC上的点，且■；；='：，17. （4分）（2015?黄浦区二模）如图，△ ABC是等边三角形，若点A绕点C顺时针旋转30°至点A 联结A B，则/ ABA度数是15°.【分析】如图，首先运用旋转变换的性质得到AC=A C, / ACA =30 °运用等腰三角形的性质得到，/ A BC=45。

九年级数学 共5页 第1页2014学年奉贤区调研测试九年级数学 2015.04（满分150分，考试时间100分钟）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤． 一、选择题：（本大题共6题，每题4分，满分24分） 1．下列计算中正确的是（▲）A .633a a a =+； B .633a a a =⋅ ； C .033=÷a a ； D .633)(a a =． 2．二元一次方程32=+y x 的解的个数是（▲）A ． 1个；B ．2个；C ．3个；D ．无数个． 3．关于反比例函数xy 2=的图像，下列叙述错误的是（▲） A ．y 随x 的增大而减小； B ．图像位于一、三象限；C ．图像是轴对称图形；D ．点（-1，-2）在这个图像上．4．一名射击运动员连续打靶8次，命中环数如图所示，这组数据的众数与中位数分别为（▲）A ．9与8；B ．8与9；C ．8与8.5；D ．8.5与9．5．相交两圆的圆心距是5，如果其中一个圆的半径是3，那么另外一个圆的半径可以是（▲）A ．2；B ．5；C ．8；D ．10． 6．如图，已知AD 是△ABC 的边BC 上的高，下列能使△ABD ≌△ACD 的条件是（▲）A ．∠B =45°；B ．∠BAC =90°；C ．BD =AC ；D ．AB =AC ．（第4题图）DCB A（第6题图）九年级数学 共5页 第2页二、填空题：（本大题共12题，每题4分，满分48分） 7．用代数式表示：a 的5倍与b 的27的差： ▲ ； 8．分解因式：1522--x x = ▲ ； 9．已知函数3+=x x f )(，那么=-)(2f ▲ ；10．某红外线遥控器发出的红外线波长为0.000 000 94m ，这个数用科学记数法表示为 ▲ ； 11．若关于x 的方程022=--k x x 有两个不相等的实数根，则k 的取值范围为 ▲ ； 12．布袋中装有2个红球和5个白球，它们除颜色外其它都相同．如果从这个布袋里随机摸出一个球，那么所摸到的球恰好为红球的概率是 ▲ ；13．已知函数b x y +-=2，函数值y 随x 的增大而▲ （填“增大”或“减小”）； 14．如果正n 边形的中心角是40°，那么n = ▲ ；15．已知△ABC 中，点D 在边BC 上，且BD =2DC ．设AB a = ，=，那么AD →等于▲ (结果用、表示)；16．小明乘滑草车沿坡比为1:2.4的斜坡下滑130米，则他下降的高度为▲米；17．我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”．如果等 腰三角形的腰长为2，“内角正度值”为45°，那么该三角形的面积等于 ▲ ；18．如图，已知钝角三角形ABC ，∠A=35°，OC 为边AB 上的中线，将△AOC 绕着点O 顺时针旋转，点C 落在BC 边上的点'C 处，点A 落在点'A 处，联结'BA ，如果点A 、C 、'A 在同一直线上，那么∠''C BA 的度数为 ▲ ；三、解答题：（本大题共7题，满分78分） 19．（本题满分10分） 计算：1o )12(45cos 22218-++--+．CBOA （第18题图）九年级数学 共5页 第3页20．（本题满分10分）解不等式组：⎪⎩⎪⎨⎧-≤-+<-x x x x 2371211513)(，将其解集在数轴上表示出来，并写出这个不等式组的最．小整数解．．．．．21．（本题满分10分，每小题满分各5分）已知：如图，在△ABC 中，AB=AC =6，BC =4，AB 的垂直 平分线交AB 于点E ，交BC 的延长线于点D ． （1）求∠D 的正弦值； （2）求点C 到直线DE 的距离．CB A（第21题图）EDS22．（本题满分10分）某学校组织为贫困地区儿童捐资助学的活动，其中七年级捐款总数为1000元，八年级捐款总数比七年级多了20%．已知八年级学生人数比七年级学生人数少25名，而八年级的人均捐款数比七年级的人均捐款数多4元．求七年级学生人均捐款数．23．（本题满分12分，每小题满分各6分）已知：如图，在四边形ABCD中，AB//CD，点E是对角线AC上一点，∠DEC=∠ABC，且CACECD⋅=2．（1）求证：四边形ABCD是平行四边形；（2）分别过点E、B作AB和AC的平行线交于点F，联结CF，若∠FCE=∠DCE，求证：四边形EFCD是菱形．D BA九年级数学共5页第4页九年级数学 共5页 第5页24．（本题满分12分，第（1）小题4分，第（2）小题8分）已知：在平面直角坐标系中，抛物线x ax y +=2的对称轴为直线x =2，顶点为A ． （1）求抛物线的表达式及顶点A 的坐标； （2）点P 为抛物线对称轴上一点，联结OA 、OP ．①当OA ⊥OP 时，求OP 的长；②过点P 作OP 的垂线交对称轴右侧的抛物 线于点B ，联结OB ，当∠OAP =∠OBP 时， 求点B 的坐标．九年级数学 共5页 第6页25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）已知：如图，线段AB =8，以A 为圆心，5为半径作圆A ，点C 在⊙A 上，过点C 作CD //AB 交⊙A 于点D （点D 在C 右侧），联结BC 、AD ． （1）若CD=6，求四边形ABCD 的面积；（2）设CD =x ，BC =y ，求y 与x 的函数关系式及自变量x 的取值范围；（3）设BC 的中点为M ，AD 的中点为N ，线段MN 交⊙A 于点E ，联结CE ，当CD 取何值时，CE //AD ．DCB （第25题图）AB（备用图）A九年级数学 共5页 第7页奉贤区初三调研考数学卷参考答案 201504一 、选择题：（本大题共8题，满分24分）1．B ； 2．D ； 3．A ； 4．C ； 5．B ； 6．D ． 二、填空题：（本大题共12题，满分48分） 7．b a 725-； 8．)3)(5(+-x x ； 9．1； 10．7104.9-⨯； 11．1->k ； 12．72； 13．减小； 14．9； 15．32+； 16．50； 17．2或1； 18．20°． 三．（本大题共7题，满分78分） 19． （本题满分10分）解：原式=1222223-+--+． (2)= 122+． ………………………………………………………………………2分20.（本题满分10分）解：由①得:2x >- ．………………………………………………………………………2分 由②得:4x ≤．………………………………………………………………………2分 所以，原不等式组的解集是24x -<≤．……………………………………………2分 数轴上正确表示解集．………………………………………………………………2分 所以，这个不等式组的最小整数解是-1．…………………………………………2分21. （本题满分10分）（1）过点A 作AH ⊥BC 于点H ………………………………………………………………1分 ∵ AB=AC ，BC =4 ∴BH =21BC =2 在△ABH 中，∠BHA=90°, ∴sin ∠BAH =31=AB BH …………………………………2分∵ DE 是AB 的垂直平分线 ∴∠BED=90° BE=3∴∠BED=∠BHA又∵∠B=∠B ∴∠BAH=∠D …………………………………………………1分九年级数学 共5页 第8页∴sin ∠D= sin ∠BAH=13……………………………………………………………1分 即∠D 的正弦值为13（2）解：过点C 作CM ⊥DE 于点M ………………………………………………………1分在△BED 中，∠BED=90°,sin ∠D =13,BE=3 ∴BD =9sin =∠DBE∴CD=5………………………………………………2分在△MCD 中，∠CMD=90°,sin ∠D =31=CD CM ∴CM=35．…………………2分 即点C 到DE 的距离为3522．（本题满分10分）解：设七年级人均捐款数为x 元，则八年级人均捐款数为)4(+x 元 ．…………………1分根据题意，得4%)201(1000251000++=-x x ．……………………………………4分 整理，得 0160122=-+x x ．……………………………………………1分解得 20,821-==x x ．……………………………………………………2分 经检验：20,821-==x x 是原方程的解，0202<-=x 不合题意，舍去．…………1分 答：七年级人均捐款数为8元．……………………………………………………………1分 23．（本题满分12分，每小题满分各6分） 证明：（1）CA CE CD ⋅=2 ∴CACDCD CE =∵∠ECD =∠DCA ∴△ECD ∽△DCA ……………………………………………2分 ∴∠ADC =∠DEC ∵∠DEC =∠ABC ∴∠ABC =∠ADC …………………1分∵AB ∥CD ∴∠ABC+∠BCD=1800 ∠BAD+∠ADC =1800∴∠BAD =∠BCD ………………………………………………………………………2分 ∴四边形ABCD 是平行四边形………………………………………………………1分（2）∵EF ∥AB BF ∥AE ∴四边形ABFE 是平行四边形∴ AB ∥EF AB=EF …………………………………………………………………2分 ∵四边形ABCD 是平行四边形∴AB ∥CD AB=CD九年级数学 共5页 第9页∴CD ∥EF CD=EF∴四边形EFCD 是平行四边形 ………………………………………………………2分 ∵CD ∥EF ∴∠FEC=∠ECD 又∵∠DCE=∠FCE ∴∠FEC=∠FCE ∴EF=FC∴平行四边形EFCD 是菱形 …………………………………………………………2分24．（本题满分12分，每小题4分）(1)∵ 抛物线x ax y +=2的对称轴为直线x =2．∴221=-a ∴41-=a ．……………………………………………………………1分 ∴抛物线的表达式为：x x y +-=241．…………………………………………………1分 ∴顶点A 的坐标为（2，1）． ……………………………………………………………2分（2）设对称轴与x 轴的交点为E ．①在直角三角形AOE 和直角三角形POE 中，AE OE OAE =∠tan ，OEPEEOP =∠tan ∵OA ⊥OP ∴EOP OAE ∠=∠ ∴OEPEAE OE =……………………………2分 ∵AE =1，OE=2 ∴PE=4…………………………………………………………1分 ∴OP=524222=+……………………………………………………………1分②过点B 作AP 的垂线，垂足为F ………………………………………………………1分 设点B （a a a +-241,），则2-=a BF ，a a EF -=241 在直角三角形AOE 和直角三角形POB 中，OE AE OAE =∠cot ，OPBPOBP =∠cot ∵OBP OAE ∠=∠， ∴21==OP BP OE AE ∵PEO BFP ∠=∠，POE BPF ∠=∠∴△BPF ∽△POE ，∴OEPFPO BP PE BF == ∵OE=2， ∴PF=1，1412+-=a a PE ∴2114122=+--a a a九年级数学 共5页 第10页解得101=a ，22=a （不合题意，舍去）…………………………………………2分 ∴点B 的坐标是（10，-15）．……………………………………………………………1分 25．解：（1）作AH ⊥CD ，垂足为点H ……………………………………………………1分∵ CD=6∴321===CD DH CH …………………………………………………1分 ∵AD=5∴AH=4………………………………………………………………1分∴28)(21=⋅+=AH AB CD S ABCD 梯形……………………………………………1分 （2）作CP ⊥AB ，垂足为点P ∵⊙A 中，AH ⊥CD ，CD=x∴x CH 21=∴x CH AP 21==…………… ………………………………1分 ∴x BP 218-=……………………………… ………………………………1分 222DH AD AH AHD Rt -=∆中，24125x -=∴2224125x AH CP -==…………………… ………………………………1分 在222BP CP BC BPC Rt +=∆中， 即222)218()4125(x x y -+-= 解得：()100889≤<-=x xy ………………………………………………2分（3）设AH 交MN 于点F ,联结AE∵BC 的中点为M ，AD 的中点为N ∴MN ∥CD∵CE ∥AD ∴DC=NE=x ………………………………………………………………1分 ∵MN ∥CD ∴AD AN DH NF =∵ 2xDH = ∴4x NF = ∴43x EF =……1分 在直角三角形AEF 和直角三角形AFN 中222EF AE AF -=222NF AN AF -= ∴2222)43(5)4()25(x x -=-∴265=x …………………………………………………………………2分 即当CD 长为265时，CE//AD ．九年级数学 共5页 第11页崇明县2014学年第二学期教学质量调研测试卷九年级数学（考试时间100分钟，满分150分）考生注意：1．本试卷含三个大题，共25题．2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效． 3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，请选择正确选项的代号并填涂在答题纸的相应位置上】1．下列运算中，正确的是 ……………………………………………………………………（ ）(A)1293=±3 (C)030-=（） (D)2139-=2．轨道交通给人们的出行提供了便捷的服务，据悉，上海轨道交通19号线即将开建，一期规划为自川桥路站至长兴岛，设6站，全长约为20600米．二期、远期将延伸到崇明岛、横沙岛，届时崇明县三岛将全通地铁．将20600用科学记数法表示应为 ………………………（ ）(A)52.0610⨯(B)320.610⨯(C)42.0610⨯(D)50.20610⨯3．从下列不等式中选择一个与12x +≥组成不等式组，如果要使该不等式组的解集为1x ≥，那么可以选择的不等式可以是 ………………………………………………………………（ ） (A)1x >-(B)2x >(C)1x <-(D)2x <4．已知点11(,)A x y 和点22(,)B x y 是直线23y x =+上的两个点，如果12x x <，那么1y 与2y 的大小关系正确的是……………………………………………………………………………（ ）(A)12y y >(B)12y y <(C)12y y =(D)无法判断5．窗花是我国的传统艺术，下列四个窗花图案中，不是．．轴对称图形的是…………………（ ）(A)(B) (C) (D)6．已知在四边形ABCD 中，AC 与BD 相交于点O ，那么下列条件中能判定这个四边形是正方形的是 ………………………………………………………………………………………（ ）九年级数学 共5页 第12页(A)AC BD =, AB CD ∥, AB CD = (B)AD BC ∥, A C ∠=∠(C)AO BO CO DO ===, AC BD ⊥(D)AO CO =, BO DO =, AB BC =九年级数学 共5页 第13页二、填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】 7．因式分解：34x x -= ▲ .8.2，那么x = ▲ ．9．如果分式242x x -+的值为0，那么x 的值为 ▲ ．10．已知关于x 的一元二次方程2610x x m -+-=有两个相等的实数根，那么m 的值为 ▲ ．11．已知在方程222232x x x x++=+中，如果设22y x x =+，那么原方程可化为关于y 的整式方程是 ▲ ． 12．布袋中有2个红球和3个黑球，它们除颜色外其他都相同，那么从布袋中取出1个球恰好是红球的概率为 ▲ ．13．某学校在开展“节约每一滴水”的活动中，从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况，将有关数据整理如下表：用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是 ▲ 吨．14．如图，在ABC ∆中，AD 是边BC 上的中线，设向量AB a = ，AD b = ，如果用向量,a b表示向量BC ，那么BC =▲ ．15．如图，已知ABC ∆和ADE ∆均为等边三角形，点D 在BC 边上，DE 与AC 相交于点F ，如果9AB =，3BD =，那么CF 的长度为 ▲ ．16. 如图，已知在O 中，弦CD 垂直于直径AB ，垂足为点E ，如果30BAD ∠=︒，2OE =，那么CD = ▲ ．17．如果一个二次函数的二次项系数为1，那么这个函数可以表示为2y x px q =++，我们将[],p q 称为这个函数的特征数．例如二次函数242y x x =-+的特征数是[]4,2-．请根据以上的信息探究下面的问题：如果一个二次函数的特征数是[]2,3，将这个函数的图像先向左平移2个单位，再向下平移3个单位，那么此时得到的图像所对应的函数的特征数为 ▲ ．（第14题图）AB C D （第15题图）AC EF D （第16题图）B九年级数学 共5页 第14页18．如图，在ABC ∆中，CA CB =，90C ∠=︒，点D 是BC的中点，将ABC ∆沿着直线EF 折叠，使点A 与点D 重合， 折痕交AB 于点E ，交AC 于点F ，那么sin BED ∠的值 为 ▲ ．三、解答题（本大题共7题，满分78分）19．（本题满分10分） 先化简，再求值：2122121x x x x x x +-÷+--+，其中6tan302x =︒-． 20．（本题满分10分）解方程组：222230x y x xy y -=⎧⎨--=⎩21．（本题满分10分，第(1)小题5分、第(2)小题5分） 在Rt ABC ∆中，90BAC ∠=︒，点E 是BC 的中点，AD BC ⊥，垂足为点D ．已知9AC =，3cos 5C =．（1）求线段AE 的长； （2）求sin DAE ∠的值．BACFD（第18题图）（第21题图）CABE D九年级数学 共5页 第15页22．（本题满分10分，第(1)小题4分，第(2)小题6分）周末，小明骑电动自行车从家里出发到野外郊游．从家出发0.5小时后到达甲地，游玩一段时间后按原速前往乙地．小明离家1小时20分钟后，妈妈驾车沿相同路线前往乙地．如图是他们离家的路程y (km)与小明离家时间x (h)的函数图像．已知妈妈驾车的速度是小明骑电动自行车速度的3倍．（1）小明骑电动自行车的速度为千米/小时，在甲地游玩的时间为小时；（2）小明从家出发多少小时的时候被妈妈追上？此时离家多远？23．（本题满分12分，每小题各6分）如图，ABC ∆中，2BC AB =，点D 、E 分别是BC 、AC 的中点，过点A 作AF BC ∥交线段DE 的延长线于点F ，取AF 的中点G ，联结DG ，GD 与AE 交于点H ．（1）求证：四边形ABDF 是菱形； （2）求证：2DH HE HC =⋅．（第22题图）)A BDHG FEC（第23题图）九年级数学 共5页 第16页24．（本题满分12分，每小题各6分）如图，已知抛物线2y ax bx c =++经过点(0,4)A -，点(2,0)B -，点(4,0)C ． （1）求这个抛物线的解析式，并写出顶点坐标；（2）已知点M 在y 轴上，OMB OAB ACB ∠+∠=∠，求点M 的坐标．（第24题图）（备用图）九年级数学 共5页 第17页25．（本题满分14分，第(1)小题5分，第(2)小题5分，第(3)小题4分）如图，在Rt ABC ∆中，90ACB ∠=︒，8AC =，4tan 3B =，点P 是线段AB 上的一个动点，以点P 为圆心，PA 为半径的P 与射线AC 的另一个交点为点D ，射线PD 交射线BC 于点E ， 点Q 是线段BE 的中点．（1）当点E 在BC 的延长线上时，设PA x =，CE y =，求y 关于x 的函数关系式，并写出定义域； （2）以点Q 为圆心，QB 为半径的Q 和P 相切时，求P 的半径；（3）射线PQ 与P 相交于点M ，联结PC 、MC ，当PMC ∆是等腰三角形时，求AP 的长．（第25题图）（备用图1）B AC （备用图2）BAC。

《2015年上海各区中考数学二模压轴题图文解析》目录2015年上海各区中考数学二模第24、25题例1 2015年宝山区嘉定区中考数学二模第24、25题图文解析/2例2 2015年奉贤区中考数学二模第24、25题图文解析/6例3 2015年虹口区中考数学二模第24、25题图文解析/10例4 2015年黄浦区中考数学二模第24、25题图文解析14例5 2015年金山区中考数学二模第24、25题图文解析/18例6 2015年静安区青浦区中考数学二模第24、25题图文解析/22例7 2015年闵行区中考数学二模第24、25题图文解析/26例8 2015年浦东新区中考数学二模第24、25题图文解析/30例9 2015年普陀区中考数学二模第24、25题图文解析34例10 2015年松江区中考数学二模第24、25题图文解析38例11 2015年徐汇区中考数学二模第24、25题图文解析42例12 2015年杨浦区中考数学二模第24、25题图文解析/46例13 2015年长宁区中考数学二模第24、25题图文解析/50例14 2015年崇明县中考数学二模第24、25题图文解析/54例15 2015年闸北区中考数学二模第24、25题图文解析/592015年上海各区中考数学二模第18题例1 2015年宝山区嘉定区中考数学二模第18题图文解析/63例2 2015年奉贤区中考数学二模第18题图文解析/64例3 2015年虹口区中考数学二模第18题图文解析/615例4 2015年黄浦区中考数学二模第18题图文解析/66例5 2015年金山区中考数学二模第18题图文解析/67例6 2015年静安区青浦区中考数学二模第18题图文解析/68例7 2015年闵行区中考数学二模第18题图文解析/69例8 2015年浦东新区中考数学二模第18题图文解析/70例9 2015年普陀区中考数学二模第18题图文解析/71例10 2015年松江区中考数学二模第18题图文解析/72例11 2015年徐汇区中考数学二模第18题图文解析/73例12 2015年杨浦区中考数学二模第18题图文解析/74例13 2015年长宁区中考数学二模第18题图文解析/75例14 2015年崇明县中考数学二模第18题图文解析/76例15 2015年闸北区中考数学二模第18题图文解析/77例 2015年上海市宝山区嘉定区中考模拟第24题如图1，在平面直角坐标系中，双曲线kyx=（k≠0）与直线y＝x＋2都经过点A(2, m)．（1）求k与m的值；（2）此双曲线又经过点B(n, 2)，过点B的直线BC与直线y＝x＋2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）在（2）的条件下，设直线y＝x＋2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．图1动感体验请打开几何画板文件名“15宝山嘉定24”，拖动点E在射线CB上运动，可以体验到，△ACE与△ACD相似，存在两种情况．思路点拨1．直线AD//BC，与坐标轴的夹角为45°．2．求△ABC的面积，一般用割补法．3．讨论△ACE与△ACD相似，先寻找一组等角，再根据对应边成比例分两种情况列方程．满分解答（1）将点A(2, m)代入y＝x＋2，得m＝4．所以点A的坐标为(2, 4)．将点A(2, 4)代入kyx=，得k＝8．（2）将点B(n, 2)，代入8yx=，得n＝4．所以点B的坐标为(4, 2)．设直线BC为y＝x＋b，代入点B(4, 2)，得b＝－2．所以点C的坐标为(0,－2)．由A(2, 4) 、B(4, 2) 、C (0,－2)，可知A、B两点间的水平距离和竖直距离都是2，B、C两点间的水平距离和竖直距离都是4．所以AB＝22，BC＝42，∠ABC＝90°．图22所以S△ABC＝12BA BC⋅＝122422⨯⨯＝8．（3）由A(2, 4) 、D(0, 2) 、C (0,－2)，得AD＝22，AC＝210．由于∠DAC＋∠ACD＝45°，∠ACE＋∠ACD＝45°，所以∠DAC＝∠ACE．所以△ACE与△ACD相似，分两种情况：①如图3，当CE ADCA AC=时，CE＝AD＝22．此时△ACD≌△CAE，相似比为1．②如图4，当CE ACCA AD=时，21021022CE=．解得CE＝102．此时C、E两点间的水平距离和竖直距离都是10，所以E(10, 8)．图3 图4考点伸展第（2）题我们在计算△ABC的面积时，恰好△ABC是直角三角形．一般情况下，在坐标平面内计算图形的面积，用割补法．如图5，作△ABC的外接矩形HCNM，MN//y轴．由S矩形HCNM＝24，S△AHC＝6，S△AMB＝2，S△BCN＝8，得S△ABC＝8．图54例 2015年上海市宝山区嘉定区中考模拟第25题在Rt △ABC 中，∠C ＝90°，BC ＝2，Rt △ABC 绕着点B 按顺时针方向旋转，使点C 落在斜边AB 上的点D ，设点A 旋转后与点E 重合，联结AE ．过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合（如图1），求cot ∠BAE 的值；（2）若点M 在边BC 上（如图2），设边长AC ＝x ，BM ＝y ，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围；（3）若∠BAE ＝∠EBM ，求斜边AB 的长．图1 图2动感体验请打开几何画板文件名“15宝山嘉定25”，拖动点A 上下运动，可以体验到，△ABE 保持等腰三角形，∠BAE ＝∠EBM 按照点M 与点B 的位置关系存在两种情况． 思路点拨1．第（1）题的特殊性是∠DEB ＝∠CAB ＝∠EBD ，△EDB 是等腰直角三角形．2．第（1）题暗示了第（2）题中蕴含着三个等角，因此寻找相似三角形．3．第（3）题∠BAE ＝∠EBM 要分两种情况考虑，各有各的特殊性．满分解答（1）如图3，当点M 与点B 重合时，EB //AC ．所以∠CAB ＝∠EBD ．又因为旋转前后∠CAB ＝∠DEB ，所以∠EBD ＝∠DEB ．所以△EDB 和△ACB 是等腰直角三角形．已知BC ＝2，所以AC ＝2，AB ＝22． 在Rt △AED 中，ED ＝2，AD ＝222-，所以cot ∠BAE ＝AD ED＝2222-＝21-．图3 图4（2）在Rt △ABC 中，BC ＝2，AC ＝x ，所以AB ＝24x +． 如图4，设EM 与AB 交于点F ．由FM //AC ，得BM BF BC BA =，即224y BFx =+．所以BF ＝242y x +． 由于BD ＝BC ＝2，所以DF ＝2422y x +-． 由∠DEB ＝∠CAB ＝∠DFE ，∠EDB 是公共角，得△DEB ∽△DFE ．所以DE 2＝DF ·DB ，即2242(2)2y x x +=-．整理，得2244x y x -=+． 定义域是0＜x ＜2．（3）已知BA ＝BE ，所以∠BAE ＝∠BEA ．当∠BAE ＝∠EBM 时，∠BAE ＝∠BEA ＝∠EBM ．按照M 、B 的位置分两种情况： ①如图5，当M 在B 右侧时，由∠BEA ＝∠EBM ，得AE //CM ．此时∠BAE ＝∠ABC ．又已知∠ABC ＝∠EBD ，所以∠ABC ＝∠EBD ＝∠EBM ＝60°．在Rt △ABC 中，AB ＝2BC ＝4．②如图6，当M 在B 左侧时，在△BAE 中，∠BAE ＝∠BEA ＝2∠ABE ．所以∠ABE ＝36°，∠BAE ＝∠BEA ＝72°．延长EA 交BC 的延长线于G ，那么∠G ＝36°，AG ＝AB ，GE ＝GB ＝2CB ＝4． 由于点A 是GE 的黄金分割点，所以512AG GE -=．所以AB ＝AG ＝252-．图5 图6考点伸展第（3）题的第②种情况，我们直接应用了黄金分割数，也可以用相似比来解． 由∠BAE ＝∠BEA ＝∠MBE ，容易得到GB ＝GE ＝4，AG ＝AB ＝BE ．由△GBE ∽△BAE ，得到EB 2＝EA ·EG ．设AB ＝BE ＝m ．于是得到24(4)m m =-．整理，得m 2＋4m －16＝0．解得252m =．6例 2015年上海市奉贤区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2＋x 的对称轴为直线x ＝2，顶点为A ．（1）求抛物线的表达式及顶点A 的坐标；（2）点P 为抛物线对称轴上一点，联结OA 、OP ．①当OA ⊥OP 时，求OP 的长；②过点P 作OP 的垂线交对称轴右侧的抛物线于点B ，联结OB ，当∠OAP ＝∠OBP 时，求点B 的坐标．图1动感体验请打开几何画板文件名“15奉贤24”，拖动点P 在抛物线的对称轴上运动，可以体验到，△BNP ∽△PMO 保持不变，当∠OAP ＝∠OBP 时，△BOP ∽△AOH ． 思路点拨1．根据等角的余角相等，通过已知的等角寻找未知的等角．2．过直角顶点P 向坐标轴画垂线，可以构造相似的直角三角形，于是通过对应边成比例，可以列方程．满分解答（1）由抛物线的对称轴为122x a =-=，可得14a =-． 所以抛物线的表达式为2211(2)144y x x x =-+=--+． 顶点A 的坐标为(2, 1)．（2）①如图2，设AP 与x 轴交于点H ．由A (2, 1)，可得tan ∠OAH ＝2．当OA ⊥OP 时，∠POH ＝∠OAH ．所以tan ∠POH ＝PH OH＝2． 因此PH ＝2OH ＝4．所以OP ＝25． 图2②如图3，当∠OAP ＝∠OBP 时，tan ∠AOH ＝tan ∠BOP ．所以2PO HO PB HA==．如图4，过点P 作PM ⊥y 轴于M ，过点B 作x 轴的垂线交直线PM 于N ．由△OMP ∽△PNB ，得2OM MP PO PN NB BP===．所以OM ＝2PN ，MP ＝2NB ． 设21(,)4B x x x -+，P (2, n )，那么2(2)n x -=-，2122()4x x n =-+-． 将n ＝4－2x 代入2114x x n -+-=，整理，得x 2－12x ＋20＝0． 解得x ＝10，或x ＝2（B 与A 重合，舍去）．所以点B 的坐标为(10, －15)．图3 图4考点伸展如果应用四点共圆的知识，结合勾股定理，那么第（2）②题可以这样做：如图3，当∠OAP ＝∠OBP 时，A 、B 、P 、O 四点共圆．此时∠OAB ＝∠OPB ＝90°．所以OB 2＝OA 2＋AB 2．设21(,)4B x x x -+，那么22222211()5(2)(1)44x x x x x x ⎡⎤+-+=+-+-+-⎢⎥⎣⎦． 整理，得x 2－12x ＋20＝0．解得x ＝10，或x ＝2．所以B (10, －15)．例 2015年上海市奉贤区中考模拟第25题如图1，已知线段AB＝8，以A为圆心，5为半径作⊙A，点C在⊙A上，过点C作CD//AB 交⊙A于点D（点D在点C右侧），联结BC、AD．（1）若CD＝6，求四边形ABCD的面积；（2）设CD＝x，BC＝y，求y与x的函数关系式及自变量x的取值范围；（3）设BC的中点为M，AD的中点为N，线段MN交⊙A于点E，联结CE，当CD取何值时，CE//AD．图1 备用图动感体验请打开几何画板文件名“15奉贤25”，拖动点C在圆上运动，可以体验到，当CE//AD 时，四边形CEND是平行四边形，四边形CEAN是平行四边形，四边形CF AG是矩形．思路点拨1．已知△ABC的三边长分别为5，8，y，构造AB边上的高CK，那么CK为两个直角三角形的公共直角边，根据勾股定理列方程，可以得到y关于x的关系式．2．当CE//AD时，注意到CE与AN、DN的关系都是平行且相等．满分解答（1）如图2，过点A作AH⊥CD，垂足为H．在△ACD中，AC＝AD＝5，CD＝6，所以CH＝DH＝3．所以AH＝4．所以S梯形ABCD＝1()2CD AB AH+⨯＝1(68)42+⨯＝28．图2 图3（2）如图3，作CK⊥AB，垂足为K，那么四边形CKAH为矩形．在△ACD中，AC＝AD＝5，CH＝DH＝12 x．8在△ABC 中，BC ＝y ，AC ＝5，AK ＝12x ，BK ＝182x -． 由CK 2＝BC 2－BK 2＝AC 2－AK 2，得222211(8)5()22y x x --=-． 整理，得898y x =-．自变量x 的取值范围是0＜x ＜10．（3）如图4，已知MN 是梯形ABCD 的中位线，MN //CD ，当CE //AD 时，四边形CEND 是平行四边形，此时CE ＝DN ＝12AD ＝52． 由CE //NA ，CE ＝NA ，得四边形CEAN 是平行四边形．所以CN ＝EA ＝CA ＝5．作CG ⊥AN 于G ，那么AG ＝12AN ＝14AD ＝54．所以DG ＝515544-=． 在Rt △CAG 中，AG ＝54，CA ＝5，由勾股定理，得CG ＝5154． 在Rt △CDG 中，CG ＝5154，DG ＝154，由勾股定理，得CD ＝562．图4 图5考点伸展第（3）题还可以用相似比来解：如图5，设直线AE 与DC 的延长线交于点P ，与⊙A 交于点Q ，那么CE 是△P AD 的中位线，因此PC ＝CD ＝x ，PE ＝EA ＝AQ ＝5．由CE //DA ，得∠1＝∠3，∠2＝∠4．又因为∠1＝∠2，所以∠3＝∠4．于是可得∠Q ＝∠5＝∠6．由△PCE ∽△PQD ，得PC PQ PE PD =．所以1552x x =．解得562x = 由△PDA ∽△PQD ，得PD PQ PA PD =．所以215102x x =．解得562x =例 2015年上海市虹口区中考模拟第24题如图1，在平面直角坐标系中，抛物线y＝ax2＋bx＋c过A(－1,0)、B(3,0)、C(2, 3)三点，与y轴交于点D．（1）求该抛物线的解析式，并写出该抛物线的对称轴；（2）分别联结AD、DC、CB，直线y＝4x＋m与线段DC交于点E，当此直线将四边形ABCD的面积平分时，求m的值；（3）设点F为该抛物线对称轴上一点，当以A、B、C、F为顶点的四边形是梯形时，请直接写出所有满足条件的点F的坐标．图1动感体验请打开几何画板文件名“15虹口24”，拖动点P运动，可以体验到，经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．拖动点F在抛物线的对称轴上运动，可以体验到，以A、B、C、F为顶点的梯形有3个．思路点拨1．已知抛物线与x轴的两个交点，设两点式比较简便．2．经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．3．过△ABC的3个顶点分别画对边的平行线，三条直线与抛物线的对称轴的3个交点，就是符合条件的点F．满分解答（1）因为抛物线与x轴交于A(－1,0)、B(3,0)两点，设y＝a(x＋1)(x－3)．将点C(2, 3)代入，得3＝－3a．解得a＝－1．所以抛物线的解析式为y＝－(x＋1)(x－3)＝－x2＋2x＋3.对称轴是直线x＝1．（2）如图2，由C(2, 3)、D(0, 3)，得CD//x轴．所以四边形ABCD是梯形．经过梯形中位线的中点，并且与两底相交的直线平分梯形的面积．梯形ABCD的中位线的中点为3(1,)2，将点3(1,)2代入y＝4x＋m，得m＝52．（3）符合条件的点F有3个，坐标分别为(1, 3)，(1,－2)，(1,－6)．10图2 图3考点伸展第（3）题这样解：过△ABC的3个顶点分别画对边的平行线，三条直线与抛物线的对称轴的3个交点，就是符合条件的点F．①如图3，当CF//AB时，点F的坐标是(1, 3)．②如图4，当BF//AC时，由tan∠CAM＝tan∠FBH，得CM FHAM BH=．所以332FH=．解得FH＝2．此时点F的坐标为(1,－2)．③如图5，当AF//CB时，由tan∠CBM＝tan∠F AH，得CM FHBM AH=．所以312FH=．解得FH＝6．此时点F的坐标为(1,－6)．图4 图512例 2015年上海市虹口区中考模拟第25题如图1，在Rt △ABC 中，∠ACB ＝90°，AB ＝13，CD //AB ，点E 为射线CD 上一动点（不与点C 重合），联结AE 交边BC 于F ，∠BAE 的平分线交BC 于点G ．（1）当CE ＝3时，求S △CEF ∶S △CAF 的值；（2）设CE ＝x ，AE ＝y ，当CG ＝2GB 时，求y 与x 之间的函数关系式；（3）当AC ＝5时，联结EG ，若△AEG 为直角三角形，求BG 的长．图1动感体验请打开几何画板文件名“15虹口25”，拖动直角顶点C 运动，可以体验到，CG ＝2GB 保持不变，△ABC 的形状在改变，EA ＝EM 保持不变．点击屏幕左下角的按钮“第（3）题”，拖动E 在射线CD 上运动，可以体验到，△AEG 可以两次成为直角三角形． 思路点拨1．第（1）题中的△CEF 和△CAF 是同高三角形，面积比等于底边的比．2．第（2）题中的△ABC 是斜边为定值的形状不确定的直角三角形．3．第（3）题中的直角三角形AEG 分两种情况讨论．满分解答（1）如图2，由CE //AB ，得313EF CE AF BA ==． 由于△CEF 与△CAF 是同高三角形，所以S △CEF ∶S △CAF ＝3∶13．（2）如图3，延长AG 交射线CD 于M ． 图2由CM //AB ，得2CM CG AB BG==．所以CM ＝2AB ＝26． 由CM //AB ，得∠EMA ＝∠BAM ．又因为AM 平分∠BAE ，所以∠BAM ＝∠EAM ．所以∠EMA ＝∠EAM ．所以y ＝EA ＝EM ＝26－x ．图3 图4（3）在Rt△ABC中，AB＝13，AC＝5，所以BC＝12．①如图4，当∠AGE＝90°时，延长EG交AB于N，那么△AGE≌△AGN．所以G是EN的中点．所以G是BC的中点，BG＝6．②如图5，当∠AEG＝90°时，由△CAF∽△EGF，得FC FA FE FG=．由CE//AB，得FC FB FE FA=．所以FA FBFG FA=．又因为∠AFG＝∠BF A，所以△AFG∽△BF A．所以∠F AG＝∠B．所以∠GAB＝∠B．所以GA＝GB．作GH⊥AH，那么BH＝AH＝132．在Rt△GBH中，由cos∠B＝BHBG，得BG＝132÷1213＝16924．图5 图6考点伸展第（3）题的第②种情况，当∠AEG＝90°时的核心问题是说理GA＝GB．如果用四点共圆，那么很容易．如图6，由A、C、E、G四点共圆，直接得到∠2＝∠4．上海版教材不学习四点共圆，比较麻烦一点的思路还有：如图7，当∠AEG＝90°时，设AG的中点为P，那么PC和PE分别是Rt△ACG和Rt △AEG斜边上的中线，所以PC＝PE＝P A＝PG．所以∠1＝2∠2，∠3＝2∠5．如图8，在等腰△PCE中，∠CPE＝180°－2(∠4＋∠5)，又因为∠CPE＝180°－(∠1＋∠3)，所以∠1＋∠3＝2(∠4＋∠5)．所以∠1＝2∠4．所以∠2＝∠4＝∠B．所以∠GAB＝∠B．所以GA＝GB．图7 图814例 2015年上海市黄浦区中考模拟第24题如图1，在平面直角坐标系中，已知点A 的坐标为(a , 3)（其中a ＞4），射线OA 与反比例函数12y x =的图像交于点P ，点B 、C 分别在函数12y x =的图像上，且AB //x 轴，AC //y 轴．（1）当点P 的横坐标为6时，求直线AO 的表达式；（2）联结BO ，当AB ＝BO 时，求点A 的坐标；（3）联结BP 、CP ，试猜想ABP ACP S S △△的值是否随a 的变化而变化？如果不变，求出ABPACPS S △△的值；如果变化，请说明理由．图1 备用图动感体验请打开几何画板文件名“15黄浦24”，拖动点A 在点B 右侧运动，观察度量值，可以体验到，△ABP 与△ACP 的面积保持相等．事实上，四边形ABDC 是矩形，△ABP 与△ACP 是同底等高的两个三角形．思路点拨1．点B 是确定的，点C 、P 随点A 的改变而改变．2．已知a ＞4隐含了点A 在点B 的右侧这个条件．满分解答（1）如图1，当x ＝6时，12y x=＝2．所以点P 的坐标为(6, 2)． 由O (0, 0)、P (6, 2)，得直线AO 的解析式为13y x =． （2）如图2，因为AB //x 轴，A (a , 3)，所以点B 的纵坐标为3．又因为点B 在反比例函数12y x=的图像上，所以B (4, 3)．因此OB ＝5． 所以当AB ＝BO ＝5时，点A 的坐标为(9, 3)．（3）如图3，过点B 向x 轴作垂线交OA 于点D ，联结CD ．由于直线OA 的解析式为3y x a =，所以点D 的坐标为12(4)a，．由于AC //y 轴，所以点C 的坐标为12()a a ，． 所以CD //x 轴．因此四边形ABDC 是矩形． 所以点B 、C 到对角线AP 的距离相等．因此△ABP 与△ACP 是同底等高的两个三角形，它们的面积相等．所以ABP ACPS S △△＝1．图2 图3考点伸展第（3）题也可以这样说理：如图3，ABP ABD S S △△＝AP AD ，ACP ACD S S △△＝AP AD，而S △ABD ＝S △ACD ，所以ABP ACP S S △△＝1． 第（3）题还可以计算说理：如图4，作PM ⊥AB 于M ，作PN ⊥AC 于N ．设点P 的坐标为12()m m ，．将点P 12()m m，代入直线OA 的解析式3y x a=，可以得到24m a =． 于是，由A (a , 3)、B (4, 3)、C 12()a a ，、P 12()m m，，可得 S △ABP ＝12AB PM ⋅＝112(4)(3)2a m --＝3416(4)2a a m m--+＝2316(4)24m m m --+， S △ACP ＝12AC PN ⋅＝112(3)()2a m a --＝34(4)2m a m a--+＝2316(4)24m m m --+． 所以S △ABP ＝S △ACP ．而事实上，如图5，由于S 1＝S 2，所以S △ABO ＝S △ACO ．所以B 、C 到AO 的距离相等．于是△ABP 与△ACP 就是同底等高的三角形．图4 图5例 2015年上海市黄浦区中考模拟第25题如图1，Rt△ABC中，∠C＝90°，∠A＝30°，BC＝2，CD是斜边AB上的高，点E 为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF与边AB、线段DE 分别交于点F、G．（1）求线段CD、AD的长；（2）设CE＝x，DF＝y，求y关于x的函数解析式，并写出它的定义域；（3）联结EF，当△EFG与△CDG相似时，求线段CE的长．图1动感体验请打开几何画板文件名“15黄浦25”，拖动点E在AC边上运动，可以体验到，△EFG 与△CDG相似存在两种情况．一种情况是FC垂直平分DE，另一种情况是EF⊥AB．思路点拨1．图形中的垂直关系较多，因此互余的角较多，相等的角较多．把相等的角都标注出来，便于分析题意．2．求y关于x的函数关系式，设法构造相似三角形．3．△EFG与△CDG都是直角三角形，分两种情况讨论相似．按照对应的锐角相等，可以推出相似时的特殊的位置关系．满分解答（1）在Rt△ABC中，∠A＝30°，BC＝2，所以AB＝4，AC＝23．在Rt△ACD中，∠A ＝30°，AC＝23，所以CD＝3，AD＝3．（2）如图2，∠CDE与∠BFC都是∠EDF的余角，所以∠CDE＝∠BFC．又因为∠DCE＝∠B＝60°，所以△CDE∽△BFD．所以CD BFCE BC=，即312yx+=．整理，得23xyx-=．定义域是32≤x＜23．图2（3）△EFG与△CDG都是直角三角形，分两种情况讨论相似：①如图3，当∠FEG＝∠DCG时，由于∠FDG＝∠DCG，所以∠FEG＝∠FDG．因此FE＝FD．所以FC垂直平分DE．此时CE＝CD＝3．16②如图4，当∠FEG＝∠CDG时，EF//CD．此时EF⊥AB．作EH⊥CD于H，那么四边形EFDH是矩形，DF＝HE．所以y＝32x．解2332xxx-=，得3393x-±=．此时3933CE-=．图3 图4考点伸展第（2）题也可以这样思考：如图5，过点E作EH⊥CD，垂足为H．在Rt△CEH中，∠CEH＝30°，CE＝x，所以CH＝12x，EH＝32x．如图6，由tan∠DEH＝tan∠DCF，得13(3)::322x x y-=．整理，得23xyx-=．图5 图6 图7 第（2）题还可以如图6这样，过点C作AB的平行线交DE的延长线于M．由tan∠M＝tan∠DCF，得CD DFCM DC=．所以CM＝23CDDF y=．由MC//AD，得CM CEAD AE=．所以323xCMx=-．由3323xy x=-，得23xyx-=．定义域的两个临界值，如图8，CE＝12CD＝32；如图9，CE＝CA＝23．图8 图9例 2015年上海市金山区中考模拟第24题已知抛物线y＝ax2＋bx－8（a≠0）经过A(－2,0)、B(4, 0)两点，与y轴交于点C．（1）求抛物线y＝ax2＋bx－8（a≠0）的解析式，并求出顶点P的坐标；（2）求∠APB的正弦值；（3）直线y＝kx＋2 与y轴交于点N，与直线AC的交点为M，当△MNC与△AOC相似时，求点M的坐标．图1动感体验请打开几何画板文件名“15金山24”，拖动点M在AC上运动，可以体验到，△MNC 与△AOC相似存在两种情况．思路点拨1．用面积法求等腰三角形P AB的腰上的高，进而可以求顶角的正弦值．2．探求△MNC与△AOC相似，可以转化为探求直角三角形MNC．满分解答（1）因为抛物线y＝ax2＋bx－8与x轴交于A(－2,0)、B(4, 0)两点，设y＝a(x＋2)(x－4)＝ax2－2ax－8a．所以－8a＝－8．解得a＝1．所以y＝x2－2x－8＝(x－1)2－9．所以顶点P的坐标为(1,－9)．（2）如图2，由A(－2,0)、B(4, 0)、P(1,－9)，得AB＝6，PB＝P A＝310．作PG⊥AB，AH⊥PB，垂足分别为G、H．由S△P AB＝1122AB PG PB AH⋅=⋅，得699105310AB PGAHPB⋅⨯===．在Rt△APH中，sin∠APB＝910331055AHPA=÷=．图2 （3）由y＝kx＋2，得点N的坐标为(0, 2)．由A(－2,0)、C(0, －8)，得直线AC的解析式为y＝－4x－8．因为△MNC与△AOC有公共的锐角∠ACO，所以分两种情况讨论相似：18①如图3，当∠MNC＝90°时，14NM OANC OC==．所以1105442NM NC===．此时点M的坐标为5(,2)2-．②如图4，当∠NMC＝90°时，过点M作x轴的垂线，过点N、C分别作y轴的垂线，构造直角三角形NEM和直角三角形MFC，那么△NEM∽△MFC．所以EN FM EM FC=．设点M的坐标为(x, －4x－8)，那么(48)(8)2(48)x xx x-----=----．解得4017x=-．此时点M的坐标为4024(,)1717-．图3 图4 图5考点伸展第（3）题也可以这样解：①如图3，当∠MNC＝90°时，MN//x轴，所以y M＝2．解方程－4x－8＝2，得52x=-．此时点M的坐标为5(,2)2-．②如图5，当∠NMC＝90°时，设直线NM交x轴于K，那么△NOK≌△AOC．所以OK＝OC＝8．所以直线NM的解析式为124y x=+．联立y＝－4x－8和124y x=+，解得4017x=-，2417y=．此时M4024(,)1717-．例 2015年上海市金山区中考模拟第25题如图1，已知在△ABC中，AB＝AC＝10，tan∠B＝43．（1）求BC的长；（2）点D、E 分别是AB、AC的中点，不重合的两动点M、N在边BC上（点M、N不与点B、C重合），且点N始终在点M的右边，联结DN、EM交于点O．设MN＝x，四边形ADOE的面积为y．①求y与x的函数关系式，并写出定义域；②当△OMN是等腰三角形且BM＝1时，求MN的长．图1动感体验请打开几何画板文件名“15金山25”，拖动点N在MC上运动，可以体验到，等腰三角形OMN存在两种情况．思路点拨1．把四边形ADOE分割为△ADE和△DOE，△DOE与△NOM是相似的．2．分三种情况讨论等腰三角形OMN，其中NM＝NO是不存在的．满分解答（1）如图2，作AF⊥BC，垂足为F．在Rt△ABF中，AB＝10，tan∠B＝43，设BF＝3m，AF＝4m，那么AB＝5m．所以5m＝10．解得m＝2．所以BF＝6，AF＝8．因为AB＝AC，AF⊥BC，所以BC＝2BF＝12．图2（2）①如图3，S△ABC＝1112848 22BC AF⋅=⨯⨯=．因为DE是△ABC的中位线，所以DE＝12BC＝6，S△ADE＝14S△ABC＝12．过点O作BC的垂线，垂足为H，交DE于G，那么GH＝12AF＝4．由DE//BC，得DE GONM HO=，即64GOx GO=-．所以246GOx=+．因此S△DOE＝11247262266 DE GOx x⋅=⨯⨯=++．所以y＝S四边形ADOE＝S△ADE＋S△DOE＝7212144 1266xx x++=++．定义域是0＜x＜12．②如图4，作EQ⊥BC，垂足为Q．在Rt△ECQ中，EC＝5，所以EQ＝4，CQ＝3．20在Rt△EMQ中，MQ＝11－3＝8，EQ＝4，所以EM＝45．如图5，在Rt△DMP中，DP＝4，MP＝3－1＝2，所以DM＝25．图3 图4 图5 因为△OMN∽△OED，所以讨论等腰△OMN可以转化为讨论等腰△OED．（I）如图6，当OM＝ON时，OE＝OD．此时点O在ED的垂直平分线上．所以BN＝CM＝11．此时MN＝22－12＝10．．（II）如图7，当MO＝MN时，EO＝ED＝6．此时MN＝MO＝45x（III）如果NM＝NO，那么DO＝DE＝6．如图8，因为DM＝25＜6，所以以D为圆心，DE为半径的⊙D与线段ME只有一个交点E，因此不存在NM＝NO的情况．图6 图7 图8考点伸展我们把图8局部放大，如图9，⊙D与直线ME的两个交点为E、O，此时点O在EM的延长线上，点N与点B重合，在点M的左侧，NO＝NM．图922例 2015年上海市静安区青浦区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2－2ax ＋c 与x 轴正半轴交于点A ，与y 轴正半轴交于点B ，它的对称轴与x 轴交于点C ，且∠OBC ＝∠OAB ，AC ＝3．（1）求此抛物线的表达式；（2）如果点D 在此抛物线上，DF ⊥OA ，垂足为F ，DF 与线段AB 相交于点G ，且32ADG AFG S S =△△，求点D 的坐标．图1动感体验请打开几何画板文件名“15静安青浦24”，拖动点D 在抛物线上运动，观察度量值，可以体验到，DG 与GF 的比值可以等于1.5，此时点D 的横坐标为3．思路点拨1．抛物线的解析式中待定两个系数，需要代入A 、B 两点的坐标列方程组．2．△ADG 与△AFG 是同高三角形，面积比等于对应的底边的比．3．把DG ∶GF ＝3∶2转化为GF ∶DF ＝2∶5，运算就简便一些．满分解答（1）由y ＝ax 2－2ax ＋c ，得抛物线的对称轴是直线x ＝1．因为AC ＝3，所以点A 的坐标为(4,0)．如图2，由∠OBC ＝∠OAB ，∠BOC ＝∠AOB ，得△BOC ∽△AOB ．于是可得OB 2＝OC ·OA ＝4．所以OB ＝2，B (0, 2)．将A (4,0)、B (0, 2)分别代入y ＝ax 2－2ax ＋c ，得1680,2.a a c c -+=⎧⎨=⎩ 解得14a =-，c ＝2．所以抛物线的表达式是211242y x x =-++．图2 图3（2）如图3，因为△ADG 与△AFG 是同高三角形，所以32ADG AFG S DG S GF ==△△． 所以25GF DF =． 由A (4,0)、B (0, 2)，得直线AB 的解析式为122y x =-+． 设D 211(,2)42x x x -++，G 1(,2)2x x -+，那么21222115242x x x -+=-++ 解得x ＝3，或x ＝4（与A 重合，舍去）．所以点D 的坐标是5(3,)4． 考点伸展第（2）题凭直觉，△ADG 的面积总要比△AFG 的面积小，但是32ADG AFG S S =△△确实是有解的． 我们分析一下方程21222115242x x x -+=-++，等号左边是可以化简、约分的． 因为1(4)222125(2)(4)4x x x x --==+-+-，所以原分式方程总有一个增根x ＝4，另一个就是一元一次方程的根．24例 2015年上海市静安区青浦区中考模拟第25题 在⊙O 中，OC ⊥弦AB ，垂足为C ，点D 在⊙O 上．（1）如图1，已知OA ＝5，AB ＝6，如果OD //AB ，CD 与半径OB 相交于点E ，求DE 的长；（2）已知OA ＝5，AB ＝6（如图2），如果射线OD 与AB 的延长线相交于点F ，且 △OCD 是等腰三角形，求AF 的长；（3）如果OD //AB ，CD ⊥OB ，垂足为E ，求sin ∠ODC 的值．图1 备用图动感体验请打开几何画板文件名“15静安青浦25”，拖动点C 运动，观察度量值，可以体验到，当CD ⊥OB 时，sin ∠ODC 的值就是黄金分割数啊．思路点拨1．反反复复的勾股定理和三角比的运算，要仔细哦．2．第（2）题等腰三角形OCD 只存在两种情况，因为OC ＜OD ．3．第（3）题中的所有直角三角形都是相似的．怎样简化错综复杂的线段间的关系呢？设⊙的半径为1，设sin ∠ODC ＝x ，然后把其他线段用x 表示出来．这个设法不多见哦． 满分解答（1）如图2，因为弦心距OC ⊥弦AB ，所以OC 平分AB ．在Rt △OAC 中，OA ＝5，AC ＝3，所以OC ＝4．在Rt △OCD 中，OC ＝4，OD ＝5，所以DC ＝224541+=．由OD//CB ，得53DE OD CE BC ==．所以554188DE DC ==．图2 图3 图4（2）因为OC ＜OD ，所以等腰三角形OCD 存在两种情况：①如图3，当DO ＝DC 时，作DH ⊥OC ，那么DH 是△OCF 的中位线．在Rt △ODH 中，OD ＝5，OH ＝2，所以DH ＝225221-=． 所以FC ＝2DH ＝221．此时AF ＝AC ＋FC ＝3221+．②如图4，当CO ＝CD 时，作CM ⊥OD ，那么CM 平分OD ．在Rt △OCM 中，OC ＝4，OM ＝12OD ＝52，所以CM ＝22539422⎛⎫-= ⎪⎝⎭． 由tan ∠COF ＝CM FC OM OC=，得3954394225CM OC FC OM ⋅==⨯÷=． 此时AF ＝AC ＋FC ＝43935+． （3）设⊙O 的半径为1，设sin ∠ODC ＝x ．如果OD //AB ，CD ⊥OB ，那么∠COD ＝90°，∠ODC ＝∠BOC ．如图5，在Rt △ODE 中，由sin ∠ODC ＝OE OD＝x ，得OE ＝x ． 如图6，在Rt △OBC 中，由sin ∠BOC ＝BC OB＝x ，得BC ＝x ． 如图7，由OD //CB ，得OD OE BC BE =．所以11x x x =-． 整理，得x 2＋x －1＝0．解得152x -±=．所以sin ∠ODC ＝512-．图5 图6 图7考点伸展看到第（3）题的结果，不由得想起了黄金分割数，那么图形中的黄金分割点在哪里？ 如图7，因为51DE OE OE DC OB OD -===，所以点E 是线段OB 的黄金分割点，点E 也是线段CD 的黄金分割点．26例 2015年上海市闵行区中考模拟第24题如图1，在平面直角坐标系中，抛物线y ＝ax 2－2ax －4与x 轴交于A 、B 两点，与y 轴交于点C ，其中点A 的坐标为(－3,0)，点D 在线段AB 上，AD ＝AC ．（1）求这条抛物线的解析式，并求出抛物线的对称轴；（2）如果以DB 为半径的⊙D 与⊙C 外切，求⊙C 的半径；（3）设点M 在线段AB 上，点N 在线段BC 上，如果线段MN 被直线CD 垂直平分，求BN CN的值．图1动感体验请打开几何画板文件名“15闵行24”，拖动点N 在BC 上运动，可以体验到，当DC 垂直平分MN 时，∠NDC ＝∠ADC ＝∠ACD ，此时DN //AC ．思路点拨1．准确描绘A 、B 、C 、D 的位置，把相等的角标注出来，利于寻找等量关系．2．第（3）题在图形中模拟比划MN 的位置，近似DC 垂直平分MN 时，把新产生的等角与前面存在的等角对比，思路就有了．满分解答（1）将点A (－3,0)代入y ＝ax 2－2ax －4，得15a －4＝0．解得415a =．所以抛物线的解析式为24841515y x x =--． 抛物线的对称轴为直线x ＝1． （2）由24844(3)(5)151515y x x x x =--=+-，得B (5, 0)，C (0,－4)． 由A (－3,0)、B (5, 0)、C (0,－4)，得 AB ＝8，AC ＝5．当AD ＝AC ＝5时，⊙D 的半径DB ＝3．由D (2, 0)、C (0,－4)，得DC ＝25因此当⊙D 与⊙C 外切时，⊙C 的半径为253（如图2所示）．（3）如图3，因为AD ＝AC ，所以∠ACD ＝∠ADC ．如果线段MN 被直线CD 垂直平分，那么∠ADC ＝∠NDC ．这时∠ACD＝∠NDC．所以DN//AC．于是35BN BDCN AD==．图2 图3考点伸展解第（3）题画示意图的时候，容易误入歧途，以为M就是点O．这是为什么呢？我们反过来计算：当DN//AC，35BNCN=时，38DNAC=，因此DM＝DN＝31588AC=．而DO＝2，你看M、O相距是多么的近啊．放大还原事实的真相，如图4所示．图4例 2015年上海市闵行区中考模拟第25题如图1，已知梯形ABCD中，AD//BC，AB＝DC＝5，AD＝4．M、N分别是边AD、BC 上的任意一点，联结AN、DN．点E、F分别在线段AN、DN上，且ME//DN，MF//AN，联结EF．（1）如图2，如果EF//BC，求EF的长；（2）如果四边形MENF的面积是△AND 面积的38，求AM的长；（3）如果BC＝10，试探求△ABN、△AND、△DNC能否两两相似？如果能，求AN的长；如果不能，请说明理由．图1 图2动感体验请打开几何画板文件名“15闵行25”，拖动点M在AD上运动，可以体验到，当EF//BC 时，EF是△AND的中位线．还可以体验到，当N是BC的中点时，△ABN、△AND和△DNC 是三个底角相等的等腰三角形．思路点拨1．由平行四边形MENF和平行四边形AEFM，可以得到E是AN的中点．2．第（2）题把四边形MENF与△AND的面积比，转化为△AEM与△MFD的和与△AND的面积比．再根据相似三角形的面积比等于对应边的比的平方列方程．3．第（3）题先探求两个三角形相似，再验证是否与第三个三角形相似．满分解答（1）如图3，由ME//DN，MF//AN，得四边形MENF是平行四边形．所以MF＝EN．如果EF//BC，那么四边形AEFM是平行四边形．所以MF＝AE．所以E是AN的中点．同理F是DN的中点．所以EF是△AND的中位线，此时EF＝12AD＝2．图3 图4 （2）如图4，设AM的长为x．28由ME //DF ，得224AEM AND S AM x S AD ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭△△． 由MF //AN ，得2244MFD AND S DM x S AD -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭△△． 所以22(4)16AEM MFD AND S S x x S ++-=△△△． 如果四边形MENF 的面积是△AND 面积的38，那么22(4)5=168x x +-． 整理，得x 2－4x ＋3＝0．解得x ＝1，或x ＝3．（3）如图5，在等腰梯形ABCD 中，保持AB ＝DC ，∠B ＝∠C ，∠1＝∠2，∠3＝∠4． 在△ABN 、△AND 、△DNC 中，保持不变的是∠B ＝∠C ．因此△ABN 与△DCN 相似时，存在两种可能：①如果=BA CD BN CN，那么BN ＝CN ．所以N 是BC 的中点． ②如果=BA CN BN CD ，那么510=5BN BN -．解得BN ＝5．所以N 也是BC 的中点． 当点N 是BC 的中点时，△ABN 与△DCN 是两个全等的等腰三角形．此时△AND 也是等腰三角形，∠1＝∠2＝∠4＝∠3．因此△ABN 、△AND 、△DNC 两两相似．由=AB AN AN AD ，得5=4AN AN ．所以=25AN ．图5考点伸展有一种传说叫做数学典型题．这道题目里的3个题目，都是典型图，都有典型结论． 如图3，联结三角形三边中点得到的三角形与原三角形相似，而且与其它三个小三角形全等．第（3）题可以推广为：如果等腰梯形ABCD 的下底BC 等于腰长的2倍，N 是下底BC 的中点，那么△ABN ∽△NCD ∽AND ．。

上海中考数学压轴题第24题分析（上）前言，成绩优秀的学生，脑子灵活，对数学有兴趣有感觉的同学，他们是特别不喜欢常规套路解题的，他们追求的是方法越巧越妙，方法越省事越舒服；但对大多数同学而言，尤其四认认真真写解答过程的女孩子来说，她们需要的是按部就班的解题步骤和规定约定俗成的烂背于心的解题套路；希望她们在漫漫地求学路上逐步找回数学感觉吧。

一、我们先来复习下二次函数的基本知识： 1、一般式：c bx ax y ++=2；2、顶点式：()k m x a y a b ac a b x a y +-=⇒-+⎪⎭⎫ ⎝⎛+=222442； 3、两根式：()()21x x x x a y --=；4、对称点式：()()m x x x x a y +--=21，其中()m x A ,1，()m x B ,2为二次函数图像的2个对称点。

5、单调性：0>a ，在⎪⎭⎫ ⎝⎛-∞-a b 2,上为减区间，在⎪⎭⎫⎝⎛+∞-,2a b 上为增区间； 6、最值：0<a ，a b ac y 442max-=；0>a ，ab ac y 442min -=。

7、①若0=b ，则对称轴为y 轴；②若0=c ，则过原点；③韦达：a b x x -=+21，acx x =21； ④弦长公式：()()a a ac b a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=-+=-=-=4442221221221218、快速配方法：aa b c a b x a cx a b x a c bx ax y ⋅⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+−−−−−−−−−→−+⎪⎭⎫ ⎝⎛+−−−−→−++=⨯-2222222系数常数项平分一次项系数除提二次项系数整理的：a b ac a b x a y 44222-+⎪⎭⎫ ⎝⎛+=； 例：⎪⎭⎫⎝⎛-⋅⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛--=-⎪⎭⎫ ⎝⎛--=-+-=3249149321293213322222x x x x x y ； 由此可得，不怕c b a ,,的系数有多复杂，都可以快速准确的配方。

2015 年上海市黄浦区中考数学二模试卷一、选择题（每题 4 分，共24 分）1．（4分）（2015•黄浦区二模）下列分数中，可以化为有限小数的是（）A．B．C．D．2．（4分）（2015•黄浦区二模）下列二次根式中最简根式是（）A．B．C．D．日期除夕初一初二初三初四初五初六最低气温（℃）445610 64这七天最低气温的众数和中位数分别是（）A．4，4 B．4，5 C．6，5 D．6，64．（4分）（2015•黄浦区二模）将抛物线y=x2向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x﹣2）2+1 C．y=（x+1）2﹣2 D．y=（x+2）2﹣15．（4分）（2015•黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4，那么这两个圆的位置关系是（）A．内含B．内切C．外切D．相交6．（4分）（2015•黄浦区二模）下列命题中真命题是（）A．对角线互相垂直的四边形是矩形B．对角线相等的四边形是矩形C．四条边都相等的四边形是矩形D．四个内角都相等的四边形是矩形二、填空题（每题4 分，共48 分）7．（4分）（2015•黄浦区二模）计算：（a2）2= ．8．（4分）（2015•房山区二模）分解因式：2x2﹣8x+8= ．9．（4分）（2015•黄浦区二模）计算：+= ．10．（4分）（2004•上海）方程=x﹣1的根是．11．（4分）（2015•黄浦区二模）如果抛物线y=（2﹣a）x2+3x﹣a的开口向上，那么a的取值范围是．12．（4分）（2015•黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为．13．（4分）（2015•黄浦区二模）将一枚质地均匀的硬币抛掷2次，硬币正面均朝上的概率是．14．（4分）（2015•黄浦区二模）如果梯形的下底长为7，中位线长为5，那么其上底长为．15．（4分）（2015•黄浦区二模）已知AB是⊙O的弦，如果⊙O的半径长为5，AB长为4，那么圆心O 到弦AB 的距离是．16．（4分）（2015•黄浦区二模）如图，在平行四边形ABCD中，点M是边CD中点，点N是边BC 上的点，且= ．设= ，= ，那么可用、表示为．17．（4分）（2015•黄浦区二模）如图，△ABC是等边三角形，若点A绕点C顺时针旋转30°至点A′，联结A′B，则∠ABA′度数是．18．（4分）（2015•黄浦区二模）如图1，点P是以r为半径的圆O外一点，点P′在线段OP上，若满足OP•OP′=r2，则称点P′是点P关于圆O的反演点．如图2，在Rt△ABO中，∠B=90°，AB=2，BO=4，圆O 的半径为2，如果点A′、B′分别是点A、B 关于圆O 的反演点，那么A′B′的长是．三、解答题（48 分）19．（6分）（2015•黄浦区二模）计算：40+﹣（﹣1）﹣1+|1﹣|．20．（6分）（2015•黄浦区二模）解方程组：．21．（6分）（2015•盘锦二模）温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：华氏度数x（℃）…0…35 …100 …摄氏度数y（℉）…32 …95 …212 …（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数．22．（6分）（2015•黄浦区二模）如图，在梯形ABCD中，AD∥BC，AB⊥BC，已知AD=2，cot∠ACB= ，梯形ABCD 的面积是9；（1）求AB 的长；（2）求tan∠ACD 的值．23．（6分）（2015•黄浦区二模）如图，在正方形ABCD中，点E在对角线AC上，点F在边BC 上，联结BE、DF，DF 交对角线AC 于点G，且DE=DG；（1）求证：AE=CG；（2）求证：BE∥DF．24．（9分）（2015•黄浦区二模）如图，在平面直角坐标系xOy中，已知点A的坐标为（a，3）（其中a＞4），射线OA与反比例函数y=的图象交于点P，点B、C分别在函数y=的图象上，且AB∥x 轴，AC∥y 轴；（1）当点P 横坐标为6，求直线AO 的表达式；（2）联结BO，当AB=BO 时，求点A 坐标；（3）联结BP、CP，试猜想：的值是否随a 的变化而变化？如果不变，求出的值；如果变化，请说明理由．25．（9分）（2015•黄浦区二模）如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF 与边AB、线段DE 分别交于点F、G；（1）求线段CD、AD 的长；（2）设CE=x，DF=y，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EF，当△EFG 与△CDG 相似时，求线段CE 的长．2015 年上海市黄浦区中考数学二模试卷参考答案与试题解析一、选择题（每题 4 分，共24 分）1．（4分）（2015•黄浦区二模）下列分数中，可以化为有限小数的是（）A．B．C．D．【考点】实数．【分析】根据分数与小数间的转化，可得答案．【解答】解：A、是无限循环小数，故A 错误；B、是无限循环小数，故B 错误；C、是有限小数，故C 正确；D、是无限循环小数，故D 错误；故选：C．【点评】本题考查了实数，利用了分数与小数的相互转化．2．（4分）（2015•黄浦区二模）下列二次根式中最简根式是（）A．B．C．D．【考点】最简二次根式．【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【解答】解：A、被开方数含开的尽的因数，故A 错误；B、被开方数含开的尽的因数，故B 错误；C、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故C 正确；D、被开方数含分母，故D 错误；故选：C．【点评】本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．日期除夕初一初二初三初四初五初六最低气温（℃）445610 64A．4，4 B．4，5 C．6，5 D．6，6【考点】众数；中位数．【分析】众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据定义即可求解．【解答】解：将一周气温按从小到大的顺序排列为4，4，4，5，6，6，10，中位数为第四个数5；4 出现了3 次，故众数为4．故选B．【点评】本题考查了众数和中位数的概念：一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．4．（4分）（2015•黄浦区二模）将抛物线y=x2向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）A．y=（x﹣1）2+2 B．y=（x﹣2）2+1 C．y=（x+1）2﹣2 D．y=（x+2）2﹣1【考点】二次函数图象与几何变换．【分析】把抛物线的平移问题转化为点平移的问题：先确定抛物线y=x2 的顶点坐标为（0，0），再根据点平移的规律得到把向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（﹣2，﹣1），然后根据顶点式写出平移后的抛物线解析式．【解答】解：抛物线y=x2的顶点坐标为（0，0），把点（0，0）向下平移1个单位，再向左平移2个单位后得到对应点的坐标为（﹣2，﹣1），所以所得抛物线的表达式是y=（x+2）2﹣1．故选：D．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a 不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．5．（4分）（2015•黄浦区二模）如果两圆的半径长分别为6与2，圆心距为4，那么这两个圆的位置关系是（）A．内含B．内切C．外切D．相交【考点】圆与圆的位置关系．【分析】根据数量关系来判断两圆的位置关系．设两圆的半径分别为R 和r，且R≥r，圆心距为d：外离，则d＞R+r；外切，则d=R+r；相交，则R﹣r＜d＜R+r；内切，则d=R﹣r；内含，则d＜R﹣r．【解答】解：∵两圆半径之差=6﹣2=4=圆心距，∴两个圆的位置关系是内切．故选B．【点评】本题考查了由两圆位置关系的知识点，利用了两圆内切时，圆心距等于两圆半径的差求解．6．（4分）（2015•黄浦区二模）下列命题中真命题是（）A．对角线互相垂直的四边形是矩形B．对角线相等的四边形是矩形C．四条边都相等的四边形是矩形D．四个内角都相等的四边形是矩形【考点】命题与定理．【分析】根据矩形的判定方法对四个命题进行判断．【解答】解：A、对角线相等的平行四边形是矩形，所以A 选项错误；B、对角线相等的平行四边形是矩形，所以B 选项错误；C、四个角都相等的四边形是矩形，所以C 选项错误；D、四个角都相等的四边形是矩形，所以D 选项正确．故选D．【点评】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．二、填空题（每题 4 分，共48 分）7．（4分）（2015•黄浦区二模）计算：（a2）2=a4．【考点】幂的乘方与积的乘方．【分析】根据幂的乘方和积的乘方的运算法则求解．【解答】解：（a2）2=a4．故答案为：a4．【点评】本题考查了幂的乘方和积的乘方，解答本题的关键是掌握幂的乘方和积的乘方的运算法则．8．（4分）（2015•房山区二模）分解因式：2x2﹣8x+8=2（x﹣2）2．【考点】提公因式法与公式法的综合运用．【专题】计算题．【分析】先提公因式2，再用完全平方公式进行因式分解即可．【解答】解：原式=2（x2﹣4x+4）=2（x﹣2）2．故答案为2（x﹣2）2．【点评】本题考查了提公因式法与公式法的综合运用，是基础知识要熟练掌握．9．（4分）（2015•黄浦区二模）计算：+= ．【考点】分式的加减法．【专题】计算题．【分析】原式通分并利用同分母分式的加法法则计算，即可得到结果．【解答】解：原式= = ，故答案为：【点评】此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．10．（4分）（2004•上海）方程=x﹣1的根是x=3．【考点】无理方程．【分析】把方程两边平方去根号后求解，注意检验．【解答】解：两边平方得7﹣x=（x﹣1）2，即（x+2）（x﹣3）=0，解得：x=﹣2 或x=3，代入原方程，当x=﹣2 时，左边==3，右边=﹣3，原方成不成立．当x=3 时，左边=，右边=2，原方程成立．故方程=x﹣1 的根是x=3，故本题答案为：x=3．【点评】在解无理方程时最常用的方法是换元法或两边平方法，用此类方法解得答案时要验根．11．（4分）（2015•黄浦区二模）如果抛物线y=（2﹣a）x2+3x﹣a的开口向上，那么a的取值范围是a＜2 ．【考点】二次函数的性质．【分析】根据二次函数的性质可知，当抛物线开口向上时，二次项系数2﹣a＞0，解不等式即可求得a 的取值．【解答】解：因为抛物线y=（2﹣a）x2+3x﹣a 的开口向上，所以2﹣a＞0，即a＜2．故答案为：a＜2．【点评】本题主要考查了二次函数的性质．用到的知识点：对于二次函数y=ax2+bx+c（a≠0）来说，当a＞0 时，抛物线y=ax2+bx+c（a≠0）开口向上；当a＜0 时，抛物线y=ax2+bx+c（a≠0）开口向下．12．（4分）（2015•黄浦区二模）某校八年级共四个班，各班寒假外出旅游的学生人数如图所示，那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40% ．【考点】条形统计图．【分析】根据条形统计图给出的数据求出外出旅游学生的总人数，再用三班外出旅游学生人数除以总人数即可得出答案．【解答】解：三班外出旅游学生人数占全年级外出旅游学生人数的百分比为×100%=40%；故答案为：40%．【点评】此题考查了条形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．13．（4分）（2015•黄浦区二模）将一枚质地均匀的硬币抛掷2次，硬币正面均朝上的概率是．【考点】列表法与树状图法．【分析】列举出所有情况，看正面都朝上的情况数占总情况数的多少即可．【解答】解：如图所示：共4 种情况，正面都朝上的情况数有1 种，所以概率是．故答案是．【点评】考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．得到所求的情况数是解决本题的关键．14．（4分）（2015•黄浦区二模）如果梯形的下底长为7，中位线长为5，那么其上底长为3．【考点】梯形中位线定理．【分析】设出梯形的上底长，直接运用梯形的中位线定理列出关于上底λ的方程，求出λ即可解决问题．【解答】解：设梯形的上底长为λ；由题意得：，解得：λ=3，故答案为3．【点评】该题主要考查了梯形的中位线定理及其应用问题；应牢固掌握梯形的中位线定理并能灵活运用．15．（4分）（2015•黄浦区二模）已知AB是⊙O的弦，如果⊙O的半径长为5，AB长为4，那么圆心O 到弦AB 的距离是．【考点】垂径定理；勾股定理．【分析】根据题意画出图形，过点O 作OD⊥AB 于点D，由垂径定理可得出AD 的长，在Rt△OAD 中，利用勾股定理及可求出OD 的长．【解答】解：如图所示：过点O 作OD⊥AB 于点D，∵AB=4，∴AD= AB= ×4=2，在Rt△OBD 中，∵OA=5，AD=2，∴OD= = = ．故答案为：．【点评】本题考查的是垂径定理及勾股定理，根据题意画出图形，利用数形结合求解是解答此题的关键．16．（4分）（2015•黄浦区二模）如图，在平行四边形ABCD中，点M是边CD中点，点N 是边BC 上的点，且= ．设= ，= ，那么可用、表示为﹣．【考点】*平面向量．【分析】首先由四边形ABCD 是平行四边形，求得= = ，又由点M 是边CD 中点，点N 是边BC 上的点，且= ，求得与，再利用三角形法则求解即可求得答案．【解答】解：∵四边形ABCD 是平行四边形，∴= = ，∵点M 是边CD 中点，点N 是边BC 上的点，且= ，∴= = ，= = ，∴= ﹣= ﹣．故答案为：﹣．【点评】此题考查了平面向量的知识．注意掌握平行四边形法则与三角形法则的应用是解此题的关键．17．（4分）（2015•黄浦区二模）如图，△ABC是等边三角形，若点A绕点C顺时针旋转30°至点A′，联结A′B，则∠ABA′度数是15°．【考点】旋转的性质．【分析】如图，首先运用旋转变换的性质得到 AC=A ′C ，∠ACA ′=30°；运用等腰三角形的性质得到，∠A ′BC=45°，借助∠ABC=60°，即可解决问题． 【解答】解：如图，由题意得： AC=A ′C ，∠ACA ′=30°；∵△ABC 为等边三角形，∴∠ACB=∠ABC=60°，AC=BC ， ∴BC=A ′C ，∠A ′BC=∠BA ′C= =45°，∴∠ABA ′=60°﹣45°=15°．【点评】该题主要考查了等边三角形的性质、等腰三角形的性质、旋转变换的性质等几何知识点及其应用问题；灵活运用旋转变换的性质等知识点来分析、判断、解答是解题的关键．18．（4 分）（2015•黄浦区二模）如图 1，点 P 是以 r 为半径的圆 O 外一点，点 P ′在线段 OP 上，若满足 OP •OP ′=r 2，则称点 P ′是点P 关于圆O 的反演点．如图 2，在 Rt △ABO 中，∠B=90°， AB=2，BO=4，圆 O 的半径为 2，如果点 A ′、B ′分别是点 A 、B 关于圆 O 的反演点，那么 A ′B ′【考点】相似三角形的判定与性质；圆周角定理． 【专题】新定义．【分析】先证明△AOB ∽△B ′OA ′，然后根据相似三角形的对应角相等可以推知 ∠OA ′B ′=∠OBA=90°，根据勾股定理即可求得．【解答】解：∵A ′、B ′分别是点 A 、B 关于圆 O 的反演点， ∴=，又∵∠O=∠O ，∴△AOB ∽△B ′OA ′， ∴∠OA ′B ′=∠OBA=90°，∵AB=2，BO=4，圆 O 的半径为 2， ∴OA=2，∴OA ′==，OB ′==1，∴A ′B ′==．的长是．故答案为：．【点评】本题考查了圆的综合题．解题时涉及到的知识点有：相似三角形的判定与性质、圆周角定理、等式的性质等．三、解答题（48 分）19．（6分）（2015•黄浦区二模）计算：40+﹣（﹣1）﹣1+|1﹣|．【考点】实数的运算；分数指数幂；零指数幂；负整数指数幂．【分析】先根据0 指数幂及负整数指数幂的计算法则、绝对值的性质及数的开方法则分别计算出各数，再根据实数混合运算的法则进行计算即可．【解答】解：原式=1+2﹣+ ﹣1=3﹣（+1）+ ﹣1=3﹣﹣1+ ﹣1=1．【点评】本题考查的是实数的运算，数值0 指数幂及负整数指数幂的计算法则、绝对值的性质及数的开方法则是解答此题的关键．20．（6分）（2015•黄浦区二模）解方程组：．【考点】高次方程．【分析】把x﹣y=1 化为x=y+1，代入方程①，求出y，再把y 值代入x=y+1，求出x 即可．【解答】解：由②得：x=y+1 ③，把③代入①得：（y+1）2﹣2y2=﹣2，即y2﹣2y﹣3=0，解得：y1=﹣1，y2=3，把y1=﹣1，y2=3 代入③得x1=0，x2=4．故方程组的解为，．【点评】本题考查的是二元二次方程组的解法，把其中的二元一次方程变形，用一个未知数表示另一个未知数，代入二元二次方程，得到一个一元二次方程，解出未知数，代入求解，得到原方程组的解．21．（6分）（2015•盘锦二模）温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：华氏度数x（℃）…0…35 …100 …摄氏度数y（℉）…32 …95 …212 …（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数．【考点】一次函数的应用．【分析】（1）设一次函数的解析式为y=kx+b，由待定系数法求出其解即可；（2）当x=﹣5 时代入（1）的解析式求出其解即可．【解答】解：（1）设y=kx+b，把（0，32）和（35，95）代入得：，解得：，∴y= ．（2）当x=﹣5 时，y=﹣9+32=23．∴某天的最低气温是﹣5℃，与之对应的华氏度数为23℉．【点评】本题考查了待定系数法求一次函数的解析式的运用，解答时求出函数的解析式是关键．22．（6分）（2015•黄浦区二模）如图，在梯形ABCD中，AD∥BC，AB⊥BC，已知AD=2，cot∠ACB= ，梯形ABCD 的面积是9；（1）求AB 的长；（2）求tan∠ACD 的值．【考点】相似三角形的判定与性质；梯形；解直角三角形．【分析】（1）根据锐角三角函数设出边长，利用梯形的面积公式列方程即可；（2）作DH⊥AC 于H，利用三角形相似，列比例式求出DH= ，AH= ，CH=AC﹣AH= ，即可求出tan∠ACD== ．【解答】解：（1）在R t ABC中，cot∠ACB==，设BC=4k，AB=3k，=（AD+BC）•AB= （2+4k）•3k=9，∴S梯形ABCD∴k=1或k=﹣（舍），∴AB=3；（2）作DH⊥AC 于H，∵AD∥BC，∴∠DAH=∠ACB，∴△ADH∽△CAB，∴= = = ，∴DH= ，AH= ，∴CH=AC﹣AH= ，∴tan∠ACD= = ．【点评】本题考查了锐角三角函数，梯形的面积，相似三角形的判定和性质，作辅助线构造相似三角形是解题的关键．23．（6分）（2015•黄浦区二模）如图，在正方形ABCD中，点E在对角线AC上，点F在边BC 上，联结BE、DF，DF 交对角线AC 于点G，且DE=DG；（1）求证：AE=CG；（2）求证：BE∥DF．【考点】正方形的性质；全等三角形的判定与性质．【专题】证明题．【分析】（1）先证∠AED=∠CGD，再证明△ADE≌△CDG，根据全等三角形的对应边相等即可得出结论；（2）先证明△BCE≌△DCE，得出对应角相等∠BEC=∠DEG，得出∠BEC=∠DGE，即可证出平行线．【解答】证明：（1）∵DE=DG，∴∠DEG=∠DGE，∴∠AED=∠CGD，∵四边形ABCD 是正方形，∴AD=CD=BC，∠DAC=∠BCE=∠DCA=45°，在△ADE 和△CDG 中，，∴△ADE≌△CDG（AAS），∴AE=CG；（2）在△BCE 和△DCE 中，，∴△BCE≌△DCE（SAS），∴∠BEC=∠DEG，∴∠BEC=∠DGE，∴BE∥DF．【点评】本题考查了正方形的性质、全等三角形的判定与性质；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．24．（9分）（2015•黄浦区二模）如图，在平面直角坐标系xOy中，已知点A的坐标为（a，3）（其中a＞4），射线OA与反比例函数y=的图象交于点P，点B、C分别在函数y=的图象上，且AB∥x 轴，AC∥y 轴；（1）当点P 横坐标为6，求直线AO 的表达式；（2）联结BO，当AB=BO 时，求点A 坐标；（3）联结BP、CP，试猜想：的值是否随a 的变化而变化？如果不变，求出的值；如果变化，请说明理由．【考点】反比例函数综合题．【分析】（1）根据自变量的值，可得函数值，根据待定系数法，可得函数解析式；（2）根据函数值，可得自变量的值，根据勾股定理，可得OB 长，根据AB=OB，可得A 点坐标；（3）联立函数解析式，可得方程组，根据解方程组，可得P 点坐标，根据自变量与函数值的对应关系，可得B、C 点坐标，根据三角形面积公式，可得答案．【解答】解：（1）当x=6时，y=2，∴P（6，2），设直线AO 的解析式为y=kx，代入P（6，2）得k=，∴直线AO 的解析式为y=x；（2）由AB∥x 轴，得B 点横坐标为4．当y=3 时，x=4，∴B（4，3）．OB= =5，∵AB=OB，∴5=a﹣4，即a=9，∴A（9，3）；（3）直线AO 的解析式为y=x，联立y=，得，解得．∴P（2，），作PM⊥AB，PN⊥AC．当x=a时，y=，即C（a，），当y=3时，x=4，即B（4，3）．AC=3﹣，PN=a﹣2 ，AB=a﹣4，PM=3﹣，=（a﹣4）（3﹣），S△ACP=（a﹣2）（3﹣），∴S△ABP∴= =1．【点评】本题考查了反比例函数综合题，（1）利用待定系数法求函数解析式；（2）利用平行x 轴直线上的点的纵坐标相等得出B 点的纵坐标，再利用函数值与自变量的关系得出B 点坐标，利用两线段相等得出A点坐标；（3）利用解方程组得出P点坐标，利用自变量与函数值的对应关系得出B、C 点坐标，利用三角形的面积公式得出答案．25．（9分）（2015•黄浦区二模）如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），联结DE，作CF⊥DE，CF 与边AB、线段DE 分别交于点F、G；（1）求线段CD、AD 的长；（2）设CE=x，DF=y，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EF，当△EFG 与△CDG 相似时，求线段CE 的长．即= = 解得 x=；【考点】相似形综合题．【分析】（1）利用特殊角的三角函数可知 sin ∠B=，tan ∠A= ，由此求得线段 CD 、AD的长；（2） 证得△CDE ∽△BFC ，得出= ，整理得出答案即可；（3） 分两种情况考虑：①当△EGF ∽△DGC 时；②当△FEG ∽△CGD 时；利用相似的性质探讨得出答案即可．【解答】解：（1）在 Rt △BCD 中， BC=2，∠B=90°﹣∠A=60°， sin ∠B= ， 即 CD=×2=， 同理 tan ∠A=， AD==3；（2）∵∠CDE=∠BFC=90°﹣∠DCF ，∠ECD=∠B=60°， ∴△CDE ∽△BFC ， ∴ = ， 即 =，∴y=﹣1，（≤x ＜2）；（3）∠EGF=∠CGD=90°①当△EGF ∽△DGC 时，∠GEF=∠GDC ， ∴EF ∥DC ， ∴ =，，②当△EG ∽△CGD 时，∴∠GEF=∠GCD=∠GDF ，∴EF=DF，又∵CF⊥DE，∴EG=DG，∴CD=CE= ；综上，CE= 或；【点评】此题考查相似的综合题，综合考查了特殊角的三角函数，相似三角形的判定与性质，注意分类讨论思想的渗透．考点卡片1.实数（1）实数的定义：有理数和无理数统称实数．（2）实数的分类：实数{有理数{正有理数0 负有理数无理数{正无理数负无理数或实数{正实数0 负实数．2.实数的运算（1）实数的运算和在有理数范围内一样，值得一提的是，实数既可以进行加、减、乘、除、乘方运算，又可以进行开方运算，其中正实数可以开平方．（2）在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．另外，有理数的运算律在实数范围内仍然适用．【规律方法】实数运算的“三个关键”1.运算法则：乘方和开方运算、幂的运算、指数（特别是负整数指数，0 指数）运算、根式运算、特殊三角函数值的计算以及绝对值的化简等．2.运算顺序：先乘方，再乘除，后加减，有括号的先算括号里面的，在同一级运算中要从左到右依次运算，无论何种运算，都要注意先定符号后运算．3.运算律的使用：使用运算律可以简化运算，提高运算速度和准确度．3.分数指数幂分数指数幂．4.幂的乘方与积的乘方（1）幂的乘方法则：底数不变，指数相乘．（a m）n=a mn（m，n 是正整数）注意：①幂的乘方的底数指的是幂的底数；②性质中“指数相乘”指的是幂的指数与乘方的指数相乘，这里注意与同底数幂的乘法中“指数相加”的区别．（2）积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘．（ab）n=a n b n（n 是正整数）注意：①因式是三个或三个以上积的乘方，法则仍适用；②运用时数字因数的乘方应根据乘方的意义，计算出最后的结果．5.提公因式法与公式法的综合运用提公因式法与公式法的综合运用．6.分式的加减法（1）同分母分式加减法法则：同分母的分式相加减，分母不变，把分子相加减．（2）异分母分式加减法法则：把分母不相同的几个分式化成分母相同的分式，叫做通分，经过通分，异分母分式的加减就转化为同分母分式的加减．：说明：①分式的通分必须注意整个分子和整个分母，分母是多项式时，必须先分解因式，分子是多项式时，要把分母所乘的相同式子与这个多项式相乘，而不能只同其中某一项相乘．②通分是和约分是相反的一种变换．约分是把分子和分母的所有公因式约去，将分式化为较简单的形式；通分是分别把每一个分式的分子分母同乘以相同的因式，使几个较简单的分式变成分母相同的较复杂的形式．约分是对一个分式而言的；通分则是对两个或两个以上的分式来说的．7.零指数幂零指数幂：a0=1（a≠0）由a m÷a m=1，a m÷a m=a m﹣m=a0可推出a0=1（a≠0）注意：00≠1．8.负整数指数幂负整数指数幂：a﹣p=1ap（a≠0，p 为正整数）注意：①a≠0；②计算负整数指数幂时，一定要根据负整数指数幂的意义计算，避免出现（﹣3）﹣2=（﹣3）×（﹣2）的错误．③当底数是分数时，只要把分子、分母颠倒，负指数就可变为正指数．④在混合运算中，始终要注意运算的顺序．9.最简二次根式最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．我们把满足上述两个条件的二次根式，叫做最简二次根式．最简二次根式的条件：（1）被开方数的因数是整数或字母，因式是整式；（2）被开方数中不含有可化为平方数或平方式的因数或因式．如：不含有可化为平方数或平方式的因数或因式的有2、3、a（a≥0）、x+y等；含有可化为平方数或平方式的因数或因式的有4、9、a2、（x+y）2、x2+2xy+y2 等．10.高次方程（1）高次方程的定义：整式方程未知数次数最高项次数高于2 次的方程，称为高次方程．（2）高次方程的解法思想：通过适当的方法，把高次方程化为次数较低的方程求解．所以解高次方程一般要降次，即把它转化成二次方程或一次方程．也有的通过因式分解来解．对于5 次及以上的一元高次方程没有通用的代数解法和求根公式（即通过各项系数经过有限次四则运算和乘方和开方运算无法求解），这称为阿贝尔定理．换句话说，只有三次和四次的高次方程可用根式求解．11.无理方程（1）定义：方程中含有根式，且开方数是含有未知数的代数式，这样的方程叫做无理方程．（2）有理方程和根式方程（无理方程）合称为代数方程．（3）解无理方程关键是要去掉根号，将其转化为整式方程．解无理方程的基本思想是把无理方程转化为有理方程来解，在变形时要注意根据方程的结构特征选择解题方法．常用的方法有：乘方法，配方法，因式分解法，设辅助元素法，利用比例性质法等．（4）注意：用乘方法（即将方程两边各自乘同次方来消去方程中的根号）来解无理方程，往往会产生增根，应注意验根．12.一次函数的应用1、分段函数问题分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．2、函数的多变量问题解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数．3、概括整合（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用．（2）理清题意是采用分段函数解决问题的关键．13.反比例函数综合题（1）应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型，是解决实际问题的关键一步，培养了学生的建模能力和从实际问题向数学问题转化的能力．在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识．（2）数形结合类综合题利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起，是分析解决问题的一种好方法．14.二次函数的性质二次函数y=ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0 时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y 随x 的增大而减小；x＞﹣时，y 随x 的增大而增大；x=﹣时，y 取得最小值，即顶点是抛物线的最低点．。