电路理论基础第三版 答案 陈希有

电路理论教程答案陈希有【篇一：《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。

当时间t2s时电流从a流向b,与参考方向相同，电流为正值；当t2s时电流从b流向a，与参考方向相反，电流为负值。

所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解：当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反，即b为高电位端，a为低电位端；当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同，即a为高电位端，b为低电位端。

答案1.3解：(a)元件a电压和电流为关联参考方向。

元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。

(b) 元件b电压和电流为关联参考方向。

元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。

(c) 元件c电压和电流为非关联参考方向。

元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。

答案1.4解：对节点列kcl方程节点③: i4?2a?3a?0，得i4?2a?3a=5a节点④: ?i3?i4?8a?0，得i3??i4?8a?3a节点①: ?i2?i3?1a?0，得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0，得i1?i2?3a?8a??1a若只求i2，可做闭合面如图(b)所示，对其列kcl方程，得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解：如下图所示(1)由kcl方程得节点①：i1??2a?1a??3a节点②：i4?i1?1a??2a节点③：i3?i4?1a??1a节点④：i2??1a?i3?0若已知电流减少一个，不能求出全部未知电流。

(2)由kvl方程得回路l1：u14?u12?u23?u34?19v回路l2：u15?u14?u45?19v-7v=12v回路l3：u52?u51?u12??12v+5v=-7v回路l4：u53?u54?u43?7v?8v??1v若已知支路电压减少一个，不能求出全部未知电压。

i答案10.1解：t ：：： 0时，电容处于开路，故u C (0 _) = 10mA 2k 「- 20V 由换路定律得：u C (0 .) +(0”20V换路后一瞬间，两电阻为串联，总电压为 u C (0 )。

所以再由节点①的KCL 方程得:i C (0 ) =10mA -i 1(0 .)二(10-5)mA =5mA答案10.2解：t ：：：0时电容处于开路，电感处于短路，3门电阻与61电阻相并联，所以45V6i(0J3A ，L(0Ji(0」= 2A(5+8 + 6 3)0 6+36+3u C (0J =8 i(0J = 24V 由换路定律得：U C (0 ) 7C (0J =24V ，匚(0.) “L (0_)=2A由KVL 得开关电压：u(0 ) --U c (0 ) 8 匚(0 .)=(-24 8 2)V 8V答案10.3解：t ：：： 0时电容处于开路，i =0 ,受控源源电压4i =0 ,所以U C (0 J =U C (0」=U 1(0」61.5V = 0.6V(9 6尸等效电阻i i (0 )=%(0 .) (2 2)k 」=5mA(b)所示。

R 段「4i (6 3)i容i时间常数二 R C 二 0 ・1st 0后电路为零输入响应，故电容电压为：u C (t)二 u C (0 ,)e~ =0.6e A0°V6“电阻电压为：“⑴工―6门 i 6门 ^C-dUc ^0.72e 10t V (t 0)dt答案10.43解：t ：：：0时电感处于短路，故L(0J= 39A=3A ，由换路定律得:6 + 3i L (0^i L (0J=3A求等效电阻的电路如图(b)所示。

等效电阻R 「6 •色卫=8」，时间常数.二L/R =0.5s6+3t 0后电路为零输入响应，故电感电流为i L (t) =i L (0 .)e^^ =3e 2t A (t _o ) 电感电压._2tu ,(t)二 L 匕二-24e V (t .0)dt31电阻电流为U 36C 汽L +U 1小2八i 3 2e A33「3「31电阻消耗的能量为：W3°= f 30i ；dt = f12/dt =12[-0.25ed=3W答案10.5解：由换路定律得i L (0.) “L (0」=0，达到稳态时电感处于短路，故LG) =20/4=5A求等效电阻的电路如图(b)所示。

答案13.3解：(1) 由公式l t I B I Tt =，已知连支电流，可求得树支电流A 1595111011010654321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡i i i i i i (2) 由公式t t U B U -=l ，已知树支电压，可求得连支电压V 321321100111110654⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡u u u (3) 由矩阵B 画出各基本回路，如图(a)~(c)所示。

将各基本回路综合在一起得题中所求线图，如图13.3(d)所示。

(a)(b)(c)(d)答案13.6解：由关联矩阵A 画出网络图，如图题13.6所示，由图写出基本割集矩阵如下：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=011101110101110001C图题13.6答案13.7解：由Tt l C B -=得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0011011011101101t B , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----==1011010001100010111000011101]|[t lB B B 由B 矩阵画出各基本回路，如图（a ）~(d)所示。

将各基本回路综合在一起得题中所求线图，如图13.7（e ）所示。

图题13.76(a)(b)(c)(d)(e)答案13.8解：由Tt l B C -=得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=101011111011100l C , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------==1011010001110010110100011100]|[tl C C C 答案13.9解：由基本回路矩阵可知：支路１、２、３为连支，４、５、６为树支，已知树支电压，可以求出全部连支电压。

=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321u u u V 628V 1264110111101t t ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-=U B U l 连支电流等于连支电压除以相应支路的电阻。

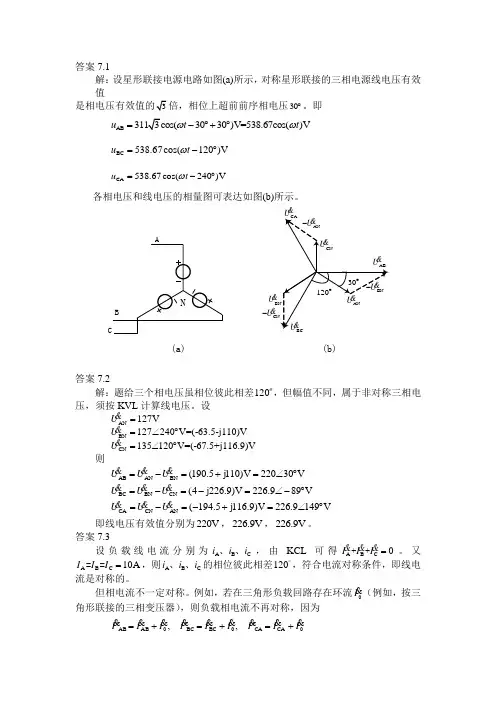
答案7.1解：设星形联接电源电路如图(a)所示，对称星形联接的三相电源线电压有效值倍，相位上超前前序相电压30︒。

即AB 3030)V=538.67cos()V u t t ωω=-︒+︒BC 538.67cos(120)V u t ω=-︒CA 538.67cos(240)V u t ω=-︒各相电压和线电压的相量图可表达如图(b)所示。

AB CN(a)&U &(b)U-&答案7.2解：题给三个相电压虽相位彼此相差120o ，但幅值不同，属于非对称三相电压，须按KVL 计算线电压。

设AN 127V U =& BN 127240V=(-63.5-j110)V U =∠︒& CN135120V=(-67.5+j116.9)V U =∠︒& 则ABANBNBC BN CN CA CN AN(190.5j 110)V 22030V (4j226.9)V 226.989V (194.5j 116.9)V 226.9149V UU U U U U U U U =-=+=∠︒=-=-=∠-︒=-=-+=∠︒&&&&&&&&& 即线电压有效值分别为220V ，226.9V ，226.9V 。

答案7.3设负载线电流分别为A B C i i i 、、，由KCL 可得A B C0I I I =&&&++。

又A B C 10A I I I ===，则A B C i i i 、、的相位彼此相差120︒，符合电流对称条件，即线电流是对称的。

但相电流不一定对称。

例如，若在三角形负载回路存在环流0I &（例如，按三角形联接的三相变压器），则负载相电流不再对称，因为CA CA 0BC BC 0AB AB ',','I I I I I I I I I &&&&&&&&&+=+=+=不满足对称条件。

教材习题3答案部分（P73）答案略 答案解：（a ） 本题考虑到电桥平衡，再利用叠加定理，计算非常简单。

（1）3V 电压源单独作用,如图(a-1)、(a-2)所示。

(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得：''182A 483I I Ω=-⨯=-Ω+Ω（2）1A 电流源单独作用，如图(a-3)所示。

(a-3)考虑到电桥平衡，"0I =，在由分流公式得："1131A A 134I =-⨯=-+ （3）叠加：'"1A I I I =+= '"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=（b ）（1）4V 电压源单独作用，如图(b-1)所示。

'I '由图(b-1)可得，'24V2V (2+2)U Ω⨯==Ω'136A I U =-=- ''21'5A I I I =+=-（2）2A 电流源单独作用，如图(b-2)所示。

(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯= 对节点②列KCL 方程得，"""1132A 4A I U I +==对节点③列KCL 方程得，"""230I I U ++=解得"5A I =（3） 叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=答案略答案略答案解 ：利用叠加定理，含源电阻网络中的电源分为一组，其作用为'I ，如图(b)所示。

S I 为一组，其单独作用的结果I '' 与S I 成比例，即："S I kI =，如图(c)所示。

答案11.1解： (1)2020001e 1e 1e e )()(-ssdt s stdt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dts s t dt t t s F ts t s st st t答案11.2解：)/1(//1)(1τττ+=+-=s s A s A s A s F 由拉氏变换的微分、线性和积分性质得：)/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F答案11.3解：设25)}({)(11+==s t f s F L ,52)}({)(22+==s t f L s F 则)5)(2(10)()(21++=s s s F s F)(1t f 与)(2t f 的卷积为)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221t t t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ对上式取拉氏变换得：)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L 由此验证)()()}(*)({2121s F s F t f t f =L 。

答案11.4解：(a)6512)(2+++=s s s s F 3221+++=s A s A3|31221-=++=-=s s s A ， 3|31221-=++=-=s s s A 所以t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ (c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s 查表得)5sin(e 53)(t t f t-=答案11.5解：(a) 由运算电路(略)求得端口等效运算阻抗为：11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z ， 112611430)(22++++=s s s s s Z i (b) 画出运算电路如图11.5(c)所示U )(2s __在端口加电流，列写节点电压方程如下⎩⎨⎧-==++-=-+)2()]()([3)(3)()]5.0/(11[)()1()()()()1(2122s U s U s U s U s s U s I s U s U s由式（２）解得)(144)(2s U s ss U ⨯+=代入式（１）得)()()1221(s I s U s ss =+-+所以1212)(2i +++=s s s s Y答案11.6解：运算电路如图11.6(b)所示。

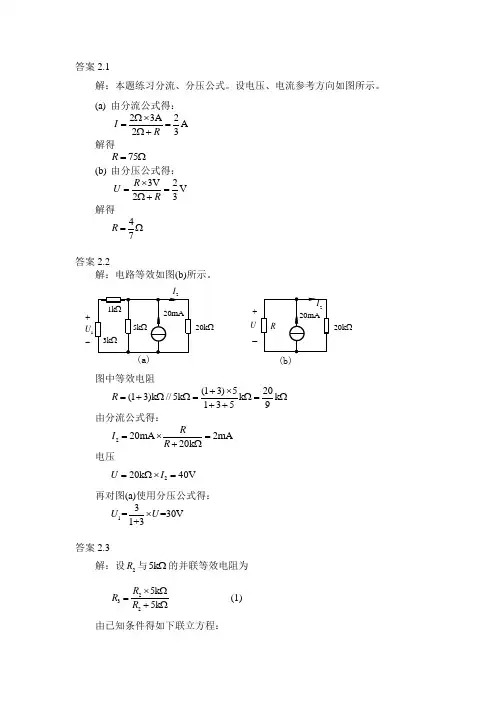
答案2.1解：本题练习分流、分压公式。

设电压、电流参考方向如图所示。

(a) 由分流公式得：23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得：3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解：电路等效如图(b)所示。

20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得：13==30V 1+3U U ⨯答案2.3解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得210k 3R =Ω答案2.4解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解：首先将电路化简成图(b)。

图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。

答案6.22解：对图(a)电路做戴维南等效，如图(b)所示。

OC U inZ (b)i j 1/(j )Z L C ωω=+ (1)SOC j I U Cω=(2) 由图(b)可知，当i 0Z =时，电阻两端电压U 与电阻R 无关，始终等于OC (0)U R ≠。

由式(1)解得1/100rad/s ω== 将式(3)代入式(2)得OC 1100A 1090V j100rad/s 0.01FU U ==∠︒⨯=∠-︒⨯90V u t ω=-（）答案6.23解：先对图(a)电路ab 端左侧电路作戴维南等效，如图(b)所示。

U iZ (b)令32000rad/s 210H 4L X L ω-==⨯⨯=Ω得等效阻抗i 4j48//8//j42(1j)4j4Z Ω⨯Ω=ΩΩΩ==+ΩΩ+Ω由OCi 1j U i Z R Cω=++知，欲使电流i 有效值为最大，电容的量值须使回路阻抗虚部为零，即：012]j 1Im[=-=++CC R Z i ωω 等效后电路如图(b)所示。

解得1250μF 2C ω==答案6.24解：应用分压公式，输出电压o U 可表示为o n1n 2U U U =-i i 1j 12j U C U R Cωω=-⨯+ i i i j 121j 2(j 1)U U CR U CR CR ωωω-=-=++ 当 0=R ， o U 超前于i U 180；当 1R Cω=，o U 超前于i U ︒90；当 ∞→R ， o U 与i U 同相位。

即当R 由零变到无穷时，o U 超前于i U 相位差从180到0变化。

答案6.25解：图示电路负载等效导纳为22221j j()j ()()R LY C C R L R L R L ωωωωωω=+=+-+++ (1) 22222222222)()(21)()(C L R LC L R L C L R R Yωωωωωωω++-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎥⎦⎤⎢⎢⎣⎡+= (2) 由式(2)可见：当)2/(12LC =ω时，Y C ω=与R 无关，电流有效值CU U Y I ω==不随R 改变。

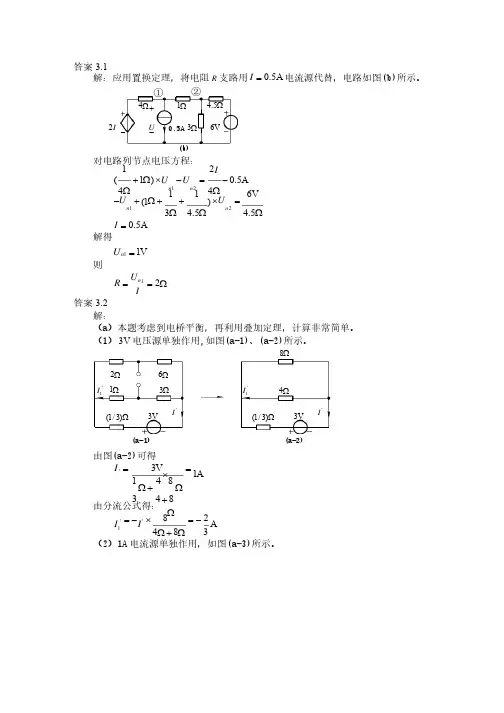
答案3.1解：应用置换定理，将电阻R 支路用0.5A I =电流源代替，电路如图电流源代替，电路如图(b)(b)(b)所示。

所示。

所示。

I2W 4-+UW1W 5.4V6W 3(b)0.5A ①②对电路列节点电压方程：对电路列节点电压方程：1212(1)0.5A 44n n I U U +W ´-=-W W12116V (1)3 4.5 4.5n n U U -+W ++´=W W W0.5A I = 解得解得11V n U = 则12n U R I==W 答案3.2解：解：（a ）本题考虑到电桥平衡，再利用叠加定理，计算非常简单。

（1）3V 电压源单独作用电压源单独作用,,如图如图(a-1)(a-1)(a-1)、、(a-2)(a-2)所示。

所示。

所示。

W 2W 6W 1W3W)3/1(V3'I '1I 8W4WW)3/1(V3'I '1I (a-1)(a-2)由图由图(a-2)(a-2)(a-2)可得可得可得'3V 1A 148348I ==´W +W + 由分流公式得：由分流公式得：''182A 483I IW =-´=-W +W （2）1A 电流源单独作用，如图电流源单独作用，如图(a-3)(a-3)(a-3)所示。

所示。

所示。

(a-3)W 2W 6W 1W3W)3/1("I "1IA1考虑到电桥平衡，考虑到电桥平衡， "0I =， 在由分流公式得：在由分流公式得： "1131A A 134I =-´=-+ （3）叠加：）叠加：'"1A I I I =+='"11117/12A I I I =+=-2111 2.007WP I W =´=（b ）（1）4V 电压源单独作用，如图电压源单独作用，如图(b-1)(b-1)(b-1)所示。

电路理论教程答案陈希有【篇一：《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。

当时间t2s时电流从a流向b,与参考方向相同，电流为正值；当t2s时电流从b流向a，与参考方向相反，电流为负值。

所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解：当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反，即b为高电位端，a为低电位端；当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同，即a为高电位端，b为低电位端。

答案1.3解：(a)元件a电压和电流为关联参考方向。

元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。

(b) 元件b电压和电流为关联参考方向。

元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。

(c) 元件c电压和电流为非关联参考方向。

元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。

答案1.4解：对节点列kcl方程节点③: i4?2a?3a?0，得i4?2a?3a=5a节点④: ?i3?i4?8a?0，得i3??i4?8a?3a节点①: ?i2?i3?1a?0，得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0，得i1?i2?3a?8a??1a若只求i2，可做闭合面如图(b)所示，对其列kcl方程，得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解：如下图所示(1)由kcl方程得节点①：i1??2a?1a??3a节点②：i4?i1?1a??2a节点③：i3?i4?1a??1a节点④：i2??1a?i3?0若已知电流减少一个，不能求出全部未知电流。

(2)由kvl方程得回路l1：u14?u12?u23?u34?19v回路l2：u15?u14?u45?19v-7v=12v回路l3：u52?u51?u12??12v+5v=-7v回路l4：u53?u54?u43?7v?8v??1v若已知支路电压减少一个，不能求出全部未知电压。

电路理论基础课后答案(哈工大陈希有)第11章题11.1 根据定义求和的象函数。

解： (1)(2)题11.2设求的象函数。

解：由拉氏变换的微分、线性和积分性质得：题11.3设(t 为纯数)。

分别求对应象函数、、，验证卷积定理。

解：设 , 则与的卷积为)()(t t t f ε=)(e )(t t t f atε-=2020001e 1e 1e e )()(-ss dt s s t dt t t s F stst st st=-=+-==∞-∞-∞-∞----⎰⎰ε20)(20)(00)(1e )(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dt s s t dt t t s F t s t s st st t ξξετd f c t bf tt f a t f f t A t f t t )()(d )(d )(,0)0(),()e 1()(011121/1⎰-++==-=--)(2t f )(2s F )/1(//1)(1τττ+=+-=s s A s A s A s F )/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F )()()(,e 2)(,e 5)(215221t f t f t f t f t f tt *===--)(1s F )(2s F )(s F 25)}({)(11+==s t f s F L 52)}({)(22+==s t f L s F )5)(2(10)()(21++=s s s F s F )(1t f )(2t f对上式取拉氏变换得：由此验证。

题11.4求下列函数的原函数。

(a) (b)(c)解：(a)， 所以(b)所以)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221tt t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L )()()}(*)({2121s F s F t f t f =L 6512)(2+++=s s s s F)2)(1(795)(23+++++=s s s s s s F 623)(2++=s s s F 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A 3|31221-=++=-=s s s A tt s s t f 321e 5e 3}3523{)(---+-=+++-=L )2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A tt t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)查表得题11.5分别求图示(a)、(b)电路的等效运算阻抗或等效运算导纳。

答案12.1解：分别对节点①和右边回路列KCL 与KVL 方程：Cq u u i i qi C L L R C C /===--==ψ将各元件方程代入上式得非线性状态方程：C q C q f f q/)/()(21=--=ψψ方程中不明显含有时间变量t ，因此是自治的。

答案12.2解：分别对节点①、②列KCL 方程： 节点①：=1i 321S 1/)(R u u i q--= 节点②：=2i 423212//)(R u R u u q--= 将)(),(222111q f u q f u == 代入上述方程，整理得状态方程：⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S 3223111R R R R q f R q f q i R q f R q f q答案12.3解：分别对节点①列KCL 方程和图示回路列KVL 方程得：⎩⎨⎧-=-=(2)(1) /323321u u R u i qS ψ 3u 为非状态变量，须消去。

由节点①的KCL 方程得：0413332432=-++-=++-R u u R u i i i i 解得)/()]()([)/()(433224114332413R R R f R q f R R R i R u u ++=++=ψ 将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得：⎩⎨⎧++-+-=+++-=Su R R R R f R R R q f R R R f R R q f q)/()()/()()/()()/()(4343224331124332243111ψψψ 答案12.4解：由KVL 列出电路的微分方程：=L u )(sin )(d d 3t R u Ri tS ωβψαψ+-=+-= 前向欧拉法迭代公式：)](sin )([31k k k k t R h ωβψαψψ+-+=+后向欧拉法迭代公式：)](sin )([1311++++-+=k k k k t R h ωβψαψψ梯形法迭代公式：)](sin )()(sin )([5.013131++++-+-+=k k k k k k t R t R h ωβψαωβψαψψ答案12.5解：由图(a)得：tu C u U t C t u Ci R R C R d d )(d dd d S -=-== (1) 由式(1)可知，当0>R i 时，0d d <t u R ，R u 单调减小；当0<R i 时，0d d >tuR ，R u 单调增加。

陈希有电路理论教程答案【篇一：电路理论基础课后答案(哈工大陈希有)第12章】图题12.1解：分别对节点①和右边回路列kcl与kvl方程：?iq?ir?ilc?c??u???u?q/clc将各元件方程代入上式得非线性状态方程：??q?f(?)?f(q/c)12???q/c方程中不明显含有时间变量t，因此是自治的。

题12.2图示电路，设u，列出状态方程。

?f(q),u?f(q)111222r图题12.2r4解：分别对节点①、②列kcl方程：节点①：??i?(u?u)/ri1?q 1s123节点②：??(u?u)/r?u/ri2?q 212324将u?f(q),u?f(q)111222代入上述方程，整理得状态方程：?q??f(q)/r?f(q)/r?i?1113223s??q?f(q)/r?f(q)(r?r)/(rr)2113223434?题12.322出电路的状态方程。

uu1解：分别对节点①列kcl方程和图示回路列kvl方程得：图题12.3?qiu (1)?1?2?3/r3????u?u(2)?2s3u3为非状态变量，须消去。

由节点①的kcl方程得：u?u3u31?i?i?i??i?0 2342rr34解得u?(u?ri)r/(r?r)?[f(q)?rf()]r/(r?r) 314233411422334将?及u3代入式(1)、(2)整理得：?q??f(q)/(r?r)?f()r/(r?r)?1113422334????f(q)r/(r?r)?f()rr/(r?r)?u211334223434s????题12.4，试分别写出用前向欧拉法、后向欧拉法和梯形法计算响?sin(?t) us图题12.4l解：由kvl列出电路的微分方程：ul?d???ri?u??)??sin(?t) sdt前向欧拉法迭代公式：????h[?)??sin(?t)]k?1kkk后向欧拉法迭代公式：????h[?)??sin(?t)]k?1kk?1k?1梯形法迭代公式：????0.5[)??(?t))??sin(?t)]k?1kkkk?1k?1题12.5?1f,u(0)?7v,u?10v电路及非线性电阻的电压电流关系如图所示。

答案15.1解： 波阻抗Ω500400102003c =⨯==++i u Z终端反射系数133c 2c 22=+-=Z R Z R N故负载承受的电压V k 15.24610200)1331(32222=⨯⨯+=+=++u N u u 答案15.2解：终端反射系数31c c 2=+-=Z Z Z Z N L L始端反射系数1cS cS 1-=+-=Z Z Z Z N这是一个多次反射过程，反射过程如图题15.2所示。

其中v l t d /= 当vlt 20<<时，反射波未达到始端，只有入射波。

mA 30500V 15c 11=Ω===+Z u i i 当vlt v l 42<<时，反射波到达始端， mA 101010302121=--=+-=+++i N N i N i i 当vlt v l 64<<时 ，始端电流为： mA 67.1631031010103022212212121=++--=+-+-=+++++i N N i N N i N N i N i i 达到稳态时mA 15)(211==∞R u i 所以⎪⎩⎪⎨⎧<<<<<<=v l t l/v v l t l/v v l t t i /64 16.67mA /42 10mA /20 mA30)(1 mA 15)(211==∞R u i图题15.2答案15.3解：波从始端传到中点所用的时间为：μs 10s 1010310325831==⨯⨯==-v l t (1)当μs 100<<t 时，入射波从始端发出，尚未到达中点所以 0)(=t i 。

(2)μs 30μs 10<<t 时，入射波已经过中点，但在终端所产生的反射波还没有到达中点。

A 2.0600600240)(c S S 1=+=+==+Z R U i t i(3) μs 60μs 30<<t 时，在终端所产生的反射波已经过中点，并于μs 40=t 时 刻到达始端。

第六章答案6.1解：将2i 和3i 改写为余弦函数的标准形式，即234cos(190)A 4cos(190180)A 4cos(10)A5sin(10)A 5cos(1090)A 5cos(80)Ai t t t i t t t ωωωωωω=-+︒=+︒-︒=+︒=+︒=+︒-︒=-︒电压、电流的有效值为12370.7V, 1.414A 2.828A, 3.54A U I I I ======== 初相位12310,100,10,80u i i i ψψψψ====-相位差111010090u i ϕψψ=-=-=- 11u i u i 与正交，滞后于； 2210100u i ϕψψ=-=︒-︒= u 与2i 同相； 3310(80)90u i ϕψψ=-=︒--︒= u 与3i 正交，u 超前于3i答案6.2()()()().a 10cos(10)V-8b arctg 10233.1V,233.1)V -6-20.8c arctg 20.889.4A,20.8cos(89.4)A 0.2d 30180A,180)A m u t U u t I i t I i t ωωωω=-︒==∠︒=+︒==∠-︒=-︒=∠︒=+︒答案6.3解：(a)利用正弦量的相量表示法的线性性质得：11221,U I n U I n ==- (b)磁通相量通常用最大值表示，利用正弦量的相量表示法的微分性质得：mj m U N ω=Φ (c) 利用正弦量的相量表示法的线性性质与微分性质得：j URI LI ω=+答案6.4解：由KCL 得电流i 的振幅相量m 1m 2m 3mI I I I =++ (2100410580)A =∠︒+∠︒+∠-︒(0.347j 1.97 3.939j0.6950.868j4.924)A =-++++-A 86.265︒-∠=电流i 的瞬时值为5cos(26.86)A i t ω=-︒答案6.5解：电压表和电流表读数为有效值，其比值为阻抗模，即/U I =将已知条件代入，得100V 15A 100V10⎧=⎪⎪=Ω 联立方程，解得13.7mH, 5.08L R ==Ω答案6.6解：(a) RC 串联电路中电阻电压与电容电压相位正交，各电压有效值关系为30V U ===电流i 的有效值为30V 3A 10C C U I I X ====Ω(b)302A 60V C C U X I ==Ω⨯=60V 1.2A 50R U I R ===ΩRC 并联电路中电阻电流与电容电流相位正交，总电流有效值为2.33I A === (c)30130C C C U X I A V ==Ω⨯=由30215C L C L L L U V U U X I I A X ==⇒===Ω并联电容、电感上电流相位相反，总电流为1L C I I I A =-= 电阻电压与电容电压相位正交，总电压为：50U V ===答案6.7解：感抗()3210rad/s 0.1H 200L X L ω==⨯⨯=Ω容抗()()3611100210rad/s 510FC X C ω--=-==-Ω⨯⨯⨯ 图(a)电路的相量模型如图(b)所示。