华师大八年级数学暑假专题辅导 平行四边形

华师大版数学八年级下册第18章《平行四边形》教学设计1一. 教材分析《平行四边形》是华师大版数学八年级下册第18章的内容，本章主要让学生掌握平行四边形的性质和判定方法，以及平行四边形的应用。

本章内容在初中数学中占据重要地位，为学生后续学习几何知识打下基础。

本节课的教学内容主要包括平行四边形的定义、性质和判定方法。

二. 学情分析八年级的学生已经学习了三角形、四边形等基本图形的知识，具备一定的空间想象能力和逻辑思维能力。

但是，对于平行四边形的性质和判定方法，学生可能还存在一定的困难。

因此，在教学过程中，要关注学生的学习情况，引导学生积极参与，提高学生的学习兴趣。

三. 教学目标1.知识与技能：使学生掌握平行四边形的定义、性质和判定方法，能运用平行四边形的知识解决实际问题。

2.过程与方法：通过观察、操作、猜想、验证等方法，培养学生的空间想象能力和逻辑思维能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队协作精神，使学生在解决实际问题中体会数学的价值。

四. 教学重难点1.重点：平行四边形的定义、性质和判定方法。

2.难点：平行四边形性质的证明和应用。

五. 教学方法1.情境教学法：通过生活实例引入平行四边形的概念，激发学生的学习兴趣。

2.动手操作法：让学生通过实际操作，观察平行四边形的性质，提高学生的动手能力。

3.小组讨论法：引导学生分组讨论，培养学生的团队协作能力和沟通能力。

4.引导发现法：教师引导学生发现平行四边形的性质，培养学生的探究能力。

六. 教学准备1.教具：多媒体课件、平行四边形模型、彩纸、剪刀等。

2.学具：学生每人准备一张彩纸，一把剪刀。

七. 教学过程1.导入（5分钟）教师通过展示生活中的平行四边形图片，如电梯、窗户等，引导学生关注平行四边形在日常生活中的应用。

提问：“你们知道这些图形是什么吗？它们有什么特点？”学生回答后，教师总结并引入平行四边形的概念。

2.呈现（10分钟）教师通过多媒体课件，展示平行四边形的定义、性质和判定方法。

学科：数学平行四边形的特征【学习目标】1．探索并掌握平行四边形的特征．2．灵活运用平行四边形的特征解决问题．3．平行四边形一般转化成三角形的问题来解决．【基础知识概述】1．平行四边形：(1)平行四边形的定义：两组对边分别平行的四边形是平行四边形．(2)平行四边形的表示：平行四边形用符号“”表示．平行四边形ABCD 记作，读作平行四边形ABCD．(3)平行四边形定义的作用：①由定义知平行四边形的两组对边分别平行．②由定义可以得出只要四边形中两组对边分别平行，那么这个四边形是平行四边形．2．平行四边形的特征：(1)平行四边形的邻角互补，对角相等．(2)平行四边形的对边平行且相等．(3)平行四边形的对角线互相平分．(4)平行四边形是中心对称图形，对角线的交点为对称中心．(5)若一条直线过平行四边形两对角线的交点，则这直线被一组对边截下的线段以对角线的交点为中点，且这条直线二等分平行四边形的面积．注意：①特征：都是通过连对角线把四边形问题转化成三角形问题来处理的，即通过平移或旋转，利用重合来证明的．②夹在两条平行线间的平行线段是指端点分别在两条平行线上的平行线段．③互相平分指两条线段有公共的中点．3．平行四边形特征的作用：可以用来证明线段相等、角相等及两直线平行等．如图12-1-1，有如下结论：⎪⎪⎩⎪⎪⎨⎧==∠=∠∠=∠==(对角线互相平分)，(对角相等)，(对边相等)，(对边平行)，是平行四边形，则如果四边形DO BO CO AO D B C A ADBC CD AB AD//BC CD //AB ABCD 4．两条平行线间的距离：(1)定义：两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线间的距离．(2)两平行线间的距离处处相等．注意：距离是指垂线段的长度，是大于0的．①平行线的位置确定后，它们的距离是定值，不随垂线段的位置改变．②平行线间的距离处处相等，因此在作平行四边形的高时，可根据需要灵活选择位置． 5．平行四边形的面积：(1)如图12-1-2①，．也就是 (a 是平行四边形任何一边长，h 必须是a 边与其对边的距离)．(2)同底(等底)同高(等高)的平行四边形面积相等．如图12-1-2②，有公共边BC ，则．注意：这里的底是相对而言的，也就是高所在的边，平行四边形任意一边都可以作底，底确定后，高也就确定了．【例题精讲】例1 如图12-1-3，已知的对角线相交于点O ，过O 作直线交AB 于E ，交CD 于F ，可得OE ＝OF ．为什么？分析：要得到OE ＝OF ，可先证得它们所在△AEO 与△CFO(△BEO 与△DFO)重合． 解：在中，∵AB ∥CD ，OD ＝OB ， ∴∠1＝∠2，∠3＝∠4，∴将△BOE 绕点O 旋转180度后与△DOF 重合．∴OE＝OF．注意：把线段与角归结为平行四边形的边，对角线或对角，利用平行四边形的特征证明．例2(1)在中，∠A︰∠B＝2︰3，求各角的度数．(2)已知的周长为28cm，AB︰BC＝3︰4，求它的各边的长．分析：(1)在平行四边形中，邻角是互补的，而对角是相等的，所以∠A与∠B必是邻角，其和为180°，可据此列式求出角度．(2)平行四边形的对边相等，所以周长为邻边之和的2倍，可以据此列式求出各边长．解：(1)由于∠A、∠B是平行四边形的两个邻角，所以∠A＋∠B＝180°．又因为∠A ︰∠B＝2︰3，不妨可设∠A＝2k，∠B＝3k，那么2k＋3k＝180°，可以解得k＝36°，则∠A＝∠C＝72°，∠B＝∠D＝108°．(2)由于在中，AB＝CD，BC＝AD．所以AB＋BC＋CD＋AD＝28，即AB＋BC ＝14．由题意得AB︰BC＝3︰4，因此可设AB＝3k，BC＝4k，那么有3k＋4k＝14，解得k ＝2，则AB＝CD＝6cm，BC＝AD＝8cm．例3如图12-1-4，已知的周长为60 cm，对角线AC、BD相交于点O，△AOB 的周长比△BOC的周长长8cm，求这个四边形各边长．分析：由平行四边形对边相等知AB＋BC＝平行四边形周长的一半＝30cm，又由△AOB 的周长比△BOC的周长长8 cm知AB—BC＝8cm，由此两式，可得各边长．解：∵四边形ABCD为平行四边形，∴AB＝CD，AD＝CB，AO＝CO．∵AB＋CD＋AD＋CB＝60，AO＋AB＋OB－(OB＋BC＋OC)＝8，∴AB十BC＝30，AB－BC＝8，∴AB＝CD＝19，BC＝AD＝11．答：这个四边形各边长分别为19 cm，11 cm，19 cm，11 cm．注意：①平行四边形的邻边之和等于平行四边形周长的一半．②平行四边形被对角线分成四个小三角形，相邻两个三角形周长之差等于邻边之差．思考：如图12-1-4，如果△AOB与△AOD的周长之差为8，而AB∶AD＝3∶2，那么的周长为多少？提示：周长为80．设AB＝3x，则AD＝2x，依题意有3x－2x＝8，∴x＝8，∴AB＝3x＝3×8＝24，AD＝2x＝2×8＝16．∴周长＝2(24＋16)＝80．例4 如图12-1-5，在中，∠B＝120°，DE⊥AB，垂足为E，DF⊥BC，垂足为F．求∠ADE，∠EDF，∠FDC的度数．分析：由平行四边形对角相等、邻角互补得∠A＝∠C，∠A＋∠B＝180°，再由垂直得到角为90°即可．解：在中，∵∠A＝∠C，AD∥BC，∴∠A＋∠B＝180°．∴∠A＝180°－∠B＝60°．∴∠C＝60°．∵DE⊥AB，DF⊥BC，∴∠ADE＝∠FDC＝90°－∠A＝90°－60°＝30°．注意：在平行四边形中求角的度数时，一般运用平行四边形的特征，即对角相等、邻角互补来进行求解．【中考考点】会利用平行四边形证明角相等，线段相等及直线平行．【命题方向】多以中档题型出现，填空、选择、计算、证明等各种形式都会涉及．【常见错误分析】例7如图12-1-7，中，AC和BD交于O，OE⊥AD于E，OF⊥BC于F，则OE＝OF．为什么？错解：∵，∴OA＝OC，∵OE⊥AD，OF⊥BC，∴∠AOE＝∠COF．又∠1＝∠2，∴△AOE旋转180°后与△COF重合，∴OE＝OF．误区分析：错误出于∠AOE＝∠COF这一步骤，原因在于默认了E，O，F三点共线，而已知条件中并没有这个结论，其实E，O，F三点共线在证题过程中应该加以证明，否则就犯了推理没有根据，理由不充足的逻辑错误．正解：解法一：∵，∴AD∥BC，∴∠3＝∠4．又OA＝OC，∠AEO＝∠CFO＝90°，∴△AOE旋转180°后与△COF重合，∴OE＝OF．解法二：∵AD ∥BC ，OE ⊥AD ∴OE ⊥BC ．又OF ⊥BC ， ∴直线OE 与OF 重合， 即E ，O ，F 三点共线， ∴∠1＝∠2．又∵OA ＝OC ，∠AEO ＝∠CFO ＝90°， ∴△AOE 旋转180°后与△COF 重合， ∴OE ＝OF ．此命题可推广如下： 已知中，AC 和BD 交于O ，过点O 作直线EF 交AD 于F ，交BC 于F ，则OE ＝OF ．求解(略)．这个推广后的命题，是平行四边形中一个十分重要的基本命题，利用它的结果可以证明很多问题成立．【学习方法指导】1．学习平行四边形的特征时，按照对角、对边、对角线的顺序去理解，便于记忆和应用．2．本节主要内容是平行四边形的定义及特征，并且要重点理解两条平行线间的距离的概念．【同步达纲练习】 一、填空题1．若一个平行四边形相邻的两内角之比为2︰3，则此平行四边形四个内角的度数分别为____________．2．在中，周长为28，两邻边之比为3︰4，则各边长为____________． 3．在中，∠A ＝30°，AB ＝7 cm ，AD ＝6 cm ，则＝____________． 4．一个平行四边形的一边长是8，一条对角线长是6，则它的另一条对角线x 的取值范围为____________．5．中，周长为20cm ，对角线AC 交BD 于点O ，△OAB 比△OBC 的周长多4，则边AB ＝____________，BC ＝____________．6．平行四边形的边长等于5和7，这个平行四边形锐角的平分线把长边分成两条线段长各是____________．7．已知等腰△ABC 的一腰AB ＝9 cm ，过底边上任一点P 作两腰平行线分别交AB 于M ，交AC 于N ，则AN 十PN ＝____________．8．平行四边形两邻边分别是4和6，其中一边上的高是3，则平行四边形的面积是____________．9．平行四边形邻边长是 4 cm 和8cm ，一边上的高是 5 cm ，则另一边上的高是____________．10．如图12-1-8，中，E 是AD 的中点，BD 与EC 相交于F ，若2S EFD =∆，则BFC S ∆＝____________．11．已知P 为内一点，，则PCD PAB S S ∆∆+＝____________．12．已知的对角线相交于点O ，它的周长为10 cm ，△BCO 的周长比△AOB 的周长多2cm ，则AB ＝____________．二、解答题13．已知，如图12-1-9，在△ABC 中，BD 是∠ABC 的平分线，DE ∥BC 交AB 于E ，EF ∥AC 交BC 于F ，则BE ＝FC ，为什么？14．如图12-1-10，中，E ，F 是对角线BD 上两点，且BE ＝FD ，连结AE ，FC ，则AE ＝FC ，试说明理由．15．如图12-1-11，中，对角线AC 长为10 cm ，∠CAB ＝30°，AB 长为6 cm ，求的面积．16．如图12-1-12，在等边△ABC中，P为△ABC内一点，PD∥AB，PE∥BC，PF∥AC，D，E，F分别在AC，AB和BC上，试说明PD＋PF＋PE＝AB．17．从平行四边形的一个锐角顶点作两条高，如果这两条高的夹角是135°，求此平行四边形的各角的度数．三、思考题18．如图12-1-13，EF过对角线的交点O，交AD于E，交BC于F，若AB＝4，BC＝5，OE＝1.5，求四边形EFCD的周长．19．以平行四边形ABCD两邻边BC、CD为边向外作正△BCP和正△CDQ，则△APQ 为正三角形，请说明理由．参考答案【同步达纲练习】 一、1．72°，108°，72°，108° 2．6，8，6，8 3．2cm 21 4．10<x<22 5．7cm ，3 cm 6．5，2 7．9 cm 8．12或189．cm 25 10．8 11．50 12．1.5cm 二、13．提示：由△BED 是等腰三角形得到BE ＝ED ，由四边形DEFC 是平行四边形得到ED ＝FC 即可．14．提示：通过△ABE 与△DCF 重合可以得出．15．2cm 30．16．延长FP 交AB 于G ，延长DP 交BC 于H ，四边形AGPD ，EBHD 为平行四边形，PD ＝AG ，PH ＝BE ，△GEP ，△PHF 为等边三角形，PE ＝EG ，PH ＝PF ＝BE ，PD ＋PF ＋PE ＝AG ＋GE ＋EB ＝AB ．17．45°，135°，45°，135°． 三、18．OE ＝OF ＝1.5，AE ＝CF ，DE ＝BF ，ED ＋CF ＝BF ＋FC ＝5，CD ＝AB ＝4，四边形EFCD 的周长为2×1.5＋5＋4＝12．19．提示：证明△ABP 、△QDA 、△QCP 三个三角形重合，可得出AP ＝AQ ＝PQ 即可．。

华师大版数学八年级下册18.1《平行四边形的性质》（第2课时）教学设计一. 教材分析华东师范大学版数学八年级下册18.1《平行四边形的性质》（第2课时）的内容主要包括平行四边形的判定、平行四边形的性质以及平行四边形的应用。

本节课的内容是学生对平行四边形知识的进一步拓展和深化，对于培养学生的空间想象能力和逻辑思维能力具有重要意义。

二. 学情分析学生在之前的学习中已经掌握了平行四边形的定义和判定，对于平行四边形的性质也有一定的了解。

但学生在应用平行四边形的性质解决实际问题时，还存在着一定的困难。

因此，在教学过程中，需要教师引导学生深入理解平行四边形的性质，提高学生运用知识解决实际问题的能力。

三. 教学目标1.知识与技能：使学生掌握平行四边形的性质，能够运用性质判定平行四边形，解决实际问题。

2.过程与方法：通过观察、操作、交流等活动，培养学生的空间想象能力和逻辑思维能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的合作精神，使学生感受到数学在生活中的应用。

四. 教学重难点1.重点：平行四边形的性质。

2.难点：运用平行四边形的性质解决实际问题。

五. 教学方法1.情境教学法：通过生活实例引入平行四边形的性质，激发学生的学习兴趣。

2.活动教学法：引导学生通过观察、操作、交流等活动，发现平行四边形的性质。

3.问题驱动法：教师提出问题，引导学生思考，培养学生解决问题的能力。

六. 教学准备1.教师准备：教材、课件、教学素材、黑板、粉笔等。

2.学生准备：课本、练习本、文具等。

七. 教学过程1.导入（5分钟）教师通过展示生活中的平行四边形图片，如教室的黑板、滑滑梯等，引导学生观察并思考：这些物体为什么是平行四边形？它们有什么共同的特点？从而引出本节课的内容——平行四边形的性质。

2.呈现（10分钟）教师通过课件展示平行四边形的性质，引导学生观察并发现平行四边形的性质。

如：对边平行且相等，对角相等，对角线互相平分等。

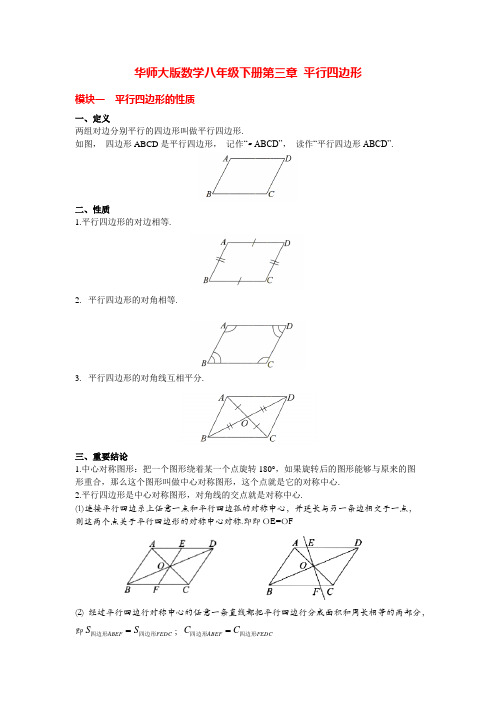
华师大版数学八年级下册第三章 平行四边形模块一 平行四边形的性质一、定义两组对边分别平行的四边形叫做平行四边形.如图， 四边形ABCD 是平行四边形， 记作“▱ABCD”， 读作“平行四边形ABCD”.二、性质1.平行四边形的对边相等.2. 平行四边形的对角相等.3. 平行四边形的对角线互相平分.三、重要结论1.中心对称图形：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心.2.平行四边形是中心对称图形，对角线的交点就是对称中心.(1)连接平行四边系上任意一点和平行四边孤的对称中心，并延长与另一条边相交于一点，则这两个点关于平行四边形的对称中心对称.即即OE=OF(2) 经过平行四边行对称中心的任意一条直线都把平行四边行分成面积和周长相等的两部分，即FEDC ABEF S S 四边形四边形=；FEDC ABEF C C 四边形四边形=典型例题例1．如图，在平行四边形ABCD中，DE平分∠ADC，AD＝6，BE＝2，则平行四边形ABCD的周长是（）A．16B．14C．20D．24练习．平行四边形ABCD中，∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分，则平行四边形ABCD的周长为cm．例2．如图，在▱ABCD中，AE⊥CD于点E，∠B＝65°，则∠DAE等于．例3．如图，平行四边形ABCD的对角线相交于点O，两条对角线的和为18，AD的长为5，则△OBC的周长为．练习．如图，在▱ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，则下列结论：①CF＝AE；②OE＝OF；③DE＝BF；④图中共有四对全等三角形．其中正确结论的个数是（）A．4B．3C．2D．1例4．如图，▱ABCD中，AC．BD为对角线，BC＝3，BC边上的高为2，则阴影部分的面积为（）A．3B．6C．12D．24例5．（1）如图，在▱ABCD中，AB＝4，BC＝6，BC边上的高AE＝2，则DC边上的高AF的长是（）A．2B．3C．4D．5（2）如图，▱ABCD与▱DCFE的周长相等，且∠BAD＝60°，∠F＝100°，则∠DAE的度数为（）A．20°B．25°C．30°D．35°（3）如图，在周长为20cm的▱ABCD中，AB≠AD，AC，BD相交于点O，OE⊥BD交AD 于E，则△ABE的周长为（）A．4cm B．6cm C．8cm D．10cm（4）如图，平行四边形ABCD中，点E在边AD上，以BE为折痕，将△ABE折叠，使点A正好与CD上的F点重合，若△FDE的周长为16，△FCB的周长为28，则FC的长为．例6.如图，在▱ABCD中，E是CD的中点，AE的延长线与BC的延长线相交于点F．求证：BC＝CF．模块二平行四边形的判定平行四边形的判定定理1.两组对边分别平行的四边形是平行四边形.AD//BC，AB//DC，四边形ABCD是平行四边形.2.两组对边分别相等的四边形是平行四边形.AB=DC，AD=BC，∴四边形ABCD是平行四边形.3.一组对边平行且相等的四边形是平行四边形.AD//BC，AD=BC，∴四边形ABCD是平行四边形.4.两组对角分别相等的四边形是平行四边形.∠=∠,∠D=BA∠C∴四边形ABCD是平行四边形.5.对角线互相平分的四边形是平行四边形.OA=OC，OB=OD，∴四边形ABCD是平行四边形.典型例题例7．如图，在四边形ABCD中，若已知AB∥CD，再添加下列条件之一，能使四边形ABCD成为平行四边形的条件是（）A．∠DAC＝∠BCA B．∠DCB+∠ABC＝180°C．∠ABD＝∠BDC D．∠BAC＝∠ACD练习．下列条件中，不能判断四边形ABCD是平行四边形的是（）A．AB∥CD，AD∥BC B．AB＝CD，AD∥BCC．AB∥CD，AB＝CD D．∠A＝∠C，∠B＝∠D例8．（1）如图，在▱ABCD中，点E、F分别在边AB和CD上，下列条件不能判定四边形DEBF一定是平行四边形的是（）A．DE＝BF B．AE＝CF C．∠ADE＝∠CBF D．∠AED＝∠CFB（2）小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带来了两块碎玻璃，其编号应该是。

初二数学平行四边形的定义和性质华东师大版【本讲教育信息】一. 教学内容：平行四边形的定义和性质二. 重点、难点：1. 重点：平行四边形的定义和性质2. 难点：平行四边形的性质平行四边形的定义三.知识梳理：平行四边形是我们常见的一种图形，它具有十分和谐的对称美。

它是什么样的对称图形呢?它又具有哪些基本性质呢?平行四边形的定义：有两组对边分别平行的四边形叫做平行四边形。

平行四边形的性质：两组对边分别平行。

即：在平行四边形ABCD中，AD∥BC，AB∥DC。

平行四边形的性质：平行线之间的距离处处相等。

平行四边形的性质：平行四边形的对边相等。

平行四边形的性质：平行四边形的对角相等。

即：在平行四边形ABCD中，AD＝BC，AB＝DC，∠A＝∠C，∠B＝∠D。

平行四边形的性质：平行四边形对角线互相平分即：在平行四边形ABCD中，已知对角线AC和BD相交于点O，OA＝OC，OB＝OD。

【典型例题】例1. 如图，在平行四边形ABCD中，已知∠A＝40°，求其他各个内角的度数。

分析：运用平行四边形的定义和性质进行解题：解：在平行四边形ABCD中，∠D＝∠B，∠C＝∠A＝40°(平行四边形的对角相等)。

又∵AD∥BC，∴∠B＝180°－∠A＝180°－40°＝140°，∴∠D＝∠B＝140°。

例2. 如图，在平行四边形ABCD中，已知AB＝8，周长等于24，求其余三条边的长。

分析：运用平行四边形的定义和性质进行解题：解：在平行四边形ABCD中，AB＝DC，AD＝BC(平行四边形对边相等)。

又∵AB＝8，AB+BC+CD+DA＝24，∴CD＝8，AD＝BC＝4。

例3.如图，在平行四边形ABCD中，已知对角线AC和BD相交于点O，△AOB的周长为15，AB＝6，那么对角线AC与BD的和是多少?分析：运用平行四边形的定义和性质进行解题：解：在平行四边形ABCD中，已知AB＝6，AO+BO+AB＝15，∴AO+BO＝15－6＝9。

《平行四边形》全章复习与巩固（基础）【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算. 【知识网络】【要点梳理】要点一、平行四边形1．定义：两组对边分别平行的四边形叫做平行四边形.2．性质：（1）对边平行且相等；（2）对角相等；邻角互补；（3）对角线互相平分；（4）中心对称图形.3．面积：高底平行四边形S 4．判定：边：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形．角：（4）两组对角分别相等的四边形是平行四边形；（5）两组邻角分别互补的四边形是平行四边形．边与角：（6）一组对边平行，一组对角相等的四边形是平行四边形；对角线：（7）对角线互相平分的四边形是平行四边形.要点诠释：平行线的性质：（1）平行线间的距离都相等；（2）等底等高的平行四边形面积相等.要点二、矩形1．定义：有一个角是直角的平行四边形叫做矩形.2．性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线互相平分且相等；（4）中心对称图形，轴对称图形.3．面积：宽＝长矩形S ４．判定：（1) 有一个角是直角的平行四边形是矩形.（2）对角线相等的平行四边形是矩形. （3）有三个角是直角的四边形是矩形.要点诠释：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半．要点三、菱形1. 定义：有一组邻边相等的平行四边形叫做菱形. 2．性质：（1）具有平行四边形的一切性质；（2）四条边相等；（3）两条对角线互相平分且垂直，并且每一条对角线平分一组对角；（4）中心对称图形，轴对称图形.3．面积：2对角线对角线高＝＝底菱形S 4．判定：（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四边相等的四边形是菱形.要点四、正方形1. 定义：四条边都相等，四个角都是直角的四边形叫做正方形.2．性质：（1）对边平行；（2）四个角都是直角；（3）四条边都相等；（4）对角线互相垂直平分且相等，对角线平分对角；（5) 两条对角线把正方形分成四个全等的等腰直角三角形；（6）中心对称图形，轴对称图形.3．面积：=S 正方形边长×边长＝12×对角线×对角线4．判定：（1）有一个角是直角的菱形是正方形；（2）一组邻边相等的矩形是正方形；（3）对角线相等的菱形是正方形；（4）对角线互相垂直的矩形是正方形；（5）对角线互相垂直平分且相等的四边形是正方形；（6）四条边都相等，四个角都是直角的四边形是正方形.【典型例题】类型一、平行四边形1、如图，在口ABCD中，点E在AD上，连接BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N．求证：四边形MFNE是平行四边形．【答案与解析】证明：∵四边形ABCD是平行四边形.∴AD＝BC,AD∥BC（平行四边形的对边相等且平行）又∵DF∥BE（已知）∴四边形BEDF是平行四边形（两组对边分别平行的四边形是平行四边形）∴DE＝BF（平行四边形的对边相等）∴AD－DE＝BC－BF，即AE＝CF又∵AE∥CF∴四边形AFCE是平行四边形（一组对边平行且相等的四边形是平行四边形）∴AF∥CE∴四边形MFNE是平行四边形（两组对边分别平行的四边形是平行四边形）【总结升华】要证明一个四边形是平行四边形首先要根据已知条件选择一种合理的判定方法，如本题中已有一边平行，只须说明另一边也平行即可，故选用“两组对边分别平行的四边形是平行四边形”来证明.举一反三：【变式】如图，等腰△ABC中，D是BC边上的一点，DE∥AC，DF∥AB,通过观察分析线段DE，DF，AB三者之间有什么关系，试说明你的结论．【答案】AB＝DE＋DF，提示：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∠C＝∠EDB∴DF＝AE．∵△ABC是等腰三角形，∴∠B＝∠C，∴∠B＝∠EDB，∴DE＝BE，∴AB＝AE＋BE＝DF＋DE2、（2015?哈尔滨）如图1，口ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD分别相交于点G，H，连接EG，FG，FH，EH．（1）求证：四边形EGFH是平行四边形；（2）如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．【思路点拨】（1）由四边形ABCD是平行四边形，得到AD∥BC，根据平行四边形的性质得到∠EAO=∠FCO，证出△OAE≌△OCF，得到OE=OF，同理OG=OH，根据对角线互相平分的四边形是平行四边形得到结论；（2）根据两组对边分别平行的四边形是平行四边形即可得到结论．【答案与解析】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAO=∠FCO，在△OAE与△OCF中，∴△OAE≌△OCF，∴OE=OF，同理OG=OH，∴四边形EGFH是平行四边形；（2）解：与四边形AGHD面积相等的所有平行四边形有口GBCH，口ABFE，口EFCD，口EGFH；∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∵EF∥AB，GH∥BC，∴四边形GBCH，ABFE，EFCD，EGFH为平行四边形，∵EF过点O，GH过点O，∵OE=OF，OG=OH，∴口GBCH，口ABFE，口EFCD，口EGFH，口ACHD它们面积=口ABCD的面积，∴与四边形AGHD面积相等的所有平行四边形有口GBCH，口ABFE，口EFCD，口EGFH．【总结升华】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行四边形的判定定理是解题的关键．类型二、矩形3、（2016春?常州期末）如图，在△ABC中，AB=AC，D为BC的中点，AE∥BC，DE∥AB．试说明：（1）AE=DC；（2）四边形ADCE为矩形．【思路点拨】（1）根据已知条件可以判定四边形ABDE是平行四边形，则其对边相等：AE=BD．结合中点的性质得到AE=CD；（2）依据“对边平行且相等”的四边形是平行四边形判定四边形ADCE是平行四边形，又由“有一内角为直角的平行四边形是矩形”证得结论．【答案与解析】证明：（1）如图，∵AE∥BC，∴AE∥BD．又∵DE∥AB，∴四边形ABDE是平行四边形，∴AE=BD．∵D为BC的中点，∴BD=DC，∴AE=DC；（2）∵AE∥CD，AE=BD=DC，即AE=DC，∴四边形ADCE是平行四边形．又∵AB=AC，D为BC的中点，∴AD⊥CD，∴平行四边形ADCE为矩形．【总结升华】本题考查了等腰三角形的性质，矩形的判定与性质以及平行四边形的性质．此题也可以根据“对角线相等的平行四边形是矩形”来证明（2）的结论．4、如图所示，在矩形ABCD中，AB＝6，BC＝8．将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处，求EF的长.【思路点拨】要求EF的长，可以考虑把EF放入Rt△AEF中，由折叠可知CD＝CF，DE＝EF，易得AC＝10，所以AF＝4，AE＝8-EF，然后在Rt△AEF中利用勾股定理求出EF的值．【答案与解析】解：设EF＝x，由折叠可得：DE＝EF＝x，CF＝CD＝6，又∵在Rt△ADC中，226810AC．∴ AF＝AC－CF＝4，AE＝AD－DE＝8－x．在Rt△AEF中，222AE AF EF，即222(8)4x x，解得：x＝3 ∴ EF＝3【总结升华】在矩形折叠问题中往往根据折叠找出相等的量，然后把未知边放在合适的直角三角形中，再利用勾股定理进行求解．举一反三：【变式】把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB ＝ 3cm，BC ＝ 5cm，则重叠部分△DEF的面积是__________2cm．【答案】5.1.提示：由题意可知BF＝DF，设FC＝x，DF＝5－x，在Rt△DFC中，222DC FC DF，解得x＝85，BF＝DE＝3.4，则DEF1=DE AB2S△＝12×3.4×3＝5.1.类型三、菱形5、如图,在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF等于( ).A.80°B.70°C.65°D.60°【答案】D；【解析】解：连结BF，由FE是AB的中垂线，知FB＝FA，于是∠FBA＝∠FAB＝＝40°.∴∠CFB＝40°＋40°＝80°,由菱形ABCD知，DC＝CB，∠DCF＝∠BCF，CF＝CF，于是△DCF≌△BCF，因此∠CFD＝∠CFB＝80°,在△CDF中, ∠CDF＝180°－40°－80°＝60°.【总结升华】运用菱形的性质可以证明线段相等、角相等、线段的平行及垂直等问题，关键是要记住它们的判定和性质.举一反三：【变式】用两张等宽的纸带交叉重叠地放在一起，重合的四边形ABCD是菱形吗？如果是菱形请给出证明，如果不是菱形请说明理由．【答案】四边形ABCD是菱形；证明：由AD∥BC，AB∥CD得四边形ABCD是平行四边形,过A，C两点分别作AE⊥BC于E，CF⊥AB于F．∴∠CFB＝∠AEB＝90°．∵AE＝CF（纸带的宽度相等）∠ABE＝∠CBF，∴Rt△ABE≌Rt△CBF,∴AB＝BC,∴四边形ABCD是菱形.类型四、正方形6、（2015春?上城区期末）如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH=2，连结CF．（1）若DG=2，求证：四边形EFGH为正方形；（2）若DG=6，求△FCG的面积．【思路点拨】（1）通过证明Rt△DHG≌△AEH，得到∠DHG=∠AEH，从而得到∠GHE=90°，然后根据有一个角为直角的菱形为正方形得到四边形EFGH为正方形；（2）作FQ⊥CD于Q，连结GE，如图，利用AB∥CD得到∠AEG=∠QGE，再根据菱形的性质得HE=GF，HE∥GF，则∠HEG=∠FGE，所以∠AEH=∠QGF，于是可证明△AEH≌△QGF，得到AH=QF=2，然后根据三角形面积公式求解．【答案与解析】（1）证明：∵四边形EFGH为菱形，∴HG=EH，∵AH=2，DG=2，∴DG=AH，在Rt△DHG和△AEH中，，∴Rt△DHG≌△AEH，∴∠DHG=∠AEH，∵∠AEH+∠AHG=90°，∴∠DHG+∠AHG=90°，∴∠GHE=90°，∵四边形EFGH为菱形，∴四边形EFGH为正方形；（2）解：作FQ⊥CD于Q，连结GE，如图，∵四边形ABCD为矩形，∴AB∥CD，∴∠AEG=∠QGE，即∠AEH+∠HEG=∠QGF+∠FGE，∵四边形EFGH为菱形，∴HE=GF，HE∥GF，∴∠HEG=∠FGE，∴∠AEH=∠QGF，在△AEH和△QGF中，∴△AEH≌△QGF，∴AH=QF=2，∵DG=6，CD=8，∴CG=2，∴△FCG的面积=CG?FQ=×2×2=2．【总结升华】本题考查了正方形的判定与性质：正方形的判定没有固定的方法，只要判定既是矩形又是菱形就可以判定；正方形具有平行四边形、矩形、菱形的所有性质．也考查了菱形和矩形的性质．7、如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过 E点作EF⊥AE交∠DCE的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由.【思路点拨】AE＝EF．根据正方形的性质推出AB＝BC，∠BAD＝∠HAD＝∠DCE＝90°，推出∠HAE＝∠CEF，根据△HEB是以∠Ｂ为直角的等腰直角三角形，得到BH＝BE，∠H＝45°，HA＝CE，根据CF平分∠DCE推出∠H＝∠FCE，根据ASA证△HAE≌△CEF即可得到答案．【答案与解析】探究：AE＝EF证明：∵△BHE为等腰直角三角形,∴∠H＝∠HEB＝45°，BH＝BE.又∵CF平分∠DCE，四边形ABCD为正方形，∴∠FCE＝12∠DCE＝45°，∴∠H＝∠FCE.由正方形ABCD知∠B＝90°，∠HAE＝90°＋∠DAE＝90°＋∠AEB,而AE⊥EF，∴∠FEC＝90°＋∠AEB，∴∠HAE＝∠FEC.由正方形ABCD知AB＝BC，∴BH－AB＝BE－BC，∴HA＝CE,∴△AHE≌△ECF （ASA）,∴AE＝EF.【总结升华】充分利用正方形的性质和题目中的已知条件，通过证明全等三角形来证明线段相等.。