当前位置：文档之家 › 第十一章 描述性统计量

第十一章 描述性统计量

  • 格式：ppt
  • 大小：497.00 KB
  • 文档页数：51

下载文档原格式

  / 51

合集下载

第十一章专题数据分析方法——描述性统计市场调研描述

第十一章专题数据分析方法——描述性统计市场调研描述


数量标志的描述方法（1）
表3 某年某工地100名工人的月工资情况 工人数（人） 10 35 20 20 15 100
厦门理工学院文化传播系 蔡清毅 14
按工资水平分组（元） 500以下 500—600 600—700 700—800 800以上 合计
2018/12/10
数量标志的描述方法（1）
注意几个问题： 第一 工资水平是连续变量 要用重叠组限
2018/12/10
厦门理工学院文化传播系 蔡清毅
4
区分不同的测量水平
区分原则：定类数据没有大小之分；定序数据
有大小之分，差值有意义；定距数据有大小之 分，差值有意义，但其比值无意义；定比数据 比值有意义。 定比定距数据可以向前化成定序或者定类数据， 但是将损失一定信息；反之，不能将定序定类 数据化成定距定比数据。
第二 组限的确定，即分组界限的确定
第三 组距大小的确定
全距 第四 组数的确定，组数＝ 组距
2018/12/10
厦门理工学院文化传播系 蔡清毅
15
数量标志的描述方法（1）
（3）不等组距变量数列 如在生命统计中，人口死亡率将人口按年龄分组
1岁以下 1—1.9岁 2—2.9岁 组距为1 5—9.9岁 10—14.9岁 组距为5 15—19.9岁 20—29.9岁 30—39.9岁 40—49.9岁 组距为10
3—3.9岁
4—4.9岁
50—59.9岁
60—64.9岁 …… 组距为5
2018/12/10
厦门理工学院文化传播系 蔡清毅
16
数量标志的描述方法（2）
某校20名学生的身高分布表
身 高 <156 156～162 162～168 168～174 174～180 >=180 累计
统计学中的描述性统计分析方法

统计学中的描述性统计分析方法

统计学中的描述性统计分析方法统计学是一门研究数据收集、整理、分析和解读的学科，它可以帮助我们更好地理解和解释数据。

描述性统计是统计学中的一个重要分支，旨在总结和揭示数据的基本特征。

在本文中，我们将介绍统计学中常用的描述性统计分析方法。

一、数据收集与整理描述性统计分析的第一步是数据收集，通过合适的调查问卷、实验或观察，我们可以获取所需的数据。

在数据收集完成后，我们需要对数据进行整理和准备，以便后续的分析。

二、测量指标在描述性统计中，我们常用各种测量指标来描绘数据的中心趋势、离散程度以及数据之间的关联性。

1. 中心趋势测量中心趋势测量用来反映数据集中的一个“典型值”。

（1）平均数（Mean）：平均数是数据集中所有观测值的总和除以观测值的数量。

它可以用来衡量数据的总体情况。

（2）中位数（Median）：中位数是将数据集按大小顺序排列后的中间值。

它可以忽略异常值的影响，更好地反映数据的中心位置。

（3）众数（Mode）：众数是数据集中出现频率最高的值。

它在描述分类数据时特别有用。

2. 离散程度测量离散程度测量用来反映数据集的分散程度。

（1）标准差（Standard Deviation）：标准差是数据集各个观测值与平均数之间的偏离度的平均值。

它反映了数据的总体分散程度。

（2）方差（Variance）：方差是各个观测值与平均数之间偏离度的平方的平均值。

它是标准差的平方。

（3）极差（Range）：极差是数据集中最大值与最小值之间的差值。

它可以用来衡量数据的全局范围。

三、数据可视化数据可视化是描述性统计分析中非常重要的一部分。

通过图表和图形的方式展示数据，可以使数据的特征更加直观地呈现出来。

1. 条形图（Bar Chart）：条形图用于对比不同类别或组之间的数据差异。

2. 折线图（Line Chart）：折线图可以展示变量随时间的变化趋势。

3. 饼图（Pie Chart）：饼图适用于展示分类数据的比例关系。

4. 散点图（Scatterplot）：散点图可以直观地显示两个变量之间的关系。

第十一章 统计分析和调查报告

第十一章 统计分析和调查报告


• 2、定序变量 • 3、定距或定比变量
第十三章 撰写研究报告
• 研究研究报告及其类型 • 研究报告是反映社会调查成果的一种书面 报告，它以文字、图表等形式将调查研究 的过程、方法和结果表现出来。其目的是 告诉有关读者，对于所研究的问题是如何 进行调查的，取得了哪些结果，这些结果 对于认识和解决这一问题有哪些理论意义 和实际意义等等
其它故事与发表情况
• 另外两种形式的故事叫做批判的故事（吸 引读者对社会问题的注意和重视）和形式 的故事（理论的表述）。 • 民族志写作惯例发生了变化。今天，被发 表的现实主义的故事越来越少，而印象主 义或坦白的故事则相对越来越多。 • 没有完美的理论，也没有完美的报告。
• 导言部分 • 普通调查报告的第一部分称作导言，它的主要任务是向读者简要地介绍 整个调查的有关背景。其中，最主要的内容包括调查的目的、调查的内 容、调查的对象、调查的时间、地点、调查的方法等等。导言的具体写 法有下列几种常见的方式。 • (1)直述式 • 即开门见山,平铺直述,直接把调查的目的,内容,对象,范围等一一写出.例 如: • 为了全面了解老年人的生活状况，加强老年人的社会保障工作，沈阳 师范大学社会学系于2003年2月至4月，在辽宁省沈阳市调查了300位老 年人的家庭与生活情况。下面是这次调查的方法及主要结果。 • (2)悬念式。 • 即先描述某种社会现象和社会问题，然后对这种社会现象和问题产生的 原因、它的影响等等提出一系列疑问，最后介绍调查的基本情况.例如: • 老年人丧偶是生活中十分普遍的现象，而老年人再婚，则是近年来出 现在我国社会中的一种新的社会现象。据有关部门统计，本市1980年再 婚老年夫妇为68对，1984年为116对，1988年为302对；1991年为： 495对；1994年为623对。促使老年人再婚比例提高的原因是什么?；社 会舆论对老年人再婚的评价如何?老年人再婚给他们的家庭及其生活带 来了哪些变化?；为了弄清这些问题，沈阳师范大学社会学系于今年3—5月，对沈阳市180对再婚老年夫妇进行了调查。
第十一章 定量数据的表示方法

第十一章 定量数据的表示方法

22
•
•
骗人的“平均数”
•
萨姆： 萨姆：对，对，对！你是对的，平均工资是每周 你是对的， 300元 可你还是蒙骗了我。 300元。可你还是蒙骗了我。 吉斯莫；我不同意！你实在是不明白。 吉斯莫；我不同意！你实在是不明白。我已经把工 资列了个表，并告诉了你，工资的中位数是200元 资列了个表，并告诉了你，工资的中位数是200元 200 可这不是平均工资，而是中等工资。 ，可这不是平均工资，而是中等工资。 萨姆：每周100元又是怎么回事呢？ 萨姆：每周100元又是怎么回事呢？ 100元又是怎么回事呢 吉斯莫：那称为众数，是大多数人挣的工资。 吉斯莫：那称为众数，是大多数人挣的工资。 吉斯莫：老弟，你的问题是出在你不懂平均数、 吉斯莫：老弟，你的问题是出在你不懂平均数、中 位数和众数之间的区别。 位数和众数之间的区别。 萨姆： 萨姆：好，现在我可懂了。我……我辞职！ 现在我可懂了。 ……我辞职！ 我辞职
24
•
中位数 将总体中的各个个体数值按照大小顺序排列， 将总体中的各个个体数值按照大小顺序排列，居于 中间位置的数值，便是中位数。 中间位置的数值，便是中位数。
•
中位数
25
中位数 1.是一种集中趋势或平均指标 1.是一种集中趋势或平均指标 2.位于中间位置的数值 2.位于中间位置的数值 • 如果数据为奇数项，中位数是中间位置的数值 如果数据为奇数项， 如果数据为偶数项， 如果数据为偶数项，中位数是中间位置两个数值的 平均数是一种位置平均数
频数分布 作用： 作用： 有助于明确未回答者的多少， 有助于明确未回答者的多少，同时也能显示不 合格答案的多少； 合格答案的多少； 可以检验奇异值和极端值； 可以检验奇异值和极端值； 根据频数分布可以划出各种统计图形。 根据频数分布可以划出各种统计图形。
社会研究方法(第四版)第十一章

社会研究方法(第四版)第十一章

.87 5.02
a 71.87 176 8212 . Y 8212 . .87 X
有了这一回归方程后，我们就可以由预测变量的值 经回归方程计算出标准变量的预测值。如另一名大学生 的身高为170厘米，则其体重的预测值为65.78公斤。
资料审核的方法主要有两种，即逻辑审核与 计算审核。 逻辑审核，即核查资料的内容是否合乎逻辑 和常识，项目之间有无互相矛盾之处，与其 他有关资料进行对照是否有明显出入等等。 计算审核，是针对数字资料进行的审查。要 检查计算有无错误。度量单位有没有错，前 后数字之间有无相互矛盾之处等等。
二、资料的转换
2 定序层次：中位值（中位数）（单选）
其意义为按大小顺序排列，处在一群数据中央位置的数值。 （1）原始资料，求中位值 例如：有9个人，他们的月工资分别如下： 47，42，50，51，92，112，71，83，108 首先作排列处理，从小到大排列 42，47，50，51，71，83，92，108，112 其次求中央位置 Md的位置=（N+1）÷2=（9+1）÷2=5 最后求中位置Md=71
二、单变量推论统计
区间估计 以样本统计量的抽样分布为理论依据，按一 定概率要求，由样本统计量的值来估计总体 参数的值所在的范围，叫做总体参数的区间 估计。 区间估计的实质就是在一定的可信度（置信 度）下，用样本统计值的某个范围来估价总 体的参数值 。范围的大小反映的是这种估计 的精确性问题，而可信度高低反映的是这种 估计的可靠性或和握性问题。
a b
两个变量（预测变量X与标准变量Y）间的回 归分析，是只有一个自变量的线性回归，也叫 一元线性回归。其回归方程为：
Y a bX
其中a,b、对一对特定数据来说是常数：
第十一章 国民经济统计基础知识 《统计学》PPT课件

第十一章 国民经济统计基础知识 《统计学》PPT课件

10 - 14
统计学
STATISTICS
二、国民经济行业分类 行业分类是国民经济的基本分类，是构成三 次产业划分和其它一些国民经济分类的基础。 在世界各国，国民经济行业分类往往以“国 家标准“的形式公布实施。随着国民经济的 不断发展，一些新的行业出现，旧的行业消 亡，我国国民经济行业分类也作过多次修订。 现行的行业分类标准将国民经济分为20个门 类，各门类下又进一步划分98个大类。
10 - 7
统计学
STATISTICS
（2）国民经济总量统计 国民经济总量统计是对一定时期内国民经济运行总成 果的统计核算，是对一国国民经济的基本规模和水平 的核算。国内生产总值核算是其中的重要内容。 （3）国民经济过程统计 国民经济过程统计从数量方面反映国民经济运行的结 果是如何产生的？ 财政政策、金融货币政策、价格 问题等是如何影响国民经济运行结果的。 。
10 - 2
统计学
STATISTICS
（一）全面系统反映国民经济运行状况 国民经济是一个非常复杂的运行系统，不同部门，不同环节之间存在着复杂 的经济联系，准确地了解这个系统难度很大。需要借助一种行之有效的工具， 国民经济核算就是这样一种工具。它通过系列 科学的核算原则和方法把描 述国民经济各个方面的基本指标有机地组织起来，将国民经济运行过程清晰 地展现出来。它既反映了国民经济运行的过程和全貌，又反映了国民经济的 主要比例和平衡关系。 美国经济学家萨谬尔森指出：“国内生产总值是20世纪最伟大的发明之一。 与太空中的卫星能够描述整个大陆的天气情况非常相似，国内生产总值能够 提供经济状况的完整图像，它能够帮助总统、国会和联邦储备委员会判断经 济是在萎缩还是在膨胀，是需要刺激还是需要控制，是处于严重衰退还是处 于通涨威胁之中。没有像国内生产总值这样的总量指标，政策制定者就会陷 入杂乱无章的数字海洋而不知所措。国内生产总值和有关数据就像灯塔一样， 帮助政策制定者引导经济向着主要的经济目标发展。”
描述性统计分析方法

描述性统计分析方法

描述性统计分析方法描述性统计分析是指对收集到的样本数据进行整理、分析和总结的过程。

它旨在通过使用统计指标和图表来描述数据的特征和分布，以便更好地理解数据，发现其中的规律和趋势。

在进行描述性统计分析时，常用的方法包括中心趋势测度、离散程度测度、分布形态描述和相关性分析等。

一、中心趋势测度中心趋势测度是用来表示数据集中趋向于某个中心的位置。

常用的中心趋势测度包括均值、中位数和众数等。

1. 均值：均值是以所有数据的数值和除以数据个数的统计量，用来表示平均水平。

均值对异常值敏感，容易受到极端值的影响。

2. 中位数：中位数是将数据按照顺序排列后，位于中间位置的数值。

中位数不会受到极端值的影响，更能反映数据的普遍情况。

3. 众数：众数是一组数据中出现频率最高的数值，可用于描述具有离散分布的数据。

二、离散程度测度离散程度测度是用来表示数据集合中数据分散程度的方法。

常用的离散程度测度有范围、方差和标准差等。

1. 范围：范围是最大值和最小值的差值，可用来衡量数据的整体变化幅度。

范围对异常值敏感，易受到极端值的影响。

2. 方差：方差是各数据与均值差的平方和的平均数，用来描述数据的平均离散程度。

方差较大时，表示数据的离散程度较高。

3. 标准差：标准差是方差的平方根，用于度量数据相对于均值的离散程度。

标准差较大时，表明数据分散程度大。

三、分布形态描述分布形态描述是对数据分布形态特征进行描述的方法。

常用的分布形态描述包括偏度和峰度等。

1. 偏度：偏度描述了数据分布曲线相对于均值偏离的大小和方向。

偏度为正表示数据分布朝右偏，为负表示数据分布朝左偏，为0表示数据均匀分布。

2. 峰度：峰度描述了数据分布曲线的陡峭程度，反映了数据分布的尖峰与平顶程度。

峰度大于0表示数据分布曲线相对于正态分布更陡峭，小于0表示数据分布曲线相对于正态分布更平顶。

四、相关性分析相关性分析用来研究两个变量之间的相关关系。

常用的相关性分析方法有协方差和相关系数。

第11章 描述统计

第11章 描述统计


3 样本与总体
人们从总体中抽取样本的目的是根据样本数据对总体的数字特征和 分布规律进行推断、估计和检验。 ●自然，由样本推断和估计总体很难做到完全精确和可靠。但是必须 采取措施获得比较精确和具有一定可靠性的推断。其措施涉及两方 面的问题：即抽取样本的方法和统计推断的方法。 ● 当样本的抽取满足下列两个条件时，样本将能很好地反映总体的统 计规律性： （1）样本容量n足够大。样本容量越大，推断的结论越准确，可 靠性越高； （2）采用随机抽样，即总体中每个个体被抽到的机会均等，即使 一个个体被抽取后，总体的成分不变。换句话说，每个样品 的抽取都是一次独立、重复试验。 ● 至于应采用的统计推断方法将在以后各章讨论
8
1 随机抽样
定义：是指从总体抽取样品时，使每个个体被抽到的机 定义 会均等以使所抽取的样本数据能够很好地代表总 体的抽样方法。 方法：鉴于实际情况产品的大小、形状、存取状态等方 方法 面的差异及条件限制，常用的随机抽样方法为： （1）简单随机抽样法： （单纯随机抽样） ① 抽签法（或掷骰子法） ② 随机数表法 （2）分层随机抽样 （3）系统随机抽样 （4）多级随机抽样
n A = 150 × n B = 60 nC = 15
1600
= 75
11
系统随机抽样法（ 系统随机抽样法（间隔随机抽样） 间隔随机抽样）
●
●
定义：当批中产品可以按某个次序排列时，给批中 定义 N N 每个 产 品 编号1～N，以 n 整数部分 n 为 抽样间隔，用简单随机抽样法在1至 N 之间 n 随机 抽 取 的 一个整数作为第一个单位产品 N 号码，每隔 − 1个产品抽取一个，直到抽出 n n个样本为止 例：某工序每天生产200件产品，规定巡检员在一 天中抽取n=10的样本进行检查，试用系统随机 抽样确定抽取的样本号码 N = 20 ，第一个样品号码用抽签法确定为13， 解： n 则被抽取的样品号码为13、33、53、…、193
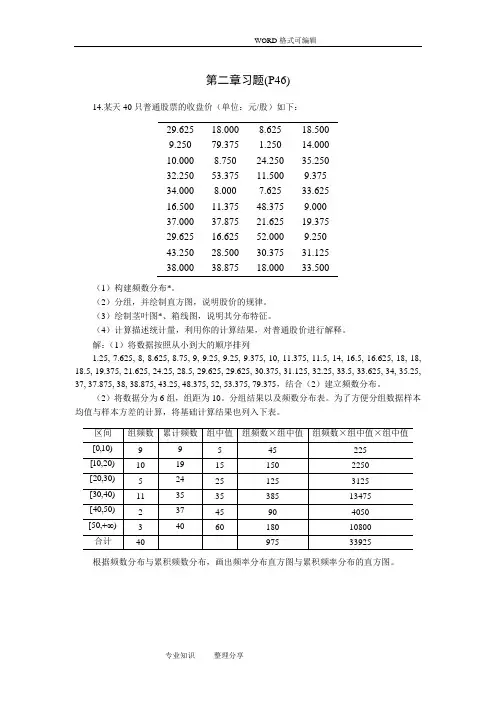
《数据、模型和决策》习题解答

《数据、模型和决策》习题解答

第二章习题(P46)14.某天40只普通股票的收盘价（单位：元/股）如下：29.625 18.000 8.625 18.5009.250 79.375 1.250 14.00010.000 8.750 24.250 35.25032.250 53.375 11.500 9.37534.000 8.000 7.625 33.62516.500 11.375 48.375 9.00037.000 37.875 21.625 19.37529.625 16.625 52.000 9.25043.250 28.500 30.375 31.12538.000 38.875 18.000 33.500（1）构建频数分布*。

（2）分组，并绘制直方图，说明股价的规律。

（3）绘制茎叶图*、箱线图，说明其分布特征。

（4）计算描述统计量，利用你的计算结果，对普通股价进行解释。

解：（1）将数据按照从小到大的顺序排列1.25, 7.625, 8, 8.625, 8.75, 9, 9.25, 9.25, 9.375, 10, 11.375, 11.5, 14, 16.5, 16.625, 18, 18, 18.5, 19.375, 21.625, 24.25, 28.5, 29.625, 29.625, 30.375, 31.125, 32.25, 33.5, 33.625, 34, 35.25, 37, 37.875, 38, 38.875, 43.25, 48.375, 52, 53.375, 79.375，结合（2）建立频数分布。

（2）将数据分为6组，组距为10。

分组结果以及频数分布表。

为了方便分组数据样本均值与样本方差的计算，将基础计算结果也列入下表。

根据频数分布与累积频数分布，画出频率分布直方图与累积频率分布的直方图。

频率分布直方图从频率直方图和累计频率直方图可以看出股价的规律。

股价分布10元以下、10—20元、30—40元占到60%，股价在40元以下占87.5%，分布不服从正态分布等等。

高等数学 第十一章 电子课件

高等数学 第十一章 电子课件


第一节
概率论
一、随机事件
（一）随机事件的概念
引例1 如果问“苹果从树上脱落，会往地上落吗？”，答案是“会”． 引例2 如果问“掷一枚骰子，能否出现7点？”，答案是“不能”． 引例3 抛掷一枚质地均匀的硬币，结果可能是正面朝上，也可能是反面朝上， 且事先无法确定抛掷的结果是什么． 引例4 在400 m短跑比赛前，运动员需通过抽签决定自己所在的跑道，且每 次抽签前都无法预测自己会在哪条跑道．
（二）概率的古典定义
在某些情况下，随机试验具有以下特征． 有限性：试验中所有可能出现的基本事件只有有限个． 等可能性：每个基本事件出现的可能性相等． 具有以上两个特点的概率模型是大量存在的，这种概率 模型称为古典概率模型，简称古典概型，也称等可能概型．
（二）概率的古典定义
定义 3 对于古典概型，设试验含有 n 个基本事件，若事件 A 包含 m 个基本事件，则事件 A
第十一章
概率统计基础
导学
概率论与数理统计是研究随机现象内在规律性的重要工具，其应用已 遍及自然科学、社会科学、工程技术、军事科学及生活实际等各领域，因 此掌握一定的概率统计知识十分必要．
本章主要介绍随机事件及其概率，随机变量及其分布，随机变量的期 望与方差，数理统计的基础知识，参数估计，假设检验及回归分析．
随机试验的一切可能结果所组成的集合称为样本空间，记作 ．随机试验的每
一个可能结果称为样本点，样本空间就是全体样本点的集合．
（一）随机事件的概念
定义1 随机试验的每一种可能的结果称为随机事件，简称事件．它通常用大写 英文字母A, B, C… 表示．
随机事件可分为基本事件和复合事件． 基本事件：在随机试验中，不可再分解的事件． 复合事件：在随机试验中，由若干个基本事件组合而成的事件．
第十一章统计决策

第十一章统计决策


E (Q(ai )) qij Pj
j 1
n
Vi
2
(ai )
(ai )
(q
j 1
n
E (Q(ai ))
ij
E (Q(ai ))) Pj
然后，在最低期望值条件下，选变异系数低的 方案为最优 * 实际决策时，通常将 期望值准则和变异系 数准则结合使用
a Min Vi
方 250 0 85 小规模投资 4、折衷准则下，选择第一种方案，即进行大规模 案 450 200 0 不生产 投资啤酒生产。 收益值为229.5万元
5、等可能准则下，选择第二种方案，即进行小规 模投资啤酒生产。收益值为105万元
二、各种准则的特点和适用场合
最大的最大收益值准则一般只有在客观情况确实很乐 观，或者即使决策失误但可以承受损失的场合才采用。 最大的最小收益值准则适用于对未来的状态非常没有 把握，或者不能承受决策失误造成损失的场合。 最小的最大后悔值准则适用于不愿放过较大的获利机 会，同时又对可能出现的损失有一定承受力的场合。 折衷准则和等可能性准则都是以各种方案的收益期望 值作为选择方案的标准。折衷准则事实上是假定未来可 能发生的状态只有两种：即最理想状态和最不理想状态。 前者发生的概率是α，后者发生的概率是（1－α）。α ＝1时，等价于乐观准则；α＝0时，等价于悲观准则。
E (Q(ai )) Max{qij } (1 ) Min{qij }
j jБайду номын сангаас
最后选择期望收益值最大的方案为最优方案。
a Max E (Q(ai ))
* i
17
一、完全不确定型决策的准则
5、等可能性准则
假定各种状态可能出现的概率相同， 首先计算各方案的收益期望值；

第十一章 相关分析


第二节 积差相关
计算积差相关系数的基本公式 • 运用标准差与离均差的计算公式
• n为成对数据的数目 • σx表示X变量的样本标准差 • σY 表示Y变量的样本标准差
第二节 积差相关
通常把公式中的 称为协方差。
所谓协方差就是两个变量离均差乘积的平均数，两列变量离 均差的乘积大小，能够反映两列变量的一致性。但不能直接 用协方差表示一致性，因为它有不同的测量单位，是一个很 不稳定的量，为了克服这一缺点，分别用各变量的标准差去 除各自的离均差，使其成为无实际测量单位的标准分数，然 后求其协方差，这样，不同测量单位表示的两列变量的一致 性便可测量，也便于比较。这就是求相关系数的公式中所以 用比率的由来。 相关系数的数值范围在正负1之间的证明
第二节 积差相关
3、相关系数显著性检验当然步骤及方法
① H0:ρ =0条件下，相关系数的显著性检验 对于总体相关系数ρ =0的零假设进行显著性检验时： 当n≥50时，r的抽样分布接近正态，其标准误为：
当n<50时，可用费舍指出的t统计量来检验相关系数的显 著性：
第二节 积差相关
检验的步骤： • 提出假设
第四节 质Байду номын сангаас量的相关
3、多列相关 1）适用资料 两列正态变量资料，其中一列为等距或等比测量数据，另 一列被认为划分为多种变量，称为名义变量。 2）计算公式
式中，Pi为每系列的次数比率，y1为每一名义变量下限的正态曲 线高度，yh 为每一名义变量上线的正态曲线高度，为每一名义变量对 偶的连续变量的平均数，St 为连续变量的标准差。 注意：a）取值范围为－1至1，相关越高，绝对值越接近于1；b）原 始数据代入积差相关的双列次数分布表计算公式，得到的值相等。

SPSS统计分析—描述性统计分析


Skewness
中位数 Median
方差
Variance
峰度
Kurtosis
众数
Mode
极小值
Minimum
和
Sum
极大值
Maximum
全距
Range
均值的标准 误差
S.E.mean
• 【Descriptive Statistics】子菜单
• ① Frequencies：产生变量值的频数分布表，并可计算常见 描述性统计量和绘制相对应的统计图。
• 执行【Analyze】/【Descriptive Statistics】/ 【Crosstabs】命令，弹出如图所示对话框
• 结果解读
1、列联表 2、卡方检验结果
3、条图
相对比描述——Ratio
• 在实际问题中，研究者有时除了希望了解变量自身的统计特 征，还希望得到两个变量相对比之间的统计描述。
适用范围：更适用于对分类变量以及不服从正态分布的连 续性变量进行描述。
• 学生身高频数表：已知有某地120名12岁男童身高数据，编 制其传统的简易频数表。
执行【Analyze】/【Descriptive Statistics】/ 【Frequencies】命令，弹出如下所示对话框
• 结果解读 1、频数表
每个格子中的理论频数T是在假定两组的发癌率相等（均等于两组 合计的发癌率）的情况下计算出来的，如第一行第一列的理论频数 为71*91/113=57.18，故卡方值越大，说明实际频数与理论频数的 差别越明显，两组发癌率不同的可能性越大。
2、卡方检验方法的适用条件
• 吸烟习惯与患病率的关系
调查339名50岁以上吸烟习惯与患慢性气管炎病的关系，如 上表所示。试问吸烟者与不吸烟者慢性气管炎患病率是否有 所不同。 ◆ 数据的预处理：WEIGHT CASE

学前教育研究方法,讲义第十一章 量化资料的处理与分析

第十一章量化资料的整理与分析本章主要内容第一节量化资料的归类整理第二节量化资料的特征描述第三节量化资料相关与因果分析第一节量化资料的归类整理一、统计表统计表是表示数字资料的一种重要方式,在对数据进行统计分类以后，一一般都用统计表的方式加以表达。

对数据进行分类以后,所得到的各种数量结果称为统计指标。

把统计指标和被说明的事物用表格的形式加以表示就构成统计表。

统计表的构造一般包括以下几个项目:序号:要写在表的左上方，序号一般以在文章中出现的先后顺序排列。

名称:又称标题，是一个表的名称，应写在表的上方。

标目:即分类的项目。

数字:数字是统计表的语言，又称统计指标。

表注:表注写于表的下面，它不是统计表的必要组成部分。

常用的统计表的类型：简单表:只列出调查名称、地点时序或统计指标名称的统计表。

分组表:只有一个标目的统计表。

复合表:有两个或两个以上标目的统计表。

二、统计图统计图就是依据数字资料，应用点、线、面、体、色彩等的描绘制成整齐而又规律，简明而又知其数量的图形。

统计图在数据的整理中占有很重要的地位。

(一)统计图的构成统计图一般采用直接坐标系，横坐标用来表示事物的组别或自变量X,纵坐标常用来表示事物出现的次数或因变量Y，除直角坐标外还有角度坐标、地理坐标等。

图号及图题:统计图的名称为图题或标题。

图目:是写在图形基线上的各种不同类别、名称、或时间空间的统计数量，即横坐标上所用的各种单位名称。

图形：是图的主要部分。

图注:凡图形或其局部或某一点,需要借助文字或数字加以补充说明的，均称为图注。

此外，一个图形要使用各种线条,这些线条因在图中的位置不同而有不同的名称。

(二)统计图的种类条形图:主要用于表示离散型的数字资料，即计数资料。

圆形图:用于表示间断性的数字资料。

线形图:用于表示连续性的数字资料。

直方图:用于表示连续性资料的频数分配。

散点图:又称点图，它是以圆点的大小和相同大小圆点的多少或疏密表示统计资料数量的大小以及变化趋势的统计图。

第十一章 统计表与统计图

第十一章统计表与统计图（一）名词解释1．统计表 2. 统计图（二）简答题1.统计表和统计图在表达资料中各有何特殊意义？2.统计表有哪些要素构成？制表的注意事项有哪些？3.统计图有哪些要素构成？绘制统计图的注意事项有哪些？4.为什么半对数线图可以描述发展速度的变化？（三）列表、制图与分析题1.某医院对麦芽根糖浆治疗急慢性肝炎161例的疗效列表，试作改进。

2．某地1952年和1972年三种死因别死亡率下表，试将该资料绘制成统计图并作分析。

表12-9 某地1952年和1972年三种死因别死亡率（1/10万）死因1952年1972年肺结核165.2 27.4心脏病72.5 83.6恶性肿瘤57.2 178.21．据下例统计资料试作统计图。

表12-10 某地居民两次粪便蠕虫卵检查结果第一次阳性率（%）第二次阳性率（%）蛔虫钩虫91.4361.2286.3931.36鞭虫17.14 16.51表12-11 某部队1997年各月传染病发病人数月份 1 2 3 4 5 6 7 8 9 10 11 12 合计传染病人数 3 4 7 14 9 14 17 104 58 12 5 2 249表12-12 224例胸膜炎病人的年龄分布年龄（岁）各组人数占全部病人的百分比11～ 4.116～ 13.521～ 44.631～ 27.141～ 8.951～合计 1.8 100.04. 某县防疫站1972年开始在城关镇建立“预防接种卡”，使计划免疫得到加强。

为说明效果，1975年5月观察了482人的锡克试验反应，其中：幼儿园儿童101人，阳性21人；小学生145人，阳性22人；中学生236人，阳性15人。

相比起来，1947年为：幼儿园儿童144人，阳性37人；小学生1417人，阳性323人；中学生359人，阳性41人。

试用适当的统计表和统计图描述上述结果，并作简要分析。

（四）是非题1.一个绘制合理的统计图可直观的反映事物间的正确数量关系。

第十一章双变量统计分析

第十一章双变量统计分析第十一章双变量统计分析在社会学研究中，不但要了解一个变量的情况，更要进一步了解一个变量与另一个变量之间的关系。

在这一讲中我们介绍几种双变量的统计分析方法。

一、交互分类表交互分类表又称列联表，是指同时依据两个变量的值，将所研究的个案分类。

交互分类的目的是将两变量分组，然后比较各组的分布状况，以寻找变量间的关系。

1、条件次数表：表10-1是交互分类表的一个例子：表10-1 500名工人的文化水平与工资收入交互分类表（人）（1）表中的次数分布是同时根据文化水平和工资收入而定，如大专以上高收入的有26人。

从表中可以清楚地知道每种文化水平的工资收入的次数分布，因此这样的表又称为条件次数表。

在表的最下一行和最右一列分别是不同文化水平和不同收入的总次数，称为边缘次数，它们的分布情况称为边缘分布；表中的其它次数，称为条件次数，每一条件下的分布称为条件分布。

(2)条件次数表有大小之分，计算的方法，通常是将因变量的数目乘上自变量的数目。

如果我们将因变量放在表的旁边，将自变量放于表的上端，则表的大小就是横行数目（rows简写r）乘上纵行数目（columns简写c），即表的大小=r×c。

这个先后次序的用意是表示前者（因变量）是受后者（自变量）影响的。

要注意的是，3×2表不同于2×3表，因为前后两个数值代表不同的变量，包含不同类别数。

2、条件百分表：条件次数表中的数字是绝对数字，由于各个类别的基数不同，相互之间无法进行比较，因而不能看出两变量之间的关系。

为克服条件次数表的这一缺点，使各个类别之间可以比较，应将表中的绝对数字转变成相对数字——百分数，这样制成的表称为条件百分表。

如上表可改成百分表为：表10-2 500名工人文化水平与工资收入的交互百分表（%）在计算条件百分表时，最好能依据下列准则：（1）每个表的顶端要有表号和标题。

加上表号，可以方便讨论和减少混乱。

简明标题，能使读者容易领会表内统计数值的意义。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中位数的作用：
不受极端数值的影响，在总体标志值差异很大 时，具有较强的代表性。
中位数的确定
（未分组资料）
【例A】某售货小组5个人，某天的销售额按 从小到大的顺序排列为440元、480元、520元、 600元、750元，则 中位数的位次为：
N 1 5 1 3 2 2
即第3个单位的标志值就是中位数 M e 520元
式中： 组的次数； 为 fi i X 为算术平均数; 为第 m 组数； X i 为第i组的标志值或组中值。
【例】某企业某日工人的日产量资料如下：
日产量（件） 工人人数（人）
X
10 11 12 13 14 合计
f
70 100 380 150 100 800
计算该企业该日全部工人的平均日产量。
解：
X
中位数的确定
（未分组资料）
【例B】若上述售货小组为6个人，某天的销 售额按从小到大的顺序排列为440元、480元、 520元、600元、750元、760元，则 中位数的位次为
N 1 6 1 3.5 2 2
中位数应为第3和第4个单位标志值的算术平 均数，即
520 600 Me 560 元 2
X 1 X 2 X N X N
X
i 1
N
i
N
式中： 为总体单位总数； X 为算术平均数; N X i 为第i 个单位的标志值。
算术平均数的计算方法
【例】 某售货小组5个人，某天的销售额
分别为520元、600元、480元、 750元、440元，则
520 600 480 750 440 5 2790 558元 5
身高
人数
（CM） （人） 164 3 165 8 166 5 167 3 168 7 169 1 170 5 171 2 172 3 174 1 总计 83
身高 人数
众数的确定方法
某年级83名女生身高资料
（CM） （人） 152 1 154 2 155 2 156 4 157 1 158 2 159 2 160 12 161 7 162 8 163 4
总体标志总量 基本形式： 平均数 总体单位总数
例：
工资总额 平均工资 职工人数 总成本 平均成本 总产量
算术
算术平均数的计算
数据集 xi ( x1 , x2 , xN 1 , xN )
算术平均数= 总体标志总量 总体单位总数
x
数据个数 N
简单算术平均数
x x N
算术平均数的计算方法 A. 简单算术平均数 ——适用于总体资料未经 分组整理、尚为原始资料 的情况
未分组数据
平均每人日销售额为：
X X N
算术平均数的计算方法
分组数据
按考试成绩分组（分） 60以下 60～70 70～80 80～90 90以上 合计 组中值 55 65 75 85 95 学生人数（人） 3 8 8 9 7 35 组中值×人数 165 520 600 765 665 2715
X
i 1 m i 1
m
i
fi
i
f
10 70 14 100 70 100
9710 12.1375 (件） 800
若上述资料为组距数列，则应取各组的组 说 中值作为该组的代表值用于计算；此时求 明 得的算术平均数只是其真值的近似值。
位置平均数 将总体各单位标志值按大小顺序排 中位数 列后，指处于数列中间位置的标志 (Median) 值，用 M e表示 中位数把标志值数列分为两个部分,一部分 标志值小于或等于它,另一部分标志值大于 或等于它.
合计
800
—
计算该企业该日全部工人日产量的中位数。
位置平均数
众数
指总体中出现次数最多的变量值， 用 M 0 表示,它不受极端数值的影响， 用来说明总体中大多数单位所达到 的一般水平。
众数（mode）：出现次数最多 即出现频率最高的变量值。
152 156 159 160 160 161 162 163 165 165 166 168 170 171 154 156 159 160 160 161 162 163 165 165 167 168 170 172 154 156 160 160 161 161 162 163 165 166 167 168 170 172 155 157 160 160 161 162 162 164 165 166 167 168 170 172 155 158 160 160 161 162 162 164 165 166 168 168 170 174 156 158 160 160 161 162 163 164 165 166 168 169 171 （CM） （人） 152 1 154 2 155 2 156 4 157 1 158 2 159 2 160 12 161 7 162 8 163 4
平均成绩为：
X 77.57
2715 35
算术平均数的计算方法 B. 加权算术平均数 ——适用于总体资料经过 分组整理形成变量数列的 情况
X 1 f1 X 2 f 2 X m f m X f1 f 2 f m
X
i 1 m i 1
m
i
fi
i
f
中位数的确定 （单值数列）
800 1 400 . 5 【例C】某企业某日工人的日产量资料如下： 2 日产量（件） 工人人数（人） 向上累计次数 f X （人） 10 70 70 11 100 170 M e 12 380 550 13 150 700 14 100 800
中位数的位次：
身高
人数
（CM） （人） 164 3 165 8 166 5 167 3 168 7 169 1 170 5 171 2 172 3 174 1 总计 83
身高 人数
众数、中位数和均值的应用场合 众数、中位数和均值都是对数据集中趋势的测度， 1、均值由全部数据计算，包含了全部数据的信息，具有 良好的数学性质，当数据接近对称分布时，具有较好的代表 性；但对于偏态分布，其代表性较差。 2、中位数是一组数据中间位置上的代表值，不受数据极 端值的影响，对于偏态分布的数据，其代表性要比均值好。 3、众数是一组数据分布的峰值，是一种位置的代表，当 数据的分布具有明显的集中趋势时，尤其对于偏态分布，众 数的代表性比均值好。 4、对接近正态的分布数据，常用均值描述数据的集中趋 势；对偏态分布，常用众数或中位数描述数据的集中趋势。 5、均值只适用于定距或定比尺度的数据；定序尺度数据 可用中位数或众数进行描述，而对定类尺度数据，只能用众 数进行描述。
11.1 集中趋势的测度
指总体中各单位的次数分布从两边向 集中趋势 中间集中的趋势，用平均指标来反映。 数值平均数
算术平均数 调和平均数 几何平均数
又称平均数，是 反映社会经济现 象总体各单位某 一数量标志在一 定时间、地点和 条件下所达到的 一般水平的综合 指标。
平众数
算术平均数