不规则三角网(TIN)的建立PPT文档资料

不规则三角网（TIN）Ⅰ 数字高程模型（DEM）地球表面高低起伏，呈现一种连续变化的曲面，这种曲面无法用平面地图来确切表示。

于是我们就利用一种全新的数字地球表面的方法——数字高程模型的方法，这种方法已被普遍广泛采用。

数字高程模型即DEM（Digital Elevation Model），是以数字形式按一定结构组织在一起，表示实际地形特征空间分布的模型，也是地形形状大小和起伏的数字描述。

DEM有三种主要的表示模型：规则格网模型，等高线模型和不规则三角网。

格网（即GRID）DEM在地形平坦的地方，存在大量的数据冗余，在不改变格网大小情况下，难以表达复杂地形的突变现象，在某些计算，如通视问题，过分强调网格的轴方向。

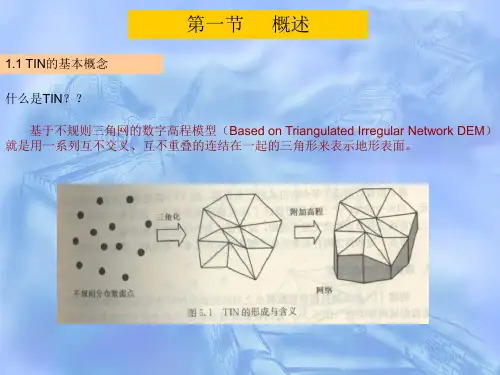
不规则三角网（简称TIN，即Triangulated Irregular Network）是另外一种表示数字高程模型的的方法（Peuker等，1978），它既减少了规则格网带来的数据冗余，同时在计算（如坡度）效率方面又优于纯粹基于等高线的方法。

不规则三角网能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置，因而它能够避免地形起伏平坦时的数据冗余，又能按地形特征点如山脊，山谷线，地形变化线等表示数字高程特征。

Ⅱ TIN的基本知识在TIN中，满足最佳三角形的条件为：尽可能的保证三角形的三个角都是锐角，三角形的三条边近似相等，最小角最大化。

TIN 是基于矢量的数字地理数据的一种形式，通过将一系列折点（点）组成三角形来构建。

形成这些三角形的插值方法有很多种，例如Delaunay 三角测量法或距离排序法。

ArcGIS 支持Delaunay 三角测量方法。

TIN 的单位是英尺或米等长度单位，而不是度分秒。

当使用地理坐标系的角度坐标进行构建时，Delaunay 三角测量无效。

创建TIN 时，应使用投影坐标系（PCS）。

TIN 模型的适用范围不及栅格表面模型那么广泛，且构建和处理所需的开销更大。

获得优良源数据的成本可能会很高，并且，由于数据结构非常复杂，处理TIN 的效率要比处理栅格数据低。

2。

1数字高程模型建模数字高程模型有两种模式[4]，一种是不规则三角网模型TIN，另一种是规则格网模型Grid。

两种模型可以相互转换，但一般大规模的地形都采用规则格网模型。

格网数字高程模型的建模方法可以有多种，最常用的方法是数字摄影测量方法，通过影像匹配自动生成数字高程模型。

当得不到立体影像，仅有地形图时，通常采用对现有地图进行扫描，获得矢量化等高线，再由等高线内插成数字高程模型。

当然，我们也可以通过外业测量的方法，获得大量高程点三维坐标，再内插成数字高程模型。

地面纹理影像可以从现有航空影像或航天遥感影像获得，也可根据地面物体的特征，人工赋予相应的纹理影像。

但不管用哪种方法，都要先将原始影像处理成数字正射影像，它有一致的比例尺，消除了投影误差，坐标与数字高程模型一致。

这样经过处理的数字正射影像才能与数字高程模型匹配，形成真实的景观模型。

由原始影像处理成数字正射影像可以有多种方法，通常有数字摄影测量方法和单片微分纠正方法。

不论哪种方法都是消除像片倾斜和投影差的过程，都要进行绝对定位使之归化比例尺和地面坐标。

2。

3三维建筑结构数据的获取与处理三维建筑结构是指房屋建筑、路桥、油罐、电视塔等各种三维实体，获得这些三维目标的框架数据主要有两种方法。

一种是用数字摄影测量方法，在立体模型上采集建筑物的框架坐标，然后通过建模软件将它们构造成体对象。

另一种方法是采用三维设计软件，如3Dmaxs，Multigen，Microstation等软件。

将设计好的三维实体导入并定位于地形景观模型中。

无论哪一种方法，都要对数据进行检核，使它们的连线正确，以利于粘贴侧面纹理。

三维实体数据检核的过程如下:(1)拓扑结构检查。

通过对每一地物的三维模型与航测像对中的立体影像的比对，检查三维模型的拓扑结构是否正确。

(2)建筑物顶部同高检查。

在现实中建筑物顶面绝大部分表现为同高的情况，而这就需要对三维建筑物模型的顶面进行同高检查，从而使点与平面符合。

2。

1数字高程模型建模数字高程模型有两种模式[4]，一种是不规则三角网模型TIN，另一种是规则格网模型Grid。

两种模型可以相互转换，但一般大规模的地形都采用规则格网模型。

格网数字高程模型的建模方法可以有多种，最常用的方法是数字摄影测量方法，通过影像匹配自动生成数字高程模型。

当得不到立体影像，仅有地形图时，通常采用对现有地图进行扫描，获得矢量化等高线，再由等高线内插成数字高程模型。

当然，我们也可以通过外业测量的方法，获得大量高程点三维坐标，再内插成数字高程模型。

地面纹理影像可以从现有航空影像或航天遥感影像获得，也可根据地面物体的特征，人工赋予相应的纹理影像。

但不管用哪种方法，都要先将原始影像处理成数字正射影像，它有一致的比例尺，消除了投影误差，坐标与数字高程模型一致。

这样经过处理的数字正射影像才能与数字高程模型匹配，形成真实的景观模型。

由原始影像处理成数字正射影像可以有多种方法，通常有数字摄影测量方法和单片微分纠正方法。

不论哪种方法都是消除像片倾斜和投影差的过程，都要进行绝对定位使之归化比例尺和地面坐标。

2。

3三维建筑结构数据的获取与处理三维建筑结构是指房屋建筑、路桥、油罐、电视塔等各种三维实体，获得这些三维目标的框架数据主要有两种方法。

一种是用数字摄影测量方法，在立体模型上采集建筑物的框架坐标，然后通过建模软件将它们构造成体对象。

另一种方法是采用三维设计软件，如3Dmaxs，Multigen，Microstation等软件。

将设计好的三维实体导入并定位于地形景观模型中。

无论哪一种方法，都要对数据进行检核，使它们的连线正确，以利于粘贴侧面纹理。

三维实体数据检核的过程如下:(1)拓扑结构检查。

通过对每一地物的三维模型与航测像对中的立体影像的比对，检查三维模型的拓扑结构是否正确。

(2)建筑物顶部同高检查。

在现实中建筑物顶面绝大部分表现为同高的情况，而这就需要对三维建筑物模型的顶面进行同高检查，从而使点与平面符合。

第一章绪论1.1研究背景地球是人类生活和活动的承载体。

多年以来，我们为了更充分的认识自然客体和改造自然，总在不懈的努力尝试用不同的方式方法来描述、表达人所处的环境，其中地形图就是一个有代表性的测绘表述变迁的缩影。

从最开始的象形符号抽象的雏形到后来的在二维介质上对三维表面进行地形写景图，地貌写景图等描述是一个进步，但写景方式不具备可量测性，所以还是很局限的。

随着测绘技术发展，地形的表达也由写景式的定性表达过渡到了以等高线为主的矢量化表达。

航空摄影测量，遥感技术提供的影响都在对三维现实世界的模拟。

但是有一个矛盾体，那就是对于地形表面形态而言，一方面我们尽可能的从几何角度去理解和描述以解决实际应用中的可量测性；另外一个方面它本身是一种三维景观现象，对于其表述要考虑生理视觉感受，我们总是希望能够尽可能的直观形象逼真。

从20世纪四十年代开始的计算机图形学、计算机辅助制图等相关学科和理论的发展，使得在测绘领域，在图形表达表述方面发生了从模拟表达时代走向了数字表达时代，有了质的飞跃。

其中地理信息系统（GIS ）及数字高程模型（DEM ）学科或技术显得尤为重要。

地理信息系统，简称GIS （Geographical Information System ）,它源于20世纪60年代初期加拿大测量学家Tomlinson 的“把地图变成数字形式的地图，以便计算机进行处理与分析”的观点，但是在技术工具处理中，则是利用计算机存贮、处理地理信息，并且在计算机软、硬件支持下，把各种资源信息和环境参数按空间分布或地理坐标，以一定的格式或者分类输入、处理、存贮、输出，用以满足其应用需要的人机交互系统。

因此GIS 的本质是在二维地理空间基础上实现对地下、地表和空中诸地理信息的数字化表达和管理。

当然地理信息系统技术发展到当前，功能不再是当初的局限于查询、检索和制图，而是丰富到空间分析、建模、决策等诸多方面，在数据管理上则从简单的栅格数据、矢量数据管理转向多元数据融合，在现实生活中应用的很活跃，也很充分。

不规则三角网（TIN）Ⅰ数字高程模型（DEM）地球表面高低起伏，呈现一种连续变化的曲面，这种曲面无法用平面地图来确切表示。

于是我们就利用一种全新的数字地球表面的方法——数字高程模型的方法，这种方法已被普遍广泛采用。

数字高程模型即DEM（Digital Elevation Model），是以数字形式按一定结构组织在一起，表示实际地形特征空间分布的模型，也是地形形状大小和起伏的数字描述。

DEM有三种主要的表示模型：规则格网模型，等高线模型和不规则三角网。

格网（即GRID）DEM在地形平坦的地方，存在大量的数据冗余，在不改变格网大小情况下，难以表达复杂地形的突变现象，在某些计算，如通视问题，过分强调网格的轴方向。

不规则三角网（简称TIN，即Triangulated Irregular Network）是另外一种表示数字高程模型的的方法（Peuker等，1978），它既减少了规则格网带来的数据冗余，同时在计算（如坡度）效率方面又优于纯粹基于等高线的方法。

不规则三角网能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置，因而它能够避免地形起伏平坦时的数据冗余，又能按地形特征点如山脊，山谷线，地形变化线等表示数字高程特征。

Ⅱ TIN的基本知识在TIN中，满足最佳三角形的条件为：尽可能的保证三角形的三个角都是锐角，三角形的三条边近似相等，最小角最大化。

TIN 是基于矢量的数字地理数据的一种形式，通过将一系列折点（点）组成三角形来构建。

形成这些三角形的插值方法有很多种，例如 Delaunay 三角测量法或距离排序法。

ArcGIS 支持 Delaunay 三角测量方法。

TIN 的单位是英尺或米等长度单位，而不是度分秒。

当使用地理坐标系的角度坐标进行构建时，Delaunay 三角测量无效。

创建TIN 时，应使用投影坐标系（PCS）。

TIN 模型的适用范围不及栅格表面模型那么广泛，且构建和处理所需的开销更大。