一次函数与实际应用

一次函数在生活中的具体应用1. 引言1.1 一次函数的定义一次函数是指形式为y=ax+b的函数，其中a和b为常数，且a不等于0。

简单来说，一次函数就是一个斜率不为零的直线函数。

在数学中，一次函数是最简单的函数之一，但却有着广泛的应用。

在一次函数中，变量之间是线性关系，可以用来描述很多现实生活中的问题。

一次函数的斜率代表了变量之间的变化率，而常数项则代表了起始值。

通过一次函数，我们可以快速地了解变量之间的关系，并进行预测和分析。

一次函数还有很多重要性质，比如通过两点确定一条直线、平行直线具有相同的斜率等。

这些性质使一次函数成为解决实际问题的有效工具。

在接下来的内容中，我们将探讨一次函数在各个领域的具体应用，包括经济学、市场营销、工程、金融学和医学。

通过这些具体案例，我们可以更好地理解一次函数在生活中的重要性和广泛应用性。

1.2 一次函数在生活中的重要性在经济学中，一次函数常常被用来描述供需关系和价格变化的规律。

通过分析一次函数的图像和方程，经济学家可以更好地预测市场走势和制定合理的政策措施，从而促进经济的稳定发展。

在市场营销领域，一次函数可以帮助企业分析销售数据、制定定价策略和评估市场需求。

借助一次函数的模型，市场营销人员可以更加准确地了解消费者的行为和喜好，从而提高产品的市场竞争力。

在工程领域，一次函数常被用来描述物体的运动轨迹和能量转化过程。

工程师利用一次函数的性质来设计各种设备和结构，确保其在实际应用中具有良好的性能和稳定性。

在金融学领域，一次函数被广泛应用于风险分析、投资组合管理和资产定价等方面。

通过构建一次函数的模型，金融学家可以更好地评估资产的价值和波动性，从而降低投资风险并获取更高的收益。

在医学领域，一次函数可以用来描述人体各个器官的生理变化和疾病进程。

医生通过对一次函数的分析和建模，可以更好地诊断疾病、制定治疗方案和预测患者的康复情况。

一次函数在生活中的重要性不可忽视，它为各个领域提供了重要的数学工具和理论基础，促进了社会的进步和发展。

一次函数生活中的实际应用题目一次函数是数学中的一种函数类型，表示为 y = kx + b 的形式，其中 k 是函数的增减速度，b 是函数的零点。

一次函数在生活中有许多实际应用，以下是一些实际问题的例子:1. 温度计：一次函数可以用来描述温度的变化情况。

当温度上升或下降时，一次函数的斜率会发生变化，而常数 b 则表示温度变化的水平方向。

例如，在摄氏 0 度和 100 度之间，温度每增加 1 度，温度计上的指针会上升多少格，就可以用一次函数来描述。

2. 流量控制：一次函数在流量控制中被广泛应用，特别是在水管和发动机的设计之中。

当水流量为恒定值时，一次函数可以用来描述水流量和水压之间的关系。

例如，如果想控制水流量为一定值，可以通过调节水管中的阀门大小来控制水压，从而实现流量的控制。

3. 存款利率：一次函数可以用来描述存款利率的变化情况。

当利率上升或下降时，一次函数的斜率会发生变化，而常数 b 则表示利率变化的水平方向。

例如，如果利率上升 1%,银行的存款利率会相应上涨多少元，就可以用一次函数来描述。

4. 股票价格：一次函数可以用来描述股票价格的变化情况。

当股票价格上升或下降时，一次函数的斜率会发生变化，而常数 b 则表示股票价格变化的水平方向。

例如，如果股票价格上升 1%,投资者获得的回报率会相应上涨多少个百分点，就可以用一次函数来描述。

5. 植物生长：一次函数可以用来描述植物的生长情况。

当植物的生长速度加快或减缓时，一次函数的斜率会发生变化，而常数 b 则表示植物的生长速度保持不变的水平方向。

例如，如果想预测植物在未来几天内的生长速度，可以使用一次函数来计算。

一次函数在生活中的具体应用1. 引言1.1 什么是一次函数一次函数是指数学中的一种特殊函数形式，通常表示为f(x) = ax + b的形式。

a和b是常数，且a不等于0。

一次函数也被称为一次多项式函数，因为它的最高次数为1。

在一次函数中，变量x的最高次数为1，这使得函数的图像呈现为一条直线。

一次函数的特点是其图像是一条直线，具有线性的特性。

这种简单的函数形式在数学建模和实际问题求解中具有重要意义。

一次函数可以描述很多实际生活中的问题，比如描述两个变量之间的线性关系，预测未来的变化趋势，进行经济预测和规划等。

在实际应用中，一次函数可以帮助我们分析经济学、物理学、工程学、社会科学和医学领域中的各种现象和问题。

通过一次函数的建模和分析，我们可以更好地理解和解决复杂的实际问题，为社会发展和个人发展提供有力的支持和指导。

了解一次函数的基本概念和应用是非常重要的。

1.2 为什么一次函数在生活中具有重要意义一次函数在生活中的重要意义在于其简单性和直观性。

一次函数是最基本的一种函数形式，具有线性关系的特点，易于理解和应用。

通过一次函数，我们可以轻松地描述许多实际问题的规律和模式，比如物体的运动轨迹、经济的增长趋势、工程中的力学关系等，为我们理解和解决问题提供了重要的工具和方法。

一次函数在生活中的重要意义还体现在其广泛应用的范围。

一次函数几乎涉及到生活的各个领域，包括经济学、物理学、工程学、社会科学、医学等，可以用来分析和描述各种不同的现象和问题。

掌握一次函数的知识和技能对我们了解世界、改善生活具有重要的意义。

一次函数在生活中的重要意义在于其简单性、直观性和广泛应用性。

通过学习和应用一次函数，我们可以更好地理解世界、解决问题，促进社会的发展和进步。

深入理解和掌握一次函数的知识对我们每个人来说都是非常重要的。

2. 正文2.1 一次函数在经济学中的应用一次函数在经济学中的应用非常广泛，经济学家们经常使用一次函数来描述和分析各种经济现象和关系。

一次函数的性质与应用一次函数，也叫线性函数，是数学中的基础函数之一。

它的一般形式可以表示为 y = ax + b，其中 a 和 b 分别是常数，a 称为斜率，b 称为截距。

一次函数的性质及其应用广泛存在于数学、经济学、物理学等各个学科领域中。

一. 一次函数的性质1. 斜率与图像关系：斜率代表直线的倾斜程度，正斜率表示直线向上倾斜，负斜率表示直线向下倾斜，斜率为零表示直线水平。

斜率的绝对值越大，越陡峭；绝对值越小，越平缓。

2. 截距与图像关系：截距表示直线与 y 轴的交点在 y 轴上的坐标。

当截距为正时，直线在 y 轴上方交 y 轴；当截距为负时，直线在 y 轴下方交 y 轴；当截距为零时，直线通过原点。

3. 函数图像的性质：一次函数的图像是一条直线。

当斜率a > 0 时，图像从左下方逐渐向右上方倾斜；当斜率 a < 0 时，图像从左上方逐渐向右下方倾斜；当斜率 a = 0 时，图像平行于 x 轴。

4. 定义域和值域：一次函数的定义域是全体实数，即 (-∞, +∞)；值域也是全体实数，即 (-∞, +∞)。

二. 一次函数的应用1. 经济学应用：一次函数可以描述经济关系中的线性关系。

例如，产量与成本之间的关系可以用一次函数表示。

斜率表示每增加一个单位产量对应的成本变化，截距表示没有产量时的固定成本。

2. 物理学应用：物理学中的运动学问题常常可以用一次函数建模。

例如，匀速直线运动中，位移与时间之间的关系可以用一次函数表示。

斜率表示物体的运动速度，截距表示物体的初始位置。

3. 工程学应用：在工程学中，一次函数可以用来描述电阻和导线的关系、温度和热量的关系等。

例如，欧姆定律描述了电流和电阻之间的线性关系。

4. 统计学应用：统计学中的线性回归分析就是建立在一次函数的基础上。

通过一次函数模型，可以对变量之间的关系进行探索和预测。

综上所述，一次函数具有明确的性质和广泛的应用。

在数学和实际问题中，了解和掌握一次函数的性质和应用，对于解决问题和做出正确的决策具有重要意义。

一次函数在生活中的应用咱们聊聊啊，这数学里头的一次函数，听起来挺高深莫测的，其实啊，它就在咱们日常生活里头溜达呢，跟咱们老百姓的日子那是息息相关，紧密得跟亲兄弟似的。

你想啊，早上起床，得琢磨着吃点啥吧？比如说，你去楼下包子铺，那价格表上写着呢，肉包子两块五一个，素包子两块一个。

这不就是一次函数嘛！你买的包子数量是X，总价是Y，Y就是X乘以单价。

肉包子的话，Y=2.5X；素包子，Y=2X。

简单吧，一口一个，吃出学问来了。

吃完早饭，该上班了。

开车去？那油费也得算算。

油价一升多少钱，咱们心里得有个数。

车子油耗多少，也得心里有谱。

这一路上，油门一踩，那就是钱在烧啊。

不过别担心，这也是一次函数在作祟。

油耗是X，油费是Y，Y=油价乘以油耗X。

省油就是省钱，这个道理大家都懂。

到了公司，得干活了。

老板说了，这个月业绩得上去，不然奖金泡汤。

这业绩和奖金的关系，嘿，又是一次函数。

业绩是X，奖金是Y，Y=奖金系数乘以业绩X。

当然啦，这个系数老板说了算，咱们只能努力提升X值，争取多拿点Y。

下了班，回家路上经过超市，得买点菜。

蔬菜水果，价格都不一样。

你挑挑拣拣，放进购物车，心里还得盘算着这得花多少钱。

挑的东西越多，钱花得越多，这也是一次函数在默默工作。

购物车里的东西重量是X，总价是Y，Y=单价乘以重量X。

勤俭持家，就得这么精打细算。

晚上，一家人围坐在一起看电视。

孩子说：“爸爸，我想学钢琴。

”你一听，心里那个激动啊，得支持孩子啊！不过，学钢琴得花钱啊。

学费按课时算，这也是一次函数。

课时是X，学费是Y，Y=课时费乘以课时X。

为了孩子的未来，这钱花得值！你看啊，这一天到晚的，咱们的生活里到处都是一次函数。

它就像个隐形的朋友，默默地陪伴着我们，帮助我们更好地规划生活、管理财务。

所以啊，别觉得数学枯燥无味、高不可攀了。

其实啊，它就在我们身边，跟咱们的生活紧密相连、息息相关。

学好数学吧朋友们！让我们的生活因数学而更加精彩、更加有序！。

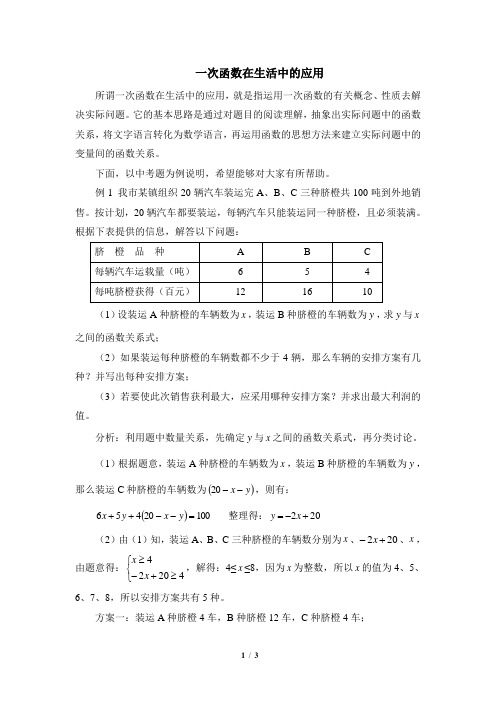
一次函数在生活中的应用所谓一次函数在生活中的应用，就是指运用一次函数的有关概念、性质去解决实际问题。

它的基本思路是通过对题目的阅读理解，抽象出实际问题中的函数关系，将文字语言转化为数学语言，再运用函数的思想方法来建立实际问题中的变量间的函数关系。

下面，以中考题为例说明，希望能够对大家有所帮助。

例1 我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售。

按计划，20辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满。

根据下表提供的信息，解答以下问题：（1）设装运A 种脐橙的车辆数为x ，装运B 种脐橙的车辆数为y ，求y 与x 之间的函数关系式；（2）如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值。

分析：利用题中数量关系，先确定y 与x 之间的函数关系式，再分类讨论。

（1）根据题意，装运A 种脐橙的车辆数为x ，装运B 种脐橙的车辆数为y ，那么装运C 种脐橙的车辆数为()y x --20，则有：()10020456=--++y x y x 整理得：202+-=x y（2）由（1）知，装运A 、B 、C 三种脐橙的车辆数分别为x 、202+-x 、x ，由题意得：⎩⎨⎧≥+-≥42024x x ，解得：4≤x ≤8，因为x 为整数，所以x 的值为4、5、6、7、8，所以安排方案共有5种。

方案一：装运A 种脐橙4车，B 种脐橙12车，C 种脐橙4车；方案二：装运A 种脐橙5车，B 种脐橙10车，C 种脐橙5车；方案三：装运A 种脐橙6车，B 种脐橙8车，C 种脐橙6车；方案四：装运A 种脐橙7车，B 种脐橙6车，C 种脐橙7车；方案五：装运A 种脐橙8车，B 种脐橙4车，C 种脐橙8车；（3）设利润为W （百元）则：()160048104162025126+-=⨯+⨯+-+⨯=x x x x W∵048<-=k ∴W 的值随x 的增大而减小要使利润W 最大，则4=x ，故选方案一1600448+⨯-=最大W ＝1408（百元）＝14.08（万元）答：当装运A 种脐橙4车，B 种脐橙12车，C 种脐橙4车时，获利最大，最大利润为14.08万元。

一次函数实际应用题解题技巧
1、先明确一次函数的定义：一次函数的定义是：一次函数是指具有单调性和可导性的函数，它可以通过一次变换把一个简单函数变换成一个新的函数。

2、明确参数：在解一次函数实际应用题时，首先要明确题目中参数的具体含义，以及函数的定义范围。

3、确定函数的性质：根据题目中给出的函数，可以确定函数的单调性、可导性和凹凸性，以及确定它是一次函数。

4、题目的读懂：需要读懂题目，理解题目的意思，确定题目的类型，以及题目所要求的具体内容。

5、利用数学公式：利用初中数学中学习的一次函数公式及其变形，把题目中的参数值带入数学公式，求解出满足条件的一次函数。

6、绘制函数图像：在确定了函数的性质和具体内容后，可以通过函数图像来进一步地分析一次函数。

7、检验结果：经过计算后，把最后得出的函数的值与题目中给出的值进行比较，以确定结果的准确性。

一次函数的应用一次函数在数学中有着广泛的应用。

在平面直角坐标系中，一次函数的图像是一条直线，其解析式为y=kx+b。

其中，k表示斜率，b表示截距。

斜率k的正负决定了直线的方向，截距b则决定了直线与y轴的交点。

正比例函数是一种特殊的一次函数，其解析式为y=kx，其中k为比例系数。

正比例函数的图像是一条经过原点的直线，斜率k决定了直线的斜率和方向。

当k>0时，随着x的增大，y也随之增大；当k<0时，随着x的增大，y则会减小。

一次函数在实际生活中也有着广泛的应用。

例如，某航空公司规定旅客携带行李的质量与运费之间的关系为一次函数。

旅客可携带的免费行李的最大质量可以通过函数图像得出。

另外，XXX从家门口骑车去单位上班，他的上班时间与路程的关系也可以用一次函数表示。

通过求解函数，我们可以得到他从单位到家门口需要的时间。

在解决实际问题时，我们还需要注意一次函数的性质。

例如，一次函数y=2x-3的图像不经过第二象限。

因此，在应用中需要注意这些性质，避免出现错误的结果。

总之，一次函数是数学中重要的概念之一，其应用也十分广泛。

在备考中，我们需要掌握其定义、性质和图像，以及应用解题的方法。

直线y=kx+b表示一次函数，其中k和b决定了直线的位置和增减性质。

当k>0时，随着x的增大，y也增大。

如果b>0，则直线会经过第一、二、三象限；如果b0，则直线会经过第一、二、四象限；如果b<0，则直线会经过第二、三、四象限。

一次函数y=kx+b可以进行平移操作，分为沿着y轴平移和沿着x轴平移。

沿着y轴平移m个单位，得到函数y=kx+b±m；沿着x轴平移n个单位，得到函数y=k(x±n)+b。

这两种平移往往是同时进行的。

直线y=kx+b与x轴的交点为(-b,0)，与y轴的交点为(0,b)，这两个交点与坐标原点构成的三角形面积为S=1/2*│-b│*│b│/k。

对于一次函数y=kx+b，当k>0时，直线上升，y随着x的增大而增加；当k-b。

一次函数在生活中的具体应用
一次函数是指函数关系中只包含一个未知数，且其次数为1的函数。

在生活中，一次函数有许多具体的应用。

以下将介绍一些常见的应用场景。

1. 财务管理：一次函数可以用来描述日常开销和收入之间的关系。

一个人每天的支出可以用y = ax + b来表示，其中x表示时间（天数），y表示支出金额（元）。

通过分析不同的数据，可以确定每天的支出情况，从而合理安排财务预算。

2. 医药剂量计算：一次函数可以用来计算医药剂量。

某种药物的剂量与体重之间的关系可以表示为y = ax + b，其中x表示体重（千克），y表示药物的剂量（毫克）。

通过确定体重，可以计算出所需的药物剂量。

4. 气象预测：一次函数可以用来预测天气变化。

某地的气温随时间的变化可以表示为y = at + b，其中x表示时间（小时），y表示气温（摄氏度）。

通过分析历史数据和天气变化规律，可以预测未来的气温变化趋势。

5. 市场需求分析：一次函数可以描述市场需求与价格之间的关系。

某商品的需求量随价格的变化可以表示为y = ax + b，其中x表示价格（元），y表示需求量（单位）。

通过分析不同价格下的需求量，可以确定最适宜的价格水平。

一次函数在生活中有着广泛的应用。

通过对数据的收集和分析，可以使用一次函数模型来描述和预测各种关系，提高决策的科学性和准确性。

一次函数在实际问题中的应用一次函数，也称为线性函数，是数学中的基础函数之一，其形式为y = kx + b，其中k和b为常数。

一次函数在实际问题中的应用广泛，它可以用来描述和解决各种与线性关系相关的情境和难题。

本文将通过几个实际问题的案例，来说明一次函数在实际问题中的应用。

案例一：速度和时间的关系在我们日常生活中，经常会遇到需要计算速度和时间关系的问题。

例如，一个汽车以等速度行驶，假设它的初始位置是0，每小时行驶60公里，我们可以用一次函数来表示汽车的位置与时间的关系。

设汽车行驶的时间为x小时，它的位置为y公里。

根据题目中给出的条件，我们可得一次函数的表达式为y = 60x。

这是一个典型的一次函数，其斜率k为60，常数b为0。

通过这个一次函数，我们可以计算出汽车在任意时间点的位置，从而回答与汽车行驶距离相关的问题。

案例二：成本和产量的关系在工业生产中，成本和产量之间通常存在着一定的线性关系。

假设某公司生产商品的成本与产量成正比，我们可以利用一次函数来描述这种关系。

设产量为x单位，成本为y单位。

根据题目给出的条件，可知产量和成本之间的关系是y = kx + b，其中k为单位产量对应的成本，b为固定成本。

通过这个一次函数，我们可以计算出不同产量对应的成本，进而进行成本和效益的分析。

案例三：温度和时间的关系在自然科学中，温度和时间之间的关系是一个常见的一次函数应用问题。

假设某地区的温度以一定的速率逐渐升高，我们可以用一次函数来描述温度和时间之间的关系。

设时间为x小时，温度为y摄氏度。

根据题目中给出的条件，我们可以得到一次函数的表达式y = kx + b，其中k为温度随时间变化的速率，b为初始温度。

利用这个一次函数，我们可以预测未来某个时间点的温度，或者计算过去某个时间点的温度。

综上所述，一次函数在实际问题中的应用十分广泛，它可以用来描述和解决与线性关系相关的问题。

通过建立一次函数模型，我们可以数学地表示和分析诸如速度、成本、温度等实际情境，从而得出有用的结论和决策。