当前位置：文档之家 › 应力状态及强度理论

应力状态及强度理论

  • 格式：doc
  • 大小：424.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学应力状态和强度理论

材料力学应力状态和强度理论

x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x ， x 定出 D1 点 由 y ， y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1，A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解： x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
A 点 横截面 m—m 上的应力为： F
A
n
m
F
A
F
m
n
F
A
2

应力状态与强度理论

应力状态与强度理论

理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时的断裂破坏。
3、最大剪应力理论（第三强度理论）：
理论认为最大剪应力是引起塑性屈服的主要 因素，只要最大剪应力τmax达到与材料性质 有关的某一极限值，材料就发生屈服。
单向拉伸下，当与轴线成45。的斜截面上的
τmax= s/2时
任意应力状态下
莫尔强度条件为：
1
Байду номын сангаас
t c
3
t
对于拉压强度不同的脆性材料，如铸铁、 岩石和土体等，在以压为主的应力状态下， 该理论与试验结果符合的较好。
综合以上强度理论所建立的强度条件， 可以写出统一的形式： σr≤[σ]
σr称为相当应力
r1 1
r2 1 2 3
r3 1 3
r4
1 2
理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时，沿纵向发生的断裂破坏。
2、最大伸长线应变理论(第二强度理论)：
理论认为最大伸长线应变是引起断裂的主要因素。
拉断时伸长线应变的极限值为
断裂准则为：
1
1 E
1
2
11
b
E
3
1 2 3 b
第二强度理论的强度条件：
1 2 3
max
1 3
2
屈服准则： 1 3 s
2
2
1 3 s
第三强度理论建立的强度条件为：
1 3
在机械和钢结构设计中常用此理论。
4、形状改变比能理论(第四强度理论)：
第四强度理论认为： 形状改变比能是引起塑性屈服的主要因素。
单向拉伸时，
1
3E
s
2的形状改变比能。

应力状态和强度理论

应力状态和强度理论

7.10 强度理论概述 低碳钢在拉伸、压缩和扭转时 低碳钢在拉伸、压缩和扭转时, 当试件的应力达 到屈服点后, 就会发生明显的塑性变形, 到屈服点后 就会发生明显的塑性变形 使其失 去正常的工作能力, 去正常的工作能力 这是材料破坏的一种基本形 塑性屈服。 叫做塑性屈服 式, 叫做塑性屈服。 铸铁拉伸或扭转时, 铸铁拉伸或扭转时 在未产生明显的塑性变形的 情况下就突然断裂, 材料的这种破坏形式, 情况下就突然断裂 材料的这种破坏形式 叫做 脆性断裂。 脆性断裂 。 石料压缩时的破坏也是这种破坏形 式。
混凝土压缩时的力学性能 使用标准立方体试块测定
端面未润滑时的破 端面润滑时的 坏形式 破坏形式
（三）最大剪应力（第三强度）理论 最大剪应力（第三强度） 认为构件的屈服是由最大剪应力引起的。 认为构件的屈服是由最大剪应力引起的。当最 最大剪应力引起的 大剪应力达到单向拉伸试验的极限剪应力时， 大剪应力达到单向拉伸试验的极限剪应力时， 构件就破坏了。 构件就破坏了。 σ1 −σ3 σ s = =τs τ max = τ s τ max =
[
]
1+µ 2 = τ E
E ∴G= 2(1+µ )
7.10 强度理论概述
1．材料破坏的基本形式
在前面的实验中, 在前面的实验中 曾接触过一些材料的 破坏现象, 破坏现象 如果以低碳钢和铸铁两种材料 为例, 它们在拉伸(压缩 压缩)和扭转试验时的破 为例 它们在拉伸 压缩 和扭转试验时的破 坏现象虽然各有不同, 坏现象虽然各有不同 但都可把它归纳为 两类基本形式, 塑性屈服和脆性断裂。 两类基本形式 即塑性屈服和脆性断裂。
第一类强度理论-----脆性断裂的理论 脆性断裂的理论 第一类强度理论
第一强度理论---第一强度理论 最大拉应力理论 第二强度理论---第二强度理论 最大伸长线应变理论

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

工程力学第9章 应力状态与强度理论

工程力学第9章 应力状态与强度理论

27
根据广义胡克定律，有
解 （1）m-m 截面的内力为：
（2）m-m 截面上 K 点的应力为：
28
29
30
9.5 强度理论
9.5.1 强度理论的概念 在第7章中介绍了杆件在基本变形情况下的强度计 算，根据杆件横截面上的最大正应力或最大切应力及相 应的试验结果，建立了如下形式的强度条件：
31
32
33
（2）第二强度理论———最大伸长线应变理论
34
（3）第三强度理论———最大切应力理论
35
（4）第四强度理论———最大形状改变比能理论
36
37
（2）校核正应力强度
（3）校核切应力强度
38
（4）按第三强度理论校核 D 点的强度
39
思考题 9.1 某单元体上的应力情况如图9.18所示，已知 σx=σy。试求该点处垂直于纸面的任意斜截面上的正应力、 切应力及主应力，从而可得出什么结论？
6
9.2.1 方位角与应力分量的正负号约定 取平面单元体位于Oxy平面内，如图9.5（a）所示。 已知x面（外法线平行于x轴的面）上的应力σx及τxy，y 面上的应力σy及τyx。根据切应力互等定理，τxy=τyx。现 在为了确定与z轴平行的任意斜截面上的应力，需要首 先对方位角α以及各应力分量的正负号作如下约定：
10
11
9.2.3 平面应力状态下的主应力 与极值切应力由式（9.1）和式（9.2）可知，当σx， σy和τxy已知时，σα和τα将随α的不同而不同，即随斜截面 方位不同，截面上的应力也不同。因而有可能存在某种 方向面，其上之正应力为极值。设α=α0时，σα取极值。 由
12
13
14
15
16

工程力学第11章 应力状态和强度理论

工程力学第11章 应力状态和强度理论

而最大正应力的方位角α0则可由下式确定
式中, 负号表示由x面到最大正应力作用面沿顺时针方向旋转。 因为 tan2α0=tan(180°+2α), 所以式(11-4) 给出两个相差90°的 α0 角, 即α0和 α0'=90°+α0(或α'0=α0-90°), 即这两个面互相垂直。 考虑到图11-8a中A、 B两点位于应力圆上同一直径两端, 即最大正应力所在截面和最小正应力所在截 面互相垂直 , 所以式 (11-4) 所求两个 α0 值即是 A 、B 两点所代表截面的方向。 它们之间的对应关系可以利用下述规则来确定 : 在 α0 和 α0+90°两个方向中 , σmax的方向总是在τx所指向的那一侧。 所以, 最大和最小正应力所在截面的方 位如图11-8b所示。 从图11-8a中还可以看出, 应力圆上存在K、M两个极值点, 由此得单元体在平 行于z轴的截面中最大和最小切应力分别为
11.2.2 平面应力状态分析的图解法
由式(11-1)和(11-2)可知, 任一斜截面α上的正应力σα和切应力τα均随参量α变 化。 所以σα和τα间必有确定的函数关系。 为建立它们间直接关系式, 先将式 (11-1)和式(11-2)改写为
式(c)、式(d)两边平方相加, 即有
从式(e)可以看出, 在以τ、σ为纵横坐标轴的平面内, 式(e)所对应的曲线为圆 (图11-5), 其圆心C的坐标为 , 半径为 , 而圆上任何一点的 纵、横坐标分别代表了单元体上某斜截面上的切应力和正应力。 此圆称为应力 圆。 并按以下步骤绘制应力圆。
的构件, 则必须研究危险点处的应力状态。 所谓一点的应力状态, 就是通过受 力构件内某一点的各个截面上应力情况。 由于构件内的应力分布一般是不均匀的, 所以在分析各个不同方向截面上的应 力时, 不宜截取构件的整个截面来研究, 而是围绕构件中的危险点截取一单元体 来分析, 以此来反映一点的应力状态。 例如, 螺旋桨轴工作时既受拉、又受扭 (图11-1a),若围绕轴表面上一点用纵、横截面截取单元体, 其应力情况如图 11-1b所示, 即处于正应力和切应力的共同作用下; 又如, 在导轨和车轮的接触 处(图11-2a), 单元体A除在垂直方向直接受压外, 由于其横向变形受到周围材 料的阻碍, 因而侧向也受到压力作用, 即单元体A处于三向受压状态。 显然, 要解决这类构件的强度问题, 除应全面研究危险点处各截面的应力外, 还 应研究材料在复杂应力作用下的破坏规律。 前者为应力状态理论的任务, 后者 则为强度理论所要研究的问题。

应力状态与强度理论

应力状态与强度理论

即为斜截面上的应力分量值。
2）证明
对下图所示应力圆可见C点的
横坐标为：
应力圆
E
D1 x , x
2a
C
D2 y , y
E
OC OB2 B2C
由于
O
D2B2C D1B1C
可得：
y
x
2
A2 B2
y D2
D1
2a 0
CF
B1 A1
x 1
应力圆
则：
B2C B1C
应力圆
OC
OB2
B1B2
/2 y
2、强度理论
强度理论概述
对单轴或纯剪切应力状态，可由实验测得的相 应的材料许用应力来建立正应力和切应力强度条件。
而当一点处的应力状态较为复杂时，因应力的 组合形式有无限多的可能性，不可能由实验的方法 来确定每一应力组合下材料的极限应力，因此需确 定引起材料破坏的共同因素。
关于材料破坏的共同因素（即破坏规律）的假 说，即称为强度理论。可根据强度理论来建立强度 条件。
主应力单元体以及主平面的方位如图c所示：
y
1
a0
x
1
(c)
2、解析法 ：
主应力
1
x
2
y
x
y
2
2
2 xy
110MPa
2 0
3
x
y
2
x
y
2
2
2 xy
40MPa
tan 2a0
2 xy x y
2 40 100 30
8 13
所以：2a0 3016' ⇒ a0 158'
习题： 251页，7-6、9
应力圆

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

应力状态分析和强度理论

应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态，当超过这一极限时，材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时，其内部应力状态会发生变化，当达到某一特定应力状态时，材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态，当超过这一极限时，材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服（即非弹性变形）的应力状态，是材料强度分析的重要依据。
根据不同的材料特性，存在多种屈服条件，如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示，用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据，当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时，材料会发生屈服和塑性变形，导致失效。该准则适用于韧性材料的失效分析，尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环，主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线，并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响，因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。

应力状态分析与强度理论

应力状态分析与强度理论

第五章 应力状态分析与强度理论一、 内容提要 1.应力状态的概念 1.1一点的应力状态通过受力构件的一点的各个截面上的应力情况的集合，称为该点的应力状态。

1.2一点的应力状态的表示方法——单元体研究受力构件内一点处的应力状态，可以围绕该点取一个无限小的正六面体，即单元体。

若单元体各个面上的应力已知或已计算出，则通过该点的其他任意方位截面上的应力就可用解析法或图解法确定。

1.3主平面、主应力单元体上切应力为零的平面称为主平面，主平面上的正应力称为主应力。

过受力构件内任一点总有三对相互垂直的主平面。

相应的主应力用1σ、2σ、3σ来表示，它们按代数值的大小顺序排列，即321σσσ≥≥。

1σ是最大主应力，3σ是最小主应力，它们分别是过一点的所有截面上正应力中的最大值和最小值。

1.4应力状态的分类（1）单向应力状态，只有一个主应力不为零，另两个主应力均为零； （2）二向或平面应力状态，两个主应力不为零，另一个为零； （3）三向或空间应力状态，三个主应力都不为零。

单向应力状态又称简单应力状态，二向、三向应力状态称为复杂应力状态。

2.平面应力状态分析的解析法在平面应力状态的单元体中，有一对平面上的应力等于零，即为主平面，其上主应力为零。

可将单元体用平面图形表示，如图5-1所示。

图5-12.1任意α斜截面上的应力当已知x σ、y σ、yx xy ττ=时，应用截面法，可得ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy yx xy yx yx +-=--++= （5-1）式中，正应力以拉应力为正，压应力为负；切应力以对单元体内任意点的矩为顺时针转向为正，反之为负；α为斜截面外法线与x 平面外法线即x 轴间的夹角，α角从x 轴量起，反时针转向为正，反之为负。

2.2主应力22min max 22xy yx y x τσσσσσσ+⎪⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫ （5-2） 式中，max σ和min σ分别表示单元体上垂直于零应力面的所有截面上正应力的最大值和最小值。

经济学应力状态和强度理论

经济学应力状态和强度理论
利用三角关系式，可以将前面所得的关于
和 的方程中的 消去，得：
(
x
y
2
)2
2
(
x
y )2
2
2x
这个方程恰好表示一个圆，这个圆称为应力圆
28
目录
二.应力圆
(
x
y )2
2
2
(
x
y )2
2
2x
R C
R
(
x
y
)2
2 x
2
x y
2
29
目录
二.应力圆
应力圆的画法
y y
y
D
x x
A x
9
目录
应力
指明
哪一个面上？
哪一点？
哪一点？ 哪个方向面？
过一点不同方向面上应力的集合，
称之为这一点的应力状态
10
目录
§7.2 平面应力状态的应力分析，主应力
一点应力状态的描述
微元
dz dy dx
dx,dy,dz 0
11
目录
§7.2 平面应力状态的应力分析，主应力
三向（空间）应力状态
xx
z
z
zx zy
τ T Wp
3
σ Mz Wz
21
目录
§7.2 平面应力状态的应力分析，主应力
z
z
zx zy
x
x
xz yz
xy
yx
y
y
2
3
1
单元体上没有切应力的面称为主平面；主平面
上的正应力称为主应力，分别用 1, 2 , 3 表示， 并且 1 2 3。该单元体称为主应力单元。

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

应力状态及强度理论

应力状态及强度理论

应力张量是一个二阶对称张量， 包含六个独立的分量，可以用 来描述物体的应力状态。
主应力和应力张量可以通过计 算得到，它们是描述物体应力 状态的重要参数。
02
强度理论
第一强度理论
总结词
最大拉应力准则
详细描述
该理论认为材料达到破坏是由于最大拉应力达到极限值，不考虑剪切应力和压 力的影响。
第二强度理论
05
实际应用
航空航天领域
飞机结构强度分析
利用应力状态及强度理论，对飞 机各部件的受力状态进行详细分 析，确保飞机在各种工况下的结 构安全。
航天器材料选择
根据材料的应力-应变关系，选择 适合航天器发射和运行阶段的材 料，确保航天器的可靠性和寿命。
航空材料疲劳寿命
评估
通过应力状态及强度理论，评估 航空材料的疲劳寿命，预防因疲 劳引起的结构失效。
03
材料失效分析
弹性失效
总结词
材料在弹性阶段发生的失效。
详细描述
当材料受到的应力超过其弹性极限时 ，会发生弹性失效。这种失效通常表 现为突然断裂或大幅度变形，且材料 不具有恢复原状的能力。
塑性失效
总结词
材料在塑性阶段发生的失效。
详细描述
当材料受到的应力超过其屈服点后，会发生塑性失效。这种 失效表现为材料发生较大的塑性变形，无法保持其原始形状 和尺寸。
土木工程领域
桥梁承载能力分析
通过对桥梁的应力分布和承载能力的分析，确保桥梁在设计寿命 内的安全性和稳定性。
建筑结构抗震设计
利用强度理论，对建筑结构进行抗震设计，提高建筑物的抗震能 力，减少地震灾害的影响。
岩土工程稳定性分析
通过对岩土工程的应力状态和强度理论的分析，评估岩土工程的 稳定性和安全性。

材料力学应力状态分析和强度理论

材料力学应力状态分析和强度理论

材料力学应力状态分析和强度理论材料力学是一门研究物质内部各个部分之间的相互作用关系的科学。

在材料力学中，应力状态分析和强度理论是非常重要的概念和方法，用来描述和分析材料的力学行为和变形性能。

材料的应力状态是指在外力作用下，物体内部各个部分所受到的力的分布情况。

应力有三个分量：法向应力、剪应力和旋转应力。

法向应力是垂直于物体表面的作用力，剪应力是平行于物体表面的作用力，旋转应力则是物体受到扭转力产生的应力分量。

应力状态的描述可以用应力矢量来表示。

应力状态分析的目的是确定材料内部各个部分的应力分布情况，进而推导出物体的变形和破坏行为。

常用的应力状态分析方法有平面应力问题、平面应变问题和三维应力问题。

平面应力问题是指在一个平面上的应变为零，而垂直于该平面的应力不为零；平面应变问题是指在一个平面上的变形为零，而垂直于该平面的应力不为零；三维应力问题则是指在空间中3个方向的应力都不为零。

强度理论是指根据材料的内部应力状态来评估其抗拉强度、抗压强度和抗剪强度等，以判断材料是否能够承受外力而不发生破坏。

常见的强度理论有最大正应力理论、最大剪应力理论和最大扭转应力理论。

最大正应力理论是指在材料的任何一个点，其法向应力都不能超过材料的抗拉强度；最大剪应力理论则是指剪应力不能超过材料的抗剪强度；最大扭转应力理论则是指旋转应力不能超过材料的极限扭转强度。

实际应用中，强度理论通常与材料的断裂理论结合起来，以评估材料的破坏行为。

材料断裂的主要原因是应力超过了材料的强度极限，从而导致材料的破坏。

为了提高材料的强度和抗拉性能，可以通过选择合适的材料、改变材料的结构和制造工艺等方法来实现。

综上所述，材料力学应力状态分析和强度理论是描述和分析材料力学行为和变形性能的重要理论和方法。

通过深入研究应力状态、应力分析和强度理论，可以为材料的设计和制造提供指导和支持，从而提高材料的强度和抗拉性能。

材料力学课件——应力状态理论和强度理论

材料力学课件——应力状态理论和强度理论

Me B
Me
B Me/Wn
P Me
C Me
C
第二节 二向应力状态下斜截面上的应力
目的 — 用一点某个微元上的应力表示其它
无限多微元上的应力 伴随结果
•应力极值 — 主应力状态 •从一个斜截面的应力构造一个单元体的应力
• 分析方法：1 解析法
•
2 图解法
二向应力状态下斜截面上的应力（续）
正应力符号规定
τα M τβ
σβ (c)
cos2
1
2
sin 2
cos2
1 sin 2
2
应力状态理论（续）
P
B
A
max A
max
M W
y
y
B
B
My
I
QS
Ib
应力状态理论（续）
P
P
A
A P/A
a) 一对横截面，两对纵截面
b)横截面，周向面，直径面 各一对
c) 同b)，但从上表面截取
应力
要指明
哪一点？
•那个面在
• 在哪一个面上？
哪个方位？
• 一点的应力状态：过一点不同方向面上应力的集合
•
称之为这一点的应力状态
•
State of the Stresses of a Given
Point
应力状态理论（续）
三向（空间）应力状态
Three-Dimensional State of Stresses
第七章 应力状态理论和强度理论
Theory of Stress State and Intensity
第一节 第二节 第三节 第四节 第五节 第六节 第七节 第八节

应力状态及强度理论

应力状态及强度理论

/
2
低碳钢
低碳钢 : σ s 240MPa; τs 200MPa
灰口铸铁 : σ Lb 98 ~ 280MPa σ yb 640 ~ 960MPa; τb 198 ~ 300MPa
铸铁
30° 40
图示单元体中应力单位为MPa
20
①求斜截面上旳应力
30
解 : x 30 y 40
60°
y
二、应力圆旳画法
y
Ox
C O
B(y ,yx)
x
xy
建立应力坐标系，如下图所示， （注意选好百分比尺）
在坐标系内画出点A( x，xy) 和B(y，yx)
x
A(x ,xy)
AB与 轴旳交点C便是圆心。
以C为圆心，以AC为半径画
圆——应力圆；
y
n 三、单元体与应力圆旳相应关系
x
xy
面上旳应力( ， ) 应力圆上一点( ， )
y
y
主单元体：
x
六个面上剪应力均为零旳单元体。
z
z
2
主平面：
剪应力为零旳截面。 x
主应力：
主平面上旳正应力。
1
主应力排序规则：按代数值大小排序：
3
σ1 σ2 σ3
三向应力状态： 三个主应力都不为零旳应力状态。（即三对平行平面上旳应
力均不为零）
二向应力状态： 一种主应力为零旳应力状态。（即仅一对平行平面上旳应力为零）
y
一、应力圆
x
y
xy
Ox
x
y
y
xy
σα
σx
σy 2
σx
σy 2
cos2α
τ xy sin2α
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图8-1 第
8章
应力状态及强度理论
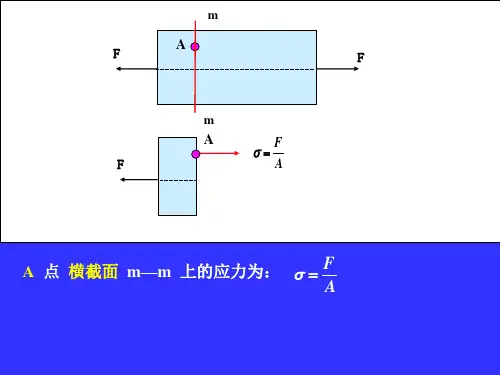
例8-1 已知应力状态如图7-1所示，试计算截
面m-m 上的正应力m σ与切应力m τ 。

解：由图可知，x 与y 截面的应力分别为
MPa x 100-=σ
MPa x 60-=τ
MPa y 50=σ
而截面m-m 的方位角则为
α= -30º
将上述数据分别代入式（7-1）与（7-2），
于是得
()()()()MPa
m 5.11460sin 6060cos 250100250100-=︒-⨯+︒---++-=σ()()()MPa m 0.3560cos 6060sin 2
50100=︒-⨯-︒---=τ 例8-2 试用图解法解例8-1（图8-2a ）。

(a) (b)
图8-2 解：首先，在τσ-平面内，按选定的比例尺，由坐标(-100，-60）与(50，60)分别确定A 和B 点图7-2b ）。

然后，以AB 为直径画圆，即得相应的应力圆。

为了确定截面m-m 上的应力，将半径CA 沿顺时针方向旋转α2=60º至CD 处，所得D 点即为截面m-m 的对应点。

按选定的比例尺，量得OE =115MPa （压应力），ED =35MPa ，由此得截面
m-m 的正应力与切应力分别为
MPa m 115-=σ
MPa m
35=τ
例 8-3 从构件中切取一微体，各截面的应力如图8-3a 所示，试用解析法与图解法确定主应力的大小及方位。

(a) (b)
图8-3 解：1.解析法
x 和y 截面的应力分别为
MPa x 70-=σ，MPa x 50=τ，0=y σ
将其代入式 (7-3）与 (7-5），得
}{MPa MPa 2696502070207022max min -=+⎪⎭
⎫ ⎝⎛--±+-=σσ ︒-=⎪⎭⎫ ⎝⎛--=⎪⎭
⎫ ⎝⎛--
=5.6202650arctan arctan max y x o σστα
由此可见，
MPa 261=σ，02=σ，MPa 963-=σ
而正应力1σ 的方位角 o α则为-62.5º(图8-3a ）。

2.图解法
按选定的在τσ-平面内，按选定的比例尺，由坐标(-70，50）与(0，-50)分别确定D 和E 点（图8-3b ）。

然后，以DE 为直径画圆即得相应的应力圆。

应力圆与坐标轴σ相交于A 和B 点，按选定的比例尺，量得OA =26MPa ，
OB =96MPa （压应力），所以，
MPa A 261==σσ； MPa A 963-==σσ
从应力圆中量得∠DCA=125º ，而且，由于自半径CD 至CA 的转向为顺时针方向，因此，主应力1σ的方位角为
︒-=︒-=∠-=5.622
1252DCA o α
例8-4 求图所示应力状态的主应力1σ，
2σ，3σ及最大正应力和最大切应力（应力单位为
MPa ）。

解：由图示单元体可知，一个主应力为-30MPa ，
待求的是其余两个主应力。

为此，分析与已知
主应力平行的斜截面上的应力情况，由主应力
公式可得 ()2222min max 3024012024012022-+⎪⎭⎫ ⎝⎛-±+=+⎪⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫x y x y x τσσσσσσ ()⎩
⎨⎧=±=MPa MPa MPa 301305080 由此可知，单元体处于三向应力状态。

三个主应力为
MPa MPa MPa 30,30,
130321-===σσσ
由相关公式可知 MPa 1301max ==σσ
()MPa MPa 802
30130231max =--=-=
σστ 例8-5 图示矩形截面梁的中性层上某点K 处，沿与轴线成450的方向贴有电阻应变片，测得线应变 545106.20-⨯-=ε, 试求梁上的载荷F 。

已知E=210 GPa ，μ=0.28 。

图8-4
图8-5
解：利用平衡方程可求得支反力
()↑=F F Ay 32 由截面法得点K 所在横截面上的剪力 ()↑=
F F s 3
2 中性层上的切应力 bh
F A F s ==
23τ 从点K 取单元体如图所示。

由纯剪切应力状态的分析知，得 0,,2113534500====-=σστσστσ
根据广义虎克定律式(8-13)，得
()()()μμτμσσε+-=+-=-=1110001354545Ebh
F E E kN Ebh F 31.8528
.01106.22.01.01021015
9450=+⨯⨯⨯⨯⨯=+=-εμ
例8-6 图8-6a)为一工字截面简支梁，已知P=30kN ，q=5kN/m,
[σ]=160MPa,[τ]=100MPa,Iz/S*max=16.9cm 。

试选择工字钢型号，并对梁作全面强度校核。

图8-6(a)
解：1) 计算梁的支反力,画出剪力图和弯矩图(图8-6b)
图8-6
2) 按弯曲正应力强度条件选工字钢型号
[]
363
max 250101601040cm M W z =⨯⨯==σ 查型钢表，选用20b 工字钢，其432500,250cm I cm W z z ==,Wz ＝309cm 3, cm 9.16*m ax =z z
S I ,截面尺寸如图8-6a)
3) 根据弯曲切应力强度条件校核
最大切应力发生在支座A 截面的中性轴上，其值为
[]ττ<=⨯⨯⨯=⋅⋅=-MPa b I S F z z s 3.2610
9.09.16104043
max *max max 4) 按主应力校核
在梁的C 截面上、腹板与翼板的交接处A 点，其正应力和切应力都比较大，需要对其强度作出校核。

从A 点取出一个单元体,计算其应力
()MPa b I y M z a c a 9.13210
9.010********.110105.37262
3=⨯⨯⨯⨯-⨯⨯=⋅⋅=---σ ()MPa b I S F z Za SC a 172
910.802500101043.914.12.1010356
3=--⨯⨯⨯⨯⨯=⋅⋅=-τ 该点的主应力为
⎩
⎨⎧-==+⎪⎭⎫ ⎝⎛±=+⎪⎭⎫ ⎝⎛±=⎭⎬⎫MPa MPa a a a 14.204.1351729.13229.132********τσσσσ 按第三强度理论，其相当应力为
[]σσσσ<=-=MPa xd 18.137313
安全。

相关主题