纯电感交流电路
- 格式:pdf
- 大小:173.77 KB
- 文档页数:4


单相交流电路概述在直流电路中,电路的参数只有电阻R 。
而在交流电路中,电路的参数除了电阻R 以外,还有电感L 和电容C 。
它们不仅对电流有影响,而且还影响了电压与电流的相位关系。
因此,研究交流电路时,在确定电路中数量关系的同时,必须考虑电流与电压的相位关系,这是交流电路与直流电路的主要区别。
本节只简单介绍纯电阻、纯电感、纯电容电路。
一、纯电阻电路纯电阻电路是只有电阻而没有电感、电容的交流电路。
如白炽灯、电烙铁、电阻炉组成的交流电路都可以近似看成是纯电阻电路,如图3—7所示。
在这种电路中对电流起阻碍作用的主要是负载电阻。
加在电阻两端的正弦交流电压为u ,在电路中产生了交流电流i ,在纯电阻电路中,龟压和电流瞬时值之间的关系,符合欧姆定律,即:/i u R =由于电阻值不随时间变化,则电流与电压的变化是一致的。
就是说,电压为最大值时,电流也同时达到最大值;电压变化到零时,电流也变化到零。
如图3—8所示。
纯电阻电路中,电流与电压的这种关系称为“同相”。
通过电阻的电流有效值为:/I U R =公式3—14是纯电阻电路的有效值。
在纯电阻电路中,电流通过电阻所做的功与直流电路的计算方法相同,即:22P UI I R U R ===二、纯电感电路纯电感电路是只有电感而没有电阻和电容的电路。
如由电匪很小的电感线圈组成的交流电路,都可近似看成是纯电感电路,如图3—9所示。
在如图3—9所示的纯电感电路中;如果线圈两端加上正弦交流电压,则通过线圈的电流i 也要按正弦规律变化。
由于线圈中电流发生变化,在线圈中就产生自感电动势,它必然阻碍线圈电流变化。
经过理论分析证明,由于线圈中自感电动势的存在,使电流达到最大值的时间,要比电压滞后90︒,即四分之一周期。
也就是说,在纯电感电路中,虽然电压和电流都按正弦规律变化,但两者不是同相的,如图3—10所示,正弦电流比线圈两端正弦电压滞后90︒,或者说,电压超前电流90︒。
理论证明,纯电感电路中线圈端电压的有效值U ,与线圈通过电流的有效值之间的关系是:L //I U L U X ω==L ω是电感线圈对角频率为叫的交流电所呈现的阻力,称为感抗,用L X 表示,即: L 2X L fL ωπ==式中 L X ——感抗(Ω);f ——频率(Hz);L ——电感(H)。

3.5 纯电感交流电路同频率
3.5 纯电感交流电路
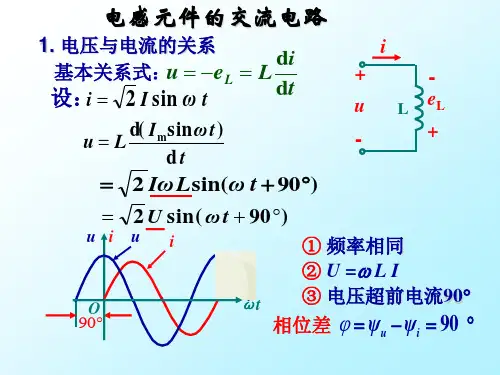
一、电压、电流的关系
2. 波形图:ωt u i
O
u , i U 3. 相量关系:(ψu = ψi +90°)
U = j X L I
I
L +
u
-i
4. 相量图:
3.5 纯电感交流电路
3.5 纯电感交流电路
二、功率关系
3. 无功功率:Q=UI= X L I2 单位:var
U2
X L
=
2. 平均功率(有功功率):P=0
P=0:电感为储能元件
【例】有一电感器,电阻可忽略不计,电感L = 0.2 H 。
把它接到220 V 工频交流电源上工作,求电感的电流和无功功率?若改接到100 V 的另一交流电源上,测得电流为0.8 A ,此电源的频率是多少?
解:(1) 接到220 V 工频交流电源时
X L =2πf L = 62.8 Ω
U 22062.8
X L I ==A = 3.5 A Q = U I = 220×3.5 var = 770 var
(2) 接到100 V 交流电源时X L 2πL
f ==100 Hz 100U 0.8I X L ==Ω=125 Ω
3.5 纯电感交流电路
总结:
1.电压电流同频率,电压超前于电流90°;
2.电压与电流的关系:
3.平均功率P =0,电感是储能元件。
4.无功功率用来说明电感与其以外电路的能量交换。
U=j X L I。





纯电感元件在正弦交流电路中的电压与电流关系
在正弦交流电路中,纯电感元件的电压与电流之间存在一定的关系。
根据电感元件的特性,其电压与电流的关系可以通过以下公式表示:
V = jωLI
其中,V表示电感元件的电压,I表示电感元件的电流,L表示电感元件的电感值,ω表示电路中的角频率。
j是虚数单位,满足j² = -1。
这个公式表明,电压与电流之间存在90度的相位差,且电压与电流之间的关系是线性的,也就是电压与电流成正比。
当电流通过电感元件时,会产生一个由电感元件本身决定的感应电动势,从而引起电压的变化。
需要注意的是,电感元件在交流电路中会引入阻抗,即纯电感元件的阻抗Z可以表示为:
Z = jωL
因此,在交流电路中,纯电感元件的电压和电流之间不仅存在幅值比例关系,还存在相位差。
这个相位差由纯电感元件的阻抗决定,通常为正90度。


教案内容、过程教法时间分配纯电感正弦交流电路一、电感元件1.自感系数和电磁感应磁通链:电流i产生的磁通为φ,线圈有N匝,那么与线圈交链的总磁通。
因为这个磁通或磁通链是由线圈本身的电流所产生,所以称为自感磁通或自感磁通链。
换算关系为1H=103 mH=106μH实际的电感线圈是用导线绕制而成的,因此除了具有电感外,还存在电阻。
如果电阻较小甚至可以忽略不计时,就可看作是理想电感元件。
对一个理想的电感线圈而言,若通过线圈的电流变动时,电流产生的磁通随之变动,而变动的磁通穿过线圈时必将引起电磁感应现象,在线圈中就会产生感应电动势,由于这种电磁感应现象是流经本线圈中的电流变化而在本线圈中引起的,因此称为自感应。
由自感现象引起的自感电动势和电流的方向选择一致时,则复习提问 10`课题引入 10`教案纸教 案 纸教 案 内 容、 过 程教 法时间分配必须指出,“无功”的含义是“交换”而不是“消耗”,它是相对 “有功”而言的,决不能理解为“无用”。
【例题】 有一电阻可以忽略的线圈接在交流电源上,已知)30314sin(2220 +=t u V,线圈的电感量L =0.7H ,求:(1)写出流过线圈电流的瞬时值表达式; (2)求电路的无功功率; (3)电压和电流的矢量图。
解:(1)因线圈的感抗Ω≈⨯==2207.0314L X L ω 电压有效值为U =220V , 流过线圈的电流有效值1220220===L X U I A 又因电流滞后电压900,而电压的初相为300 则电流的初相为 60903090-=-=-=u i ϕϕ.所以流过线圈电流的瞬时表达式为: )60314sin(2 -=t i A (2)电路的无功功率为: 2201220=⨯==UI Q L (Var) (3)电压和电流的矢量图如图所示小结 5`。
电感器在交流电路中的作用首先,电感器可以用来限制电流的变化率。
当交流电压施加在电感器上时,电感器的磁场会相应地变化,并且产生一个抗拒电流变化的作用。
这意味着电感器会限制通过它的电流的变化速度。
这样一来,在电路中加入电感器可以使电流的变化更加平滑,防止电流的突然变化引起电路中其他元件的损坏。
其次,电感器还可以用来调整电路的频率响应。
在电路中,电感器和电容器通常以特定的组合形式被使用,形成一个谐振电路。
电感器在谐振电路中起到调谐的作用,决定了电路的共振频率。
通过调节电感器的数值,可以改变电路的频率响应特性,使电路对特定频率的信号有更高或更低的增益。
此外,电感器还可以用来滤除电路中的高频噪声。
高频噪声是指频率高于所需信号频率的杂散信号。
由于电感器对频率较高的电流变化有较强的抵抗力,它可以在电路中起到滤波的作用。
通过将电感器与电容器和电阻器等元件组合在一起,可以构建一个低通滤波器,用于去除高频噪声,使电路输出的信号更加纯净和稳定。
此外,电感器还可以用来储存和释放电能。
当电感器通过电流时,它会在磁场中储存能量。
当电流停止流动时,电感器会以相反的电势释放储存的能量。
这种特性使得电感器可以用来构建一种电子开关,例如继电器。
继电器是一种通过电磁吸合和释放来控制电路开关状态的装置。
电感器在继电器中起到存储和释放能量的作用,使得继电器可以实现远距离的控制和调节。
最后,电感器还可以用于变压器和感应线圈等电子器件中。
在变压器中,电感器将电能从一个线圈传递到另一个线圈,实现电压的变换。
在感应线圈中,电感器通过磁场的变化诱导出电压或电流,用于无线能量传输和感应加载等应用。
总之,电感器在交流电路中起着至关重要的作用。
它通过限制电流的变化率、调整电路的频率响应、滤除高频噪声、储存和释放能量等方式,使得电路可以更加稳定可靠地工作。
电感器的应用范围广泛,包括电子通讯、电力系统、电动机驱动等领域。
在现代电子技术发展的过程中,电感器的功能和性能不断得到改善和完善,为电路设计和应用提供了更多的选择和灵活性。
纯电感交流电路欧姆定律符号法表示形式为纯电感交流电路是电工学中的经典问题,它的欧姆定律符号法表示形式为什么如此重要呢?
首先,我们需要了解欧姆定律的概念。
欧姆定律是电学中最基本的定律之一,它描述了电流、电压和电阻之间的关系,即电流等于电压除以电阻。
在直流电路中,欧姆定律一般用V-I符号法表示,其中V表示电压,I表示电流,R表示电阻,通过这个符号法可以很方便地分析直流电路的特性。
然而,对于交流电路来说,情况就有些不同了。
因为交流电路中,除了电阻还存在电感、电容等元件,它们的特性和直流电路中的电阻是不同的。
因此,在分析交流电路时,需要采用不同的符号法。
对于纯电感交流电路来说,由于没有电阻,因此无法用V-I符号法表示。
相反,需要采用更为抽象的符号法来描述电路特性。
在这个符号法中,电压和电流的关系是通过欧姆定律的变形得到的。
具体来说,我们可以利用电感的特性,将电压和电流表示为正弦函数,然后通过欧姆定律变形得到它们之间的关系。
这个表示形式的优点在于,可以很方便地分析纯电感交流电路的特性。
同时,这种符号法也为后续的电路分析提供了基础,为我们理解更为复杂的交流电路奠定了基础。
总之,纯电感交流电路的欧姆定律符号法表示形式是电工学中的重要内容。
它不仅为我们分析纯电感交流电路的特性提供了基础,还为我们理解更为复杂的交流电路提供了帮助。
因此,我们应该认真学
习这个表示形式,并尽可能地将它应用到实际问题中。
纯电感正弦交流电路1、含义:交流电路中只有电感线圈作负载的电路。
2、电流与电压的关系在电感线圈两端加上交流电U L ,线圈中必定产生交流电流i ,因而线圈中将产生感生电动势,其大小:e L =-Lti ∆∆ 则线圈两端的电压u L =- e L =-L ti ∆∆ 通过线圈的电流i= t sin I m ω 在0-2π即第一个41周期内:电流从0→I m ,ti∆∆>0且最大→0,电压e Lm →0。
在2π-π即第二个41周期内:电流从I m →0,ti∆∆<0且0→最大负值,电压0→-e Lm 。
在π-23π即第三个41周期内: 电流从0→-I m ,ti∆∆<0且最大负值→0,电压-e Lm →0。
在23π-2π即第四个41周期内: 电流从-I m →0,ti∆∆>0且0→最大,电压0→e Lm 。
结论: 在纯电感电路中,电感两端的电压超前电流90度,或电流滞后电压90度. i= t sin I m ω u=U Lm sin(ωt+2π) 电流一电压最大值之间的关系:LI L:2L U I L L lm m ωωω===U UI 或得两边同除于 设X L =ωL 代入上式:LLX U I =在纯电感正弦交流电路中,电流和电压的最大值及有效值之间符合欧姆定律. 3、感抗:1)、计算:X L =ωL=2πfL 2)、特点:“通直阻交” 3)、注意:IU X LL =只表示电压与电流的最大值或有效值之比。
iu x LL ≠不是瞬时值之比 4、电路的功率:1)、瞬时功率电压瞬时值u 和电流瞬时值i 的乘积,称为瞬时功率。
用P 表示。
即:p= U Lm sin(ωt+2π)t sin I m ω= U Lm sin ωt t sin I m ω=21U Lm I m sin2ωt = U L Isin2ωt电感元件的瞬时功率P 是按正弦规律变化的,其频率为电流频率的2倍。
纯电感交流电路欧姆定律表达式为欧姆定律是电学中一条非常重要的定律,它描述了电阻中电流与电压之间的关系。
然而,在纯电感交流电路中,由于电感的存在,电流与电压之间的关系并不遵循欧姆定律。
那么,在纯电感交流电路中,我们该如何表达欧姆定律呢?在纯电感交流电路中,电感的作用是储存电能和阻碍电流的变化。
当电路中的电感与电源相连时,会产生电流的变化,即交流电流。
而根据法拉第电磁感应定律,电感中的电压与电流的变化率成正比。
因此,我们可以使用以下表达式来描述纯电感交流电路中电流与电压之间的关系:V = L * di/dt其中,V表示电感的电压,L表示电感的感值,di/dt表示电流的变化率。
这个表达式可以看作是欧姆定律在纯电感交流电路中的推广。
从这个表达式中,我们可以看出,在纯电感交流电路中,电流与电压之间的关系是非线性的。
当电流的变化率较小时,电流与电压的关系近似为线性关系。
但是,当电流的变化率较大时,电流与电压之间的关系将变得复杂,甚至可以出现反向的情况。
在纯电感交流电路中,电感的作用是储存电能,并且可以改变电流的相位。
当电源的电压变化时,电感会产生电压的反向变化,从而改变电流的相位。
这种相位差的变化是纯电感交流电路中的一个重要特性,它使得纯电感交流电路在电子设备中具有广泛的应用。
在实际应用中,我们经常会遇到纯电感交流电路的设计和分析问题。
通过欧姆定律表达式,我们可以更好地理解纯电感交流电路中电流与电压之间的关系,从而更好地设计和优化电路。
同时,我们还可以利用这个表达式来计算电感的感值,以满足电路设计的要求。
纯电感交流电路欧姆定律表达式是描述纯电感交流电路中电流与电压之间关系的重要工具。
它使我们能够更好地理解纯电感交流电路的特性,并在实际应用中进行电路设计和分析。
通过深入研究和应用这个表达式,我们可以更好地利用电感的特性,实现更高效、稳定的电子设备。