随机变量的函数变换

第六章 随机变量函数第一节 一维随机变量函数一、一维随机变量函数1、一元波雷尔函数：设)(x f 为一元实函数,若1B ∈∀B ,有11})(|{)(B ∈∈=-B x f x B f ，则称)(x f 为一元波雷尔函数. 可以证明：连续函数、单调函数都是波雷尔函数.2、定义：设),,(P S F 为一概率空间，X 为S 上的一维随机变量，)(x f 为一元波雷尔函数, S e ∈∀,规定: ))(()(e X f e Y =R ∈,称Y 为X 的函数. 记作)(X f Y =.显然,1B ∈∀B ,F ∈∈=∈=--)}()(|{}))((|{)(11B f e X e B e X f e B Y ， 故Y 也是S 上的一维随机变量.二、离散型设X 的概率分布为X 1x 2x … k x… P1p 2p…kp…)(X f Y =为X 的函数，那么}{~k k y Y P q Y ==,其中 ∑-∈-=∈=====)(11)}({})({}{k i y fx i k k k k p y fX P y X f P y Y P q .特别,当f 为一一对应函数时,令)(k k x f y =, 有k k k k p x X P y fX P q ===∈=-}{)}({1,那么Y)(1x f )(2x f… )(k x f … P1p2p …kp…例1 设X 的概率分布为X-1 01 P1/3 1/2 1/6求：(1)1-X ;(2)X 2-;(3)2X 的概率分布. 解:列表计算1/3 1/2 1/6 X -1 0 1 1-X -2 -1 0 X 2- 2 0 -2 2X1 0 1所以 (1) 1-X 的概率分布为:1-X-2 -1 0 P1/3 1/2 1/6 (2) X 2-的概率分布为:X 2--2 0 2 P 1/6 1/2 1/3 (3) 2X 的概率分布为: 2X0 1 P1/2 1/2例2 设()kk X P X 2/1}{~==，N ∈k ，)2sin(X Y π=，求Y 的概率分布.解: 显然Y 的可能取值为1,0,1-.由已知条件知:∑∑∞=+∞=⎪⎭⎫⎝⎛=+===014021}14{}1{n n n n X P Y P ∑∑∑∞=-∞=∞==-⨯=⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛====1112131411141414121}2{}0{n n n nn n X P Y P ,152}0{}1{1}1{==-=-=-=Y P Y P Y P .所以Y 的概率分布为:Y-1 0 1 P2/15 1/3 8/15三、连续型设)(~x X ϕ，)(X f Y = 1、 分布函数法先求出⎰≤=≤=≤=yx f Y dx x y X f P y Y P y F )()(})({}{)(ϕ；(2) 再求出)()(y F y Y Y '=ϕ.例3 设)(~x X ϕ,||X Y =,则)()()(y y y X X Y -+=ϕϕϕ，0>y . 解:(1)当0≤y ，0)(=y F Y ,因此0)(=y Y ϕ；(2) 当0>y ,)()(}{}|{|)(y F y F y X y P y X P y F X X Y --=≤≤-=≤=, 那么)()()()()(y y y F y F y X X X XY -+=-'-'=ϕϕϕ.2、公式法(1) 设)(~x X ϕ,)(X f Y =,0)(>'x f ，)(-∞=f α，)(+∞=f β,)(y h 为)(x f 的反函数,则 )()]([)(y h y h y X Y '=ϕϕ，βα<<y .证明:因0)(>'x f ,则)(x f y =存在反函数)(y h x =,且0)(>'y h ,那么)(y h 递增.显然βα≤≤)(X f ,且})({}{)(y X f P y Y P y F Y ≤=≤=.① 当α≤y 时, 0)(=y F Y ,⇒0)(=y Y ϕ； ② 当β≥y 时, 1)(=y F Y ,⇒0)(=y Y ϕ； ③ 当βα<<y 时,)]([)}({)}()]([{)(y h F y h X P y h X f h P y F X Y =≤=≤=, 所以 )()]([)()(y h y h y F y X Y Y '='=ϕϕ.(1)’ 设)(~x X ϕ,)(X f Y =,0)(<'x f ，)(+∞=f α，)(-∞=f β,)(y h 为)(x f 的反函数,则 |)(|)]([)(y h y h y X Y '=ϕϕ，βα<<y .证明:同(1),只是0)(<'y h ,那么)(y h 递减. 当βα<<y 时,)}({1)}({)}()]([{)(y h X P y h X P y h X f h P y F Y <-=≥=≥= )]([1y h F X -=, 所以|)(|)]([)()]([)()(y h y h y h y h y F y X X Y '='-='=ϕϕϕη.例4 设)(~x X ϕ,b aX Y +=,)0(≠a ，则⎪⎭⎫⎝⎛-=a b y a y X Y ϕϕ||1)(,+∞<<∞-y .解:令b ax x f y +==)(,那么-∞=α，+∞=β，ab y y h -=)(,ay h 1)(=',⎪⎭⎫⎝⎛-='=a b y a y h y h y X X Y ϕϕϕ||1|)(|)]([)(,+∞<<∞-y .例5 设),(~2σμN X ,σμ-=X Y ,，则)1,0(~N Y . 解: b aX Y +=,01>=σa ,σμ-=b ,于是()μσσϕϕϕ+=⎪⎭⎫⎝⎛-=y a b y ay XX Y 1)(,()22][222212yy ee --+-==πσπσσμμσ, +∞<<∞-y .例6 设),(~2σμN X ,b aX Y +=,)0(≠a ，则),(~22σμa b a N Y +.证明: 222)(||21||1)(σμσπϕϕ---=⎪⎭⎫⎝⎛-=a b y X Y ea ab y a y2222)]([||21ab a y e a σμσπ+--=，+∞<<∞-y所以 ),(~22σμa b a N Y +.(2)设)(~x X ϕ,b x a <<,)(X f Y =,0)(>'x f ，)(b f =α，)(a f =β,)(y h 为)(x f 的反函数,则)()]([)(y h y h y X Y '=ϕϕ，βα<<y . 证明:因0)(>'x f ,则)(x f y =在),(b a 上存在反函数)(y h x =,且0)(>'y h ,那么)(y h 递增.显然βα≤≤)(X f ,且})({}{)(y X f P y Y P y F Y ≤=≤=. ① 当α≤y 时, 0)(=y F Y ,⇒0)(=y Y ϕ； ② 当β≥y 时, 1)(=y F Y ,⇒0)(=y Y ϕ； ③ 当βα<<y 时,)]([)}({)}()]([{)(y h F y h X P y h X f h P y F X Y =≤=≤=, 所以 )()]([)()(y h y h y F y X Y Y '='=ϕϕ.(2)’ 设)(~x X ϕ,b x a <<,)(X f Y =,0)(<'x f ，)(a f =α，(b f =β,)(y h 为)(x f 的反函数,则|)(|)]([)(y h y h y X Y '=ϕϕ，βα<<y . 证明:同(2),只是0)(<'y h ,那么)(y h 递减. 当βα<<y 时,)}({1)}({)}()]([{)(y h X P y h X P y h X f h P y F Y <-=≥=≥= )]([1y h F X -=,所以|)(|)]([)()]([)()(y h y h y h y h y F y X X Y Y '='-='=ϕϕϕ.例7 设)2,2(~ππ-U X ,X A Y sin =,)0(>A ，求)(y Y ϕ.解:已知x A x f y sin )(==,0)(>'x f ,)2,2(ππ-∈x ,A -=α,A =β,Ay y h arcsin)(=,221)(yA y h -='，又 ⎩⎨⎧>≤=.2/|| ,0 ,2/|| ,1/ )(πππϕt t t X所以 ⎪⎩⎪⎨⎧<<--='=. ,0 , ,1|)(|)]([ )(22其他A y A yA y h y h y XY πϕϕ(3) 设)(~x X ϕ,)(X f Y =,)()(x f x f i =,i I x ∈,且在i I 导数恒不为零,)(y h i 为)(x f i 的反函数, }),(|{i i i I x x f y y J ∈==,i I 为互不相交的区间,.,,2,1m i =,则 iJ y i mi i XY y h y h y ∈='=∑|)(|)]([)(1ϕϕ.证明：由(2)知, |)(|)]([)()(y h y h y i i X X f i '=ϕϕ,i J y ∈.∑∑=∈≤=≤=≤=mi iI e X Y y X fP y X f e P y X f e P y F i1)(})({})(|{})(|{)(iJ y i mi i Xmi i Y Y y h y h y X f P dyd dyy dF y ∈=='=≤==∑∑|)(|)]([})({)()(11ϕϕ.例8 设)(~x X ϕ,2X Y =,则)]()([21)(y y yy X X Y -+=ϕϕϕ，0>y .证明:令0,0,)(,)(121><-===y x y y h x x f y ，0,0,)(,)(222><===y x y y h x x f y ,那么),0(21+∞==J J .由(3)知 )]()([21|)(|)]([)(021y y yy h y h y X X y i i i XY -+='=>=∑ϕϕϕϕ,0>y .例9 设)1,0(~N X ,2X Y =,则)1()21,21(~22χ∆=Γ=X Y .解: )(1)]()([21)(y yy y y y X X X Y ϕϕϕϕ=-+=()21121212)2/1(2/1211---Γ==eyeyy π,0>y .所以 )21,21(~2Γ=XY .四、随机变量存在定理设定义在R 上的函数)(x F 满足：(1)R ∈∀x ,1)(0≤≤x F ；(2))(x F 为单调不减函数；(3)0)(lim =-∞→x F x ,1)(lim =+∞→x F x ；(4))(x F 为右连续函数.则)(x F 必为某一维随机变量的分布函数.事实上,取)1,0(~U X ,定义})(|sup{)(x t F t x G <=,则)(X G Y =的分布函数为)(x F .说明: ① 由此可见满足分布函数(1)-(4)的)(x F 可确定一个随机变量.②利用数学或物理的方法产生)1,0(中均匀分布随机变量的子样(称为均匀分布随机数)，再利用变换)(X G Y =可得到任意分布)(x F 的随机数.这在蒙特卡洛方法中具有重要性．证明:①先证明)(x G 单调不减,那么)(x G 是波雷尔函数.R ∈<∀21x x ,若1)(x t F <,有2)(x t F <⇒})(|{})(|{11x t F t x t F t <⊂<⇒})(|sup{})(|sup{21x t F t x t F t <≤<⇒)()(21x G x G ≤. 所以)(x G 单调不减.其次证明)(x G 的定义域)1,0(⊃D .因X 的值域为)1,0(, 这样)(X G 就是一维随机变量.)1,0(∈∀r ,因(3),必R ∈'''∃x x ,,使得)()(x F r x F ''<<'. 因r x F <')(,有})(|{r t F t x <∈',于是})(|{r t F t <非空；又})(|{r t F t s <∈∀,有)()(x F r s F ''<<,因(2),有x s ''<, 于是})(|{r t F t <有界,这样})(|sup{)(r t F t r G <=存在,. 于是D r ∈,那么D ⊂)1,0(.③ 再证明R ∈∀x ，有x y F x G y <⇔<)()(，这样 )()(y F x y x G ≤⇔≤.“⇐”x y F <)(,因(4),则y y >'∃,使得x y F y F <'<)()(， 这样 )(})(|sup{x G x t F t y y =<≤'<“⇒”)(x G y <，因})(|sup{)(x t F t x G <=,则})(|{ x t F t y <∈'∃， 使得y y x G x G '<--])([)(,即y y '<,又因(2),有x y F y F <'≤)()(. ④ 最后证明)(X G Y =的分布函数为)(x F .因)1,0(~U X ,故x x F X =)(,10≤≤x ,而由(1)知1)(0≤≤y F , 因此 R ∈∀y ，)()]([)}({})({}{)(y F y F F y F X P y X G P y Y P y F X Y ==≤=≤=≤=.第二节 n 维随机变量一、n 维随机变量1、定义：设),,(P S F 为一概率空间，k X ，)(n N k ∈为S 上的一维随机变 量，称),,,(21n X X X X =为S 上的n 维随机变量.符号约定：设nn n y y y y x x x x R ∈==),,,( ),,,,(2121 ,规定： ① y x <⇔k k y x <；n k ,,2,1 =.②y x ≤⇔k k y x ≤，)(n N k ∈.③将),,,(21n x x x x =写成列(column)向量) (21'n x x x ,即==),,,(21n x x x x ) (21'n x x x .) (),,,(2121'==n n X X X X X X X .2、X 关于J X 的边缘分布：),,,(21mk k k I X X X X =.)(),,,(21n N k k k I m ⊂= 表示)(},,,{21n N k k k m ⊂ .3、X 的分布：}{B P ∈X , n B B ∈. 其中可证：=∈}{B X F ∈∈∈},)(|{S e B e X e .4、分布函数(1)定义：设),,(P S F 为一概率空间，X 为S 上的n 维随机变量, n x R ∈∀,规定}{)(x X P x F ≤=.称)(x F 为X 的分布函数.(2) 性质① n x R ∈∀,1)(0≤≤x F .② )(x F 关于k x 为单调不减右连续函数，)(n N k ∈. ③ 0)(lim =-∞→x F J x ,)(n N J ⊂；1),,,(=+∞+∞+∞ F .④ ),,,(lim }{)(21n x J JJ x x x F x XP x FJ JX +∞→=≤=,)(n N J J =+.5、相互独立: 设),,,(21m X X X X =,)(x F 为X 的分布函数, 而),,,(21kkn k k k X X X X =为k n 维随机变量, )(k k x F 是k X 的分布函数,m k ,,2,1 =，恒有)(x F ∏==mk k kx F1)(，则称m X X X ,,,21 相互独立.注：① 若mmn m n X X ,,,,,,11111X X 独立,即X 独立， 则m X X X ,,,21 独立.②m X X X ,,,21 独立⇔kn k B B ∈∀，m k ,,2,1 =恒有}{}{}{},,,{22112211m m m m B X P B X P B X P B X B X B X P ∈∈∈=∈∈∈ .③ 若),,,(21m X X X X =相互独立 ⇒kJ J J X X X ,,,21独立,)(21m N J J J k ⊂+++ .6、随机变量序列}{n X 的独立：若}{n X 中任意有限个随机变量独立，则称}{n X 独立.n 维离散型随机变量1、定义：设),,(P S F 为一概率空间，),,,(21n X X X X =为S 上的n 维随机变量，若X 的取值为有限个或可数个(至多可数)，称X 为S 上的n 维离散型随机变量.显然：X 为S 上的n 维离散型随机变量⇔i X ),,2,1(n i =均为S 上的一维离散型随机变量.2、概率分布：假设X 所有可能取的值为I x ),,,(21ni i i x x x =，nn i i i I N ∈=),,,(21 ，令},,,{}{2121ni n i i I I x X x X x X P x X P p ====== ,称其为n 维随机变量X 的概率分布.3、分布律性质(1)0≥I p ; (2) 1=∑II p ;(1)(2)为离散型随机变量的特征性质. 反之亦然.(3) ∑∈=∈Bx I I p B X P }{,n B B ∈；(4)n X X X ,,,21 独立⇔nI N∈∀,恒有}{}{}{}{2121n i n i i I x X P x X P x X P x X P ===== .4、IJ p Y X ~),(的边缘分布,n I N ∈,mJ N ∈(1)),(Y X 关于X 的边缘分布：∑=∙JIJ I p p X ~.(2)),(Y X 关于Y 的边缘分布：∑=∙IIJ J p p Y ~.5、IJ p Y X ~),(的条件分布(1)在I x X =的条件下Y 的分布：∙===I IJ I J p p x X y Y P }|{.在J y Y =的条件下X 的分布：JIJ J I p p y Y X X P ∙===}|{.三、n 维连续型随机变量1、定义：设),,(P S F 为一概率空间，X 为S 上的n 维随机变量，)(x F 为X 的分布函数,若存在非负可积函数)(x ϕ，对n x R ∈∀,有⎰≤=xt dt t x F )()(ϕ,则称X为n 维连续型随机变量. )(x ϕ为X 的概率密度函数.记作)(~x X ϕ. 注：(1) )(x F 为连续函数；(2) )(x ϕ意义与一维相同.2、性质(1)0)(≥x ϕ; (2)⎰∈=nx dxx R1)(ϕ；(1)(2)为连续型随机变量的特征性质. 反之亦然.(3)⎰∈=∈Bx dx x B X P )(}{ϕ,nB B∈；(4)n B B ∈∀,若0)(=B m ,有0}{=∈B X P .(5)n X X X ,,,21 独立⇔nn R x x x x ∈=∀),,,(21 ,恒有∏==nk k X X x x k1)()(ϕϕ.3、 X 关于J X 的边缘分布： ⎰=JJ dx x x )()(ϕϕ，)(n N J J =+.4、在J J x X =的条件下L X 的分布： )()()|(J L J J L x x x x ϕϕϕ+=，)(n N L J ⊂+. 例1 (均匀分布) 在n A B ∈(0)(>A m )中任取一点X ，则X 的密度函数为：⎪⎩⎪⎨⎧∉∈=. ,0 , )(1)(A x A x A m x ，ϕ 此时，记：)(~A U X .例2 (n 维正态分布) 设)(~),,,(21x X X X X n ϕ =,n R ∈μ,C 为n 阶正定对称矩阵，且)()(211212||)2(1)(μμπϕ-'---=x Cx eC x n,n x R ∈称X 服从n 维正态分布，记作),(~C N X μ.特别,当2=n 时, ),(21μμμ=,因⎪⎪⎭⎫ ⎝⎛=22211211c cc c C 为二阶正定对称矩阵,于是⎪⎪⎭⎫ ⎝⎛=22121211c cc c C ,且011>c ,0||2122211>=-C c c c ,那么022>c , 令111c =σ,222c =σ,221112c c c =ρ，这样1||<ρ,⎪⎪⎭⎫⎝⎛=22212121σσρσσρσσC , ⎪⎪⎭⎫ ⎝⎛--=-212121221||1σσρσσρσσC C, )1(||22222ρσσ-=C , 于是 )()(211212||)2(1)(μμπϕ-'---=x C x eC x n⎥⎥⎦⎤⎢⎢⎣⎡-+-------=2222212121212)())((2)()1(21221121σμσσμμρσμρρσπσy y x x e，这正是二维正态分布.第三节 n 维随机变量函数一、n 维随机变量函数1、n 元波雷尔函数：设)(x f 为n 元实函数,若1B ∈∀B , 有n B x f x B fB ∈∈=-})(|{)(1，则称)(x f 为n 元波雷尔函数.可以证明：连续函数是波雷尔函数.2、定义：设),,(P S F 为一概率空间，X 为S 上的n 维随机变量，)(x f 为n 元波雷尔函数, S e ∈∀,规定: ))(()(e X f e Y =R ∈,称Y 为X 的函数. 记作)(X f Y =.3、显然：1B ∈∀B ,F ∈∈=∈=--)}()(|{}))((|{)(11B fe X e B e Xf e B Y ，故Y 也是S 上的一维随机变量.二、离散型设X 的概率分布为}{I x X P =,n I N ∈,)(X f Y =为X 的函数， 则Y 的概率分布为)}({I x f Y P =.例1 设),(Y X 的概率分布为YX -1 1-1 1/4 1/3 1 1/6 1/4求：(1)Y X +；(2) Y X -2 的概率分布.解:列表计算P),(Y X Y X + Y X -2 1/4 (-1,-1) -2 -1 1/3 (-1,1) 0 -3 1/4 (1,1) 2 1 1/6 (1,-1) 0 3所以:(1) Y X +的概率分布为:Y X +-2 0 2 P1/4 1/2 1/4(2)Y X -2的概率分布为:Y Z -2-3 -1 13 P1/3 1/4 1/4 1/6例2 设)(~i i P X λ,2,1=i 独立, 21X X Z +=则 )(~2121λλ++=P X X Z . 解：Z 的可能取值为 ,2,1,0,而∑=-====+==ki i k X i XP k X X P k Z P 02121},{}{}{∑∑=---=-=-===ki ik iki ei k ei i k X P i XP 02102121)!(!}{}{λλλλ)(21210)(2121!)()!(!!!λλλλλλλλ+--=+-+=-=∑ek i k i k k eki k i ki ，0N k ∈,所以)(~2121λλ++=P X X Z .三、连续型1、分布函数法: 设),(~),(y x Y X ϕ，),(Y X f Z =,为S 上的二维随机变量, (1) 先求出⎰⎰≤=≤=≤=zy x f Z dxdyy x z Y X f P z Z P z F ),(),(}),({}{)(ϕ,R ∈∀z ；(2) 再求出)()(z F z Z Z '=ϕ.2、随机变量四则运算公式: 设二维随机变量),(~),(y x Y X ϕ.(1)Y X Z +=,则 ⎰+∞∞--=dx x z x z Z ),()(ϕϕ，或⎰+∞∞--=dyy y z z Z),()(ϕϕ.若X 与Y 独立，则⎰+∞∞--=dx x z x z Y XZ )()()(ϕϕϕ.证明：⎰⎰⎰⎰+∞∞--∞-≤+==xz z y x Z dyy x dx dxdyy x z F ),(),()(ϕϕ⎰⎰⎰⎰∞-+∞∞-+∞∞-∞-=--=-====zzyx t dx x t x dt dtx t x dx ),(),(ϕϕ⎰⎰⎰∞-∞-+∞∞-=⎥⎦⎤⎢⎣⎡-=zzdt t dt dx x t x )(),(ζϕϕ,所以⎰+∞∞--=dx x z x z Z ),()(ϕϕ.例3 设)1,0(~N X i ,2,1=i 独立,则)2,0(~21N X X Z +=. 证明：由 222222)(z xz x x z x +-=-+ 22222222)2(22222z z x z z zxx +⎪⎭⎫ ⎝⎛-=+⎪⎭⎫ ⎝⎛+-=, 从而 ⎰⎰+∞∞----+∞∞-=-=dx eedx x z x z x z xX X Z 2)(2222121)()()(πϕϕϕ⎰⎰∞+∞-⎪⎭⎫ ⎝⎛--⋅-∞+∞-⎪⎭⎫ ⎝⎛--⋅-⎪⎭⎫ ⎝⎛-==2221221222222222222222z x d eedx eez x z z x zπππ ()2222221⋅-=z eπ,R ∈z . 所以)2,0(~N Z .注：一般地，设),(~2i i i N Z σμ,2,1=i 独立,则),(~22212121σσμμ+++=N X X Z .4 设),(~λi i r X Γ,2,1=i 独立, 21X X Z +=则 ),(~2121λr r X X Z +Γ+=.证明: ⎰⎰+∞+∞∞--=-=)()()()()(2121dx x z x dx x z x z X X X X Z ϕϕϕϕϕ,① 当0≤z 时, 0)(=z Z ϕ； ② 当0>z 时,⎰⎰------ΓΓ=-=zx z r r r r zX X Z dx ex z r exr dx x z x z 0)( 12 x11 0221121)()()()()()(λλλλϕϕϕ⎰⎰---+-=--+--⋅ΓΓ===-ΓΓ=111121 0112121212121)1()()()()()()(dt t tz r r edx x z xr r er r r r zxzt zr r r r z λλλλλzr r e z A 121)(λλλ--+=，又因 ) ()()()(1210121r r A z d ez A dz z zr r Z +Γ===⎰⎰+∞--++∞∞-λλϕλ,⇒[]121) (-+Γ=r r A ，这样 []z121 1121212121)()() ()(λλλλλϕ--++--+-+Γ=+Γ=ezr r ez r r z r r r r zr r Z .所以),(~21λr r Z +Γ.(2)Y X Z -=,则 ⎰+∞∞--=dx z x x z Z ),()(ϕϕ.若X 与Y 独立，则⎰+∞∞--=dx z x x z Y XZ )()()(ϕϕϕ.证明：⎰⎰⎰⎰+∞∞--∞-≤-==zx z y x Z dy y x dx dxdyy x z F ),(),()(ϕϕ⎰⎰⎰⎰∞-+∞∞-+∞∞-∞-=--=-====zzyt x dx t x x dt dtt x x dx ),(),(ϕϕ,所以 ⎰+∞∞--=dx z x x z Z ),()(ϕϕ.独立时简单证明: 因 )()(y y Y Y -=-ϕϕ,于是⎰⎰+∞∞-+∞∞---+-=-==dx z x x dx x z x z z Y XY XY X Z )()()()()()()(ϕϕϕϕϕϕ.(3) XY Z =,则 ⎰+∞∞-=dy y yz y z Z ),(||1)(ϕϕ，或⎰+∞∞-=dx xzx x z Z ),(||1)(ϕϕ.若X 与Y 独立，则⎰+∞∞-=dx xzx x z Y X Z )()(||1)(ϕϕϕ.证明：⎰⎰⎰⎰⎰⎰∞+∞-∞-∞+≤+==),(),(),()(yzyzzxy Z dxy x dy dx y x dy dxdyy x z F ϕϕϕ⎰⎰⎰⎰∞+∞-∞-∞-=+===01),(1),(zzxyt dt yy yt dydt yy yt dyϕϕ⎰⎰⎰⎰∞+∞-∞-∞-+=00),(||1),(||1zzdt y yt y dydt y yt y dyϕϕ⎰⎰⎰⎰∞-+∞∞-+∞∞-∞-==zzdy y yt y dtdt y yt y dy),(||1),(||1ϕϕ所以 ⎰+∞∞-=dy y yz y z Z ),(||1)(ϕϕ.例5 设),(~),(y x Y X ϕ,且⎩⎨⎧<≤<= . ,0,10 8),(其他，y x xy y x ϕXY Z =,求)(z Z ϕ.解:⎰⎰==+∞∞-1),(1),(||1)(dy y yz ydy y yz y z Z ϕϕϕz z y d y yz yZZZ ln 481110-==+=⎰⎰⎰,10<<z .(4) YX Z =,则 ⎰+∞∞-=dy y yz y z Z ),(||)(ϕϕ.若X 与Y 独立，则⎰+∞∞-=dy y yz y z Y XZ )()(||)(ϕϕϕ.证明：⎰⎰⎰⎰⎰⎰+∞∞-∞-+∞≤+==),(),(),()(zyzyzyxZ dx y x dy dx y x dy dxdyy x z F ϕϕϕ⎰⎰⎰⎰+∞∞-∞--∞=+===00),(),(zzxty ydty ty dy ydt y ty dy ϕϕ⎰⎰⎰⎰+∞∞-∞-∞-+=00),(||),(||zzdt y ty y dy dt y ty y dy ϕϕ⎰⎰⎰⎰∞-+∞∞-+∞∞-∞-==zzdyy ty y dt dt y ty y dy ),(||),(||ϕϕ所以 ⎰+∞∞-=dy y yz y z Z ),(||)(ϕϕ.例5 设)(~i Exp X i ,2,1=i 独立, 21X X Z =,求)(z Z ϕ. 解: ⎰⎰+∞+∞∞-==)()()()(||)(2121dy y yz y dy y yz y z X X X X Z ϕϕϕϕϕ，① 当0≤z 时, 0)(=z Z ϕ；当0>z 时, ⎰+∞--=22)(dy eyez yzyZ ϕ22)2(122)2(2)2()2(2])2[()2()2(2z z y z d ez z yz +=+Γ=+++=⎰+∞+--.所以 ⎪⎩⎪⎨⎧≤>+=.0 ,0 ,0 ,)2(2)(2z z z z Z ϕ四、最大、最小公式设),,,(21n X X X 为S 上的n 维随机变量,且n X X X ,,,21 独立.(1) },,,max{21n X X X Z =，则∏==ni X Z z Fz F i1)()(.证明: }},,,{max{}{)(21z X X X P z Z P z F n Z ≤=≤= },,,{21z X z X z X P n ≤≤≤=∏==≤≤≤=ni X n z Fz X P z X P z X P i121)(}{}{}{ .(2)},,,min{21n X X X Z =，则∏=--=ni X Z z F z F i1)](1[1)(.证明: }},,,{min{1}{1}{)(21z X X X P z Z P z Z P z F n Z >-=>-=≤=},,,{121z X z X z X P n >>>-=∏=--=>>>-=ni X n z F z X P z X P z X P i 121)](1[1}{}{}{1 .例6 设)(~i i Exp X λ,2,1=i 独立,},max{211X X Z =,},min{212X X Z =, 求)(1z Z ϕ,)(2z Z ϕ.解:已知 xX i i ex F λ--=1)(,0>x ,那么① )1)(1()()()(21211zzX X Z eez F z F z F λλ----==,0>z ,zzzZ Z eeez F z )(2121212111)()()(λλλλλλλλϕ+---+-+='=，0>z .⎩⎨⎧≤>+-+=+---.0 ,0,0 ,)( )()(212121211z z e e e z z z z Z λλλλλλλλϕ② zX X Z ez F z F z F )(212121)](1)][(1[1)(λλ+--=---=,0>z ,zZ Z ez F z )(212122)()()(λλλλϕ+-+='=，0>z .所以 ⎩⎨⎧≤>+=+-.0 ,0,0 ,)( )()(21212z z e z z Z λλλλϕ五、函数的独立性设m X X X ,,,21 独立，),,,(21kkn k k k X X X X =，)(k k k X f Y =，m k ,,2,1 =.则 m Y Y Y ,,,21 也独立.证明：121,,,B ∈∀m B B B ,有},,,{2211m m B Y B Y B Y P ∈∈∈)}(,),(),({121221111m m m B f X B f X B f X P ---∈∈∈= )}({)}({)}({121221111m m m B f X P B f X P B f X P ---∈∈∈=}{}{}{2211m m B Y P B Y P B Y P ∈∈∈=例8 设),(~2i i i N X σμ,m i ,,2,1 =独立,则),(~1211∑∑∑====mi i mi i mi iN XY σμ.例9 设),(~λi i r X Γ,m i ,,2,1 =独立, 则),(~11λ∑∑==Γ=mi i mi ir XY .例10 设X 与Y 独立，且)(),(y x Y X ϕϕ,),(y x ϕ均连续, 而)(),(~),(22y x q y x Y X +=ϕ,则X 与Y 均服从正态分布.引理:设)(x f 与)(y g )0,(≥y x 都连续不恒为0,且0,≥∀y x 恒有)()()(y x h y g x f +=,则xka x f =)(,0≥x ，此处a k ,是常数, 0>a .证明:①先证明0)0(≠f .反证.假设0)0(=f ，则0)(≡x h .)(y g 不恒为0,故00≥∃y ,使得0)(0≠y g ,,那么0)()()(00≡+=y g y x h x f ,这与)(x f 不恒为0矛盾,故0)0(≠f .同理可证0)0(≠g .② 由于)()()0()0()(x h x g f g x f ==,那么)()0()0()()0()()0()(x p g f x h g x g f x f ===, 于是)()0()0()()0()()0()()()(y x p g f y x h g y g f x f y p x p +=+==,0,≥y x . ③ 再证明 0)1(≠p .反证. 假设0)1(=p ⇒0)1()1(==⎥⎦⎤⎢⎣⎡p n p n⇒0)1(lim )0(==→∞n p p n .而1)0()0()0(==f f p ,故0)1(≠p .④ 因)()()(y x p y p x p +=,0,≥y x .则 x a x p =)(⇒x x ka a f x f ==)0()(.此处a k ,是常数,且 0)21()21()1(>==p p p a .例10证明: 因X 与Y 独立,则)(),()()(22y x q y x y x Y X +==ϕϕϕ.考虑在第一象限1D 中,令)()()(22x x x f X X ϕϕ==,)()()(22y y x g Y Y ϕϕ==, 显然都连续不恒为0,再令 )()(2222y x q y x h +=+,于是 )()()(2222y x h y g x f +=,因此2)()(2x X ka x f x ==ϕ,0)0()0()1(>=g f h a .由于σπσπσπϕσ222)(12222k dx ek dx a kdx x xx====⎰⎰⎰+∞∞--+∞∞-+∞∞-,有σπ21=k ,其中,因⎰+∞∞-dx a x2收敛,于是10<<a ,这样0ln 21>-=aσ.从而22221)(σσπϕxX ex -=，在其他三象限同样有此结果,于是),0(~2σN X .由对称性知道, ),0(~2σN Y .六、随机变量的变换)(~x X ϕ为S 上的n 维随机变量，)(x f y =为nn R R →的变换,)(x f y =在其定义域x D 上雅可比行列式0≠∂∂=xyJ ，y D 为其值域， 则)(x f y =有逆变换)(y h x =,)(X f Y =也是S 上的n 维随机变量，且1)]([)]([)(-=∂∂=Jy h yx y h y X X Y ϕϕϕ，y D y ∈. 证明：n y R ∈∀,有⎰≤=≤=yx f XY dx x y X f P y F )()(})({)(ϕ,0≠∂∂xy ,x D x ∈,故)(x f t =有逆变换)(t h x =,且0≠∂∂tx ，那么⎰⎰≤≤∂∂==yt X yx f X Y dt tx t h dx x y F )]([)()()(ϕϕ.又⎰≤=yt YY dt t y F )()(ϕ,故 yx y h y X Y ∂∂=)]([)(ϕϕ，y D y ∈.华东师大《数学分析(下)》例11 设),(~),(y x Y X ϕ，Y X Z +=,则 ⎰+∞∞--=dx x z x z Z ),()(ϕϕ.证明：令Y X Z +=,X W =,定义域和值域都是2R ,且雅可比行列式为10111-==∂∂∂∂∂∂∂∂=y w x w yzx z J , 而逆变换),(w z h 为W X =,W Z Y -=.这样),(W Z 的密度函数为),(),()],([),(11w z w y x J w z h w z -===-ϕϕϕϕ，于是⎰⎰+∞∞-+∞∞--=-=dx x z x dww z w z Z ),(),()(ϕϕϕ.。

随机变量函数分布随机变量函数分布是概率论中的重要概念，它描述了一个随机变量经过函数转换后的分布情况。

在实际问题中，我们常常需要通过随机变量的函数来描述某种现象的规律或特性。

本文将介绍随机变量函数分布的基本概念和常见的分布形式。

一、随机变量函数分布的定义随机变量函数分布指的是一个随机变量经过某种函数转换后的概率分布情况。

在数学上，对于一个随机变量X和一个函数Y=f(X)，我们可以描述函数Y的概率分布，也就是Y的取值在各个区间内的概率。

通常情况下，我们可以通过概率密度函数或累积分布函数来描述随机变量函数分布。

二、常见的随机变量函数分布形式1. 线性变换最简单的随机变量函数分布形式就是线性变换。

设X是一个随机变量，Y=aX+b是X的线性变换，其中a和b为常数。

如果知道X的分布情况，就可以通过线性变换得到Y的分布。

具体地，如果X服从均匀分布，则Y也会服从均匀分布。

2. 指数变换指数变换是常用的随机变量函数形式之一。

如果X服从指数分布，经过指数变换Y=e^X后，Y会服从对数正态分布。

指数变换在描述某些事件的时间间隔时非常有用，比如描述两次地震事件之间的时间间隔。

3. 幂变换幂变换是一种常见的函数形式，如果X服从正态分布，Y=X^2后，Y会服从卡方分布。

幂变换在统计学中的应用非常广泛，比如方差分析和回归分析中就经常用到幂变换来处理数据。

三、实际应用举例在实际问题中，随机变量函数分布具有广泛的应用。

比如在金融领域中，可以通过随机变量函数分布来描述股票价格的涨跌情况，进而进行风险管理和投资决策。

在生物学领域中，可以通过随机变量函数分布来描述基因的变异情况，进而研究遗传特性。

总的来说，随机变量函数分布是概率论中一个重要的概念，它通过函数转换描述了随机变量的特性和规律。

通过研究随机变量函数分布，我们可以更好地理解现实世界中复杂的随机变量关系，从而进行更加精确的建模和分析。

人工智能的数学基础】随机变量的变量替换定理下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!人工智能的数学基础：随机变量的变量替换定理引言人工智能领域涉及广泛的数学概念和技术，其中概率论和数理统计是其重要的数学基础之一。

逆变换法求随机变量的原理
逆变换法求随机变量的基本原理是:
1. 对给定的随机变量X,先求出其分布函数或特征函数。

2. 根据X的分布函数或特征函数,确定一个中间变量Y,使Y满足已知的一些标准分布,如标准正态分布。

3. 利用分布函数或特征函数的可逆性,建立随机变量X和中间变量Y之间的一一对应关系。

4. 将关于Y的分布函数或特征函数表达成关于X的形式。

5. 最终得到随机变量X的分布律。

6. 逆变换法主要用于求解变量转化后的分布,特别是确定难以直接求得的分布。

7. 常用的逆变换方法有Box-Cox变换、幂变换等。

8. 逆变换法需要运用分布函数或特征函数的基本理论知识。

9. 应用复杂,但可以推导出许多不规则分布的精确分布。

10. 需要仔细推导求解过程,正确运用相关公式。

综上所述,这就是逆变换法求随机变量分布的一般思路和原理。

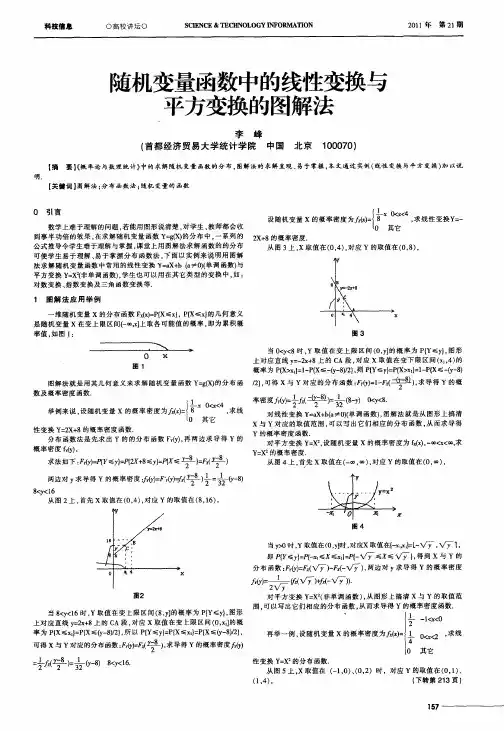
随机变量函数中的线性变换与平方变换的图解法
线性变换与平方变换是随机变量函数的一类变换，它用于描述实验中观察到的随机变量之间的关系。

本文主要介绍线性变换与平方变换的图解法，并讨论它们之间的区别和特点。

线性变换是指把一个随机变量变换成另一个同样可以表示为一组常数乘以原来随机变量的新的随机变量的变换。

它的图解法可以用四象限散点绘图来表示，如图1所示，以一个变
量Y为横轴，另一个变量X为纵轴，变换前原变量X和Y在图中表示为正方形，变换后
新变量X'和Y'形成直线，其斜率可以由图中给出，公式可表示为：Y'/X' = kY/X。

图1 线性变换的图解法
平方变换是把一个随机变量X变换为X^2的随机变量Y的变换，它的图解法可以用交叉
散点图来表示，如图2所示，以一个变量X为横轴，另一个变量Y为纵轴，表示X^2 = Y，公式可表示为Y = X^2。

综上所述，线性变换与平方变换的图解法有所不同。

前者是从一个正方形变成一条斜率，而后者是从一个点变成一条曲线。

同时，它们都是研究随机变量之间联系，表现出不同随
机变量之间的内在联系的一种变换方式。

概率论变量变换法概率论变量变换法是一种求解随机变量函数的分布的方法，它利用随机变量之间的函数关系，通过积分或者求和的方式，得到新的随机变量的概率分布。

概率论变量变换法有两种常见的形式：一元变换和多元变换。

一元变换是指已知一个随机变量X的分布，求另一个随机变量Y=f(X)的分布。

一元变换的方法有两种：累积分布函数法和密度函数法。

累积分布函数法是利用Y=f(X)的累积分布函数F_Y(y)等于F_X(f^{-1}(y))或者1-F_X(f^{-1}(y))，根据X的累积分布函数F_X(x)求出F_Y(y)，然后求导得到Y 的密度函数f_Y(y)。

密度函数法是利用Y=f(X)的密度函数f_Y(y)等于f_X(f^{-1}(y))乘以f^{-1}(y)对y的导数的绝对值，根据X的密度函数f_X(x)求出f_Y(y)。

一元变换的例子有指数分布、正态分布、卡方分布、t分布等。

多元变换是指已知n个随机变量X_1,X_2,...,X_n的联合分布，求另外m个随机变量Y_1,Y_2,...,Y_m=g(X_1,X_2,...,X_n)的联合分布。

多元变换的方法有两种：雅可比行列式法和矩母函数法。

雅可比行列式法是利用(Y_1,Y_2,...,Y_m)和(X_1,X_2,...,X_n)之间的雅可比行列式J=\frac{\partial(Y_1,Y_2,...,Y_m)}{\partial(X_1,X_2 ,...,X_n)}，根据(X_1,X_2,...,X_n)的联合密度函数f_{X_1,X_2,...,X_n}(x_1,x_2,...,x_n)求出(Y_1,Y_2,...,Y_m)的联合密度函数f_{Y_1,Y_2,...,Y_m}(y_1,y_2,...,y_m)，其中f_{Y_1,Y_2,...,Y_m}(y_1,y_2,...,y_m)=f_{X_1,X_2,... ,X_n}(g^{-1}(y_1,y_2,...,y_m))|J|。