平面向量高考经典试题教学内容

专题12 平面向量文考纲解读明方向分析解读 1.从“方向”与“大小”两个方面理解平面向量的概念.2.结合图形理解向量的线性运算,熟练掌握平行四边形法则与三角形法则.3.向量共线的条件要结合向量数乘的意义去理解,并能灵活应用.4.向量的概念与运算是必考内容.5.本节在高考中主要考查平面向量的线性运算及其几何意义,分值约为5分,属中低档题.分析解读 1.理解平面向量基本定理的实质,理解基底的概念,会用给定的基底表示向量.2.掌握求向量坐标的方法,掌握平面向量的坐标运算.3.能够根据平面向量的坐标运算解决向量的共线、解三角形等有关问题.4.用坐标表示的平面向量共线的条件是高考考查的重点,分值约为5分,属中低档题.两向量垂直及分析解读 1.理解数量积的定义、几何意义及其应用.2.掌握向量数量积的性质及运算律;掌握求向量长度的方法.3.会用向量数量积的运算求向量夹角,判断或证明向量垂直.4.利用数形结合的方法和函数的思想解决最值等综合问题.2018年高考全景展示1．【2018年浙江卷】已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量b满足b2−4e·b+3=0，则|a−b|的最小值是A. −1B. +1C. 2D. 2−【答案】A【解析】分析:先确定向量所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值.点睛：以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.2．【2018年天津卷文】在如图的平面图形中，已知,则的值为A. B. C. D. 0【答案】C【解析】分析：连结MN，结合几何性质和平面向量的运算法则整理计算即可求得最终结果.详解：如图所示，连结MN，由可知点分别为线段上靠近点的三等分点，则，由题意可知：，，结合数量积的运算法则可得：.本题选择C选项.点睛：求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．3．【2018年文北京卷】设向量a=（1,0），b=（−1,m）,若，则m=_________.【答案】点睛：此题考查向量的运算，在解决向量基础题时，常常用到以下：设，则①；②.4．【2018年江苏卷】在平面直角坐标系中，A为直线上在第一象限内的点，，以AB为直径的圆C与直线l交于另一点D．若，则点A的横坐标为________．【答案】3【解析】分析：先根据条件确定圆方程，再利用方程组解出交点坐标，最后根据平面向量的数量积求结果.点睛：以向量为载体求相关变量的取值或范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程或解不等式或求函数值域，是解决这类问题的一般方法.2017年高考全景展示1.【2017北京，文7】设m , n 为非零向量，则“存在负数λ，使得m =λn ”是“m ·n <0”的 （A ）充分而不必要条件 （B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件【答案】A 【解析】试题分析：若0λ∃<，使m n λ=，即两向量反向，夹角是0180，那么0cos1800m n m n m n ⋅==-<T ，若0m n ⋅<，那么两向量的夹角为(0090,180⎤⎦ ，并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分不必要条件，故选A. 【考点】1.向量；2.充分必要条件.【名师点睛】判断充分必要条件的的方法：1.根据定义，若,p q q p ⇒≠>，那么p 是q 的充分不必要 ，同时q 是p 的必要不充分条件，若p q ⇔，那互为充要条件，若p q <≠>，那就是既不充分也不必要条件，2.当命题是以集合形式给出时，那就看包含关系，若:,:p x A q x B ∈∈,若A B ≠⊂，那么p 是q 的充分必要条件，同时q 是p 的必要不充分条件，若A B =，互为充要条件，若没有包含关系，就是既不充分也不必要条件，3.命题的等价性，根据互为逆否命题的两个命题等价，将p 是q 条件的判断，转化为q ⌝是p ⌝条件的判断.2.【2017课标II ，文4】设非零向量a ，b 满足+=-b b a a 则 A.a ⊥b B. =b a C. a ∥b D. >b a 【答案】A【考点】向量数量积 【名师点睛】(1)向量平行：1221//a b x y x y ⇒=，//,0,a b b a b λλ≠⇒∃∈=R ,111BA AC OA OB OC λλλλ=⇔=+++ (2)向量垂直：121200a b a b x x y y ⊥⇔⋅=⇔+=，(3)向量加减乘： 221212(,),||,||||cos ,a b x x y y a a a b a b a b ±=±±=⋅=⋅<>3.【2017浙江，10】如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC ＝AD ＝2，CD ＝3，AC 与BD 交于点O ，记1·I OAOB ＝，2·I OB OC ＝，3·I OC OD ＝，则A ．321I I I <<B ．231I I I <<C ．213I I I <<D ．312I I I <<【答案】C 【解析】试题分析：因为90AOB COD ∠=∠>，所以0(,)OB OC OA OB OC OD OA OC OB OD ⋅>>⋅>⋅<< 选C ．【考点】 平面向量数量积运算【名师点睛】平面向量的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用． 利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．列出方程组求解未知数．本题通过所给条件结合数量积运算，易得90AOB COD ∠=∠>，由AB ＝BC ＝AD ＝2，CD ＝3，可求OC OA <，OD OB <，进而解得213I I I <<． 4.【2017山东，文11】已知向量a =（2,6）,b =(1,)λ- ,若a ||b ,则λ= . 【答案】3- 【解析】【考点】向量共线与向量的坐标运算【名师点睛】平面向量共线的坐标表示问题的常见类型及解题策略(1)利用两向量共线求参数．如果已知两向量共线,求某些参数的取值时,利用“若a ＝(x 1,y 1),b ＝(x 2,y 2),则a ∥b 的充要条件是x 1y 2＝x 2y 1”解题比较方便．(2)利用两向量共线的条件求向量坐标．一般地,在求与一个已知向量a 共线的向量时,可设所求向量为λa (λ∈R ),然后结合其他条件列出关于λ的方程,求出λ的值后代入λa 即可得到所求的向量． (3)三点共线问题．A ,B ,C 三点共线等价于AB →与AC →共线.5.【2017北京，文12】已知点P 在圆22=1x y +上，点A 的坐标为(-2,0)，O 为原点，则AO AP ⋅的最大值为_________． 【答案】6 【解析】试题分析：||||cos ||||2(21) 6.AO AP AO AP AO AP θ⋅=⋅≤⋅≤⨯+=所以最大值是6. 【考点】1.向量数量积；2.向量与平面几何【名师点睛】本题考查了转化与化归能力，因为AO 是确定的，所以根据向量数量积的几何意义若AO AP ⋅最大，即向量AP 在AO 方向上的投影 最大，根据数形结合分析可得当点P 在圆与x 轴的右侧交点处时最大，根据几何意义直接得到运算结果236⨯=.6.【2017课标3，文13】已知向量(2,3),(3,)a b m =-=，且a b ⊥，则m = . 【答案】2【解析】由题意可得：2330,2m m -⨯+=∴=.【考点】向量数量积【名师点睛】(1)向量平行：1221//a b x y x y ⇒=，//,0,a b b a b λλ≠⇒∃∈=R ,111BA AC OA OB OC λλλλ=⇔=+++ (2)向量垂直：121200a b a b x x y y ⊥⇔⋅=⇔+=，(3)向量加减乘： 221212(,),||,||||cos ,a b x x y y a a a b a b a b ±=±±=⋅=⋅<>7.【2017浙江，14】已知向量a ，b 满足1,2,==a b 则++-a b a b 的最小值是________，最大值是_______．【答案】4，【解析】【考点】平面向量模长运算【名师点睛】本题通过设入向量,a b 的夹角θ，结合模长公式， 解得5c o sa b a b ++-=+转化能力和最值处理能力有一定的要求．8.【2017天津，文14】在△ABC 中，60A ∠=︒，AB =3，AC =2.若2BD DC =，AE AC AB λ=-（λ∈R ），且4AD AE ⋅=-，则λ的值为 .【答案】 311【解析】【考点】1.平面向量基本定理；2.向量数量积.【名师点睛】平面向量问题中，向量的线性运算和数量积是高频考点，当出现线性运算问题时，向要选好基底向量，如本题就要灵活使用向量,AB AC ，要注意结合图形的性质，灵活运用向量的运算解决问题，当涉及到向量数量积时，要记熟向量数量积的公式、坐标公式、几何意义等.9.【2017课标1，文13】已知向量a =（–1，2），b =（m ，1）．若向量a +b 与a 垂直，则m =________． 【答案】7 【解析】试题分析：由题得(1,3)a b m +=-，因为()0a b a +⋅=，所以(1)230m --+⨯=，解得7m = 【考点】平面向量的坐标运算 ，垂直向量【名师点睛】如果a ＝(x 1，y 1)，b ＝(x 2，y 2)(b ≠0)，则a ⊥b 的充要条件是x 1x 2+y 1y 2＝0．10.【2017江苏，12】如图,在同一个平面内，向量OA ,OB ,OC 的模分别为OA 与OC 的夹角为α,且tan α=7,OB 与OC 的夹角为45°.若OC mOA nOB =+(,)m n ∈R , 则m n += ▲.【答案】3【解析】由tan 7α=可得sin 10α=，cos 10α=，根据向量的分解，易得cos 45cos sin 45sin 0n m n m αα⎧︒+=⎪⎨︒-=⎪⎩0210m n m =⎪-=⎪⎩，即510570n m n m +=⎧⎨-=⎩，即得57,44m n ==，所以3m n +=. 【考点】向量表示【名师点睛】(1)向量的坐标运算将向量与代数有机结合起来，这就为向量和函数、方程、不等式的结合提供了前提，运用向量的有关知识可以解决某些函数、方程、不等式问题.(2)以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解不等式或求函数值域，是解决这类问题的一般方法.(3)向量的两个作用：①载体作用：关键是利用向量的意义、作用脱去“向量外衣”，转化为我们熟悉的数学问题；②工具作用：利用向量可解决一些垂直、平行、夹角与距离问题.11.【2017江苏，16】 已知向量(cos ,sin ),(3,[0,π].x x x ==∈a b （1）若a ∥b ,求x 的值；（2）记()f x =⋅a b ,求()f x 的最大值和最小值以及对应的x 的值.【答案】（1）5π6x =（2）0x =时，取得最大值，为3； 5π6x =时，取得最小值，为-.【考点】向量共线，数量积【名师点睛】(1)向量平行：1221//a b x y x y ⇒=，//,0,a b b a b λλ≠⇒∃∈=R ,111BA AC OA OB OC λλλλ=⇔=+++ (2)向量垂直：121200a b a b x x y y ⊥⇔⋅=⇔+=，(3)向量加减乘： 221212(,),||,||||cos ,a b x x y y a a a b a b a b ±=±±=⋅=⋅<>2016年高考全景展示1.[2016高考新课标Ⅲ文数]已知向量1(2BA =uu v ,1),2BC =uu u v 则ABC ∠=（ ）(A)300(B) 450(C) 600(D)1200【答案】A 【解析】考点：向量夹角公式．【思维拓展】（1）平面向量a 与b 的数量积为·cos a b a b θ＝，其中θ是a 与b 的夹角，要注意夹角的定义和它的取值范围：0180θ︒≤≤︒；（2）由向量的数量积的性质有||=a a a ·，·cos a b a bθ=， ·0a b a b ⇔⊥＝，因此，利用平面向量的数量积可以解决与长度、角度、垂直等有关的问题．2.【2016高考天津文数】已知△ABC 是边长为1的等边三角形，点E D ,分别是边BC AB ,的中点，连接DE 并延长到点F ，使得EF DE 2=，则⋅的值为（ ） （A ）85- （B ）81 （C ）41 （D ）811【答案】B 【解析】试题分析：设BA a =，BC b =，∴11()22DE AC b a ==-，33()24DF DE b a ==-， 1353()2444AF AD DF a b a a b =+=-+-=-+，∴25353144848AF BC a b b ⋅=-⋅+=-+=，故选B.考点：向量数量积【名师点睛】研究向量数量积，一般有两个思路，一是建立直角坐标系，利用坐标研究向量数量积；二是利用一组基底表示所有向量，两种实质相同，坐标法更易理解和化简. 平面向量的坐标运算的引入为向量提供了新的语言——“坐标语言”，实质是“形”化为“数”．向量的坐标运算，使得向量的线性运算都可用坐标来进行，实现了向量运算完全代数化，将数与形紧密结合起来．3.【2016高考四川文科】已知正三角形ABC 的边长为32，平面ABC 内的动点P ，M 满足1AP =uu u r ，PM MC =uuu r uuu r，则2BM uuu r 的最大值是( )(A)443 (B) 449 (C) 43637+ (D) 433237+【答案】B 【解析】考点：1.向量的数量积运算；2.向量的夹角；3.解析几何中与圆有关的最值问题.【名师点睛】本题考查平面向量的数量积与向量的模，由于结论是要求向量模的平方的最大值，因此我们要把它用一个参数表示出来，解题时首先对条件进行化简变形，本题中得出120ADC ADB BDC ∠=∠=∠=︒，且2DA DB DC ===，因此我们采用解析法，即建立直角坐标系，写出,,,A B C D 坐标，同时动点P的轨迹是圆，()(22214x y BM +++=，因此可用圆的性质得出最值．因此本题又考查了数形结合的数学思想．4.【2016高考新课标2文数】已知向量a =(m ,4)，b =(3,-2)，且a ∥b ，则m =___________.【答案】6- 【解析】考点：平面向量的坐标运算 ，平行向量.【名师点睛】如果a ＝(x 1，y 1)，b ＝(x 2，y 2)(b ≠0)，则a ∥b 的充要条件是x 1y 2－x 2y 1＝0.5.【2016高考北京文数】已知向量=a b ，则a 与b 夹角的大小为_________. 【答案】30【解析】试题分析：两向量夹角为603030.-=23cos ,222a b a b a b⋅<>===⋅⋅，且两个向量夹角范围是[]0,π，所以夹角为30，故填：30. 考点：平面向量数量积【名师点睛】由向量数量积的定义θcos ||||⋅⋅=⋅(θ为，的夹角)可知，数量积的值、模的乘积、夹角知二可求一，再考虑到数量积还可以用坐标表示，因此又可以借助坐标进行运算.当然，无论怎样变化，其本质都是对数量积定义的考查.求解夹角与模的题目在近年高考中出现的频率很高，应熟练掌握其解法. 6.【2016高考新课标1文数】设向量a =(x ,x +1),b =(1,2),且a ⊥b ,则x = .【答案】23- 【解析】试题分析：由题意, 20,2(1)0,.3x x x ⋅=++=∴=-a b 考点：向量的数量积及坐标运算【名师点睛】全国卷中向量大多以客观题形式出现,属于基础题.解决此类问题既要准确记忆公式,又要注意运算的准确性.本题所用到的主要公式是：若()()1122,,,x y x y ==a b ,则1122x y x y ⋅=+a b .7.【2016高考浙江文数】已知平面向量a ，b ，|a |=1，|b |=2，a ·b =1．若e 为平面单位向量，则|a ·e |+|b ·e |的最大值是______．【解析】考点：平面向量的数量积和模.【思路点睛】先设a ，b 和e 的坐标，再将转化为三角函数，进而用辅助角公式将三角函数进行化简，最后用三角函数的性质可得三角函数的最大值，进而可得a e b e ⋅+⋅的最大值．8.【2016高考山东文数】已知向量1,-()()16,-4a b ==，．若()a tab ⊥+，则实数t 的值为________． 【答案】5- 【解析】 试题分析：()()()()6,4,6,41,12100ta b t t ta b a t t t +=+--+⋅=+--⋅-=+=，解得5t =-考点：平面向量的数量积【名师点睛】本题主要考查平面向量的数量积、平面向量的坐标运算.解答本题，关键在于能从()a tab ⊥+出发，转化成为平面向量的数量积的计算.本题能较好的考查考生转化与化归思想、基本运算能力等.。

原创精品资源学科网独家享有版权，侵权必究！
1
（九）平面向量
1．平面向量的实际背景及基本概念
（1）了解向量的实际背景.
（2）理解平面向量的概念，理解两个向量相等的含义.
（3）理解向量的几何表示.
2．向量的线性运算
（1）掌握向量加法、减法的运算，并理解其几何意义.
（2）掌握向量数乘的运算及其几何意义，理解两个向量共线的含义.
（3）了解向量线性运算的性质及其几何意义.
3．平面向量的基本定理及坐标表示
（1）了解平面向量的基本定理及其意义.
（2）掌握平面向量的正交分解及其坐标表示.
（3）会用坐标表示平面向量的加法、减法与数乘运算.
（4）理解用坐标表示的平面向量共线的条件.
4．平面向量的数量积
（1）理解平面向量数量积的含义及其物理意义.
（2）了解平面向量的数量积与向量投影的关系.
（3）掌握数量积的坐标表达式，会进行平面向量数量积的运算.
（4）能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系.
5．向量的应用
（1）会用向量方法解决某些简单的平面几何问题.
（2）会用向量方法解决简单的力学问题与其他一些实际问题.。

【最新】《平面向量》专题一、选择题1．如图所示，ABC ∆中，点D 是线段BC 的中点，E 是线段AD 的靠近A 的三等分点，则AC =u u u v（ ）A ．43AD BE +u u uv u u u vB ．53AD BE +u u uv u u u vC ．4132AD BE +u u uv u u u vD ．5132AD BE +u u uv u u u v【答案】B 【解析】 【分析】利用向量的加减运算求解即可 【详解】 据题意，2533AC DC DA BD AD BE ED AD BE AD AD AD BE =-=+=++=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r．故选B ． 【点睛】本题考查向量加法、减法以及向量的数乘运算，是基础题2．已知菱形ABCD 的边长为2，60ABC ∠=︒，则BD CD ⋅=u u u v u u u v（）A ．4B ．6C ．23D ．43【答案】B 【解析】 【分析】根据菱形中的边角关系，利用余弦定理和数量积公式，即可求出结果． 【详解】 如图所示，菱形形ABCD 的边长为2，60ABC ∠=︒，∴120C ∠=︒，∴22222222cos12012BD =+-⨯⨯⨯︒=， ∴23BD =，且30BDC ∠=︒，∴|||3 302|326BD CD BD CD cos =⨯⨯︒=⨯⨯=⋅u u u r u u u r u u u r u u u r ，故选B ． 【点睛】本题主要考查了平面向量的数量积和余弦定理的应用问题，属于基础题.．3．在平面直角坐标系中，()1,2A -，(),1B a -，(),0C b -，,a b ∈R ．当,,A B C 三点共线时，AB BC ⋅u u u r u u u r的最小值是（ ）A ．0B ．1C ．2D ．2【答案】B 【解析】 【分析】根据向量共线的坐标表示可求得12b a =-，根据数量积的坐标运算可知所求数量积为()211a -+，由二次函数性质可得结果.【详解】由题意得：()1,1AB a =-u u u r ，(),1BC b a =--u u u r，,,A B C Q 三点共线，()()111a b a ∴⨯-=⨯--，即12b a =-，()1,1BC a ∴=-u u u r， ()2111AB BC a ∴⋅=-+≥u u u r u u u r ，即AB BC ⋅u u u r u u u r 的最小值为1.故选：B . 【点睛】本题考查平面向量的坐标运算，涉及到向量共线的坐标表示和数量积的坐标运算形式，属于基础题.4．如图，在直角梯形ABCD 中，AB ∥DC ，AD ⊥DC ，AD ＝DC ＝2AB ，E 为AD 的中点，若(,)CA CE DB R λμλμ=+∈u u u r u u u r u u u r，则λ＋μ的值为（ ）A ．65B ．85C ．2D ．83【答案】B 【解析】【分析】建立平面直角坐标系，用坐标表示,,CA CE DB u u u r u u u r u u u r ，利用(,)CA CE DB R λμλμ=+∈u u u r u u u r u u u r，列出方程组求解即可. 【详解】建立如图所示的平面直角坐标系，则D (0，0).不妨设AB ＝1，则CD ＝AD ＝2，所以C (2，0)，A (0，2)，B (1，2)，E (0，1)，(2,2),(2,1),(1,2)CA CE DB ∴=-=-=u u u r u u u r u u u rCA CE DB λμ=+u u u r u u u r u u u r Q∴(－2，2)＝λ(－2，1)＋μ(1，2)，2222λμλμ-+=-⎧∴⎨+=⎩解得6525λμ⎧=⎪⎪⎨⎪=⎪⎩则85λμ+=.故选：B 【点睛】本题主要考查了由平面向量线性运算的结果求参数，属于中档题.5．如图，圆O 是等边三角形ABC 的外接圆，点D 为劣弧AC 的中点，则OD =u u u r（ ）A ．2133BA AC +u uu r u u u rB ．2133BA AC -u uu r u u u rC ．1233BA AC +u uu r u u u rD ．4233BA AC +u uu r u u u r【答案】A 【解析】 【分析】连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，列出相应式子得出结论. 【详解】解：连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，则()()221121332333OD BO BE BA BC BA BA AC BA AC ===⨯+=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u uu r u u u r . 故选：A.【点睛】本题考查向量的表示方法，结合几何特点，考查分析能力，属于中档题.6．已知A ，B ，C 是抛物线24y x =上不同的三点，且//AB y 轴，90ACB ∠=︒，点C 在AB 边上的射影为D ，则CD =（ ） A ．4 B ．22C ．2D ．2【答案】A 【解析】 【分析】画出图像，设222112112,,,,,444y y y A y B y C y ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，12y y >， 由90ACB ∠=︒可求221216y y -=，结合221244y y CD =-即可求解 【详解】如图：设222112112,,,,,444y y y A y B y C y ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，12y y >， 由90ACB ∠=︒可得0CA CB ⋅=u u u r u u u r ，222212121212,,,44y y y y CA y y CB y y ⎛⎫⎛⎫--=-=-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r ，()222221212004y y CA CB y y ⎛⎫-⋅=⇔--= ⎪⎝⎭u u u r u u u r ，即()()222122212016y y y y ---= 解得221216y y -=（0舍去），所以222212124444y y y y CD -=-==故选：A 【点睛】本题考查抛物线的几何性质与向量的综合应用，计算能力，逻辑推理能力，属于中档题7．已知5MN a b =+u u u u r r r ，28NP a b =-+u u u r r r ，3()PQ a b =-u u u r r r ，则（ ）A ．,,M N P 三点共线B ．,,M N Q 三点共线C ．,,N P Q 三点共线D ．,,M P Q 三点共线【答案】B 【解析】 【分析】利用平面向量共线定理进行判断即可. 【详解】因为28NP a b =-+u u u r r r ,3()PQ a b =-u u u r r r所以()2835NQ NP PQ a b a b a b =+=-++-=+u u u r u u u r u u u r r r r r r r ,因为5MN a b =+u u u u r rr ,所以MN NQ =u u u u r u u u r由平面向量共线定理可知,MN u u u u r 与NQ uuur 为共线向量,又因为MN u u u u r 与NQ uuur 有公共点N ,所以,,M N Q 三点共线.故选: B 【点睛】本题考查利用平面向量共线定理判断三点共线;熟练掌握共线定理的内容是求解本题的关键;属于中档题、常考题型.8．已知菱形ABCD 的边长为4，60ABC ∠=︒，E 是BC 的中点2DF AF =-u u u r u u u r，则AE BF ⋅=u u u r u u u r（ ）A ．24B ．7-C ．10-D ．12-【答案】D 【解析】 【分析】根据平面向量的基本定理,将AE BF ⋅u u u r u u u r用基底,AB AD u u u r u u u r 表达,再根据平面向量的数量积公式求解即可. 【详解】由已知得13AF AD =u u u r u u u r ,12BE BC =u u u r u u u r ,AD BC =u u u r u u u r,所以1122AE AB BC AB AD =+=+u u u r u u u r u u u r u u u r u u u r ,13BF AF AB AD AB =-=-u u ur u u u r u u u r u u u r u u u r .因为在菱形ABCD 中,60ABC ∠=︒,所以120BAD ∠=︒.又因为菱形ABCD 的边长为4,所以1||||cos1204482AB AD AB AD ⎛⎫⋅=⋅︒=⨯⨯-=- ⎪⎝⎭u u u r u u u r u u u r u u u r ,所以1123AE BF AB AD AB AD ⎛⎫⎛⎫⋅=+⋅-+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r221111||||16(8)16126666AB AB AD AD --⋅+=--⨯-+⨯=-u u u r u u u r u u u r u u u r .故选：D 【点睛】本题考查平面向量的线性运算及向量的数量积,考查推理论证能力以及数形结合思想.9．已知P 为边长为2的正方形ABCD 所在平面内一点，则PC uuu r ()PB PD +⋅u u ur u u u r 的最小值为（ ） A ．1- B ．3-C ．12-D ．32-【答案】A 【解析】 【分析】建立坐标系，写出各点坐标，表示出对应的向量坐标，代入数量积整理后即可求解． 【详解】建立如图所示坐标系，设(,)P x y ，则(0,0),(2,0),(2,2),(0,2)A B C D ，所以(2,2),(2,)(,2)(22,22)PC x y PB PD x y x y x y =--+=--+--=--u u u r u u u r u u u r，故223131()(2)(22)(2)(22)222222PC PB PD x x y y x y ⎛⎫⎛⎫⋅+=--+--=--+-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r223322122x y ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭所以当32x y ==时，PC uuu r ()PB PD +⋅u u u r u u u r 的最小值为1-.故选：A ． 【点睛】本题考查利用坐标法求向量数量积的最值问题，涉及到向量的坐标运算，考查学生的运算求解能力，是一道中档题.10．如图，已知1OA OB ==u u u v u u u v ，2OC =u u u v ，4tan 3AOB ∠=-，45BOC ∠=︒，OC mOA nOBu u u v u u u v u u u v =+，则mn等于（ ）A ．57B ．75C ．37D ．73【答案】A 【解析】 【分析】依题意建立直角坐标系，根据已知角，可得点B 、C 的坐标，利用向量相等建立关于m 、n 的方程，求解即可． 【详解】以OA 所在的直线为x 轴，过O 作与OA 垂直的直线为y 轴，建立直角坐标系如图所示：因为1OA OB ==u u u r u u u r ，且4tan 3AOB ∠=-，∴34cos sin 55AOB AOB ∠=-∠=，，∴A （1，0），B （3455-，），又令θAOC ∠=，则θ=AOB BOC ∠-∠，∴413tan θ413--=-=7，又如图点C 在∠AOB 内，∴cos θ=10，sin θ=10,又OC u u u v =C （1755，）， ∵OC mOA nOB =+u u u r u u u r u u u r ，（m ，n ∈R ），∴（1755，）=（m,0）+（3455n n -，）=(m 35n -，45n ） 即15= m 35n -，7455n =，解得n=74，m=54，∴57m n =， 故选A ． 【点睛】本题考查了向量的坐标运算，建立直角坐标系，利用坐标解决问题是常用的处理向量运算的方法，涉及到三角函数的求值，属于中档题．11．在ABC V 中，D 、P 分别为BC 、AD 的中点，且BP AB AC λμ=+u u u r u u u r u u u r，则λμ+=（ ） A ．13- B ．13C ．12-D ．12【答案】C 【解析】 【分析】由向量的加减法运算，求得BP BD DP BD PD =+=-u u u r u u u r u u u r u u u r u u u r，进而得出()()22BP AB AC BD PD λμμλλμ=+=-++u u u r u u u r u u u r u u u r u u u r，列式分别求出λ和μ，即可求得λμ+.【详解】解：已知D 、P 分别为BC 、AD 的中点， 由向量的加减法运算， 得BP BD DP BD PD =+=-u u u r u u u r u u u r u u u r u u u r，2AB AD DB BD PD =+=-+u u u r u u u r u u u r u u u r u u u r ， 2AC AD DC BD PD =+=+u u u r u u u r u u u r u u u r u u u r ，又()()22BP AB AC BD PD λμμλλμ=+=-++u u u r u u u r u u u r u u u r u u u r Q ，则1221μλλμ-=⎧⎨+=-⎩，则12λμ+=-. 故选：C.【点睛】本题考查平面向量的加减法运算以及向量的基本定理的应用.12．已知椭圆2222:1(0)x y T a b a b +=>>的离心率为32，过右焦点F 且斜率为()0k k >的直线与T 相交于A ，B 两点，若3AF FB =uu u r uu r，则k =（ ）A ．2B 3C 2D ．1【答案】C 【解析】 【分析】由32e =可得3a =，3b =，可设椭圆的方程为222334x y c +=，()()1122,,,A x y B x y ，并不妨设B 在x 轴上方，由3AF FB =uu u r uu r得到12123430x x c y y +=⎧⎨+=⎩，再由22211334x y c +=，22222334x y c +=得到A 、B 两点的坐标，利用两点的斜率公式计算即可. 【详解】因为2231c b e a a ==-=，所以2a b =，所以3a =，3b =，则椭圆方程22221x y a b+=变为222334x y c +=. 设()()1122,,,A x y B x y ，不妨设B 在x 轴上方，则210,0y y ><，又3AF FB =uu u r uu r，所以()()1122,3,c x y x c y --=-，所以()121233c x x c y y ⎧-=-⎨-=⎩，12123430x x cy y +=⎧⎨+=⎩因为A ，B 在椭圆上，所以22211334x y c +=，①22222334x y c +=②. 由①—9×②，得2121212123(3)(3)3(3)(3)84x x x x y y y y c +-++-=-，所以21234(3)84c x x c ⨯-=-，所以12833x x c -=-， 所以123x c =，2109x c =，从而1y =，2y =所以2(,)33A c -，10(,)99B c c，故9102393k c c +==- 故选：C. 【点睛】本题考查直线与椭圆的位置关系，当然本题也可以利用根与系数的关系来解决，考查学生的数学运算求解能力，是一道中档题.13．已知向量(b =r ，向量a r 在b r方向上的投影为6-，若()a b b λ+⊥r r r ，则实数λ的值为（ ） A ．13B ．13-C ．23D ．3【答案】A 【解析】 【分析】设(),a x y =r，转化条件得62x +=-，()4x λ=-，整体代换即可得解.【详解】 设(),a x y =r，Q a r 在b r方向上的投影为6-，∴6a b b⋅==-r rr即12x +=-. 又 ()a b b λ+⊥r r r，∴()0a b b λ+⋅=r r r即130x y λ++=，∴()4x λ+=-即124λ-=-，解得13λ=. 故选：A. 【点睛】本题考查了向量数量积的应用，属于中档题.14．已知平面向量,,a b c r r r 满足()()2,21a b a b a c b c ==⋅=-⋅-=r r r r r r r r ，则b c -r r 的最小值为（ ）A B C ．2-D ．12【答案】A【解析】【分析】根据题意，易知a r 与b r 的夹角为60︒，设(=1a r ，()20b =，r ，(),c x y =r ，由()()21a c b c -⋅-=r r r r ，可得221202x y x +-+=，所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值， 利用圆心和点()20，的距离与半径的差，即可求出结果.【详解】因为2a b a b ==⋅=r r r r ，所以a r 与b r 的夹角为60︒，设(=1a r ，()20b =，r ，(),c x y =r ，因为()()21a c b c -⋅-=r r r r ，所以221202x y x +-+=，又b c -=r r所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值，又圆221202x y x +-+=的圆心坐标为1⎛ ⎝⎭，所以点()20，与圆221202x y x +-+=上一动点距离的最小值为=. 故选：A.【点睛】本题考查向量的模的最值的求法，考查向量的数量积的坐标表示，考查学生的转换思想和运算能力，属于中档题．15．在ABC V 中，D 为边AC 上的点，若2133BD BA BC =+u u u r u u u r u u u r ，AD DC λ=u u u v u u u v ，则λ=（ ）A ．13B ．12C ．3D ．2【答案】B【解析】【分析】 根据2133BD BA BC =+u u u v u u u v u u u v ，将,AD DC u u u r u u u r 都用基底()BA BC u u u r u u u r ，表示，再根据AD DC λ=u u u v u u u v 求解. 【详解】 因为2133BD BA BC =+u u u v u u u v u u u v ， 所以1122,+3333AD BD BA BA BC DC BC BD BA BC =-=-+=-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ， 因为AD DC λ=u u u v u u u v ， 所以λ=12， 故选：B【点睛】 本题主要考查平面向量的基本定理和共线向量定理，还考查运算求解的能力，属于中档题. 16．已知向量(sin ,cos )a αα=r ，(1,2)b =r ，则以下说法不正确的是（ ）A ．若//a b r r ，则1tan 2α=B ．若a b ⊥r r ，则1tan 2α=C ．若()f a b α=⋅r r 取得最大值，则1tan 2α= D ．||a b -r r 1 【答案】B【解析】【分析】A 选项利用向量平行的坐标表示来判断正确性.B 选项利用向量垂直的坐标表示来判断正确性.C 选项求得()f α的表达式，结合三角函数最值的求法，判断C 选项的正确性.D 选项利用向量模的运算来判断正确性.【详解】A 选项，若//a b r r ，则2sin cos αα=，即1tan 2α=，A 正确.B 选项，若a b ⊥r r ，则sin 2cos 0αα+=，则tan 2α=-，B 不正确.C 选项，si (n )2cos in()f a b ααααϕ+==⋅=+r r ，其中tan 2ϕ=.取得最大值时，22k παϕπ+=+，22k πϕπα=+-，tan 2tan 2k πϕπα=+-⎛⎫ ⎪⎝⎭1tan 22tan παα⎛⎫=== ⎪⎝⎭-，则1tan 2α=，则C 正确. D 选项，由向量减法、模的几何意义可知||a b -r r1，此时a =r，,a b r r 反向.故选项D 正确.故选：B【点睛】 本小题主要考查向量平行、垂直的坐标表示，考查向量数量积的运算，考查向量减法的模的几何意义，属于中档题.17．已知,A B 是圆22:16O x y +=的两个动点，524,33AB OC OA OB ==-u u u v u u u v u u u v ，若M 分别是线段AB 的中点，则·OC OM =u u u v u u u u v （ ） A．8+B．8-C ．12 D ．4【答案】C【解析】【分析】【详解】 由题意1122OM OA OB =+u u u u r u u u r u u u r ，则2252115113322632OC OM OA OB OA OB OA OB OA OB ⎛⎫⎛⎫⋅=-⋅+=-+⋅ ⎪ ⎪⎝⎭⎝⎭u u u v u u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v ，又圆的半径为4，4AB =uu u r ，则,OA OB u u u r u u u r 两向量的夹角为π3．则8OA OB ⋅=u u u v u u u v ，2216OA OB ==u u u v u u u v ，所以12OC OM ⋅=u u u r u u u u r ．故本题答案选C ．点睛：本题主要考查平面向量的基本定理.用平面向量的基本定理解决问题的一般思路是:先选择一组基底,并且运用平面向量的基本定理将条件和结论表示成基底的线性组合,在基底未给出的情况下进行向量的运算,合理地选取基底会给解题带来方便.进行向量运算时,要尽可能转化到平行四边形或三角形中.18．三角形ABC 中，5BC =，G ，O 分别为三角形ABC 的重心和外心，且5GO BC ⋅=u u u r u u u r ，则三角形ABC 的形状是（ ）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．上述均不是【答案】B【解析】【分析】 取BC 中点D ，利用GO GD DO =+u u u r u u u r u u u r代入计算，再利用向量的线性运算求解．如图，取BC 中点D ，连接,OD AD ，则G 在AD 上，13GD AD =，OD BC ^， ()GO BC GD DO BC GD BC DO BC ⋅=+⋅=⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r221111()()()53326GD BC AD BC AB AC AC AB AC AB =⋅=⋅=⨯+⋅-=-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ， ∴2223025AC AB BC -=>=，∴2220AB BC AC +-<，由余弦定理得cos 0B <，即B 为钝角，三角形为钝角三角形．故选：B ．【点睛】本题考查平面向量的数量积，考查向量的线性表示，考查余弦定理．解题关键是取BC 中点D ，用,AB AC u u u r u u u r 表示出,GD BC u u u r u u u r ．19．已知向量()1,3a =-v ，()3,b m =v ，若a b ⊥v v ，则2a b +v v 等于（ ）A ．10B ．16C ．52D ．410【答案】C【解析】【分析】 先利用向量垂直的坐标表示求出实数m 的值，得出向量b r 的坐标，并计算出向量2a b +r r ，最后利用向量模的坐标运算得出结果．【详解】 ()1,3a =-r Q ，()3,b m =r ，a b ⊥r r ，则1330a b m ⋅=⨯-=r r ，得1m =，()3,1b ∴=r ，则()()()221,33,15,5a b +=-+=-r r ，因此，()2225552a b +=+-=r r C.【点睛】本题考查向量垂直的坐标表示以及向量模的坐标运算，意在考查学生对这些公式的理解掌握情况，考查运算求解能力，属于中等题．20．已知向量(),1a x =-r ， (3b =r ，若a b ⊥r r ，则a =r （ ） A 2 B 3 C ．2 D ．4【解析】由a b r r ⊥，(),1a x =-r ， (b r =，可得：x 0x ，==，即)1a =-r所以2a ==r 故选C。

baC B Aa b C C -=A -AB =B1.向量加法运算：⑴三角形法则的特点：首尾相连．⑵平行四边形法则的特点：共起点．2.向量减法运算：⑴三角形法则的特点：共起点，连终点，方向指向被减向量．⑵坐标运算：设()11,a x y =，()22,b x y =，则()1212,a b x x y y -=--． 设A 、B 两点的坐标分别为()11,x y ，()22,x y ，则()1212,x x y y AB =--． 3.向量数乘运算：⑴实数λ与向量a 的积是一个向量的运算叫做向量的数乘，记作a λ． ①a a λλ=；②当0λ>时，a λ的方向与a 的方向相同；当0λ<时，a λ的方向与a 的方向相反；当0λ=时，0a λ=．⑵运算律：①()()a a λμλμ=；②()a a a λμλμ+=+；③()a b a b λλλ+=+． ⑶坐标运算：设(),a x y =，则()(),,a x y x y λλλλ==．4. 平面向量基本定理：如果1e 、2e 是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数1λ、2λ，使1122a e e λλ=+．（不共线的向量1e 、2e 作为这一平面内所有向量的一组基底）。

5.平面向量的数量积：⑴()cos 0,0,0180a b a b a b θθ⋅=≠≠≤≤．零向量与任一向量的数量积为0．⑵性质：设a 和b 都是非零向量，则①0a b a b ⊥⇔⋅=．②当a 与b 同向时，a b a b ⋅=；当a 与b 反向时，a b a b ⋅=-；22a a a a ⋅==或a a a =⋅．③ab a b ⋅≤．⑶运算律：①a b b a ⋅=⋅；②()()()a b a b a b λλλ⋅=⋅=⋅；③()a b c a c b c +⋅=⋅+⋅． ⑷坐标运算：设两个非零向量()11,a x y =，()22,b x y =，则1212a b x x y y ⋅=+．若(),a x y =，则222a x y =+，或2a x y =+设()11,a x y =，()22,b x y =，则12120a b x x y y ⊥⇔+=．设a 、b 都是非零向量，()11,a x y =，()22,b x y =，θ是a 与b 的夹角，则：12cos a b a bx θ⋅==+．6.向量共线定理：向量()0a a ≠与b 共线，当且仅当有唯一一个实数λ，使b a λ=． 设()11,a x y =，()22,b x y =，其中0b ≠，则当12210x y x y -=时，向量a 、()0b b ≠共线． 7.分点坐标公式：设点P 是线段12P P 上的一点，1P 、2P 的坐标分别是()11,x y ，()22,x y ，当12λP P =PP 时，点P 的坐标是1212,11x x y y λλλλ++⎛⎫⎪++⎝⎭． 【高考真题讲解】1．(2014·辽宁卷) 设a ，b ，c 是非零向量，已知命题p ：若a ·b ＝0，b ·c ＝0，则a ·c ＝0，命题q ：若a ∥b ，b ∥c ，则a ∥c ，则下列命题中真命题是 ( )A ．p ∨qB ．p ∧qC ．)()(q p ⌝∧⌝D ．)(q p ⌝∨2．(·14全国卷Ⅰ) 已知A ，B ，C 为圆O 上的三点，若AO →＝12(AB →＋AC →)，则AB →与AC →的夹角为________． 3．(2014·四川卷) 平面向量a ＝(1，2)，b ＝(4，2)，c ＝ma ＋b (m ∈R)，且c 与a 的夹角等于c 与b 的夹角，则m ＝( )A ．－2B ．－1C ．1D ．2 4. (14·全国卷Ⅰ)设D 、E 、F 分别为△ABC 的三边BC 、CA 、AB 的中点，则=+（ ）A ． B.21 C. D. 215. (14福建)设M 为平行四边形ABCD 对角线的交点，O 为平行四边形ABCD 所在平面内任意一点，则+++等于 （ ）A ． B. 2 C. 3 D. 46. （11浙江）若平面向量,αβ满足1,1a β=≤，且以向量,αβ为邻边的平行四边形的面积为12，则α与β的夹角θ的取值范围是 。

高考数学一轮复习平面向量多选题(讲义及答案)及答案一、平面向量多选题1．在三棱锥M ABC -中，下列命题正确的是（ ）A ．若1233AD AB AC =+，则3BC BD = B ．若G 为ABC 的重心，则111333MG MA MB MC =++C ．若0MA BC ⋅=，0MC AB ⋅=，则0MB AC ⋅=D ．若三棱锥M ABC -的棱长都为2，P ，Q 分别为MA ，BC 中点，则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图，在每个三角形中利用向量的线性运算可得. 【详解】对于A ，由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-，即2CD DB =，则32BD BD DC BC =+=，故A 错误； 对于B ，由G 为ABC 的重心，得0GA GB GC ++=，又MG MA AG =+，MG MB BG =+，MG MC CG =+，3MA MB MC MG ∴++=，即111333MG MA MB MC =++，故B 正确；对于C ，若0MA BC ⋅=，0MC AB ⋅=，则0MC MA BC AB ⋅+⋅=，即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅，即0MB AC ⋅=，故C 正确；对于D ，111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()2112PQ MB MC MA MB MC MA ∴=+-=+-，又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=，1PQ ∴==，故D 错误. 故选：BC 【点睛】关键点睛：本题考查向量的运算，用已知向量表示某一向量的三个关键点： (1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．2．定义空间两个向量的一种运算sin ,a b a b a b ⊗=⋅，则关于空间向量上述运算的以下结论中恒成立的有（ ） A ．()()a b a b λλ⊗=⊗ B ．a b b a ⊗=⊗C ．()()()a b c a c b c +⊗=⊗+⊗D ．若()11,a x y =，()22,b x y =，则122a b x y x y ⊗=- 【答案】BD 【分析】对于A,B,只需根据定义列出左边和右边的式子即可,对于C,当λab 时,()()1sin ,a b c b c b c λ+⊗=+⋅,()()()sin ,sin,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅,显然不会恒成立. 对于D,根据数量积求出cos ,a b ,再由平方关系求出sin ,a b 的值,代入定义进行化简验证即可. 【详解】解：对于A ：()()sin ,a b a b a b λλ⊗=⋅，()sin ,a b a b a bλλλ⊗=⋅，故()()a b a b λλ⊗=⊗不会恒成立；对于B ，sin ,a b a b a b ⊗=⋅，=sin ,b a b a b a ⊗⋅，故a b b a ⊗=⊗恒成立； 对于C ，若λab ，且0λ>，()()1sin ,a b c b c b c λ+⊗=+⋅，()()()sin,sin ,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅，显然()()()a b c a c b c +⊗=⊗+⊗不会恒成立； 对于D ，1212cos ,x x y y a b a b+=⋅，212sin ,1a b a b ⎛ ⎪=- ⎪⋅⎭，即有222121212121x x y yx x y y ab a b a b a a b ⎛⎫⎛⎫++ ⎪⊗=⋅⋅-=⋅- ⎪ ⎪ ⎪⋅⎭⎭21y =⎪+⎭==1221x y xy =-.则1221a b x y x y ⊗=-恒成立. 故选：BD. 【点睛】本题考查向量的新定义，理解运算法则正确计算是解题的关键，属于较难题.3．下列关于平面向量的说法中正确的是（ ）A ．已知,a b 均为非零向量，若//a b ，则存在唯一的实数λ，使得λabB ．已知非零向量(1,2),(1,1)a b ==，且a 与a λb +的夹角为锐角，则实数λ的取值范围是5,3⎛⎫-+∞ ⎪⎝⎭C ．若a c b c ⋅=⋅且0c ≠，则a b =D ．若点G 为ABC 的重心，则0GA GB GC ++= 【答案】AD 【分析】由向量共线定理可判断选项A ；由向量夹角的的坐标表示可判断选项B ；由数量积的运算性质可判断选项C ；由三角形的重心性质即向量线性运算可判断选项D. 【详解】对于选项A ： 由向量共线定理知选项A 正确；对于选项B ：()()()1,21,11,2a b λλλλ+=+=++，若a 与a λb +的夹角为锐角，则()()122530a a b λλλλ⋅+=+++=+>解得53λ>-，当a 与a λb +共线时，()221λλ+=+，解得：0λ=，此时(1,2)a =，()1,2a b λ+=，此时a b =夹角为0，不符合题意，所以实数λ的取值范围是()5,00,3⎛⎫-⋃+∞ ⎪⎝⎭，故选项B 不正确； 对于选项C ：若a c b c ⋅=⋅，则()0c a b ⋅-=，因为0c ≠，则a b =或c 与a b -垂直， 故选项C 不正确；对于选项D ：若点G 为ABC 的重心，延长AG 与BC 交于M ，则M 为BC 的中点，所以()1222AG GM GB GC GB GC ==⨯⨯+=+，所以0GA GB GC ++=，故选项D 正确.故选：AD 【点睛】易错点睛：两个向量夹角为锐角数量积大于0，但数量积大于0向量夹角为锐角或0，由向量夹角为锐角数量积大于0，需要检验向量共线的情况. 两个向量夹角为钝角数量积小于0，但数量积小于0向量夹角为钝角或π.4．已知直线1:310l mx y m --+=与直线2:310l x my m +--=相交于点P ，线段AB 是圆()()22:114C x y +++=的一条动弦，G 为弦AB 的中点，23AB =（ ）A ．弦AB 的中点轨迹是圆B ．直线12,l l 的交点P 在定圆()()22222x y -+-=上 C ．线段PG 长的最大值为421 D ．PA PB ⋅的最小值642+ 【答案】ABC 【分析】对于选项A ：设()00,G x y ，利用已知条件先求出圆心到弦AB 的距离CG ，利用两点之间的距离公式即可得到结论；对于选项B ：联立直线的方程组求解点P 的坐标，代入选项验证即可判断；对于选项C ：利用选项A B 结论，得到圆心坐标和半径，利用1112max PG PG r r =++求解即可；对于选项D ：利用平面向量的加法法则以及数量积运算得到23PA PB PG ⋅==-，进而把问题转化为求1112min PG PG r r=--问题，即可判断.【详解】对于选项A ：设()00,G x y，2AB =G 为弦AB 的中点， GB ∴=，而()()22:114C x y+++=， 半径为2，则圆心到弦AB 的距离为1CG ==，又圆心()1,1C --，()()2200111x y ∴+++=，即弦AB 的中点轨迹是圆. 故选项A 正确； 对于选项B ：由310310mx y m x my m --+=⎧⎨+--=⎩，得222232113211m m x m m m y m ⎧++=⎪⎪+⎨-+⎪=⎪+⎩， 代入()()2222x y -+-整理得2， 故选项B 正确；对于选项C ：由选项A 知：点G 的轨迹方程为：()()22111x y +++=，由选项B 知：点P 的轨迹方程为：()()22222x y -+-=，()()11121,1,1,2,2,G r P r∴--=所以线段1112max 11PG PG r r =++=+=，故选项C 正确； 对于选项D ：()()PA PB PG GA PG GB ⋅=+⋅+()2PG PG GA GB GA GB =+⋅++⋅ 22203PG PG GB PG =+⋅-=-，故()()2minmin3PA PBPG ⋅=-，由选项C 知：1112min 11PG PG r r =--=-=，所以()()2min136PA PB⋅=-=-，故选项D 错误； 故选：A B C. 【点睛】关键点睛：本题考查了求圆的轨迹问题以及两个圆上的点的距离问题.把两个圆上的点的距离问题转化为两个圆的圆心与半径之间的关系是解决本题的关键.5．已知向量(2,1)a =，(cos ,sin )(0)b θθθπ=，则下列命题正确的是（ ）A ．若a b ⊥，则tan θ=B ．若b 在a 上的投影为12-，则向量a 与b 的夹角为23πC ．存在θ，使得||||||a b a b +=+D ．a b 【答案】BCD 【分析】若a b ⊥，则tan θ=A 错误； 若b 在a 上的投影为12-，且||1b =，则2πcos ,3a b 〈〉=，故B 正确；若b 在a 上的投影为12-，且||1b =，故当a,b 0<>=，|||||a b a b =+|+，故C 正确；2cos sin a b θθ+==)θϕ+， a b D 正确.【详解】若a b ⊥，则2cos sin 0a b θθ+==，则tan θ=A 错误； 若b 在a 上的投影为12-，且||1b =，则1||cos 2b a b 〈〉=-，，2πcos ,3a b 〈〉=，故B 正确；若2()2a b a b a b =+22++，222(||||)||||2||||a b a b a b +=++，若|||||a b a b =+|+，则||||cos ||||a b a b a b a b 〈〉=，=，即cos ,1a b 〈〉=，故a,b 0<>=，|||||a b a b =+|+，故C正确；2cos sin a b θθ+==)θϕ+，因为0πθ≤≤，π02ϕ<<，则当π2θϕ+=时，a b ，故D 正确，故选：BCD ． 【点睛】本题主要考查平面向量的数量积的计算和应用，考查数量积的运算律，意在考查学生对这些知识的理解掌握水平.6．已知,,a b c 是同一平面内的三个向量，下列命题中正确的是（ ） A ．||||||a b a b ⋅≤B ．若a b c b ⋅=⋅且0b ≠，则a c =C ．两个非零向量a ，b ，若||||||a b a b -=+，则a 与b 共线且反向D ．已知(1,2)a =，(1,1)b =，且a 与a b λ+的夹角为锐角，则实数λ的取值范围是5,3⎛⎫-+∞ ⎪⎝⎭【答案】AC 【分析】根据平面向量数量积定义可判断A ；由向量垂直时乘积为0，可判断B ；利用向量数量积的运算律，化简可判断C ；根据向量数量积的坐标关系，可判断D. 【详解】对于A ，由平面向量数量积定义可知cos ,a b a b a b ⋅=，则||||||a b a b ⋅≤，所以A 正确，对于B ，当a 与c 都和b 垂直时，a 与c 的方向不一定相同，大小不一定相等，所以B 错误，对于C ，两个非零向量a ，b ，若||||||a b a b -=+，可得22()(||||)a b a b -=+，即22||||a b a b -⋅=，cos 1θ=-，则两个向量的夹角为π，则a 与b 共线且反向，故C 正确； 对于D ，已知(1,2)a =，(1,1)b =且a 与a b λ+的夹角为锐角， 可得()0a a b λ⋅+>即2||0a a b λ+⋅>可得530λ+>，解得53λ>-， 当a 与a b λ+的夹角为0时，(1,2)a b λλλ+=++，所以2220λλλ+=+⇒= 所以a 与a b λ+的夹角为锐角时53λ>-且0λ≠，故D 错误； 故选:AC. 【点睛】本题考查了平面向量数量积定义的应用，向量共线及向量数量积的坐标表示，属于中档题.7．关于平面向量有下列四个命题，其中正确的命题为（ ） A ．若a b a c ⋅=⋅，则b c =；B ．已知(,3)a k =，(2,6)b =-，若//a b ，则1k =-；C ．非零向量a 和b ，满足||||||a b a b ==-，则a 与a b +的夹角为30º；D ．0||||||||a b a b a b a b ⎛⎫⎛⎫+⋅-= ⎪ ⎪⎝⎭⎝⎭【答案】BCD 【分析】通过举反例知A 不成立，由平行向量的坐标对应成比例知B 正确，由向量加减法的意义知，C 正确，通过化简计算得D 正确． 【详解】对A ，当0a = 时，可得到A 不成立； 对B ，//a b 时，有326k =-，1k ∴=-，故B 正确． 对C ，当||||||a b a b ==-时，a 、b 、a b -这三个向量平移后构成一个等边三角形，a b + 是这个等边三角形一条角平分线，故C 正确．对D ，22()()()()110||||||||||||a b a b a b a a a b b b +⋅-=-=-=，故D 正确． 故选：BCD ． 【点睛】本题考查两个向量的数量积公式，两个向量加减法的几何意义，以及共线向量的坐标特点．属于基础题．8．设a 、b 是两个非零向量，则下列描述正确的有（ ） A ．若a b a b +=-，则存在实数λ使得λa bB ．若a b ⊥，则a b a b +=-C ．若a b a b +=+，则a 在b 方向上的投影向量为aD ．若存在实数λ使得λa b ，则a b a b +=-【答案】AB 【分析】根据向量模的三角不等式找出a b a b +=-和a b a b +=+的等价条件，可判断A 、C 、D 选项的正误，利用平面向量加法的平行四边形法则可判断B 选项的正误.综合可得出结论. 【详解】当a b a b +=-时，则a 、b 方向相反且a b ≥，则存在负实数λ，使得λa b ，A选项正确，D 选项错误；若a b a b +=+，则a 、b 方向相同，a 在b 方向上的投影向量为a ，C 选项错误； 若a b ⊥，则以a 、b 为邻边的平行四边形为矩形，且a b +和a b -是这个矩形的两条对角线长，则a b a b +=-，B 选项正确. 故选：AB. 【点睛】本题考查平面向量线性运算相关的命题的判断，涉及平面向量模的三角不等式的应用，考查推理能力，属于中等题.二、立体几何多选题9．如图，在直三棱柱111ABC A B C -中，12AC BC AA ===，90ACB ∠=︒，D ，E ，F 分别为AC ，1AA ，AB 的中点．则下列结论正确的是（ ）A ．1AC 与EF 相交B ．11//BC 平面DEF C ．EF 与1AC 所成的角为90︒D ．点1B 到平面DEF 32【答案】BCD 【分析】利用异面直线的位置关系，线面平行的判定方法，利用空间直角坐标系异面直线所成角和点到面的距离，对各个选项逐一判断． 【详解】对选项A ，由图知1AC ⊂平面11ACC A ，EF 平面11ACC A E =，且1.E AC ∉由异面直线的定义可知1AC 与EF 异面，故A 错误；对于选项B ，在直三棱柱111ABC A B C -中，11B C //BC ．D ，F 分别是AC ，AB 的中点， //∴FD BC ，11B C ∴ //FD ．又11B C ⊄平面DEF ，DF ⊂平面DEF ，11B C ∴ //平面.DEF 故B 正确；对于选项C ，由题意，建立如图所示的空间直角坐标系，则(0C ，0，0)，(2A ，0，0)，(0B ，2，0)，1(2A ，0，2)，1(0B ，2，2)，1(0C ，0，2)，(1D ，0，0)，(2E ，0，1)，(1F ，1，0)．(1EF ∴=-，1，1)-，1(2AC =-，0，2)． 1·2020EF AC =+-=，1EF AC ∴⊥，1EF AC ∴⊥． EF 与1AC 所成的角为90︒，故C 正确；对于选项D ，设向量(n x =，y ，)z 是平面DEF 的一个法向量． (1DE =，0，1)，(0DF =，1，0)， ∴由n DE n DF ⎧⊥⎨⊥⎩，，，即·0·0n DE n DF ⎧=⎨=⎩，，，得00.x z y +=⎧⎨=⎩，取1x =，则1z =-，(1n ∴=，0，1)-， 设点1B 到平面DEF 的距离为d ． 又1(1DB =-，2，2)， 1·102322DB n d n-+-∴===， ∴点1B 到平面DEF 32，故D 正确．故选：BCD【点睛】本题主要考查异面直线的位置关系，线面平行的判定，异面直线所成角以及点到面的距离，还考查思维能力及综合分析能力，属难题．10．如图，正方体1111ABCD A B C D -的棱长为3，点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动，且满足直线//BM 平面1D EF ，则（ ）A ．过1D ，E ，F 的平面截正方体所得截面为等腰梯形B ．三棱锥1D EFM -的体积为定值C ．动点M 10D ．过B ，E ，M 的平面截正方体所得截面面积的最小值为10【答案】BCD【分析】由题做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，进而计算即可排除A 选项；根据//BM 平面1D EF ，由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确；取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知M 的轨迹为线段HI 10，故C 选项正确；过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，易知过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而得当H 位于点I 时，截面面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=【详解】解：对于A 选项，如图，取BF 中点G ，连接1A G ，由点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=，故四边形11A D EG 为平行四边形，故11//AG D E ，由于在11A B G △，F 为1B G 中点，当N 为11A B 中点时，有11////NF A G D E ，故过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，此时22133532D N ⎛⎫=+= ⎪⎝⎭，223110EF =+=，故梯形1D EFN 不是等腰梯形，故A 选项错误；对于B 选项，三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积，由于//BM 平面1D EF ，故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积，三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积，而三棱锥1D BEF -的体积为定值，故B 选项正确； 对于C 选项，取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知1////HB AG NF ，1//BI D F ，由于1,HI BI I NF D F F ==，故平面//BHI 平面1D EF ，故M 的轨迹为线段HI ，其长度为10，故C 选项正确；对于D 选项，过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，则过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，易知当H 位于点I 时，平行四边形BPOE 边BP 最小，且为AB ，此时截面平行四边形BPOE 的面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=，故D 选项正确；故选：BCD【点睛】本题解题的关键在于根据题意，依次做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而讨论AD 选项，通过//BM 平面1D EF ，并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确，通过构造面面平行得M 的轨迹为线段HI ，进而讨论C 选项，考查回归转化思想和空间思维能力，是中档题.。

考点20 平面向量【考纲要求】1.了解向量的实际背景．2.了解向量线性运算的性质及其几何意义．3.了解平面向量的基本定理及其意义．4.了解平面向量的数量积与向量投影的关系．5.理解平面向量的概念及向量的几何表示，理解两个向量相等的含义．6.理解用坐标表示的平面向量共线的条件．7.理解平面向量数量积的含义及其物理意义．8.掌握向量加法、减法的运算，并理解其几何意义．9.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义 ． 10.掌握平面向量的正交分解及其坐标表示．11.掌握数量积的坐标表达式，会进行平面向量数量积的运算．12.能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系． 13.会用向量方法解决某些简单的实际问题． 14会用坐标表示平面向量的加法、减法与数乘运算． 【命题规律】高考对平面向量的考查，在选择题或填空题中一般是平面向量的线性运算、坐标运算，用向量方法解决平面几何问题，在解答题中也会出现与共线向量、数量积有关的问题. 【典型高考试题变式】 （一）平面向量的坐标运算例1.【2017∙山东卷】已知向量a =（2,6）,b =(1,)λ- ，若//a b ，则λ= . 【答案】3-【解析】由//a b 得62λ-=，解得3λ=-.【名师点睛】平面向量共线的坐标表示问题的常见类型及解题策略:（1）利用两向量共线求参数．如果已知两向量共线,求某些参数的取值时,利用“若a ＝(x 1,y 1),b ＝(x 2,y 2),则a ∥b 的充要条件是x 1y 2＝x 2y 1”解题比较方便．(2)利用两向量共线的条件求向量坐标．一般地,在求与一个已知向量a 共线的向量时,可设所求向量为λa (λ∈R ),然后结合其他条件列出关于λ的方程,求出λ的值后代入λa 即可得到所求的向量．(3)三点共线问题．A ,B ,C 三点共线等价于AB →与AC →共线.【变式1】【改变条件】已知向量a =（2,6），a +b =(1,)λ- ，若//a b ，则λ= . 【答案】3【解析】由已知可得b )6,3(--=λ，因为//a b ，所以12218-=-λ，解得3=λ. 【变式2】【改变结论】已知向量a =（2,6），b =(1,)λ- ，若//a b ，则a+λb = .【答案】(5,15)【解析】由//a b 得62λ-=，解得3λ=-，所以a+λb =)15,5()9,3()6,2(=+.例2.【2017∙新课标卷】已知向量=a (2,3)-，=b (3,)m 且⊥a b ，则=m . 【答案】2【解析】由题意可得：2330m -⨯+=，所以2m =. 【名师点睛】向量垂直：121200a b a b x x y y ⊥⇔⋅=⇔+=.【变式1】【改变例题中的条件】已知向量=a )2,1(-，=b （m ，1）．若向量+a b 与a 垂直，则=m ________．【答案】7【解析】由题得()1,3m +=-a b ，因为向量+a b 与a 垂直，所以()0+⋅=a b a ， 所以(1)230m --+⨯=，解得7m =.【变式2】【改变例题中的结论】已知向量=a (2,3)-，=b (3,)m 且⊥a b ，则|a +b |= .【解析】由题意0⋅=a b ，2(1)0x x ++=，23x =-.所以+a b =)37,1(，所以a +b |=358)37(122=+.（二）平面向量的夹角例 3. 【2016∙北京卷】已知向量=a b ，则a 与b 夹角的大小为_________.【答案】30【名师点睛】由向量数量积的定义θcos ||||⋅⋅=⋅b a b a (θ为，的夹角)可知，数量积的值、模的乘积、夹角知二可求一，再考虑到数量积还可以用坐标表示，因此又可以借助坐标进行运算.当然，无论怎样变化，其本质都是对数量积定义的考查.求解夹角与模的题目在近年高考中出现的频率很高，应熟练掌握其解法.【变式1】【改变已知条件】已知向量a ，(1,0)=-b ，则a 与b 夹角的大小为_________.【答案】32π【解析】由已知得210)1()3(1)0,1()3,1(cos 2222-=+-⋅+-⋅=θ，因为],0[πθ∈，所以32πθ=.【变式2】【改变例题中的结论】已知向量=a b ，若a 与b 夹角为θ，则=θtan _________.【答案】33【解析】由已知得231)3()3(1)1,3()3,1(cos 2222=+⋅+⋅=θ，因为],0[πθ∈， 所以6πθ=，所以33tan =θ. （三）数量积的运用例4.【2017∙天津卷】在△ABC 中，60A ∠=︒，AB =3，AC =2. 若2BD DC =，AE AC AB λ=-（λ∈R ），且4AD AE ⋅=-，则λ的值为 .【答案】311【解析】32cos603AB AC ⋅=⨯⨯=，1233AD AB AC =+， 所以12212()()34934333333AD AE AB AC AC AB λλλ⋅=+⋅-=⨯+⨯-⨯-⨯=-，所以113=λ.【名师点睛】平面向量问题中，向量的线性运算和数量积是高频考点，当出现线性运算问题时，向要选好基底向量，如本题就要灵活使用向量,AB AC ，要注意结合图形的性质，灵活运用向量的运算解决问题，当涉及到向量数量积时，要记熟向量数量积的公式、坐标公式、几何意义等.【变式1】【改变例题的条件】在等边△ABC 中，若2=AB ，2BD DC =，AE AC AB λ=-（λ∈R ），且4AD AE ⋅=-，则λ的值为 .【答案】25-【变式2】【改变例题的条件与结论】已知△ABC 是边长为1的等边三角形，点E D ,分别是边BC AB ,的中点，连接DE 并延长到点F ，使得EF DE 2=，则⋅的值为 . 【答案】81【解析】设BA a =，BC b =，所以11()22DE AC b a ==-，33()24DF DE b a ==-，1353()2444AF AD DF a b a a b =+=-+-=-+，所以25353144848AF BC a b b ⋅=-⋅+=-+=.（四）平面向量与三角函数的交汇例5. 【2017∙江苏卷】 已知向量(cos ,sin ),(3,[0,π].x x x ==∈a b（1）若a ∥b ，求x 的值；（2）记()f x =⋅a b ，求()f x 的最大值和最小值以及对应的x 的值.【解析】（1）因为 co ()s ,sin x x =a ，(3,=b ，//a b ，所以3sin x x =. 若cos 0x =，则sin 0x =，与22sin cos 1x x +=矛盾，故cos 0x ≠.于是tan x =又[]0,πx ∈，所以5π6x =.（2）()(πcos ,sin 3,3cos )6()f x x x x x x =⋅=⋅=-=+a b .因为[]0,πx ∈，所以ππ7π[,]666x +∈，从而π1cos()6x -+剟. 于是，当ππ66x +=，即0x =时，()f x 取到最大值3；当π6x +=π，即5π6x =时，()f x 取到最小值-.【名师点睛】向量的两个作用：①载体作用：关键是利用向量的意义、作用脱去“向量外衣”，转化为我们熟悉的数学问题；②工具作用：利用向量可解决一些垂直、平行、夹角与距离问题.【变式1】【改变例题的结论】已知向量(cos ,sin ),(3,[0,π].x x x ==∈a b （1）若a ⊥b ，求x 的值；（2）记()f x =⋅a b ，解不等式()f x ≥【解析】（1）因为 co ()s ,sin x x =a ，(3,=b ，⊥a b ，所以3cos 0x x =. 所以3tan =x . 因为],0[π∈x ，所以3π=x .【变式2】【改变例题中的条件与结论】设向量a ＝(3sin x ，sin x )，b ＝(cos x ，sin x )，]2,0[π∈x ．（1）若|a |＝|b |，求x 的值；（2）设函数f (x )＝a ·b ，求f (x )的最大值．【解析】（1）由|a |2＝(3sin x )2＋sin 2x ＝4sin 2x ，|b |2＝cos 2x ＋sin 2x ＝1，及|a |＝|b |，得4sin 2x ＝1.又]2,0[π∈x ，从而sin x ＝21，所以x ＝6π. （2）)(x f ＝a ·b ＝3sin x ·cos x ＋sin 2x ＝23sin 2x －21cos 2x ＋21＝)62sin(π-x ＋21，当3π=x ]2,0[π∈时，)62sin(π-x 取最大值1. 所以)(x f 的最大值为23. 【数学思想】①数形结合思想:向量兼具代数的抽象与严谨和几何的直观与形象，向量本身是一个数形结合的产物，在利用向量解决问题时，要注意数与形的结合、代数与几何的结合、形象思维与逻辑思维的结合．②分类讨论思想:对向量的方向、向量的位置关系、参数进行讨论． ③转化与化归思想.【温馨提示】①作两个向量的差时，要注意向量的方向是指向被减向量的终点．②在向量共线的重要条件中易忽视“a ≠0”，否则λ可能不存在，也可能有无数个． ③注意能作为基底的两个向量必须是不共线的．④要区分点的坐标与向量坐标的不同，尽管在形式上它们完全一样，但意义完全不同，向量坐标中既有方向也有大小的信息．⑤0与实数0的区别：0a ＝0≠0，a ＋(－a )＝0≠0，a ·0＝0≠0；②0的方向是任意的，并非没有方向，0与任何向量平行，我们只定义了非零向量的垂直关系．⑥a·b ＝0不能推出a ＝0或b ＝0，因为a·b ＝0时，有可能a ⊥b . 【典例试题演练】1.【2017∙河北省武邑中学调研】已知向量()2,1a =-，()1,3b =-，则（ ）A. //a bB. a b ⊥C. ()//a a b - D. ()a ab ⊥- 【答案】D【解析】由()1,2a b ---＝， ()2,1a =-，得 ()220a b a -⋅=-=，所以()a ab ⊥-，故选D.2. 【2018∙河南郑州一中测试】在ABC ∆中， D 为BC 边的中点，若()2,0BC =，()1,4AC =，则AD =（ ）A. ()2,4-B. ()0,4-C. ()2,4D. ()0,4 【答案】D【解析】()()11,41,02AD AC DC AC BC =-=-=-=()0,4.故选D. 3.【2018∙广州市海珠区测试】已知向量,a b 的夹角为60||2|2|2a a b =-=，，，则||b =（ ）A. 4B. 2 D. 1 【答案】D4. 【2016∙湖北省优质高中联考】已知向量()()()3,1,1,3,,2a b c k ===-，若()//a c b -，则向量a 与向量c 的夹角的余弦值是（ ）A ．5 B ．15 C ．5- D ．15- 【答案】A【解析】()3,3k c a -=-，因为()//a c b -，所以133)3(⨯=⨯-k ，解得2=k ，当2=k 时，5522104,cos =⨯=⋅>=<c a c a c a，故选A ．5. 【2017∙江西赣中南五校联考】ABC ∆外接圆圆心O ，半径为1，2AO AB AC =+且OA AB =，则向量BA 在向量BC 方向的投影为（ ）A ．21 B ．23 C ．21- D ．23-【答案】A【解析】因为-+-=⇒+=22，所以-=，所以C B O ,,三点共线，即AC AB ⊥1==，所以2=BC ， 所以()1BA BC BA AC AB ⋅=⋅-=，故向量在向量BC 上的投影为21，故选A ． 6.【2017∙湖北省黄石市调研】已知向量()()1,3,sin ,cos a b αα==且//a b ，则tan α=（ ）A ．3B ．3-C ．13D ．13- 【答案】C【解析】由//a b ，得3sin cos αα=，所以tan α=13，故选C. 7. 【2017∙河北省衡水中学联考】 已知平面向量,a b 满足()5a a b +=，且2,1a b ==，则向量a 与b夹角的余弦值为（ ）A B ．-．12 D ．12-【答案】C【解析】22()cos ,42cos ,5a a b a a b a a b a b a b ⋅+=+⋅=+⋅<>=+<>=，所以1cos ,2a b <>=，故选C. 8.【2017∙湖南永州市模拟，11】已知向量a 与向量b 的夹角为23π，且2a b ==，又向量c xa yb =+（x R ∈且0x ≠，y R ∈），则x c的最大值为（ ）A B ．13D ．3 【答案】A9.【2017∙四川巴中市“零诊”】已知向量(,1)a t =与(4,)b t =共线且方向相同，则=t .【答案】2【解析】由题意得24t =，所以2t =±，当2t =-时，a ，b 方向相反，舍去，故2t =. 10. 【2017∙云南、四川、贵州联考】在矩形ABCD 中，30CAB ∠=，||AC AD AC =，则AC AB =______.【答案】12【解析】||||c o s 60|A C A D A C A D A C ⋅=⋅=，||2AD =，故||4AC =，||23AB =，所以||||cos3012AC AB AC AB ⋅=⋅=.11. 【2017∙江西南昌摸底】已知平面向量(1,2)a =，(3,2)b =-，若ka b +与3a b -垂直，则实数k = .【答案】19【解析】1a b ⋅=，所以由()(3)0ka b a b +⋅-=得5313130,19.k k k -⨯+-== 12. 【2017∙河北唐山市摸底】已知向量()()cos15,sin15,cos75,sin 75a b ==，则2a b -=___________． 【答案】313.【2018∙江苏省南京市调研】在△ABC 中，3=AB ，2=AC ，120=∠BAC ，BM BC λ=．若17·3AM BC =-，则实数λ的值为______． 【答案】13【解析】因为3,2,120AB AC BAC ==∠=，所以由余弦定理可得BC = 又根据余弦定理可得cosABC ∠=， ()2AM BC BM BA BC BC BA BC λ⋅=-⋅=-⋅ 171933λ=-=-，解得13λ=． 14. 【2017∙河南省南阳市六校联考】已知()1,2a =， ()3,4b =-.（1）若5ka b +=，求k 的值；（2）求a b +与a b -的夹角.【解析】（1）()()()1,23,43,24ka b k k k +=+-=-+，由5ka b +=5=，解得0k =或2k =-. （2）()()2,6,4,2a b a b +=--=-2,64,2cos ,2a b a b -⋅-∴〈+-〉==- 0a b a b a b a b π+-〈+-〉∈与夹角，（，），34a b a b π∴+-与夹角为. 15. 【2016∙河南中原名校一联】在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知向量()B A cos ,cos =，()b c a -=2,，且//．（1）求角A 的大小；（2）若4=a ，求ABC ∆面积的最大值．（2）由余弦定理得A bc c b a cos 2222-+=，bc bc bc bc c b =-≥-+=∴21622，因此16≤bc ，当且仅当4==c b 时，等号成立； 因此ABC ∆面积34sin 21≤=A bc S ，因此ABC ∆面积的最大值34．。

平面向量经典例题讲解讲课时间:___________姓名：___________课时：___________讲课教师：___________一、选择题（题型注释）1． 空间四边形OABC 中，OA a =,OB b =, OC c =,点M 在OA 上，且MA OM 2=，N 为BC 的中点，则MN =（ ）A．121-a b c +B 211a b c ++ C 112-a b c + D221-a b c + 【答案】B 【解析】点，则1()2ON OB OC =+，12()2MN ON OM OB OC OA=-=+-=112b c a +-，选B 考点：向量加法、减法、数乘的几何意义；2．已知平面向量a ，b 满足||1=a ，||2=b ，且()+⊥a b a ，则a 与b 的夹角是（ ）（A （（C ）（D 【答案】D 【解析】试题分析：2()()00a b a a b a a a b +⊥∴+⋅=∴+⋅=，||1=a ，||2=b ，设夹角为θ，则2112cos a a b +⋅=+⨯ 考点：本题考查向量数量积的运算点评：两向量垂直的充要条件是点乘积得0，用向量运算得到cos θ的值，求出角3．若OA 、OB 、OC 三个单位向量两两之间夹角为60OA OB OC ++= A.3 C.6 【答案】D 【解析】试题分析： OA 、OB 、OC 三个单位向量两两之间夹角为60°222222232coa b c a b c ab bc ac a b ++=+++++=+6=考点:向量的数量积.4．在平行四边形ABCD 中，AC 与BD 交于点O E ，是线段OD 的中点，AE 的延长线与CD 交于点F ,若AC a =，BD b =，则AF =( )A.1142a b +B.1233a b + C.1124a b + D.2133a b + 【答案】D 【解析】试题分析：由题意可知，AEB ∆与FED ∆相似，且相似比为3:1，所以13DF DC =,由向量加减法的平行四边形法则可知，,AB AD a AD AB b +=-=，解得，,a b a bAD AB +-==可知，121AF AD DF AD AB a b =+=+=+,故D 正确。

平面向量一. 教学内容：平面向量二. 教学重点、难点及教学要求：1. 理解向量的概念，掌握向量的几何表示，了解共线向量的概念。

2. 掌握向量的加法和减法。

3. 掌握实数与向量的积，理解两个向量共线的充要条件。

4. 了解平面向量的基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算。

5. 掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度、垂直等问题，掌握向量垂直的条件。

6. 掌握两点间距离公式，以及线段的定比分点和中点公式，并且能熟练运用，掌握平移公式。

三. 知识串讲（一）向量的基本运算1. 有关概念（1）向量—既有大小又有方向的量叫做向量常用有向线段表示向量（3）共线向量（平行向量）—方向相同或相反的向量叫做平行向量（即共线向量）。

向量可以在平面（空间）平行移动而不变。

规定：零向量与任一向量平行。

［练习］2. 向量的加法、减法与数乘。

（1）向量的加法是用三角形法则来定义的。

例如：如图：向量的多边形法则：多个向量相加，将它们顺序“头尾相接”，则以第一个向量的起点为起点，以最后一个向量的终点为终点的向量，即为这多个向量的和向量。

（3）实数与向量的积（此不等式表示三角形两边之和大于第三边，两边之差小于第三边，也称为三角不等式） 这个定理表明：平面内的任一向量都可以沿两个不共线向量分解为唯一一对向量的 所有向量的一组基底。

［练习］解：在平行四边形ABCD 中分析：∵点在上，可知与共线，得，再用以为起点P AB AP AB AP t AB O →→→→=→证明：∵A 、P 、B 三点共线则存在唯一实数t ，注意：这是一个充分必要条件命题，可判定三点共线。

_______________分析：∵与共线平行存在实数，使，即a b m a m b e k e →→⇔→=→→+→()12（二）向量的坐标运算3. 向量平行的坐标表示（三）平面向量的数量积1. 数量积的概念规定：零向量与任一向量的数量积为零。

2013高考试题解析分类汇编（理数）5：平面向量一、选择题错误！未指定书签。

．（2013年高考上海卷（理））在边长为1的正六边形ABCDEF 中,记以A为起点,其余顶点为终点的向量分别为12345,,,,a a a a a ;以D 为起点,其余顶点为终点的向量分别为12345,,,,d d d d d .若,m M 分别为()()i j k r s t a a a d d d ++⋅++的最小值、最大值,其中{,,}{1,2,3,4,5}i j k ⊆,{,,}{1,2,3,4,5}r s t ⊆,则,m M 满足 （ ）A ．0,0m M =>B ．0,0m M <>C ．0,0m M <=D ．0,0m M <<D ．【解答】作图知，只有0AF DE AB DC ⋅=⋅>，其余均有0i r a d ⋅≤，故选D ．错误！未指定书签。

．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））已知点()()1,3,4,1,A B AB -则与向量同方向的单位向量为 （ ）A ．3455⎛⎫ ⎪⎝⎭，- B ．4355⎛⎫ ⎪⎝⎭，-C ．3455⎛⎫- ⎪⎝⎭，D ．4355⎛⎫- ⎪⎝⎭，A(3,4)AB =-，所以||5AB =，所以同方向的单位向量是134(,)555AB =-，选A.错误！未指定书签。

．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））设0,P ABC ∆是边AB 上一定点,满足AB B P410=,且对于边AB 上任一点P ,恒有C P B P 00∙≥∙.则（ ）A ．090=∠ABCB ．090=∠BAC C ．AC AB =D ．BC AC =D以AB 所在的直线为x 轴，以AB 的中垂线为y 轴建立直角坐标系，设AB=4，C （a ，b ），P （x ，0）则BP 0=1，A （﹣2，0），B （2，0），P 0（1，0） 所以=（1，0），=（2﹣x ，0），=（a ﹣x ，b ），=（a ﹣1，b ）因为恒有所以（2﹣x ）（a ﹣x ）≥a ﹣1恒成立整理可得x 2﹣（a+2）x+a+1≥0恒成立所以△=（a+2）2﹣4（a+1）≤0即△=a 2≤0所以a=0，即C 在AB 的垂直平分线上所以AC=BC 故△ABC 为等腰三角形 故选D错误！未指定书签。

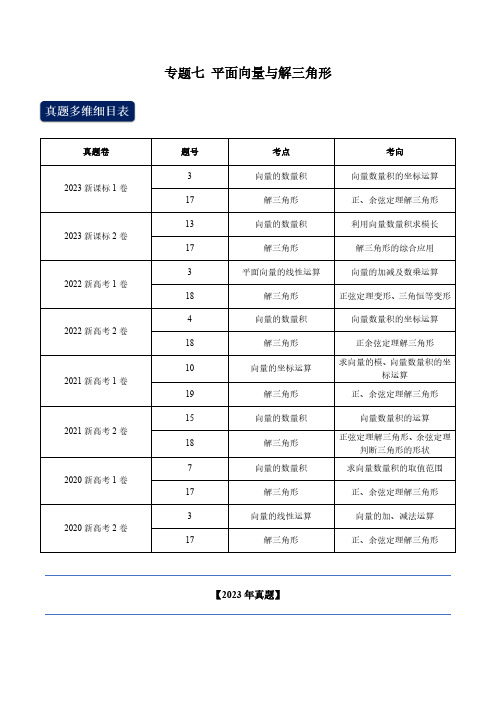
专题七平面向量与解三角形真题卷题号考点考向2023新课标1卷3 向量的数量积向量数量积的坐标运算17 解三角形正、余弦定理解三角形2023新课标2卷13 向量的数量积利用向量数量积求模长17 解三角形解三角形的综合应用2022新高考1卷3 平面向量的线性运算向量的加减及数乘运算18 解三角形正弦定理变形、三角恒等变形2022新高考2卷4 向量的数量积向量数量积的坐标运算18 解三角形正余弦定理解三角形2021新高考1卷10 向量的坐标运算求向量的模、向量数量积的坐标运算19 解三角形正、余弦定理解三角形2021新高考2卷15 向量的数量积向量数量积的运算18 解三角形正弦定理解三角形、余弦定理判断三角形的形状2020新高考1卷7 向量的数量积求向量数量积的取值范围17 解三角形正、余弦定理解三角形2020新高考2卷3 向量的线性运算向量的加、减法运算17 解三角形正、余弦定理解三角形【2023年真题】1.（2023·新课标I 卷 第3题）已知向量(1,1)a = ，(1,1).b=− 若()()a b a b λµ+⊥+，则( ) A. 1λµ+=B.1λµ+=− C. 1λµ= D. 1λµ=−【答案】D 【解析】 【分析】本题考查向量的数量积运算，结合向量垂直，向量的数量积为0，为较易题. 【解答】解：22()()()()2(1)0a b a b a a b b λµλµλµλµ+⋅+=++⋅+=+=，所以1;λµ=−故选.D2. （2023·新课标II 卷 第13题）已知向量a ，b 满足||a b − |||2|a b a b +=− ，则||b = __________【答案】【解析】 【分析】本题考查向量模及向量数量积的运算，属于基础题． 将两等式分别平方，然后化简计算即可． 【解答】 解：将原式平方：化简可得：即23b =，故||b =3. （2023·新课标I 卷 第17题）已知在ABC 中，3A B C +=，2sin()sin .A C B −=(1)求sin A ；(2)设5AB =，求AB 边上的高.【答案】解：(1)3A B C +=，3C C π∴−=，解得.4C π=2sin()sin A C B ∴−=可化为2sin()sin()44A A πππ−=−−，即32sin()sin()44A A ππ−=−，A A A A=，整理得sin3cosA A=，将1cos sin3A A=代入22sin cos1A A+=，得210sin19A=，29sin10A∴=，sin A=(2)由(1)知sin A=，1cos sin3A A==4Cπ=，又sin sinAC ABB C=，sinsinAB BACC∴==AB∴边上的高sin 6.h AC A===【解析】本题考查了三角恒等变换与解三角形的相关知识，属于中等题.(1)根据题意，结合A B Cπ++=可直接求出C，再将C代入2sin()sinA C B−=进行恒等变换得sin3cosA A=，最后再结合同角三角函数的基本关系即可求解；(2)结合三角恒等变换、正弦定理，分别求出sin B和AC，即可得AB边上的高sinAC A的值.4.（2023·新课标II卷第17题）记ABC的内角A，B，C的对边分别为a，b，c，已知ABC，D为BC的中点，且 1.AD=(1)若3ADCπ∠=，求tan B；(2)若228b c+=，求b，.c【答案】解：(1)ABCS=，D为BC的中点，ADCS∴11sin122AD CD ADC CD⋅⋅∠=××=，解得2CD=，则 2.BD=过点A作AE CD⊥于点E，则在ADE中，AE=12DE=，∴在Rt AEB中，52BE BD DE=+=，tanAEBBE==(2) 在ABC 中，1()2AD AB AC =+，222222111||()(||||2)(2cos )444AD AB AC AB AC AB AC c b bc A ∴=+=++⋅=++ ，11(82cos )4bc A ∴=+，即cos 2bc A =−，又1sin 2ABC S bc A == ，sin bc A ∴，sintancos bc A Abc A ∴==23A π∴=，sin A =， 4.bc =再将4b c=代入228b c +=，即可解得 2.b c == 【解析】本题考查了解三角形的综合应用，属于中等题.(1)结合三角形面积和中点关系进行求解；(2)观察题目所给条件，结合中线的向量表示和三角形面积进行求解.【2022年真题】5.（2022·新高考I 卷 第3题）在ABC 中，点D 在边AB 上，2.BD DA =记CA m = ，CD n = ，则CB =( ) A. 32m n −B. 23m n −+C. 32m n +D. 23m n +【答案】B 【解析】 【分析】本题主要考查向量的加减及数乘运算，属于基础题. 【解答】解：2133CD CA CB =+ ，3223.CB CD CA m n =−=−+6.（2022·新高考II 卷 第4题）已知向量(3,4)a = ，(1,0)b = ，c a tb =+ ，若,,a c b c <>=<> ，则实数t =( ) A. 6− B. 5−C. 5D. 6【答案】C 【解析】 【分析】本题考查了向量的坐标运算和夹角运算，属于基础题。

专题07平面向量考纲解读三年高考分析1.平面向量的实际背景及基本概念(1)了解向量的实际背景.(2)理解平面向量的概念,理解两个向量相等的含义.(3)理解向量的几何表示.2.向量的线性运算(1)掌握向量加法、减法的运算,并理解其几何意义.(2)掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.(3)了解向量线性运算的性质及其几何意义.3.平面向量的基本定理及坐标表示(1)了解平面向量的基本定理及其意义.(2)掌握平面向量的正交分解及其坐标表示.(3)会用坐标表示平面向量的加法、减法与数乘运算.(4)理解用坐标表示的平面向量共线的条件.4.平面向量的数量积(1)理解平面向量数量积的含义及其物理意义.(2)了解平面向量的数量积与向量投影的关系.(3)掌握数量积的坐标表达式,会进行平面向量数量积的运算.(4)能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.向量的应用(1)会用向量方法解决某些简单的平面几何问题.(2)会用向量方法解决简单的力学问题与其他一些实际问题.平面向量基本定理和向量的坐标运算是考查的重点，解题时常用到等价转化的数学思想和数形结合的数学思想，考查学生的逻辑推理能力、数学运算能力，题型以选择填空题为主，中等难度. 1、主要考查平面向量的线性运算(加法、减法、数乘向量)及其几何意义、共线向量定理常与三角函数、解析几何交汇考查，有时也会有创新的新定义问题；题型以选择题、填空题为主，属于中低档题目．偶尔会在解答题中作为工具出现.2、主要考查利用数量积的定义解决数量积的运算、投影、求模与夹角等问题，考查利用数量积的坐标表示求两个向量的夹角、模以及判断两个平面向量的平行与垂直关系．一般以选择题、填空题的形式考查，偶尔会在解答题中出现，属于中档题.3、主要考查平面向量基本定理、向量加法、减法、数乘向量的坐标运算及平面向量共线的坐标表示，考查向量线性运算的综合应用，考查学生的运算推理能力、数形结合能力，常与三角函数综合交汇考查，突出向量的工具性．一般以选择题、填空题形式考查，偶尔有与三角函数综合在一起考查的解答题，属于中档题.1．【2019年全国新课标2理科03】已知（2，3），（3，t），||＝1，则•（）A．﹣3 B．﹣2 C．2 D．3【解答】解：∵（2，3），（3，t），∴（1，t﹣3），∵||＝1，∴t﹣3＝0即（1，0），则• 2故选：C．2．【2019年新课标1理科07】已知非零向量，满足||＝2||，且（）⊥，则与的夹角为（）A．B．C．D．【解答】解：∵（）⊥，∴，∴，∵，∴．故选：B．3．【2019年北京理科07】设点A，B，C不共线，则“与的夹角为锐角”是“||＞||”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：点A，B，C不共线，“与的夹角为锐角”⇒“||＞||”，“||＞||”⇒“与的夹角为锐角”，∴设点A，B，C不共线，则“与的夹角为锐角”是“||＞||”的充分必要条件．故选：C．4．【2018年新课标1理科06】在△ABC中，AD为BC边上的中线，E为AD的中点，则（）A．B．C．D．【解答】解：在△ABC中，AD为BC边上的中线，E为AD的中点，（），故选：A．5．【2018年新课标2理科04】已知向量，满足||＝1，1，则•（2）＝（）A．4 B．3 C．2 D．0【解答】解：向量，满足||＝1，1，则•（2）＝22+1＝3，故选：B．6．【2018年浙江09】已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足4•3＝0，则||的最小值是（）A． 1 B． 1 C．2 D．2【解答】解：由4•3＝0，得，∴（）⊥（），如图，不妨设，则的终点在以（2，0）为圆心，以1为半径的圆周上，又非零向量与的夹角为，则的终点在不含端点O的两条射线y（x＞0）上．不妨以y为例，则||的最小值是（2，0）到直线的距离减1．即．故选：A．7．【2018年北京理科06】设，均为单位向量，则“|3|＝|3|”是“⊥”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：∵“|3|＝|3|”∴平方得||2+9||2﹣6•9||2+||2+6•，即1+9﹣6•9+1+6•，即12•0，则•0，即⊥，则“|3|＝|3|”是“⊥”的充要条件，故选：C．8．【2018年天津理科08】如图，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD＝120°，AB＝AD ＝1．若点E为边CD上的动点，则的最小值为（）A．B．C．D．3【解答】解：如图所示，以D为原点，以DA所在的直线为x轴，以DC所在的直线为y轴，过点B做BN⊥x轴，过点B做BM⊥y轴，∵AB⊥BC，AD⊥CD，∠BAD＝120°，AB＝AD＝1，∴AN＝AB cos60°，BN＝AB sin60°，∴DN＝1，∴BM，∴CM＝MB tan30°，∴DC＝DM+MC，∴A（1，0），B（，），C（0，），设E（0，m），∴（﹣1，m），（，m），0≤m，∴m2m＝（m）2（m）2，当m时，取得最小值为．故选：A．9．【2017年新课标2理科12】已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（）的最小值是（）A．﹣2 B．C．D．﹣1【解答】解：建立如图所示的坐标系，以BC中点为坐标原点，则A（0，），B（﹣1，0），C（1，0），设P（x，y），则（﹣x，y），（﹣1﹣x，﹣y），（1﹣x，﹣y），则•（）＝2x2﹣2y+2y2＝2[x2+（y）2]∴当x＝0，y时，取得最小值2×（），故选：B．10．【2017年新课标3理科12】在矩形ABCD中，AB＝1，AD＝2，动点P在以点C为圆心且与BD相切的圆上．若λμ，则λ+μ的最大值为（）A．3 B．2C．D．2【解答】解：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC＝2，CD＝1，∴BD∴BC•CD BD•r，∴r，∴圆的方程为（x﹣1）2+（y﹣2）2，设点P的坐标为（cosθ+1，sinθ+2），∵λμ，∴（cosθ+1，sinθ+2）＝λ（1，0）+μ（0，2）＝（λ，2μ），∴cosθ+1＝λ，sinθ+2＝2μ，∴λ+μcosθsinθ+2＝sin（θ+φ）+2，其中tanφ＝2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选：A．11．【2017年浙江10】如图，已知平面四边形ABCD，AB⊥BC，AB＝BC＝AD＝2，CD＝3，AC与BD 交于点O，记I1•，I2•，I3•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I3【解答】解：∵AB⊥BC，AB＝BC＝AD＝2，CD＝3，∴AC＝2，∴∠AOB＝∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0••，•0，即I3＜I1＜I2，故选：C．12．【2017年北京理科06】设，为非零向量，则“存在负数λ，使得λ”是“•0”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：，为非零向量，存在负数λ，使得λ，则向量，共线且方向相反，可得•0．反之不成立，非零向量，的夹角为钝角，满足•0，而λ不成立．∴，为非零向量，则“存在负数λ，使得λ”是•0”的充分不必要条件．故选：A．13．【2019年天津理科14】在四边形ABCD中，AD∥BC，AB＝2，AD＝5，∠A＝30°，点E在线段CB的延长线上，且AE＝BE，则•．【解答】解：∵AE＝BE，AD∥BC，∠A＝30°，∴在等腰三角形ABE中，∠BEA＝120°，又AB＝2，∴AE＝2，∴，∵，∴又，∴•＝﹣125×2＝﹣1故答案为：﹣1．14．【2019年新课标3理科13】已知，为单位向量，且•0，若2，则cos，．【解答】解：22，∵（2）2＝4459，∴||＝3，∴cos，．故答案为：15．【2019年江苏12】如图，在△ABC中，D是BC的中点，E在边AB上，BE＝2EA，AD与CE交于点O．若•6•，则的值是．【解答】解：设λ（），μμ（）＝（1﹣μ）μμ∴，∴，∴（），，6•6（）×（）（），∵•，∴，∴3，∴．故答案为：16．【2019年浙江17】已知正方形ABCD的边长为1．当每个λi（i＝1，2，3，4，5，6）取遍±1时，|λ1λ2λ3λ4λ5λ6|的最小值是，最大值是．【解答】解：正方形ABCD的边长为1，可得，，•0，|λ1λ2λ3λ4λ5λ6|＝|λ1λ2λ3λ4λ5λ5λ6λ6|＝|（λ1﹣λ3+λ5﹣λ6）（λ2﹣λ4+λ5+λ6）|，由于λi（i＝1，2，3，4，5，6）取遍±1，可得λ1﹣λ3+λ5﹣λ6＝0，λ2﹣λ4+λ5+λ6＝0，可取λ5＝λ6＝1，λ1＝λ3＝1，λ2＝﹣1，λ4＝1，可得所求最小值为0；由λ1﹣λ3+λ5﹣λ6，λ2﹣λ4+λ5+λ6的最大值为4，可取λ2＝1，λ4＝﹣1，λ5＝λ6＝1，λ1＝1，λ3＝﹣1，可得所求最大值为2．故答案为：0，2．17．【2018年江苏12】在平面直角坐标系xOy中，A为直线l：y＝2x上在第一象限内的点，B（5，0），以AB为直径的圆C与直线l交于另一点D．若0，则点A的横坐标为．【解答】解：设A（a，2a），a＞0，∵B（5，0），∴C（，a），则圆C的方程为（x﹣5）（x﹣a）+y（y﹣2a）＝0．联立，解得D（1，2）．∴．解得：a＝3或a＝﹣1．又a＞0，∴a＝3．即A的横坐标为3．故答案为：3．18．【2018年新课标3理科13】已知向量（1，2），（2，﹣2），（1，λ）．若∥（2），则λ＝．【解答】解：∵向量（1，2），（2，﹣2），∴（4，2），∵（1，λ），∥（2），∴，解得λ．故答案为：．19．【2018年上海08】在平面直角坐标系中，已知点A（﹣1，0）、B（2，0），E、F是y轴上的两个动点，且||＝2，则的最小值为．【解答】解：根据题意，设E（0，a），F（0，b）；∴；∴a＝b+2，或b＝a+2；且；∴；当a＝b+2时，；∵b2+2b﹣2的最小值为；∴的最小值为﹣3，同理求出b＝a+2时，的最小值为﹣3．故答案为：﹣3．20．【2017年江苏12】如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα＝7，与的夹角为45°．若m n（m，n∈R），则m+n＝．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα＝7．∴cosα，sinα．∴C．cos（α+45°）（cosα﹣sinα）．sin（α+45°）（sinα+cosα）．∴B．∵m n（m，n∈R），∴m n，0n，解得n，m．则m+n＝3．故答案为：3．21．【2017年新课标1理科13】已知向量，的夹角为60°，||＝2，||＝1，则|2|＝．【解答】解：【解法一】向量，的夹角为60°，且||＝2，||＝1，∴4•4＝22+4×2×1×cos60°+4×12＝12，∴|2|＝2．【解法二】根据题意画出图形，如图所示；结合图形2；在△OAC中，由余弦定理得||2，即|2|＝2．故答案为：2．22．【2017年浙江15】已知向量、满足||＝1，||＝2，则||+||的最小值是，最大值是．【解答】解：记∠AOB＝α，则0≤α≤π，如图，由余弦定理可得：||，||，令x，y，则x2+y2＝10（x、y≥1），其图象为一段圆弧MN，如图，令z＝x+y，则y＝﹣x+z，则直线y＝﹣x+z过M、N时z最小为z min＝1+3＝3+1＝4，当直线y＝﹣x+z与圆弧MN相切时z最大，由平面几何知识易知z max即为原点到切线的距离的倍，也就是圆弧MN所在圆的半径的倍，所以z max．综上所述，||+||的最小值是4，最大值是．故答案为：4、．23．【2017年天津理科13】在△ABC中，∠A＝60°，AB＝3，AC＝2．若2，λ（λ∈R），且4，则λ的值为．【解答】解：如图所示，△ABC中，∠A＝60°，AB＝3，AC＝2，2，∴（），又λ（λ∈R），∴（）•（λ）＝（λ）•λ＝（λ）×3×2×cos60°32λ×22＝﹣4，∴λ＝1，解得λ．故答案为：．1．【山东省聊城市2019届高三三模】在正方形ABCD 中，E 为DC 的中点，若AE AB AC λμ=+u u u r u u u r u u u r，则λμ+的值为（ ） A ．12-B ．12C ．1-D ．1【答案】B 【解析】由题得1111111122222222AE AD AC BC AC AC AB AC AB AC =+=+=-+=-+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ,11,1,22λμλμ∴=-=∴+=.故选：B2．【江西省鹰潭市2019届高三第一次模拟】已知向量a r与b r 的夹角为120︒，3a =r，||13a b +=rr，则||b =r（ ） A ．1B ．3C ．4D ．5【答案】C 【解析】解：根据条件，222||2a b a a b b +=+⋅+r r r r r r 293||||13b b =-+=r r ；∴解得4b =r，或1-（舍去）．故选C ．3．【山东省安丘市、诸城市、五莲县、兰山区2019届高三5月校际联合】已知1a =r ，2b =r ()a ab ⊥-r r r ，则向量a r 在b r方向上的正射影的数量为（ ）A ．1B 2C ．12D ．22【答案】D 【解析】由()a a b ⊥-r r r 得()0a a b ⋅-=r r r ，所以1a b a a ⋅=⋅=r r r r，所以向量a r 在b r方向上的正射影的数量为2cos ,22a b a a b b⋅===r rr r r r ，故选D.4．【辽宁省朝阳市重点高中2019届高三第四次模拟】已知P 为等边三角形ABC 所在平面内的一个动点，满足()BP BC R λλ=∈u u u r u u u r ，若2AB =u u u r ，则()AP AB AC u u u v u u u v u u u v⋅+=（ ）A ．23B ．3C ．6D ．与λ有关的数值【答案】C 【解析】如图：以BC 中点为坐标原点O ，以BC 方向为x 轴正方向，OA 方向为y 轴正方向，建立平面直角坐标系，因为2AB =u u u r ，则3AO =u u u r因为P 为等边三角形ABC 所在平面内的一个动点，满足()BP BC R λλ=∈u u u r u u u r， 所以点P 在直线BC ，所以AP uu u r 在AO uuur 方向上的投影为AO u u u v ，因此2()226AP AB AC AO AP AO ⋅+=⋅==u u u r u u u r u u u r u u u r u u u r u u u r .故选C5．【北京市朝阳区2019届高三第二次（5月)综合练习】已知平面向量,a b r r 的夹角为23π，且1,2a b ==r r ，则a b +=r r（ ）A ．3B ．3C ．7D ．7【答案】B 【解析】22221||||||2||||cos 14212332a b a b a b π⎛⎫+=++=++⨯⨯⨯-= ⎪⎝⎭r r r r r r ,所以a b +=r r3故选:B.6．【山东省淄博市部分学校2019届高三5月阶段性检测】如图，已知等腰梯形ABCD 中，24,5,AB DC AD BC E ====是DC 的中点，P 是线段BC 上的动点，则EP BP ⋅u u u r u u u r的最小值是（ ）A ．95- B ．0C ．45-D ．1【答案】A 【解析】由等腰梯形的知识可知5cos B = 设BP x =，则5CP x =，∴2565·()?··1?·((5)?·(1)55EP BP EC CP BP EC BP CP BP x x x x x u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v =+=+=-+-=-，05x Q 剟∴当35x =时，·EP BP u u u v u u u v 取得最小值95-．故选：A ．7．【广东省2019届高三适应性考试】已知ABC ∆，点M 是边BC 的中点，若点O 满足230OA OB OC ++=u u u r u u u r u u u r r，则（ ）A ．0OM BC •=u u u u r u u u rB ．0OM AB •=u u u u r u u u rC ．//OM BC u u u u r u u u rD ．//OM AB u u u u r u u u r【答案】D 【解析】点M 是边BC 的中点，可得2OM OB OC =+u u u u r u u u r u u u r，230OA OB OC u u u r u u u r u u u r r ++=，可得OA OC ++u u u r u u u r 2（OB OC +u u u r u u u r）23OA OB OA +=-+u u u r u u u ru u u r 40OM =u u u u r r ，即2（OA OB u u u r u u u r -）+120OM =u u u u r r ， 可得AB =u u u r6OM u u u u r ， 即OM u u u u r ∥AB u u u r ，故选：D ．8．【内蒙古呼伦贝尔市2019届高三模拟统一考试】已知菱形ABCD 的边长为2，60ABC ∠=︒，则BD CD ⋅=u u u r u u u r（）A ．4B ．6C ．23D ．3【答案】B 【解析】 如图所示，菱形形ABCD 的边长为2，60ABC ∠=︒，∴120C ∠=︒，∴22222222cos12012BD =+-⨯⨯⨯︒=， ∴23BD =30BDC ∠=︒，∴|||3302|326BD CD BD CD cos =⨯⨯︒==⋅u u u r u u u r u u u r u u u r， 故选B ．9．【山东省临沂市2019年普通高考模拟考试】在ABC ∆中，AB AC AB AC +=-u u u r u u u r u u u r u u u r，2AB =，1AC =，E ，F 为AB 的三等分点，则CE CF u u u v u u u v⋅=（ ）A ．89B ．109C ．179D ．259【答案】C 【解析】因为AB AC AB AC +=-u u u r u u u r u u u r u u u r ，所以22AB AC AB AC +=-u u u r u u u r u u u r u u u r ，化为AB AC 0⋅=uu u r uu u r，因为2AB =，1AC =，所以224,1AB AC ==u u u r u u u r ，又因为E ，F 为AB 的三等分点，所以()()E C CF CA AE CA AF ⋅=+⋅+uu r uu u r uu r uu u r uu r uu u r1233CA AB CA AB ⎛⎫⎛⎫=+⋅+ ⎪ ⎪⎝⎭⎝⎭u u ur u u u r u u u r u u u r2229CA AB CA AB =++⋅u u u r u u u r u u u r u u u r21714099=+⨯+=，故选C.10．【湖南省师范大学附属中学2019届高三下学期模拟（三)】在ABC ∆中，90A ∠=︒，1AB =，2AC =，设点D 、E 满足AD AB λ=u u u r u u u r ，(1)AE λ=-u u u r ()AC R λ∈u u u r ，若5BE CD ⋅=u u u r u u u r，则λ=（ ）A ．13- B ．2 C ．95D ．3【答案】D 【解析】因为90A ∠=︒，则•0AB AC =u u u r u u u r，所以()()BE CD AE AB AD AC •=-•-u u u r u u u r u u u r u u u r u u u r u u u r22[(1)]()(1)4(1)34AC AB AB AC AC AB λλλλλλλ=--•-=---=---=-u u u u r u u u r u u u r u u u r u u u r u u u r .由已知，345λ-=，则3λ=. 选D .11．【广东省深圳市高级中学2019届高三适应性考试】在平行四边形ABCD 中，113,2,,D,32AB AD AP AB AQ A ====uu u r uu u r uuu r uuu r 若CP C 12,Q ⋅=uu r uu u r则ADC ∠=( )A ．56πB ．34π C ．23π D ．2π【答案】C 【解析】如图所示,平行四边形ABCD 中, 3,2AB AD ==,11,32AP AB AQ AD ==u u u r u u u r u u u r u u u r ，23CP CB BP AD AB ∴=+=--u u u r u u u r u u u r u u u r u u u r ，12CQ CD DQ AB AD =+=--u u u r u u u r u u u r u u u r u u u r ,因为12CP CQ ⋅=u u u r u u u r,所以2132CP CQ AD AB AB AD ⎛⎫⎛⎫⋅=--⋅-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r22214323AB AD AB AD =++⋅u u ur u u u r u u u r u u u r222143232cos 12323BAD =⨯+⨯+⨯⨯⨯∠=, 1cos 2BAD ∠=，,3BAD π∴∠= 所以233ADC πππ∠=-=，故选C. 12．【广东省2019届高考适应性考试】若向量a r ，b r ，c r满足a b ≠r r ，0c ≠r r ，且()()0c a c b -⋅-=r r r r ，则a b a bc++-r r r r r 的最小值是（ ） A 3 B ．22C ．2D ．32【答案】C 【解析】设向量a OA =r u u u r ，b OB =r u u u r ，c OC =r u u u r ,则由()()0c a c b -⋅-=r r r r 得0AC BC ⋅=u u u r u u u r,即C 的轨迹为以AB 为直径的圆，圆心为AB 中点M ，半径为1||2AB u u ur ，因此11||||||(||)||22c OC OM r OA OB AB =≤+=++r u u u r u u u u r u u u r u u u r u u u r1111(||)(||)(||)(||)2222OA OB OA OB a b a b =++-=++-u u u r u u u r u u u r u u u r r r r r 从而2a b a bc++-≥r r r r r ，选C. 13．【江苏省徐州市2018-2019学年高三考前模拟检测】已知12,e e u v u u v 是夹角为3π的两个单位向量，向量122a e e =+v u v u u v ，12b ke e =-v u v u u v ，若0a b ⋅=v v，则实数k 的值为____．【答案】54【解析】()()121202ke a b e e e ⋅==+-⋅v v u v u u v u v u u v ，因为22121e e ==u v u u v ，1212e e ⋅=u v u u v ，所以1522022a b k k k ⋅=-+-=-=v v ， 所以54k =，填54.14．【广东省肇庆市2019届高中毕业班第三次统一检测】在ABC ∆中，3AB =，2BC =，7AC =，则BA BC ⋅=u u u v u u u v______．【解析】解：在ABC ∆中，3AB =，2BC =，7AC =，可得9471cos 2322B +-==⨯⨯，则13232BA BC ⋅=⨯⨯=u u u r u u u r .故答案为：3．15．【2019年湖北省武汉市高考数学(5月份)模拟】已知向量(1,2)a =v，(2,1)b =v ，(1,)c n =v，若(23)a b c -⊥v v v，则n =_____【答案】4 【解析】23(4,1)a b -=-v r；∵()23a b c -⊥v v r ；∴()230a b c -=v vr g；∴4n =． 故答案为：4．16．【江西省南昌市江西师范大学附属中学2019届高三三模】已知平面向量1a =r，2b =r ，223a b r r +=，则a r 在b r方向上的射影为_____．【答案】12【解析】223a b +=r Q r ()222222448412a b a ba ab b a b ∴+=+=+⋅+=+⋅=r r r r rr r r r r解得：1a b ⋅=r ra ∴r 在b r 方向上的射影为：1cos ,2a b a a b br r r r r r ⋅== 本题正确结果：1217．【河南省八市重点高中联盟“领军考试”2019届高三】已知向量()cos ,sin a θθ=r，向量(1,22b =-r ，则3a b -r r的最大值是______.【解析】由题意，向量()cos ,sin a θθ=r ，则()33cos ,3sin a θθ=r，所以向量3a r的终点在以原点为圆心，3为半径的圆上，又由3b =r，则其终点也在此圆上，当3a r 与b r反向时，3a b -r r 为最大，最大值为6.18．【天津市北辰区2019届高考模拟考试】平行四边形ABCD 中，4,2,4AB AD AB AD ==⋅=u u u v u u u v，点P 在边CD 上，则AP PC ⋅u u u r u u u r的取值范围是______． 【答案】250,4⎡⎤⎢⎥⎣⎦【解析】因为点P 在边CD 上，所以设()01DP λDC λAB λ==≤≤u u u r u u u ru u u r ， 则 λAP AD DP A A D B =+=+u u u r u u u r u u u r u u u r u u u r ，() 1PC λAB -=u u ur u u u r ， 所以()()1PC A AP D λλAB AB ⋅=+⋅-u u u r u u u r u u u r u u u r u u u r()()223 141161612445224λλλλλλ⎛⎫=-+-⨯=-++=-- ⎪⎝+⎭，又01λ≤≤，所以2504AP PC ≤⋅≤u u u r u u u r ，故答案为250,4⎡⎤⎢⎥⎣⎦．19．【四川省名校联盟2019届高考模拟信息卷（一)】直线x y a +=与圆C ：()2212x y -+=交于A ，B 两点，向量CA u u u r ，u u rCB 满足CA CB CA CB +=-u u u r u u u r u u u r u u u r ，则实数a 的取值集合为______.【答案】{}12,12+ 【解析】解：由CA u u u r ，u u r CB 满足CA CB CA CB +=-u u u r u u u r u u u r u u u r ，得CA CB ⊥u u u r u u u r ，圆C ：()2212x y -+=的圆心为()1,0，半径为2，点C 到直线x y a +=的距离为1，由112a d -==，得12a =±.故实数a 的取值集合为{}12,12-+.20．【江西省临川一中2019届高三年级考前模拟】如图，点D 在ABC ∆的边AC 上，且3CD AD =，2BD =，10cos24ABC ∠=，则3AB BC +的最大值为________．165【解析】 因为10cos24ABC ∠=， 所以22101cos 2cos 121244ABC ABC ⎛∠∠=-=-= ⎝⎭因为3CD AD =，所以3uu u r uu u rCD DA =即()3uu u r uu u r uu r uu u r BD BC BA BD -=-，整理得到3144uu u r uu r uu u r BD BA BC =+，两边平方后有22291316168uu u r uu r uu u r uu r uu u rBD BA BC BA BC =++⋅，所以22913216168u u r u u u r u u r u u u r BA BC BA BC =++⋅即2291312||||161684u u r u u ur u u r u u u r BA BC BA BC =++⋅⨯， 整理得到2233292u u r u u u r u u r u u u r BA BC BA BC =++⋅，设,uu r uu u r c BA a BC ==，所以()22239329322c a ac c a ac =++=+-，因为2933332222ac a c a c ⨯⨯+⎛⎫=≤⨯ ⎪⎝⎭，所以()()()()2222935323333288c a ac c a c a c a =+-≥+-+=+，8325355c a ⨯+≤=，当且仅当855a =，515c =时等号成立，故填165 5.1．在平行四边形ABCD中，，边AB、AD的长分别为2、1，若M、N分别是边BC、CD上的点，且满足，则的最大值为5．【解答】解：设k，则k∈[0，1]；建立如图所示的坐标系，则A（0，0），B（2，0），D（，），C（，），由k，k，可得k（2k，k），同理可得（2k，），∴•（2k）（2k）k＝﹣k2﹣2k+5＝﹣（k+1）2+6，∵k∈[0，1]，∴﹣（k+1）2+6≥﹣1+6＝5，•的最大值是5，当且仅当M、N与点C重合时取得最大值．故答案为：D．2．已知，，若，则k＝8．【解答】解：2（9，2+2k），3（﹣1，6﹣k）；∵（2）∥（3），∴9（6﹣k）﹣（﹣1）（2+2k）＝0，解得k＝8．故答案为：8．3．已知非零向量，满足4||＝3||，若⊥（﹣4）则，夹角的余弦值为【解答】解：∵非零向量，满足4||＝3||，若⊥（﹣4），∴||||，且•（﹣4）40，即．设，夹角为θ，则cosθ，故答案为：．4．已知向量，且，则与的夹角为．【解答】解：∵；∴；∴4k＝3；∴；∴，且；设与的夹角为θ，则：；又0≤θ≤π；∴．故答案为：．5．已知，且，共线，则向量在方向上的投影为．【解答】解：由，且，共线，得1×（﹣4）﹣2t＝0，解得t＝﹣2．∴向量在方向上的投影为．故答案为：．。

平面向量【题型1 平面向量共线定理及其应用】 (4)【题型2 平面向量基本定理及其应用】 (5)【题型3 平面向量的数量积】 (7)【题型4 平面向量的模的问题】 (8)【题型5 平面向量夹角与垂直问题】 (9)【题型6 极化恒等式】 (10)【题型7 向量与解三角形综合】 (10)【题型8 向量与几何最值、范围问题】 (11)【题型9 向量在几何中的其他应用】 (12)平面向量是高考的必考内容之一.从近几年的高考情况来分析，平面向量的数量积、模、夹角是高考考查的重点、热点，试题主要以选择题、填空题的形式呈现，常常以平面图形为载体，考查数量积、模、夹角与垂直的条件等问题，也时也会与平面解析几何、三角函数、不等式等知识相结合，以工具的形式出现，试题难度中等.学生在高考复习中应注意加强对平面向量的数量积、模、夹角等知识的掌握，能灵活运用向量知识解决有关问题.【知识点1 平面向量线性运算问题的解题策略】1.平面向量线性运算问题的求解思路：(1)解决平面向量线性运算问题的关键在于熟练地找出图形中的相等向量，并能熟练运用相反向量将加减法相互转化；(2)在求向量时要尽可能转化到平行四边形或三角形中，运用平行四边形法则、三角形法则及三角形中位线定理、相似三角形对应边成比例等平面几何的性质，把未知向量转化为用已知向量线性表示.2.向量线性运算的含参问题的解题策略：与向量的线性运算有关的参数问题，一般是构造三角形，利用向量运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数的值.3.利用共线向量定理解题的策略：(1)是判断两个向量共线的主要依据.注意待定系数法和方程思想的运用.(2)当两向量共线且有公共点时，才能得出三点共线，即A,B,C三点共线共线.(3)若与不共线且，则(4)λ,μ为实数)，若A,B,C三点共线，则λ+μ=1.【知识点2 平面向量基本定理的解题策略】1.应用平面向量基本定理求向量的实质应用平面向量基本定理求向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.一般将向量“放入”相关的三角形中，利用三角形法则列出向量间的关系.2.用平面向量基本定理解决问题的一般思路：用平面向量基本定理解决问题的一般思路是：先选择一个基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决.注意同一个向量在不同基底下的分解是不同的，但在每个基底下的分解都是唯一的.【知识点3 平面向量坐标运算的方法技巧】1.平面向量坐标运算的技巧(1)向量的坐标运算主要是利用向量加、减、数乘运算的法则来进行求解的，若已知有向线段两端点的坐标，则应先求向量的坐标.(2)解题过程中，常利用向量相等其坐标相同这一原则，通过列方程(组)来进行求解.【知识点4 平面向量数量积问题的解题方法】1.平面向量数量积的两种运算方法(1)基底法：当已知向量的模和夹角时，可利用定义法求解，适用于平面图形中的向量数量积的有关计算问题；(2)坐标法：当平面图形易建系求出各点坐标时，可利用坐标法求解.2.夹角与垂直问题根据平面向量数量积的性质：若，为非零向量，则(夹角公式)等，可知平面向量的数量积可以用来解决有关角度、垂直问题.3.向量的模的求解思路：(1)坐标法：当向量有坐标或适合建坐标系时，可用模的计算公式；(2)公式法：利用，把向量的模的运算转化为数量积运算；(3)几何法：利用向量的几何意义，即利用向量加减法的平行四边形法则或三角形法则作出向量，再利用余弦定理等方法求解. 【知识点5 极化恒等式】1.极化恒等式的证明过程与几何意义(1)平行四边形对角线的平方和等于四边的平方和：2222||||2(||||)a b a b a b ++−=+r r r r r r .证明：不妨设,AB a AD b ==u u u r r u u u r r ，则C A a b =+u u u r r r ，DB a b =−u u u r r r，()22222C AC A a ba ab b ==+=+⋅+u u u r u u u r r r r r r ①， ()222222DB DB a ba ab b ==−=−⋅+u u u r u u u r r r r r r r ②，①②两式相加得：()()22222222AC DB a b AB AD +=+=+u u u r u u u r r r u u u r u u u r .(2)极化恒等式：上面两式相减，得：()()2214a b a b ⎡⎤+−−⎢⎥⎣⎦r rr r ————极化恒等式平行四边形模式：2214a b AC DB ⎡⎤⋅=−⎣⎦r r .(3)几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14． 【知识点6 平面向量的应用的方法技巧】1.平面向量的应用的解题方法；平面向量的应用方向主要是平面几何问题，往往涉及角和距离，转化成平面向量的夹角、模的问题，主要解题方法有：(1)坐标法：把几何图形放在适当的坐标系中，就赋予了有关点与向量具体的坐标，这样就能进行相应的代数运算和向量运算，从而使问题得到解决.(2)基向量法：适当选取一组基底，写出向量之间的联系，利用向量共线构造关于设定未知量的方程来进行求解.(3)利用向量运算进行转化，化归为三角函数的问题或三角恒等变换问题是常规的解题思路和方法，以向量为载体考查三角形问题时，要注意正弦定理、余弦定理等知识的应用.2.平面向量中的最值（范围）问题的两类求解思路：(1)“形化”，即利用平面向量的相关知识将问题转化为平面几何中的最值或范围问题，然后结合平面图形的特征直接进行判断；(2)“数化”，即利用平面向量的坐标运算，把问题转化为代数中的函数最值与值域、不等式的解集、方程有解等问题，然后利用函数、不等式、方程的有关知识来解决．【题型1 平面向量共线定理及其应用】【例1】（2023·江苏·统考模拟预测）在△ABC 中，AD ⃗⃗⃗⃗⃗ =2DB ⃗⃗⃗⃗⃗⃗ ，点P 在CD 上，且AP⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +13AB ⃗⃗⃗⃗⃗ (m ∈R)，则m =（ ）A ．15B ．14C ．13D ．12【变式1-1】（2023下·江苏连云港·高一校考阶段练习）设e 1⃗⃗⃗ ，e 2⃗⃗⃗ 是两个不共线的向量，已知AB ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ −ke 2⃗⃗⃗ ，CB ⃗⃗⃗⃗⃗ =e 1⃗⃗⃗ +3e 2⃗⃗⃗ ，CD ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ −e 2⃗⃗⃗ ，若三点A ，B ，D 共线，则k 的值为（ ）A ．－8B ．8C ．6D ．－6【变式1-2】（2023·陕西安康·统考一模）已知O 是△ABC 内一点，2OA ⃗⃗⃗⃗⃗ +3OB ⃗⃗⃗⃗⃗ +mOC ⃗⃗⃗⃗⃗ =0⃗ ，若△AOB 与△ABC 的面积之比为47，则实数m 的值为（ ）A ．−103B ．103C ．−203D ．203【变式1-3】（2023·全国·高一专题练习）在△OAB 中，OA ⃗⃗⃗⃗⃗ =3OC ⃗⃗⃗⃗⃗ ，OB ⃗⃗⃗⃗⃗ =2OD ⃗⃗⃗⃗⃗⃗ ，AD ，BC 的交点为M ，过M 作动直线l 分别交线段AC ，BD 于E ，F 两点.若OE ⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗ ，OF ⃗⃗⃗⃗⃗ =μOB ⃗⃗⃗⃗⃗ (λ,μ>0)，则λ+μ的最小值为（ ）A ．3+√35B ．2+2√37C ．3+2√35D ．3+2√25【题型2 平面向量基本定理及其应用】【例2】（2023·广东汕头·统考三模）如图，点D 、E 分别AC 、BC 的中点，设AB ⃗⃗⃗⃗⃗ =a ，AC ⃗⃗⃗⃗⃗ =b ⃗ ，F 是DE 的中点，则AF⃗⃗⃗⃗⃗ =（ ）A ．12a +12b⃗ B ．−12a +12b⃗ C ．14a +12b⃗ D ．−14a +12b⃗【变式2-1】（2023·河北沧州·校考模拟预测）在△ABC中BE⃗⃗⃗⃗⃗ =12EC⃗⃗⃗⃗⃗ ,BF⃗⃗⃗⃗⃗ =12(BA⃗⃗⃗⃗⃗ +BC⃗⃗⃗⃗⃗ )，点P为AE与BF的交点，AP⃗⃗⃗⃗⃗ =λAB⃗⃗⃗⃗⃗ +μAC⃗⃗⃗⃗⃗ ，则λ−μ=（）A．0B．14C．12D．34【变式2-2】（2023·湖南娄底·娄底市第三中学校联考三模）2000多年前，古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割.所谓黄金分割点，指的是把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，黄金分割比为√5−12.如图，在矩形ABCD中，AC与BD相交于点O，BF⊥AC,DH⊥AC,AE⊥BD,CG⊥BD，且点E为线段BO的黄金分割点，则BF⃗⃗⃗⃗⃗ =（）A．3−√52BA⃗⃗⃗⃗⃗ +5+√510BG⃗⃗⃗⃗⃗ B．3−√52BA⃗⃗⃗⃗⃗ +5−√510BG⃗⃗⃗⃗⃗C．√5−12BA⃗⃗⃗⃗⃗ +5−√510BG⃗⃗⃗⃗⃗ D．3−√52BA⃗⃗⃗⃗⃗ +√55BG⃗⃗⃗⃗⃗【变式2-3】（2023·重庆江北·校考一模）如图，在△ABC中，点D是边AB上一点且BD=2AD，E是边BC的中点，直线AE和直线CD交于点F，若BF是∠ABC的平分线，则|BC||BA|=（）A．4B．3C．2D．12【题型3 平面向量的数量积】【例3】（2023·辽宁朝阳·朝阳市第一高级中学校考模拟预测）已知向量a =(1,2)，b ⃗ =(3,4)，c =(5,m )（m ∈R ），则(2a −b ⃗ )⋅c =（ ）A ．5B ．−5C ．5mD ．−5m【变式3-1】（2023·全国·模拟预测）已知向量a ，b ⃗ 满足a =λb ⃗ (λ>0)，|b ⃗ |=2，|a −b ⃗ |=1，则(a +b ⃗ )⋅a =（ ）A ．3B ．15C ．-3或15D ．3或15【变式3-2】（2023·广东佛山·统考一模）设四边形ABCD 为矩形，|AB⃗⃗⃗⃗⃗ |=6，|AD ⃗⃗⃗⃗⃗ |=4，若点M ，N 满足BM ⃗⃗⃗⃗⃗⃗ =13MC ⃗⃗⃗⃗⃗⃗ ，DN ⃗⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ ，则AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =（ ） A ．28B ．32C ．36D ．40【变式3-3】（2023·广东广州·华南师大附中校考一模）如图，在等腰梯形ABCD 中，AB ∥ CD,AB =5,AD =4,DC =1,E 是线段AB 上一点，且AE =4EB ，动点P 在以E 为圆心，1为半径的圆上，则DP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的最大值为（ ）A ．√3−√21B ．2√3−6C ．√21−6D ．−√3【题型4 平面向量的模的问题】【例4】（2023·四川成都·成都七中校考一模）若向量a 、b ⃗ 满足：|a |=1，(a +b ⃗ )⊥a ，|2a −b ⃗ |=√10，则|b⃗ |=（ ） A ．2 B ．√2 C ．10 D ．√10【变式4-1】（2023·全国·模拟预测）已知向量a =(x,1)，b ⃗ =(2,y)，c =(x,y).若(a +b ⃗ )⊥(a −b ⃗ )，且a //b ⃗ ，则|c |=（ ）A ．√2B ．√3C ．√5D ．√6【变式4-2】（2023·四川甘孜·统考一模）已知平面向量a ,b ⃗ ,|a |=2,|b ⃗ |=1，且a 与b ⃗ 的夹角为π3，则|a −2b⃗ |=（ ）A ．√5B ．4C ．2D ．0【变式4-3】（2023上·安徽·高二校联考期中）如图，在长方形 ABCD 中，AB =6,AD =4，点 P 满足DP ⃗⃗⃗⃗⃗ =λDC⃗⃗⃗⃗⃗ ，其中λ∈[0,23]，则|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |的取值范围是（ ）A．[4,5]B．[8,10]C．[4,√17]D．[2√17,10]【题型5 平面向量夹角与垂直问题】【例5】（2023·陕西西安·校联考模拟预测）向量a，b⃗满足|a|=4，|b⃗|=1，(2a−3b⃗)⋅b⃗=3，则向量a，b⃗夹角的余弦值为（）A．23B．34C．−34D．−23【变式5-1】（2023·全国·模拟预测）已知向量a=(−1,−2)，b⃗=(4,−2)，若(a−λb⃗)⊥(a+μb⃗)，则（）A．4λμ=1B．4λμ=−1C．4(λ+μ)=1D．4(λ+μ)=−1【变式5-2】（2023·四川巴中·南江中学校考模拟预测）已知平面向量a=(2,0)，b⃗=(1,√3)，则向量a−b⃗与a−12b⃗的夹角为（）A．π6B．π3C．2π3D．5π6【变式5-3】（2023·全国·模拟预测）已知△ABC 中，AO ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +(1−λ)AC ⃗⃗⃗⃗⃗ ，且O 为△ABC 的外心．若BA ⃗⃗⃗⃗⃗ 在BC⃗⃗⃗⃗⃗ 上的投影向量为μBC ⃗⃗⃗⃗⃗ ，且cos∠AOC ∈[13,23]，则μ的取值范围为（ ） A ．[23,56]B ．[15,310]C ．[43,53]D ．[15,35]【题型6 极化恒等式】【例6】（2023·福建宁德·校考二模）在平行四边形ABCD 中，已知DE ⃗⃗⃗⃗⃗ =12EC ⃗⃗⃗⃗⃗ ，BF ⃗⃗⃗⃗⃗ =12FC ⃗⃗⃗⃗⃗ ，|AE ⃗⃗⃗⃗⃗ |=√2，|AF⃗⃗⃗⃗⃗ |=√6，则AC ⃗⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ = ．【变式6-1】（2023·四川乐山·统考一模）已知正方形ABCD 边长为2√2，MN 是正方形ABCD 的外接圆的一条动弦，|MN |=2，P 为正方形ABCD 边上的动点，则MP ⃗⃗⃗⃗⃗⃗ ⋅PN ⃗⃗⃗⃗⃗⃗ 的最大值为 .【变式6-2】（2022·全国·高一假期作业）设三角形ABC ，P 0是边AB 上的一定点，满足P 0B =14AB ，且对于边AB 上任一点P ，恒有PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ ≥P 0B ⃗⃗⃗⃗⃗⃗⃗ ⋅P 0C ⃗⃗⃗⃗⃗⃗⃗ ，则三角形ABC 形状为 .【变式6-3】（2022·湖北省直辖县级单位·湖北省仙桃中学校考模拟预测）如图直角梯形ABCD 中，EF 是CD 边上长为6 的可移动的线段，AD =4，AB =8√3，BC =12 ，则BE ⃗⃗⃗⃗⃗ ⋅BF⃗⃗⃗⃗⃗ 的取值范围为 .【题型7 向量与解三角形综合】【例7】（2023·上海普陀·曹杨二中校考模拟预测）已知点O 为△ABC 的外心，且AO ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ +BO ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ <CO ⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ ，则△ABC 为（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定【变式7-1】（2023·山东济南·统考三模）在△ABC 中，若|AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ |=2,|BC ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ |=3，则△ABC 面积的最大值为（ ）A ．38B ．34C ．1D ．√52【变式7-2】（2023·福建厦门·厦门一中校考二模）在△AOB 中，已知|OB⃗⃗⃗⃗⃗ |=√2，|AB ⃗⃗⃗⃗⃗ |=1，∠AOB =45°，若OP ⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗ +μOB ⃗⃗⃗⃗⃗ ，且λ+2μ=2，μ∈[0,1]，则OA ⃗⃗⃗⃗⃗ 在OP ⃗⃗⃗⃗⃗ 上的投影向量为me （e 为与OP ⃗⃗⃗⃗⃗ 同向的单位向量），则m 的取值范围是（ ）A ．[−√22,1] B ．[√22,1] C ．(−√22,1] D ．(√22,1]【变式7-3】（2023下·江苏扬州·高一统考期中）如图，在平面四边形ABCD 中，AB ⊥BC ，∠BCD =60°，∠ADC =150°，BE =3EC ，CD =2√33，BE =√3，若点F 为边AD 上的动点，则EF⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的最小值为（ ）A ．1B ．1516C ．3132D ．2【题型8 向量与几何最值、范围问题】【例8】（2023·贵州毕节·统考二模）等腰三角形ABC 内接于半径为2的圆O 中，AB =AC =2，且M 为圆O 上一点，则MO ⃗⃗⃗⃗⃗⃗ ⋅MA ⃗⃗⃗⃗⃗⃗ +MB ⃗⃗⃗⃗⃗⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ 的最大值为（ ）A ．2B ．5C ．14D ．16【变式8-1】（2023·山东日照·统考一模）已知正六边形ABCDEF 的边长为2，P 是正六边形ABCDEF 边上任意一点，则PA⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ 的最大值为（ ） A ．13 B ．12 C ．8 D ．2√3【变式8-2】（2023·重庆·统考模拟预测）在正方形ABCD 中，动点E 从点B 出发，经过C ，D ，到达A ，AE ⃗⃗⃗⃗⃗ =λAB⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ ，则λ+μ的取值范围是（ ） A ．[−1,1] B ．[0,1] C ．[−1,2] D ．[0,2]【变式8-3】（2023·河南郑州·统考模拟预测）已知△ABC 中，AB =AC =2√2，|AB ⃗⃗⃗⃗⃗ +λBC ⃗⃗⃗⃗⃗ |min =2(λ∈R )，AM ⃗⃗⃗⃗⃗⃗ =12MB ⃗⃗⃗⃗⃗⃗ ，AP ⃗⃗⃗⃗⃗ =sin 2α⋅AB ⃗⃗⃗⃗⃗ +cos 2α⋅AC⃗⃗⃗⃗⃗ ，α∈[π6,π3]，则|MP ⃗⃗⃗⃗⃗⃗ |的取值范围为（ ） A ．[4√23,4√53] B ．[43,4√53] C ．[√173,√413] D ．[43,√413]【题型9 向量在几何中的其他应用】【例9】（2023·甘肃天水·统考二模）已知非零向量AB ⃗⃗⃗⃗⃗ 与AC ⃗⃗⃗⃗⃗ 满足AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗|AB ⃗⃗⃗⃗⃗ |=CA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗|AC ⃗⃗⃗⃗⃗ |且AB ⃗⃗⃗⃗⃗|AB ⃗⃗⃗⃗⃗|·AC⃗⃗⃗⃗⃗ |AC⃗⃗⃗⃗⃗ |=12，则△ABC 为（ ）A ．三边均不相等的三角形B ．直角三角形C ．等腰非等边三角形D ．等边三角形【变式9-1】（2023·江西抚州·校考模拟预测）△ABC 是等腰直角三角形，C =90°，AB =2，D 为AB 的中点，动点E 在边AC 上，线段CD 与BE 交于点P ，设t =BP⃗⃗⃗⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ ，当动点E 自点C 向点A 运动的过程中，下列说法正确的是（ ）A ．t 一直增大B ．t 一直减小C ．t 先增大后减小D ．t 为定值【变式9-2】（2023·吉林·统考三模）已知A ､B 为平面上的两个定点，且|AB⃗⃗⃗⃗⃗ |=2，该平面上的动线段PQ 的端点P ､Q ，满足|AP ⃗⃗⃗⃗⃗ |≤5，AP ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =6，AQ ⃗⃗⃗⃗⃗ =−2AP⃗⃗⃗⃗⃗ ，则动线段PQ 所形成图形的面积为（ ） A ．36 B ．60C ．72D ．108【变式9-3】（2023·浙江·校联考二模）如图，正方形ABCD 的中心与圆O 的圆心重合，P 是圆O 的动点，则下列叙述不正确的是（ ）A ．PA ⃗⃗⃗⃗⃗ ⋅PC⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ 是定值； B ．PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ +PD ⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗ 是定值； C ．|PA⃗⃗⃗⃗⃗ |+|PB ⃗⃗⃗⃗⃗ |+|PC ⃗⃗⃗⃗⃗ |+|PD ⃗⃗⃗⃗⃗ |是定值； D ．PA ⃗⃗⃗⃗⃗ 2+PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2+PD ⃗⃗⃗⃗⃗ 2是定值．1．（2023·北京·统考高考真题）已知向量a ，b ⃗ 满足a +b ⃗ =(2,3),a −b ⃗ =(−2,1)，则|a |2−|b⃗ |2=（ ）A ．−2B ．−1C ．0D ．12．（2023·全国·统考高考真题）已知向量a =(3,1),b ⃗ =(2,2)，则cos⟨a +b ⃗ ,a −b ⃗ ⟩=（ ） A ．117B ．√1717C ．√55D ．2√553．（2023·全国·统考高考真题）已知向量a ,b ⃗ ,c 满足|a |=|b ⃗ |=1,|c |=√2，且a +b ⃗ +c =0⃗ ，则cos〈a −c ,b ⃗ −c 〉=（ ） A ．−45B ．−25C ．25D ．454．（2023·全国·统考高考真题）已知⊙O 的半径为1，直线P A 与⊙O 相切于点A ，直线PB 与⊙O 交于B ，C 两点，D 为BC 的中点，若|PO |=√2，则PA ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ 的最大值为（ ） A ．1+√22B ．1+2√22C ．1+√2D ．2+√25．（2023·全国·统考高考真题）已知向量a =(1,1),b ⃗ =(1,−1)，若(a +λb ⃗ )⊥(a +μb ⃗ )，则（ ） A ．λ+μ=1 B ．λ+μ=−1 C ．λμ=1 D ．λμ=−16．（2022·全国·统考高考真题）已知向量a =(2,1)，b ⃗ =(−2,4)，则|a −b ⃗ |（ ） A ．2 B ．3C ．4D ．57．（2022·全国·统考高考真题）在△ABC 中，点D 在边AB 上，BD =2DA ．记CA ⃗⃗⃗⃗⃗ =m ⃗⃗ ，CD ⃗⃗⃗⃗⃗ =n ⃗ ，则CB ⃗⃗⃗⃗⃗ =（ ） A ．3m ⃗⃗ −2n ⃗B ．−2m ⃗⃗ +3n ⃗C ．3m ⃗⃗ +2n ⃗D ．2m ⃗⃗ +3n ⃗8．（2023·全国·统考高考真题）已知向量a ，b ⃗ 满足|a −b ⃗ |=√3，|a +b ⃗ |=|2a −b ⃗ |，则|b ⃗ |= ．9．（2022·浙江·统考高考真题）设点P 在单位圆的内接正八边形A 1A 2⋯A 8的边A 1A 2上，则PA ⃗⃗⃗⃗⃗ 12+PA 2⃗⃗⃗⃗⃗⃗⃗ 2+⋯+PA ⃗⃗⃗⃗⃗ 82的取值范围是 ．10．（2022·天津·统考高考真题）在△ABC 中，CA ⃗⃗⃗⃗⃗ =a ,CB ⃗⃗⃗⃗⃗ =b ⃗ ，D 是AC 中点，CB ⃗⃗⃗⃗⃗ =2BE ⃗⃗⃗⃗⃗ ，试用a ,b ⃗ 表示DE ⃗⃗⃗⃗⃗ 为 ，若AB ⃗⃗⃗⃗⃗ ⊥DE ⃗⃗⃗⃗⃗ ，则∠ACB 的最大值为 .平面向量小题【题型1 平面向量共线定理及其应用】 (4)【题型2 平面向量基本定理及其应用】 (6)【题型3 平面向量的数量积】 (9)【题型4 平面向量的模的问题】 (11)【题型5 平面向量夹角与垂直问题】 (13)【题型6 极化恒等式】 (15)【题型7 向量与解三角形综合】 (18)【题型8 向量与几何最值、范围问题】 (22)【题型9 向量在几何中的其他应用】 (25)平面向量是高考的必考内容之一.从近几年的高考情况来分析，平面向量的数量积、模、夹角是高考考查的重点、热点，试题主要以选择题、填空题的形式呈现，常常以平面图形为载体，考查数量积、模、夹角与垂直的条件等问题，也时也会与平面解析几何、三角函数、不等式等知识相结合，以工具的形式出现，试题难度中等.学生在高考复习中应注意加强对平面向量的数量积、模、夹角等知识的掌握，能灵活运用向量知识解决有关问题.(1)解决平面向量线性运算问题的关键在于熟练地找出图形中的相等向量，并能熟练运用相反向量将加减法相互转化；(2)在求向量时要尽可能转化到平行四边形或三角形中，运用平行四边形法则、三角形法则及三角形中位线定理、相似三角形对应边成比例等平面几何的性质，把未知向量转化为用已知向量线性表示.2.向量线性运算的含参问题的解题策略：与向量的线性运算有关的参数问题，一般是构造三角形，利用向量运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数的值.3.利用共线向量定理解题的策略：(1)是判断两个向量共线的主要依据.注意待定系数法和方程思想的运用.(2)当两向量共线且有公共点时，才能得出三点共线，即A,B,C三点共线共线.(3)若与不共线且，则.(4)λ,μ为实数)，若A,B,C三点共线，则λ+μ=1.【知识点2 平面向量基本定理的解题策略】1.应用平面向量基本定理求向量的实质应用平面向量基本定理求向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.一般将向量“放入”相关的三角形中，利用三角形法则列出向量间的关系.2.用平面向量基本定理解决问题的一般思路：用平面向量基本定理解决问题的一般思路是：先选择一个基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决.注意同一个向量在不同基底下的分解是不同的，但在每个基底下的分解都是唯一的.【知识点3 平面向量坐标运算的方法技巧】1.平面向量坐标运算的技巧(1)向量的坐标运算主要是利用向量加、减、数乘运算的法则来进行求解的，若已知有向线段两端点的坐标，则应先求向量的坐标.(2)解题过程中，常利用向量相等其坐标相同这一原则，通过列方程(组)来进行求解. 【知识点4 平面向量数量积问题的解题方法】1.平面向量数量积的两种运算方法(1)基底法：当已知向量的模和夹角时，可利用定义法求解，适用于平面图形中的向量数量积的有关计算问题；(2)坐标法：当平面图形易建系求出各点坐标时，可利用坐标法求解. 2.夹角与垂直问题根据平面向量数量积的性质：若，夹角公式)，等，可知平面向量的数量积可以用来解决有关角度、垂直问题.3.向量的模的求解思路：(1)坐标法：当向量有坐标或适合建坐标系时，可用模的计算公式；(2)公式法：利用，把向量的模的运算转化为数量积运算；(3)几何法：利用向量的几何意义，即利用向量加减法的平行四边形法则或三角形法则作出向量，再利用余弦定理等方法求解.【知识点5 极化恒等式】1.极化恒等式的证明过程与几何意义(1)平行四边形对角线的平方和等于四边的平方和：2222||||2(||||)a b a b a b ++−=+.证明：不妨设,AB a AD b ==，则C A a b =+，DB a b =−，()22222C 2AC A a b a a b b ==+=+⋅+①， ()222222DB DB a ba ab b ==−=−⋅+②，①②两式相加得： ()()22222222AC DB a bAB AD+=+=+.(2)极化恒等式：上面两式相减，得：()()2214a b a b ⎡⎤+−−⎢⎥⎣⎦————极化恒等式平行四边形模式：2214a b AC DB ⎡⎤⋅=−⎣⎦.(3)几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14． 【知识点6 平面向量的应用的方法技巧】1.平面向量的应用的解题方法；平面向量的应用方向主要是平面几何问题，往往涉及角和距离，转化成平面向量的夹角、模的问题，主要解题方法有：(1)坐标法：把几何图形放在适当的坐标系中，就赋予了有关点与向量具体的坐标，这样就能进行相应的代数运算和向量运算，从而使问题得到解决.(2)基向量法：适当选取一组基底，写出向量之间的联系，利用向量共线构造关于设定未知量的方程来进行求解.(3)利用向量运算进行转化，化归为三角函数的问题或三角恒等变换问题是常规的解题思路和方法，以向量为载体考查三角形问题时，要注意正弦定理、余弦定理等知识的应用.2.平面向量中的最值（范围）问题的两类求解思路：(1)“形化”，即利用平面向量的相关知识将问题转化为平面几何中的最值或范围问题，然后结合平面图形的特征直接进行判断；(2)“数化”，即利用平面向量的坐标运算，把问题转化为代数中的函数最值与值域、不等式的解集、方程有解等问题，然后利用函数、不等式、方程的有关知识来解决．【题型1 平面向量共线定理及其应用】【例1】（2023·江苏·统考模拟预测）在△ABC 中，AD ⃗⃗⃗⃗⃗ =2DB ⃗⃗⃗⃗⃗⃗ ，点P 在CD 上，且AP ⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +13AB ⃗⃗⃗⃗⃗ (m ∈R)，则m =（ ）A ．15B ．14C ．13D ．12【解题思路】将AB ⃗⃗⃗⃗⃗ =32AD ⃗⃗⃗⃗⃗ 代入AP ⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +13AB ⃗⃗⃗⃗⃗ (m ∈R)，利用共线定理推论可得. 【解答过程】因为AD ⃗⃗⃗⃗⃗ =2DB ⃗⃗⃗⃗⃗⃗ ，所以AB ⃗⃗⃗⃗⃗ =32AD ⃗⃗⃗⃗⃗ ， 所以AP ⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +13AB ⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +13×32AD ⃗⃗⃗⃗⃗ =mAC ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ ，又P ，C ，D 三点共线，所以m +12=1，得m =12.故选：D.【变式1-1】（2023下·江苏连云港·高一校考阶段练习）设e 1⃗⃗⃗ ，e 2⃗⃗⃗ 是两个不共线的向量，已知AB ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ −ke 2⃗⃗⃗ ，CB ⃗⃗⃗⃗⃗ =e 1⃗⃗⃗ +3e 2⃗⃗⃗ ，CD ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ −e 2⃗⃗⃗ ，若三点A ，B ，D 共线，则k 的值为（ ）A ．－8B ．8C ．6D ．－6【解题思路】根据三点A ，B ，D 共线，可得存在唯一实数λ使AB⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗⃗ ，进而可得出答案. 【解答过程】由已知得DB ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ −CD ⃗⃗⃗⃗⃗ =e 1⃗⃗⃗ +3e 2⃗⃗⃗ −(2e 1⃗⃗⃗ −e 2⃗⃗⃗ )=−e 1⃗⃗⃗ +4e 2⃗⃗⃗ ， ∵三点A ，B ，D 共线，∴存在唯一实数λ使AB ⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗⃗ ， ∴2e 1⃗⃗⃗ −ke 2⃗⃗⃗ =λ(−e 1⃗⃗⃗ +4e 2⃗⃗⃗ )=−λe 1⃗⃗⃗ +4λe 2⃗⃗⃗ ， ∴{2=−λ−k =4λ ，解得{λ=−2k =8.故选：B.【变式1-2】（2023·陕西安康·统考一模）已知O 是△ABC 内一点，2OA ⃗⃗⃗⃗⃗ +3OB ⃗⃗⃗⃗⃗ +mOC ⃗⃗⃗⃗⃗ =0⃗ ，若△AOB 与△ABC 的面积之比为47，则实数m 的值为（ ）A ．−103B ．103C ．−203D ．203【解题思路】由2OA ⃗⃗⃗⃗⃗ +3OB ⃗⃗⃗⃗⃗ +mOC ⃗⃗⃗⃗⃗ =0⃗ 确定O 点的位置，再利用△AOB 与△ABC 的面积之比列方程来求得m 的值.【解答过程】由2OA ⃗⃗⃗⃗⃗ +3OB ⃗⃗⃗⃗⃗ =−mOC ⃗⃗⃗⃗⃗ 得25OA ⃗⃗⃗⃗⃗ +35OB ⃗⃗⃗⃗⃗ =−m 5OC ⃗⃗⃗⃗⃗ ， 设−m 5OC ⃗⃗⃗⃗⃗ =OD ⃗⃗⃗⃗⃗⃗ ，则OD ⃗⃗⃗⃗⃗⃗ =25OA ⃗⃗⃗⃗⃗ +35OB ⃗⃗⃗⃗⃗ .由于25+35=1，所以A ，B ，D 三点共线，如图所示， ∵OC ⃗⃗⃗⃗⃗ 与OD ⃗⃗⃗⃗⃗⃗ 反向共线，m >0，∴|OD⃗⃗⃗⃗⃗⃗ ||OC⃗⃗⃗⃗⃗ |=m5，∴|OD⃗⃗⃗⃗⃗⃗ ||CD ⃗⃗⃗⃗⃗ |=m5m 5+1=mm+5，∴S△AOB S △ABC=|OD ⃗⃗⃗⃗⃗⃗ ||CD⃗⃗⃗⃗⃗ |=m m+5=47⇒m =203.故选：D.【变式1-3】（2023·全国·高一专题练习）在△OAB 中，OA ⃗⃗⃗⃗⃗ =3OC ⃗⃗⃗⃗⃗ ，OB ⃗⃗⃗⃗⃗ =2OD ⃗⃗⃗⃗⃗⃗ ，AD ，BC 的交点为M ，过M 作动直线l 分别交线段AC ，BD 于E ，F 两点.若OE ⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗ ，OF ⃗⃗⃗⃗⃗ =μOB ⃗⃗⃗⃗⃗ (λ,μ>0)，则λ+μ的最小值为（ ）A ．3+√35B ．2+2√37C ．3+2√35D ．3+2√25【解题思路】利用平面向量共线定理的推论得到λ、μ的关系，进而利用均值定理即可求得λ+μ的最小值 【解答过程】由A 、M 、D 三点共线，可得存在实数t ，使OM⃗⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +(1−t)OD ⃗⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +12(1−t)OB ⃗⃗⃗⃗⃗ 又由B 、M 、C 三点共线，可得存在实数m ，使得 OM⃗⃗⃗⃗⃗⃗ =mOB ⃗⃗⃗⃗⃗ +(1−m)OC ⃗⃗⃗⃗⃗ =mOB ⃗⃗⃗⃗⃗ +13(1−m)OA ⃗⃗⃗⃗⃗ 则{t =13(1−m)m =12(1−t) ，解之得{t =15m =25，则OM ⃗⃗⃗⃗⃗⃗ =15OA ⃗⃗⃗⃗⃗ +25OB ⃗⃗⃗⃗⃗又OE ⃗⃗⃗⃗⃗ =λOA⃗⃗⃗⃗⃗ ，OF ⃗⃗⃗⃗⃗ =μOB ⃗⃗⃗⃗⃗ (λ,μ>0)， 则OM ⃗⃗⃗⃗⃗⃗ =15λOE ⃗⃗⃗⃗⃗ +25μOF ⃗⃗⃗⃗⃗ ，由E 、M 、F 三点共线，可得15λ+25μ=1 则λ+μ=(λ+μ)(15λ+25μ)=35+μ5λ+2λ5μ≥35+2√μ5λ×2λ5μ=3+2√25（当且仅当λ=√2+15，μ=√2+25时等号成立） 则λ+μ的最小值为3+2√25， 故选：D.【题型2 平面向量基本定理及其应用】【例2】（2023·广东汕头·统考三模）如图，点D 、E 分别AC 、BC 的中点，设AB ⃗⃗⃗⃗⃗ =a ，AC ⃗⃗⃗⃗⃗ =b ⃗ ，F 是DE 的中点，则AF⃗⃗⃗⃗⃗ =（ ）A ．12a +12b⃗ B ．−12a +12b⃗ C ．14a +12b⃗ D ．−14a +12b⃗ 【解题思路】根据向量的运算，利用基底向量a ,b ⃗ 表示AF ⃗⃗⃗⃗⃗ 即可. 【解答过程】因为点D 、E 分别BC 的中点，F 是DE 的中点， 所以AF⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ +12DE ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ +14AB ⃗⃗⃗⃗⃗ . 即AF ⃗⃗⃗⃗⃗ =14a +12b ⃗ . 故选：C.【变式2-1】（2023·河北沧州·校考模拟预测）在△ABC 中BE⃗⃗⃗⃗⃗ =12EC ⃗⃗⃗⃗⃗ ,BF ⃗⃗⃗⃗⃗ =12(BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )，点P 为AE 与BF 的交点，AP⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ ，则λ−μ=（ ） A ．0B ．14C ．12D ．34【解题思路】利用平面向量基本定理得到AP ⃗⃗⃗⃗⃗ =(1−k )AB ⃗⃗⃗⃗⃗ +12kAC ⃗⃗⃗⃗⃗ ，AP ⃗⃗⃗⃗⃗ =13mAC ⃗⃗⃗⃗⃗ +23mAB ⃗⃗⃗⃗⃗ ，从而列出方程组，求出k,m ，得到λ=12,μ=14，求出答案.【解答过程】因为BF⃗⃗⃗⃗⃗ =12(BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )，所以F 为AC 中点， B,P,F 三点共线，故可设BP⃗⃗⃗⃗⃗ =kBF ⃗⃗⃗⃗⃗ ，即AP ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =k(AF ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )， 整理得AP ⃗⃗⃗⃗⃗ =kAF ⃗⃗⃗⃗⃗ +(1−k )AB ⃗⃗⃗⃗⃗ =(1−k )AB ⃗⃗⃗⃗⃗ +12kAC ⃗⃗⃗⃗⃗ ， 因为BE ⃗⃗⃗⃗⃗ =12EC ⃗⃗⃗⃗⃗ ，所以AE ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ −12AE ⃗⃗⃗⃗⃗ ，即AE⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ ， A,P,E 三点共线，可得AP ⃗⃗⃗⃗⃗ =mAE ⃗⃗⃗⃗⃗ =m (13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ )=13mAC ⃗⃗⃗⃗⃗ +23mAB ⃗⃗⃗⃗⃗ ， 所以{2m3=1−km 3=12k ，解得{k =12m =34，可得AP ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +14AC ⃗⃗⃗⃗⃗ ，则λ=12,μ=14，λ−μ=14. 故选：B.【变式2-2】（2023·湖南娄底·娄底市第三中学校联考三模）2000多年前，古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割.所谓黄金分割点，指的是把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，黄金分割比为√5−12.如图，在矩形ABCD 中，AC 与BD 相交于点O ，BF ⊥AC,DH ⊥AC,AE ⊥BD,CG ⊥BD ，且点E 为线段BO 的黄金分割点，则BF⃗⃗⃗⃗⃗ =（ ）A ．3−√52BA ⃗⃗⃗⃗⃗ +5+√510BG ⃗⃗⃗⃗⃗ B ．3−√52BA ⃗⃗⃗⃗⃗ +5−√510BG ⃗⃗⃗⃗⃗ C ．√5−12BA ⃗⃗⃗⃗⃗+5−√510BG⃗⃗⃗⃗⃗ D ．3−√52BA ⃗⃗⃗⃗⃗ +√55BG⃗⃗⃗⃗⃗ 【解题思路】由题意得BE ⃗⃗⃗⃗⃗ =√5−12BO ⃗⃗⃗⃗⃗ ，结合矩形的特征可用BG ⃗⃗⃗⃗⃗ 表示出BO ⃗⃗⃗⃗⃗ ，再利用向量加减法法则及数乘向量运算法则即可作答.【解答过程】由题意得BE ⃗⃗⃗⃗⃗ =√5−12BO ⃗⃗⃗⃗⃗ ，显然BE =DG ，BO =OD =12BD ， 同理有AF ⃗⃗⃗⃗⃗ =√5−12AO ⃗⃗⃗⃗⃗ ，DG ⃗⃗⃗⃗⃗ =√5−12DO ⃗⃗⃗⃗⃗⃗ ，所以BG⃗⃗⃗⃗⃗ =(2−√5−12)BO ⃗⃗⃗⃗⃗ =5−√52BO ⃗⃗⃗⃗⃗ ，故BO ⃗⃗⃗⃗⃗ =5−√5⃗⃗ =√5(√5−1)⃗⃗ ， 因为BF ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AF ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +√5−12AO ⃗⃗⃗⃗⃗=BA⃗⃗⃗⃗⃗ +√5−12(BO ⃗⃗⃗⃗⃗−BA⃗⃗⃗⃗⃗ )=3−√52BA ⃗⃗⃗⃗⃗ +√5−12BO ⃗⃗⃗⃗⃗ ， 所以BF ⃗⃗⃗⃗⃗ =3−√52BA ⃗⃗⃗⃗⃗ +√55BG⃗⃗⃗⃗⃗ . 故选：D.【变式2-3】（2023·重庆江北·校考一模）如图，在△ABC 中，点D 是边AB 上一点且BD =2AD ，E 是边BC 的中点，直线AE 和直线CD 交于点F ，若BF 是∠ABC 的平分线，则|BC ||BA |=（ ）A ．4B ．3C ．2D ．12【解题思路】首先根据BF 是∠ABC 的平分线，则存在一个实数λ使得BF ⃗⃗⃗⃗⃗ =λ(BA ⃗⃗⃗⃗⃗|BA ⃗⃗⃗⃗⃗ |+BC ⃗⃗⃗⃗⃗|BC ⃗⃗⃗⃗⃗ |)， 再替换向量BC⃗⃗⃗⃗⃗ =2BE ⃗⃗⃗⃗⃗ 和BA ⃗⃗⃗⃗⃗ =32BD ⃗⃗⃗⃗⃗⃗ ，利用平面向量基本定理的推论，即可求解. 【解答过程】因为BF 是∠ABC 的平分线，所以存在一个实数λ使得BF ⃗⃗⃗⃗⃗ =λ(BA ⃗⃗⃗⃗⃗ |BA ⃗⃗⃗⃗⃗ |+BC⃗⃗⃗⃗⃗ |BC ⃗⃗⃗⃗⃗ |)，（根据角平分线的条件，选择合适的基底）因为E 是边BC 的中点，所以BF ⃗⃗⃗⃗⃗ =λ(BA ⃗⃗⃗⃗⃗ |BA ⃗⃗⃗⃗⃗ |+2BE⃗⃗⃗⃗⃗ |BC ⃗⃗⃗⃗⃗ |)，又点A ，E ，F 共线，所以λ|BA ⃗⃗⃗⃗⃗ |+2λ|BC ⃗⃗⃗⃗⃗ |=1①．（三点共线的应用：OA⃗⃗⃗⃗⃗ =λOB ⃗⃗⃗⃗⃗ +μOC ⃗⃗⃗⃗⃗ （λ，μ为实数），若A ，B ，C 三点共线，则λ+μ=1） 因为BD =2AD ，所以BF ⃗⃗⃗⃗⃗ =λ(32BD⃗⃗⃗⃗⃗⃗ |BA ⃗⃗⃗⃗⃗ |+BC ⃗⃗⃗⃗⃗|BC ⃗⃗⃗⃗⃗ |)，又点C ，F ，D 共线，所以3λ2|BA ⃗⃗⃗⃗⃗ |+λ|BC ⃗⃗⃗⃗⃗ |=1②，联立①②，得12|BA⃗⃗⃗⃗⃗ |=1|BC ⃗⃗⃗⃗⃗ |，则|BC⃗⃗⃗⃗⃗ ||BA ⃗⃗⃗⃗⃗ |=2，即|BC ||BA |=2. 故选：C ．【题型3 平面向量的数量积】【例3】（2023·辽宁朝阳·朝阳市第一高级中学校考模拟预测）已知向量a =(1,2)，b ⃗ =(3,4)，c =(5,m )（m ∈R ），则(2a −b ⃗ )⋅c =（ ）A ．5B ．−5C ．5mD ．−5m【解题思路】求出向量2a −b ⃗ 的坐标，根据数量积坐标表示，即可求得答案. 【解答过程】由题意向量a =(1,2)，b ⃗ =(3,4)，c =(5,m )可得2a −b ⃗ =(−1,0)， 故(2a −b ⃗ )⋅c =(−1,0)⋅(5,m)=−5， 故选：B.【变式3-1】（2023·全国·模拟预测）已知向量a ，b ⃗ 满足a =λb ⃗ (λ>0)，|b ⃗ |=2，|a −b ⃗ |=1，则(a +b ⃗ )⋅a =（ ）A ．3B ．15C ．-3或15D ．3或15【解题思路】对|a −b ⃗ |=1两边同时平方，将a =λb ⃗ (λ>0)代入可求出λ的值，可求出|a |，代入(a +b ⃗ )⋅a 即可得出答案.【解答过程】因为向量a =λb ⃗ (λ>0)，所以a ⋅b ⃗ =|a |·|b ⃗ |=λ|b ⃗ |2=4λ， 又|a −b ⃗ |2=|a |2−2a ⋅b ⃗ +|b ⃗ |2=4λ2−8λ+4=1， 解得:λ=12或32，即|a |=1或|a |=，所以当|a |=1时，(a +b ⃗ )⋅a =a ⋅b ⃗ +|a |2=2+1=3； 当|a |=3时，(a +b ⃗ )⋅a =a ⋅b ⃗ +|a |2=6+9=15， 故(a +b ⃗ )⋅a =3或15． 故选：D.【变式3-2】（2023·广东佛山·统考一模）设四边形ABCD 为矩形，|AB ⃗⃗⃗⃗⃗ |=6，|AD ⃗⃗⃗⃗⃗ |=4，若点M ，N 满足BM ⃗⃗⃗⃗⃗⃗ =13MC ⃗⃗⃗⃗⃗⃗ ，DN ⃗⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ ，则AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =（ ） A ．28B ．32C ．36D ．40【解题思路】根据矩形的几何性质，结合平面向量的线性运算，可得答案.【解答过程】由BM ⃗⃗⃗⃗⃗⃗ =13MC ⃗⃗⃗⃗⃗⃗ ，则BM ⃗⃗⃗⃗⃗⃗ =14BC ⃗⃗⃗⃗⃗ ；由DN ⃗⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ ，则DN⃗⃗⃗⃗⃗⃗ =23DC ⃗⃗⃗⃗⃗ ， 在矩形ABCD 中，由AB ⊥AD ，则AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ =0，AM⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ )⋅(AD ⃗⃗⃗⃗⃗ +DN ⃗⃗⃗⃗⃗⃗ )=(AB ⃗⃗⃗⃗⃗ +14BC ⃗⃗⃗⃗⃗ )⋅(AD ⃗⃗⃗⃗⃗ +23DC ⃗⃗⃗⃗⃗ ) =(AB⃗⃗⃗⃗⃗ +14AD ⃗⃗⃗⃗⃗ )⋅(AD ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ +23|AB ⃗⃗⃗⃗⃗ |2+14|AD ⃗⃗⃗⃗⃗ |2+16AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ =23×36+14×16=28.故选：A.【变式3-3】（2023·广东广州·华南师大附中校考一模）如图，在等腰梯形ABCD 中，AB ∥ CD,AB =5,AD =4,DC =1,E 是线段AB 上一点，且AE =4EB ，动点P 在以E 为圆心，1为半径的圆上，则DP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的最大值为（ ）A ．√3−√21B ．2√3−6C ．√21−6D ．−√3【解题思路】过点D 作DO ⊥AB ，垂足为O ，以O 为坐标原点，建立如图所示的平面直角坐标系，利用DP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =DE⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ +EP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ ，通过坐标运算和数量积的定义来求解最值. 【解答过程】过点D 作DO ⊥AB ，垂足为O ， 以O 为坐标原点，建立如图所示的平面直角坐标系， 则A (−2,0),C(1,2√3),D(0,2√3),E (2,0)，则DP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =(DE ⃗⃗⃗⃗⃗ +EP ⃗⃗⃗⃗⃗ )⋅AC ⃗⃗⃗⃗⃗ =DE ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ +EP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ ， 其中DE⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =(2,−2√3)⋅(3,2√3)=6−12=−6， EP⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|EP ⃗⃗⃗⃗⃗ ||AC ⃗⃗⃗⃗⃗ |cos⟨EP ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ⟩=1×√9+12cos⟨EP ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ⟩=√21cos⟨EP ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ⟩， 当cos⟨EP ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ⟩=1，即EP ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ 同向时，EP ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 取最大值√21， 所以DP⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的最大值为√21−6.故选：C.【题型4 平面向量的模的问题】【例4】（2023·四川成都·成都七中校考一模）若向量a 、b ⃗ 满足：|a |=1，(a +b ⃗ )⊥a ，|2a −b ⃗ |=√10，则|b⃗ |=（ ） A ．2B ．√2C ．10D ．√10【解题思路】由平面向量垂直可得出a ⋅b ⃗ =−1，再利用平面向量数量积的运算性质可求得|b ⃗ |的值. 【解答过程】因为向量a 、b ⃗ 满足：|a |=1，(a +b ⃗ )⊥a ，|2a −b ⃗ |=√10， 则(a +b ⃗ )⋅a =a 2+a ⋅b ⃗ =1+a ⋅b ⃗ =0，所以，a ⋅b ⃗ =−1， 所以，|2a −b ⃗ |2=4a 2−4a ⋅b ⃗ +b ⃗ 2=4+4+|b ⃗ |2=10，故|b ⃗ |=√2. 故选：B.【变式4-1】（2023·全国·a =(x,1)，b ⃗ =(2,y)，c =(x,y).若(a +b ⃗ )⊥(a −b ⃗ )，且a //b ⃗ ，则|c |=（ ）A ．√2B ．√3C ．√5D ．√6【解题思路】利用向量的数量积运算将向量垂直的条件转化为(a +b ⃗ )⋅(a −b ⃗ )=a 2−b ⃗ 2=0，然后利用向量的模的坐标运算公式和向量共线的坐标关系得到方程组，求解即得x,y 的值，进而计算向量c =(x,y)的模. 【解答过程】因为a =(x,1)，b⃗ =(2,y)， 由(a +b ⃗ )⊥(a −b ⃗ )可得，(a +b ⃗ )⋅(a −b ⃗ )=a 2−b ⃗ 2=0， 即(x 2+1)−(4+y 2)=0，整理得x 2−y 2=3. 又因为a ∥b⃗ ，所以xy =2， 联立{x 2−y 2=3xy =2，解得{x =2y =1 或{x =−2y =−1 ，故|c |=√x 2+y 2=√5， 故选C.【变式4-2】（2023·四川甘孜·统考一模）已知平面向量a ,b ⃗ ,|a |=2,|b ⃗ |=1，且a 与b ⃗ 的夹角为π3，则|a −2b⃗ |=（ ）A ．√5B ．4C ．2D ．0【解题思路】|a −2b ⃗ |平方展开后，利用向量的数量积定义进行运算即可. 【解答过程】因为|a −2b ⃗ |2=a 2−4a ⋅b ⃗ +4b ⃗ 2 =4−4×2×1×cos π3+4=4， 所以|a −2b ⃗ |=2， 故选：C.【变式4-3】（2023上·安徽·高二校联考期中）如图，在长方形 ABCD 中，AB =6,AD =4，点 P 满足DP ⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ ，其中λ∈[0,23]，则|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |的取值范围是（ ）A ．[4,5]B ．[8,10]C ．[4,√17]D ．[2√17,10]【解题思路】建立平面直角坐标系，写出点的坐标，得到P (6λ,4)，λ∈[0,23]，从而求出|PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |=√(6−12λ)2+64，求出最值.【解答过程】以A 为坐标原点，AB,AD 所在直线分别为x,y 轴，建立平面直角坐标系， 则A (0,0),B (6,0),D (0,4),C (6,4)，设P (s,t )，因为DP⃗⃗⃗⃗⃗ =λDC ⃗⃗⃗⃗⃗ ，所以(s,t −4)=λ(6,0)，即s =6λ,t =4， 故P (6λ,4)，λ∈[0,23]，则PA⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ =(−6λ,−4)+(6−6λ,−4)=(6−12λ,−8)， 则|PA⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |=√(6−12λ)2+64，因为λ∈[0,23]，所以6−12λ∈[−2,6]，(6−12λ)2∈[0,36]， 故|PA⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ |=√(6−12λ)2+64∈[8,10].故选：B.【题型5 平面向量夹角与垂直问题】【例5】（2023·陕西西安·校联考模拟预测）向量a ，b ⃗ 满足|a |=4，|b ⃗ |=1，(2a −3b ⃗ )⋅b ⃗ =3，则向量a ，b⃗ 夹角的余弦值为（ ） A ．23B ．34C ．−34D ．−23【解题思路】由|a |=4，|b ⃗ |=1，且(2a −3b ⃗ )·b ⃗ =2，从而可求解. 【解答过程】由题意知|a |=4，|b⃗ |=1， 又因为(2a −3b ⃗ )⋅b ⃗ =2a ⋅b ⃗ −3b ⃗ 2=2|a ||b ⃗ |cos⟨a ,b ⃗ ⟩−3|b ⃗ |2=3， 解之得：cos⟨a ,b ⃗ ⟩=34，故B 项正确 故选：B.【变式5-1】（2023·全国·模拟预测）已知向量a =(−1,−2)，b ⃗ =(4,−2)，若(a −λb ⃗ )⊥(a +μb ⃗ )，则（ ）A ．4λμ=1B ．4λμ=−1C ．4(λ+μ)=1D ．4(λ+μ)=−1【解题思路】用坐标表示向量a −λb ⃗ ,a +μb ⃗ ，根据向量垂直的坐标运算建立方程，并化简得结果. 【解答过程】法一：用坐标表示向量a −λb ⃗ ,a +μb⃗ 由题意可知，a −λb ⃗ =(−1−4λ,−2+2λ),a +μb ⃗ =(−1+4μ,−2−2μ)， 由(a −λb ⃗ )⊥(a +μb⃗ )得， (−1−4λ)(−1+4μ)+(−2+2λ)(−2−2μ)=0， 整理得，5−20λμ=0，。