视距测量
- 格式:doc
- 大小:104.50 KB
- 文档页数:15

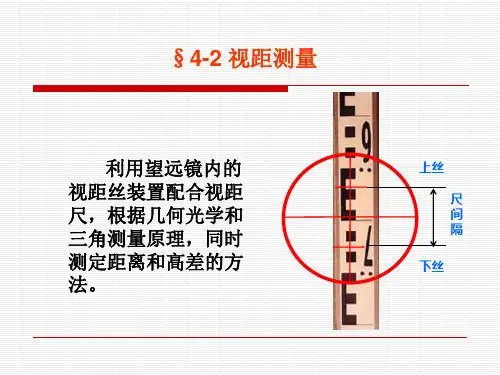
第四章→第二节→视距测量一、视距测量的概念视距测量是根据几何光学原理,利用仪器望远镜筒内的视距丝在标尺上截取读数,应用三角公式计算两点距离,可同时测定地面上两点间水平距离和高差的测量方法。
视距测量的优点是,操作方便、观测快捷,一般不受地形影响。
其缺点是,测量视距和高差的精度较低,测距相对误差约为1/200~1/300。
尽管视距测量的精度较低,但还是能满足测量地形图碎部点的要求,所以在测绘地形图时,常采用视距测量的方法测量距离和高差。
二、视距测量的计算公式(一)望远镜视线水平时测量平距和高差的计算公式如图4-7 所示,测地面两点的水平距离和高差,在点安置仪器,在点竖立视距尺,当望远镜视线水平时,水平视线与标尺垂直,中丝读数为,上下视距丝在视距尺上的位置读数之差称为视距间隔,用表示。
1、水平距离计算公式设仪器中心到物镜中心的距离为,物镜焦距为,物镜焦点到点的距离为,由图4-7可知两点间的水平距离为,根据图中相似三角形成比例的关系得两点间水平距离为:(4-7)式中:为视距乘常数,用表示,其值在设计中为100。
为视距加常数,仪器设计为0。
则视线水平时水平距离公式:(4-8)式中—视距乘常数其值等于100。
—视距间隔。
2、高差的计算公式:两点间的高差由仪器高和中丝读数求得,即:(4-9)式中:—仪器高,地面点至仪器横轴中心的高度。
(二)望远镜视线倾斜时测量平距和高差的公式在地面起伏比较大的地区进行视距测量时,需要望远镜倾斜才能照准视距标尺读取读数,此时视准轴不垂直于视距标尺,不能用式4-8计算距离和高差。
如图4-8所示,下面介绍视准轴倾斜时求水平距离和高差的计算公式。
视线倾斜时竖直角为,上下视距丝在视距标尺上所截的位置为,,视距间隔为,求算、两点间的水平距离。
首先将视距间隔换算成相当于视线垂直时的视距间隔之距离,按式4-8求出倾斜视线的距离′,其次利用倾斜视线的距离′.2和竖直角计算为水平距离。
因上下丝的夹角很小,则认为∠和∠为90°,设将视距尺旋转角,根据三角函数得视线倾斜时水平距离计算式为式(4-10),两点高差计算公式为式(4-11)。


视距测量名词解释
1.视距:指观测者从观察位置到目标点的直线距离,也称为视线距离。
2. 视差:是指同一物体在不同位置被观察时,由于观察者的位置不同而产生的物体位置的差异。
视差可以用来确定物体的深度。
3. 视线:指观测者注视目标点时眼睛和目标点之间的直线。
4. 视角:是指从观察者位置出发,通过两个边缘点,能够囊括的视野范围。
5. 视平面:指从观测者位置出发,垂直于视线的平面。
6. 视线偏移:是指由于观测者移动位置而发生的视线方向变化。
7. 视距误差:是指由于测量时存在的误差而引起的视距测量结果与实际值之间的偏差。
8. 视距纠正:是指对视距误差进行校正,使测量结果更加准确。
9. 视距测量仪:是一种用来测量视距的仪器,常用于地形测绘、建筑设计、交通规划等领域。
常见的视距测量仪包括激光测距仪和全站仪等。
- 1 -。

视距测量的概念
视距测量是指测量一个物体或目标与观察者之间的实际距离。
在地理学、天文学、航空、军事等领域中,视距测量有重要的应用。
视距测量通常会考虑到地球的曲率,因为地球是近似球体,两个点之间的距离会因地球的曲率而产生差异。
视距测量的公式可以根据地球的曲率进行修正,以得到更准确的距离值。
在航空和军事中,视距测量通常使用雷达、激光测距仪或目测等方式进行。
这些技术可以通过测量信号的传播时间、反射率等参数来计算目标与观察者之间的距离。
视距测量还可以用于确定两个物体之间的可见距离。
在大气条件良好的情况下,可见距离通常受限于大气散射、折射、吸收等因素。
通过测量可见距离,可以评估环境的清晰度和透明度,对于航空、交通管理等领域具有重要意义。
总之,视距测量是测量物体或目标与观察者之间实际距离的方法和过程,它在不同领域中有着广泛的应用价值。



视距测量的原理
视距测量是通过测量两个点之间的视线距离来确定它们之间的实际距离。
其基本原理是利用视觉系统中的视觉焦点和视差现象。
首先,视觉焦点是指人眼在观察某个目标时的焦点位置。
在测量中,通过调节人眼的焦距,使其聚焦于目标上。
通过测量人眼焦点位置的变化,可以得到目标到观察者之间的视线距离。
其次,视差现象是指当两个眼睛观察同一个目标时,由于眼睛之间的距离,目标在两个眼睛中的位置会有所不同。
观察者可以通过比较两个眼睛所观察到目标的位置差异,来判断目标的距离。
在实际测量中,常用的视距测量方法有三角测距法和激光测距法两种。
三角测距法基于三角形的几何关系,通过测量观察者、目标以及一个已知距离点之间的角度和距离,来计算目标到观察者的距离。
激光测距法利用激光束的特性,通过测量激光束发射和接收的时间以及光速来计算目标到观察者的距离。
总结起来,视距测量的基本原理是利用视觉焦点和视差现象来测量目标到观察者之间的距离。
这种测量方法广泛应用于地理测量、工程测量和航空导航等领域。

视距测量原理我们需要了解一些基本概念。
在视距测量中,我们通常使用的是目视距离,也就是从眼睛到目标物体的直线距离。
视距测量可以在不同的环境和条件下进行,例如在平地、水面或者山区等地形中。
视距测量原理的核心是利用物体的视角和距离之间的关系来计算目标物体的距离。
根据三角学的原理,我们可以得出以下公式:距离= 高度 / tan(视角/2)。
其中,高度是观察者和目标物体之间的垂直距离,视角是观察者所能看到的目标物体的角度。
在实际应用中,我们可以通过测量目标物体的高度和视角,然后代入公式计算出目标物体与观察者之间的距离。
例如,在测量远处的建筑物高度时,我们可以站在建筑物附近,用测距仪测量建筑物的高度,然后通过测量建筑物的视角,就可以计算出建筑物与观察者的距离。
视距测量原理在很多领域都有广泛的应用。
在军事领域中,视距测量可以用于确定目标物体的距离和大小,从而帮助军事人员进行作战规划和战术部署。
在建筑和工程领域中,视距测量可以用于测量建筑物的高度和距离,从而帮助设计师和工程师进行规划和设计。
在航海和航空领域中,视距测量可以用于导航和定位,帮助船舶和飞机确定自身位置和目标位置。
视距测量原理也有一些局限性。
首先,由于测量过程中可能存在误差,所以视距测量结果并不是绝对准确的。
其次,视距测量受到环境条件的限制,例如天气、光线和地形等因素都会对测量结果产生影响。
此外,视距测量也受到目标物体本身特性的限制,例如目标物体的形状、颜色和表面材料等都会对测量结果产生影响。
为了提高视距测量的准确性和可靠性,科学家和工程师们不断进行研究和创新。
例如,他们提出了激光测距技术,利用激光束测量目标物体与观察者之间的距离。
这种技术可以通过测量激光束的传播时间和光速来计算出距离,具有高精度和远距离测量能力。
视距测量原理是一种简单而有效的距离测量方法,具有广泛的应用前景。
通过了解视距测量原理,我们可以更好地理解和应用这一测量方法,从而为各个领域的科研和工程提供支持。


视距测量的原理
视距测量是利用水准仪的望远镜内十字丝分划板上的视距丝在视距尺(水准尺)上读数,根据光学和几何学原理,同时测定仪器到地面点的水平距离和高差的一种方法。
视距测量的原理基于几何光学和光线传播的原理。
当光线通过一个介质界面时,会发生折射。
折射是光线改变传播方向的现象,它的大小与两个介质的折射率有关。
在视距测量中,我们通常假设大气是均匀的,即折射率是常数。
这样,通过测量光线的折射角度,就可以计算出视距的大小。
视距测量的基本原理是通过测量上下丝读数之差来计算视距。
上、下丝读数之差称为视距间隔或尺间隔。
根据相似三角形和几何学原理,可以推导出视距公式:D=Kl,其中D为水平距离,K为视距常数,l为上下丝读数之差。
通过这个公式,可以求出仪器到地面点的水平距离。
同时,在测量高差时,可以通过望远镜视线水平时的视距读数和已知仪器高i来计算高差h:h=i-v,其中i为仪器高,v为视距读数。
总之,视距测量的原理是通过测量光线的折射角度和上下丝读数之差来计算水平距离和高差。
在实际应用中,需要根据具体的测量要求和条件选择合适的仪器和测量方法,以确保测量结果的准确性和可靠性。
第四章→第二节→视距测量一、视距测量的概念视距测量是根据几何光学原理,利用仪器望远镜筒内的视距丝在标尺上截取读数,应用三角公式计算两点距离,可同时测定地面上两点间水平距离和高差的测量方法。
视距测量的优点是,操作方便、观测快捷,一般不受地形影响。
其缺点是,测量视距和高差的精度较低,测距相对误差约为1/200~1/300。
尽管视距测量的精度较低,但还是能满足测量地形图碎部点的要求,所以在测绘地形图时,常采用视距测量的方法测量距离和高差。
二、视距测量的计算公式(一)望远镜视线水平时测量平距和高差的计算公式如图4-7 所示,测地面两点的水平距离和高差,在点安置仪器,在点竖立视距尺,当望远镜视线水平时,水平视线与标尺垂直,中丝读数为,上下视距丝在视距尺上的位置读数之差称为视距间隔,用表示。
1、水平距离计算公式设仪器中心到物镜中心的距离为,物镜焦距为,物镜焦点到点的距离为,由图4-7可知两点间的水平距离为,根据图中相似三角形成比例的关系得两点间水平距离为:(4-7)式中:为视距乘常数,用表示,其值在设计中为100。
为视距加常数,仪器设计为0。
则视线水平时水平距离公式:(4-8)式中—视距乘常数其值等于100。
—视距间隔。
2、高差的计算公式:两点间的高差由仪器高和中丝读数求得,即:(4-9)式中:—仪器高,地面点至仪器横轴中心的高度。
(二)望远镜视线倾斜时测量平距和高差的公式在地面起伏比较大的地区进行视距测量时,需要望远镜倾斜才能照准视距标尺读取读数,此时视准轴不垂直于视距标尺,不能用式4-8计算距离和高差。
如图4-8所示,下面介绍视准轴倾斜时求水平距离和高差的计算公式。
视线倾斜时竖直角为,上下视距丝在视距标尺上所截的位置为,,视距间隔为,求算、两点间的水平距离。
首先将视距间隔换算成相当于视线垂直时的视距间隔之距离,按式4-8求出倾斜视线的距离′,其次利用倾斜视线的距离′和竖直角计算为水平距离。
因上下丝的夹角很小,则认为∠和∠为90°,设将视距尺旋转角,根据三角函数得视线倾斜时水平距离计算式为式(4-10),两点高差计算公式为式(4-11)。
视距测量高差计算公式
视距测量计算公式:F=h/L。
视距测量是利用水准仪的望远镜内十字丝分划板上的视距丝在视距尺(水准尺)上读数,根据光学和几何学原理,同时测定仪器到地面点的水平距离和高差的一种方法。
水准仪(英文:level)是建立水平视线测定地面两点间高差的仪器。
原理为根据水准测量原理测量地面点间高差。
主要部件有望远镜、管水准器(或补偿器)、垂直轴、基座、脚螺旋。
按结构分为微倾水准仪、自动安平水准仪、激光水准仪和数字水准仪(又称电子水准仪)。
按精度分为精密水准仪和普通水准仪。
一、视距测量的概念视距测量是根据几何光学原理,利用仪器望远镜筒内的视距丝在标尺上截取读数,应用三角公式计算两点距离,可同时测定地面上两点间水平距离和高差的测量方法。
视距测量的优点是,操作方便、观测快捷,一般不受地形影响。
其缺点是,测量视距和高差的精度较低,测距相对误差约为1/200~1/300。
尽管视距测量的精度较低,但还是能满足测量地形图碎部点的要求,所以在测绘地形图时,常采用视距测量的方法测量距离和高差。
二、视距测量的计算公式(一)望远镜视线水平时测量平距和高差的计算公式如图4-7 所示,测地面两点的水平距离和高差,在点安置仪器,在点竖立视距尺,当望远镜视线水平时,水平视线与标尺垂直,中丝读数为,上下视距丝在视距尺上的位置读数之差称为视距间隔,用表示。
1、水平距离计算公式设仪器中心到物镜中心的距离为,物镜焦距为,物镜焦点到点的距离为,由图4-7可知两点间的水平距离为,根据图中相似三角形成比例的关系得两点间水平距离为:(4-7)式中:为视距乘常数,用表示,其值在设计中为100。
为视距加常数,仪器设计为0。
则视线水平时水平距离公式:(4-8)式中—视距乘常数其值等于100。
—视距间隔。
2、高差的计算公式:两点间的高差由仪器高和中丝读数求得,即:(4-9)式中:—仪器高,地面点至仪器横轴中心的高度。
(二)望远镜视线倾斜时测量平距和高差的公式在地面起伏比较大的地区进行视距测量时,需要望远镜倾斜才能照准视距标尺读取读数,此时视准轴不垂直于视距标尺,不能用式4-8计算距离和高差。
如图4-8所示,下面介绍视准轴倾斜时求水平距离和高差的计算公式。
视线倾斜时竖直角为,上下视距丝在视距标尺上所截的位置为,,视距间隔为,求算、两点间的水平距离。
首先将视距间隔换算成相当于视线垂直时的视距间隔之距离,按式4-8求出倾斜视线的距离′,其次利用倾斜视线的距离′和竖直角计算为水平距离。
因上下丝的夹角很小,则认为∠和∠为90°,设将视距尺旋转角,根据三角函数得视线倾斜时水平距离计算式为式(4-10),两点高差计算公式为式(4-11)。
(4-10)(4-11)将(4-10)式代入(4-11)式化简后得:(4-12)式中:—上、下视距丝在标尺上的读数之差。
—仪器高度。
—十字丝的中丝在标尺上的读数。
—视距乘常数(=100)。
—视线倾斜时的竖直角。
为了计算简便,在实际工作中,通常使中横丝照准标尺上与仪器同高处,使,则上述计算高差的公式简化为:(4-13)现在视距测量的计算工具主要是电子计算器,最好使用程序型的计算器,事先将视距计算公式和高差计算公式输入到计算器中,使用快捷方便,不容易出现计算错误。
三、视距测量观测方法1、如图4-8所示,将经纬仪安置于点,量取仪器高度(仪器横轴中心至地面点的距离),在点竖立视距尺。
2、望远镜照准点视距尺,使中丝读数为仪器高,分别读取上、下丝读数。
3、转动竖盘水准管定平螺旋,使气泡居中(或打开竖盘自动归零装置)。
读取竖盘读数。
4、根据视距间隔、竖直角,按式(4-10)、式(4-13)计算水平距离和高差。
四、视距测量的误差及注意事项影响视距测量精度的因素很多,但主要有以下几个方面,在测量时应加以注意。
1、视距尺倾斜误差视距公式是在视距尺铅垂竖直的条件下推得的,视距尺倾斜对视距测量的影响与竖直角的大小有关,竖直角越大对视距测量的影响越大,特别在山区测量时,应尽量扶直视距尺。
2、读数误差的影响用视距丝在视距尺上读数的误差是影响视距测量精度的主要因素。
读数误差与视距尺最小分划的宽度、距离远近、望远镜的放大倍数及成像的清晰程度等因素有关。
所以在作业时,应使用厘米刻划的板尺。
应根据测量精度限制最远视距,使成像清晰,消除视差,读数仔细。
3、外界条件的影响实验证明,当视线接近地面,垂直折光引起视距尺上的读数误差较大。
因此观测时应尽可能使视线离地面1米以上以减少大气折光的影响。
避免在烈日强光等不利天气条件下进行观测。
第二节视距测量视距测量是用望远镜内的视距丝装置,根据光学原理同时测定距离和高差的一种方法。
这种方法具有操作方便、速度快、一般不受地形限制等优点。
虽然精度较低(普通视距测量仅能达到1/200~1/300的精度),但能满足测定碎部点位置的精度要求。
所以视距测量被广泛地应用于地形测图中。
一、视距测量原理视距测量所用的仪器主要有经纬仪、水准仪和平板仪等。
进行视距测量,要用到视距丝和视距尺。
视距丝即望远镜内十字丝平面上的上下两根短丝,它与横丝平行且等距离,如图8-3所示。
视距尺是有刻划的尺子,和水准尺基本相同。
图8-3 视距丝1.视线水平时的水平距离和高差公式如图8-4所示,在A点安置经纬仪,在B点竖立视距尺,用望远镜照准视距尺,当望远镜视线水平时,视线与尺子垂直。
如果视距尺上M、N点成像在十字丝分划板上的两根视距丝m、n处,那么视距尺上MN 的长度,可由上、下视距丝读数之差求得。
上、下视距丝读数之差称为视距间隔或尺间隔,用l表示。
图8-4 视线水平时的视距测量原理在图8-4中,为上、下视距丝的间距,为视距间隔,f为物镜焦距,δ为物镜中心到仪器中心的距离。
由相似△m′Fn′和△MFN可得即因此,由图8-4得令,则有(8-1)式中K——视距乘常数,通常K=100;C——视距加常数。
式(8-1)是用外对光望远镜进行视距测量时计算水平距离的公式。
对于内对光望远镜,其加常数C 值接近零,可以忽略不计,故水平距离为(8-2)同时,由图8-4可知,A、B两点间的高差h为(8-3)式中i——仪器高(m);v——十字丝中丝在视距尺上的读数,即中丝读数(m)。
2.视线倾斜时的水平距离和高差公式在地面起伏较大的地区进行视距测量时,必须使望远镜视线处于倾斜位置才能瞄准尺子。
此时,视线便不垂直于竖立的视距尺尺面,因此式(8-2)和式(8-3)不能适用。
下面介绍视线倾斜时的水平距离和高差的计算公式。
如图8-5所示,如果我们把竖立在B点上视距尺的尺间隔MN,化算成与视线相垂直的尺间隔M′N′,就可用式(8-2)计算出倾斜距离L。
然后再根据L和垂直角α,算出水平距离D和高差h。
图8-5 视线倾斜时的视距测量原理从图8-5可知,在△EM′M和△EN′N中,由于φ角很小(约34′),可把∠EM′M和∠EN′N视为直角。
而∠MEM′=∠NEN′=α,因此式中M′N′就是假设视距尺与视线相垂直的尺间隔l′,MN是尺间隔l,所以将上式代入式(8-2),得倾斜距离L因此,A、B两点间的水平距离为:(8-4)式(8-4)为视线倾斜时水平距离的计算公式。
由图8-5可以看出,A、B两点间的高差h为:式中h′——高差主值(也称初算高差)。
(8-5)所以(8-6)式(8-6)为视线倾斜时高差的计算公式。
二、视距测量的施测与计算1.视距测量的施测(1)如图8-5所示,在A点安置经纬仪,量取仪器高i,在B点竖立视距尺。
(2)盘左(或盘右)位置,转动照准部瞄准B 点视距尺,分别读取上、下、中三丝读数,并算出尺间隔l。
(3)转动竖盘指标水准管微动螺旋,使竖盘指标水准管气泡居中,读取竖盘读数,并计算垂直角α。
(4)根据尺间隔l、垂直角α、仪器高i及中丝读数v,计算水平距离D和高差h。
2.视距测量的计算例8-1 以表8-1中的已知数据和测点1的观测数据为例,计算A、1两点间的水平距离和1点的高程。
解表8-1为视距测量记录计算表。
表8-1 视距测量记录与计算手簿测站:A测站高程:+45.37m 仪器高:1.45m 仪器:DJ6三、视距测量的误差来源及消减方法1.用视距丝读取尺间隔的误差读取视距尺间隔的误差是视距测量误差的主要来源,因为视距尺间隔乘以常数,其误差也随之扩大100倍。
因此,读数时注意消除视差,认真读取视距尺间隔。
另外,对于一定的仪器来讲,应尽可能缩短视距长度。
2.垂直角测定误差从视距测量原理可知,垂直角误差对于水平距离影响不显著,而对高差影响较大,故用视距测量方法测定高差时应注意准确测定垂直角。
读取竖盘读数时,应严格令竖盘指标水准管气泡居中。
对于竖盘指标差的影响,可采用盘左、盘右观测取垂直角平均值的方法来消除。
3.标尺倾斜误差标尺立不直,前后倾斜时将给视距测量带来较大误差,其影响随着尺子倾斜度和地面坡度的增加而增加。
因此标尺必须严格铅直(尺上应有水准器),特别是在山区作业时。
4.外界条件的影响(1)大气垂直折光影响由于视线通过的大气密度不同而产生垂直折光差,而且视线越接近地面垂直折光差的影响也越大,因此观测时应使视线离开地面至少1m以上(上丝读数不得小于0.3m)。
(2)空气对流使成像不稳定产生的影响。
这种现象在视线通过水面和接近地表时较为突出,特别在烈日下更为严重。
因此应选择合适的观测时间,尽可能避开大面积水域。
此外,视距乘常数K的误差、视距尺分划误差等都将影响视距测量的精度。
COS(+2°18′48″)角度与弧度间换算关系就十分明了了。
因为360度=2π,所以,1度=π/180≈弧度,1弧度=180/π≈度。
弧度与角度的关系,在EXCEL里面把角度和弧度相互转换DEGREES函数的功能是将用弧度表示的参数转换为角度,RADIANS函数的功能是将用角度表示的参数转换为弧度。
这两个函数的表达式为:DEGREES(angle)RADIANS(angle)其中DEGREES函数的参数angle表示待转换的弧度,RADIANS函数的参数angle表示需要转换成弧度的角度。
示例如图所示●在B2中输入公式“=DEGREES(PI()/4)”,pi/4弧度对应的角度。
●在B3中输入公式“=DEGREES(-PI()/3)”,-pi/3弧度对应的角度。
●在B4中输入公式“=RADIANS(120)”,120度对应的弧度值。
●在B5中输入公式“=RADIANS(45)”,45度对应的弧度值。
一、角的两种单位“ 弧度”和“度”是度量角大小的两种不同的单位。
就像“米”和“市尺”是度量长度大小的两种不同的单位一样。
在flash里规定:在旋转角度(rotation)里的角,以“度”为单位;而在三角函数里的角要以“弧度”为单位。
这个规定是我们首先要记住的!!!例如:rotation2--是旋转“2度”;sin(π/2)--是大小为“π/2弧度”的角的正弦。
二、弧度的定义所谓“弧度的定义”就是说,1弧度的角大小是怎样规定的我们知道“度”的定义是,“两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。
当这段弧长正好等于圆周长的360分之一时,两条射线的夹角的大小为1度。
(如图1)那么,弧度又是怎样定义的呢弧度的定义是:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。
当这段弧长正好等于圆的半径时,两条射线的夹角大小为1弧度。