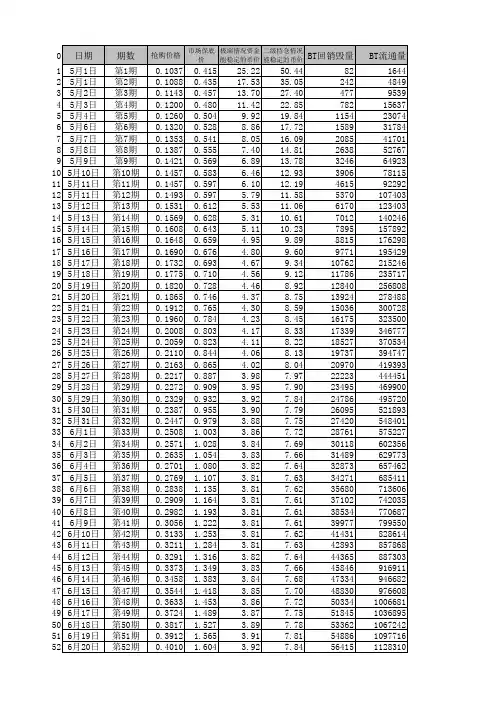
数学模型2

实验二： 微分方程模型Matlab 求解与分析一、实验目的[1] 掌握解析、数值解法，并学会用图形观察解的形态和进行解的定性分析； [2] 熟悉MATLAB 软件关于微分方程求解的各种命令；[3] 通过范例学习建立微分方程方面的数学模型以及求解全过程； [4] 熟悉离散 Logistic 模型的求解与混沌的产生过程。

二、实验原理1. 微分方程模型与MATLAB 求解解析解用MATLAB 命令dsolve(‘eqn1’,’eqn2’, ...) 求常微分方程（组）的解析解。

其中‘eqni'表示第i 个微分方程，Dny 表示y 的n 阶导数,默认的自变量为t 。

（1） 微分方程 例1 求解一阶微分方程 21y dxdy+= (1) 求通解 输入：dsolve('Dy=1+y^2')输出：ans =tan(t+C1)（2）求特解 输入：dsolve('Dy=1+y^2','y(0)=1','x')指定初值为1，自变量为x 输出：ans =tan(x+1/4*pi)例2 求解二阶微分方程 221()04(/2)2(/2)2/x y xy x y y y πππ'''++-=='=-原方程两边都除以2x ，得211(1)04y y y x x'''++-= 输入:dsolve('D2y+(1/x)*Dy+(1-1/4/x^2)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x')ans =- (exp(x*i)*(pi/2)^(1/2)*i)/x^(1/2) +(exp(x*i)*exp(-x*2*i)*(pi/2)^(3/2)*2*i)/(pi*x^(1/2))试试能不用用simplify 函数化简 输入: simplify(ans)ans =2^(1/2)*pi^(1/2)/x^(1/2)*sin(x) （2）微分方程组例3 求解 d f /d x =3f +4g ; d g /d x =-4f +3g 。

数学建模论文题目：一个医药公司的新药研究部门为了掌握一种新止痛剂的疗效，设计了一个药物试验，给患有同种疾病的病人使用这种新止痛剂的以下4个剂量中的某一个：2 g，5 g，7 g和10 g，并记录每个病人病痛明显减轻的时间（以分钟计）. 为了解新药的疗效与病人性别和血压有什么关系，试验过程中研究人员把病人按性别及血压的低、中、高三档平均分配来进行测试. 通过比较每个病人血压的历史数据，从低到高分成3组，分别记作0.25，0.50和0.75. 实验结束后，公司的记录结果见下表（性别以0表示女，1表示男）.请你为该公司建立一个数学模型，根据病人用药的剂量、性别和血压组别，预测出服药后病痛明显减轻的时间.病人序号病痛减轻时间／min用药剂量／g性别血压组别1 352 0 0.252 43 2 0 0.503 55 2 0 0.754 47 2 1 0.255 43 2 1 0.506 57 2 1 0.757 26 5 0 0.258 27 5 0 0.509 28 5 0 0.7510 29 5 1 0.2511 22 5 1 0.5012 29 5 1 0.7513 19 7 0 0.2514 11 7 0 0.5015 14 7 0 0.7516 23 7 1 0.2517 20 7 1 0.5018 22 7 1 0.7519 13 10 0 0.2520 8 10 0 0.5021 3 10 0 0.7522 27 10 1 0.2523 26 10 1 0.5024 5 10 1 0.75一、摘要在农某医药公司为了掌握一种新止痛药的疗效，设计了一个药物实验，通过观测病人性别、血压和用药剂量与病痛时间的关系，预测服药后病痛明显减轻的时间。

我们运用数学统计工具m i n i t a b软件，对用药剂量，性别和血压组别与病痛减轻时间之间的数据进行深层次地处理并加以讨论概率值P （是否<0.05）和拟合度R -S q 的值是否更大（越大，说明模型越好）。

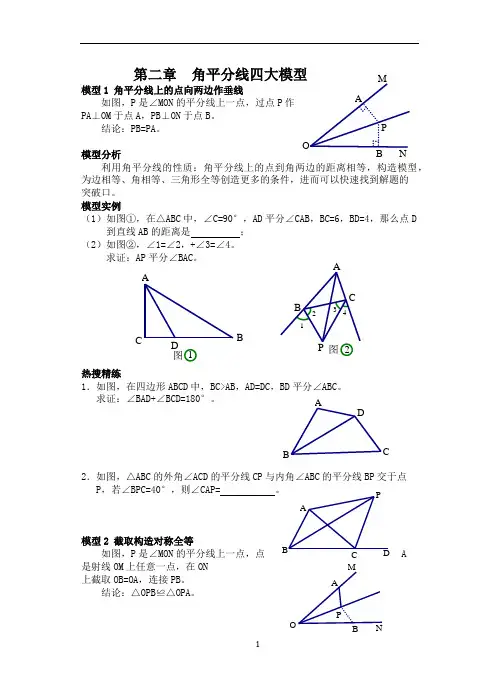
N MOA B P 2图4321A CP B D AB C图1A B D C AB D CPP ONM BA 第二章 角平分线四大模型模型1 角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B 。

结论：PB=PA 。

模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口。

模型实例（1）如图①，在△ABC 中，∠C=90°，AD 平分∠CAB ，BC=6，BD=4，那么点D到直线AB 的距离是 ； （2）如图②，∠1=∠2，+∠3=∠4。

求证：AP 平分∠BAC 。

热搜精练1．如图，在四边形ABCD 中，BC>AB ，AD=DC ，BD 平分∠ABC 。

求证：∠BAD+∠BCD=180°。

2．如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ，若∠BPC=40°，则∠CAP= 。

模型2 截取构造对称全等如图，P 是∠MON 的平分线上一点，点A 是射线OM 上任意一点，在ON 上截取OB=OA ，连接PB 。

结论：△OPB ≌△OPA 。

图2DP AB C D C 1图P B A ABC DA BC DE DC B AP ONM B A 模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧。

模型实例（1）如图①所示，在△ABC 中，AD 是△ABC 的外角平分线，P 是AD 上异于点A 的任意一点，试比较PB+PC 与AB+AC 的大小，并说明理由；（2）如图②所示， AD 是△ABC 的内角平分线，其他条件不变，试比较 PC-PB 与AC-AB 的大小，并说明理由。

乒乓球的弹跳罗基斯第模型[问题]罗基斯第模型一个乒乓球离球拍的高度为h0，落在球拍上反弹，设恢复系数为e，不计空气阻力。

(1)如果e为常数，讨论球的高度变化的规律。

如果e2与高度h n成线性关系e2=μ(1–h n/H0)(2.1)其中H0是最大高度，μ是参数。

对于不同的参数讨论小球高度的变化规律。

(2)当参数连续变化时，分析最后分布的高度。

(3)计算前几个分岔点。

(4)用李雅普洛夫指数判断混沌的发生。

[解析](1)当球从高度h n下落到球拍上之前速度为v(2.2)n球与球拍碰撞后反弹的速度为v'n=ev n(2.3)球反弹的高度为h n+1=e2h n(2.4)如果e<1，则球的反弹高度随次数不断减小；如果e=1，则球反弹后始终保持初始高度；如果e>1，例如球拍每次加一个向上的冲击力，则球的高度随次数不断增加。

e2与高度的线性关系说明：如果球的高度较大，则恢复系数较小，反之较大。

设相对高度为x n=h n/H0，则下一次上升的相对高度为x n+1=μ(1–x n)x n，(n=0,1,2,…)(2.5)这是著名的罗基斯第模型。

由于相对高度0≤x n≤1，而(1–x n)x n的最大值为1/4，所以参数的值在0到4之间。

球的高度强烈依赖参数。

[算法](1)先取一个参数，再取一个相对高度，通过迭代算法计算下一次碰撞后的高度，画出高度点，依此类推。

再取另一高度参数，重新通过迭代算法计算高度，画出高度点，依此类推。

[程序]MATH2_1.m如下。

%乒乓球与球拍的碰撞高度clear%清除变量u=input('请输参数(参考值:0.5,2,3.25,3.5,3.56,3.8):');%键盘输入初始相对高度(1)xn=0.9;%第1个的初始相对高度(2)figure%开创图形窗口plot(0,xn,'.')%画高度点text(0,xn,num2str(xn),'FontSize',16)%标记第1个的初始高度grid minor%加细网格title(['乒乓球与球拍的碰撞高度(\it\mu\rm=',num2str(u),')'],'FontSize',16)%标题n=50;%迭代次数axis([0,n,0,1])%坐标范围hold on%保持图像for j=1:n%按次数循环xn=u*(1-xn)*xn;%计算下一次的相对高度(3)plot(j,xn,'.')%画高度点end%结束循环xn=0.1;%取初始相对高度(4)plot(0,xn,'ro')%画高度点text(0,xn,num2str(xn),'FontSize',16)%初始高度for j=1:n%按次数循环xn=u*(1-xn)*xn;%计算下一次的相对高度(5)plot(j,xn,'ro')%画高度点end%结束循环[说明](1)程序执行时要用户用键盘输入参数，提供6个参数选择。

专题08 角平分线的重要模型（二）非全等类角平分线在中考数学中都占据着重要的地位，角平分线常作为压轴题中的常考知识点，需要掌握其各大模型及相应的辅助线作法，且辅助线是大部分学生学习几何内容中的弱点，，本专题就角平分线的非全等类模型作相应的总结，需学生反复掌握。

模型1.双角平分线模型（导角模型） 【模型解读】双角平分线模型（导角模型）指的是当三角形的内角（外角）的平分线相交时，可以导出平分线的夹角的度数。

【模型图示】条件：BD ，CD 是角平分线.结论：1902BDC A∠=︒+∠1902BDC A ∠=︒-∠12BDC A ∠=∠ 1．（2022·广东·九年级专题练习）BP 是∠ABC 的平分线，CP 是∠ACB 的邻补角的平分线，∠ABP =20°，∠ACP =50°，则∠P =（ ）4231AFCB4321DAA．30°B．40°C．50°D．60°【答案】A【分析】据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出∠P 的度数．【详解】∠BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，∠∠ABP=∠CBP=20°，∠ACP=∠MCP=50°，∠∠PCM是△BCP的外角，∠∠P=∠PCM−∠CBP=50°−20°=30°，故选：A．【点睛】本题考查三角形外角性质以及角平分线的定义，解题时注意：一个三角形的外角等于与它不相邻的两个内角的和．2．（2022·山东·济南中考模拟）如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．∠ABC；(1)求证：∠AOC＝90°＋12(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．∠MK=ML，角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC 与∠A的数量关系，并说明理由．（4）如图4，△ABC外角∠CBM、∠BCN的平分线交于点Q，∠A＝64°，∠CBQ，∠BCQ的平分线交于点P，则∠BPC＝°，延长BC至点E，∠ECQ的平分线与BP的延长线相交于点R，则∠R＝°．【分析】（1）根据三角形的内角和角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A与∠1表示出∠2，再利用∠E与∠1表示出∠2，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB，然后再根据三角形的内角和定理列式整理即可得解；（4）结合（1）（2）（3）的解析即可求得．【解答】解：（1）∵PB、PC分别平分∠ABC和∠ACB，∴∠PBC=12∠ABC，∠PCB=12∠ACB（角平分线的性质），∴∠BPC+∠PBC+∠PCB＝180°（三角形内角和定理），∴∠BPC＝180°﹣（∠PBC+∠PCB）＝180°﹣（12∠ABC+12∠ACB）＝180°−12（∠ABC+∠ACB）＝180°−12（180°﹣∠A）＝180°﹣90°+12∠A＝90°+12∠A＝90°+12×64°＝122°．故答案为：122°；（2）∵BE是∠ABD的平分线，CE是∠ACB的平分线，∴∠ECB=12∠ACB，∠ECD=12∠ABD．∵∠ABD是△ABC的外角，∠EBD是△BCE的外角，∴∠ABD＝∠A+∠ACB，∠EBD＝∠ECB+∠BEC，∴∠EBD=12∠ABD=12（∠A+∠ACB）＝∠BEC+∠ECB，即12∠A+∠ECB＝∠ECB+∠BEC，∴∠BEC=12∠A=12α；（3）结论∠BQC＝90°−12∠A．∵∠CBM与∠BCN是△ABC的外角，∴∠CBM＝∠A+∠ACB，∠BCN＝∠A+∠ABC，∵BQ，CQ分别是∠ABC与∠ACB外角的平分线，∴∠QBC=12（∠A+∠ACB），∠QCB=12（∠A+∠ABC）．∵∠QBC+∠QCB+∠BQC＝180°，∴∠BQC＝180°﹣∠QBC﹣∠EQB＝180°−12（∠A+∠ACB）−12（∠A+∠ABC），＝180°−12∠A−12（∠A+∠ABC+∠ACB）＝180°−12∠A﹣90°＝90°−12∠A；（4）由（3）可知，∠BQC＝90°−12∠A＝90°−12×64°=58°，由（1）可知∠BPC＝90°+12∠BQC＝90°+12×58°=119°；由（2）可知，∠R=12∠BQC＝29°故答案为119，29．【点评】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．4．（2022·辽宁沈阳·九年级期中）阅读下面的材料，并解决问题(1)已知在∠ABC中，∠A=60°，图1-3的∠ABC的内角平分线或外角平分线交于点O，请直接写出下列角度的度数，如图1，∠O＝；如图2，∠O＝；如图3，∠O＝；∠A(2)如图4，点O是∠ABC的两条内角平分线的交点，求证：∠O＝90°+12(3)如图5，在∠ABC中，∠ABC的三等分线分别与∠ACB的平分线交于点O1O2，若∠1＝115°，∠2＝135°，求∠A的度数．模型2.角平分线加平行线等腰现（角平分线+平行线）【模型解读】1）过角平分线上一点作角的一边的平行线，构造等腰三角形；2）有角平分线时，过角一边上的点作角平分线的平行线，交角的另一边的直线于一点，也可构造等腰三角形。

第11 讲全等模型(二)手拉手模型板块一初识手拉手模型(1)双等边三角形模型1 异侧双等边模型2 同侧双等边条件:AB=AC,AD=AE,∠BAC=∠DAE=60°结论:△ABD≌△ACE,∠BFC=∠BAC=60°典例精讲【例】如图,AB=AD,AC=AE,∠BAD=∠CAE=60°,,BE,CD 交于点P,连接AP.(1)求证:BE=CD;(2)求∠BPD 的度数;(3)求证:PA 平分∠DPE.实战演练如图,AB=AD,AE=AC,∠BAD=∠CAE=60°,直线BE,CD 交于点P,连接AP.(1)求证:BE=CD;(2)求∠BPA 的度数.初识手拉手模型(2)双等腰直角三角形模型 1 异侧双等腰直角三角形模型2 同侧双等腰直角三角形条件:AB=AC,AD=AE,∠BAC=∠DAE=90°结论:△ABD≌△ACE,BD⊥CE典例精讲【例】如图,AB=AC,AD=AE,∠BAC=∠DAE=90°,,连接BD,CE 交于点 P.(1)求证:△ABD≅△ACE;(2)判断 BD,CE 的关系并证明;(3)连接 PA,求∠APB的度数.实战演练如图，∠BAD=∠CAE=90°,AB=AD,AE=AC.,点 D 在 CE 上,AF⊥CB,,垂足为F.(1)求证:BC⊥CE;(2)若BF=2,求CD-DE 的长.板块三初识手拉手模型(3)双等腰三角形条件:AB=AC,AD=AE,∠BAC=∠DAE结论:△ABD≌△ACE,∠BAC=∠BFC模型 1 异侧双等腰三角形模型 2 同侧双等腰三角形典例精讲【例】如图1,AB=AC,AD=AE,∠BAC=∠DAE=α,直线BD,CE 交于点 P,连接AP.(1)求证:BD=CE;(2)求∠APB 的度数(用α表示);(3)将图形旋转至如图2所示的位置，其余条件不变，直接写出∠APB= (用α表示).实战演练如图,AD=AB,AC=AE,∠DAB=∠EAC,G,F 分别为DC,BE 的中点.若∠DAB=α,探究∠AGF 与α的数量关系.板块四构造手拉手模型模型1 构双等边三角形模型 2 构双等腰直角三角形等边△ABC等腰直角△ABC,∠BAC=90°典例精讲题型一构双等边三角形【例1】如图,在△ABC中,AB=AC,∠ADB=∠BAC=60°.求.∠ADC的度数.题型二构双等腰直角三角形【例2】如图,在△ABC 中,.AB=AC,∠BAC=90°,∠ADB=45°.求∠ADC的度数.题型三构双等腰三角形【例3】如图,在.△ABC中,AB=AC,∠BAC=120°,∠ADB=30°.求∠ADC的度数.实战演练1.已知,在△ABC中,AB=AC,D 为BC上一点,AD=DE,∠ADE=∠BAC=α. (1)如图1,若α=90°,求∠DCE 的度数.(2)如图2,若α=120°,求∠DCE 的度数.2.如图,在△ABC中,AB=AC,∠ADB=∠ABC..求证:DA 平分.∠BDC.3.如图,P 为等边。

实验05 数学规划模型㈡（2学时）（第4章数学规划模型）1.（求解）汽车厂生产计划（LP，整数规划IP）p101~102(1) (LP)在模型窗口中输入以下线性规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3≥ 0并求解模型。

★(1) 给出输入模型和求解结果（见[101]）：(2) (IP)在模型窗口中输入以下整数规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3均为非负整数并求解模型。

LINGO函数@gin见提示。

★(2) 给出输入模型和求解结果（见[102]模型、结果）：2.（求解）原油采购与加工（非线性规划NLP ，LP 且IP ）p104~107模型：已知 ⎪⎩⎪⎨⎧≤≤+≤≤+≤≤=)15001000(63000)1000500(81000)5000(10)(x x x x x xx c注：当500 ≤ x ≤ 1000时，c (x ) = 10 × 500 + 8( x – 500 ) = (10 – 8 ) × 500 + 8x112112221112212211112112122211122122max 4.8() 5.6()()500100015000.50.6,,,,0z x x x x c x x x x x x x x x x x x x x x x x x =+++-+≤++≤≤≥+≥+≥2.1解法1（NLP ）p104~106将模型变换为以下的非线性规划模型：1121122212311122122111121121222123122312311122122max4.8()5.6()(1086)50010000.50.6(500)0(500)00,,500,,,,0z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++-+++≤++≤≥+≥+=++-=-=≤≤≥LINGO 软件设置：局部最优解，全局最优解，见提示。